Design of adaptive sliding mode controllers for a class of perturbed fractional-order nonlinear systems

Abstract

In this paper, a design methodology of the adaptive sliding mode controller was proposed for a class of multi-input fractional-order nonlinear systems with matched and unmatched perturbations to solve state regulation problems. The sliding surface is firstly introduced, and then the controller is designed with adaptive mechanisms and perturbation estimator embedded. Due to the employed adaptive and perturbation estimation mechanisms, the upper bounds of the perturbations and perturbation estimation errors do not need to be known in advance. The resultant control scheme is capable of driving the controlled states into the equilibrium point and stays thereafter within a finite time. Finally, a numerical example is given for demonstrating the feasibility of the proposed control scheme.

1 Introduction

Owing to fractional derivatives and integrals providing a powerful tool in describing the memory and hereditary properties of different substances, many researchers have recently pointed out that fractional calculus is well suited for modeling and describing of properties of many practical processes, such as thermal systems [1], power systems [2], financial systems [3], electromechanical systems [4], biological systems [5], hyperchaotic systems [6] and viscoelastic materials [7]. As a result, fractional calculus has also been applied to many practical applications by engineers and physicists [7,8,9,10,11].

Sliding mode control (SMC) is a well-known nonlinear control design method because of its robustness against matched perturbations encountered in the systems [12, 13]. In the past few decades, SMC has been used in many different integer order (IO) systems such as mobile robots [14, 15], DC–DC boost converters [16] and vehicle systems [17]. With the development of fractional calculus, the controls of FO systems by using SMC technique have also applied to various kinds of nonlinear systems [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. However, it is noted that the designers have to know in advance the upper bounds of the perturbations when utilizing the control schemes proposed in [22,23,24,25,26,27,28,29,30], and in [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] designers only considered matched perturbations.

In order to alleviate or eliminate the restrictions of the researches mentioned above [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36], in this paper, we also designed an adaptive sliding mode controller for a class of multi-input FO nonlinear systems with matched and unmatched perturbations to solve the regulation problems. The novelties of this research are as follows. (1) A fractional derivative estimator is proposed in this research, which can be utilized to estimate the perturbations encountered in the system, and adaptation mechanisms are embedded in the proposed control scheme so that the designers do not need to know in advance the upper bounds of the perturbations as well as perturbation estimation errors. (2) The dynamic equations of the plant considered in this research are more generalized than those in [27,28,29,30,31,32,33] since the control schemes in [27,28,29,30,31,32,33] do not allow the input gain uncertainty to appear in the second differential equation, and we replaced the state $\mathbf x_2$ in the first differential equation with function ${\mathbf g} (\mathbf x_2)$. The major improvement in the proposed control scheme is that it can be applied to a class of FO nonlinear systems with unmatched perturbations and it is capable of driving the state trajectory into the equilibrium point and stays thereafter within a finite time as well, which may not be achievable by using the control schemes developed in [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Finally, a numerical example is illustrated by using computer simulation for showing the feasibility of the proposed control scheme.

2 System descriptions and problem formulations

Consider a class of multi-input nonlinear FO systems with matched and unmatched perturbations governed by

$$\begin{aligned} \begin{array}{lll} D^{\alpha }{\mathbf {x}}_1&{}=&{}{\mathbf {f}_1}(t, {\mathbf {x}}_1)+{\mathbf {G}_1}(t, {\mathbf {x}}_1){\mathbf g} (\mathbf x_2)+\triangle \mathbf {p}_1(t,\mathbf x), \\ D^{\alpha }{\mathbf {x}}_2&{}=&{}{\mathbf {f}_2}(t, \mathbf x)+{\mathbf {G}_2}(t, \mathbf x){\mathbf u}+\triangle \mathbf {p}_2(t,\mathbf x,{\mathbf u}), \end{array} \end{aligned}$$

(1)

where $\alpha \in R$ and $\alpha \in (0,1)$; $\mathbf {x}\triangleq [\mathbf x_1^T \quad \mathbf x_2^T ]^T \in R^n$ is the measurable state vector, $\mathbf {x}_2\in R^{m\times 1}$, ${\mathbf g} (\mathbf {x}_2)\in R^{m\times 1}$, $\mathbf {x}_1\triangleq [x_{11},x_{12},\ldots ,x_{1(n-m)}]^T\in R^{n-m}$, and $n\le 2m$. The nonlinear vectors $\mathbf f_1(t, {\mathbf {x}}_1)$, $\mathbf f_2(t, \mathbf {x})$ and ${\mathbf g} (\mathbf x_2)$ are known, and $\mathbf f_1(t, {\mathbf {x}}_1)=\mathbf 0$ if ${\mathbf x}_1=\mathbf 0$. The matrices $\mathbf {G}_1$ and $\mathbf {G}_2$ are also known. The vector $\mathbf u\in R^{s\times 1}$ is the control input, and $m\le s$. The vectors $\triangle \mathbf p_i(\bullet ), 1\le i\le 2$, are unknown uncertainties, parameter variations and/or external disturbances. The aim of this paper is to design a sliding mode controller with perturbation estimation scheme such that the state trajectory $\mathbf x(t)$ of (1) can reach zero within a finite time. In order to achieve this purpose, we assume that the following assumptions are valid throughout this paper:

$\mathbf {A1}$: The matrices $\mathbf G_1(t, {\mathbf x}_1)$ and $\mathbf G_2(t, {\mathbf x})$ have full row rank for all ${\mathbf x}$ and t in the domain of interest; these imply that the matrices ${\mathbf G}_j^+\triangleq {\mathbf G}_j^T(\mathbf G_j{\mathbf G_j}^T)^{-1}, j=1,2$, exist.

$\mathbf {A2}$: The vector ${\mathbf {f}_1}(t, {\mathbf x}_1)$ and matrix ${\mathbf G}_1^+$ are continuously differentiable with respect to ${\mathbf {x}_1}$.

$\mathbf {A3}$: [37] The unmatched and matched perturbations fulfill the following inequalities

$$\begin{aligned} \Vert \triangle \mathbf {p}_1(t,\mathbf x)\Vert \le \gamma _1\beta _1(\mathbf x), \ \Vert \triangle {\mathbf {p}}_2(t,\mathbf x,\mathbf u)\Vert \le \beta _2(\mathbf x,\mathbf u), \end{aligned}$$

in the domain of interest for all t and $\mathbf x$, where $\gamma _1$ is an unknown positive constant, $\beta _1(\mathbf {x})$ is a known positive function, and $\beta _2(\mathbf x,\mathbf u)$ is an unknown positive function. In addition, $\beta _1(\mathbf x)=0$ if $\mathbf x=\mathbf 0$, and the function $\beta _2(\mathbf x,\mathbf u)$ is bounded if $\mathbf x$ and $\mathbf u$ are bounded. In this paper, the notation ${\Vert \cdot \Vert }$ stands for the Euclidean norm of a vector or the induced two-norm of a matrix.

$\mathbf {A4}$: ${\mathbf g} ({\mathbf {x}}_2)=\mathbf 0$ implies ${\mathbf {x}}_2=\mathbf 0$, and $\big (\partial \mathbf g/ \partial \mathbf x_2\big )^{-1}$ exists.

Remark 1

The vector ${\mathbf g}(\mathbf x_2)$ of plant (1) considered in [27,28,29,30,31,32,33] is ${\mathbf g} (\mathbf x_2)=\mathbf x_2$; however, the vector ${\mathbf g}(\mathbf x_2)$ considered in this paper may be a function of $\mathbf x_2$.

The following theorem will be utilized in the stability analysis in Sect. 6.

Theorem 1

If there exists a continuous and positive definite function $V(\mathbf {x}(t),t)$ satisfying the following differential inequality:

$$\begin{aligned} D^{\alpha }V(\mathbf {x}(t),t)\le -\,k, \end{aligned}$$

(2)

where k is a positive constant, and $\alpha \in (0,1)$, then $V \equiv 0, \forall t\ge T$. The finite time T is given by

$$\begin{aligned} T=\Big ({\frac{\varGamma (\alpha +1)}{k}}V(\mathbf {x}_0, 0)\Big )^{\frac{1}{\alpha }}, \end{aligned}$$

(3)

where $t_0=0$ is initial time and $\varGamma (x)\triangleq \int ^\infty _0e^{-t}t^{x-1}\hbox {d}t$ is the Euler’s Gamma function [38].

Proof

From (2), it is seen that

$$\begin{aligned} D^{\alpha } \Big (\int ^t_{0} \dot{V}(\mathbf {x}(\tau ),\tau ) \hbox {d}\tau \Big )\le -\,k. \end{aligned}$$

(4)

Multiplying fractional integral operator $D^{-\alpha }$ to both side of (4), we obtain

$$\begin{aligned} \int ^t_{0} \dot{V}(\mathbf {x}(\tau ),\tau ) d\tau \le D^{-\alpha }(-\,k). \end{aligned}$$

(5)

By using the following equation [38],

$$\begin{aligned} {}_{t_0}D_t^{-\alpha }f(t)={\frac{1}{\varGamma (\alpha )}} \int ^t_{t_0} {\frac{f(\tau )}{(t-\tau )^{1-{\alpha }}}}\hbox {d}\tau , \end{aligned}$$

From (5), we obtain

$$\begin{aligned} \int ^t_{0} \dot{V}(\mathbf {x}(\tau ),\tau ) \hbox {d}\tau&\le -\,k{\frac{1}{\varGamma (\alpha )}} \int ^t_{0} {\frac{1}{(t-\tau )^{1-{\alpha }}}}\hbox {d}\tau \nonumber \\&=-\,{\frac{kt^\alpha }{\alpha \varGamma (\alpha )}}. \end{aligned}$$

(6)

Then by using the reduction formula $\varGamma (x+1)=x\varGamma (x)$ [39], from (6) one can obtain

$$\begin{aligned} V(\mathbf {x}(t),t)-V(\mathbf {x}_0,0) \le -\,{\frac{kt^\alpha }{\varGamma (\alpha +1)}}. \end{aligned}$$

The preceding equation also implies that the finite time T is given by (3). $\square$

3 Design of sliding surface

According to the methodology of sliding mode control, one should design a sliding surface function $\varvec{\sigma }$ and a control function $\mathbf u$ such that once the controlled system enters the sliding surface and remains on the surface thereafter, the desired system’s performance and control’s objective can be realized. Hence in the first step, we design the sliding surface function as

$$\begin{aligned} \varvec{\sigma }(\mathbf x_1)={\mathbf x_1}. \end{aligned}$$

(7)

By using (1), one obtains the fractional derivative of $\varvec{\sigma }$ from (7) as

$$\begin{aligned} D^{\alpha }{\varvec{\sigma }}=D^\alpha {\mathbf {x}}_{1}={\mathbf {f}_1}+{\mathbf {G}_1}\mathbf {g}(\mathbf {x}_2)+\triangle \mathbf {p}_1. \end{aligned}$$

(8)

Design another function $\varvec{\phi }$ as

$$\begin{aligned} \varvec{\phi }(t, \mathbf x)=\mathbf {g}(\mathbf {x}_2)-\varvec{\eta }(t, {\mathbf x}_1), \end{aligned}$$

(9)

where

$$\begin{aligned}&\varvec{\eta }(t, {\mathbf x}_1)\nonumber \\&\quad ={\left\{ \begin{array}{ll} -\,{\mathbf G}_1^+\Big [\mathbf f_1(t, \mathbf {x}_1)+\hat{\gamma }_1(t) \Vert \varvec{\zeta }_1(\varvec{\sigma })\Vert \varvec{\sigma }+\lambda _1{\frac{\varvec{\sigma }}{\Vert \varvec{\sigma }\Vert }}\Big ], \\ \hbox {if}\quad {\varvec{\sigma }}\ne \mathbf 0 \\ \mathbf 0, \quad \hbox {if}\quad {\varvec{\sigma }}=\mathbf 0 \end{array}\right. } \end{aligned}$$

(10)

The scalar $\lambda _1$ is a designed positive constant, and the adaptive gain $\hat{\gamma }_1(t)\ge 0,\ \forall t$ will be introduced later. For obtaining the function $\varvec{\zeta }_1$ in (10), one can utilize the similar method as in [37] to compute the upper bound of $\triangle \mathbf {p}_1$ as

$$\begin{aligned} \Vert \triangle \mathbf p_{1}(t, \mathbf x)\Vert\le & {} \gamma _1\Vert {\varvec{\zeta }}_1(\varvec{\sigma })\Vert \Vert \varvec{\sigma }\Vert \nonumber \\&+\,\gamma _1\Vert {\varvec{\zeta }}_2(\varvec{\sigma },\varvec{\phi })\Vert \Vert \varvec{\phi }\Vert , \end{aligned}$$

(11)

where

$$\begin{aligned}&{\varvec{\zeta }}_1(\varvec{\sigma })=\int ^1_0{\frac{\partial \beta _1(\varvec{\mu }_1, \mathbf {0})}{\partial \varvec{\mu }_1}}{\Big |_{\varvec{\mu }_1=\varvec{\sigma }\omega }}\hbox {d}\omega \ \in R^{(n-m)\times 1}, \\&{\varvec{\zeta }}_2(\varvec{\sigma }, \varvec{\phi })=\int ^1_0{\frac{\partial \beta _1(\varvec{\sigma }, \varvec{\mu }_2)}{\partial \varvec{\mu }_2}}{\Big |_{\varvec{\mu }_2=\varvec{\phi }\omega }}\hbox {d}\omega \ \in R^{m\times 1}. \end{aligned}$$

Substituting (9) and (10) into (8), one can see that the dynamic equation of $\varvec{\sigma }$ for $\varvec{\sigma }\ne \mathbf 0$ is

$$\begin{aligned} D^{\alpha }{\varvec{\sigma }}&=-\,\lambda _1{\frac{\varvec{\sigma }}{\Vert \varvec{\sigma }\Vert }}-\hat{\gamma }_1(t) \Vert \varvec{\zeta }_1(\varvec{\sigma })\Vert \varvec{\sigma }+\triangle \mathbf {p}_1+{\mathbf {G}_1}{\varvec{\phi }}. \end{aligned}$$

(12)

Now define the first Lyapunov function candidate as

$$\begin{aligned} V_1=\Vert \varvec{\sigma }\Vert +\frac{1}{2}{\tilde{\gamma }}^2_1, \end{aligned}$$

(13)

where ${\tilde{\gamma }}_1(t)\triangleq \hat{\gamma }_1(t)-\gamma _1$ is the adaptive error of the unknown constant $\gamma _1$. By using (11), we can obtain the fractional derivative of (13) along the trajectory of (12) for $\varvec{\sigma }\ne \mathbf 0$ as

$$\begin{aligned} D^{\alpha }V_1&\le \frac{\varvec{\sigma }^T}{\Vert \varvec{\sigma }\Vert }\Big \{-\lambda _1{\frac{\varvec{\sigma }}{\Vert \varvec{\sigma }\Vert }}-\hat{\gamma }_1(t) \Vert \varvec{\zeta }_1(\varvec{\sigma })\Vert \varvec{\sigma }+\triangle \mathbf {p}_1\nonumber \\&\quad +\,{\mathbf {G}_1}{\varvec{\phi }}\Big \}+{\tilde{\gamma }}_1D^{\alpha }\hat{\gamma }_1 \nonumber \\&\le -\,\lambda _1-\big (\hat{\gamma }_1(t)-\gamma _1 \big )\Vert \varvec{\zeta }_1(\varvec{\sigma })\Vert \Vert \varvec{\sigma }\Vert \nonumber \\&\quad +\,\gamma _1\Vert \varvec{\zeta }_2(\varvec{\sigma },\varvec{\phi })\Vert \nonumber \\&\quad \times \, \Vert \varvec{\phi }\Vert +\frac{\varvec{\sigma }^T}{\Vert \varvec{\sigma }\Vert }{\mathbf {G}_1}{\varvec{\phi }} +\big (\hat{\gamma }_1(t)-\gamma _1 \big )D^{\alpha }\hat{\gamma }_1. \end{aligned}$$

(14)

According to (14), one may design the adaptive gain $\hat{\gamma }_1(t)$ for adapting the unknown constant $\gamma _1$ as

$$\begin{aligned} D^{\alpha }{\hat{\gamma }}_1(t)=\Vert \varvec{\zeta }_1(\varvec{\sigma })\Vert \Vert \varvec{\sigma }\Vert , \quad {\hat{\gamma }}_1(0)=0. \end{aligned}$$

(15)

Substituting (15) into (14) for $\varvec{\sigma }\ne \mathbf 0$ yields

$$\begin{aligned} D^{\alpha }{V}_1&\le -\lambda _1+\gamma _1\Vert \varvec{\zeta }_2(\varvec{\sigma },\varvec{\phi })\Vert \Vert \varvec{\phi }\Vert +\frac{\varvec{\sigma }^T}{\Vert \varvec{\sigma }\Vert }{\mathbf {G}_1}{\varvec{\phi }}. \end{aligned}$$

(16)

If $\varvec{\sigma }=\mathbf 0$, then from (13) and (15), one can obtain $V_1={\tilde{\gamma }}_1^2/2$ and $D^{\alpha }{\hat{\gamma }}_1=0$. Hence $D^{\alpha }{V}_1\le \tilde{\gamma }_1D^{\alpha }\tilde{\gamma }=\tilde{\gamma }_1D^{\alpha }\hat{\gamma }_1=0$. Therefore, it can be seen that, if state $\varvec{\phi }$ reaches zero in a finite time and stays thereafter, i.e., $\varvec{\phi }=\mathbf {0}$ and $D^{\alpha }{\varvec{\phi }}=\mathbf {0}$ (this will be shown in Sect. 6), Eq. (16) becomes $D^\alpha V_1\le -\lambda _1.$ Hence the Lyapunov function $V_1$ will converge to zero within a finite time if $\varvec{\sigma }\ne \mathbf 0$ in accordance with Theorem 1, and $V_1$ will stop decreasing if $\varvec{\sigma }=\mathbf 0$. Therefore, the sliding variable $\varvec{\sigma }$ will also reach zero within a finite time. Note that $\hat{\gamma }_1(t)$ will reach a finite nonzero limit in accordance with (15), and this will be explained in Sect. 6.

On the other hand, when the controlled system enters the sliding surface in a finite time, from (7) and (10) one can see that the state $\mathbf {x}_1=\mathbf 0$ and $\varvec{\eta }(t, {\mathbf x}_1)=\mathbf 0$ within a finite time too. According to (9), vector $\mathbf {g}(\mathbf {x}_2)$ will tend to zero within a finite time. Hence the state $\mathbf x_{2}$ will also tend to zero in accordance with assumption A4.

Fig. 1

Block diagram of fractional derivative estimator

4 Design of fractional derivative estimator

In order to reduce the chattering phenomenon and save control energy, we propose a design method of fractional derivative estimator (FDE). The idea of designing this FDE is quite similar to that of AIVSDE developed by Cheng and Chang [40]. The block diagram of the proposed FDE is shown in Fig. 1, where r(t) is the input signal, $\hat{k}_r (t)$ is an adaptive gain, which will be explained later. The notation $D^{-\alpha }$ stands for the fractional integral operator; $k_1, k_2$, and $k_b$ are adjustable positive constant gains specified by the designer and y(t) is output.

The idea of designing the FDE shown in Fig. 1 is to force the magnitude of the error signal e(t) to be as small as possible in a finite time. Then the signal x(t) will approach the signal r(t), and the output signal y(t) in Fig. 1 will approach the fractional derivative of the input signal r(t) since $y(t)=D^{\alpha }x(t)$.

The following theorem proves that under certain mild conditions the signal $\sigma (t)$ depicted in Fig. 1 will approach zero in a finite time, and the fractional derivative estimation error e(t) will be asymptotically stable.

Theorem 2

Consider the FDE shown in Fig. 1 with $k_2>1$. Suppose that $|r(t)|\le {\bar{k}}_0$ and $|D^{\alpha }r(t)|\le {\bar{k}}_1$ are fulfilled in a finite time, where ${\bar{k}}_0$ and ${\bar{k}}_1$ are unknown constants. The adaptive gain ${\hat{k}}_r (t)$ is given by the adaptive law

$$\begin{aligned} D^{\alpha }\hat{k}_r (t)={\left\{ \begin{array}{ll} \beta _r, &{}\hbox {if}\quad {\sigma (t)}\ne 0 \\ 0, &{}\hbox {if}\quad {\sigma (t)}= 0 \end{array}\right. }, \quad \hat{k}_r(0)=\delta >0 \end{aligned}$$

where $\beta _r$ is a designed positive constant. Then $\sigma (t)$ will approach zero within a finite time, the fractional derivative estimation error e(t) will reach zero asymptotically, and the adaptive gain $\hat{k}_r(t)$ is bounded.

Proof

The proof of this theorem is very similar to that in [40], and hence it is omitted in this paper. $\square$

5 Design of controllers

In order to drive the state trajectories of the controlled system into the designated sliding surface in a finite time, we design the proposed controller as

$$\begin{aligned} \mathbf u=-\,{\mathbf G}_2^+\big [\mathbf u_f+\mathbf u_s], \end{aligned}$$

(17)

where

$$\begin{aligned} \mathbf u_f&=\mathbf f_2+\varvec{\psi }(t)+\Big (\frac{\partial {\mathbf g}}{\partial {\mathbf {x}}_2}\Big )^{-1}\Big (c_0\varvec{\phi }+{\mathbf p}_\mathrm{est}(t)\Big ), \end{aligned}$$

(18)

$$\begin{aligned} \mathbf u_s&={\left\{ \begin{array}{ll} \Big (\frac{\partial {\mathbf g}}{\partial {\mathbf {x}}_2}\Big )^{-1}\Big (\big [-c_0\Vert \varvec{\phi }\Vert +\lambda _2+\hat{\gamma }_2(t)\beta _3(\mathbf {x})\big ]\frac{\varvec{\phi }(t)}{\Vert \varvec{\phi }(t)\Vert }\Big ),\\ \hbox {if}\quad \varvec{\phi }\ne \mathbf 0 \\ \mathbf 0, \quad \hbox {if}\quad \varvec{\phi }=\mathbf 0 \end{array}\right. } \end{aligned}$$

(19)

where $c_0$ and $\lambda _2$ are designed positive constants. In addition, the adaptive laws $\hat{\gamma }_2(t)$ and $\varvec{\psi }(t)$ are specified, respectively, as

$$\begin{aligned} D^{\alpha }{\hat{\gamma }}_2(t)&= {\left\{ \begin{array}{ll} \beta _3(\mathbf {x}),\quad \quad &{}\hbox {if}\quad \varvec{\phi }\ne \mathbf 0 \\ \mathbf 0, \quad \quad &{}\hbox {if}\quad \varvec{\phi }=\mathbf 0 \end{array}\right. }, \quad {\hat{\gamma }}_2(0)=0 \end{aligned}$$

(20)

$$\begin{aligned} D^{\alpha }{\varvec{\psi }}(t)&= {\left\{ \begin{array}{ll} -\,\Big [h_1\delta (\mathbf {u})+h_2\Vert \varvec{\psi }\Vert \Big ]\frac{\varvec{\psi }(t)}{\Vert \varvec{\psi }(t)\Vert },&{}\hbox {if}\quad \varvec{\psi }(t)\ne \mathbf 0 \\ -\,\varvec{\theta }, &{}\hbox {if}\quad \varvec{\psi }(t)=\mathbf 0 \end{array}\right. } \end{aligned}$$

(21)

where $\varvec{\theta }$ is a designed vector with positive entries. The other positive constants $h_1, h_2$ and functions $\delta (\mathbf {u}), \beta _3(\mathbf x)$ are introduced in the next section.

Fig. 2

Perturbation estimation mechanism for computing ${\mathbf p}_\mathrm{est}$

The perturbation estimation signal $\mathbf {p}_\mathrm{est}(t)$ in (18) is designed in a similar way as in [37]. By using (1), (9) and (17), one can see that

$$\begin{aligned} D^{\alpha }{\varvec{\phi }}&=\frac{\partial \mathbf {g}}{\partial {\mathbf {x}_{\mathbf{2}}}}(-\,\varvec{\psi }(t)-\mathbf {u}_s+\triangle \mathbf {p}_2)\nonumber \\&\quad -\,c_0\varvec{\phi }-{\mathbf {p}}_\mathrm{est}-D^{\alpha }{\varvec{\eta }}. \end{aligned}$$

(22)

Now design a nominal signal ${\varvec{\phi }}_{(\mathrm nom)}(t)$ as

$$\begin{aligned} D^\alpha {\varvec{\phi }}_{(\mathrm nom)}=-\,c_0{\varvec{\phi }}_{(\mathrm nom)}-{\mathbf p}_\mathrm{est}-\frac{\partial \mathbf {g}}{\partial {\mathbf {x}_{\mathbf{2}}}}\mathbf {u}_s, \end{aligned}$$

(23)

where $\ c_0>\alpha \pi /2$. Then subtracting (23) from (22) yields

$$\begin{aligned}&D^\alpha \big (\varvec{\phi }-\varvec{\phi }_{(\mathrm nom)}\big )+c_0\big (\varvec{\phi }-\varvec{\phi }_{(\mathrm nom)}\big )\nonumber \\&\quad =\frac{\partial \mathbf {g}}{\partial \mathbf {\mathbf {x}_2}}\Big (-\varvec{\psi }(t)+\varDelta {\mathbf {p}_{2}}\Big )-D^{\alpha }{\varvec{\eta }}. \end{aligned}$$

(24)

Let $\hat{\mathbf {p}}(t)$ be the output of the FDE developed in Sect. 4. This FDE is used to estimate the signal $D^\alpha \big (\varvec{\phi }-\varvec{\phi }_{(\mathrm nom)}\big )$ since $\varvec{\phi }$ and $\varvec{\phi }_{(\mathrm nom)}$ are measurable and differentiable. Hence one obtains that

$$\begin{aligned} \hat{\mathbf {p}}(t)= D^\alpha \big (\varvec{\phi }-\varvec{\phi }_{(\mathrm nom)}\big )+\varvec{\omega }(t), \end{aligned}$$

(25)

where $\varvec{\omega }(t)$ is the fractional derivative estimation error. If the FDE is designed properly, then $\varvec{\omega }(t)$ is small in accordance with Theorem 2.

The perturbation estimation signal in this paper is then designed as

$$\begin{aligned} \mathbf {p}_\mathrm{est}=\hat{\mathbf {p}}(t)+c_0\big (\varvec{\phi }-\varvec{\phi }_{(\mathrm nom)}\big ). \end{aligned}$$

(26)

The block diagram for implementing the signal $\mathbf {p}_\mathrm{est}$ is depicted in Fig. 2. From (24), (25), and (26), one can define the perturbation estimation error as

$$\begin{aligned} \triangle \tilde{\mathbf {p}}_2(t)&\triangleq \frac{\partial \mathbf {g}}{\partial \mathbf {\mathbf {x}_2}}\big [{-\,\varvec{\psi }(t)+\varDelta \mathbf {p}_{2}}\big ]\nonumber \\&\quad -D^{\alpha }{\varvec{\eta }}-\mathbf {p}_\mathrm{est}=-\,\varvec{\omega }(t). \end{aligned}$$

(27)

6 Stability analysis

According to the analysis in Sect. 3, one can see that the trajectory of $\mathbf x$ will reach zero within a finite time once the state $\varvec{\phi }$ approaches zero and stays thereafter. Therefore, the main purpose of this section is to show that the designed controller (17) indeed has the ability to drive the trajectory of $\varvec{\phi }$ to zero in a finite time. The stability of the proposed control system is addressed in the following theorem.

Theorem 3

Consider the dynamic system (1) with assumptions $\mathbf {A1}$ to $\mathbf {A4}$. Suppose that there exist known positive constants $h_1$, $h_2,$ and an unknown positive constant $\gamma _2$ satisfying the following inequality

$$\begin{aligned} \Vert \ \triangle \tilde{\mathbf {p}}_2(t)\Vert \le \gamma _2\beta _3(\mathbf x)+h_1\delta (\mathbf {u})+h_2\Vert \varvec{\psi }(t)\Vert \end{aligned}$$

(28)

$\forall \ t,\ \mathbf x$ in the domain of interest, where $\beta _3(\mathbf x)$ and $\delta (\mathbf {u})$ are known positive functions and $\varvec{\psi }(t)$ is the state variable defined in (21).

If the controller (17) with adaptive laws (15), (20) and (21) are employed, then

(a) the function $\varvec{\phi }$ and state variable $\mathbf {x}$ will approach zero within a finite time;

(b) the adaptive gains $\hat{\gamma }_1$ and $\hat{\gamma }_2$ are all bounded, and $\hat{\gamma }_1, \hat{\gamma }_2$ will reach a finite limit, respectively, as $t\rightarrow \infty$;

(c) the nominal signal $\varvec{\phi }_{(\mathrm nom)}$ and the estimation signal $\mathbf {p}_\mathrm{est}(t)$ are all bounded.

Proof

(a) Define the second Lyapunov function candidate as

$$\begin{aligned} V_2=\Vert \varvec{\phi }\Vert +\frac{1}{2}\tilde{\gamma }^2_2+\Vert \varvec{\psi }\Vert , \end{aligned}$$

(29)

where $\tilde{\gamma }_2(t)\triangleq \hat{\gamma }_2(t)-\gamma _2$ is the adaptive error of the unknown positive constant $\gamma _2$. All the possible cases that may occur in the derivative of (29) are analyzed as follows.

$\mathbf {Case}$${\mathbf 1}$ : $\varvec{\phi }\ne \mathbf 0$ and $\varvec{\psi }\ne \mathbf 0$

By using (19), (27) and (28), one computes the fractional derivative of (29) along the trajectories of (22) and (20) as

$$\begin{aligned} D^{\alpha } V_2&\le \frac{\varvec{\phi }^T}{\Vert \varvec{\phi }\Vert } D^{\alpha }\varvec{\phi }+\tilde{\gamma }_2D^{\alpha }{\hat{\gamma }}_2+\frac{\varvec{\psi }^{T}(t)}{\Vert \varvec{\psi }(t)\Vert }D^{\alpha }\varvec{\psi }\nonumber \\&=-\,\lambda _2-\hat{\gamma }_2\beta _3(\mathbf {x})+\frac{\varvec{\phi }^T}{\Vert \varvec{\phi }\Vert }\triangle \tilde{\mathbf {p}}_2(t)+\tilde{\gamma }_2D^{\alpha }{\hat{\gamma }}_2\nonumber \\&\quad +\,\frac{\varvec{\psi }^{T}(t)}{\Vert \varvec{\psi }(t)\Vert }D^{\alpha }\varvec{\psi }\nonumber \\&\le -\,\lambda _2-\hat{\gamma }_2\beta _3(\mathbf {x})+\gamma _2\beta _3(\mathbf {x})+h_1\delta (\mathbf {u})+h_2\Vert \varvec{\psi }\Vert \nonumber \\&\quad +\,(\hat{\gamma }_2-\gamma _2)D^{\alpha }{\hat{\gamma }}_2+\frac{\varvec{\psi }^{T}(t)}{\Vert \varvec{\psi }(t)\Vert }D^{\alpha }\varvec{\psi }\nonumber \\&=-\,\lambda _2+h_1\delta (\mathbf {u})+h_2\Vert \varvec{\psi }\Vert +\frac{\varvec{\psi }^{T}(t)}{\Vert \varvec{\psi }(t)\Vert }D^{\alpha }\varvec{\psi }. \end{aligned}$$

(30)

By using (21), one can further simplify (30) as

$$\begin{aligned} D^{\alpha } V_2&\le -\,\lambda _2<0. \end{aligned}$$

(31)

Equation (31) clearly indicates that the function $V_2$ is bounded, hence the trajectories of $\varvec{\phi }, \hat{\gamma }_2$ and $\varvec{\psi }$ are all bounded, and the state $\varvec{\phi }$ will be driven toward zero within a finite time in this case. Noted that the state $\varvec{\psi }$ is asymptotically stable due to $\varvec{\psi }^TD^{\alpha }\varvec{\psi }<0$ in accordance with (21), and it also means that the state $\varvec{\psi }$ will not reach zero and stay thereafter in a finite time. The adaptive gain $\hat{\gamma }_2$ will not reach zero in a finite time either, this is explained in part (b). When $\varvec{\phi }$ reaches zero in a finite time, the stability of the controlled system is analyzed in case 3 and case 4.

$\mathbf {Case}$${\mathbf 2}$ : $\varvec{\phi }\ne \mathbf 0$ and $\varvec{\psi }=\mathbf 0$

From the fractional derivative of (30), it is seen that

$$\begin{aligned} D^{\alpha } V_2&\le -\lambda _2+h_1\delta (\mathbf {u}). \end{aligned}$$

In this case, $D^{\alpha }V_2$ may be greater or smaller than zero. From (21), it is seen that $\mathbf {\varvec{\psi }=0}$ and $D^{\alpha }\varvec{\psi }\ne \mathbf 0$, it means that the trajectory of $\varvec{\psi }$ will not stay in the surface $\varvec{\psi }=\mathbf 0$ and will cross the surface $\varvec{\psi }=\mathbf 0$ immediately (that is, $\varvec{\psi }\ne \mathbf 0$ in the next time interval). Hence the status of the system will switch to another case with $\varvec{\psi }\ne \mathbf 0$. Noted that the states $\varvec{\phi }$ and $\hat{\gamma }_2$ are still bounded in this case due to the continuity of these trajectories.

$\mathbf {Case}$${\mathbf 3}$ : $\varvec{\phi }=\mathbf 0$ and $\varvec{\psi }\ne \mathbf 0$

From (29), it is seen $V_2=\frac{1}{2}\tilde{\gamma }^2_2+\Vert \varvec{\psi }\Vert$. By noting that $D^{\alpha }{\hat{\gamma }}_2=0$ in (20), and using (21) for $\varvec{\psi }\ne \mathbf 0$, one is able to compute $D^{\alpha }V_2$ as

$$\begin{aligned} D^{\alpha }V_2=\frac{\varvec{\psi }^{T}(t)}{\Vert \varvec{\psi }(t)\Vert }D^{\alpha }\varvec{\psi }=-h_1\delta (\mathbf {u})-h_2\Vert \varvec{\psi }\Vert <0. \end{aligned}$$

One can see that $V_2$ is a bounded function and the magnitude of $V_2$ will still decrease in this case. Hence one can conclude that $\varvec{\psi }$ and $\hat{\gamma }_2(t)$ are bounded in this case.

$\mathbf {Case}$${\mathbf 4}$ : $\varvec{\phi }=\mathbf 0$ and $\varvec{\psi }=\mathbf 0$

In this case, it is seen that $V_2=\frac{1}{2}\tilde{\gamma }^2_2$. Hence $D^{\alpha }V_2=0$ in accordance with (20). Therefore, the value of $V_2$ will not decrease and both $V_2$ and $\hat{\gamma }_2(t)$ are bounded in this case.

According to the previous stability analysis from case 1 to case 4 and Theorem 1, it can be seen that variable $\varvec{\phi }(t)$ will approach zero and stay thereafter in a finite time. According to (16), the Lyapunov function $V_1$ will also converge to zero in a finite time once $\varvec{\phi }=\mathbf 0$. Therefore, the controlled state variable $\mathbf {x}$ will tend to zero within a finite time in accordance with the analysis of Sect. 3.

(b) From (15) and (20), it is seen that adaptive gains ${\hat{\gamma }}_j(t)$, $j=1, 2$, are monotonically increasing and are all bounded above in accordance with the analysis of part (a). Therefore, there exist finite constants $\gamma _{j\infty }$, $j=1, 2$, such that $\underset{t\rightarrow \infty }{\lim }\hat{\gamma }_{j}(t)$$=\gamma _{j\infty }$, $j=1, 2$ [41] (Proposition 2.14, page 83).

(c) According to (10), one can see that the function $\varvec{\eta }$ depends on state $\mathbf {x}_1$ and t, and hence the fractional derivative of $\varvec{\eta }$ is given by

$$\begin{aligned} D^{\alpha }\varvec{\eta }&=\frac{\partial \varvec{\eta }}{\partial \mathbf {x}_1}D^{\alpha }\mathbf {x}_1+\frac{\partial \varvec{\eta }}{\partial t} \nonumber \\&=\frac{\partial \varvec{\eta }}{\partial \mathbf {x}_1}\big [{\mathbf {f}_1}+{\mathbf {G}_1}{\mathbf g} (\mathbf x_2)+\triangle \mathbf {p}_1(t,\mathbf x)\big ]+\frac{\partial \varvec{\eta }}{\partial t}. \end{aligned}$$

(32)

According to the previous stability analysis, the states $\mathbf {x}_1, \mathbf {x}_2$ and $\varvec{\eta }$ are all bounded and will approach zero within a finite time, which also implies that $D^{\alpha }\varvec{\eta }$ is bounded in accordance with (32). Since $\varvec{\psi }^TD^{\alpha }\varvec{\psi }<0$ in (21), the signal $\varvec{\psi }$ is bounded. Hence the right-hand side of (24) is bounded in accordance with the assumption $\mathbf {A3}$ and the analysis of part (a). Hence according to Theorem 4.3 in [42], one can see that $\varvec{\phi }-\varvec{\phi }_{(\mathrm nom)}$ is bounded since $\frac{\partial \mathbf {g}}{\partial \mathbf {\mathbf {x}_2}}\big (-\varvec{\psi }(t)+\varDelta {\mathbf {p}_{2}}\big )-D^{\alpha }{\varvec{\eta }}$ is bounded and $c_0>\alpha \pi /2$. Therefore, $\varvec{\phi }_{(\mathrm nom)}$ must be bounded, and from (26) the signal $\mathbf {p}_\mathrm{est}$ must be bounded due to $\hat{\mathbf {p}}(t)$ is bounded. $\square$

Note that: The function $\beta _3(\mathbf x)$ may be a non-vanishing function.

7 Numerical example

Consider a multi-input perturbed nonlinear FO system described by (1), where the fractional order is $\alpha =0.65$, and $\mathbf {g}(\mathbf {x})=[x_{21}+x_{22}\ \ x_{22}\ \ x_{21}+x_{23}]^T$. The state variables are $\mathbf {x_1}\triangleq [x_{11}\ \ x_{12}]^T$, $\mathbf {x_2}\triangleq [x_{21}\ \ x_{22}\ \ x_{23}]^T$. The known nonlinear vectors and matrices $\mathbf f_i$, $\mathbf G_i$, $1\le i\le 2$, are given by $\mathbf f_1(t, \mathbf x_1)=[ \sin (t)x_{11}^2\ \ x_{12}^2 ]^T$, $\mathbf f_2(t, \mathbf x)=[x_{11}x_{21}\cos (t)$$\cos (x_{12})x_{22}$${x_{23}^2}x_{22}+\sin (t)]^T$,

$$\begin{aligned} \mathbf G_1(t, {\mathbf x_1})&= \begin{bmatrix} x_{12}\sin (t)&x_{11}^2&1\\ 0&1&\cos (x_{11}) \end{bmatrix}, \\ \mathbf G_2(t, \mathbf x)&= \begin{bmatrix} 5&\cos (t)&x_{22}x_{12}\\ 1&2&0 \\ \sin (t)&\sin (x_{11}x_{22})&3 \end{bmatrix}. \end{aligned}$$

The vector $\mathbf u \triangleq [u_1\quad u_2\quad u_3]^T$ represents the control input. For demonstrating the robustness of the proposed control scheme and computer simulation, we assume that the unknown perturbations $\triangle \mathbf {p}_i$, $1\le i\le 2$, are

$$\begin{aligned}&\triangle {\mathbf p}_1(t, \mathbf x)= \begin{bmatrix} 0.5x_{21}\cos (x_{11}t)\\ -\,x_{21}x_{22}^2 \end{bmatrix}, \\&\triangle {\mathbf p}_2(t, \mathbf x, \mathbf u)= \begin{bmatrix} -\,x_{12}^2u_2\\ \sin (t)u_3\\ x_{12}x_{23}^2+\sin (t) \end{bmatrix}. \end{aligned}$$

Fig. 3

The trajectory of function $\varvec{\phi }$

Fig. 4

The trajectory of sliding surface $\varvec{\sigma }$

Fig. 5

The trajectory of state variable $\mathbf x_1$

Fig. 6

The trajectory of state variable $\mathbf x_2$

Fig. 7

The trajectory of function $\varvec{\phi }_{(\mathrm nom)}$

Fig. 8

The trajectories of adaptive gains

Fig. 9

The trajectory of control input ${\mathbf u}$

The controller and sliding surface function are designed in accordance with (17) and (7), respectively. The designed parameters are chosen to be $(\lambda _1,\lambda _2,c_0, h_1, h_2$, $k_1, k_2, k_b)=(0.1, 3, 25, 1, 1, 1, 5, 2)$, $\varvec{\theta }=[ 0.1\ \ 0.1\ \ 0.1 ]^T$. The nonlinear positive vanishing functions $\beta _1$ in assumption $\mathbf {A3}$, $\beta _3$ and $\delta (\mathbf {u})$ in (28) are given by

$$\begin{aligned}&\delta (\mathbf {u})\triangleq \Vert \mathbf {u}\Vert ,\quad \beta _1(\mathbf x)\triangleq \Vert \mathbf x_1\Vert \Vert \mathbf x_2\Vert +\Vert \mathbf x_2\Vert ^2, \\&\beta _3(\mathbf x)\triangleq 0.2\Vert \mathbf x_1\Vert \Vert \mathbf x_2\Vert +0.25\Vert \mathbf x_1\Vert \Vert \mathbf x_2\Vert ^2+0.3. \end{aligned}$$

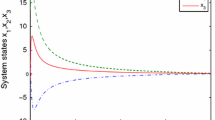
The initial condition $\mathbf x(0)$ is assumed to be $\mathbf x(0)\!=\![2\ \ -1\ \ 1.5\ \ -2\ \ 0.7]^T$. The results of computer simulation with step time 0.0001 s are shown from Figs. 3, 4, 5, 6, 7, 8 and 9. Figure 3 shows that the function $\varvec{\phi }$ tends to zero within 8.32 s, and the controlled system enters the sliding surface in 11.19 s, as displayed in Fig. 4. The state variables $\mathbf x_i, 1\le i\le 2$, as illustrated in Figs. 5 and 6, all reach zero within 11.21 s. The functions $\varvec{\phi }_{(\mathrm nom)}$, adaptive gains ${\hat{\gamma }}_1, {\hat{\gamma }}_2$ and control input $\mathbf u$ are all bounded, as depicted from Figs. 7, 8 and 9, respectively.

8 Conclusion

In this paper, an adaptive SMC scheme is successfully proposed for a class of perturbed FO nonlinear systems with matched and unmatched perturbations to solve regulation problems. The advantages of the proposed control system are as follows. (1) The proposed control scheme can be applied to systems with unmatched perturbations. (2) There is no need to know in advance the upper bounds of perturbations and perturbation estimation errors due to the embedded perturbation estimator and adaptive mechanisms. (3) The resultant control system is able to drive the controlled state trajectories into equilibrium point within a finite time. For future study, solving the tracking problems is worth considering.