1 Introduction

Over the past decades, fractional calculus has attracted increasing concerns of researchers, which has been widely applied in the fields of engineering and physics, such as system control [1], electromechanics [2] and signal processing [3]. So far, integer-order nonlinear systems have been studied extensively [4–7]. Since the mathematical model of a real plant can be accurately described via the fractional-order differential method [8, 9], many systems can be expressed as fractional differential equations, for example fractional-order economic system [10], fractional-order biological population model [11], fractional-order financial system [12] and fractional-order chaotic and hyperchaotic systems [13–19]. Recently, the synchronization of fractional-order chaotic systems has been extensively investigated because of the potential applications in electrical engineering and secure communication. Therefore, it is significant to develop the synchronization control of fractional-order chaotic systems based on fractional calculus.

The chaotic synchronization is that the synchronization errors asymptotically approach zero for the trajectories of drive system and response system. Since the synchronization was firstly realized between two identical chaotic systems by Pecora and Carroll [20, 21], the chaotic synchronization has been developed quickly and many synchronization control schemes for fractional-order chaotic systems have been proposed including impulsive control [22], active control [23], adaptive control [24], generalized projective control [25] and passive control [26]. In addition, it is well known that sliding mode control is an effective robust control scheme and the sliding mode control scheme has the features of fast global convergence and high robustness to external disturbances [27]. In recent years, sliding mode control has been investigated for linear and nonlinear systems [28–31] and many important results have been reported for the synchronization of fractional-order chaotic systems by using the sliding mode control strategy. In [32, 33], from the stability theory of fractional-order systems and active sliding mode control method, the synchronization was achieved for two fractional-order chaotic systems. The sliding mode synchronization control was realized for uncertain fractional-order Duffing–Holmes systems in [34]. In [35], the stabilization and synchronization were investigated for a class of chaotic fractional-order systems via a novel fractional-order sliding mode method. A robust fractional-order sliding mode scheme was proposed, and the synchronization was realized for uncertain fractional-order chaotic systems in [36]. In [37], a new three-dimensional fractional-order chaotic system was presented and its adaptive sliding mode synchronization was studied. The synchronization was studied for a class of fractional-order arbitrary dimensional hyperchaotic systems based on the sliding mode control method in [38]. The above-mentioned works focused on synchronization of fractional-order chaotic systems via sliding mode control approach. In practice, many real physical systems are subjected to exogenous disturbance and the disturbance may lead to oscillations and even increase instability of systems; it is significant to investigate the synchronization of fractional-order chaotic systems with external disturbance. According to the conclusion above, the bounded assumption for fractional derivative of disturbances was introduced [34]. In [36, 38], unknown disturbances in fractional-order systems were tackled by adaptive estimation method. However, the nonlinear FODO has rarely been considered in synchronization control of fractional-order chaotic systems in the literature.

Since the nonlinear disturbance observer can approximate unknown disturbance well, it can be employed to restrain the interference of external disturbance. In the past decades, many design techniques of integer-order disturbance observer have been reported. In [39], a disturbance observer-based control was proposed for nonlinear systems with disturbances. The nonlinear disturbance observer was developed for robot manipulators in [40]. In [41], an adaptive fuzzy tracking control scheme was explored based on disturbance observer for multi-input and multi-output nonlinear systems. By using the terminal sliding mode technique, a disturbance observer-based adaptive sliding mode control scheme was proposed for near-space vehicles (NSV) in [42]. In [43], a Nussbaum disturbance observer was designed for NSV. On the basis of the terminal sliding mode technique and the disturbance observer method, an anti-disturbance control scheme was presented for NSV in [44]. With such experience of the applications of disturbance observers, it is necessary to design nonlinear FODO to compensate for the effects caused by unknown disturbances.

Inspired by the above discussions, we develop a synchronization control scheme to synchronize fractional-order chaotic systems with unknown external disturbances based on a designed nonlinear FODO and a simple sliding mode surface. To illustrate the effectiveness of the given synchronization control method, a modified fractional-order Jerk system is analyzed by using the proposed synchronization control scheme.

The organization of the paper is as follows. Section 2 details the problem formulation. The nonlinear FODO is designed in Sect. 3. The sliding mode surface is constructed, and the sliding mode synchronization controller is proposed based on the developed nonlinear FODO in Sect. 4. A modified fractional-order Jerk system is presented, and the effectiveness of the proposed synchronization control method is demonstrated via numerical simulation in Sect. 5, followed by some concluding remarks in Sect. 6.

2 Problem statement and preliminaries

Fractional calculus is an extension to integer-order calculus. Several existing definitions of fractional derivatives are given in [45], where the Caputo definition is used in engineering applications extensively. We firstly introduce the following Caputo definition.

Definition 1

[45] For the function g(t), the Caputo fractional derivative of fractional-order \(\alpha \) is defined as follows:

$$\begin{aligned} D^\alpha g(t) = \frac{1}{{{\varGamma } (m - \alpha )}}\int _{{t_0}}^t {\frac{{{g^{(m)}}(\tau )}}{{{{(t - \tau )}^{\alpha - m + 1}}}}} \hbox {d}\tau . \end{aligned}$$
(1)

where \(m - 1 < \alpha < m\), \(m = [\alpha ] + 1\), \([\alpha ]\) denotes the integer part of \(\alpha \), and the \({\varGamma } ( \cdot )\) is gamma function, which is defined as \({\varGamma } (m - \alpha ) = \int _0^\infty {{t^{m - \alpha - 1}}{e^{ - t}}} \hbox {d}t\). The main advantage of (1) is that Caputo derivative of a constant is equal to zero. In this paper, the fractional-order chaotic systems will be described by using Caputo definition with lower limit of integral \({t_0} = 0\) and the order \(0 < \alpha < 1\).

Definition 2

[46] The Mittag–Leffler function with two parameters is defined as

$$\begin{aligned} {E_{{\alpha _1},{\alpha _2}}}(z) = \sum \limits _{k = 0}^\infty {\frac{{{z^k}}}{{{\varGamma } (k{\alpha _1} + {\alpha _2})}}} \end{aligned}$$
(2)

where \({\alpha _1} > 0\), \({\alpha _2} > 0\), z stands for set of complex numbers.

On the basis of the Caputo definition of fractional derivative, the fractional-order chaotic system will be introduced.

Consider the following fractional-order chaotic system as the drive system:

$$\begin{aligned} D^\alpha x(t) = Ax(t) + f(x(t)). \end{aligned}$$
(3)

where \(A \in {R^{n \times n}}\) denotes a constant matrix, \(x(t) = {({x_1}(t),{x_2}(t), \ldots , {x_n}(t))^T} \in {R^n}\) is a state vector, \(f(x(t)) = {({f_1}(x(t)),{f_2}(x(t)), \ldots ,{f_n}(x(t)))^T} \in {R^n}\) is the nonlinear function vector.

The response system is defined as follows:

$$\begin{aligned} D^\alpha y(t) = Ay(t) + f(y(t)) + d(t) + u(t). \end{aligned}$$
(4)

where \(y(t) = {({y_1}(t),{y_2}(t), \ldots , {y_n}(t))^T} \in {R^n}\) is the state vector, \(f(y(t)) = ({f_1}(y(t)),{f_2}(y(t)),\ldots , {f_n}(y(t)))^T \in {R^n}\) is the nonlinear function vector, \(d(t)\; = \;({d_1}(t),{d_1}(t),\ldots ,{d_n}(t))^T \in {R^n}\) is the unknown bounded disturbance, and \(u(t) = {({u_1}(t),{u_1}(t), \ldots , {u_n}(t))^T} \in {R^n}\) is the control input.

This paper aims at developing a FODO-based adaptive sliding mode synchronization control scheme, so that the synchronization is realized between two identical fractional-order chaotic systems in the presence of external unknown disturbances. On the basis of the designed sliding mode controller, the response system can well synchronize the drive system under the proper condition. In order to obtain the main results, the following lemmas, properties and assumption are introduced.

Lemma 1

[47] Let \(\chi (t) \in \mathfrak {R}\) be a continuous and derivable function. Then, for any time instant \(t \ge {t_0}\), we have

$$\begin{aligned} \frac{1}{2}D^{\alpha }{\chi ^2}(t) \le \chi (t)D^{\alpha }\chi (t). \end{aligned}$$
(5)

where \(0 < \alpha < 1\).

Lemma 2

[48] Consider the following fractional-order system

$$\begin{aligned} {D^\alpha }q(t) \le - {b_0}q(t) + {b_1} \end{aligned}$$
(6)

then there exists a constant \(t_1>0\) such that for all \(t \in ({t_1},\infty )\), we have

$$\begin{aligned} \left\| {q(t)} \right\| \le \frac{{2{b_1}}}{{{b_0}}} \end{aligned}$$
(7)

where q(t) is the state variable and \(b_0\) and \(b_1\) are two positive constants.

Property 1

[49] If \({g_1}\) is a constant and the order \({\beta _2} > 0\), the Caputo fractional derivative satisfies the following condition:

$$\begin{aligned} {D^{{\beta _2}}}{g_1} = 0. \end{aligned}$$
(8)

Property 2

[49] The Caputo fractional derivative satisfies the following linear characteristic:

$$\begin{aligned} {D^\alpha }\left[ {a_1}{g_2}(t) + {a_2}{g_3}(t)\right] = {a_1}{D^\alpha }{g_2}(t) + {a_2}{D^\alpha }{g_3}(t).\nonumber \\ \end{aligned}$$
(9)

where \({g_2}(t)\) and \({g_3}(t)\) are functions and \({a_1}\) and \({a_2}\) are constants.

Assumption 1

For the external disturbance \(d_i(t)\) with \(i = 1,2, \ldots ,n\), the Caputo fractional derivative of \(d_i(t)\) is bounded, that is \(\left| {{D^\alpha }{d_i}(t)} \right| \le {\zeta _i}\) and \({\zeta _i}>0\) is an unknown positive constant.

3 Design of fractional-order disturbance observer

In this section, a nonlinear FODO will be designed to approximate the external disturbance in the response system (4). Without loss of generality, according to the response system (4), we have

$$\begin{aligned} {D^\alpha }{y_i}(t) = {\theta _i} + {f_i}(y(t)) + {u_i}(t) + {d_i}(t) \end{aligned}$$
(10)

where \({\theta _i}\) is ith element of Ay(t), \({y_i}(t)\) is the ith element of y(t), \({f_i}(y(t))\) is the ith element of f(y(t)), \(u_i(t)\) is the ith element of u(t), \({d_i}(t)\) is the ith element of d(t) and \(i = 1,2, \ldots ,n\).

Since d(t) in (4) is unknown, d(t) cannot be applied to developing synchronization control for the drive system (3) and the response system (4). To overcome the above problem, a fractional-order nonlinear disturbance observer is designed to estimate disturbance.

To design the nonlinear FODO, an auxiliary variable is introduced based on the design technique of integer-order disturbance observer as follows [41]:

$$\begin{aligned} {\phi _i}(t) = {d_i}(t) - {\sigma _i}{y_i}(t) \end{aligned}$$
(11)

where \({\sigma _i}>0\) is a constant to be determined.

Combining (10) and (11), the Caputo fractional derivative of \({\phi _i}(t)\) can be written as

$$\begin{aligned} {D^\alpha }{\phi _i}(t)= & {} {D^\alpha }{d_i}(t) - {\sigma _i}{D^\alpha }{y_i}(t)\nonumber \\= & {} - {\sigma _i}({\theta _i} + {f_i}(y(t)) + {d_i}(t) ) \nonumber \\&-\,{\sigma _i}{u_i}(t)+ {D^\alpha }{d_i}(t)\nonumber \\= & {} - {\sigma _i}({\theta _i} + {f_i}(y(t)) + {\phi _i}(t) + {\sigma _i}{y_i}(t) )\nonumber \\&-\,{\sigma _i}{u_i}(t) + {D^\alpha }{d_i}(t) \end{aligned}$$
(12)

To obtain the disturbance estimate, the estimate of intermediate variable \({\phi _i}(t)\) is described as

$$\begin{aligned} {D^\alpha }{{\hat{\phi }}_i(t)}= & {} - {\sigma _i}({\theta _i} + {f_i}(y(t)) + {\sigma _i}{y_i}(t)) \nonumber \\&-\,{\sigma _i}{{\hat{\phi }}_i}(t) - {\sigma _i}{u_i}(t) \end{aligned}$$
(13)

where \({{\hat{\phi }}_i}\) is the estimate of \( \phi _i\).

According to (11), the disturbance \(d_i(t)\) can be estimated as

$$\begin{aligned} {{\hat{d}}_i}(t) = {{\hat{\phi }}_i}(t) + {\sigma _i}{y_i}(t) \end{aligned}$$
(14)

Define \({{\tilde{d}}_i}(t) = {d_i}(t) - {{\hat{d}}_i}(t)\). Considering (11) and (14), we have

$$\begin{aligned} {{\tilde{\phi }}_i}(t) = {\phi _i}(t) - {{\hat{\phi }}_i}(t) = {d_i}(t) - {{\hat{d}}_i}(t) = {{\tilde{d}}_i}(t) \end{aligned}$$
(15)

Considering (12) and (13), the Caputo fractional derivative of \({{\tilde{\phi }}_i}(t)\) can be written as

$$\begin{aligned} {D^\alpha }\tilde{\phi }_i (t) = - {\sigma _i}{{\tilde{\phi }}_i}(t) + {D^\alpha }{d_i}(t) \end{aligned}$$
(16)

On the basis of the above discussions, in order to analyze the convergence of disturbance estimate error \({{\tilde{d}}_i}(t)\), a Lyapunov function candidate can be chosen as

$$\begin{aligned} {V_d} = \frac{1}{2}\tilde{d}_i^2(t) = \frac{1}{2}\tilde{\phi }_i^2(t) \end{aligned}$$
(17)

Invoking (17) and Lemma 1, the Caputo fractional derivative of \(V_d\) is described as

$$\begin{aligned} {D^\alpha }{V_d}(t) \le {{\tilde{\phi }}_i}(t){D^\alpha }{{\tilde{\phi }}_i}(t) \end{aligned}$$
(18)

Substituting (16) into (18), we obtain

$$\begin{aligned} {D^\alpha }{V_d}(t) \le {{\tilde{\phi }}_i}(t)( - {\sigma _i}{{\tilde{\phi }}_i}(t) + {D^\alpha }{d_i}(t)) \end{aligned}$$
(19)

According to (19) and Assumption 1, we have

$$\begin{aligned} {D^\alpha }{V_d}(t)\le & {} - {\sigma _i}\tilde{\phi }_i^2(t) + \frac{1}{2}\tilde{\phi }_i^2(t) + \frac{1}{2}\zeta _i^2\nonumber \\= & {} - \left( {\sigma _i} - \frac{1}{2}\right) \tilde{\phi }_i^2(t) + \frac{1}{2}\zeta _i^2\nonumber \\= & {} - {B_0}{V_d}(t) + {B_1} \end{aligned}$$
(20)

where \({B_0} = 2{\sigma _i} - 1\) and \({B_1} = \frac{1}{2}\zeta _i^2\). To ensure the estimated error is bounded, the nonlinear FODO control gain \({\sigma _i}\) should be chosen to make \({\sigma _i}>0.5\). The conclusion that the signals \(\tilde{\phi }_i (t)\) and \(\tilde{d}_i (t)\) are bounded can be drawn from (20) and Lemma 2.

On the basis of Lemma 2 and (20), we obtain

$$\begin{aligned} \left| {{V_d}(t)} \right| \le \frac{{\zeta _i^2}}{{2({\sigma _i} - 0.5)}} \end{aligned}$$
(21)

which means

$$\begin{aligned} \left| {{{\tilde{d}}_i}(t)} \right| \le \sqrt{\frac{{\zeta _i^2}}{{({\sigma _i} - 0.5)}}} \end{aligned}$$
(22)

According to (22), the disturbance estimation error \({{\tilde{d}}_i}\) is upper bounded. For the external disturbance \(d_i(t)\) with \(i = 1,2, \ldots ,n\), the disturbance approximation error \({{\tilde{d}}_i}(t) = {d_i}(t) - {{\hat{d}}_i}(t)\) satisfies \(\left| {{{\tilde{d}}_i}(t)} \right| \le {\kappa _i}\) and \({\kappa _i}>0\) is an unknown positive constant. In actual application, the upper bound of \(\left| {{{\tilde{d}}_i}(t)} \right| \) is difficult to determine; therefore, the estimated value \({{\hat{\kappa }}_i}\) of \({\kappa _i} \) is introduced, where \(i = 1,2, \ldots ,n\).

The above design procedure of nonlinear FODO can be summarized in the following theorem:

Theorem 1

Consider the response system (4) and the nonlinear FODO is designed as (13) and (14). The disturbance estimate error of the proposed nonlinear FODO is bounded.

On the basis of the above-mentioned analyses, Theorem 1 can be easily proven.

4 Synchronization control of fractional-order chaotic systems

In this section, the nonlinear FODO-based adaptive sliding mode control scheme will be proposed to guarantee the trajectories of drive system (3) and response system (4) which are ultimately bounded synchronization. To design the synchronization control scheme, we firstly define error state \(e(t) = y(t) - x(t)(e(t) = ({e_1}(t),{e_2}(t), \ldots , {e_n}(t))^T \in {R^n})\). From (3) and (4), the corresponding synchronization error system is as follows:

$$\begin{aligned} D^\alpha e(t) = Ae(t) + f(y(t)) - f(x(t)) + d(t) + u(t)\nonumber \\ \end{aligned}$$
(23)

To investigate the stabilization of fractional-order synchronization error system (23), a simple sliding mode surface is defined as

$$\begin{aligned} {s_i}(t) = {e_i}(t). \end{aligned}$$
(24)

where \(i = 1,2, \ldots ,n\)

From (24), we have

$$\begin{aligned} {D^\alpha }{s_i}(t)= & {} {D^\alpha }{e_i}(t)\nonumber \\= & {} {A_i}e(t) + {f_i}(y(t)) - {f_i}(x(t)) \nonumber \\&+\,{d_i}(t) + {u_i}(t) \end{aligned}$$
(25)

where \({A_i}\) denotes the ith line of A and \(f_i(x(t))\) denotes the \(i\hbox {th}\) element of f(x(t)).

Using the adaptive sliding control approach, the desired synchronization control input is designed as

$$\begin{aligned} {u_i}(t)= & {} - {A_i}e(t) - \left( f_i(y(t)) - f_i(x(t))\right) - {\eta _i}s_i(t)\nonumber \\&-\,{{\hat{\kappa }}_i}\hbox {sign}({s_i}(t))- \hat{d}_i(t) \end{aligned}$$
(26)

where \(\hbox {sign}(\cdot )\) is the sign function and \({\eta _i}>0\) is a design constant. Meanwhile, the estimated value \({{\hat{\kappa }}_i}\) is updated by

$$\begin{aligned} {D^\alpha }{{\hat{\kappa }}_i} = {\gamma _i}\left( \left| {{s_i}(t)} \right| - {{\hat{\kappa }}_i}\right) \end{aligned}$$
(27)

where \({\gamma _i} > 0\) is a design constant.

If the synchronization control scheme is designed as (26) for fractional-order synchronization error system (23), the sliding mode surface satisfies that the sliding mode surface \({s_i}(t)\) is bounded stable in the form of

$$\begin{aligned} \left| {{s_i}(t)} \right| \le a \end{aligned}$$
(28)

where \(a>0\) is a unknown constant.

From (24) and (28), one obtains

$$\begin{aligned} \left| {{e_i}(t)} \right| \le a \end{aligned}$$
(29)

According to the above discussion, if the sliding surface \({s_i}(t) \) is bounded, then the synchronization error \({e_i}(t)\) is also bounded. Therefore, the nonlinear FODO-based adaptive sliding mode synchronization control scheme for fractional-order chaotic systems with unknown disturbances can be summarized in the following theorem and will be proved by using fractional-order Lyapunov method.

Theorem 2

For the synchronization error system (23) with \(0 < \alpha <1\), the sliding mode surface is designed according to (24). The external unknown bounded disturbance is estimated by using the designed nonlinear FODO (13) and (14). Then, the synchronization error e(t) is ultimately bounded stable under the adaptive sliding control scheme (26) and (27).

Proof

To analyze the convergence of synchronization error e(t), we consider the Lyapunov candidate function as

$$\begin{aligned} V(t)= & {} \sum \limits _{i = 1}^n {\frac{1}{2}s_i^2(t)} + \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{d}_i^2(t)} \nonumber \\&+ \sum \limits _{i = 1}^n {\frac{1}{2}{{\left( \frac{1}{{\sqrt{{\gamma _i}} }}({{{\hat{\kappa }}_i} - {\kappa _i}})\right) ^2}}} \end{aligned}$$
(30)

According to Property 2 and (30), we have

$$\begin{aligned} D^\alpha V(t)= & {} \sum \limits _{i = 1}^n {\frac{1}{2}D^\alpha s_i^2(t)} + \sum \limits _{i = 1}^n {\frac{1}{2}D^\alpha {{\left( \frac{1}{{\sqrt{{\gamma _i}} }}{{\tilde{\kappa }}_i}\right) ^2}}} \nonumber \\&+\sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(31)

where \({{\tilde{\kappa }}_i} = {{\hat{\kappa }}_i} - {\kappa _i}\).

From Lemma 1, (31) can be written as

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n {{s_i(t)}D^\alpha {s_i(t)}} + \sum \limits _{i = 1}^n {\frac{1}{{\sqrt{{\gamma _i}} }}{{\tilde{\kappa }}_i}D^\alpha \left( \frac{1}{{\sqrt{{\gamma _i}}}}{{\tilde{\kappa }}_i}\right) }\nonumber \\&+ \sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(32)

Based on Property 2, (32) is equivalent to

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n {{s_i(t)}D^\alpha {s_i(t)}} + \sum \limits _{i = 1}^n {\frac{1}{{{\gamma _i}}}{{\tilde{\kappa }}_i}D^\alpha {{\tilde{\kappa }}_i}}\nonumber \\&+ \sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(33)

On the basis of (25), one has

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n {s_i(t)}\left( {A_i}e(t) + {f_i}(y(t))- {f_i}(x(t))\right) \nonumber \\&+ \sum \limits _{i = 1}^n {{s_i(t)}\left( {d_i}(t) + {u_i}(t)\right) } + \sum \limits _{i = 1}^n {\frac{1}{{{\gamma _i}}}{{\tilde{\kappa }}_i}{D^\alpha }{{\tilde{\kappa }}_i}} \nonumber \\&+ \sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(34)

Referring to Property 1 and \({{\tilde{\kappa }}_i} = {{\hat{\kappa }}_i} - {\kappa _i}\), we obtain

$$\begin{aligned} {D^\alpha }{{\tilde{\kappa }}_i} = {D^\alpha }{{\hat{\kappa }}_i} \end{aligned}$$
(35)

According to (27) and (35), we have

$$\begin{aligned} \sum \limits _{i = 1}^n {\frac{1}{{{\gamma _i}}}{{\tilde{\kappa }}_i}{D^\alpha }{{\tilde{\kappa }}_i}}= & {} \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left( \left| {{s_i}(t)} \right| - {{\hat{\kappa }}_i}\right) } \nonumber \\= & {} \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left| {{s_i}(t)} \right| - } \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}{{\hat{\kappa }}_i}} \nonumber \\\le & {} \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left| {{s_i}(t)} \right| - } \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{\kappa }_i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2}\nonumber \\ \end{aligned}$$
(36)

Invoking (36), we obtain

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n {s_i(t)}\left( {A_i}e(t) + {f_i}(y(t)) - {f_i}(x(t))\right) \nonumber \\&+ \sum \limits _{i = 1}^n {{s_i(t)}({d_i}(t) + {u_i}(t))}+ \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left| {{s_i}(t)} \right| }\nonumber \\&- \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{\kappa }_i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2} +\sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)}\nonumber \\ \end{aligned}$$
(37)

Substituting (26) into (37) yields

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n {s_i(t)}\left( - {\eta _i}{s_i}(t)+ {{\tilde{d}}_i}(t) -{{\hat{\kappa }}_i}\hbox {sign}({s_i(t)})\right) \nonumber \\&+ \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left| {{s_i}(t)} \right| } - \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{\kappa }_i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2} \nonumber \\&+\sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(38)

Furthermore, (38) can be rewritten as

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n { - {\eta _i}s_i^2(t)} + \sum \limits _{i = 1}^n {\left| {{s_i}(t)} \right| \left| {{{\tilde{d}}_i}(t)} \right| } \nonumber \\&+ \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left| {{s_i}(t)} \right| } - \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{\kappa }_i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2} \nonumber \\&- \sum \limits _{i = 1}^n {{{\hat{\kappa }}_i}\left| {{s_i}(t)} \right| } +\sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(39)

with

$$\begin{aligned} \sum \limits _{i = 1}^n {{{\tilde{\kappa }}_i}\left| {{s_i}(t)} \right| } - \sum \limits _{i = 1}^n {{{\hat{\kappa }}_i}\left| {{s_i}(t)} \right| } = - \sum \limits _{i = 1}^n {{\kappa _i}\left| {{s_i}(t)} \right| } \end{aligned}$$
(40)

According to (40), it yields

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n { - {\eta _i}s_i^2(t)} - \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{\kappa }_i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2} \nonumber \\&+\sum \limits _{i = 1}^n {\frac{1}{2}{D^\alpha }\tilde{d}_i^2(t)} \end{aligned}$$
(41)

Considering (20) and (41), we have

$$\begin{aligned} D^\alpha V(t)\le & {} \sum \limits _{i = 1}^n { - {\eta _i}s_i^2(t)} - \sum \limits _{i = 1}^n {\frac{1}{2}\tilde{\kappa }_i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2} \nonumber \\&\sum \limits _{i = 1}^n { - ({\sigma _i} - \frac{1}{2})\tilde{d}_i^2(t)} + \sum \limits _{i = 1}^n {\frac{1}{2}\zeta _i^2} \nonumber \\\le & {} - {B_2}V(t) + {B_3} \end{aligned}$$
(42)

where \({B_2} = \min (2{\eta _i},1,2{\sigma _i} - 1)\) and \({B_3} = \sum \limits _{i = 1}^n {\frac{1}{2}\zeta _i^2} + \sum \limits _{i = 1}^n {\frac{1}{2}\kappa _i^2} \).

To ensure the synchronization error is bounded, the corresponding design parameters \({\eta _i}\) and \({\sigma _i}\) should be chosen to make \({\eta _i}>0\) and \({\sigma _i}>0.5\). According to (42) and Lemma 2, it may directly show that the signals s(t), e(t) and \({{\tilde{d}}_i}(t)\) are ultimately bounded. From Lemma 2 and (42), we obtain

$$\begin{aligned} \left| {V(t)} \right| \le \frac{{\sum \nolimits _{i = 1}^n {\zeta _i^2} + \sum \nolimits _{i = 1}^n {\kappa _i^2} }}{{{B_2}}} \end{aligned}$$
(43)

which implies

$$\begin{aligned} \left\| {s(t)} \right\| \le \sqrt{\frac{{2\left( \sum \limits _{i = 1}^n {\zeta _i^2} + \sum \limits _{i = 1}^n {\kappa _i^2} \right) }}{{{B_2}}}} \end{aligned}$$
(44)

From the inequality (44), the synchronization error e(t) and s(t) will be ultimately bounded as \(t \rightarrow \infty \). Therefore, the synchronization error system (23) is bounded stable based on Lemma 2. The bounded synchronization of drive system (3) and response system (4) is achieved. This concludes the proof.\(\square \)

Remark 1

Since the response system (4) is with the unknown time-varying disturbance, the nonlinear FODO is employed to estimate the disturbance in this paper. To develop the disturbance observer, Assumption 1 is introduced. This assumption means that the Caputo derivative of the disturbance is bounded. If the Caputo derivative of the disturbance is unbounded, the estimation performance of nonlinear FODO could be poor. Thus, Assumption 1 is necessary for the disturbance.

Remark 2

As for the proposed nonlinear FODO, we can see that the estimated error with suitable transient performance can be obtained by appropriately adjusting design parameter \({\sigma _i}\). For example, the approximation error could be decreased by increasing the value of \({\sigma _i}\). Therefore, appropriate parameter should be chosen based on the performance of whole systems.

5 Simulation example

5.1 Modified fractional-order Jerk system

In [50], a new chaotic generator was investigated by constructing a three-segment piecewise-linear odd function with variable break point. From the differential equation of chaotic generator in [50], the modified fractional-order Jerk system is given as follows:

$$\begin{aligned} D^\alpha {x_1}(t)= & {} {x_2}(t)\nonumber \\ D^\alpha {x_2}(t)= & {} {x_3}(t)\nonumber \\ D^\alpha {x_3}(t)= & {} - {\varepsilon _1}{x_1}(t) - {x_2}(t) - {\varepsilon _2}{x_3}(t) - {f_3}(x(t))\nonumber \\ \end{aligned}$$
(45)

where the parameters \({\varepsilon _1} = 1.5\), \({\varepsilon _2} = 0.35\) and \({f_3}(x(t))\) is a piecewise-linear function defined by

$$\begin{aligned} {f_3}(x(t))= & {} \frac{1}{2}({\vartheta _0} - {\vartheta _1})(\left| {{x_1}(t) + 1} \right| - \left| {{x_1}(t) - 1} \right| ) \nonumber \\&+\,{\vartheta _1}{x_1}(t) \end{aligned}$$
(46)

where \({\vartheta _0} < - 1 < {\vartheta _1} < 0\) and \({\vartheta _0}=-2.5,\,{\vartheta _1}=-0.5\).

Table 1 Equilibrium points of the modified fractional-order Jerk system
Full size table

According to the system (45) and the piecewise-linear function (46), the three equilibrium points of the modified fractional-order Jerk system are given in Table 1. The Jacobian matrix for system (45) can be written as

$$\begin{aligned} J = \left[ {\begin{array}{*{20}{c}} 0&{}1&{}0\\ 0&{}0&{}1\\ { - 1.5 - \frac{{\partial {f_3}(x(t))}}{{\partial {x_1}(t)}}}&{}{ - 1}&{}{ - 0.35} \end{array}} \right] . \end{aligned}$$
(47)

On the basis of Table 1, the corresponding eigenvalues for equilibrium point \({Q_ 0 }\) are \({\lambda _1} = 0.6228\) and \({\lambda _{2,3}} = - 0.4864 \pm 1.1701j\). And, for equilibrium points \({Q_ + }\) and \({Q_ - }\), the eigenvalues are \({\lambda _1} = -0.7614\) and \({\lambda _{2,3}}= 0.2057 \pm 1.1274j\). When the fractional-order \(\alpha = 0.98\) is chosen, we obtain the following characteristic equation of the equilibrium points \({Q_ + }\) and \({Q_ - }\):

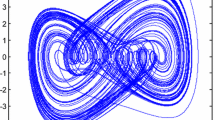
$$\begin{aligned} {\lambda ^{294}} + 0.35{\lambda ^{196}} + {\lambda ^{98}} + 1 = 0 \end{aligned}$$
(48)

with unstable \({\lambda _{1,2}}= 1.0013 \pm 0.0142j\), and \(\left| {\arg ({\lambda _{1,2}})} \right| = 0.0142 < {\pi / {2\vartheta }} = 0.0157\), in which \(\vartheta = 100\) (\(\vartheta \) is the lowest common multiple of fractional-order denominator). Thus, the modified fractional-order Jerk system (45) with chaotic dynamic behaviors is based on the theorem in [51]. When the initial values are chosen as \({(1,1,1)^T}\) and the fractional-order \(\alpha =0.98\), the fractional-order modified Jerk system exhibits chaotic behaviors as shown in Fig. 1.

Fig. 1
figure 1

Chaotic behaviors of modified fractional-order Jerk system. a \({x_1}(t) - {x_2}(t)\) plane, b \({x_1}(t) - {x_3}(t)\) plane, c \({x_2}(t) - {x_3}(t)\) plane, d \({x_3}(t) - {x_1}(t) - {x_2}(t)\) space

Full size image

5.2 Numerical simulation of synchronization control

In this section, to illustrate the effectiveness of the proposed synchronization controller, the synchronization of modified fractional-order Jerk system (45) is investigated. Consider the fractional-order chaotic system (45) as drive system. From (4), the response system is defined as follows:

$$\begin{aligned} D^\alpha {y_1}(t)= & {} {y_2}(t) + {d_1}(t) + {u_1}(t)\nonumber \\ D^\alpha {y_2}(t)= & {} {y_3}(t) + {d_2}(t) + {u_2}(t)\nonumber \\ D^\alpha {y_3}(t)= & {} - {\varepsilon _1}{y_1}(t) - {y_2}(t) -{\varepsilon _2}{y_3}(t) \nonumber \\&- {f_3}(y(t)) + {d_3}(t) +{u_3}(t) \end{aligned}$$
(49)

where \({d_1}(t)\), \({d_2}(t)\) and \({d_3}(t)\) are unknown bounded disturbances. \({u_1}(t)\), \({u_2}(t)\) and \({u_3}(t)\) are designed synchronization control inputs. \({f_3}(y(t))\) is defined as

$$\begin{aligned} {f_3}(y(t))= & {} \frac{1}{2}({\vartheta _0} - {\vartheta _1})(\left| {{y_1}(t) + 1} \right| - \left| {{y_1}(t) - 1} \right| )\nonumber \\&+\,{\vartheta _1}{y_1}(t) \end{aligned}$$
(50)

According to (45) and (49), the synchronization error system can be written as

$$\begin{aligned} D^\alpha {e_1}(t)= & {} {e_2}(t) + {d_1}(t) + {u_1}(t)\nonumber \\ D^\alpha {e_2}(t)= & {} {e_3}(t) + {d_2}(t) + {u_2}(t)\nonumber \\ D^\alpha {e_3}(t)= & {} - {\varepsilon _1}{e_1}(t) - {e_2}(t) - {\varepsilon _2}{e_3}(t) \nonumber \\&- {f_3}(y(t)) + {f_3}(x(t)) + {d_3}(t) + {u_3}(t)\nonumber \\ \end{aligned}$$
(51)
Fig. 2
figure 2

Comparison result of \({2^{0.98}}\cos (2t + \frac{{0.98\pi }}{2})\) and \({D^\alpha }\cos (2t)\)

Full size image
Fig. 3
figure 3

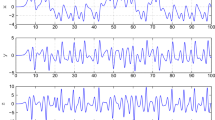
Synchronization control results of modified fractional-order Jerk system. a Synchronization state of \({x_1}(t)\) and \({y_1}(t)\), b synchronization state of \({x_2}(t)\) and \({y_2}(t)\), c synchronization state of \({x_3}(t)\) and \({y_3}(t)\), d synchronization error \({e_1}(t)\), \({e_2}(t)\) and \({e_3}(t)\)

Full size image
Fig. 4
figure 4

Disturbance observer results. a \(d_1(t)\) and \(\hat{d}_1(t)\), b \(d_2(t)\) and \(\hat{d}_2(t)\), c \(d_3(t)\) and \(\hat{d}_3(t)\), d observation errors \({\tilde{d}_1}(t)\), \({\tilde{d}_2}(t)\) and \({\tilde{d}_3}(t)\)

Full size image

Referring to the designed controller (26), the synchronization controller can be written as

$$\begin{aligned} {u_1}(t)= & {} - {e_2}(t) - {\eta _1}{s_1}(t) - {{\hat{\kappa }}_1}\hbox {sign}({s_1}(t)) - {{\hat{d}}_1}(t)\nonumber \\ {u_2}(t)= & {} - {e_3}(t) - {\eta _2}{s_2}(t) - {{\hat{\kappa }}_2}\hbox {sign}({s_2}(t)) - {{\hat{d}}_2}(t)\nonumber \\ {u_3}(t)= & {} {\varepsilon _1}{e_1}(t) + {e_2}(t) + {\varepsilon _2}{e_3}(t) + {f_3}(y(t)) \nonumber \\&- {f_3}(x(t)) - {\eta _3}{s_3}(t) - {{\hat{\kappa }}_3}\hbox {sign}({s_3}(t)) - {{\hat{d}}_3}(t)\nonumber \\ \end{aligned}$$
(52)

Substituting (52) into (51), we have

$$\begin{aligned} {D^\alpha }{e_1}(t)= & {} - {\eta _1}{s_1}(t) - {{\hat{\kappa }}_1}\hbox {sign}({s_1}(t)) + {{\tilde{d}}_1}(t)\nonumber \\ {D^\alpha }{e_2}(t)= & {} - {\eta _2}{s_2}(t) - {{\hat{\kappa }}_2}\hbox {sign}({s_2}(t)) + {{\tilde{d}}_2}(t)\nonumber \\ {D^\alpha }{e_3}(t)= & {} - {\eta _3}{s_3}(t) - {{\hat{\kappa }}_3}\hbox {sign}({s_3}(t)) + {{\tilde{d}}_3}(t) \end{aligned}$$
(53)

where \({D^\alpha }{{\hat{\kappa }}_i} = {\gamma _i}(\left| {{s_i}(t)} \right| - {{\hat{\kappa }}_i})\) with \({\gamma _i} > 0\) and \(i=1,2,3\).

To demonstrate the effectiveness of the proposed nonlinear FODO-based adaptive sliding mode synchronization control scheme, the numerical simulation results are presented for the modified fractional-order Jerk system under the following conditions: the initial conditions \({x_0}(t) = {(1,1,1)^T}\), \({y_0}(t) = (1.2,0.6,0.5)^T\), \({{\hat{\kappa }}_0} = {(0.1,0.1,0.1)^T}\) and \(\hat{\phi }_0(t)= {(0.1,0.1,0.1)^T}\), and the designed parameters are chosen as \(\alpha = 0.98\), \({\sigma _1}={\sigma _2}={\sigma _3}=50\), \({\gamma _1} = {\gamma _2} = {\gamma _3} = 0.1\) and \({\eta _1}={\eta _2}={\eta _3}=50\). The disturbance is assumed as \({d_1}(t) = \cos (2t)\), \({d_2}(t) = \cos (2t)\) and \({d_3}(t) = \cos (2t)\). On the basis of the result in [52], we have \({\rho _1}{D^\alpha }\cos ({\rho _2}t) = {\rho _1}\frac{1}{2}{(j{\rho _2})^m}{t^{m - \alpha }}({E_{1,m - \alpha + 1}}(j{\rho _2}t) + {( - 1)^n}{E_{1,m - \alpha + 1}}( - j{\rho _2}t))\) with j denotes the unit of imaginary part with \({\rho _1}\) and \({\rho _2}\) which are arbitrary numbers. In this paper, the parameter \(m=1\) and the fractional-order \(\alpha =0.98\). Thus, \({\rho _1}\rho _2^\alpha \cos ({\rho _2}t + \frac{{\pi \alpha }}{2})\) can be used to approximate \({\rho _1}{D^\alpha }\cos ({\rho _2}t)\). The comparison result is shown in Fig. 2 for the case of \({\rho _1}=1\) and \({\rho _2}=2\). According to Fig. 2, Assumption 1 is satisfied.

The numerical results are shown in Figs. 3 and 4 under the proposed nonlinear FODO-based adaptive sliding mode control scheme. The state synchronization results of drive system (45) and response system (49) are given in Fig. 3a–c. It is shown that good synchronization performance is achieved. Figure 3d shows the synchronization errors \({e_1}(t)\), \({e_2}(t)\) and \({e_3}(t)\) are convergent. Furthermore, the observation performance of the proposed FODO (13) and (14) is presented in Fig. 4. It is evident in Fig. 4 that the observer is effective and feasible. According to the simulation results, the drive system (45) and the response system (49) are bounded synchronization under the designed sliding mode controller (26) and the adaptive update law (27). Therefore, the proposed nonlinear FODO-based adaptive sliding mode synchronization control scheme is valid for fractional-order chaotic systems with external disturbance.

6 Conclusion

In this paper, the nonlinear FODO-based adaptive sliding mode synchronization control scheme has been studied for fractional-order chaotic systems in the presence of external disturbance. A nonlinear FODO has been developed to approximate the unknown disturbances. A sliding mode synchronization controller has been designed based on the nonlinear FODO for synchronization of fractional-order chaotic systems. Furthermore, an example is given in the present paper, i.e., the synchronization between two modified fractional-order Jerk systems. The numerical simulations show the effectiveness of the proposed nonlinear FODO-based adaptive sliding mode synchronization control scheme.