1 Introduction

Nowadays, information security is becoming an increasingly important topic due to the rapid progress of communication network and information technology [1], especially the security of images. Actually, images from various sources for various applications are required to be confidential between the transmitter and the receiver, such as medical imaging systems, architectural drawings, military image databases, and so on. Due to some intrinsic features of images, such as high correlation among adjacent pixels, bulk volume of data, real-time requirement and high redundancy, traditional encryption algorithms, such as the Advanced Encryption Standard AES [2], may not be the most desired applicants for secure image transmission. Since chaos has the properties of unpredictability, high sensitive dependence on initial conditions and parameters, ergodicity, quasi-randomness, etc., secure image transmission based on chaotic system attracts more and more researchers’s attentions. Effectively, new encryption schemes are presented in [3,4,5,6,7,8,9,10]. In [3] the scheme is based on PWLCM chaotic system. In [4], a new scheme based on the combination of chaos cellular automata and weighed histogram is presented. A coding and substitution frame for encryption based on hyperchaotic systems is introduced in [5]. In [6,7,8], the authors propose encryption algorithms using complex chaotic systems. A new transmission scheme based on chaotic system and SPIHT technique is proposed in [9, 10].

The pioneering work of Pecora and Carrol [11] has aroused great interest as a potential means for secure communications. Accordingly, several cryptosystems based on chaos synchronization have been proposed [12, 13]. In these cryptosystems, one will encrypt the original information by the pseudorandom signal. This latter is generated using a master chaotic oscillator (transmitter). Subsequently, one will transmit the unintelligible information, which is the combination of a variable of the chaotic transmitter with the original information, through the communication channel. The exact synchronization of the master (transmitter) and the slave (receiver) allows the recovery of the original information. In another instance, the synchronization may be regarded as a special case of state observer design problem [14]. In [15], the transmitter is a chaotic oscillator in which the original information is introduced in its dynamic. The receiver is an observer, where not only the states are estimated but also the transmitted information which is considered as an unknown input.

Chaos theory and applications of continuous fractional-order system are becoming a great research topic [16]. Despite this, discrete-time fractional-order chaotic system theory and applications are not well documented in the literature. Indeed, it is well known that fractional-order difference equation is a new field and the only works devoted to this topic concern the linear case [17, 18]. Because of several advantages of discrete-time systems, various studies have been consecrated to this category of systems. Effectively, it is frequently desirable to derive discrete models which represent the dynamics of systems, which are often in continuous time. This is mainly due to the measurements, which are usually, in practice, carried out at specific time intervals. More importantly, digital simulations can be performed easily and quickly, which improve the speed of encryption.

Recently, fractional-order calculus have received considerable interest and have found many applications in recent studies in various fields [19, 20]. With the development of this discipline, the attention was paid to the study of chaotic behavior for fractional-order systems [21,22,23,24,25]. Indeed, due to the complex geometric interpretation of the nonlocal effects of fractional derivatives in space or time [26], fractional-order chaotic systems exhibit higher nonlinearity and degrees of freedom and have more complex random sequences compared to integer-order chaotic systems. These advantages attract the attention of researchers to the application of fractional-order chaotic system in secure communication [27,28,29,30,31]. Effectively, the interest of using the fractional-order chaotic systems in secure transmission is to improve the security by adding the fractional-orders derivative as new parameters to the security key. The identification of the added parameters is very difficult and more complex, which makes the cryptosystem based on fractional-order chaotic systems advantageous and distinctive compared to the integer order ones. But the research of secure image transmission based on fractional-order chaotic systems is very few and it is a great valuable research topic [32,33,34,35].

In the present work, we propose a novel secure image transmission scheme based on fractional-order modified-Hénon system and we focus on the synchronization of this system via a delayed observer. The proposed scheme is composed of a transmitter and a receiver. At the transmitter level, an encryption function is used to encrypt an original image. Then, the ciphered image is introduced by the inclusion method in the dynamics of the fractional-order modified-Hénon system in order to increase the robustness of the proposed scheme against hacker’s attacks. At the receiver level, a delayed observer with the aim of recovering the original image is developed. The performance of the proposed transmission scheme is highlighted by the fact that a sole transmission channel is used for the synchronization. Two main theoretical contributions of our work are presented. Firstly, observability and observability matching condition of nonlinear discrete-time fractional-order systems are studied. Secondly, a dead beat observer for this class of systems is developed. The finite-time convergence is the main advantage of this observer. In practical case, a new secure image transmission scheme is proposed. Different analysis have been done to demonstrate the highly robustness of the presented method, which confirms the security and the good feature of the proposed scheme.

The remaining of the paper is organized as follows. In Sect. 2, some preliminaries and definitions of nonlinear discrete-time fractional-order systems are recalled. In Sect. 3, some results on the observability and on discrete observability matching condition of this class of systems are established. In Sect. 4, the proposed transmission scheme is presented. In Sect. 5, the simulation results illustrating the synchronization and the reconstruction of the transmitted image and the security analysis are provided. Finally, some concluding remarks and some perspectives to improve the proposed scheme are given.

2 Preliminaries

In this section, some definitions on the fractional-order discrete-time systems are given. In [36], the \(\alpha \) order difference operation was specified using Grunwald-Letnikov definition as follows:

$$\begin{aligned} {\varDelta }^{\alpha }x(k)=\frac{1}{h^{\alpha }}\sum \limits _{j=0}^k (-1)^j \left( \begin{array}{l} \alpha \\ j \end{array}\right) x(k-j) \end{aligned}$$
(1)

where the fractional order \(\alpha \in {\mathbb {R}}^{*+}\), i.e., the set of strictly positive real numbers, \(h\in {\mathbb {R}}^{*+}\) is a sampling period taken equal to unity in all what follows, and \(k\in {\mathbb {N}}\) represents the discrete time. We define

$$\begin{aligned} \left( \begin{array}{l} \alpha \\ j \end{array}\right) = \left\{ \begin{array}{ll} 1 &{} \text {for } j=0\\ \frac{\alpha (\alpha -1)\cdots (\alpha -j+1)}{j!} &{} \text {for }j>0 \end{array} \right. \end{aligned}$$
(2)

Let us consider now the discrete-time state-space model of integer order, i.e., when \(\alpha \) is equal to unity:

$$\begin{aligned} x(k+1) = f(x(k))+g(x(k))u(k) \end{aligned}$$
(3)

where \(x(k)\in {\mathbb {R}}^n\) is the n-dimensional state vector and \(u(k)\in {\mathbb {R}}\) is the input control, f(x) and g(x) are smooth vector fields for \(x\in {\mathbb {R}}^n\). The state vector is written as

$$\begin{aligned} x(k)=[x_1(k)\, x_2(k) \ldots x_n(k)]^T \end{aligned}$$

The first-order difference for \(x(k+1)\) is defined as

$$\begin{aligned} {\varDelta }^1x(k+1)=x(k+1)-x(k) \end{aligned}$$

Therefore, using (3), we deduce that

$$\begin{aligned} {\varDelta }^1x(k+1)=f(x(k))+g(x(k))u(k)-x(k) \end{aligned}$$
(4)

The \(\alpha \)-order difference is indicated in the same way that the first-order difference as follows

$$\begin{aligned} {\varDelta }^{\alpha }x(k+1)=f(x(k))+g(x(k))u(k)-x(k) \end{aligned}$$
(5)

Noting the \(\alpha \) order difference (1), we obtain

$$\begin{aligned} {\varDelta }^{\alpha }x(k+1)=x(k+1)+\sum _{j=1}^{k+1}(-1)^{j} \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) x(k+1-j) \end{aligned}$$
(6)

Equation (6) can be rewritten as

$$\begin{aligned} {\varDelta }^{\alpha }x(k+1)= & {} x(k+1)-\alpha x(k) \nonumber \\&+\sum _{j=2}^{k+1}(-1)^{j} \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) x(k+1-j) \end{aligned}$$
(7)

Substituting (7) into (5), we obtain

$$\begin{aligned} x(k+1)=&f(x(k))+g(x(k))u(k)+(\alpha -1)x(k) \nonumber \\&-\sum \limits _{j=2}^{k+1}(-1)^j\left( {\begin{array}{c}\alpha \\ j\end{array}}\right) x(k-j+1) \end{aligned}$$
(8)

Introducing the new variables \(C_p= (-1)^{p+1}\left( {\begin{array}{c}\alpha \\ p+1\end{array}}\right) \) and \(p=j-1\), it follows that

$$\begin{aligned} x(k+1)=&f(x(k))+g(x(k))u(k)+(\alpha -1)x(k) \nonumber \\&-\sum \limits _{p=1}^k C_p x(k-p) \end{aligned}$$
(9)

In this model, the differentiation order \(\alpha \) is taken the same for all the state variables \(x_i(k)\), \(i=1,\ldots , n\), this is referred to as a commensurate order. But in general, the differentiation order may be different for each state \(x_i\), then the system is called of incommensurate order.

We can state that System (9) presents an infinite long memory property, and we can easily verify that the coefficient \(C_p\) decreases as the iteration p increases. Then, it is reasonable to truncate the memory for practical use and for computation process. Therefore, the short memory principle can be used to specify a more exploitable fractional-order nonlinear system.

The limited length of memory is denoted by L. Then, System 9 can be rewritten as follows

$$\begin{aligned} x(k+1)=&f(x(k))+g(x(k))u(k)+(\alpha -1)x(k) \nonumber \\&-\sum \limits _{p=1}^L C_p x(k-p) \end{aligned}$$
(10)

Remark 1

The model described by (10) can be classified as a discrete-time system with a time-delay in the state, such as the system (10) has a varying number of steps of time-delays, equal to L.

3 Observability and observability matching condition of nonlinear discrete-time fractional-order systems

In this section, the observability and observability matching condition features for nonlinear discrete-time fractional-order systems are introduced.

3.1 Observability

In this part, we study the observability properties of nonlinear discrete-time fractional-order systems. Firstly, we give some definitions on the observability of nonlinear discrete-time systems. Then, we aim at extending this concept to the fractional-order systems.

Let us consider System (3) as before, but now together with an output map.

$$\begin{aligned} \left\{ \begin{array}{l} x(k+1)=f(x(k)) +g(x(k))u(k)\\ y(k)=h(x(k)) \end{array}\right. \end{aligned}$$
(11)

where \(y(k)\in {\mathbb {R}}\) is the output vector, \(h(x):{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is the output map of the system.

In [37], some definitions of the notion of observability for this class of systems are found.

Definition 1

Indistinguishability

Two states \(x^{1}, x^{2}\in {\mathbb {R}}^n\), are said to be indistinquishable (denoted \(x^{1}Ix^{2}\)) for (11) if, for every admissible input function u, the output function \(h(x^{1}(k))\), \(k\ge 0\), of the system for initial state \(x^{1}(0)=x_0^{1}\), and the output function \(h(x^{2}(k)), k\ge 0\), of the system for initial state \(x^{2}(0)=x_0^{2}\), such that \(x_0^{2}\ne x_0^{1}\), are identical on their common domain of definition.

Definition 2

A state \(x^{0}\) is said to be observable, if, for each \(x^{1}\in {\mathbb {R}}^n\), \(x^{0}Ix^{1}\) implies \(x^{0}=x^{1}\).

Definition 3

A state \(x^{0}\) is said to be locally observable, if there exists a neighborhood \(W_{x^{0}}\) of \(x^{0}\), such that, for each \(x^{1}\in W_{x^{0}}\), \(x^{0}Ix^{1}\) implies \(x^{0}=x^{1}\).

Definition 4

A system (11) is (locally) observable, if each state \(x\in {\mathbb {R}}^n\) enjoys this property.

The observation space will prove to be essential for local observability.

Definition 5

Consider the nonlinear system (11). The observation space O of (11) is the linear space of functions on \({\mathbb {R}}^n\) given as follows.

$$\begin{aligned} O = [h, h\circ f, \ldots , h\circ f^{(n-1)}]^T \end{aligned}$$
(12)

where “\(\circ \)” denotes the usual composition function, “\(\circ {f^{(j)}}\)” denotes the function f composed j times.

The observability codistribution, denoted as \(\mathrm{d}O\), is defined by the observability space O as follows

$$\begin{aligned} \mathrm{d}O=\text {span } \{\mathrm{d} h, \mathrm{d} h\circ f, \ldots , \mathrm{d} h\circ f^{(n-1)}\} \end{aligned}$$
(13)

Theorem 1

Consider the system (11). Assume that

$$\begin{aligned} \text {dim}\; \mathrm{d}O = n \end{aligned}$$
(14)

then the system is locally observable.

Now, let us consider the fractional-order discrete-time system defined as follows

$$\begin{aligned} \left\{ \begin{array}{l} x(k+1)=f(x(k))+g(x(k))u(k)+(\alpha -1)x(k)\\ \qquad \qquad \qquad -\sum \limits _{p=1}^L C_{p} x(k-p) \\ y(k)=h(x(k)) \end{array}\right. \end{aligned}$$
(15)

As mentioned in Remark 1, the system (15) can be classified as a discrete-time system with time-delay in the state. To study the observability of this system, we consider the augmented system obtained from the following change of coordinates

$$\begin{aligned} \left\{ \begin{array}{l} Z_1(k)=x(k)\\ Z_2(k)=x(k-1)\\ \vdots \\ Z_{L+1}(k)=x(k-L)\\ \end{array}\right. \end{aligned}$$
(16)

where \(Z_1,Z_2,\ldots ,Z_{L+1} \in {\mathbb {R}}^n\). Then, we obtain the augmented system in the new coordinates presented as follows

$$\begin{aligned} \left\{ \begin{array}{l} Z_1(k+1)=f(Z_1(k))+g(Z_1(k))u(k)\\ \qquad \qquad +(\alpha -1)Z_1(k)-\sum \limits _{p=1}^L C_{p} Z_{p+1}(k)\\ Z_2(k+1)=Z_1(k)\\ \vdots \\ Z_j(k+1)=Z_{j-1}(k)\\ \vdots \\ Z_{_{L+1}}(k+1)=Z_{L}(k)\\ y(k)=h(Z_1(k)) \end{array}\right. \end{aligned}$$
(17)

where \(j=2,\ldots , L+1\).

The system (17) can be rewritten as follows

$$\begin{aligned} \left\{ \begin{array}{l} Z(k+1)=F(Z(k))+G(Z(k)) u(k)\\ y(k)=H(Z(k)) \end{array}\right. \end{aligned}$$
(18)

where \(Z(k)=[Z_1, Z_2, \ldots , Z_{L+1}]\in {\mathbb {R}}^{n'}\) is the new state vector and \(n'=n(L+1)\).

Proposition 1

The observation space \(O'\) of (15) is also given as the linear space of functions on \({\mathbb {R}}^{n'}\) given as follows.

$$\begin{aligned} O' = [H, H\circ F, \ldots , H\circ F^{(n'-1)}]^T \end{aligned}$$
(19)

with F is the vector field of the augmented system (18) and H is the output function.

In this case, the observability codistribution is given as follows

$$\begin{aligned} \mathrm{d}O'=\text {span } \{\mathrm{d}H, \mathrm{d} H\circ F, \ldots , \mathrm{d} H\circ F^{(n'-1)}\} \end{aligned}$$
(20)

The main theorem concerning local observability reads as follows

Theorem 2

The nonlinear discrete-time fractional-order system modeled by (18) is locally observable if and only if

$$\begin{aligned} \text {dim}\; \mathrm{d}O'=n' \end{aligned}$$
(21)

Proof

Assume \(\text {dim}\; \mathrm{d}O'=n'\). Then, there exist \(n'\) functions \({\varGamma }_i(.)={\varGamma }_1, \ldots , {\varGamma }_{n'}\in O\), where \({\varGamma }_1=H, {\varGamma }_2=H\circ F, \ldots , {\varGamma }_{n'}=H\circ F^{(n'-1)}\), whose differentials are linear independent at \(Z^{0}\). By continuity, they remain independent in a neighborhood \(W_{Z^{0}}\) of \(Z^{0}\). Therefore, \({\varGamma }_i(.)\) define a smooth mapping from \({\mathbb {R}}^{n'}\) to \({\mathbb {R}}\), which, restricted to \(W_{Z^{0}}\), is injective. Let \(Z^{1}\in W_{Z^{0}}\), if \(Z^{1}IZ^{0}\), in particular, for all \(i=1,\ldots , n'\), it must hold \({\varGamma }_i(Z^{0})={\varGamma }_i(Z^{1})\). By the injectivity of \({\varGamma }_i(.)\), \(i=1,\ldots ,n'\), it follows that \(Z^{0}=Z^{1}\). Thus \(Z^{0}\) is a locally observable state. \(\square \)

3.2 Observability matching condition

In this part, we start by presenting the property of observability matching condition of discrete-time nonlinear systems. Then, we propose a new theorem for the fractional-order discrete-time nonlinear systems. To this end, let us consider the nonlinear analytic system given by Eq. (11). The observability matching condition of System (11) is defined as given in [39] by the following definition.

Definition 6

The observability matching condition is:

$$\begin{aligned} \left( (\mathrm{d} h)\; (\mathrm{d} h\circ f)\;\cdots (\mathrm{d} h\circ f^{(n-1)})\right) ^T g=(0 \ldots 0 \; *)^T \end{aligned}$$
(22)

where “*” means a non-null term almost everywhere in the neighborhood of \(x=0\).

To study the observability matching condition of the fractional-order discrete-time system defined by (15), the following theorem is given.

Theorem 3

The observability matching condition of nonlinear fractional-order discrete-time systems modeled by (15) is

$$\begin{aligned} \left( (\mathrm{d} h)\; (\mathrm{d} h\circ {\tilde{f}})\;\cdots (\mathrm{d} h\circ {\tilde{f}}^{(n-1)})\right) ^T g=(0 \ldots 0 \; *)^T \end{aligned}$$
(23)

where \({\tilde{f}}=f(x(k))+(\alpha -1) x(k)+\beta (x)\). and \(\beta (x(k))\in {\mathbb {R}}^n\) is the \(n-\)dimensional vector of linear functions with respect to the delayed state \(x(k-j)\), with \(j=1\ldots ,L\) given by

$$\begin{aligned} \beta (x(k))=[\beta _1(x_1(k)),\beta _2(x_2(k)),\cdots ,\beta _n(x_n(k))]^T \end{aligned}$$

with \(\beta _i(x_i(k))=-\sum \nolimits _{j=1}^L C_{ij} x_i(k-j)\) with \(i=1,\ldots ,n\), and \(C_{ij}= (-1)^{j+1} \left( {\begin{array}{c}\alpha _i\\ j+1\end{array}}\right) \).

Proof

Let us consider the system (15) which can be presented as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x(k+1)=f(x(k))+g(x(k))u(k)\\ \qquad \qquad +(\alpha -1) x(k) +\beta (x(k))\\ y(k)=h(x(k)) \end{array}\right. \end{aligned}$$
(24)

Define the derivative of \(\beta _i(x_i)\) with respect to \(x_i\) as \(\dfrac{\mathrm{d}\beta _i(x_i)}{d x_i}\). As mentioned above, the function \(\beta _i(x_i)\) is linear with respect to \(x_i(k-j)\) and coefficients \(C_{ij}\) are constants, then we obtain

$$\begin{aligned} \dfrac{\mathrm{d}\beta _i(x_i)}{d x_i}=-\sum \limits _{j=1}^L C_{ij} \end{aligned}$$
(25)

System (24) may be rewritten in the following form:

$$\begin{aligned} \left\{ \begin{array}{l} x(k+1)={\tilde{f}}(x(k))+g(x(k)) u(k)\\ y(k)=h(x(k)) \end{array}\right. \end{aligned}$$
(26)

Then, applying Definition 6 completes the proof. \(\square \)

The observability and the observability matching condition of System (15) guarantee the left invertibility property, i.e., the possibility of recovering all the states and the input u from the output y(k) and its iterations.

4 Proposed secure image transmission scheme

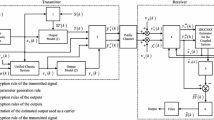
Based on the fractional-order modified-Hénon system, we propose a secure image transmission scheme. The synoptic block diagram of the proposed scheme is shown by Fig. 1 which is composed mainly of a transmitter and a receiver. In what follows, the developed method is presented.

Fig. 1
figure 1

Global scheme of the proposed secured transmission system

Full size image

4.1 Description of the fractional-order modified-Hénon system

In this subsection, we present the discrete-time hyperchaotic system which consists on fractional-order modified-Hénon system. Firstly, we consider the discrete-time modified-Hénon’s map given by a simplified version as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x_1(k+1)=a-x_2^{2}(k)-b x_3(k)\\ x_2(k+1)=x_1(k) \\ x_3(k+1)=x_2(k) \\ y(k)=x_2(k) \end{array} \right. \end{aligned}$$
(27)

where \(x=[x_1\; x_2 \; x_3]^{T}\in {\mathbb {R}}^{3}\) denotes the state vector and \(y(k)\in {\mathbb {R}}\) is the output.

Using Eq. (10), a corresponding fractional-order discrete-time modified-Hénon system of (27) is expressed by:

$$\begin{aligned} \left\{ \begin{array}{l} x_1(k+1)=a-x_2^{2}(k)-b x_3(k)+(\alpha _1-1) x_1(k)\\ \qquad +\beta _1 (x_1(k))\\ x_2(k+1)=x_1(k)+(\alpha _2-1) x_2(k)+\beta _2 (x_2(k))\\ x_3(k+1)=x_2(k)+(\alpha _3-1) x_3(k)+\beta _3 (x_3(k))\\ y(k)=x_2(k) \end{array} \right. \end{aligned}$$
(28)

where \(\beta _{1}=-\sum \nolimits _{j=1}^{L} C_{1j} x_1(k-j)\);\(\beta _{2}=-\sum \nolimits _{j=1}^{L} C_{2j} x_2(k-j)\); \(\beta _{3}=-\sum \nolimits _{j=1}^{L} C_{3j} x_3(k-j)\) and \(0<\alpha _1\le 1\), \(0<\alpha _2\le 1\), \(0<\alpha _3\le 1\) are the fractional orders.

Fig. 2
figure 2

Lyaponuv exponents of the fractional-order modified-Hénon system for \(L=1\)

Full size image
Fig. 3
figure 3

Phase portrait of the states \(x_1(k)-x_3(k)\) of the fractional-order modified-Hénon system

Full size image

Remark 2

Note that if we set \(\alpha _i=1\), for \(i=1,\ldots ,3\) in (28), by the fact that all \(C_{ij}\) vanish for \(\alpha _i=1\), we obtain the integer-order modified-Hénon system (27).

Actually, System (28) exhibits hyperchaotic behavior for \(\alpha _1=0.97\), \(\alpha _2=0.94\), \(\alpha _3=0.91\), \(a=1.68\), \(b=0.1\). Initial conditions \(x_1(0)=0.2\), \(x_2(0)=0.5\) and \(x_3(0)=0.1\) are chosen interior the strange attractor basin. In fact, the computation of the Lyapunov exponents establishes presence of hyperchaos since two positive exponents are found. In this paper, Lyapunov exponents of fractional-order discrete-time systems are calculated by adapting the Wolf et al. algorithm [38] with some changes. In order to simplify the calculation, we choose the size of memory \(L=1\), and the corresponding augmented system will present 6 Lyapunov exponents. In Fig. 2, the Lyapunov exponents of System (28) are shown, where two exponents are positive \((\lambda _1=0.168, \mathrm {and}, \lambda _2=0.139)\), which proves the hyperchaotic behavior of the system.

The chaotic behavior of System (28)is illustrated by the simulation results given bellow. Figure 3 presents the phase portrait in the plane \((x_1, x_3)\). Figures 4 and 5, respectively, illustrate the sensitivity of System (28) to small changes of orders \(\alpha _1\) and a. The bifurcation diagram, obtained by varying the parameter a of the fractional-order modified-Hénon system, is given by Fig. 6. We can see, from this diagram, that System (28) presents a chaotic behavior when \(a\in [1.3, 1.7]\).

Fig. 4
figure 4

State \(x_1(k)\) of the fractional-order modified-Hénon system for small changes \(10^{-15}\) of parameter \(\alpha _1\)

Full size image
Fig. 5
figure 5

State \(x_2(k)\) of the fractional-order modified-Hénon system for small changes \(10^{-15}\) of parameter a

Full size image
Fig. 6
figure 6

Bifurcation diagram of \(x_3\) with \(a\in [0, 1.7]\)

Full size image

4.2 Description of the transmitter

In the sender, fractional-order modified-Hénon System (28) generates chaotic signals \(x_1, x_2, x_3\). Then, we encrypt the original image with generated pseudorandom sequences in order to obtain ciphered image. The encryption function used in this work is the XOR operation. The choice of this operation is justified by the simple and useful way of encrypting and decrypting the information. To further improve the security and robustness of the transmission scheme, the encrypted image (the output of the XOR operation) is inserted by inclusion method in the same chaotic system dynamics.

The complete procedure of the encryption algorithm of the proposed scheme can be described as following:

Step 1 We represent the original image by matrix \(A_{M\times N}\) (where M and N are the row and column of the image). Then, we form a decimal set \(A=\{A_1,A_2,\ldots ,A_{M\times N}\}\) by arranging the pixels by order from left to right and from top to bottom. This set is transformed on a binary set,

$$\begin{aligned} B(k)=de2bi(A(k))=\{B_1,B_2,\ldots ,B_{M\times N\times 8}\} \end{aligned}$$

where de2bi converts decimal numbers to binary vectors.

Step 2 We consider that System (28) is perfectly synchronized after \(N_c\) number of iterations. Then, we iterate the system for \(N_f=M\times N\times 8\) after \(N_c\) values and that to void the transient effects, so we obtain a chaotic decimal sequences \(\{x_1(k), x_3(k)\}\). These sequences are preprocessed as follows:

$$\begin{aligned} C(k)= & {} c x_1^2(k) + d (x_1(k)+x_3(k)) + e x_3^2(k)\\ D(k)= & {} \text {mod}(abs(f C(k))-abs(g C(k))\times 10^{12},255)\\ K(k)= & {} de2bi(\text {round}(D(k))) \end{aligned}$$

where c, d, e, f, g and h are the new secret keys and \(\text {mod}(x; y)\) returns the remainder after division x / y, \(\text {round}(x)\) rounds the elements of x to the nearest integers, abs(x) returns the absolute value of x.

Step 3 We encrypt the original image using XOR function, presented by the symbol \( \oplus \). The cipher sequence \(m_c(k)\) is obtained as follows:

$$\begin{aligned} m_c(k)=B(k) \oplus K(k) \end{aligned}$$
(29)

Step 4 The cipher sequence \(m_c(k)\) to send is introduced in the third component of System (28) as an input. Then, we obtain:

$$\begin{aligned} \left\{ \begin{array}{l} x_1(k+1)=a-x_2^{2}(k)-b x_3(k)+(\alpha _1-1)x_1(k)+\beta _{1}(x_1(k)) \\ x_2(k+1)=x_1(k)+(\alpha _2-1)x_2(k)+\beta _{2}(x_2(k)) \\ x_3(k+1)=x_2(k)+(\alpha _3-1)x_3(k)+\beta _{3}(x_3(k))+m_c(k) \\ y(k)=x_2(k) \end{array} \right. \end{aligned}$$
(30)

In our application, the input \(u(k)=m_c(k)\) and the vector \(g(x(k))=[0\quad 0\quad 1]^T\).

Step 5 The state variable \(x_2\) considered as the system output is transmitted to the receiver.

4.3 Description of the receiver

In this subsection, based on the works [40,41,42,43], a step-by-step delayed observer is designed and used to resolve the synchronization problem, and to allow the reconstruction of the states and the unknown input (message). Firstly, we will verify the observability and the observability matching condition of the proposed fractional-order discrete-time system. Then, the step-by-step delayed observer is designed.

4.3.1 Study of the step-by-step delayed observer design

In this part, we will study the observability and the observability matching condition of System (30).

4.3.2 a. Observability of the system

To study the observability of System (30), one can use the change of coordinates given by (16) and obtains the corresponding augmented system. In order to simplify the equations of this System, we choose \(L=2\). The initial system is given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} x_1(k+1)=\;a-x_2^{2}(k)-\;b\; x_3(k)+(\alpha _1-1)\;x_1(k)\\ \qquad -C_{11}x_1(k-1)-C_{12}x_1(k-2)\\ x_2(k+1)=x_1(k)+(\alpha _2-1)x_2(k)-C_{21}x_2(k-1)\\ \qquad -C_{22}x_2(k-2)\\ x_3(k+1)=x_2(k)+(\alpha _3-1)x_3(k)-C_{31}x_3(k-1)\\ \qquad -C_{32}x_3(k-2)+m_c(k)\\ y(k)=x_2(k) \end{array}\right. \end{aligned}$$
(31)

After the change of coordinates presented before, we give the augmented system of System (31) as follows

$$\begin{aligned} \left\{ \begin{array}{l} z_1(k+1)=a-z_2^{2}(k)-b x_3(k)+(\alpha _1-1)z_1(k)\\ \qquad -C_{11}z_4(k)-C_{12}z_7(k) \\ z_2(k+1)=z_1(k)+(\alpha _2-1)z_2(k)-C_{21}z_5(k)\\ \qquad -C_{22}z_8(k) \\ z_3(k+1)=z_2(k)+(\alpha _3-1)z_3(k)-C_{31}z_6(k)\\ \qquad -C_{32}z_9(k)+m_c(k) \\ z_4(k+1)=z_1(k)\\ z_5(k+1)=z_2(k)\\ z_6(k+1)=z_3(k)\\ z_7(k+1)=z_4(k)\\ z_8(k+1)=z_5(k)\\ z_9(k+1)=z_6(k)\\ Y(k)=z_2(k) \end{array} \right. \end{aligned}$$
(32)

Using Theorem 2, we find that

$$\begin{aligned} \text {dim} (\mathrm{d}H, \mathrm{d}H\circ F, \ldots , \mathrm{d}H\circ F^{(8)})^T=9 \end{aligned}$$
(33)

We can deduce that System (32) is observable, which means that all states may be reconstructed. This result motivates the good choice of the output \(y(k)=x_2(k)\).

4.3.3 b. Observability matching condition of the system

In this part, we check the observability matching condition of System (30). In our application, one can see from the system that the information is inserted in the third component of the system. Then, we have

$$\begin{aligned} g = \left( \begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right) \end{aligned}$$

Let us calculate \([\mathrm{d} h \quad \mathrm{d}h\circ {\tilde{f}}\quad \mathrm{d} h\circ {\tilde{f}}^{(2)}]^T \)

Knowing that \(h(x)=x_2\), we clearly obtain \(\mathrm{d} h=[0\quad 1\quad 0]\).

Now, we calculate \(h\circ {\tilde{f}}\)

$$\begin{aligned} h\circ {\tilde{f}}&= x_2(k+1)\nonumber \\&=x_1(k)+(\alpha _2-1)x_2(k)-C_{21}x_2(k-1)\nonumber \\&\quad -C_{22}x_2(k-2) \end{aligned}$$
(34)

we obtain \(\mathrm{d} h\circ {\tilde{f}}=[1 \quad \gamma _1 \quad 0]\)

Then, we calculate \(h\circ {\tilde{f}}^{(2)}\)

$$\begin{aligned} h\circ {\tilde{f}}^{(2)}= & {} x_1(k+1)+(\alpha _2-1) x_2(k+1)-C_{21}x_2(k) \nonumber \\&-C_{22}x_2(k-1) \nonumber \\= & {} a-x_2^2(k)-bx_3(k)+(\alpha _1-1)x_1(k) \nonumber \\&-C_{11}x_1(k-1) -C_{12}x_1(k-2) \nonumber \\&+(\alpha _2-1)[x_1(k)+(\alpha _2-1)x_2(k) \nonumber \\&-C_{21}x_2(k-1)-C_{22}x_2(k-2)] \nonumber \\&-C_{21}x_2(k)-C_{22}x_2(k-1) \end{aligned}$$
(35)

we obtain \(\mathrm{d} h\circ {\tilde{f}}^{(2)}=[1 \quad \gamma _2 \quad \gamma _3]\)

where: \( \left\{ \begin{array}{l} \gamma _1=(\alpha _2-1)-C_{21}-C_{22} \\ \gamma _2=\alpha _1+\alpha _2-2-C_{11}-C_{12}\\ \gamma _3=(\alpha _2-1)^2-2x_2-(\alpha _2-1)(-C_{21}-C_{22})\\ \qquad -C_{21}-C_{22}\\ \end{array}\right. \)

Using Eq. (23), given by Theorem 3, we obtain

$$\begin{aligned} \left( \begin{array}{l} \mathrm{d} h\\ \mathrm{d}h\circ {\tilde{f}}\\ \mathrm{d} h\circ {\tilde{f}}^{(2)} \end{array}\right) g&= \left( \begin{array}{lll} 0&{}1&{}0 \\ 1 &{} \gamma _1 &{}0 \\ \gamma _2 &{} \gamma _3 &{} -b \end{array}\right) \left( \begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right) \nonumber \\&= \left( \begin{array}{l} 0 \\ 0 \\ -b \end{array}\right) \end{aligned}$$
(36)

we know that \(b\ne 0\), which implies that the observability matching condition is satisfied. Then, the choice of the vector g(x) is justified.

Remark 3

The matching condition of our system is satisfied even if the size of memory L becomes higher.

4.3.4 Step-by-step delayed observer

To show that an observable system is always constructible, i.e., a step-by-step delayed observer can be designed, we give the proposition as presented below.

Proposition 2

Let the nonlinear discrete-time fractional-order chaotic system (30) with unknown input be locally observable and satisfying the observability matching condition. Then, the system is constructible, i.e., there exists a map \(\varphi :{\mathbb {R}} \rightarrow {\mathbb {R}}^3\) such that the state x(k) of the system can be exactly reconstructed in terms of the output and finite string of obtained outputs, in the form:

$$\begin{aligned} xo_2(k)= & {} \varphi _2(y(k)) \\= & {} y(k) \end{aligned}$$
$$\begin{aligned} xo_1(k-1)= & {} \varphi _1(y(k),y(k-1)) \nonumber \\= & {} y(k){-}(\alpha _2-1)y(k-1) {-}\beta _2 (y(k-1)) \nonumber \\ xo_3(k-2)= & {} \varphi _3(y(k),y(k-1),y(k-2)) \nonumber \\= & {} \dfrac{1}{b}(a-y^2(k-2) +(\alpha _1-1) (y(k-1) \nonumber \\&-(\alpha _2-1)y(k-2) -\beta _2(y(k-2))) \nonumber \\&-y(k)+\beta _1(\varphi _1(y(k-1),y(k-2))) \nonumber \\&+ (\alpha _2-1)y(k-1)+ \beta _2(y(k-1)))\nonumber \\ \end{aligned}$$
(37)

where \(\varphi =[\varphi _1, \varphi _2, \varphi _3]^T\).

Moreover, there exists a map \(\psi :{\mathbb {R}}^3 \rightarrow {\mathbb {R}}\) such that the unknown input \(mo_c(k)\) of the system can be exactly reconstructed in terms of the obtained estimated states in the form:

$$\begin{aligned} mo_c(k-3)= & {} \psi (xo_1,xo_2,xo_3) \nonumber \\= & {} xo_3(k-2)-xo_2(k-3) \nonumber \\&-(\alpha _3-1)xo_3(k-3) \nonumber \\&+\beta _3(xo_3(k-3)) \end{aligned}$$
(38)

Proof

Rewrite System (30) as follows

$$\begin{aligned} x_1(k+1)= & {} f_1(x_1(k),x_2(k),x_3(k)) \\ x_2(k+1)= & {} f_2(x_1(k),x_2(k)) \\ x_3(k+1)= & {} f_3(x_2(k),x_3(k))+m_c(k) \end{aligned}$$
$$\begin{aligned} y(k)=x_2(k) \end{aligned}$$
(39)

It is clear that the estimated state \(xo_2\) can be expressed as follows

$$\begin{aligned} xo_2(k)= & {} y(k) \nonumber \\= & {} \varphi _2(y(k)) \end{aligned}$$
(40)

If we take one delay to the second expression of System (39), we obtain

$$\begin{aligned} xo_2(k)= & {} f_2(xo_1(k-1),xo_2(k-1)) \nonumber \\= & {} xo_1(k-1)+(\alpha _2-1)xo_2(k-1) \nonumber \\&+\beta _2(xo_2(k-1)) \end{aligned}$$
(41)

where \(\beta _2(xo_2(k-1))=\sum _{j=1}^{L}C_{2j}xo_{2}(k-j-1)\).

Then, from Eq. (41), we can deduce \(xo_1(k-1)\) as follows

$$\begin{aligned} xo_1(k-1)= & {} y(k)-(\alpha _2-1)y(k-1) -\beta _2 (y(k-1)) \nonumber \\= & {} \varphi _1(y(k),y(k-1)) \end{aligned}$$
(42)

If we take two delays to the first expression of System (39), we obtain

$$\begin{aligned} xo_1(k-1)= & {} f_1(xo_1(k-2),xo_2(k-2),xo_3(k-2)) \nonumber \\= & {} a-xo_2^2(k-2)-b xo_3(k-2)+(\alpha _1-1) \nonumber \\&xo_1(k-2)+ \beta _1(xo_1(k-2)) \end{aligned}$$
(43)

where \(\beta _1(xo_1(k-2))=\sum _{j=1}^{L}C_{1j}xo_{1}(k-j-2)\).

Then, from Eq. (43), we can deduce \(xo_3(k-2)\) as follows

$$\begin{aligned} xo_3(k-2)= & {} \dfrac{1}{b}[a-y^2(k-2)+(\alpha _1-1)(y(k-1) \nonumber \\&-\,(\alpha _2-1)y(k-2)-\beta _2(y(k-2)))-y(k) \nonumber \\&+\,\beta _1(xo_1(k-2))+(\alpha _2-1)y(k-1) \nonumber \\&+\,\beta _2(y(k-1))] \nonumber \\= & {} \varphi _3(y(k),y(k-1),y(k-2)) \end{aligned}$$
(44)

If we take three delays to the third expression of System (39), we find

$$\begin{aligned} xo_3(k-2)= & {} f_3(x_2(k-3),x_3(k-3))+m_c(k-3) \nonumber \\= & {} xo_2(k-3)+(\alpha _3-1)xo_3(k-3) \nonumber \\&+\,\beta _3(xo_3(k-3))+mo_c(k-3) \end{aligned}$$
(45)

where \(\beta _3(xo_3(k-3))=\sum _{j=1}^{L}C_{3j}xo_{3}(k-j-3)\).

Using the estimated states \(xo_1,xo_2,xo_3\) and from the Eq. (45), the estimated input is obtained as follows

$$\begin{aligned} mo_c(k-3)= & {} xo_{3}(k-2)-xo_2(k-3) \nonumber \\&-(\alpha _{3}-1)xo_{3}(k-3)+\beta _3(xo_3(k-3)) \nonumber \\= & {} \psi (xo_1,xo_2,xo_3) \end{aligned}$$
(46)

The result follows. \(\square \)

Finally, the decryption of the cipher image is done in the same way as the encryption of the real image, except that the key Ko(k), as shown in Fig. 1, is obtained from the delayed discrete-time observer given by Eqs. (37) and (38) with the same parameters. Then, the recovered image is obtained.

5 Simulation results

In this section, some simulation results will be illustrated. Firstly, we present the simulation results on the synchronization of the transmitter given by System (30) and its observer given by Eqs. (37) and (38). Secondly, some results of the robustness of the proposed transmission scheme are shown.

5.1 Simulation results on the synchronization

In the following, we insert the original information, which is the Greens image of size \(128\times 128\) pixels, in System (30). As shown below, Figs. 7, 8 and 9 illustrate the simulation results for recovering the states \(x_1(k),x_3(k)\) and the input m(k), respectively. The reconstruction of these latters is done step-by-step and is perfect. The phase planes of the states \(x_1(k)\), \(x_3(k)\) and the message m(k), respectively, are given in Figs. 10, 11 and 12.

Fig. 7
figure 7

States time responses: \(x_1(k)\) (transmitter) and \(xo_{1}(k)\) (receiver)

Full size image
Fig. 8
figure 8

States time responses: \(x_3(k)\) (transmitter) and \(xo_{3}(k)\) (receiver)

Full size image
Fig. 9
figure 9

Messages responses: m(k) (transmitter) and mo(k) (receiver)

Full size image
Fig. 10
figure 10

Phase plane \(x_1(k)\) versus \(xo_1(k)\)

Full size image
Fig. 11
figure 11

Phase plane \(x_3(k)\) versus \(xo_3(k)\)

Full size image
Fig. 12
figure 12

Phase plane m(k) versus mo(k)

Full size image
Fig. 13
figure 13

The Greens gray original image, the encrypted image, the decrypted image and their corresponding gray histogram

Full size image
Fig. 14
figure 14

The Lena gray original image, the encrypted image, the decrypted image and their corresponding gray histogram

Full size image

5.2 Robustness of the proposed transmission scheme

In order to prove the security of the proposed transmission scheme, the following analysis are performed. The original images are the Greens and Lena images of size \(128\times 128\) pixels.

5.2.1 Statistical analysis

In the following, the good confusion property of the proposed method will be shown. To this end, two types of statistical analysis, histogram and correlation, are presented.

Histogram analysis The original, encrypted and decrypted Greens and Lena images and their histograms are shown in Figs. 13 and 14. These figures show that the histograms of the encrypted images are fairly uniform and are completely different from those of the original images. To ensure this uniformity, the chi-square test is applied and is given by the following formula:

$$\begin{aligned} \chi ^2 = \sum \limits _{i=0}^{255} \frac{(o_i-e_i)^2}{e_i} \end{aligned}$$
(47)

where \(o_i\) are the observed frequencies of each gray level \((0-255)\) in the encrypted image histogram’s, and \(e_i\) is the expected frequency of the uniform distribution, given here by \(e_i=(n\times m){/}256\), where n and m present the image size’s. The calculation results of the chi-square test of the two encrypted images histogram’s, Figs. 13d and 14d, with a significant level of 0.05 are presented in Table 1. From the results of Table 1, one can observe that the obtained values are lower than the critical value \(\chi _{255,0.05}^2=293\). Thus, we conclude that the distribution of the tested histograms is uniform, which means that the proposed method does not reveal any information for the statistical analysis.

Table 1 Chi-square test of histograms
Full size table
Fig. 15
figure 15

Correlations of two horizontal, vertical and diagonal adjacent pixels in the Greens gray original image and encrypted image

Full size image

Correlation analysis Adjacent pixels having strong correlation is an essential characteristic of digital images without compression. An effective secure image transmission scheme should be able to remove this sort of relationship. Consequently, it is appropriate to test the correlation between the values of two adjacent pixels of our images. So, we calculate the correlation coefficient in each direction by the following equation

$$\begin{aligned} \text {cov}(x,y)=\frac{\frac{1}{N}\sum \nolimits _{i=1}^N(x_i-{\bar{x}}) (y_i-{\bar{y}})}{\sqrt{\left( \frac{1}{N}\sum \nolimits _{i=1}^N (x_i-{\bar{x}})^2\right) \left( \frac{1}{N}\sum \nolimits _{i=1}^N (y_i-{\bar{y}})^2\right) }} \end{aligned}$$
(48)

where N in the total number of pixel pairs and \({\bar{x}}=\frac{1}{N}\sum \nolimits _{i=1}^Nx_i\), \({\bar{y}}=\frac{1}{N}\sum \nolimits _{i=1}^Ny_i\), \((x_i,y_i)\) is the ith pair of adjacent pixels in the same direction. Figure 15 illustrates the correlation distribution of two horizontally, vertically and diagonally neighboring pixels in the original Greens image and that in the cipher Greens image. Table 2 presents the results of the correlation coefficients of Greens and Lena images, which are far apart. Therefore, the proposed scheme is highly secure against statistical attacks.

Table 2 Correlation coefficients in the original images and encrypted images
Full size table

5.2.2 Information entropy analysis

The entropy of an information is an important characteristic of randomness and is calculated by the succeeding formula:

$$\begin{aligned} H(S)= \sum \limits _{i=0}^{n} p(x_i) \log _2 \frac{1}{p(x_i)} \end{aligned}$$
(49)

where \(p(x_i)\) presents the probability of appearance of the information value \(x_i\). For a true random source which produce \(2^L\) symbols, the entropy should be L. In this work, we take a 256-gray-scale image in which the pixel data have \(2^8\) possible values. Then, the entropy of a true random image must be 8. However, the entropy value of practical information is smaller than the ideal one. Therefore, the ideal value of information entropy after encryption is as close as possible to 8. The results of information entropies for different original images and their corresponding cipher images are listed in Table 3. From this table, it is clear that entropies are close to 8, so the proposed transmission scheme has a good property of information entropy.

Table 3 Information entropy of original and encrypted images
Full size table
Fig. 16
figure 16

Decryption attempts using incorrect keys and their corresponding histogram. a Incorrect parameter a, b gray scale, c incorrect fractional-order \(\alpha _1\), d gray scale, e incorrect coefficient f and f gray scale

Full size image

5.2.3 Sensitivity analysis

Sensitivity analysis permits the revelation of some information concerning the secret key of a secure transmission scheme. In this work, we verify the key sensitivity of our proposed scheme using decryption image obtained by key that is a little different from the original one. To this end, the number of pixels change rate (NPCR) is employed and is defined as follows:

$$\begin{aligned} \text {NPCR}=\frac{\sum \nolimits _{i,j}D(i,j)}{M\times N}\times 100\,\% \end{aligned}$$
(50)

where \(C_1\) and \(C_2\) are two images with the same size \(M\times N\), the gray-scale values of the pixels at position (i, j) of \(C_1\) and \(C_2\) are denoted as \(C_1(i,j)\) and \(C_2(i,j)\), respectively. D(i, j) is determined by \(C_1(i,j)\) and \(C_2(i,j)\), namely, if \(C_1(i,j)=C_2(i,j)\) then \(D(i,j)=0\) otherwise \(D(i,j)=1\).

In what follows, we take any of three different incorrect keys to decrypt a same ciphered image. Firstly, we decrypt the cipher image 13b using an incorrect parameter \(a+10^{-15}\), then using an incorrect fractional order \(\alpha _1+10^{-15}\) and finally using an incorrect coefficient \(f+10^{-13}\) with other keys the same. The decryption Greens images and its corresponding histograms are shown in Fig. 16, we see that the decrypted images are completely different from the original image 14a and their histograms are nearly uniformly distributed, which means that our proposed scheme provides a high key sensitivity. Table 4 shows the NPCR of original and recovered images with different keys, we find that the NPCR under correct secret keys is small enough, however, under other a small difference with correct one the NPCR is close to 100 %.

Table 4 NPCR of original image and recovered image with different keys
Full size table

5.2.4 Key space analysis

An effective secure transmission scheme should possess a very large key space, and that owing to make brute-force attack infeasible. In this work, we will evaluate the level of security produced by the secret key. Therefore, we generate the sequences, K and Ko, from the fractional-order modified-Hnon system. To this end, we assume that the initial conditions are known and we consider the fractional derivative orders \((\alpha _1, \alpha _2)\) and the parameters (a, b, c, d, e, f, g, h) to construct a secret key for our transmission scheme, the order \(\alpha _3\) is not considered because of the system dynamics. Then, we determine the size N of the key space which represents the finite set of all possible keys. Table 5 illustrates the sensitivity of parameters of fractional-order modified-Hénon system, in which the size of the interval of variation of its parameters is \(s_i=0.1\).

Table 5 Sensitivity to parameters
Full size table

From this table, one can calculate the size of the key space of our scheme as follows

$$\begin{aligned} N= \prod \limits _{i=1}^{9}= 10^{(14\times 4+12\times 2+11\times 3)}=10^{113}\gg 2^{128} \end{aligned}$$

This result satisfies the requirement of resisting the brute-force attack.

5.2.5 Robustness to noise

During the transmission process, cipher image may be influenced by noise. Therefore, the transmission scheme should be able to resist the noise attacks. In this part, we will look at two different noise types: Salt and Pepper noise and Gaussian noise, which are added to the cipher image. In order to evaluate the performance of our transmission scheme in resisting the noise attacks, the peak signal-to-noise ratio (PSNR) test is performed. The definition of PSNR is described as follows,

$$\begin{aligned} \text {PSNR}=10\times \log _{10}\left( \frac{255^2}{\text {MSE}}\right) \end{aligned}$$
(51)

where MSE is the mean squared error between the original image I and the decrypted image \(I'\), which is given by

$$\begin{aligned} \text {MSE}=\frac{1}{M\times N}\sum \limits _{i=1}^M \sum \limits _{j=1}^N[I(i,j)-I'(i,j)]^2 \end{aligned}$$
(52)
Table 6 The PSNR of decrypted images under different noise types
Full size table

Table 6 displays the PSNR values of the decrypted images such as the cipher images are attacked by different noises. The results demonstrate that the proposed transmission scheme can resist the noise attack. Indeed, larger PSNR value means more similarity to the original image. When the value of \(\text {PSNR} \ge 30\), the human eyes cannot percept differences between the plain-image and the decrypted image.

5.2.6 Speed performance

The running speed of the encryption algorithm is an important factor for a well applicable cryptosystem. In this work, we implement the proposed algorithm by using Matlab R2015. The speed performance is tested in a personal computer with an Intel(R) Core (TM) i5, CPU 2.20 GHZ, 4.00Go Memory, and the operating system is Microsoft Windows 8.1 Professionnel. Table 7 shows the encryption time of the proposed method.

Table 7 Encryption time of the proposed scheme
Full size table

5.2.7 Comparisons with other schemes

In the following, details on comparisons with other schemes are presented in Table 8. Indicators include \(\chi ^2\) test, correlation coefficients of horizontal, vertical and diagonal adjacent pixels, information entropy, NPCR for the key sensitivity and key space. From Table 8, it can be concluded that the proposed scheme has good performance.

Table 8 Comparisons between different schemes on performance
Full size table

6 Conclusion

In this paper, we have proposed a novel image transmission scheme using fractional-order chaotic discrete-time systems. The message was encrypted by an encryption function before sending it by a chaotic carrier. Various methods for security analysis are employed, such as statistical analysis and sensitivity analysis, and illustrated by the simulation results. The corresponding results show that the proposed transmission scheme can resist different attacks.

Finally, one of our prospects for improving the presented work is to design an optimal protocol for real-time key transmission. In this case, an adaptation of the transmitted data in a given communication network, such as wireless networks, should be carried out. Another idea for enhancing the transmission scheme security is to use more complex encryption functions in the proposed algorithm and transmit more complex data, such as color images. Once these objectives are reached, practical implementation will be planned on programmable devices, such as Arduino boards and FPGA circuits.