Abstract
In this paper, a novel technique for synthesizing static anti-windup compensator (AWC) is explored for dynamic nonlinear plants with state interval time-delays, exogenous input disturbance, and input saturation nonlinearity, by means of reformulated Lipschitz continuity property. A delay-range-dependent approach, based on Wirtinger-based inequality, is employed to derive a condition for finding the static AWC gain. By using the Lyapunov–Krasovskii functional, reformulated Lipschitz continuity property, Wirtinger-based inequality, sector conditions, bounds on delay, range of time-varying delay, and \(\mathcal {L}_2\) gain reduction, several conditions are derived to guarantee the global and local stabilization of the overall closed-loop system. Further, when the lower time-delay bound is zero, the delay-dependent stabilization condition is derived for saturated nonlinear time-delay systems as a particular scenario of the suggested static AWC design approach. Furthermore, a static AWC design strategy is also provided when a delay-derivative bound is not known. An application to the nonlinear dynamical system is employed to demonstrate the usefulness of the proposed methodologies. A comparative numerical analysis with the existing literature is provided to show the superiority of the proposed AWC results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Time-delays and actuator saturation nonlinearities are frequently encountered in many fields of engineering and nonlinear science. Controlling linear, nonlinear, and time-delay systems under input nonlinearity is getting significant research consideration, throughout the past years [1,2,3,4]. All real-world dynamical systems are subjected to practical restrictions [5, 6], such as constrained dimensions and restricted control capability. A control signal is delivered to a plant via actuators, and a practical actuator cannot supply an unrestrained energy signal. The careless treatment of the input actuator saturation not only causes performance degradation such as oscillations, divergence, undershoots, overshoots, and instability, but also leads to fatalities (see [7,8,9] and references therein). Controller design without considering the windup phenomenon produces undesirable performance as an aftermath of the actuator saturation [9, 10]. Over the past decade, several techniques have been developed to mitigate the windup effects, such as robust and \(H_\infty \) optimal control based schemes [11], adaptive fuzzy control [12], linear matrix inequality (LMI)-based optimization techniques [8, 9, 13], full-order dynamic anti-windup compensator (AWC) [9], low-order AWC [14], internal model control (IMC)-based anti-windup [15], observer-based AWC [16], static AWC [13], and dynamic anti-windup [8, 17]. Some outcomes on AWC synthesis for linear systems [11, 18], feedback-linearizable nonlinear plants [17], Takagi–Sugeno fuzzy systems [19], Lipschitz nonlinear systems [8, 9], Markovian jump models [20], Euler–Lagrange nonlinear systems [21], and nonlinear dynamic inversion structures [22] have been previously reported.
Feedback linearization-based multi-variable nonlinear AWC methodology for constrained nonlinear multi-variable systems is suggested in [23], by employing nonlinear \(\mu \)-analysis. A set of conditions is derived to ensure the local stabilization and performance of the system. Further, the IMC-based AWC of [24] is extended to multi-variable nonlinear systems. Static AWC for time-varying uncertain Markovian jump systems with moderately unidentified transition rates is investigated in [20]. Further, the developed result is extended to the two types of Markovian jump systems with totally known and unknown transition rates. The LMI-based technique is recommended in [25] and an approach for finding a static AWC gain by employing a generalized sector condition along with enlargement of a region of stability is studied. A one-step instantaneous design of multi-objective \(H_\infty \) controller and a static anti-windup for a class of nonlinear systems under actuator constraints have been studied in [26]. Necessary conditions for designing global and local AWC to mitigate the windup effects in nonlinear systems are anticipated. IMC-based AWC approach, for nonlinear plant with mathematical modeling errors, by utilizing input-output linearization techniques, is explored in [27]. Decoupled and IMC-based AWC architectures are explored in [9], and global and regional AWC synthesis for Lipschitz nonlinear systems are deliberated in the same study. LMI-based static AWC for nonlinear parameter-varying (NPV) systems is presented in the recent work [28], and the resultant scheme is successfully implemented for an NPV DC-servo system.
Due to a wide range of applications of time-delay systems in field of nonlinear science, networked dynamical systems, industrial plants, chemical processes, pneumatic structures, neural networks, electric power grids, transmission lines, chemical and biological processes, extensive consideration has been dedicated to the control of systems with time-delay during the past years [4, 19, 29, 30]. In numerous practical control systems, both the time-delay and actuator saturation nonlinearity are present concurrently. Both of these two complications are major sources of performance retrogression and instability [4, 29]. The stabilization problem of uncertain time-delay plants with unknown delays and actuator saturation is studied in [31] by employing the Razumikhin technique. Lyapunov-based static AWC synthesis guaranteeing a wide basin of attraction and the rapid convergency of states of saturated linear time-delay systems has been formulated in [32]. Nonlinear delayed AWC architectures are developed to attain the compensation for windup consequences in nonlinear time-delay systems in [33]. Several LMIs are derived to design dynamic AWC for linear, nonlinear, and time-delay systems. While in [34], the nonlinear delayed AWC methodology of [33] has been extended using linear parameter-varying (LPV) and Lipschitz reformulation techniques. The stabilization problem of dynamical nonlinear systems with state time-delay and saturation nonlinearity is an interesting research problem. Therefore, further efforts are still required to explore the windup compensation techniques for nonlinear time-delay systems.
AWC methodologies for nonlinear control systems with and without time-delay have been previously presented in the works [8, 9, 21, 33, 34]. In comparison with these conventional schemes, the current study presents a new anti-windup design for a class of nonlinear systems with state interval delays, exogenous input disturbance, and input actuator saturation. The proposed AWC design technique does not require the state of a plant. AWC methods such as [8, 9, 21, 33, 34] are based on the supposition that all the states of the plant are accessible to the AWC block for compensation, as well as activation. However, the utilization of additional hardware to access all the states of a plant through sensors can be costly and sometimes unrealizable. IMC-based schemes [35] can only be used to compensate the saturation effects in asymptotically stable plants and can offer poor performance when the dynamics of a plant is slow. In contradistinction to the dynamic AWC methodologies like [8, 9, 33, 34], the proposed static AWC is simple to implement as the static anti-windup is composed of a constant proportional gain. Further, the proposed AWC is activated upon saturation of the control signal and deactivated immediately on termination of the windup.
A new technique for global or local static AWC design for delayed nonlinear models with state varying time-delays, exogenous input disturbance, and input actuator saturation is proposed in this study. Several static AWC design conditions are developed by means of the Lyapunov–Krasovskii functional, Wirtinger-based inequality, reformulation of the Lipschitz continuity, sector constraints, bound on delay and its derivative, and \(\mathcal {L}_2\) gain reduction. Local AWC design conditions are provided for the case when global stabilization condition cannot be achieved. Further, when the lower time-delay bound is zero or the delay-derivative bound is not known, the delay-dependent and delay-rate-independent stabilization conditions are derived for saturated nonlinear time-delay systems as particular cases of the suggested static AWC design approach. A new delay-range-dependent-based static AWC synthesis technique by using linear parameter-varying (LPV) theory for the Lipschitz nonlinear time-delay systems under input saturation limitation and state delay is formulated. In contrast to the existing works like [33, 34], improved delay-range-dependent methodology based on Wirtinger-based inequality has been used to attain feasibility result for a larger delay range. Hopfield neural network (HNN) is used to demonstrate the usefulness of the proposed methodologies and to show the superiority over the existing techniques.
This article is arranged into five sections. Section 2 presents explanation of systems used in the study and their reformulation. In Sect. 3, static anti-windup compensator synthesis approaches are provided. Section 4 renders the simulation results. Section 5 presents concluding remarks of the study.
Notations The symbol \(Q^\mathrm{T}\) signifies transpose of a real matrix Q. \(Q>0\) and \(Q\ge 0\) represent a symmetric positive and a positive semi-definite matrices. The ith row of Q is defined as \(Q_{(i)}\). \(||w(t)||\) symbolizes the Euclidean norm of a vector w(t). \(||w(t)||_2=[\int _0^\infty ||x||^2{\text {d}}t]^{1/2}\) denotes the \(\mathcal {L}_2\) norm. The saturation and dead-zone nonlinearities are indicated by 
and \(\zeta _z(.) \), respectively. \({\text {diag}}(\phi _1(t), \phi _2(t),\phi _3(t), \ldots ,\phi _n(t))\) implies a diagonal matrix. If \(\varphi (t)=(\varphi _1(t), \varphi _2(t),\varphi _3(t), \ldots ,\varphi _n(t))^\mathrm{T}\) and \(z(t)=(z_1(t), z_2(t),z_3(t), \ldots ,z_i(t))^\mathrm{T}\), then an auxiliary vector formed by \(\varphi (t)\) and z(t) can be defined \(\varphi (t)^{z_i(t)}=(z_1(t), z_2(t),z_3(t), \ldots ,z_n(t),\varphi _{i+1}(t), \varphi _{i+2}(t), \varphi _{i+3}(t), \ldots ,\varphi _{n}(t))^\mathrm{T}\). The canonical basis vector of \(\mathbb {R}^n\) is defined as \(e_n(i)=(0,0,0, \ldots ,0, 1,0,0,0, \ldots ,0)^\mathrm{T}\), where 1 is the ith term.
2 System description and reformulation
Consider the following nonlinear time-delay system described by
where \(x(t) \in \mathbb {R}^n\) represents the state, \(w(t) \in \mathbb {R}^q\) denotes the exogenous input, 
signifies the saturated control input, \(y(t) \in \mathbb {R}^p\) indicates the output, and \(z(t) \in \mathbb {R}^k\) represents the exogenous output. \(A_p \in \mathbb {R}^{n \times n}\), \(A_d \in \mathbb {R}^{n \times n}\), \(B_p \in \mathbb {R}^{n \times m}\), \(B_{pw} \in \mathbb {R}^{n \times q}\), \(C_y \in \mathbb {R}^{p \times n}\), \(D_y \in \mathbb {R}^{p \times m}\), \(D_{yw} \in \mathbb {R}^{p \times q}\), \(C_z \in \mathbb {R}^{k \times n}\), and \(D_{zw} \in \mathbb {R}^{k \times q}\) represent the appropriate constant matrices. \(f_p(t,x)\), \(f_d(x(t-h(t)))\), 
, h(t), and \(\theta (t)\) represent the nonlinear dynamics, nonlinear time-delay function, saturation nonlinearity, unknown time-varying delay and initial condition for \([-\tau _2 \quad 0]\), respectively. The unknown time-varying delay h(t) is presumed to fulfil
where \(\tau _1 \), \( \tau _2\) and d denote the lower delay bound, upper delay bound, and the delay variation, respectively. We define, \(\tau _{21}=\tau _2-\tau _1\). In order to design a static AWC for nonlinear time-delay system, we take the subsequent assumptions on the nonlinear dynamic \(f_p(t,x)\), nonlinear time-delay function \(f_d(x(t-h(t)))\), and \(w(t) \in \mathbb {R}^q\):
Assumption 1
The nonlinear function \(f_p(t,x)\) and nonlinear time-delay function \(f_d(x(t-h(t)))\), for all x(t), \(\bar{x}(t)\)\(\in \mathbb {R}^n\), fulfil the subsequent Lipschitz continuity condition:
where \(L_p\) and \(L_d\) are constant matrices.
Assumption 2
The exogenous input signal \(w(t) \in \mathbb {R}^q\) satisfies the energy bound for a constant scalar \(\lambda \), given by
The feedback stabilizing nominal controller, which provides the required tracking performance and stabilization of the closed-loop system, has the form
where \(x_c(t) \in \mathbb {R}^c\) and \(u_c(t) \in \mathbb {R}^m\) signify the states and output of a controller, respectively. \(A_c\), \(C_c\), \(B_c\), and \(D_c\) indicate the controller matrices. To compensate the undesirable effects of saturation nonlinearity, the AWC gains, \(E_{awc1}\) and \(E_{awc2}\), are incorporated in the control system such that
where 
designates the dead-zone nonlinearity. Reformulated Lipschitz property is useful for employing the linear parameter-varying (LPV) approach. According to [13, 36], for any two vectors \(Y(t)= (y_1(t), y_2(t),y_3(t), \ldots ,y_n(t))^\mathrm{T}\) and \(X(t)= (x_1(t), x_2(t),x_3(t), \ldots ,x_n(t))^\mathrm{T}\), a region \(B_\varphi \subseteq \mathbb {R}^r\) can be defined as
The nonlinear dynamics \(f_p\left( {x(t)} \right) :{\mathbb {R}^n} \rightarrow {\mathbb {R}^n}\) and nonlinear time-delay function \(f_d\left( {x(t-h(t))} \right) :{\mathbb {R}^n} \rightarrow {\mathbb {R}^n}\) in Assumption 1 can be rewritten as
where \({{{ A}}_{fp}}({\varTheta _{fp}}) = \sum \nolimits _{i = 1}^n {\sum \nolimits _{j = 1}^n {{f_{pij}}\left( {{e_n}(i)e_n^\mathrm{T}(j)} \right) } }\) and \({{{A}}_{fd}}({\varTheta _{fd}}) = \sum \nolimits _{i = 1}^n {\sum \nolimits _{j = 1}^n {{f_{dij}}\left( {{e_n}(i)e_n^\mathrm{T}(j)} \right) } }\). We have
where the bounds for \({f_{dij}}\) and \({f_{dij}}\) are considered as \({{\underline{\lambda }}_{f_{pij}}} \le {f_{pij}} \le {\bar{\lambda } _{f_{pij}}}\) and \({{\underline{\lambda }}_{f_{dij}}} \le {f_{dij}} \le {\bar{\lambda } _{f_{dij}}},\) respectively. For the condition \(f_p(0) = f_d(0) = 0\), we have
Both the functions \({f_{pij}} (x^{\bar{x}_{j-1}},x^{\bar{x}_{j}})\) and \({f_{dij}} (x^{\bar{x}_{j-1}},x^{\bar{x}_{j}})\) have lower and upper bounds, the matrices \({{{A}}_{fp}}({\varTheta _{fp}})\) and \({{{ A}}_{fd}}({\varTheta _{fd}})\) belong to convex sets \(W_{fp}\) and \(W_{fd}\), where the set of vertices are
Using the equivalent Lipschitz conditions, the nonlinear dynamics \(f_p\left( {x(t)} \right) \) and nonlinear time-delay function \(f_d\left( {(t-h(t))} \right) \) can be rewritten as
The system attained by employing the delayed nonlinear system (1), controller (8), and reformulated Lipschitz property in (18) and (19) is represented as
where
The subsequent lemma is useful for deriving the proposed static AWC synthesis conditions.
Lemma 1
[30] Consider a scalar \(h(t)>0\) and a matrix \(Q=Q^\mathrm{T}>0\). The integral inequality
holds, for all continuous function \(\chi (t)\) in [0, h(t)], where \(\varOmega =\int _0^{h(t)}\chi (\alpha ){\mathrm{d}}\alpha -\frac{2}{h(t)}\int _0^{h(t)}\int _a^t\chi (r){\mathrm{d}}r{\mathrm{d}}s\).
The goal of this research paper is to propose LMI-based global and local static AWC design approaches to handle the saturation effects in nonlinear time-delay systems.
3 Static anti-windup synthesis
Several conditions are derived for determining the static AWC gains \(E_{awc1}\) and \(E_{awc2}\) in this section. We first derive global static AWC result in Theorem 1 for given static anti-windup compensator gains \(E_{awc1}\) and \(E_{awc2}\).
Theorem 1
Consider the nonlinear time-delay system (1), satisfying the time-varying delay bounds (2) and (3), and Assumptions 1 and 2. For a given controller (8) along with the suggested anti-windup compensator gains \(E_{awc1}\) and \(E_{awc2}\), suppose that there exist symmetric matrices \(P>0\), \(Q_1>0\), \(Z_1>0\), \(Q_2>0\), \(Z_2>0\), and \(Q_3>0\), a diagonal matrix \(W>0\), and a scalar \(\sigma >0\) in such a way that the subsequent inequalities are fulfilled.
Then, the complete closed-loop system obtained by employing the system (1) and controller (8) assurances the following:
- 1.
The overall system (20) is globally asymptotically stable if \(w(t)=0\).
- 2.
The \(\mathcal {L}_2\) gain of the mapping from w(t) to z(t) is restricted by \(\gamma =\sqrt{\sigma }\), if \(w(t) \in \mathcal {L}_2.\)
Proof
We consider a Lyapunov–Krasovskii functional as
the time-derivative of \(V(t,\chi )\) is obtained as
By employing the closed-loop system (20), the inequality (26) yields
By applying Lemma 1, the integral term \(\tau _1\int _{t-\tau _1}^{t}\dot{\chi }^\mathrm{T}(\alpha )Z_1\dot{\chi }(\alpha ){\text {d}}\alpha \) in (27) can be defined as
where \(\psi _1(t)=\chi (t-\tau _1)+\chi (t)-\frac{2}{\tau _1}\int _{t-\tau _1}^t\chi (\alpha ){\text {d}}\alpha \). Inequality (28) can be represented as
By application of Lemma 1, the term \(\tau _{21}\int _{t-\tau _2}^{t-\tau _1}\dot{\chi }^\mathrm{T}(\alpha )Z_2\dot{\chi }(\alpha ){\text {d}}\alpha \) can be written as
where \(\beta (t)=\frac{h(t)-\tau _1}{\tau _2-\tau _1}\), \(\psi _2(t)=\chi (t-\tau _2)+\chi (t-h(t))-2(\tau _2-h(t))^{-1}\int _{t-\tau _2}^{t-h(t)}\chi (\theta ){\text {d}}\theta \), and \(\psi _3(t)= \chi (t-\tau _1)+\chi (t-h(t))-2(h(t)-\tau _1)^{-1}\int _{t-h(t)}^{t-\tau _1}\chi (\theta ){\text {d}}\theta \). The inequality (30) can be further written as
In order to minimize the effect of exogenous input, we define the following objective function:
For \(W\in \mathbb {R}^{m\times m}>0\), the dead-zone function authenticates
By using (20), (29), (31), and (33), the inequality (32) reveals
where
The inequality (34) can be written as
The inequality (38) can be further transformed as
where
The condition (22) is obtained by applying Schur complement to \(\varPi ^{(1)}<0\) and \(\varPi _2^{(1)}<0\) and further replacing \(\sigma =\gamma ^2\), \(M_1=Z_1^{-1}\), and \(M_2=Z_2^{-1}\). If \(w(t)=0\), the condition (32) yields \(\dot{V}(t,\chi )<0\), as \(z^\mathrm{T}(t)z(t)>0\), which authenticates that system (20) is asymptotically stable. The following inequality is obtained by integrating the condition (32) from \(t = 0\) to \(t = T>0\):
If \(\chi (0)=0\), we have \({V}(0,\chi )=0\), therefore, \(\int _{0}^{t}z^\mathrm{T}(\alpha )z(\alpha ){\text {d}}\alpha <\gamma ^2\int _{0}^{t}w(\alpha )^\mathrm{T}w(\alpha ){\text {d}}\alpha \) is obtained from (43) as \({V}(t,\chi )>0\), which further implies \(||z(t)||_2^2\le \gamma ^2 ||w(t)||_2^2\). It ensures that the \(\mathcal {L}_2\) gain from w(t) to z(t) is less than \(\gamma \), which completes the proof.
\(\square \)
Remark 1
Looking at the literature, various techniques, such as [4, 8, 9, 19, 33, 34], have been proposed to deal with saturation effects in linear, nonlinear, and time-delay systems. In contrast to the delay-dependent approach [19] and delay-independent method [4], we have used an improved delay-range-dependent technique to derive the design condition. Unlike the dynamic windup compensation methodologies (for example [8, 9, 33, 34]), we have suggested a static AWC technique for nonlinear time-delay systems which is attractive due to several reasons: First, the proposed static AWC is computationally simple compared to a dynamic AWC. Second, unlike the dynamic AWC in [8, 9, 16, 21, 33, 34], the anticipated static AWC synthesis methodology eliminates the requirements of the state of the system for feedback. Note that all states of a plant are not attainable in most practical circumstances. Further, the practical implementation of a static AWC is relatively simple. A novel delay-range-dependent static AWC synthesis methodology for Lipschitz nonlinear time-delay systems with input saturation limitation and state delays is proposed in our work.
Remark 2
This work uses the Lipschitz reformulation property [13, 36] to design a static AWC for nonlinear time-delay systems. In contrast to the conventional Lipschitz conditions [8, 9, 33], the reformulated Lipschitz property can be used to synthesize a less conservative static AWC for nonlinear systems particularly for large values of the Lipschitz constants (see [13, 36] for more details). To further demonstrate the superiority of the Lipschitz reformulation property as in [13], consider the nonlinear functions \( f_{p}(\xi ) = \tanh (\xi )\) and \( f_{p}(\xi ) = \sin (\xi ) \). The traditional Lipschitz condition [8, 9, 33] does not differentiate among the two nonlinear functions. However, according to Lipschitz reformulation property, we have \(0 \le {f_{p11}}={\tanh (\xi )}/\xi \le 1\) and \(0.2172 \le {f_{p11}}={\sin (\xi )}/\xi \le 1\). The linear parameter-varying (LPV) theory provides an effective approach to represent nonlinear dynamics. The conventional Lipschitz conditions [8, 9, 33, 37] do not signify all the properties of a nonlinear function, whereas the reformulated Lipschitz condition is the premium one that includes all the characteristics of the Lipschitz nonlinearities.
Remark 3
Lyapunov–Krasovskii functional (LKF)-based LMI techniques [38] are widely used to analyze stability and to design controller for linear and nonlinear time-delay systems. These techniques can be used to attain robust analysis, exponential stability with an assured decay rate and design of a compensator. However, selection of LKF, reducing the complexity and conservatism involved in handling the time-derivative of the LKF, is always a challenging and an open problem for control engineering community. Looking at the literature, various techniques, such as the integral inequalities [39], Jensen inequality [40], modified Jensen inequality [41], the reciprocally convex approach [42], cross terms [43], and free-matrix-based inequality (FMBI) [33], are used to deal with the integral terms involved in manipulating the time-derivative of LKFs. Nevertheless, conservatism is involved in all of these methods due to poor handling of the integral terms in derivative of the LKF. Most recently, Wirtingers integral inequality [30] has been introduced to reduce the above-mentioned conservatism. It provides an improved method to manage the time-derivative of the LKF. In this work, we used the improved delay-rage-dependent stability treatment based on Wirtingers integral inequality to derive the condition for finding the static AWC gains.
Theorem 1 can be used to synthesize a static anti-windup for given values of gains \(E_{awc1}\) and \(E_{awc2}\). In Theorem 2, we deliver an LMI-based methodology for calculating the suggested AWC gains \(E_{awc1}\) and \(E_{awc2}\).
Theorem 2
Consider the nonlinear time-delay system (1), satisfying the time-varying delay bounds (2) and (3), and Assumptions 1 and 2. Suppose that there exist symmetric matrices \(X>0\), \(\bar{Q}_1>0\), \(\bar{Z}_1>0\), \(\bar{Q}_2>0\), \(\bar{Z}_2>0\), and \(\bar{Q}_3>0\), a matrix \(\mathbb {V}_{awc}\), a diagonal matrix \(U>0\), and a positive scalar \(\sigma \) in such a way that the subsequent matrix inequalities are fulfilled.
where
Then, the complete closed-loop system obtained by employing (1) and (8) assurances the following:
- 1.
The overall system (20) is globally asymptotically stable if \(w(t)=0\).
- 2.
The \(\mathcal {L}_2\) gain of the mapping from signal w(t) to z(t) is restricted from \(\gamma =\sqrt{\sigma }\), if \(w(t) \in \mathcal {L}_2.\)
Further, anti-windup compensator can be attained via \(\mathbb {E}_{awc}=\mathbb {V}_{awc}U^{-1}.\)
Proof
By applying congruence transformation using the diagonal structure \({\text {diag}}(\varGamma _1,I,W,\varGamma _1)\), where \(\varGamma _1={\text {diag}}(X,X,X,X),\) to the inequalities in (22) and further by using \(U=W^{-1}\), \(X=P^{-1}\), \(\bar{Z}_i=P^{-1}{Z}_iP^{-1}\), \(\varSigma _i=P^{-1}\bar{Z}_i^{-1}P^{-1}\), for \(i=1,2,\)\(\bar{Q}_1=P^{-1}Q_1P^{-1}\), \(\bar{Q}_2=P^{-1}Q_2P^{-1}\), \(\bar{Q}_3=P^{-1}Q_3P^{-1}\), and \(\mathbb {V}_{awc}=\mathbb {E}_{awc}U\), we acquire
where
and \(\bar{\varXi }_{11}^{(2)}(\varTheta _{fp})=X\mathbb {A}_p^\mathrm{T}+\mathbb {A}_pX+X\mathcal {A}_{fp}^\mathrm{T}(\varTheta _{fp})+\mathcal {A}_{fp}(\varTheta _{fp})X+\sum _{i=1}^{3}\bar{Q}_i-4\bar{Z}_1+\mathbb {C}_z^\mathrm{T}\mathbb {C}_z\). The LMIs in (44) are acquired by applying the Schur complement to condition (48). \(\square \)
Remark 4
Theorem 1 can be used to synthesize a static AWC for given static anti-windup compensator gains \(E_{awc1}\) and \(E_{awc2}\). However, it may be a tedious job to design a static AWC from the constraints in Theorem 1, because a lot of tuning struggles will be required for attaining suitable AWC gains \(E_{awc1}\) and \(E_{awc2}\). In contrast to Theorem 1, Theorem 2 provides an LMI-based methodology based on the iterative solution of LMI constraints and the cone complementary linearization (CCL) technique for calculating the static AWC gains \(E_{awc1}\) and \(E_{awc2}\). The iterative approach for finding AWC gains will be discussed later.
When \(\tau _1=0\), the result of Theorem 2 reduces to the subsequent corollary.
Corollary 1
Consider a system (1), satisfying the time-varying delay bounds (2) and (3) and Assumptions 1 and 2. Suppose that there exist symmetric matrices \(X>0\), \(\bar{Q}_1>0\), \(\bar{Z}_1>0\), \(\bar{Q}_2>0\), \(\bar{Z}_2>0\), and \(\bar{Q}_3>0\), a matrix \(\mathbb {V}_{awc}\), a diagonal matrix \(U>0\), and a positive scalar \(\sigma \) in such a way that the subsequent matrix inequalities are fulfilled.
where
Then, the complete closed-loop system obtained by employing (1) and (8) assurances the following:
- 1.
The overall system (20) is globally asymptotically stable if \(w(t)=0\).
- 2.
The \(\mathcal {L}_2\) gain of the mapping from w(t) to z(t) is restricted by \(\gamma =\sqrt{\sigma }\), if \(w(t) \in \mathcal {L}_2.\)
Further the anti-windup compensator gains can be calculated as \(\mathbb {E}_{awc}=\mathbb {V}_{awc}U^{-1}\).
When the information on derivative bound of time-delay is unknown, the constraint in Theorem 2 can be reduced to the following corollary by substituting \(Q_3=0\).
Corollary 2
Consider a nonlinear time-delay system (1), satisfying the time-varying delay bounds (2) and (3), and Assumptions 1 and 2. Suppose that there exist symmetric matrices \(X>0\), \(\bar{Q}_1>0\), \(\bar{Z}_1>0\), \(\bar{Q}_2>0\), \(\bar{Z}_1>0\), and \(\bar{Q}_3>0\), a matrix \(\mathbb {V}_{awc}\), a diagonal matrix \(U>0\), and a positive scalar \(\sigma \) in such a way that the subsequent matrix inequalities are fulfilled.
where
Then, the complete closed-loop system obtained by employing the nonlinear time-delay systems (1) and controller (8) assurances the following:
- 1.
The overall system (20) is globally asymptotically stable if \(w(t)=0\).
- 2.
The \(\mathcal {L}_2\) gain of the mapping from w(t) to z(t) is restricted by \(\gamma =\sqrt{\sigma }\), if \(w(t) \in \mathcal {L}_2.\)
Further, the anti-windup compensator gain can be obtain as \(\mathbb {E}_{awc}=\mathbb {V}_{awc}U^{-1}.\)
Remark 5
The anti-windup approach for linear time-delay systems by employing delay-independent (unknown time-delay), delay-dependent (\(\tau _1=0\)), and delay-range-dependent (\(\tau _1 \le h(t) \le \tau _2\)) methodologies have been considerably proposed in the literature such as [19, 32, 33]. Nevertheless, there is an insignificant study on anti-windup technique for delayed nonlinear models, (see [19, 33, 34]). Delay-range-dependent-based static AWC schema of delayed nonlinear process using Wirtinger-based inequality, reformulated Lipschitz continuity property, and LPV approach has not been addressed until now. In contrast to [4, 19, 33, 34], the proposed static AWC result is less conservative and more suitable in practice. The employed methods in our study can be used to mitigate the saturation effects in delayed nonlinear systems with non-zero lower delay bound, large range of delay, and larger value of bounds on nonlinearity along with a simple static gain for compensation. Further, a static AWC design methodology for delayed nonlinear systems with zero lower delay bound has been suggested in Corollary 1 as a particular scenario of the suggested static AWC approach in Theorem 2. Furthermore, a static AWC design strategy is also provided in Corollary 2 derived from Theorem 2 by substituting \(Q_3=0\), when a delay-derivative bound is not known. The novel results in Corollaries 1 and 2 are promising due to the application of Wirtinger-based inequality and LPV approach, which further validates the novelty of the proposed methodology of Theorem 2.
In Theorems 1 and 2, we formulated global static AWC results, while in Theorem 3, we propose a local static AWC design approach.
Theorem 3
Consider a nonlinear time-delay system (1), satisfying the time-varying delay bounds (2) and (3), and Assumptions 1 and 2. Suppose that there exist symmetric matrices \(X>0\), \(\bar{Q}_1>0\), \(\bar{Z}_1>0\), \(\bar{Q}_2>0\), \(\bar{Z}_2>0\), and \(\bar{Q}_3>0\), matrices \(\mathbb {V}_{awc}\), \(U>0\), and N, and positive scalars \(v<1\) and \(\sigma \) in such a way that the subsequent matrix inequalities are fulfilled.
where
Then the given controller (8) along with the proposed static AWC guaranteed the following.
- 1.
The overall system (20) is locally asymptotically stable \(\forall \)\(\chi (0)\in {V}(0,\chi )<1\), if \(w(t)=0\).
- 2.
The \(\mathcal {L}_2\) gain of the mapping from signal w(t) to z(t) is restricted from \(\gamma =\sqrt{\sigma }\), if \(||w||_2^2\le \delta ^{-1}\), where \(\delta ^{-1}=(v^{-1}-1)/\gamma \).
- 3.
For all \({V}(0,\chi )<1\) and \(||w(t)||_2^2\le \delta ^{-1}\), states of (20) remain within the ellipsoidal \(\chi ^\mathrm{T}(t)v X^{-1}\chi (t)\le 1\).
The AWC gain guaranteeing the local stability and performance of the complete system (20) can be computed via \(\mathbb {E}_{awc}=\mathbb {V}_{awc}U^{-1}\).
Proof
For any arbitrary vector \(\bar{w}(t) \in \mathbb {R}^m\), consider an auxiliary region \(S(u(t),\bar{w}(t)) \subseteq \mathbb {R}^m\) defined as
Then, dead-zone nonlinearities authenticate the subsequent local sector condition
where
By employing (20) and (63), the auxiliary region \(S(u(t),\bar{w}(t)) \subseteq \mathbb {R}^m\) can be written as
By using (26) and (62), we define the following performance objective function:
Further, by means of (20) and Lemma 1 in a manner analogous to the proof of Theorem 1, the inequality (65) yields
The inequality (66) can be further written as
where
where \(\varXi _{16}^{(3)}=P\mathbb {B}_{awc}\mathbb {E}_{awc}-P\mathbb {B}_{\zeta _z}+\mathbb {G}_c^\mathrm{T}W\). By employing Schur complement to \(\bar{\varPi }_1^{(3)}<0\) and \(\bar{\varPi }_2^{(3)}<0\) and meanwhile taking \(\sigma =\gamma ^2\), it yields
where
Condition (57) is acquired by applying congruence transformation, the diagonal structure, \({\text {diag}}(\varGamma _1,I, W,\varGamma _1,I)\) to (69) and further by using \(U=W^{-1}\), \(X=P^{-1}\), \(\bar{S}_i=P^{-1}S_iP^{-1}\), for \(i=1,2,3\), \(\bar{Q}_j=P^{-1}Q_jP^{-1}\), for \(i=1,2\), \(N=\mathbb {G}_cP^{-1}\), and \(\mathbb {V}_{awc}=\mathbb {E}_{awc}U\). As \(\zeta _z^\mathrm{T}(u_c(t))W(\bar{w}(t)-\zeta _z(u_c(t)))\ge 0\), the inequality (65) can be written as
If \(w(t)=0\), the condition \(\dot{V}(t,\chi )<0\) ensures that the system (20) is stable. Under zero initial condition, we have \({V}(0,\chi )=0\), henceforth, \(\int _{0}^{t}z^\mathrm{T}(t)z(t)<\gamma ^2\int _{0}^{t}w(t)^\mathrm{T}w(t)\), which can be written as \(||z(t)||_2^2\le \gamma ^2 ||w(t)||_2^2\). It ensures that the \(\mathcal {L}_2\) gain from w(t) to z(t) is less than \(\gamma \). For \(||w(t)||_2^2\le \delta ^{-1}\), the zero initial condition \({V}(0,\chi )<1\) implies that \(\chi ^\mathrm{T}(0)X^{-1}\chi (0)<1\) as \(z^\mathrm{T}(t)z(t)>0\). Therefore, the inequality (73) can written as
where \(v^{-1}=1+\gamma \delta ^{-1}\). Note that \(1<v^{-1}\) and \(v^{-1}>\gamma \delta ^{-1}\); therefore, we have \(\chi ^\mathrm{T}(t)P\chi (t)\le \gamma \delta ^{-1}\subseteq \chi (t)^\mathrm{T}P\chi (t)\le v^{-1}\) and, further \(\chi ^\mathrm{T}(t)P\chi (t)\le 1\subseteq \chi (t)^\mathrm{T}P\chi (t)\le v^{-1}\). As a result, all the states of the close-loop system remains in ellipsoidal basin \(\xi (t)^\mathrm{T}vP\xi (t)\le 1\) for all \(t>0\) and for all exogenous signal satisfying the condition \(||w(t)||_2^2\le \delta ^{-1}\). \(\chi (t)^\mathrm{T}vX^{-1}\chi (t)\le 1\) into the auxiliary region \(S(u(t),\bar{w}(t))\) in (64) and further applying the Schur complement and congruence transformation, we obtain (57). \(\square \)
Remark 6
Global and regional static AWC synthesis methods for nonlinear systems with delayed states are formulated in Theorems 2 and 3, respectively. In contrast to those techniques of [17, 44], it does not require the exponential stability, bounded input, and state stability for the open-loop systems. Further, unlike the techniques of [17, 21, 44], the proposed approaches do not require feedback-linearizable property of a nonlinear system. The dynamic-based AWC [33] is designed by employing free-matrix-based inequality (FMBI), while the AWC [34] is based on the Jensen inequality approach. In contrast to [33, 34], we used Wirtinger integral inequality to achieve an improve result. Unlike FMBI and Jensen inequality approaches, the Wirtinger integral inequality permits us to consider a more precise integral inequality (see Table 1 for detail). Furthermore, the proposed constraints in Theorem 3 (compared to Theorem 2) are derived on the basis of a comprehensive (local) sector condition and can be employed to design a static AWC for unstable and oscillatory nonlinear time-delay systems. The AWC design for more complex systems, such as complex dynamical networks [45], two-dimensional (2-D) system [46] and one-sided Lipschitz nonlinear systems [47], can be considered in the further studies.
Remark 7
It is important to note that the constraints in Theorems 2 and 3 contain nonlinear terms \(\varSigma _1=P^{-1}\bar{Z}_1^{-1}P^{-1}\) and \(\varSigma _2=P^{-1}\bar{Z}_2^{-1}P^{-1}\). The nonlinear terms in Theorems 2 and 3 can be solved by means of the following linearization approach [48]:
where \(\bar{\varSigma }_i=\varSigma _i^{-1}\), \(\tilde{Z}_i=\bar{Z}_i^{-1}\), and \(\tilde{X}=X^{-1}\).
4 Simulation results
The proposed anti-windup is validated via its application to the nonlinear Hopfield neural networks (HNNs) [49] in this section. Owing to the abundant applications of HNNs and their generalizations in nonlinear science, signal processing, pattern recognition, optimization solvers, and computations associated with memories, significant research attention has been given to HNNs during the last couples of years [49,50,51]. In many applications, stability of the neural networks is an important dynamical aspect. Meanwhile, time-delays and actuator saturation are the main causes of performance degradation and instability; therefore, this study investigates the tracking and stability of HNNs in the presence of time-delays and actuator saturation. Consider a nonlinear Hopfield neural network [50] with multiple inputs and outputs represented by
Closed-loop response of nonlinear Hopfield neural network system: a unsaturated closed-loop output \(y_{1}(t)\) and b unsaturated control signal \(u_{c1}(t)\)
Closed-loop response of nonlinear Hopfield neural network system: a unsaturated closed-loop output \(y_{2}(t)\) and b Unsaturated control signal \(u_{c2}(t)\)
The output feedback controller is designed without considering the saturating input
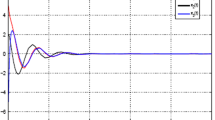
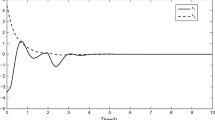
where \(r_1(t)\) and \(r_2(t)\) are the reference inputs. The unconstrained closed-loop response \(y_{p1}(t)\) and nominal control signal \(u_{c1}(t)\) of the nonlinear HNN to a square wave input of magnitude of one are shown in Fig. 1a, b. Likewise, the unconstrained closed-loop response \(y_{p2}(t)\) and nominal control signal \(u_{c2}(t)\) of the nonlinear HNN to a square wave input of magnitude of 0.5 are presented in Fig. 2a, b. As we can see from Figs. 1 and 2, the unconstrained closed-loop responses \(y_{p1}(t)\) and \(y_{p2}(t)\) follow the desired square wave references in the absence of actuator saturation. However, saturation is the physical limitation of all actuators, as none of the transducer can pass unlimited power. Therefore, an actuator saturation always exists in practical control systems and the controller design without bearing in mind the windup effect can cause unsatisfactory response when the nominal control signal exceeds the limits of the saturation. Consequently, there should be some mitigation technique to deal with the saturation effects. We select the time-varying delay bounds as \(0.1\sec \le h(t)\le 0.25\sec \), delay rate as \(\dot{\tau }(t)\le 0.5\) and saturation bounds as \(\pm 1\) and \(\pm 0.8\) for \(u_{c1}(t)\) and \(u_{c2}(t)\), respectively. By solving the set of LMIs of Theorem 3, accompanied by the linearization approach (74), we obtain the anti-windup gains as
The effects of saturation are then studied with and without the proposed AWC. The simulation results clearly reveal that the windup effect is removed by applying the proposed compensation technique. Figure 3 represents the response of \(y_1(t)\), which is showing overshoot and undershoot in following the reference signal. By applying the proposed static AWC, the overshoot and undershoot in following the reference signal are removed, which is also clear in the \(u_{c1}(t)\) plot. Figure 4 represents the improvement in response of \(y_2(t)\) and control signal \(u_{c2}(t)\) by the application of the anticipated static AWC methodology.
Closed-loop response of nonlinear Hopfield neural system with and without the suggested AWC approach: a saturated closed-loop output \(y_{1}(t)\) and b saturated control signal 
Closed-loop response of nonlinear Hopfield neural network system with and without the suggested AWC approach: a saturated closed-loop output \(y_{2}(t)\) and b saturated control signal 
A comparative investigation of our suggested static AWC with the existing dynamic AWC technique of [33] has been presented. Tables I summarizes the AWC gains, \(E_{awc1}\) and \(E_{awc2}\), obtained by solving the constraints of the suggested static AWC in Theorem 3 and the dynamic AWC in Theorem 2 of [33] for different values of delay bounds \(\tau _1\) and \(\tau _2\). The recommended static AWC scheme is feasible for a larger delay range, whereas the methodology provided in [33] produces infeasible result for \(\tau _1=1\) and \(\tau _2=10\). Unlike to the dynamic AWC technique presented in [33], the proposed static AWC is less conservative and computationally more effective, because we employed an LPV approach and Lipschitz reformulation technique for the efficient treatment of the Lipschitz nonlinearities, instead of conventional Lipschitz condition. Further, an improved Wirtinger-based inequality, instead of free-matrix-based inequality, is used to derive the delay-range-dependent conditions for determining the AWC gains. Table 1 clearly reveals the less conservativeness and supremacy of our suggested static AWC method in contrast to the windup compensation methodologies delivered in the previous works.
5 Conclusions
This paper focused on the static AWC design for dynamical nonlinear time-delay plants with state delays and input saturation nonlinearity by employing the delay-range-dependent stability tactic. A novel technique was proposed for designing a static AWC for delayed nonlinear systems with state delays, exogenous input disturbance, and input actuator saturation by means of reformulated Lipschitz continuity property. A delay-range-dependent technique based on the Wirtinger-based inequality was employed to derive a condition for calculating the AWC gains. By using the Lyapunov–Krasovskii functional, Wirtinger-based inequality, sector conditions, bound on delays, time-varying range of delay, and \(\mathcal {L}_2\) gain reduction, several conditions were derived to guarantee local and global stabilization and performance of the overall closed-loop system. Local AWC design conditions were provided, in case when global stabilization condition cannot be achieved. In contrast to the existing methods, the proposed approach is based on static AWC gain, which is simple to implement, and provides relaxation in control parameters (like range of the delay). A novel delay-range-dependent static AWC synthesis technique by using linear parameter-varying theory for Lipschitz nonlinear time-delay systems with input saturation limitation and state delay was formulated. Compared with the existing works, an improved delay-range-dependent methodology based on Wirtinger-based inequality has been used to attain a larger delay range. This advanced time-delay approach provides an improved methodology to manage the time-derivative of the LKF. An iterative convex approach based on cone complementary linearization is provided to obtain the static AWC gains. In contrast to the conventional Lipschitz condition, the reformulated Lipschitz continuity property is used to achieve less conservative outcomes, which provides an effective approach to represent the nonlinear dynamics. An application example was provided to demonstrate the usefulness of the proposed nonlinear AWC methodologies under time-delays.
References
Cai, X., Liu, L., Zhang, W.: Saturated control design for linear differential inclusions subject to disturbance. Nonlinear Dyn. 58(3), 487 (2009)
Zhou, N., Liu, Y.-J., Tong, S.-C.: Adaptive fuzzy output feedback control of uncertain nonlinear systems with nonsymmetric dead-zone input. Nonlinear Dyn. 63(4), 771–778 (2011)
Zheng, Z., Huang, Y., Xie, L., Zhu, B.: Adaptive trajectory tracking control of a fully actuated surface vessel with asymmetrically constrained input and output. IEEE Trans. Control Syst. Technol 26(5), 1851–1859 (2018)
da Silva Jr, J.M.G., Tarbouriech, S., Garcia, G.: Anti-windup design for time-delay systems subject to input saturation an lmi-based approach. Eur. J. Control 12(6), 622–634 (2006)
Lin, D., Wang, X., Yao, Y.: Fuzzy neural adaptive tracking control of unknown chaotic systems with input saturation. Nonlinear Dyn. 67(4), 2889–2897 (2012)
Agha, R., Rehan, M., Ahn, C.K., Mustafa, G., Ahmad, S.: Adaptive distributed consensus control of one-sided lipschitz nonlinear multiagents. IEEE Trans. Syst. Man Cybern. Syst PP(99), 1–11 (2017). https://doi.org/10.1109/TSMC.2017.2764521
Ran, M., Wang, Q., Dong, C., Ni, M.: Multistage anti-windup design for linear systems with saturation nonlinearity: enlargement of the domain of attraction. Nonlinear Dyn. 80(3), 1543–1555 (2015)
Hussain, M., us Saqib, N., Rehan, M.: Nonlinear dynamic regional anti-windup compensator (RAWC) schema for constrained nonlinear systems. In: 2016 International Conference on Emerging Technologies (ICET), pp. 1–6. IEEE (2016)
Rehan, M., Hong, K.-S.: Decoupled-architecture-based nonlinear anti-windup design for a class of nonlinear systems. Nonlinear Dyn. 73(3), 1955–1967 (2013)
Lee, S., Kwon, O., Park, J.H.: Regional asymptotic stability analysis for discrete-time delayed systems with saturation nonlinearity. Nonlinear Dyn. 67(1), 885–892 (2012)
Turner, M.C., Herrmann, G., Postlethwaite, I.: Incorporating robustness requirements into antiwindup design. IEEE Trans. Autom. Control 52(10), 1842–1855 (2007)
Zhou, Q., Li, H., Wu, C., Wang, L., Ahn, C.K.: Adaptive fuzzy control of nonlinear systems with unmodeled dynamics and input saturation using small-gain approach. IEEE Trans. Syst. Man Cybern. Syst. 47(8), 1979–1989 (2017)
Wang, N., Pei, H., Tang, Y.: Anti-windup-based dynamic controller synthesis for Lipschitz systems under actuator saturation. IEEE/CAA J. Autom. Sin. 2(4), 358–365 (2015)
Kerr, M.L., Turner, M.C., Postlethwaite, I.: Practical approaches to low-order anti-windup compensator design: a flight control comparison. IFAC Proc. Vol. 41(2), 14162–14167 (2008)
Weston, P.F., Postlethwaite, I.: Linear conditioning for systems containing saturating actuators. Automatica 36(9), 1347–1354 (2000)
Yang, S.-K.: Observer-based anti-windup compensator design for saturated control systems using an LMI approach. Comput. Math. Appl. 64(5), 747–758 (2012)
Yoon, S.-S., Park, J.-K., Yoon, T.-W.: Dynamic anti-windup scheme for feedback linearizable nonlinear control systems with saturating inputs. Automatica 44(12), 3176–3180 (2008)
Chen, Y., Fei, S., Zhang, K.: Stabilization of impulsive switched linear systems with saturated control input. Nonlinear Dyn. 69(3), 793–804 (2012)
Ting, C.-S., Chang, Y.-N.: Robust anti-windup controller design of time-delay fuzzy systems with actuator saturations. Inf. Sci. 181(15), 3225–3245 (2011)
Wei, Y., Zheng, W.X., Xu, S.: Static anti-windup design for a class of markovian jump systems with partial information on transition rates. Int. J. Robust Nonlinear Control 26(11), 2418–2435 (2016)
Morabito, F., Teel, A.R., Zaccarian, L.: Nonlinear antiwindup applied to Euler–Lagrange systems. IEEE Trans. Robot. Autom. 20(3), 526–537 (2004)
Valmórbida, G., Tarbouriech, S., Turner, M., Garcia, G.: Anti-windup design for saturating quadratic systems. Syst. Control Lett. 62(5), 367–376 (2013)
Kendi, T.A., Doyle, F.J.: An anti-windup scheme for multivariable nonlinear systems. J. Process Control 7(5), 329–343 (1997)
Kendi, T., Doyle, F.: An anti-windup scheme for input-output linearization. In: Proceedings of European Control Conference, pp. 2653–2658 (1995)
Silva, J., Oliveira, M., Coutinho, D., Tarbouriech, S.: Static anti-windup design for a class of nonlinear systems. Int. J. Robust Nonlinear Control 24(5), 793–810 (2014)
Rehan, M., Khan, A.Q., Abid, M., Iqbal, N., Hussain, B.: Anti-windup-based dynamic controller synthesis for nonlinear systems under input saturation. Appl. Math. Comput. 220, 382–393 (2013)
Hu, Q., Rangaiah, G.: Anti-windup schemes for uncertain nonlinear systems. IEE Proc. Control Theory Appl. 147(3), 321–329 (2000)
us Saqib, N., Rehan, M., Iqbal, N., Hong, K.-S.: Static antiwindup design for nonlinear parameter varying systems with application to dc motor speed control under nonlinearities and load variations. IEEE Trans. Control Syst. Technol. https://doi.org/10.1109/TCST.2017.2692745
Mobayen, S.: Robust tracking controller for multivariable delayed systems with input saturation via composite nonlinear feedback. Nonlinear Dyn. 76(1), 827–838 (2014)
Seuret, A., Gouaisbaut, F.: Wirtinger-based integral inequality: application to time-delay systems. Automatica 49(9), 2860–2866 (2013)
Niculescu, S.-I., Dion, J.-M., Dugard, L.: Robust stabilization for uncertain time-delay systems containing saturating actuators. IEEE Trans. Autom. Control 41(5), 742–747 (1996)
Ahmed, A., Rehan, M., Iqbal, N.: Delay-dependent anti-windup synthesis for stability of constrained state delay systems using pole-constraints. ISA Trans. 50(2), 249–255 (2011)
Hussain, M., Rehan, M.: Nonlinear time-delay anti-windup compensator synthesis for nonlinear time-delay systems: a delay-range-dependent approach. Neurocomputing 186, 54–65 (2016)
Akram, A., Hussain, M., us Saqib, N., Rehan, M.: Dynamic anti-windup compensation of nonlinear time-delay systems using LPV approach. Nonlinear Dyn. 90(1), 513–533 (2017)
Edwards, C., Postlethwaite, I.: Anti-windup schemes with closed-loop stability considerations. In: 1997 European Control Conference (ECC), pp. 2658–2663. IEEE (1997)
Zemouche, A., Boutayeb, M.: On LMI conditions to design observers for lipschitz nonlinear systems. Automatica 49(2), 585–591 (2013)
Zewei, Z., Liang, S., Yao, Z.: Attitude tracking control of a 3-DOF helicopter with actuator saturation and model uncertainties. In: 2016 35th Chinese Control Conference (CCC), pp. 5641–5646. IEEE (2016)
Boyd, S., El Ghaoui, L., Feron, E., Balakrishnan, V.: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia (1994)
Moon, Y.S., Park, P., Kwon, W.H., Lee, Y.S.: Delay-dependent robust stabilization of uncertain state-delayed systems. Int. J. Control 74(14), 1447–1455 (2001)
Shao, H.: New delay-dependent stability criteria for systems with interval delay. Automatica 45(3), 744–749 (2009)
Briat, C.: Convergence and equivalence results for the jensen’s inequality—application to time-delay and sampled-data systems. IEEE Trans. Autom. Control 56(7), 1660–1665 (2011)
Park, P., Ko, J.W., Jeong, C.: Reciprocally convex approach to stability of systems with time-varying delays. Automatica 47(1), 235–238 (2011)
Kim, J.-H.: Note on stability of linear systems with time-varying delay. Automatica 47(9), 2118–2121 (2011)
Herrmann, G., Menon, P., Turner, M., Bates, D., Postlethwaite, I.: Anti-windup synthesis for nonlinear dynamic inversion control schemes. Int. J. Robust Nonlinear Control 20(13), 1465–1482 (2010)
Selvaraj, P., Sakthivel, R., Ahn, C.K.: Observer-based synchronization of complex dynamical networks under actuator saturation and probabilistic faults. IEEE Trans. Syst. Man Cybern. Syst. (2018). https://doi.org/10.1109/TSMC.2018.2803261
Arif, I., Tufail, M., Rehan, M., Ahn, C.K.: A novel word length selection method for a guaranteed \({H}_\infty \) interference rejection performance and overflow oscillation-free realization of 2-D digital filters. Multidimens. Syst. Signal Process. https://doi.org/10.1007/s11045-017-0504-x
Rehan, M., Jameel, A., Ahn, C.K.: Distributed consensus control of one-sided lipschitz nonlinear multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. https://doi.org/10.1109/TSMC.2017.2667701
El Ghaoui, L., Oustry, F., AitRami, M.: A cone complementarity linearization algorithm for static output-feedback and related problems. IEEE Trans. Autom. Control 42(8), 1171–1176 (1997)
Li, W.-J., Lee, T.: Hopfield neural networks for affine invariant matching. IEEE Trans. Neural Netw. 12(6), 1400–1410 (2001)
Ahn, C.K.: Adaptive \({H}_\infty \) anti-synchronization for time-delayed chaotic neural networks. Prog. Theor. Phys. 122(6), 1391–1403 (2009)
Ahn, C.K.: An \({H}_\infty \) approach to stability analysis of switched hopfield neural networks with time-delay. Nonlinear Dyn. 60(4), 703–711 (2010)
Acknowledgements
This work was supported in parts by the Higher Education Commission (HEC) of Pakistan through PhD scholarship of the first author (phase II, batch II program) and the National Research Foundation of Korea through the Ministry of Science, ICT and Future Planning under Grant NRF-2017R1A1A1A05001325.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hussain, M., Rehan, M., Ahn, C.K. et al. Static anti-windup compensator design for nonlinear time-delay systems subjected to input saturation. Nonlinear Dyn 95, 1879–1901 (2019). https://doi.org/10.1007/s11071-018-4666-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-018-4666-3