Dynamics of superregular breathers in the quintic nonlinear Schrödinger equation

Abstract

In this paper, we consider an extended nonlinear Schrödinger equation that includes fifth-order dispersion with matching higher-order nonlinear terms. Via the modified Darboux transformation and Joukowsky transform, we present the superregular breather (SRB), multipeak soliton and hybrid solutions. The latter two modes appear as a result of the higher-order effects and are converted from a SRB one, which cannot exist for the standard NLS equation. These solutions reduce to a small localized perturbation of the background at time zero, which is different from the previous analytical solutions. The corresponding state transition conditions are given analytically. The relationship between modulation instability and state transition is unveiled. Our results will enrich the dynamics of nonlinear waves in a higher-order wave system.

1 Introduction

Wave evolution in different physical fields is governed by the nonlinear partial differential equations [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Though the nonlinear Schrödinger (NLS) equation contains only the lowest-order dispersion and lowest-order nonlinearity, it can well describe the propagation and dynamics of nonlinear pulses in diverse physics, including water waves [15], nonlinear optics [16], plasma [17], Bose–Einstein condensates [18, 19] and several other cases. The integrability of this equation [20] enables us to get such analytical solutions as solitons, breathers [21] and rogue waves [22,23,24,25,26,27,28,29,30,31], which have been observed in numerous experiments in these areas [32,33,34,35,36,37]. In many cases, the dynamics of a system influenced by modulation instability (MI) is also described by the NLS equation. In particular, there are some special interests on the nonlinear evolution stage and long-time dynamics, which are beyond the linear stability analysis. Zhakarov and Gelash [38, 39] proposed a kind of breather solution of the NLS equation, namely the superregular breather (SRB) solution. They further claimed that the SRB solution starts with infinitesimally small localized perturbation and could be used to describe the nonlinear stage of MI [38,39,40]. The SRBs are unique nonlinear wave structures on a plane-wave background formed by a nonlinear superposition of pairs of quasi-Akhmediev breathers [38,39,40]. This unique feature has been observed in both optics and hydrodynamics, based on exact superregular breather solution of the standard NLS equation [40]. However, in order to claim that one has characterized the nonlinear stage of MI, one must study solutions generated by generic initial conditions [41, 42]. Biondini and Mantzavinos [41, 42] have studied the nonlinear stage of the MI by characterizing the initial value problem for the focusing NLS equation with nonzero boundary conditions at infinity. As shown in [41], for generic perturbations of the background, the signature of MI lies precisely in the portion of the continuous spectrum which is the nonlinearization of the unstable Fourier modes. In fact, it was also shown in [41] that there are classes of initial conditions that are modulational unstable but that do not generate any discrete spectrum. These classes include small localized perturbations of the background. Since these perturbations generate no discrete spectrum, they do not produce SRBs. Moreover, as shown in [42], small localized perturbations of the background lead to a universal wedge-shaped structure. Asymptotically in time, the spatial domain divides into three regions: a far left and a far right field, in which the solution is approximately equal to its initial value, and a central region in which the solution has oscillatory behavior described by slow modulations of the periodic traveling wave solutions [42].

The above studies show that the NLS equation is a good candidate describing various physical mechanisms in different contexts. Nevertheless, to increase the wave amplitude, we have to consider the higher-order effects which do not exist in the simplest NLS equation [43]. In studies of pulse propagation in optical fibers, for transmitting the ultrashort pulses whose durations are shorter than 100 fs, the higher-order effects such as the third-order dispersion, self-steepening and delayed nonlinear response have to be taken into account. Thus, it is necessary to study the other integrable models of the whole hierarchy except for the NLS equation. Two extensions of the hierarchy to third- and fourth-order terms are known as the Hirota equation [44] and Lakshmanan–Porsezian–Daniel (LPD) equation [45,46,47,48]. More recently, the quintic equation of the hierarchy has been studied by Hoseini and Marchant [49]. The quintic nonlinear Schrödinger (QNLS) equation reads as [50,51,52,53],

$$\begin{aligned} \begin{array}{l} i\,q_t+S[q(x,t)]-i\,\varepsilon \,Q[q(x,t)]=0, \end{array} \end{aligned}$$

(1.1)

where S[q(x, t)] is the second-order NLS operator,

$$\begin{aligned} \begin{array}{l} S[q(x,t)]=\frac{1}{2}q_{xx}+q |q|^2, \end{array} \end{aligned}$$

(1.2)

while Q[q(x, t)] is the fifth-order quintic operator,

$$\begin{aligned} \begin{array}{lll} Q[q(x,t)]&{}=&{}q_{xxxxx}+10|q|^2 q_{xxx}+10 (q|q_x|^2)_x\\ &{}&{}+\,20q^*q_x q_{xx}+30|q|^4q_x. \end{array} \end{aligned}$$

(1.3)

and $\varepsilon$ is an arbitrary real parameter and can be varied and set close to an experimental value. This flexibility allows us to make reasonable adjustments for the actual physical phenomenon to be approximated in future experiments. Here x is the propagation variable, and t is the transverse variable (time in a moving frame). The function |q(x, t)| is the envelope of the waves. A series of works on this equation have been done including the Darboux transformation [50], conservation laws [51], breather solutions [52], and breather-to-soliton conversions [53].

Well recent studies suggest that advanced improvement in NLS equation could lead to some qualitatively new characteristics for rogue waves and breathers [54, 55]. Increasing the value of higher-order terms causes the observation of the compression effects of the breathers in the LPD equation [56]. These effects could make the rogue wave twisted in the Sasa–Satsuma equation [57,58,59]. The state transitions among breathers and other types of nonlinear waves such as the multipeak soliton, anti-dark soliton, periodic wave and W-shaped soliton can appear as a result of the existence of the higher-order effects [53, 60,61,62,63,64,65,66,67]. And the rogue waves can be also converted into the W-shaped solitons [68, 69]. In particular, the higher-order effects affect the MI, the growth rate of which shows a nonuniform distribution characteristic in the low perturbation frequency region and opens up a stability region as the background frequency changes [63,64,65,66,67,68,69].

In the present work, based on the QNLS equation, we mainly concentrate the dynamics of the SRB solutions and their state transition induced by the fifth-order effects. By means of the Darboux transformation, we first show that the SRB solutions still exist in the NLS equation in spite of the fifth-order dispersion with matching higher-order nonlinear terms. Further, we transform the SRBs into the multipeak solitons while keep the small localized perturbation unchanged. Such transition occurs under a special condition where the radial and angle satisfy a transition equation. The transformed solitons are expected to be observed in future optical experiments. We finally reveal the relationship between transformed soliton and linear MI.

2 The SRB solutions and state transitions

In this section, via the Darboux transformation and method in Refs. [38, 39], we discuss the characteristics of the SRB solutions for the QNLS equation. Due to the fifth-order dispersion with matching higher-order nonlinear terms, we show that the SRB solutions can be transformed into other two types of ones, i.e., the multipeak soliton solution and hybrid solution.

2.1 The SRB solutions

Equation (1.1) is the compatibility condition for the following overdetermined linear system for a matrix function $\varPsi$ [50]

$$\begin{aligned} \begin{aligned}&\varPsi _x=U \varPsi =(\lambda U_0+U_1) \varPsi ,\\&\varPsi _t=V \varPsi =\left( \begin{array}{cc} A &{} B \\ -\,B^* &{} -\,A \\ \end{array} \right) \varPsi , \end{aligned} \end{aligned}$$

(2.1)

with U and V being $2\times 2$ matrices,

$$\begin{aligned} \varPsi =&(\varphi , \psi )^\mathrm{T},\\ U_0=&\left( \begin{array}{cc} -i &{}\quad 0 \\ 0 &{}\quad i \\ \end{array} \right) ,\qquad U_1=\left( \begin{array}{cc} 0 &{}\quad q \\ -q^* &{}\quad 0 \\ \end{array} \right) ,\\ A=&-16 i \lambda ^5 \varepsilon +8 i \lambda ^3 \varepsilon |q|^2\\&+4\lambda ^2 \varepsilon \left( q q_x^*-q_xq^*\right) -i \lambda ^2\\&-2 i \lambda \varepsilon \left( q q_{xx}^*+q^* q_{xx}-|q_x|^2+3|q|^4\right) \\&+\frac{1}{2} i |q|^2 \\&+\varepsilon \left( q^* q_{xxx}-q q_{xxx}^*+q_x q_{xx}^*-q_{xx} q_x^*\right. \\&\left. +\,6|q|^2 q^*q_x-6|q|^2q_x^*q\right) ,\\ B=&16 \lambda ^4 \varepsilon q+8 i \lambda ^3 \varepsilon q_x-4 \lambda ^2 \varepsilon \left( q_{xx}+2|q|^2 q\right) \\&-2 i \lambda \varepsilon \left( q_{xxx}+6 |q|^2 q_x\right) +\lambda q\\&+\varepsilon \left( q_{xxxx}+8 |q|^2 q_{xx}\right. \\&+\left. 2 q^2 q_{xx}^*+4 |q_x|^2 q+6 q_x^2 q^*+6 |q|^4 q\right) \\&+\frac{1}{2} i q_x, \end{aligned}$$

where $\lambda$ is an eigenvalue parameter and $\varphi$ and $\psi$ are two linear complex functions. Using the Darboux transformation, we can give the N-order solutions of Eq. (1.1)

$$\begin{aligned} q^{[n]}=q^{[0]}-2\,i\,\frac{\varDelta _{1}}{\varDelta }, \end{aligned}$$

(2.2)

with

$$\begin{aligned} \begin{aligned}&\varDelta _{1}=\begin{vmatrix} \varphi _{1}&\psi _{1}&\cdots&\lambda _{1}^{n-2} \varphi _{1}&\lambda _{1}^{n-2}\psi _{1}&\lambda _{1}^{n-1} \varphi _{1}&\lambda _{1}^{n} \varphi _{1}\\ \varphi _{2}&\psi _{2}&\cdots&\lambda _{2}^{n-2} \varphi _{2}&\lambda _{2}^{n-2} \psi _{2}&\lambda _{2}^{n-1} \varphi _{2}&-\lambda _{2}^{n} \varphi _{2}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ \varphi _{2n}&\psi _{2n}&\cdots&\lambda _{2n}^{n-2} \varphi _{2n}&\lambda _{2n}^{n-2} \psi _{2n}&\lambda _{2n}^{n-1} \varphi _{2n}&-\lambda _{2n}^{n} \varphi _{2n} \end{vmatrix},\\&\varDelta =\begin{vmatrix} \varphi _{1}&\psi _{1}&\cdots&\lambda _{1}^{n-2} \varphi _{1}&\lambda _{1}^{n-2}\psi _{1}&\lambda _{1}^{n-1} \varphi _{1}&\lambda _{1}^{n-1} \psi _{1}\\ \varphi _{2}&\psi _{2}&\cdots&\lambda _{2}^{n-2} \varphi _{2}&\lambda _{2}^{n-2} \psi _{2}&\lambda _{2}^{n-1} \varphi _{2}&\lambda _{2}^{n-1} \psi _{2}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ \varphi _{2n}&\psi _{2n}&\cdots&\lambda _{2n}^{n-2} \varphi _{2n}&\lambda _{2n}^{n-2} \psi _{2n}&\lambda _{2n}^{n-1} \varphi _{2n}&\lambda _{2n}^{n-1} \psi _{2n} \end{vmatrix}. \end{aligned} \end{aligned}$$

Hereby, $q^{[0]}$ is a certain particular solution of Eq. (1.1) and $\varPsi _{j}=(\varphi _{j}, \psi _{j})^\mathrm{T}$ are the fundamental matrix solutions of Lax Pair (2.1). Choosing N complex numbers $\lambda _{j}$ corresponding to $\varPsi _{j}$, we can obtain the new solution of Eq. (1.1) by Expression (2.2).

In order to obtain the breather solutions, we consider the plane-wave solution $q^{[0]}=c\,\mathrm{e}^{i\,(a\,x+b\,t)}$ as the initial one, where c, b and a represent the amplitude, wave number and frequency, respectively. Further, to facilitate the SRB solutions, we perform the Joukowsky transform to $\lambda$ as follows

$$\begin{aligned} \lambda =- i \frac{c}{2}\left( \xi +\frac{1}{\xi }\right) -\frac{a}{2}, \qquad \xi =R\,\mathrm{e}^{i\,\alpha }, \end{aligned}$$

(2.3)

which maps the plane of $\lambda$ onto the outer part of the circle of unit radius. The parameters R (radius) and $\alpha$ (angle) are the polar coordinates of the point. Then, the first-order breather solution can be written in the following form ($n=1$):

$$\begin{aligned} q_{B}^{[1]}=c\left( 1-2\left( R+\frac{1}{R}\right) \cos \alpha \,\frac{\varphi _{1}\psi _{1}^{*}}{|\varphi _{1}|^{2}+|\psi _{1}|^{2}}\right) \,q^{[0]}, \end{aligned}$$

(2.4)

with

$$\begin{aligned} \lambda _{1}= & {} -\frac{a}{2}+\frac{c}{2}\left( R-\frac{1}{R}\right) \sin \alpha -i\,\frac{c}{2}\left( R+\frac{1}{R}\right) \cos \alpha ,\\ h_R= & {} \frac{c}{2}\left( R-\frac{1}{R}\right) \cos \alpha ,h_I=\frac{c}{2}\left( R+\frac{1}{R}\right) \sin \alpha ,\\ \omega _R= & {} 2(-a+5\,a^{4}\,\varepsilon -40\,a^{2}\,c^{2}\,\varepsilon +16\,c^{4}\,\varepsilon )\\&-\,c\,(R-R^{-1})(1-20\,a^{3}\,\varepsilon +50\,a\,c^{2}\,\varepsilon )\sin {\alpha }\\&+\,4\,c^{2}(-5\,a^{2}+3\,c^{2})(R^{2}+R^{-2})\varepsilon \,\cos {2\alpha }\\&-\,10\,a\,c^{3}(R^{3}-R^{-3})\varepsilon \sin {3\alpha }\\&+\,2\,c^{4}\,(R^{4}+R^{-4})\varepsilon \cos {4\alpha },\\ \omega _I= & {} -c\,(R+R^{-1})(1-20\,a^{3}\,\varepsilon +50\,a\,c^{2}\,\varepsilon )\cos {\alpha }\\&-\,4\,c^{2}(-5\,a^{2}+3\,c^{2})(R^{2}-R^{-2})\varepsilon \,\sin {2\alpha }\\&-\,10\,a\,c^{3}(R^{3}+R^{-3})\varepsilon \cos {3\alpha }\\&-\,2\,c^{4}\,(R^{4}-R^{-4})\varepsilon \sin {4\alpha }, \end{aligned}$$

In Eq. (2.4), the parameters $\theta$ and $\mu$, respectively, define the location and phase of the breather. The group velocity and phase velocity of the breather can be given by

$$\begin{aligned} \quad \,V_{\mathrm{ph}}=-\frac{h_{R}\,\omega _{I}}{h_{I}}-\omega _{R},\quad V_{\mathrm{gr}}=-\omega _{R}+\frac{h_{I}\,\omega _{I}}{h_{R}}.\quad \end{aligned}$$

(2.5)

Similarly, the second-order breather solution via Expression (2.2) can be given by ($n=2$)

$$\begin{aligned} q_{B}^{[2]}=c\bigg (1-i\,\bigg (R^{2}-\frac{1}{R^{2}}\bigg )\sin 2\alpha \,\frac{N_{R}+i N_{I}}{\varDelta }\bigg )\,\mathrm{e}^{i\,\rho }, \end{aligned}$$

(2.6)

with

$$\begin{aligned} N_{R}= & {} \left( R+\frac{1}{R}\right) \cos \alpha \left[ \left( |\psi _{1}|^{2}-\right. |\varphi _{1}|^{2}\right) \varphi _{2}\psi _{2}^{*}\\&+\left. \,\left( |\varphi _{2}|^{2}-|\psi _{2}|^{2}\right) \varphi _{1}\psi _{1}^{*}\right] , \\ N_{I}= & {} -\left( R-\frac{1}{R}\right) \sin \alpha \left[ \left( |\psi _{1}|^{2}+|\varphi _{1}|^{2}\right) \varphi _{2}\psi _{2}^{*}\right. \\&+\,\left( |\varphi _{2}|^{2}+|\psi _{2}|^{2}\right) \left. \varphi _{1}\psi _{1}^{*}\right] , \\ \varDelta= & {} \sin ^{2}\alpha \left( R-\frac{1}{R}\right) ^{2}(|\varphi _{1}|^{2}|\varphi _{2}|^{2}+|\psi _{1}|^{2}|\psi _{2}|^{2})\\&+\,4\,\cos ^{2}\alpha (|\varphi _{1}|^{2}|\psi _{2}|^{2}+|\psi _{1}|^{2}|\varphi _{2}|^{2})\\&-\,\cos ^{2}\alpha \left( R+\frac{1}{R}\right) ^{2}(\varphi _{1}\psi _{2}\psi _{1}^{*}\varphi _{2}^{*}+\psi _{1}\varphi _{2}\varphi _{1}^{*}\psi _{2}^{*})\\&+\,\left( R-\frac{1}{R}\right) ^{2}(|\varphi _{1}|^{2}|\psi _{2}|^{2}+|\psi _{1}|^{2}|\varphi _{2}|^{2}),\\ \varphi _{1}= & {} \frac{\mathrm{e}^{A_{1}-i\,\alpha }}{R}+\mathrm{e}^{-A_{1}},\psi _{1}=\frac{\mathrm{e}^{-A_{1}-i\,\alpha }}{R}+\mathrm{e}^{A_{1}},\\ A_{1}= & {} h\,x+\omega \,t+\frac{1}{2}(\mu _{1}-i\,\theta _{1}),\\ \varphi _{2}= & {} \frac{\mathrm{e}^{A_{2}-i\,\alpha }}{R}+\mathrm{e}^{-A_{2}},\psi _{2}=\frac{\mathrm{e}^{-A_{2}-i\,\alpha }}{R}+\mathrm{e}^{A_{2}},\\ A_{2}= & {} h^{*}\,x+\omega ^{\star }\,t+\frac{1}{2}(\mu _{2}-i\,\theta _{2}),\\ \\ \omega ^{\star }= & {} h^*(\omega ^{\star }_R+i\,\omega ^{\star }_I)\\= & {} h^*\,\left[ 2 a^4 \varepsilon -4 a^3 \lambda _2 \varepsilon +8 a^2 \varepsilon \left( \lambda _2 ^2-3 c^2\right) \right. \\&+\,a \left( 24 c^2 \lambda _2 \varepsilon -16 \lambda _2 ^3 \varepsilon -1\right) \\&\left. +\,2 \left( 6 c^4 \varepsilon -8 c^2 \lambda _2 ^2 \varepsilon +\lambda _2 +16 \lambda _2 ^4 \varepsilon \right) \right] . \end{aligned}$$

In fact, solution (2.6) includes two sets of parameters $R_{j}$, $\alpha _{j}$, $\theta _{j}$ and $\mu _{j}$ for $j=1, 2$. Hereby, we only consider the case $R_{1}=R_{2}=R$ and $\alpha _{1}=-\,\alpha _{2}=\alpha$ for the SRBs in opposite directions. This is depicted in Fig. 1.

Fig. 1

(Color online) Uniformization of symmetrical eigenvalue parameters of second-order breather with the help of Joukowsky transform with the same small parameter $\sigma$ and symmetrical angle $\alpha$

Fig. 2

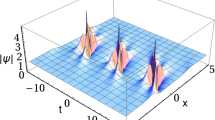
(Color online) Intensity distribution of fundamental modes $(I=|q|^2)$ with the same $\alpha$ (= $\pi /3$) as $R\rightarrow 1.5$. a Akhmediev breather ($R=1$), b quasi-Akhmediev breather ($R=1.2$), c general breather ($R=1.5$). The solid lines represent the group velocity $V_{\mathrm{gr}}$, while the dashed lines describe the phase velocity $V_{\mathrm{ph}}$

Solutions (2.4) and (2.6) describe different types of nonlinear waves depending on the values of the parameters R and $\alpha$. The case $R>1$ and $\alpha =0$ is response for the Kuznetsov–Ma breather, while $R=1$ and $\alpha \ne 0$ give rise to the Akhmediev breather. When $\alpha \rightarrow 0$, solution (2.4) describes the Peregrine rogue wave. In addition, we set $R=1+\sigma$ ($\sigma$ is a small parameter), which could lead to the observation of quasi-annihilation at the moment of collision. Conversely, the case $R=1$ will cause two Akhmediev breathers with opposite values of angular parameter completely annihilate each other. In order to illustrate the effect of R on the breather more clearly, Fig. 2 is plotted to show the conversion process from a Akhmediev breather ($R=1$) to a quasi-Akhmediev breather ($R=1.2$) to a general breather ($R=1.5$) as the value of R grows. Two additional phase-shift parameters $\theta$ and $\mu$ affect the shape and amplitude of the perturbation. The degree of complexity of the wave profile at the area of collision depends on the difference between $\theta _{1}+\theta _{2}$ and $\pi$. For example, the most effective annihilation appears when $\theta _{1}+\theta _{2}$ approaches $\pi$. This will allow us to observe the SRBs. For the detailed discussion of the effects of parameters $\theta$ and $\mu$, one can refer to Refs. [38, 39].

Fig. 3

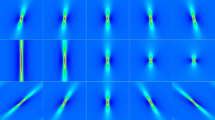
(Color online) Intensity distribution $(I=|q|^2)$ of a first-order quasi-AB and the three modes of second-order breather solution ($R=1.13$, $\alpha =0.6$, $\mu _{1,2}=0$, $c=1$, $a=0.5$ and $\varepsilon =0.1$) with the following phase shifts: b ghost case: $\theta _{1,2}=0$, c amplification case: $\theta _{1,2}=\pi$, d superregular case: $\theta _{1,2}=\frac{\pi }{2}$. Notice that the amplitudes $|q^{[2]}(0,0)|^{2}$ are b 5.4104, c 18.7145, d 1.1636, respectively

In Fig. 3a, we display the first-order breather solution of the QNLS equation with $R=1.13$, $\alpha =0.6$, $\mu _{1,2}=0$, $c=1$, $a=0.5$ and $\varepsilon =0.1$. This type of solution is periodic in neither time nor space while it is periodic along the line connecting the peak maxima. Figure 3b describes the ghost interaction of breathers. The collision point is just another maximum of either breather solution. Each breather then appears seemingly without influence of the collision process. Figure 3c characterizes the synchronized collision between two SRBs from which we can observe a second-order rogue wave at the origin. Figure 3d is plotted for the quasi-annihilation of SRBs at the origin. Such phenomena correspond to the cases $\theta _{1,2}=0$, $\theta _{1,2}=\frac{\pi }{2}$ and $\theta _{1,2}=\pi$, respectively. And $\mu _{1,2}=0$, $R=1.13$ and $\alpha =0.6$ for all cases. Hereby, we are particularly focused on the last interaction since it has more physical and practical significance. It is well known that the Akhmediev breathers develop from periodic perturbations in Benjamin–Feir instability that require the whole infinite space [40]. While the two quasi-Akhmediev breathers reduce to a small localized perturbation (LP) of the background at time zero, which is shown in Fig. 4 clearly. Further, the perturbation $\delta q=1-q^{[2]}$ on the continuous wave can be approximated by

$$\begin{aligned} \begin{aligned}&\delta q=q_{B}^{[2]}-c\,\mathrm{e}^{i\,\rho }\\&\approx 4\,i\,c\,\sigma \frac{\cosh {(i\,\alpha +2\,V_{G}\,h_{R}t)}\cos (2\,\sin \alpha \,x-\frac{\theta _{1}-\theta _{2}}{2})}{\cosh (2\,\sigma \,x\,\cos \alpha )}, \end{aligned} \end{aligned}$$

(2.7)

the temporal width of which increases with decreasing $\sigma$, whereas the amplitude decreases. This means that the small parameter $\sigma$ plays an important role in the LP. Note that $\delta q$ possesses a perturbed frequency $2\sin \alpha$.

Fig. 4

(Color online) The development of the quasi-annihilation of breathers with the same parameters as in Fig. 3d. Red solid line is small perturbation at the moment $t=0$. Blue dashed line is the breathers solution at the moment $t=5$

Despite the fifth-order dispersion and nonlinearity terms, the SRB solutions still exist in the QNLS equation. Additionally, these terms have no influence on the small LP, at first glance. However, as previous studies pointed out, the higher-order effects can lead to the state transition between breather and soliton [53, 60, 62,63,64]. Therefore, we will expect to observe some new phenomena in next part.

Fig. 5

(Color online) Phase diagrams of fundamental nonlinear modes in the Re($\xi$)–Im($\xi$) plane ($\xi = R$ $\mathrm{e}^{i\alpha }$) with (a) $a\ne a_{s1}$ and (b) $a= a_{s1}$. a shows well-known breathing modes including “GB” (general breather), “QAB” (quasi-Akhmediev breather),“AB” (Akhmediev breather), “KMB” (Kuznetsov–Ma breather), and “PRW” (Peregrine rogue wave), while for the same pole (i.e., the same R, $\alpha$), b displays non-breathing modes including “MPS” (multipeak soliton), “QPW” (quasiperiodic wave), “PW” (periodic wave), “SPS” (single-peak soliton), and “WSS” (W-shaped soliton)

2.2 The multipeak soliton solution

As shown in Ref. [53], the breathers can be converted into solitons when the fifth-order dispersion parameter $\varepsilon$, real part $\lambda _{r}$, and imaginary part $\lambda _{i}$ of the eigenvalue satisfy the following equation [53]

$$\begin{aligned} \begin{aligned}&2\,\varepsilon [a^{3}-4\,a^{2}\lambda _{r}-2\,a(3\,c^{2}-6\,\lambda _{r}^{2}+2\,\lambda _{i}^{2})\\&\quad +\,8\lambda _{r}(c^{2}-4\,\lambda _{r}^{2}+4\,\lambda _{i}^{2})]=1\,\qquad i=1, 2. \end{aligned} \end{aligned}$$

(2.8)

Here, Eq. (2.8) is formulated in polar coordinate form to facilitate the transformation. To convert two quasi-Akhmediev breathers into solitons completely, we use two different sets of values of the radius and angle as follows

$$\begin{aligned} R_1= & {} 1+\sigma _1, \,\,\,R_2=1+\sigma _2, \,\,\,\nonumber \\ \sigma _1\ne & {} \sigma _2, \,\,\,\alpha _1\ne -\alpha _2. \end{aligned}$$

(2.9)

In this case, Eq. (2.8) can be expressed in forms of

$$\begin{aligned} \begin{aligned} \varepsilon&=R_i^3\Big /\bigg [4 \sin (\alpha _{i} ) \left( 2 R_i^2 \left( R_i^2-1\right) \left( 5 a^2-c^2-2\right) -1\right) \\&~~~~~+10 a R_i \left( 2 R_i^2 \left( a^2-c^2-2\right) +R_i^4 +1\right) \\&~~~~~-4 R_i \left( R_i^4-R_i^2+1\right) \cos (2 \alpha _{i} ) (5 a+2 R_i \sin (\alpha _{i} ))\\&~~~~~+4 \sin (3 \alpha _{i} )\bigg ], \,\,i=1, 2. \end{aligned} \end{aligned}$$

(2.10)

Equation (2.10) is the state transition equation in polar coordinates. It includes four important parameters, namely the radius R, the angle $\alpha$, the frequency a and the higher-order term $\varepsilon$. Thus, for the given $\varepsilon$ and a, we can realize the state transition by the manipulation of the other two parameters $R_{i}$ and $\alpha _{i}$. On the other hand, one can easily check that Eq. (2.10) is equivalent to the condition

$$\begin{aligned} \begin{aligned} V_{\mathrm{gr}, i}=V_{\mathrm{ph}, i}, \qquad i=1, 2. \end{aligned} \end{aligned}$$

(2.11)

Interestingly, Eq. (2.11) suggests that the transformed solitons appear as a result of the case where the group velocity and phase velocity of the SRB solution have an equal value. Note that both $V_{\mathrm{gr}, i}$ and $V_{\mathrm{ph}, i}$ are related to the frequency a that can be flexibly adjusted. So we can satisfy condition (2.11) by controlling the value of a. Solving Eq. (2.11), we obtain the values of $a_{i}=a_{s,i}$ for $i=1, 2$. For the fixed $R_{i}$, $\alpha _{i}$ and $\varepsilon$, using $a_{i}=a_{s,i}$ in Eq. (2.10) will lead to the conversion between the SRBs and solitons. Therefore, we have different routes to realize the state transition by the manipulation of the eigenvalue ($R_{i}, \alpha _{i}$) or the frequency a. Similar to the case in Refs. [63, 64], the solitons also have different types of nonlinear modes with the corresponding eigenvalues. Hereby, we demonstrate the phase diagrams of fundamental nonlinear modes in Fig. 5.

The independence of the two sets of eigenvalue parameters ($R_{i}$ and $\alpha _{i}$, $i=1, 2$) allows us to conveniently control the two transformed solitons. But these two eigenvalue parameters should be associated with the same values of $\varepsilon$ and a. Each set of $R_{i}$ and $\alpha _{i}$ meeting Eq. (2.10) can turn a SRB into a multipeak soliton. However, we have to require the amplitude of the small LP almost unchanged after the conversion except for its shape. This means that not all values of $R_{i}$ and $\alpha _{i}$ are suitable for transformations. Only the $R_{i}$ and $\alpha _{i}$ whose values do not significantly increase the amplitude of the small LP can be considered. On the other hand, the two quasi-Akhmediev breathers are required to have different group velocity to prevent the overlap. In addition to R and $\alpha$, one can find the group velocity is related to three other parameters, namely a, c and $\varepsilon$. The parameter c denotes the background amplitude and is generally taken as 1 while $\varepsilon$ is a system parameter. Consequently, we mainly control the group velocity of the two SRBs by adjusting the value of the frequency a. The condition

$$\begin{aligned} \begin{aligned} V_{\mathrm{gr}, i}=V_{\mathrm{gr}, j}, \quad i\ne j. \end{aligned} \end{aligned}$$

(2.12)

will result in the overlap of two SRBs which have been studied in Ref. [60]. Solving Eq. (2.12) with respect to a, we have $a=a_{f}$. We omit this case since it does not involve LP. Instead, under the condition

$$\begin{aligned} \begin{aligned} V_{\mathrm{gr}, i}\approx V_{\mathrm{gr}, j}, \qquad i\ne j, \end{aligned} \end{aligned}$$

(2.13)

the group velocity of one of solitons is closed to that of another one. This could allow us to observe some novel nonlinear modes in the nonlinear stage of MI. Therefore, we consider the case $a\approx a_{f}$. It should be pointed out that we fail to obtain $a_{f}$ analytically due to the computational complexity. However, we show how the parameter a affects the group velocity and phase velocity in Fig. 6. Conditions (2.11), (2.12) and (2.13), respectively, correspond to the cases $a=a_{s,i}$, $a=a_{f}$, and $a\approx a_{f}$. So in conclusion, we can choose the suitable value of the frequency a to manipulate the dynamics of the SRBs and solitons.

Fig. 6

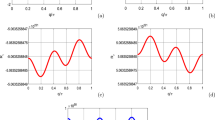
(Color online) Evolution of $V_{\mathrm{gr},i}$ and $V_{\mathrm{ph},i}$ ($i = 1, 2$) with a. The conditions $V_{\mathrm{gr}, i}=V_{\mathrm{ph}, i}$, $V_{\mathrm{gr}, i}=V_{\mathrm{gr}, j}$ and $V_{\mathrm{gr}, i}\approx V_{\mathrm{gr}, j}$, respectively, correspond to the cases $a=a_{s,i}$, $a=a_{f}$, and $a\approx a_{f}$

Fig. 7

(Color online) a The quasi-annihilation of two multipeak solitons (they have the similar velocities) propagating in same directions with $R_{1}=1.03$, $R_{2}=1.08$, $\alpha _{1}=0.6$, $\alpha _{2}=0.715$, $\mu _{1,2}=0$, $\theta _{1,2}=\frac{\pi }{2}$, $c=1$, $a=0.5$ and $\varepsilon =-\,0.049$. b is the global scenario of development of a small localized perturbation. A small localized perturbation experiences two major phases of developments, i.e., the beating pattern and two multipeak soliton state

As mentioned, the solution of Eq. (2.10) is complicated and has to be found numerically. Solving Eq. (2.10) for a fixed values of $\varepsilon$ and a (for example $\varepsilon =-\,0.049$ and $a=0.5$) provides us with two solutions, i.e., $R_{1}=1.03$, $\alpha _{1}=0.6$ and $R_{2}=1.08$, $\alpha _{2}=0.715$. In this case, the two transformed solitons have the similar velocity but they do not overlap. The corresponding wave profile is shown in Fig. 7a from which we observe that two quasi-Akhmediev breathers are converted into the stable multipeak solitons in the same direction over a period of time. Fig. 7b depicts a global scene of collision between two multipeak solitons clearly. The fifth-order dispersion and nonlinear term inhibit the periodic oscillations of the SRBs during their propagations. We also note that these two solitons have the same propagation direction, which breaks the limit of definition of SRB in opposite directions in Refs. [38, 39]. Unfortunately, we have not found the transformed solitons with different directions since this case will produce a larger LP. Such case is worth further study. Another interesting phenomenon is that a beating pattern appears before the formation of the multipeak solitons, which is depicted in Fig. 8a. The beating patterns are formed by the nonlinear superposition of two general breathers, as reported in Refs. [52, 60]. This occurs when the directions of propagation of the two colliding breathers coincide. Nevertheless, the velocities of two waves in Fig. 7a are similar but not identical. Thus, the beating pattern is different from the previous ones and shows the feature of the short-lived life. As shown in Fig. 8b, at the branch point (BP), the beating structure is beginning to divide into two multipeak solitons. It is difficult to give the position of this point analytically. It may be associated with the separation distance between the two waves. Hereby, we define the position of the BP on which two main peaks of the solitons are formed and present its coordinate numerically ($t=141.14$, $x=213.47$).

Fig. 8

(Color online) a The beating pattern [area A in enlarged Fig. 7a]. b The BP [area B in enlarged Fig. 7a]

Fig. 9

Quasi-annihilation of a multipeak soliton and a superregular breather with $R_{1}=R_{2}=1.13, \alpha _{1}=-\,\alpha _{2}=0.6, \mu _{1,2}=0, \theta _{1,2}=\frac{\pi }{2}, c=1, a=-\,0.1271$ and $\varepsilon =0.1$. b is the cross-sectional view of a at $t=0$ and $t=20$

2.3 The hybrid solution

In this part, we are concerned with another type of state transition that only involves one multipeak soliton. In this case, the eigenvalue parameters meet the following condition

$$\begin{aligned} R_{1}=R_{2}=R=1+\sigma , \qquad \alpha _{1}=-\alpha _{2}=\alpha . \end{aligned}$$

(2.14)

The above relation indicates that the two sets of parameters ($R_{j}, \alpha _{j}$) for $j=1, 2$ relate to each other. The values of the radiuses are equal, while the angles are antisymmetric. Consequently, if one of quasi-Akhmediev breathers is converted into a soliton, then the other one cannot be transformed. The governing equation for such transition is given by

$$\begin{aligned} \begin{aligned} \varepsilon&=R^3\Big /\bigg [4 \sin (\alpha ) \left( 2 R^2 \left( R^2-1\right) \left( 5 a^2-c^2-2\right) -1\right) \\&~~~~~+10 a R \left( 2 R^2 \left( a^2-c^2-2\right) +R^4 +1\right) \\&~~~~~-4 R \left( R^4-R^2+1\right) \cos (2 \alpha ) (5 a+2 R \sin (\alpha ))\\&~~~~~+4 \sin (3 \alpha )\bigg ], \end{aligned} \end{aligned}$$

(2.15)

which is equivalent to the following relation

$$\begin{aligned} \begin{aligned}&V_{\mathrm{ph},1}=V_{\mathrm{gr},1}. \end{aligned} \end{aligned}$$

(2.16)

As depicted in Fig. 9, one can observe the collision between a stable multipeak soliton and a breather with fast group velocity in opposite directions. The two waves reduce to a small localized perturbation of the background at time zero as before. This again confirms the fact that the higher-order effects can lead to more nonlinear wave patterns. In addition, by selecting the suitable values of $R_{i}$ and $\alpha _{i}$ for $i=1, 2$, we could observe other types of nonlinear waves such as the anti-dark solitons, W-shaped solitons and M-shaped solitons in the nonlinear stage of MI.

3 The relation between state transition and linear MI

To reveal the relation between the state transition and linear MI, we perform the linear stability analysis of the background wave $q^{[0]}$ via adding small-amplitude perturbed Fourier modes p, i.e., $q_{p} = [c + p]\mathrm{e}^{i \rho }$, where $p = f_{+}\mathrm{e}^{i(\varLambda x-\varOmega t)} + f_{-}^{*} \mathrm{e}^{-i(\varLambda x-\varOmega ^{*} t)}$ with small amplitudes $f_{+}$, $f_{-}^{*}$, perturbed frequency $\varLambda$, and wave number $\varOmega$. Substituting the perturbed solution $q_{p}$ into Eq. (1), followed by the linearization process in Refs. [68, 69], leads to the following dispersion relation

$$\begin{aligned} \begin{aligned} \varOmega =&\varLambda \,[a-5\,a^{4}\,\epsilon +10\,a^{2}\,\epsilon \,(6\,c^{2}-\varLambda ^{2})\\&-\epsilon \,(30\,c^{4}-10\,c^{2}\,\varLambda ^{2}\,+\varLambda ^{4})]\\&\pm \,\frac{\sqrt{\varLambda ^{2}-4\,c^{2}}}{2}\Big |\varLambda [1-10\,a\,\epsilon (2\,a^{2}-6\,c^{2}+\varLambda ^{2})]\Big |. \end{aligned} \end{aligned}$$

(3.1)

MI exists when $\mathrm{Im}(\varOmega )>0$ (thus MI exists in the region $\varLambda <2c$ with $\varLambda [1-10\,a\,\epsilon (2\,a^{2}-6\,c^{2}+\varLambda ^{2})]\ne 0)$ and is described by the growth rate $G=k\, \mathrm{Im}(\varOmega )>0$ , where $k>0$ is a real number. Namely, a small-amplitude perturbations in this case suffer MI and grow exponentially like $\exp (G\,t)$ at the expense of pump waves.

Fig. 10

(Color online) Distribution of linear MI growth rate $G=k\,\mathrm{Im}(\varOmega )>0$ on $(\varLambda ,a)$ plane with $c=1$, $\epsilon =0.1$, $k=2$. The abscissa values of the red points in (10) correspond to three roots of Eq. (3.3), namely $a_{j}$ for $j=1, 2, 3$

As mentioned, $\delta q$ possesses a perturbed frequency $\varLambda =2\sin \alpha$ which belongs to the linear MI region $|\varLambda |<2$. Conversely, the MI is absent and the small perturbation cannot be amplified. In addition, the transformed solitons generated from the SRB solutions have close relations with the linear MI in the presence of higher-order effects. Figure 10 shows the MI growth rate distribution with $\varepsilon \ne 0$. It is obviously found that the higher-order effects affect the distribution characteristic of MI growth rate in the subregion $-\,2<\varLambda <2$. There are three asymmetric modulation stability (MS) regions where the corresponding MI growth rate is equal to zero. Further, the MS regions can be given analytically by

$$\begin{aligned} \epsilon =\frac{1}{10\,a\left( 2\,a^{2}-6\,c^{2}+\varLambda ^{2}\right) }, \end{aligned}$$

(3.2)

which is shown by the solid lines in Fig. 10. If the value of $\varLambda$ in Eq. (3.2) is closed to zero, we have

$$\begin{aligned} \epsilon =\frac{1}{10\,a\left( 2\,a^{2}-6\,c^{2}\right) }. \end{aligned}$$

(3.3)

Solving Eq. (3.2) with respect to a, we have

$$\begin{aligned} \,a_{1}= & {} -\frac{1}{2}\left( \frac{4\times 5^{\frac{1}{3}}\,c^{2}\epsilon }{M^{\frac{1}{3}}}+\frac{M^{\frac{1}{3}}}{5^{\frac{1}{3}}\,\epsilon }\right) , \end{aligned}$$

(3.4a)

$$\begin{aligned} \,a_{2}= & {} \frac{5^{\frac{1}{3}}\,(1+i\,\sqrt{3})\,c^{2}\epsilon }{M^{\frac{1}{3}}}+\frac{(1-i\,\sqrt{3})\,M^{\frac{1}{3}}}{4\times 5^{\frac{1}{3}}\,\epsilon }, \end{aligned}$$

(3.4b)

$$\begin{aligned} \,a_{3}= & {} \frac{5^{\frac{1}{3}}\,(1-i\,\sqrt{3})\,c^{2}\epsilon }{M^{\frac{1}{3}}}+\frac{(1+i\,\sqrt{3})\,M^{\frac{1}{3}}}{4\times 5^{\frac{1}{3}}\,\epsilon }, \end{aligned}$$

(3.4c)

with

$$\begin{aligned} M=-\,\epsilon ^{2}+\sqrt{\epsilon ^{4}-1600\,c^{6}\epsilon ^{6}}. \end{aligned}$$

Interestingly, state transition condition (2.8) can also be converted into Eq. (3.3) as we consider the rogue wave eigenvalue $\lambda =-\frac{a}{2}+c\,i$. In this case, the SRBs are transformed into the W-shaped solitons. This indicates that the W-shaped solitons appears in a MS region where the perturbation frequency satisfies $\varLambda =0$ and the frequency of the background wave $a=a_{j}$ for $j=1, 2, 3$ [also see the red points in Fig. 10].

4 Conclusions

To conclude, we have studied the dynamics of SRB solutions governed by the QNLS equation that includes the fifth-order dispersion with matching higher-order nonlinear terms. We have shown that the SRB solutions can also exist for the QNLS equation. We have presented the multipeak soliton and hybrid solutions, both of which are caused by the higher-order effects. All three types of solutions reduced to small localized perturbations of the background at time zero. We have revealed the relationship between the state transition and the linear MI.