1 Introduction

It is well known that the modified Korteweg–de Vries (mKdV) equation is a fundamental completely integrable nonlinear partial differential equation admitted the N-soliton solution [1], and has significant applications in various physical contexts such as the generation of supercontinuum in optical fibres [2], propagation of solitons in lattice [3], nonlinear Alfvén waves propagating in plasma [4], physical experiments of ion acoustic solitons in plasmas [5] and fluid mechanics [6]. In focusing case, the mKdV equation can be written as

$$\begin{aligned} u_{t}+\alpha (6u^2u_{x}+u_{xxx})=0, \end{aligned}$$
(1)

where \(u=u(t,x)\) is a real function with evolution variable t and transverse variable x. The inverse scattering transform, Hirota bilinear technique and Darboux transformation (DT) were developed to derive the explicit N-soliton solution for Eq. (1) along the past few decades [1, 7, 8].

In recent years, the construction of rational solutions for integrable nonlinear equations has been becoming a topic of continued interesting in the description of rogue waves [9], which are originally referred to huge waves occurring erratically and unexpectedly on the ocean surfaces [10], and nowadays, they are extended in a wide range of research fields, for instance, optics [11], Bose–Einstein condensation [12], plasmas [13] and even finance [14]. Among the rogue wave theoretics, the Peregrine soliton, a simplest rational solution of the nonlinear Schrödinger (NLS) equation given over 30 years ago, plays a prototypical role in mathematics to model rogue waves in many physical branches [15]. It depicts a doubly localized (temporally and spatially) wave featuring a single hump whose amplitude is three times larger than the average crest and two holes with zero amplitude. Analytically, the Peregrine soliton can be seen as a special limiting case of the periodic Akhmediev breather [16] or Kuznetsov–Ma soliton [17, 18]. More recently, periodic solutions, rational solutions and the generation of rogue waves in Eq. (1) have been reported by many authors [19,20,21,22]. As are emphasized by them, this type of rational solutions plays the role of rogue waves in the mKdV equation and can present different descriptions in hydrodynamics from that in the NLS equation. Besides, it is noted that, these rational solutions may appear in diverse physical fields, the electromagnetic waves in quantized films, internal waves in stratified flows [23] and so on.

Since rogue wave investigations have flourish developed in several scientific fields, one should go beyond the standard NLS equation to model more general and complex physical systems. In this direction, some integrable physical systems including higher-order perturbation terms such as the Hirota equation [24,25,26] and Sasa–Satsuma equation [27] have been taken widespread attention, and actually, these equations usually possess some novel characteristics. Most notably, as we argue, the breathers and rogue waves in them can convert to new types of solitons due to the existence of the higher-order perturbation terms [28,29,30,31,32,33]. But, the standard NLS equation does not allow the conversion of breathers or rogue waves into solitons.

In this paper, we investigate an extended modified Korteweg–de Vries (emKdV) equation, which takes the form

$$\begin{aligned}&u_{t}+\alpha (6u^2u_{x}+u_{xxx})+\beta \left( 30u^4u_{x}+10u_{x}^3\right. \nonumber \\&\quad \left. +\,40uu_{x}u_{xx}+10u^2u_{xxx}+u_{xxxxx}\right) =0, \end{aligned}$$
(2)

where \(\alpha \ll 1\) and \(\beta \ll 1\) stand for the third- and fifth-order dispersion coefficients matching with the relevant nonlinear terms, respectively. As is known, the Painlevé test and multi-soliton solutions via the simplified Hirota’ direct method for Eq. (2) have been recently studied by Wazwaz and Xu [34]. In this paper, our aim is to construct the infinitely many conservation laws [35,36,37] for Eq. (2) based on its Lax pair, and to derive the periodic and rational solutions through the N-fold DT together with the limit approach [38,39,40,41,42,43,44,45,46].

The present paper is organized as follows. Section 2 gives the infinitely many conservation laws for Eq. (2) based on the Lax pair. Section 3 constructs the Nth-order periodic solution for Eq. (2) via the N-fold DT. Section 4 derives the Nth-order rational solution for Eq. (2) from the generalized DT by using the limit approach. Explicit expressions of the periodic and rational solutions from first to second order are presented, and some typical types of the nonlinear wave structures are shown. In the last section, we give the conclusions of this paper.

2 Lax pair and conservation laws

To begin with, the Lax pair of Eq. (2) can be given through the AKNS technique [47]:

$$\begin{aligned} \varPhi _{x}= & {} (\lambda \sigma _{3}+U)\varPhi ,\quad U= \left( \begin{array}{cc} 0 &{}\quad u \\ -u &{}\quad 0 \\ \end{array} \right) ,\end{aligned}$$
(3a)
$$\begin{aligned} \varPhi _{t}= & {} V\varPhi ,\quad V= \left( \begin{array}{cc} A &{}\quad B \\ C &{}\quad -A \\ \end{array} \right) , \end{aligned}$$
(3b)

where \(\sigma _{3}\) is the Pauli matrix,

$$\begin{aligned} A= & {} -16 \beta \lambda ^5-(8 \beta u^2+4 \alpha ) \lambda ^3-\left( 6 \beta u^4+2 \alpha u^2 \right. \nonumber \\&\quad \left. +\,4 \beta u u_{xx} -2 \beta u_{x}^2\right) \lambda ,\\ B= & {} -16 \beta u \lambda ^4-8 \beta u_{x} \lambda ^3-\left( 8 \beta u^3 +4 \alpha u \right. \nonumber \\&\quad +\left. 4 \beta u_{xx} \right) \lambda ^2 -(12 \beta u^2 u_{x} +2 \beta u_{xxx} \\&\quad +2 \alpha u_{x} ) \lambda -6 \beta u^5-2\alpha u^3-10 \beta u^2 u_{xx} \nonumber \\&\quad -10 \beta u u_{x}^2-\beta u_{xxxx} -\alpha u_{xx},\\ C= & {} -B(-\lambda ). \end{aligned}$$

Here \(\varPhi =(\psi ,\varphi )^T\), \(\lambda \) is a spectral parameter. From the compatibility condition \(U_{t}-V_{x}+[\lambda \sigma _{3}+U,V]=0\) one can easily get Eq. (2). In order to obtain the infinitely many conservation laws for Eq. (2), we denote \(\omega =\frac{\varphi }{\psi }\), then we can get the following Riccati equation

$$\begin{aligned} u\omega _{x}=-u^2\omega ^2-2\lambda u\omega -u^2. \end{aligned}$$
(4)

By substituting the ansatz

$$\begin{aligned} u\omega =\sum _{n=0}^{\infty }\dfrac{\omega _{n}}{(-2\lambda )^{n+1}} \end{aligned}$$
(5)

into Eq. (4) and equating the powers of \(\lambda \), we have

$$\begin{aligned} \omega _{0}=u^2,\quad \omega _{1}=uu_{x}, \end{aligned}$$
(6)

and

$$\begin{aligned} \omega _{n+1}=u\left( \dfrac{\omega _{n}}{u}\right) _{x}+\sum _{i=0}^{n-1}\omega _{i}\omega _{n-i-1},\ (n=1,2,3,\ldots ),\nonumber \\ \end{aligned}$$
(7)

which give rise to

$$\begin{aligned} \omega _{2}= & {} uu_{xx}+u^4,\quad \omega _{3}=uu_{xxx}+5u^3u_{x},\nonumber \\ \omega _{4}= & {} uu_{xxxx}+7u^3u_{xx}+11u^2u_{x}^2+2u^6,\nonumber \\ \omega _{5}= & {} u(22u^4u_{x}+9 u^2 u_{xxx}+38uu_{x}u_{xx}\nonumber \\&\quad +11u_{x}^3+u_{xxxxx}). \end{aligned}$$
(8)

Moreover, by resorting to the compatibility condition of \((\ln \psi )_{xt}=(\ln \psi )_{tx}\), we have

$$\begin{aligned} (\lambda +u\omega )_{t}=(A+B\omega )_{x}, \end{aligned}$$

then a recursive formula of the infinitely many conservation laws for Eq. (2) that satisfy

$$\begin{aligned} \partial _{t}\omega _{n}(t,x,u)=\partial _{x}J_{n}(t,x,u),\ n=0,1,\ldots , \end{aligned}$$

can be written as follows

$$\begin{aligned} J_{n}= & {} \dfrac{1}{u}\left( \dfrac{\omega _{n+4}}{2^4}B_{1}-\dfrac{\omega _{n+3}}{2^3}B_{2}+ \dfrac{\omega _{n+2}}{2^2}B_{3}\right. \nonumber \\&\left. -\dfrac{\omega _{n+1}}{2}B_{4}+\omega _{n}B_{5}\right) , \end{aligned}$$
(9)

where \(B_{j}\) (\(j=1,2,\ldots ,5\)) are the coefficients of \(\lambda ^{5-j}\) in B, \(\omega _{n}\) and \(J_{n}\) represent the conservative densities and associated flows, respectively. By inserting the first few conservative densities (6) and (8) into Eq. (9), we arrive at the first two associated flows

$$\begin{aligned} J_{0}= & {} -\alpha (3 u^4+2 u u_{xx}-u_{x}^2)-\beta (10 u^6+20 u^3 u_{xx}\nonumber \\&\quad +10 u^2 u_{x}^2+2 u u_{xxxx}-2 u_{x} u_{xxx}+u_{xx}^2),\nonumber \\ J_{1}= & {} -\alpha u (6 u^2 u_{x}+u_{xxx})-\beta u (30 u^4 u_{x}+10 u^2 u_{xxx} \nonumber \\&\quad +40 u u_{x} u_{xx}+10 u_{x}^3+u_{xxxxx}). \end{aligned}$$
(10)

3 Periodic solutions

In this section, we derive the general Nth-order periodic solution from a nonzero constant seed solution for Eq. (2) by virtue of the N-fold DT. We first present the elementary DT for Eq. (2) basing on the DT for the standard AKNS system and its relevant reductions [8].

Suppose \(\varPhi _{1}=(\psi _{1},\varphi _{1})^{T}\) be a special solution for the linear system (3) at \(u=u[0]\) and \(\lambda =\lambda _{1}\), then it is known that the following DT

$$\begin{aligned} \varPhi [1]= & {} T[1]\varPhi ,\quad T[1]=I-\frac{2\lambda _{1}}{\lambda +\lambda _{1}}\frac{\varPhi _{1}\varPhi _{1}^{T}}{\varPhi _{1}^{T}\varPhi _{1}}, \end{aligned}$$
(11)
$$\begin{aligned} u[1]= & {} u[0]+4\lambda _{1}\frac{\psi _{1}\varphi _{1}}{\psi _{1}^2+\varphi _{1}^2}, \end{aligned}$$
(12)

convert the linear system (3) into

$$\begin{aligned} \varPhi [1]_{x}&=(\lambda \sigma _{3}+U[1])\varPhi [1],\quad U[1]= \left( \begin{array}{cc} 0 &{}\quad u[1] \\ -u[1] &{}\quad 0 \\ \end{array} \right) ,\\ \varPhi [1]_{t}&=V[1]\varPhi [1],\quad V= \left( \begin{array}{cc} A[1] &{}\quad B[1] \\ C[1] &{}\quad -A[1] \\ \end{array} \right) , \end{aligned}$$

where A[1], B[1] and C[1] have the same form of polynomials with respect to \(\lambda \) as A, B and C except that the original potential u is replaced with the new one u[1], I is the unit matrix. Moreover, it is easy to check that, the inverse matrix of T[1] such that \(T[1]T[1]^{-1}=I\) can be presented in the form

$$\begin{aligned} T[1]^{-1}=I+\frac{2\lambda _{1}}{\lambda -\lambda _{1}}\frac{\varPhi _{1}\varPhi _{1}^{T}}{\varPhi _{1}^{T}\varPhi _{1}}. \end{aligned}$$
(13)

In what follows, we generalize the aforementioned elementary DT into the N-fold case. Assume that \(\varPhi _{l}=(\psi _{l},\varphi _{l})^{T}\) (\(l=1,2,\ldots ,N\)) be N special solutions for the linear system (3) at \(u=u[0]\) and \(\lambda =\lambda _{l}\). Similarly, according to iterative rule of the one-degree Darboux matrix of (11) and its inverse form (13), we can express the N-fold DT in terms of

$$\begin{aligned} T_{N}=T[N]T[N-1]\cdots T[1]=I+\displaystyle \sum _{i=1}^{N}\dfrac{D_{i}}{\lambda +\lambda _{i}},\\ \end{aligned}$$

and

$$\begin{aligned} T_{N}^{-1}=T[1]^{-1}T[2]^{-1}\cdots T[N]^{-1}=I+\displaystyle \sum _{i=1}^{N}\dfrac{E_{i}}{\lambda -\lambda _{i}}, \end{aligned}$$

where \(D_{i}=|x_{i}\rangle \langle y_{i}|\) and \(E_{i}=|v_{i}\rangle \langle w_{i}|\), here \(|\cdot \rangle \) and \(\langle \cdot |\) denote two-dimensional column vector and row vector, respectively.

Note that \(T_{N}T_{N}^{-1}=I\) leads to \(\langle y_{l}|T_{N}^{-1}|_{\lambda =-\lambda _{l}}=0\). Moreover, in view of the equation

$$\begin{aligned} \varPhi _{l}^{T}|T_{N}^{-1}|_{\lambda =-\lambda _{l}}=0, \end{aligned}$$

we can obtain \(\langle y_{l}|=\varPhi _{l}^{T}\). Thus, by resorting to \(T_{N}|_{\lambda =\lambda _{l}}\varPhi _{l}=0\) we have

$$\begin{aligned} \varPhi _{l}+\sum _{i=1}^{N}\dfrac{|x_{i}\rangle \varPhi _{i}^{T}}{\lambda +\lambda _{i}}\left| \right. _{\lambda =\lambda _{l}}\varPhi _{l}=0,~(l=1,2,\ldots ,N), \end{aligned}$$

which implies

$$\begin{aligned} (|x_{1}\rangle ,|x_{2}\rangle ,\ldots ,|x_{N}\rangle )= & {} -(\varPhi _{1},\varPhi _{2},\ldots ,\varPhi _{N})M^{-1}, M_{ij}\nonumber \\= & {} \dfrac{\varPhi _{i}^{T}\varPhi _{j}}{\lambda _{j}+\lambda _{i}},1\le i,j\le N. \end{aligned}$$

On the other hand, by returning to the definition of the N-fold Darboux transformation, we get

$$\begin{aligned} T_{Nx}+T_{N}(\lambda \sigma _{3}+U)=(\lambda \sigma _{3}+U[N])T_{N}, \end{aligned}$$

that is,

$$\begin{aligned}&\left( \displaystyle \sum _{i=1}^{N}\dfrac{D_{i}}{\lambda +\lambda _{i}}\right) _{x}+ \left( I+\displaystyle \sum _{i=1}^{N}\dfrac{D_{i}}{\lambda +\lambda _{i}}\right) (\lambda \sigma _{3}+U)\\&\quad =(\lambda \sigma _{3}+U[N])\left( I+\displaystyle \sum _{i=1}^{N}\dfrac{D_{i}}{\lambda +\lambda _{i}}\right) , \end{aligned}$$

then by comparing the coefficient of \(\lambda ^{0}\) in the above equation as \(\lambda \rightarrow +\infty \), we obtain

$$\begin{aligned} U+\left( \sum _{i=1}^{N}D_{i}\right) \sigma _{3}=\sigma _{3}\left( \sum _{i=1}^{N}D_{i}\right) +U[N], \end{aligned}$$

which gives rise to

$$\begin{aligned}&u[N]=u[0]-2\sum _{i=1}^{N}(D_{i})_{12} =u\\&\quad -2(|x_{1}\rangle ^{1},|x_{2}\rangle ^{1},\ldots ,|x_{N}\rangle ^{1})(\varphi _{1},\varphi _{2},\ldots ,\varphi _{N})^{T}, \end{aligned}$$

where \(|x_{i}\rangle ^{1}\) \((i=1,2,\ldots ,N)\) stands for the first rank of \(|x_{i}\rangle \). In addition, it can be computed from the aforementioned equations that

$$\begin{aligned} (|x_{1}\rangle ^{1},|x_{2}\rangle ^{1},\ldots ,|x_{N}\rangle ^{1})=-(\psi _{1},\psi _{2},\ldots ,\psi _{N})M^{-1}. \end{aligned}$$

At this point, through the simple calculation, we can rewrite the expressions of T[N] and u[N] as the compact determinant forms, we conclude that

$$\begin{aligned} \varPhi [N]= & {} T_{N}\varPhi ,T_{N}=I-XM^{-1}(\lambda I+S)^{-1}X^{T}, \end{aligned}$$
(14)
$$\begin{aligned} u[N]= & {} u[0]-2\sum _{i=1}^{N}(D_{i})_{12}=u[0]-2\frac{\det (M_{1})}{\det (M)},\nonumber \\ \end{aligned}$$
(15)

where \(X=(\varPhi _{1},\varPhi _{2},\ldots ,\varPhi _{N}),S=\mathrm{diag}(\lambda _{1},\lambda _{2},\ldots ,\lambda _{N}),\)

$$\begin{aligned} M= & {} \left( \begin{array}{cccc} \dfrac{\varPhi _{1}^{T}\varPhi _{1}}{2\lambda _{1}} &{}\quad \dfrac{\varPhi _{1}^{T}\varPhi _{2}}{\lambda _{2}+\lambda _{1}} &{}\quad \cdots &{}\quad \dfrac{\varPhi _{1}^{T}\varPhi _{N}}{\lambda _{N}+\lambda _{1}} \\ \dfrac{\varPhi _{2}^{T}\varPhi _{1}}{\lambda _{1}+\lambda _{2}} &{}\quad \dfrac{\varPhi _{2}^{T}\varPhi _{2}}{2\lambda _{2}} &{}\quad \cdots &{}\quad \dfrac{\varPhi _{2}^{T}\varPhi _{N}}{\lambda _{N}+\lambda _{2}} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \dfrac{\varPhi _{N}^{T}\varPhi _{1}}{\lambda _{1}+\lambda _{N}} &{}\quad \dfrac{\varPhi _{N}^{T}\varPhi _{2}}{\lambda _{2}+\lambda _{N}} &{}\quad \cdots &{}\quad \dfrac{\varPhi _{N}^{T}\varPhi _{N}}{2\lambda _{N}} \\ \end{array} \right) ,\\ M_{1}= & {} \left( \begin{array}{ccccc} \dfrac{\varPhi _{1}^{T}\varPhi _{1}}{2\lambda _{1}} &{}\quad \dfrac{\varPhi _{1}^{T}\varPhi _{2}}{\lambda _{2}+\lambda _{1}} &{}\quad \cdots &{}\quad \dfrac{\varPhi _{1}^{T}\varPhi _{N}}{\lambda _{N}+\lambda _{1}} &{}\quad \varphi _{1} \\ \dfrac{\varPhi _{2}^{T}\varPhi _{1}}{\lambda _{1}+\lambda _{2}} &{}\quad \dfrac{\varPhi _{2}^{T}\varPhi _{2}}{2\lambda _{2}} &{}\quad \cdots &{}\quad \dfrac{\varPhi _{2}^{T}\varPhi _{N}}{\lambda _{N}+\lambda _{2}} &{}\quad \varphi _{2}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ \dfrac{\varPhi _{N}^{T}\varPhi _{1}}{\lambda _{1}+\lambda _{N}} &{}\quad \dfrac{\varPhi _{N}^{T}\varPhi _{2}}{\lambda _{2}+\lambda _{N}} &{}\quad \cdots &{}\quad \dfrac{\varPhi _{N}^{T}\varPhi _{N}}{2\lambda _{N}} &{}\quad \varphi _{N}\\ \psi _{1} &{}\quad \psi _{2} &{}\quad \cdots &{}\quad \psi _{N} &{}\quad 0\\ \end{array} \right) . \end{aligned}$$
Fig. 1
figure 1

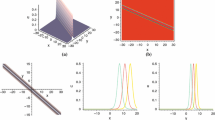
a, b The first-order periodic solution (18) at \(\beta =-0.1\) and \(\beta =-0.2\) with \(\alpha =1,u_{0}=1,\kappa _{1}=0.1\)

Full size image
Fig. 2
figure 2

a, b The second-order rational solution (19) at \(\kappa _{1}=0.5,\kappa _{2}=0.3\) and \(\kappa _{1}=0.5,\kappa _{2}=0.2\) with \(\alpha =1,\beta =-0.2,u_{0}=1\)

Full size image

Next, we choose \(u[0]=u_{0}\) (\(u_{0}\ne 0\)) as the seed solution to generate periodic solutions for Eq. (2). By substituting \(u[0]=u_{0}\) into the linear system (3) and taking \(\lambda =u_{0}(1-2\kappa ^2)\) such that \(|\kappa |<1\), we obtain the solution

$$\begin{aligned} \varPhi (\kappa )= \left( \begin{array}{c} \dfrac{1}{\kappa }\sin (\rho )+\dfrac{1}{\sqrt{1-\kappa ^2}}\cos (\rho ) \\ -\dfrac{1}{\kappa }\sin (\rho )+\dfrac{1}{\sqrt{1-\kappa ^2}}\cos (\rho ) \\ \end{array} \right) , \end{aligned}$$
(16)

where

$$\begin{aligned} \rho= & {} 2u_{0}\kappa \sqrt{1-\kappa ^2}[x-2(8\beta u_{0}^4(1-2\kappa ^2)^4\\&+\,4\beta u_{0}^4(1-2\kappa ^2)^2+2\alpha u_{0}^2(1-2\kappa ^2)^2\\&+\,3\beta u_{0}^4+\alpha u_{0}^2)t]. \end{aligned}$$

By taking \(\varPhi _{j}=(\psi _{j},\varphi _{j})^T=\varPhi (\kappa )|_{\kappa =\kappa _{j}}\) be N special solutions of the linear system (3) under the constant seed solution \(u=u_{0}\) and \(\lambda _{j}=u_{0}(1-2\kappa _{j}^2)\) with \(\kappa _{i}\ne \kappa _{j}\) for \(i\ne j\), we can provide the Nth-order periodic solution for Eq. (2) from the formula (15) in a compact form

$$\begin{aligned} u[N]=u_{0}\left[ 1-2\frac{\det (P_{1})}{\det (P)}\right] , \end{aligned}$$
(17)

where

$$\begin{aligned} P= & {} \left( \begin{array}{cccc} P_{11} &{}\quad P_{12} &{}\quad \cdots &{}\quad P_{1N} \\ P_{21} &{}\quad P_{22} &{}\quad \cdots &{}\quad P_{2N} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ P_{N1} &{}\quad P_{N2} &{}\quad \cdots &{}\quad P_{NN} \\ \end{array} \right) ,\\ P_{1}= & {} \left( \begin{array}{ccccc} P_{11} &{}\quad P_{12} &{}\quad \cdots &{}\quad P_{1N} &{}\quad \varphi _{1}\\ P_{21} &{}\quad P_{22} &{}\quad \cdots &{}\quad P_{2N} &{}\quad \varphi _{2}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ P_{N1} &{}\quad P_{N2} &{}\quad \cdots &{}\quad P_{NN} &{}\quad \varphi _{N}\\ \psi _{1}/u_{0} &{}\quad \psi _{2}/u_{0} &{}\quad \cdots &{}\quad \psi _{N}/u_{0}&{}\quad 0 \end{array} \right) , \end{aligned}$$

with

$$\begin{aligned} P_{ij}=\dfrac{\psi _{j}\psi _{i}+\varphi _{j}\varphi _{i}}{2u_{0}(1-\kappa _{j}^2-\kappa _{i}^2)},1\le i,j\le N. \end{aligned}$$

Explicitly, by taking \(N=1\) for Eq. (17), one obtains the first-order periodic solution

$$\begin{aligned} u[1]_{p}=u_{0}\left[ 1-2\dfrac{\cos (2\rho _{1})+(2\kappa _{1}^2-1)}{\cos (2\rho _{1})+1/(2\kappa _{1}^2-1)}\right] , \end{aligned}$$
(18)

where

$$\begin{aligned} \rho _{1}= & {} 2u_{0}\kappa _{1}\sqrt{1-\kappa _{1}^2}[x-2(8\beta u_{0}^4(1-2\kappa _{1}^2)^4\\&+\,4\beta u_{0}^4(1-2\kappa _{1}^2)^2+2\alpha u_{0}^2(1-2\kappa _{1}^2)^2\\&+\,3\beta u_{0}^4+\alpha u_{0}^2)t]. \end{aligned}$$

Figure 1 shows the first-order periodic solution (18) with two different values of the higher-order effect coefficient. The maximum amplitude of this periodic solution is \(-(4\kappa _{1}^2-3)u_{0}\), and the minimum amplitude is \((4\kappa _{1}^2-1)u_{0}\). It is shown that, the amplitude of the periodic solution maintains constant, and the distance between two peaks is always the same. Furthermore, the period of the solution is \(T=\pi /\left( 2u_{0}\kappa _{1}\sqrt{1-\kappa _{1}^2}\right) \) along the x axis.

Analogously, for \(N=2\) in Eq. (17), the second-order periodic solution can be worked out as

$$\begin{aligned} u[2]_{p}=u_{0}\left[ 1-2\dfrac{N_{p}^{(2)}}{D_{p}^{(2)}}\right] , \end{aligned}$$
(19)

where

$$\begin{aligned} D_{p}^{(2)}= & {} D_{11}D_{22}-D_{12}D_{21},\ N_{p}^{(2)}=\left( D_{12}\psi _{1}\varphi _{2}\right. \\&\left. +D_{21}\psi _{2}\varphi _{1}-D_{11}\psi _{2}\varphi _{2}-D_{22}\psi _{1}\varphi _{1}\right) /u_{0}, \end{aligned}$$

with

$$\begin{aligned} D_{11}= & {} \dfrac{2\kappa _{1}^2\cos (2\rho _{1})-\cos (2\rho _{1})+1}{2u_{0}\kappa _{1}^2(2\kappa _{1}^2 -1)(\kappa _{1}^2-1)},\\ D_{22}= & {} \dfrac{2\kappa _{2}^2\cos (2\rho _{2})-\cos (2\rho _{2})+1}{2u_{0}\kappa _{2}^2(2\kappa _{2}^2 -1)(\kappa _{2}^2-1)},\\ D_{12}= & {} D_{21}=\\&-\dfrac{\sqrt{1-\kappa _{1}^2}\sqrt{1-\kappa _{2}^2}\sin (\rho _{1})\sin (\rho _{2}) +\kappa _{1}\kappa _{2}\cos (\rho _{1})\cos (\rho _{2})}{u_{0}\kappa _{1}\kappa _{2}\sqrt{1-\kappa _{1}^2}\sqrt{1-\kappa _{2}^2} (\kappa _{1}^2+\kappa _{2}^2-1)},\\ \rho _{j}= & {} 2u_{0}\kappa _{j}\sqrt{1-\kappa _{j}^2}[x-2(8\beta u_{0}^4(1-2\kappa _{j}^2)^4\\&+\,4\beta u_{0}^4(1-2\kappa _{j}^2)^2+2\alpha u_{0}^2(1-2\kappa _{j}^2)^2\\&+\,3\beta u_{0}^4+\alpha u_{0}^2)t],\quad j=1,2. \end{aligned}$$

Figure 2 displays the second-order doubly periodic lattice-like structure with different choices of the parameters \(\kappa _{2}\) by fixing \(\kappa _{1}\). It is computed that the maximum amplitude of the higher-order periodic solution is \([-4(\kappa _{1}^2+\kappa _{2}^2)+5]u_{0}\) and the minimum value is \([4(\kappa _{1}^2+\kappa _{2}^2)-3]u_{0}\).

Therefore, the sum of the maximum and minimum amplitudes is always \(2u_{0}\) and independents on \(\alpha \) and \(\beta \). In Fig. 2a, the maximum amplitude of the solution is 3.64 and the minimum value is \(-1.64\), while in Fig. 2b, the corresponding values are 3.84 and \(-1.84\). Particularly, it is apparently exhibited that the distance between two peaks in Fig. 2b is narrower than that in Fig. 2a when by decreasing the value of \(\kappa _{2}\) with the fixed number of \(\kappa _{1}\).

4 Rational solutions

In this section, in order to derive the Nth-order rational solution for Eq. (2), we should utilize the limit approach to construct the generalized DT. We impose a small perturbation on the spectral parameter \(\lambda \), namely \(\lambda =\lambda _{1}+2u_{0}f^2\). Here \(\lambda _{1}=u_{0}\) is a fixed spectral parameter, f is a small complex parameter. Then, we have another form of the solution for the linear system (3)

$$\begin{aligned} \varPhi _{1}(f)= \left( \begin{array}{c} C_{1}e^{A}-C_{2}e^{-A} \\ C_{1}e^{-A}-C_{2}e^{A} \\ \end{array} \right) , \end{aligned}$$
(20)

where

$$\begin{aligned} C_{1}= & {} \frac{(1+2f^2+2f\sqrt{1+f^2})^{\frac{1}{2}}}{2f\sqrt{1+f^2}},\\ C_{2}= & {} \frac{(1+2f^2-2f\sqrt{1+f^2})^{\frac{1}{2}}}{2f\sqrt{1+f^2}}, \end{aligned}$$

and

$$\begin{aligned} A= & {} 2u_{0}f\sqrt{1+f^2}[x-2(8\beta u_{0}^4(1+2f^2)^4\\&+\,4\beta u_{0}^4(1+2f^2)^2+2\alpha u_{0}^2(1+2f^2)^2\\&+3\beta u_{0}^4+\alpha u_{0}^2)t+\displaystyle \sum _{i=1}^{N-1}s_{i}f^{2i}], \end{aligned}$$

with \(\varPhi _{1}(f)=(\psi _{1}(f),\varphi _{1}(f))^T\) and \(s_{i}\) are real constants.

In this case, it is ready to prove that \(\varPhi _{1}(f)\) can be expanded as the following Taylor series

$$\begin{aligned} \varPhi _{1}= & {} \varPhi _{1}^{[0]}+\varPhi _{1}^{[2]}f^{2}+\cdots +\varPhi _{1}^{[N-1]}f^{2(N-1)}\nonumber \\&+\,\mathcal {O}(f^{2N}), \end{aligned}$$
(21)

where \(\varPhi _{1}^{[i]}=(\psi _{1}^{[i]},\varphi _{1}^{[i]})^{T}=\lim \limits _{f\rightarrow 0} \frac{\displaystyle 1}{\displaystyle 2i!}\frac{\displaystyle \partial ^{2i}\varPhi _{1}}{\displaystyle \partial f^{2i}},~i=0,1,\ldots ,N-1.\) Furthermore, we denote

$$\begin{aligned}&\dfrac{\psi _{1}(f^*)\psi _{1}(f)+\varphi _{1}(f^*)\varphi _{1}(f)}{2u_{0}(1+f^2+f^{*2})}\nonumber \\&\quad =\sum _{i,j=1}^{N}Q^{[i,j]}f^{2(j-1)}f^{*2(i-1)}+ \mathcal {O}\left( (ff^{*})^{2N}\right) ,\nonumber \\ \end{aligned}$$
(22)

where

$$\begin{aligned} Q^{[ij]}= & {} \dfrac{1}{2(i-1)!2(j-1)!}\dfrac{\partial ^{2(i+j-2)}}{\partial f^{2(j-1)}\partial f^{*2(i-1)}}\\&\dfrac{\psi _{1}(f^*)\psi _{1}(f)+\varphi _{1}(f^*)\varphi _{1}(f)}{2u_{0}(1+f^2+f^{*2})}\Bigg |_{f,f^{*}=0}, \end{aligned}$$

with \(f^{*}\) is another complex small parameter. At this point, by virtue of the special solution \(\varPhi _{1}(f)\) and its transpose form \(\varPhi _{1}^{T}(f^{*})\) , we can construct the generalized DT through the iterative rule as follows.

For the one-fold generalized DT, we define

$$\begin{aligned}&T_{1}^{[0]}=I-\dfrac{2\lambda _{1}}{\lambda +\lambda _{1}}\dfrac{\varPhi _{1}\varPhi _{1}^{T}}{\varPhi _{1}^{T}\varPhi _{1}}\Bigg |_{f,f^{*}\rightarrow 0},\\&\left( T_{1}^{[0]}\right) ^{-1}=I+\dfrac{2\lambda _{1}}{\lambda -\lambda _{1}} \dfrac{\varPhi _{1}\varPhi _{1}^{T}}{\varPhi _{1}^{T}\varPhi _{1}}\Bigg |_{f,f^{*}\rightarrow 0}. \end{aligned}$$

For the two-fold generalized DT, we can use the limit approach to obtain the eigenfunctions of the new Lax pair (\(\varPhi [1],u[1]\)), namely

$$\begin{aligned} \varPhi _{1}[1]= & {} \lim \limits _{f\rightarrow 0}\dfrac{T_{1}^{[0]}|_{\lambda =\lambda _{1}+2u_{0}f^2}\varPhi _{1}}{f^2}\\= & {} T_{1}^{[0]}|_{\lambda =\lambda _{1}}\dfrac{1}{2!}\dfrac{\mathrm{d}^2}{\mathrm{d}f^2}\varPhi _{1}|_{f=0} +\dfrac{u_{0}}{\lambda _{1}}\varPhi _{1}|_{f=0},\\ \varPhi _{1}^{T}[1]= & {} \lim \limits _{f^{*}\rightarrow 0}\dfrac{\varPhi _{1}^{T} \left( T_{1}^{[0]}\right) ^{-1}|_{\lambda =-\lambda _{1}+2u_{0}f^{*}}}{f^{*2}}\\= & {} \dfrac{1}{2!}\dfrac{\mathrm{d}^2}{\mathrm{d}f^{*2}}\varPhi _{1}^{T}|_{f^{*}=0} \left( T_{1}^{[0]}\right) ^{-1}|_{\lambda =-\lambda _{1}}\\&-\dfrac{u_{0}}{\lambda _{1}} \varPhi _{1}^{T}|_{f^{*}=0}. \end{aligned}$$

It then holds that

$$\begin{aligned}&T_{1}^{[1]}=I-\dfrac{2\lambda _{1}}{\lambda +\lambda _{1}}\dfrac{\varPhi _{1}[1]\varPhi _{1}^{T}[1]}{\varPhi _{1}^{T}[1]\varPhi _{1}[1]}\Bigg |_{f,f^{*}\rightarrow 0},\\&\left( T_{1}^{[0]}\right) ^{-1}=I+\dfrac{2\lambda _{1}}{\lambda -\lambda _{1}} \dfrac{\varPhi _{1}[1]\varPhi _{1}^{T}[1]}{\varPhi _{1}^{T}[1]\varPhi _{1}[1]}\Bigg |_{f,f^{*}\rightarrow 0}. \end{aligned}$$

Continuing the above process, we have

$$\begin{aligned} \varPhi _{1}[j]= & {} \lim \limits _{f\rightarrow 0} \dfrac{\left( T_{1}^{[j-1]}\cdots T_{1}^{[1]}T_{1}^{[0]}\right) |_{\lambda =\lambda _{1} +2u_{0}f^2}}{f^{2j}}\varPhi _{1},\\ \varPhi _{1}^{T}[j]= & {} \lim \limits _{f^{*}\rightarrow 0}\varPhi _{1}^{T} \dfrac{\left[ \left( T_{1}^{[0]}\right) ^{-1}\left( T_{1}^{[1]}\right) ^{-1} \cdots \left( T_{1}^{[j-1]}\right) ^{-1}\right] |_{\lambda =-\lambda _{1}+2u_{0}f^{*2}}}{(f^{*})^{2j}},\\ j= & {} 1,2,\ldots . \end{aligned}$$

Therefore, the N-fold generalized DT can be presented in the compact determinant form, namely

$$\begin{aligned} \varPhi [N]= & {} T_{N}\varPhi ,\quad T_{N}=T_{1}^{[N-1]}T_{1}^{[N-2]}\cdots T_{1}^{[0]}, \end{aligned}$$
(23)
$$\begin{aligned} u[N]= & {} u[0]-2\sum _{j=1}^{N-1}\left( D_{1}^{[j]}\right) _{12}=u_{0}-2\frac{\det (Q_{1})}{\det (Q)},\nonumber \\ \end{aligned}$$
(24)

where

$$\begin{aligned} T_{1}^{[j]}= & {} I+\dfrac{D_{1}^{[j]}}{\lambda +\lambda _{1}},\ \left( T_{1}^{[j]}\right) ^{-1}=I+\dfrac{E_{1}^{[j]}}{\lambda -\lambda _{1}},\\ D_{1}^{[j]}= & {} -2\lambda _{1}\dfrac{\varPhi _{1}[j]\varPhi _{1}^{T}[j]}{\varPhi _{1}^{T}[j]\varPhi _{1}[j]},\quad E_{1}^{[j]}=2\lambda _{1} \dfrac{\varPhi _{1}[j]\varPhi _{1}^{T}[j]}{\varPhi _{1}^{T}[j]\varPhi _{1}[j]}, \end{aligned}$$

in which

$$\begin{aligned} \displaystyle \varPhi _{1}[j]= & {} \sum _{l=0}^{j}\frac{\varOmega ^{l}}{2(j-l)!}\dfrac{\mathrm{d}^{2(j-l)}}{\mathrm{d}f^{2(j-l)}}\varPhi _{1}|_{f\rightarrow 0}, \varOmega ^{l}\\= & {} \sum _{0\le i_{s}\le j-l-1}\prod _{s=1}^{j-l}\left( \dfrac{u_{0}}{\lambda _{1}}\right) ^{l} T_{1}^{[i_{s}]},\\ \displaystyle \varPhi _{1}^{T}[j]= & {} \sum _{l=0}^{j}\dfrac{\mathrm{d}^{2(j-l)}}{\mathrm{d}f^{*2(j-l)}} \varPhi _{1}^{T}|_{f^{*}\rightarrow 0}\frac{\varLambda ^{l}}{2(j-l)!}, \varLambda ^{l}\\= & {} \sum _{0\le i_{s}\le j-l-1}\prod _{s=1}^{j-l}\left( -\dfrac{u_{0}}{\lambda _{1}}\right) ^{l} \left( T_{1}^{[i_{s}]}\right) ^{-1}, \end{aligned}$$

and

$$\begin{aligned} Q= & {} \left( \begin{array}{cccc} Q^{[11]} &{}\quad Q^{[12]} &{}\quad \cdots &{}\quad Q^{[1N]} \\ Q^{[21]} &{}\quad Q^{[22]} &{}\quad \cdots &{}\quad Q^{[2N]} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ Q^{[N1]} &{}\quad Q^{[N2]} &{}\quad \cdots &{}\quad Q^{[NN]} \\ \end{array} \right) , \\ Q_{1}= & {} \left( \begin{array}{ccccc} Q^{[11]} &{}\quad Q^{[12]} &{}\quad \cdots &{}\quad Q^{[1N]} &{}\quad \varphi _{1}^{[0]}\\ Q^{[21]} &{}\quad Q^{[22]} &{}\quad \cdots &{}\quad Q^{[2N]} &{}\quad \varphi _{1}^{[1]}\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ Q^{[N1]} &{}\quad Q^{[N2]} &{}\quad \cdots &{}\quad Q^{[NN]} &{}\quad \varphi _{1}^{[N-1]}\\ \psi _{1}^{[0]} &{}\quad \psi _{1}^{[1]}&{}\quad \cdots &{}\quad \psi _{1}^{[N-1]}&{}\quad 0 \end{array} \right) . \end{aligned}$$

As in Eq. (24) we provide a unified representation of the Nth-order rational solution in a simple determinant form for Eq. (2). For \(N=1\), we can give the explicit first-order rational solution

$$\begin{aligned}&u[1]=u_{0}\left[ -1\right. \nonumber \\&\quad \left. +\dfrac{4}{4 u_{0}^2 x^2-48 u_{0}^4 (5\beta u_{0}^2+\alpha ) x t +144 u_{0}^6 (5\beta u_{0}^2+\alpha )^2 t^2+1}\right] .\nonumber \\ \end{aligned}$$
(25)

This solution corresponds to the Peregrine soliton of the NLS equation [15] and looks like a soliton on a nonzero constant background [20], see Fig. 3. The maximum amplitude of it is \(3u_{0}\) and occurs at

$$\begin{aligned} t=\frac{1}{6 u_{0}^2(5\beta u_{0}^2+\alpha )}x. \end{aligned}$$
Fig. 3
figure 3

a, b The first-order rational solution (25) at \(\beta =-0.2\) and \(\beta =-0.22\) with \(\alpha =1,u_{0}=1\)

Full size image
Fig. 4
figure 4

a, b The second-order rational solution (26) at \(\beta =-0.15\) and \(\beta =-0.1\) with \(\alpha =1,u_{0}=1,s_{1}=0\)

Full size image
Fig. 5
figure 5

a, b The second-order rational solution (26) at \(\beta =-0.15\) and \(\beta =-0.1\) with \(\alpha =1,u_{0}=1,s_{1}=30\)

Full size image

Moreover, it is calculated that

$$\begin{aligned} \int _{-\infty }^{\infty }\left( u[1]^2-u_{0}[1]^2\right) \mathrm{d}x=0, \end{aligned}$$

and

$$\begin{aligned} \int _{-\infty }^{\infty }(u[1]-u_{0}[1])^2\mathrm{d}x=4\pi \mathrm{sgn}(u_{0})u_{0}, \end{aligned}$$

where \(u_{0}[1]=\lim _{x\rightarrow \pm \infty }u[1]=-u_{0}\), which indicates that the energy of the pump [48] is preserved, and the energy of the Peregrine pulse [48] keeps a constant. We note that, the choice of \(\beta =-\alpha /(5 u_{0}^2)\) corresponds to the stationary rational solution of Eq. (2) with higher-order effects, see Fig. 3a.

Afterwards, in terms of \(N=2\) in Eq. (24), one obtains

$$\begin{aligned} u[2]=u_{0}\left[ 1+2\dfrac{N_{r}^{(2)}}{D_{r}^{(2)}}\right] , \end{aligned}$$
(26)

where

$$\begin{aligned} N_{r}^{(2)}= & {} -124416 u_{0}^{12} \gamma ^4 t^4\\&\quad +82944 u_{0}^{10} \gamma ^3 x t^3 \\&\quad -(20736 u_{0}^8 \gamma ^2 x^2 +1728 u_{0}^6 \gamma (95 \beta u_{0}^2 \\&\quad +11 \alpha )) t^2 \\&\quad +(2304 u_{0}^6 \gamma x^3+576 u_{0}^4 (55 \beta u_{0}^2+7 \alpha ) x \\&\quad +864 u_{0}^4 \gamma s_{1}) t \\&\quad -96 u_{0}^4 x^4 -144 s_{1} u_{0}^2 x-144 u_{0}^2 x^2+18,\\ D_{r}^{(2)}= & {} 2985984 u_{0}^{18} \gamma ^6 t^6 \\&\quad -2985984 u_{0}^{16} \gamma ^5 x t^5 \\&\quad +(1244160 u_{0}^{14} \gamma ^4 x^2 -20736 u_{0}^{12} (145 \beta u_{0}^2 \\&\quad +13 \alpha ) \gamma ^3) t^4 \\&\quad -(276480 u_{0}^{12} \gamma ^3 x^3 -41472 u_{0}^{10} (35 \beta u_{0}^2 \\&\quad +3 \alpha ) \gamma ^2 x-20736 u_{0}^{10} \gamma ^3 s_{1}) t^3 \\&\quad +(34560 u_{0}^{10} \gamma ^2 x^4-17280 u_{0}^8 (13 \beta u_{0}^2+\alpha ) \gamma x^2 \\&\quad -10368 u_{0}^8 \gamma ^2 s_{1} x \\&\quad +144 u_{0}^6 (9475 \beta ^2 u_{0}^4+2270 \alpha \beta u_{0}^2 +139 \alpha ^2)) t^2 \\&\quad -(2304 u_{0}^8 \gamma x^5 -384 u_{0}^6 (25 \beta u_{0}^2+\alpha ) x^3 \\&\quad -1728 u_{0}^6 \gamma s_{1}x^2 \\&\quad +144 u_{0}^4 (125 \beta u_{0}^2+17 \alpha ) x \\&\quad +144 u_{0}^4 s_{1}(95 \beta u_{0}^2+11 \alpha )) t \\&\quad +64 u_{0}^6 x^6-96 u_{0}^4 s_{1} x^3 \\&\quad +48 u_{0}^4 x^4 +36 u_{0}^2 s_{1}^2 \\&\quad +72 u_{0}^2 s_{1} x+108 u_{0}^2 x^2+9, \end{aligned}$$

with \(\gamma =5\beta u_{0}^2+\alpha \).

In this circumstance, it can be calculated that, when setting \(\beta \ne -\frac{\alpha }{10 u_{0}^2},\) the second-order solution exhibits a doubly localized high-peak structure which can be seen as a collision of a dark soliton and a bright soliton, see Fig. 4a. The collision point is (0, 0), and the maximum amplitude of the peak is \(5u_{0}\).

Noteworthily, when \(\beta =-\frac{\alpha }{10 u_{0}^2}\), we can show that, the doubly localized high-peak wave can be converted into a new type of soliton, namely the W-shaped soliton, see Fig. 4b. Here, we should point out that, this conversion can only exist in the higher-order systems such as the emKdV equation considered in this paper, while for the standard mKdV equation, it is impossible to appear. The maximum amplitude of this W-shaped soliton is \(5u_{0}\) and arrives at

$$\begin{aligned} t=\frac{1}{6 u_{0}^2(5\beta u_{0}^2+\alpha )}x. \end{aligned}$$

The minimum amplitude of it is \(-u_{0}\) and reaches at

$$\begin{aligned} t=\frac{1}{6 u_{0}^2(5\beta u_{0}^2+\alpha )}x\pm \frac{\sqrt{3}}{6\alpha u_{0}^3}. \end{aligned}$$

In addition, it is pointed out by Chowdury et al. [20], the second-order rational solution of the mKdV equation cannot be separated into three components like the NLS equation, while the nonzero free parameter \(s_{1}\) can produce a “differential shift” effecting on the peak along the trough of the “depressed soliton”, see Fig. 5a. The maximum amplitude of the high peak in this case is also 5, but the critical point shifts from (0, 0) to \((-5.63,-3.75)\). Further, it should be emphasized that, unlike the doubly localized high-peak wave, when \(s_{1}\ne 0\), the W-shaped soliton can be separated into a dark soliton and a bright soliton, see Fig. 5b.

5 Conclusion

In summary, we investigated the conservation laws, periodic and rational solutions for the emKdV equation which can be seen as a higher-order integrable generalization of the standard mKdV equation. We constructed the N-fold DT and obtained the general Nth-order periodic solution under a nonzero constant background. Further, we derived a unified representation of the Nth-order rational solution from the generalized DT by resorting to the limit approach. Explicitly, the periodic and rational solutions from first to second order were presented, and the doubly periodic lattice-like and doubly localized high-peak waves were shown. Remarkably, we interestingly found that the stationary rational soliton and the W-shaped soliton can only exist in the emKdV equation as a result of the higher-order effects. Our results may be useful to better understand the nonlinear wave phenomena in various physical systems where the mKdV equation governs.