1 Introduction and model formulation

Pests can cause significant crop yield declines, even massive crop failure. In addition, they can reduce the quality of farm products. Therefore, countries around the world have set up special organizations to study the control strategy of agricultural pests, for example Office of Pest Management Policy established by USA, Department of Agriculture in 1997 [1], the Pest Management Regulatory Agency (PMRA) created by Canadian government in 1995 [2]. Since then, various types methods such as mechanical pest control, physical pest control, elimination of breeding grounds, pesticides and biological pest control have been implemented in practice [3]. But evidences show that a single measure has its drawback so that may not work well, such as low efficiency or doing harm to the environment: pest resistance [4, 5], pesticide residues and pest resurgence [6, 7]. Then, integrated pest management (IPM) was proposed [8], which utilizes a combination of agricultural, biological, chemical, physical and cultural methods to control pests effectively. Different to the traditional ways, the goal of IPM is not to eradicate pests, instead to suppress pest populations so that it is below the economic injury level (EIT) [9]. Therefore, IPM not only can control pests effectively, but also can protect ecosystems in maximum extent. It has already attracted many scholars’ attentions [10–15], and a large number of mathematical models have been established since the day it was invented to explain how IPM plays a role in the process of pest control. But, as an old saying says: There are two sides for every coin, IPM has its own problems such as causing system population changes radically. Mathematically, this change can be described by impulsive differential equations (IDEs), and numerous models with periodic impulsive manual intervention based on predator–prey model [16–26, 29] have been developed to study the IPM [27, 28, 30–37].

In practice, control measures based on number or density of pests seem more reasonable. It then leads to mathematical models with state feedback control [38–51]. For example, Tang et al. [52, 53] established a pest management system with one state-dependent pulse and discussed the existence of the order one periodic solutions. Zhang et al. [54] proposed a Beddington–DeAngelis prey–predator system with harvesting and impulsive state feedback control and studied the existence and stability of predator-free periodic solution. Pang et al. [55] investigated the periodic solution of a delayed pest management system with logistic growth and impulsive state feedback control. Recently, Wang and Tang [56] established the following pest management system with one state-dependent pulse

(1.1)

where \(P_{\max }\in [0,1)\) denotes the maximal killing proportion, \(\theta _1\) is the half-saturation constant.

In [57], Chen et al. considered the following model with logistic growth and Holling’s type III functional response

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\dot{x}(t)=ax(t)-bx^2(t)-\frac{\alpha x^2(t)y(t)}{x^2(t)+\beta ^2}}, \\ \displaystyle {\dot{y}(t)=y(t)\left( -c+\frac{k\alpha x^2(t)}{x^2(t)+\beta ^2}\right) }. \end{array}\right. } \end{aligned}$$
(1.2)

It should be noted that as a basic model, system (1.2) considered density constraints of prey populations and interaction between prey population and predator population, and the authors gave a qualitatively analysis and got the conditions for the global stability of nontrivial equilibrium points and conditions for the existence and uniqueness of limit cycles around the positive equilibrium point. While from the point of view of pest control, people always want to control pests in a limited amount of time, and considering the cost, environmental, efficiency and other factors, in a certain period of time, according to the number of pests, manual intervention to the system in order to control pests is necessary. Then, based on system (1.2) and motivated by references [56], we are proposing our model here

$$\begin{aligned} \begin{array}{ll} \left. \begin{array}{l} \displaystyle {\dot{x}(t)=ax(t)-bx^2(t)-\frac{\alpha x^2(t)y(t)}{x^2(t)+\beta ^2}}, \\ \displaystyle {\dot{y}(t)=y(t)\left( -c+\frac{k\alpha x^2(t)}{x^2(t)+\beta ^2}\right) },\\ \end{array} \right\} &{}\,x\ne h_1,\\ \left. \begin{array}{l} \displaystyle {\Delta {x}(t)=-p(x(t))x(t)}, \\ \displaystyle {\Delta {y}(t)=-qy(t)+\mu _1}, \\ \end{array} \right\}&\,x=h_1, \end{array} \end{aligned}$$
(1.3)

where \(\Delta x(t)=x(t^{+})-x(t), \Delta y(t)=y(t^{+})-y(t);\) \(h_1\) is the EIL; q is the mortality of natural enemies due to pesticide and \(\mu _1\) is the quantity of natural enemies released once. To be biological meaningful, we restrict our study in region \(R_{+}^{2}=\{(x,y)|x\ge 0,y\ge 0\}.\) Simplifying by transformations

$$\begin{aligned} x&=\beta \sqrt{\frac{c}{k\alpha -c}}x^{\prime },\\ y&=\frac{\beta \sqrt{c(k\alpha -c)}y^{\prime }}{\alpha },\\ \mathrm{d}t&=\frac{cx'^2+k\alpha -c}{c(k\alpha -c)}\mathrm{d}t^{\prime } \end{aligned}$$

and dropping all primes yield (1.4), where

$$\begin{aligned}&C_0=\frac{a}{c}, \quad C_1=-\frac{b\beta }{c}\sqrt{\frac{c}{k\alpha -c}},\quad C_2=\frac{a}{k\alpha -c},\\&C_3=-\frac{b\beta }{k\alpha -c}\sqrt{\frac{c}{k\alpha -c}},\quad h=\frac{h_1}{\beta \sqrt{\frac{c}{k\alpha -c}}},\\&\mu =\frac{\mu _1}{\frac{\beta }{\alpha }\sqrt{c(k\alpha -c)}},\quad \theta =\frac{\theta _1}{\beta \sqrt{\frac{c}{k\alpha -c}}}. \end{aligned}$$

Our aim in this paper is to investigate the periodic solutions associated with control strategy for the proposed mathematical model. And for system (1.2), the authors have analyzed the existence and stability of order one periodic solutions by using Lambert W function and related skills of impulsive semidynamics system. In system (1.4), we shall discuss the existence of the order one periodic solutions by using geometrical method (successor function), which is different from the ones in system (1.2) and [52, 53]. This paper is structured as follows: Sect. 2 introduces some basic concepts and fundamental results, which are necessary for future discussions. In Sect. 3, we will investigate the periodic behavior of solutions of system (1.4) under impulsive state feedback control. Then, we show an example and carry out numerical simulations in Sect. 4, from which it can be seen that all simulations agree with the theoretical results. We finally conclude our paper in Sect. 5.

$$\begin{aligned} \begin{array}{ll} \left. \begin{array}{l} \displaystyle \dot{x}(t)=x(t)(C_0+C_1x(t)+C_2x^2(t)\\ \quad \quad \quad \ +\,C_3x^3(t))-x^2(t)y(t), \\ \displaystyle {\dot{y}(t)=y(t)(-1+x^2(t)),}\\ \end{array} \right\} &{}\,x\ne h,\\ \left. \begin{array}{l} \displaystyle {\Delta {x}(t)=-\frac{P_{\mathrm{\max }}x(t)}{x(t)+\theta }x(t)}, \\ \displaystyle {\Delta {y}(t)=-qy(t)+\mu }, \\ \end{array} \right\}&\,x=h, \end{array} \end{aligned}$$
(1.4)

2 Preliminaries

Definition 1

[58] Consider

(2.1)

We call M the impulsive set and a continuous mapping \(I:I(M)=N\) the impulse function, here N is referred as the phase set. Furthermore, a semicontinuous system is a set defined by the solution maps of system (2.1) and denoted as \((\mho , f, I, M).\)

Given initial mapping point \(P\notin M.\) Then, we have the following definition.

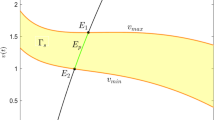
Definition 2

[58] Let \(P\in N\) be the initial mapping point, \(f(P,T)=P_{1}\in M,\) \(I(P_{1})=P^{+}\in N\) and coordinates of point \(P, P_{1}\) and \(P^{+}\) be denoted by \((P_x,P_y), (P_{1x},P_{1y})\) and \((P^{+}_x,P^{+}_y)\), respectively. Then, function

$$\begin{aligned} F(P)=F(P^{+})-F(P)=P^{+}_y-P_y \end{aligned}$$

is the successor function of point P (see Fig. 1).

Fig. 1
figure 1

The schematic of successor function of the point P

Full size image

Definition 3

[58] If there exists a point \(P\in N\) such that \(f(P,T)=P_1\in M\) and \(I(P_1)=P\in N,\) then f(P, T) is called an order one periodic solution of system (2.1).

Lemma 1

[58] Let \((X,\Pi )\) be a continuous dynamic system and given two points \(P_1,P_2,\) in the pulse phase. If \(F(P_1)F(P_2)<0,\) then there exists a point P between \(P_1\) and \(P_2\) such that \(F(P)=0,\) that is, the system has an order one periodic solution, where F is the successor function.

Lemma 2

(Analogue of Poincaré Criterion [59, 60]) The T-periodic solution \(x=\phi (t), y=\varphi (t)\) of model

(2.2)

is orbitally asymptotically stable if \(|\mu _2|<1,\) where \(\mu _2\) is the multiplier given by

$$\begin{aligned} \mu _{2}= & {} \prod _{k=1}^{q}\Delta _{k}\exp \left[ \int _{0}^{T}\left( \frac{\partial \Gamma }{\partial x}(\phi (t),\varphi (t))\right. \right. \nonumber \\&\left. \left. +\frac{\partial \Sigma }{\partial y}(\phi (t),\varphi (t))\right) dt\right] \end{aligned}$$
(2.3)

with

$$\begin{aligned} \displaystyle {\Delta _{k}=\frac{\varGamma _{+}\left( \frac{\partial \Theta _2}{\partial y}\frac{\partial \Phi }{\partial x}-\frac{\partial \Theta _2}{\partial x}\frac{\partial \Phi }{\partial y}+\frac{\partial \Phi }{\partial x}\right) +\Sigma _{+}\left( \frac{\partial \Theta _1}{\partial x}\frac{\partial \Phi }{\partial y}-\frac{\partial \Theta _1}{\partial y}\frac{\partial \Phi }{\partial x}+\frac{\partial \Phi }{\partial y}\right) }{\Gamma \frac{\partial \Phi }{\partial x}+\Sigma \frac{\partial \varPhi }{\partial y}}} \end{aligned}$$
(2.4)

and \(\Gamma ,\Sigma ,\frac{\partial \Theta _1}{\partial x},\frac{\partial \Theta _1}{\partial y},\frac{\partial \Theta _2}{\partial x},\frac{\partial \Theta _2}{\partial y},\frac{\partial \Phi }{\partial x},\frac{\partial \Phi }{\partial y}\) are calculated at the point \((\phi (t_{k}), \varphi (t_{k}))\) and \(\Gamma _{+}=\Gamma (\phi (t_{k}^{+}),\varphi (t_{k}^{+})),\) \(\Sigma _{+}=\Sigma (\phi (t_{k}^{+}),\varphi (t_{k}^{+})).\)

We next list some qualitative results of system (1.4) when without neglecting impulsive effect. More precisely, consider

$$\begin{aligned} {{\left\{ \begin{array}{ll} \dot{x}(t)=x(t)(C_0+C_1x(t)+C_2x^2(t)\\ \quad \quad \quad +\,C_3x^3(t))-x^2(t)y(t), \\ \dot{y}(t)=y(t)(-1+x^2(t)). \end{array}\right. }} \end{aligned}$$
(2.5)

Then, Chen and Zhang [57] proved

Theorem 1

(Sec. II in [57]) System (2.5) has at most three equilibrium points in region \(x\ge 0, y\ge 0\) when \(k\alpha >c.\) More precisely, it

  1. 1.

    when \(C_2+C_3<0,\) has two equilibria O(0, 0) and \(R(x^+, 0)\) with O(0, 0) is a saddle point and \(R(x^+, 0)\) a stable node;

  2. 2.

    when \(C_2+C_3=0,\) has two equilibria O(0, 0) and \(R(x^+, 0),\) moreover O(0, 0) is a saddle point, \(R(x^+, 0)\) is a stable critical node;

  3. 3.

    when \(C_2+C_3>0,\) has three equilibria: two saddle points O(0, 0) and \(R(x^+,0),\) and a positive equilibrium \(S(1, y^*).\) Moreover, if \(2C_3+C_2-C_0<0\) and \((2C_3+C_2-C_0)^2-8(C_0+C_1+C_2+C_3)<0, S(1, y^*)\) is a globally asymptotically stable focus.

Here

$$\begin{aligned} y^*=C_0+C_1+C_2+C_3,\quad x^+=-\frac{C_2}{C_3}. \end{aligned}$$

3 The order one periodic solutions of system (1.4) induced by nonlinear impulsive state feedback control

For system (1.4), it is easy to verify that (a) the pulse set is \(M=\{(x,y)|x=h\},\) and the image set is \(N=\{(x,y)|x=\left( 1-P_\mathrm{{\max }}{h}/(h+\theta )\right) h, 0\le y\le \mu \};\) (b) it has four nullclines with two X-nullclines: \(L:y={C_0}/{x}+C_1+C_2x+C_3x^2\) and Y-axis and two Y-nullclines: \(L^{\prime }:x=1\) and X-axis.

Next, we study the existence of order one periodic solution of system (1.4), which is then followed by the stability of it.

3.1 The existence

Noticing the pulse set is \(x=h\) and the Y-nullcline is \(x=1,\) we can prove the following theorems.

Theorem 2

If \(h\le 1,\) then there exists a point \(P\in N: x=\left( 1-P_{\mathrm{\max }}{h}/(h+\theta )\right) h\) such that \(F(P)=0,\) namely system (1.4) has an order one periodic solution.

Proof

Due to the similarity in proof, we only prove the case when \(h=1.\) In this case, we have the pulse set \(\{M: x=1\}\) and the phase set \(\{N: x=1-P_{\max }/(1+\theta )\}.\) Our goal here is to find a point \(P\in N\) such that \(F(P)=0.\) We prove this by finding two points \(P_1, P_2\in N\) satisfying \(F(P_1)F(P_2)<0\)

Let the intersection of N and L be \(A(A_x, A_y).\) Then, system (1.4) has an orbit \(L_1\) tangent to N at point A and intersects with M at a point denoted by \(A_1({A_1}_x, {A_1}_y).\) As a result, the orbit \(L_1\) jumps back to N from M since M is the pulse set. We then denote the associated phase point by \(A_1^+({{A}^+}_x,{{A}^+}_y).\) Using definition 2, \(A^+\) is the successor point of A and the successor function is \(F(A)={{A}^+}_y-A_y.\) According to the sign of F(A),  we have three cases to discuss. If \(F(A)=0,\) we then proved the conclusion and the order one periodic solution consists of orbit \(L_1\) and \(AA^+\).

If \(F(A)<0,\) then we know \(A^+\) is below point A on N, see Fig. 2b. In order to achieve our goal, we should find at least one point \(Q\in N\) such that \(F(Q)>0.\) To this end, we choose a point \(S\in N\) as far as possible away from the x axis. And the orbit \(L_2\) starting from S intersects with N at point \(B(B_x, B_y),\) and intersects with M at point \(B_1,\) then pulses to \(B^+.\) Since point \(S\in N\) is as far as possible away from the x axis, then point B can be very close to the x axis. Thus, we have that the successor function of point B is \(F(B)={{B}^+}_y-B_y>0,\) by Lemma 1, we get that system (1.4) has an order one periodic solution.

Fig. 2
figure 2

The schematic for the case in Theorem 2. a The successor point of A exactly is point A. b The successor point of A is below point A. c The successor point of A is above point A

Full size image

Similar argument will give the case \(F(A)>0,\) see Fig. 2c.

This completes the proof. \(\square \)

Next, we can prove the following theorem.

Theorem 3

When \(0<\left( 1-P_{\mathrm{\max }}{h}/(h+\theta )\right) h<1\) and \(1<h<x^{+},\) system (1.4) has an order one periodic solution.

Proof

As discussed in the previous theorem, we here only need to show that there exists a point \(P\in N\) such that \(F(P)=0.\)

In this case, we consider the trajectory \(L_0\) of system (1.4) tangency to \(x=h\) at point \(H(H_x,H_y),\) see Fig. 3. If trajectory \(L_0\) of system intersects with phase set N at most once, then by the geometrical methods [61], there exists a trajectory \(L_1\) tangent to N at a point, A say and then it intersects with M at some point denoted by \(A_1,\) then pulses to point \(A^+.\) We then have two subcases here, (a): \(F(A)={{A}^+}_y-A_y<0,\) please see Fig. 3a; and b: \(F(A)={{A}^+}_y-A_y>0,\) see Fig. 3b. Then as what we discussed in the proof of previous theorem, we can find an order one periodic solution for system (1.4).

Fig. 3
figure 3

The schematic for the case in Theorem 3 a The successor point of A is below point A. b The successor point of A is above point A. c The successor point of A is above point A. d The successor point of A is below point A

Full size image

Now, if the orbit \(L_0\) intersect phase set twice, the intersection point is denoted by \(A^{\prime }(A^{\prime }_x, A^{\prime }_y)\) and \(B^{\prime }(B^{\prime }_x, B^{\prime }_y),\) respectively, with \(A^{\prime }_y>B^{\prime }_y.\) Then, we consider the phase points \(A^{\prime }+({A^{\prime }+}_x, {A^{\prime }+}_y).\) According to the sign of \(F(A^{\prime })={A^{\prime }+}_y-A^{\prime }_y,\) we have two subcases to be discussed as well, please see Fig. 3d, where \(F(A^{\prime })=A^{+}_y-A_y>0\) and Fig. 3d where \(F(B^{\prime })={A^+}_y-B^{\prime }_{y}<0.\) Similarly, we can also show the existence of order one periodic solution. This completes the proof. \(\square \)

Remark 1

When \(\left( 1-P_{\mathrm{\max }}{h}/{h+\theta }\right) h>1,\) we can still find periodic solution. But the number of the pests maintains at a higher level in this case, from the point view of pest management, it does not have practical significance.

3.2 The stability

Theorem 4

Let \((x,y)=(\phi (t), \varphi (t))\) be a periodic solution of system (1.4), \(f(C_0,t)\) be the orbit beginning from \(C_0(\phi (0), \varphi (0)),\) where \(\phi (0)=\left( 1-P_\mathrm{{\max }}\frac{h}{h+\theta }\right) h\) and

$$\begin{aligned} \delta =\int _0^T\left( C_1\phi +2C_2\phi ^2+3C_3\phi ^3-\phi \varphi \right) dt. \end{aligned}$$

Then, if condition (3.1) holds, then the order one periodic solution passing through point \((h, \varphi (T))\) of system (1.4) is orbitally asymptotically stable.

$$\begin{aligned} \varphi (0)<\frac{(1-q)(C_0+C_1h+C_2h^2+C_3h^3-(C_0+C_1\phi (0) +C_2\phi (0)^2+C_3\phi (0)^3)e^{\delta })+h\mu }{h-(1-q)\phi (0)e^{\delta }} \end{aligned}$$
(3.1)

Proof

Let initial value be \(C_0(\phi (0), \varphi (0))\) and assume orbit \(f(C_0,t)\) intersects with M at \(C_1(\phi (T),\varphi (T))\) and then jumps to \(C_1^{+}(\phi (T^{+}),\varphi (T^{+}).\) Then, we have

$$\begin{aligned} f(C_0,T)=C_1,C_1^{+}=I(C_1)=C_0, \end{aligned}$$

thus \(\phi (T^{+})=\left( 1-P_{\max }\frac{h}{h+\theta }\right) \phi (T)=\phi (0),\varphi (T^{+})=(1-q)\varphi (T)+\mu =\varphi (0)\) and \(\phi (T)=h.\) According to Lemma 2, let

$$\begin{aligned} {\left\{ \begin{array}{ll} \Gamma (x,y)=x(C_0+C_1x+C_2x^2+C_3x^3)-x^2y,\\ \Sigma (x,y)=y(-1+x^2),\\ \Theta _1(x,y)=-\frac{P_{\mathrm{\max }}x}{x+\theta }x,\\ \Theta _2(x,y)=-qy+\mu ,\\ \Phi (x,y)=x-h. \end{array}\right. } \end{aligned}$$

By a direct calculation, we get

$$\begin{aligned}&\frac{\partial \Theta _1}{\partial x}=-P_{\mathrm{\max }}\frac{x(x+2\theta )}{(x+\theta )^2},\quad \frac{\partial \Theta _1}{\partial y}=0,\\&\frac{\partial \Theta _2}{\partial x}=0,\quad \frac{\partial \Theta _2}{\partial y}=-q,\\&\frac{\partial \Phi }{\partial x}=1,\quad \frac{\partial \Phi }{\partial y}=0,\\&\int _0^T\frac{\partial \Gamma }{\partial x}\mathrm{d}t = \int _0^T\Big (C_0+2C_1x+3C_2x^2\\&\quad \quad \quad \quad \quad \quad \quad \ +\,4C_3x^3-2xy\Big )dt\\&\quad \quad \quad \quad \quad \quad =\ln \left( \frac{\phi (T)}{\phi (0)}\right) +\delta ,\\&\int _0^T\frac{\partial \Sigma }{\partial y}\mathrm{d}t = \int _0^T(-1+x^2)\mathrm{d}t=\ln \left( \frac{\varphi (T)}{\varphi (0)}\right) , \end{aligned}$$

where \(\delta =\int _0^T\left( C_1x+2C_2x^2+3C_3x^3-xy\right) \mathrm{d}t.\) Thus, we have

$$\begin{aligned} \int _0^T\left( \frac{\partial \Gamma }{\partial x}+\frac{\partial \Sigma }{\partial y}\right) \mathrm{d}t=\ln \left( \frac{\phi (T)}{\phi (0)}\right) +\ln \left( \frac{\varphi (T)}{\varphi (0)}\right) +\delta . \end{aligned}$$

From Lemma 2, we have

$$\begin{aligned} \Delta _1=\frac{\Gamma (\phi (T^+),\varphi (T^+))(1-q)}{\Gamma (\phi (T),\varphi (T))} \end{aligned}$$

where

$$\begin{aligned} \Gamma (\phi (T^+),\varphi (T^+))= & {} \phi (0)(C_0+C_1\phi (0)+C_2\phi (0)^2\\&+\,C_3\phi (0)^3-\phi (0)\varphi (0)),\\ \Gamma (\phi (T),\varphi (T))= & {} \phi (T)(C_0+C_1\phi (T)+C_2\phi (T)^2\\&+\,C_3\phi (T)^3-\phi (T)\varphi (T)), \end{aligned}$$

and note that, \(\phi (T)=h,\phi (0)=\left( 1-P_{\max }\frac{h}{h+\theta }\right) h\) and \((1-q)\varphi (T)+\mu =\varphi (0),\) we have

$$\begin{aligned}&\mu _2=\Delta _1\exp \left\{ \int _0^T{\left( \frac{\partial \Gamma }{\partial x}+\frac{\partial \Sigma }{\partial y}\right) \mathrm{d}t}\right\} \\&\quad =\frac{C_0+C_1\phi (0)+C_2\phi (0)^2+C_3\phi (0)^3-\phi (0)\varphi (0)}{C_0+C_1h+C_2h^2+C_3h^3-h\frac{\varphi (0)-\mu }{1-q}}\\&\quad \quad \times \,\frac{\varphi (0)-\mu }{\varphi (0)}e^{\delta }\\&\quad <\frac{C_0+C_1\phi (0)+C_2\phi (0)^2+C_3\phi (0)^3-\phi (0)\varphi (0)}{C_0+C_1h+C_2h^2+C_3h^3-h\frac{\varphi (0)-\mu }{1-q}}e^{\delta }. \end{aligned}$$

Therefore, if condition (3.1) holds, then the periodic solution is stable. This completes the proof. \(\square \)

4 An example and numerical simulations

In this section, we will give an example and some numerical simulations to illustrate the existence of periodic solutions. To this end, set \(a=1, b=0.2, c=0.5, \alpha = 0.1, \beta = 2, k=8, P_\mathrm{{\max }}=0.6, \theta =2, q=0.4.\) Then \(A_0=2, A_1=-1.0328<0, A_2=3.3333>0, A_3=-1.7213<0.\) We then consider system (4.1).

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} \displaystyle \dot{x}(t)=x(t)(2-1.0328x(t)+3.3333x^2(t)\\ \quad \quad \quad \quad -\,1.7213x^3(t))-x^2(t)y(t) \\ \displaystyle {\dot{y}(t)=y(t)(-1+x^2(t))},\\ \end{array} \right\} &{}\,x\ne h,\\ \left. \begin{array}{l} \displaystyle {\Delta {x}(t)=-\frac{0.6x(t)}{x(t)+2}x(t)}, \\ \displaystyle {\Delta {y}(t)=-0.4y(t)+\mu }, \\ \end{array} \right\}&\,x=h, \end{array}\right. } \end{aligned}$$
(4.1)

By calculation, we obtain \(x^*=1, y^*=2.5792.\) The direction field of shows that system (4.1) has a stable focus \((x^*, y^*)=(1,2.5792),\) please see Fig. 4.

Fig. 4
figure 4

System (4.1) has a stable focus

Full size image

Let the initial value be (0.5,2), and following the theoretical results, we have the following cases (the impulsive set, phase set and the corresponding figure can be seen in Table 1).

Table 1 Impulse set, phase set and the corresponding figure
Full size table

Case I: \(h=1.\) We have \((1-\frac{P_{\mathrm{\max }}h}{h+\theta })h=0.8.\) By regulating \(\mu ,\) there are the following cases: The orbit of system has a tendency to leap upward (\(\mu =1\)) or down (\(\mu =0.6\)) under the effect of the pulse. Figure 5a, d shows that the system (4.1) has one order one periodic solution.

Fig. 5
figure 5

Illustration of basic behavior of solutions of the system (4.1) when \(h=1.\) In (a) and (d), the red orbit represents phase portrait of x(t) and y(t) with impulsive effect, and the blue represents phase portrait of x(t) and y(t) without impulsive effect. In (b) (c) (e) and (f), the red curve represent time series of x(t) and y(t) with impulsive effect, and the blue represents time series of x(t) and y(t) without impulsive effect. a Phase portrait of x(t) and y(t). b Time series of x(t). c Time series of y(t). d Phase portrait of x(t) and y(t). e Time series of x(t). f Time series of y(t)

Full size image

Case II: \(h<1.\) Let \(h=0.8,\) then \((1-\frac{P_{\max }h}{h+\theta })h=0.6629.\) Similar results can appear like case I by regulating \(\mu \) with \(\mu =1\) (Fig. 6a) or \(\mu =0.6\) (Fig. 6d).

Fig. 6
figure 6

Illustration of basic behavior of solutions of the system (4.1) when \(h=0.8.\) In (a) and (d), the red orbit represents phase portrait of x(t) and y(t) with impulsive effect, and the blue represents phase portrait of x(t) and y(t) without impulsive effect. In (b) (c) (e) and (f), the red curve represent time series of x(t) and y(t) with impulsive effect, and the blue represents time series of x(t) and y(t) without impulsive effect. a Phase portrait of x(t) and y(t). b Time series of x(t). c Time series of y(t). d Phase portrait of x(t) and y(t). e Time series of x(t). f Time series of y(t)

Full size image

Case III: \(h>1, (1-\frac{P_{\max }h}{h+\theta })h<1.\) Let \(h=1.05,\) then \((1-\frac{P_{\max }h}{h+\theta })h=0.8331<1.\) By regulating \(\mu ,\) we can conclude that the system (4.1) has one order one periodic solution (see Fig. 7a, d).

Fig. 7
figure 7

Illustration of basic behavior of solutions of the system (4.1) when \(h=1.05.\) In (a) and (d), the red orbit represents phase portrait of x(t) and y(t) with impulsive effect, and the blue represents phase portrait of x(t) and y(t) without impulsive effect. In (b) (c) (e) and (f), the red curve represent time series of x(t) and y(t) with impulsive effect, and the blue represents time series of x(t) and y(t) without impulsive effect. a Phase portrait of x(t) and y(t). b Time series of x(t). c Time series of y(t). d Phase portrait of x(t) and y(t). e Time series of x(t). f Time series of y(t)

Full size image

5 Conclusion

In present paper, based on a prey–predator model with the Holling’s type III functional response, a pest management system with nonlinear state feedback control is proposed and analyzed. The integrated pest management strategy according to number of pests is considered. By the qualitative theory of differential equations and geometrical analysis, the existence and stability of periodic solutions of the model were discussed. Numerical simulations verified our theoretical results.