1 Introduction

Feedback stabilization for nonlinear systems is a well-known issue in the control theory and still an open problem for researchers [10, 19, 24, 26]. The stability analysis of nonlinear systems under time delays is usually more difficult compared with systems without time delays [7, 13, 22]. Time delay is a property of many dynamical systems such as, communications, embedded systems, mechanical, tele-operation, biological, electrical, and many other applications [8, 20, 29].

Now, the issue is why the time-delay systems are still a direct problem, since the stability and stabilization problems of dynamical systems subject to nonlinearities are of interest due to the fact that such systems, especially time-delays systems, include a wide variety of practical systems and devices, like servo systems, flexible systems, etc. Indeed, smooth and nonsmooth nonlinearities often occur in a real control process, due to physical, technological, safety constraints, even inherent characteristic of considered systems [11]. Significant efforts have been done to solve such problems, and many control approaches have been used. For example, those based on fuzzy control [25], adaptive control [16, 32], intermittent control [27], impulsive control [21], switching control [30], neural networks, and so on. Such methods have been developed for linear and for nonlinear time-delay systems.

Indeed, in [25], the problems of stability analysis and stabilization for a class of discrete-time Takagi–Sugeno (T–S) fuzzy systems with stochastic perturbation and time-varying state delay are investigated. Authors [25] designed a novel fuzzy Lyapunov–Krasovskii function in order to reduce the conservatism of stability conditions. The work in [32] deals with adaptive stabilization for a class of uncertain high-order nonlinear systems with time delays, and a procedure is developed to design the continuous adaptive state feedback controller without over-parameterization. [27] proposed a pinning synchronization control scheme in complex networks with nondelay and delay couplings, which uses two switched periods to provide intermittent control. Another type of control is named impulsive control. In fact, authors in [14] have used some analysis techniques such as reduction to absurdity and some new useful criteria for global exponential stability in order to validate the impulsive control law.

From practical point of view, systems with perturbations cause instability. Many researches have devoted themselves to design effective control approaches to guarantee the system stability [1, 5, 6, 9, 12, 18, 28]. Indeed, in citeHam01, the global stabilization problem for a relatively broad class of nonlinear plants is discussed. Author in [12] designs a nonlinear state feedback control law for a class of nonlinear perturbed system taking into account the fact that the nonlinear part is uniformly globally Lipchitz continuous along with a nongrowth condition.

In this work, we have treated the case where the system presents a perturbation term, which could result from errors in modeling the nonlinear system aging of parameters, or uncertainties and disturbances which exist in any realistic problems [2, 4, 17]. We do not know the term perturbation, but we know some information about it, like knowing an upper bound on it. The main contribution of this paper lies in the following aspects. Firstly, compared with [12] and based on the work of [18], an extended class of nonlinear time-varying dynamical system under unknown time-varying delay and a new control law are presented. Next, according to the designed control law, some new criteria are given to ensure the practical and the exponential stability of the origin of the addressed system. Besides, an illustrative example with simulation results shows the performance of the suggested control strategy.

The paper is organized as follows. In Sect. 2, the practical stability definition is presented. In Sect. 3, the system description is shown. According to the designed control law, some assumptions are provided in order to prove the stability of the controlled system. In Sect. 4, an illustrative example is described and the simulation results are presented in order to show the performances of the suggested control strategy. Finally, some concluding remarks and perspectives are given in Sect. 5.

2 Preliminary

We consider the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}\left( t \right) =f\left( t,x(t),x\left( t-\tau \left( t \right) \right) \right) \,\,t\ge t_{0}\\ x\left( t \right) =\phi \left( t-t_{0} \right) , \quad \forall t\in [t_{0}-\tau ,t_{0}] \end{array}\right. } \end{aligned}$$
(2.1)

where \(\tau ={ sup} \left( \tau \left( t \right) \right) _{t\in \mathbb {R}_{+}}\) and x(t) is the system solution with initial function \(\phi \) verifying:

$$\begin{aligned} x\left( s+t_{0} \right) =\phi (s), \quad \forall s\in [-\tau ,0], \end{aligned}$$

\(\phi \) is a constant function in the Banach space \(C_{n,\tau }:=C\left( \left[ -\tau ,0 \right] ,\mathbb {R}^{n} \right) \) with norm :

$$\begin{aligned} \left\| \phi \right\| _{\tau }:={\max }_{s\in \left[ -\tau ,0 \right] }\left\| \phi \left( s \right) \right\| , \end{aligned}$$

\(f:\mathbb {R}^{+}\times \mathbb {R}^{n}\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}\) is a piecewise continuous in t and locally Lipschitz in the state and \(\tau \) is the delay.

The definition of the practical stability introduced in [3] is presented as follows:

Definition 1

Equation (2.1) is said to be globally uniformly practically exponentially stable if there exists a ball \(B_{r}=\{x\in \mathbb {R}^{n}:\Vert x \Vert \le r\}\) such that \(B_{r}\) is globally uniformly practically exponentially stable, it means that:

There exists \(r>0\) such that for all \(t\ge t_{0}\) and \(\phi \in C_{n,\tau }\),

$$\begin{aligned} \left\| x(t) \right\| \le \lambda _{1}\left\| \varphi \right\| { exp} {\left( -\lambda _{2}\left( t-t_{0} \right) \right) +\,r}, \end{aligned}$$

with \(\lambda _{1}>0, \lambda _{2}>0.\)

3 Stabilization

In this paper, we examine the class of nonlinear dynamical systems modeled by the following state equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}\left( t \right) \!=\!f\left( t,x\left( t \right) \right) \!+\!g\left( t,x\left( t \right) \right) \left[ h\left( t,x_{\tau \left( t \right) } \right) \!+\!u\left( t \right) \right] \\ \qquad \qquad \!+\,\varphi \left( x\left( t \right) ,u\left( t \right) \right) \\ x\left( t \right) =\phi \left( t-t_{0} \right) \quad t\in [t_{0}-\tau ^{*},t_{0}] \end{array}\right. } \end{aligned}$$
(3.1)

where \(x(t)\in \mathbb {R}^{n}\) is the state of the system, \(u(t)\in \mathbb {R}^{q}\) is the input, \(x_{\tau (t)}=x\left( t-\tau \left( t \right) \right) \) is the delayed state with

$$\begin{aligned}&x=\left( {\begin{array}{c} x_{1} \\ \cdot \\ \cdot \\ \cdot \\ x_{n} \\ \end{array}} \right) , x_{\tau (t)}=\left( {\begin{array}{c} x_{1,\tau (t)} \\ \cdot \\ \cdot \\ \cdot \\ x_{n,\tau (t)} \\ \end{array}} \right) ; f :{\mathbb {R}\times \mathbb {R}}^{n}\rightarrow \mathbb {R}^{n},\\&g :{\mathbb {R}\times \mathbb {R}}^{n}\rightarrow \mathbb {R}^{n\times q}, h :\mathbb {R}\times \mathbb {R}^{n}\rightarrow \mathbb {R}^{q},\\&\varphi :\mathbb {R}^{n}\times \mathbb {R}^{q}\rightarrow \mathbb {R}^{n}, \end{aligned}$$

\(\tau ^{*}>0\) denotes the known upper bound of \(\tau (t), f(t,0) = 0, h(t,0) = 0, \forall t \in \mathbb {R} \;\mathrm{and }\, \varphi (0,u) =0\, \forall u \in \mathbb {R}^q\). The known functions \(f\left( t, x\left( t \right) \right) \), \(g\left( t, x\left( t \right) \right) \), and the unknown function \(h\left( t, x_{\tau \left( t \right) } \right) \), \(\varphi \left( x\left( t \right) ,u\left( t \right) \right) \) are continuous, uniformly bounded with respect to time, and locally uniformly bounded with respect to the state.

Assume that the following assumptions are satisfied:

  • (A1) There exists an increasing nonnegative continuous function \(\psi :\mathbb {R}_{+}\rightarrow \mathbb {R}\) such that:

    $$\begin{aligned}&\left\| h\left( t, x_{\tau \left( t \right) } \right) \right\| \le \psi \left( \left\| x_{\tau \left( t \right) } \right\| \right) , \end{aligned}$$
    (3.2)

  • (A2) The origin \(x=0\) of the nominal system \(\dot{x}\left( t \right) =f\left( t,x\left( t \right) \right) +g\left( t,x\left( t \right) \right) u\left( t \right) \) is stabilizable. Also, there exists a \(C^{1}\) function \(V\left( .,. \right) {: \mathbb {R}\times \mathbb {R}}^{n}\rightarrow \mathbb {R}^{{+}}\) and \(u_{1} :\mathbb {R}\rightarrow \mathbb {R}^{q}\) which satisfies:

    $$\begin{aligned}&\lambda _{1}\left\| x \right\| ^{2}\le V\left( t,x \right) \le \lambda _{2}\left\| x \right\| ^{2}, \end{aligned}$$
    (3.3)
    $$\begin{aligned}&\frac{\partial V(t,x)}{\partial t}+\nabla _{x}^{T}V\left( t,x \right) \left( f\left( t,x\left( t \right) \right) \right. \nonumber \\&\quad \left. +\,g\left( t,x\left( t \right) \right) u_{1} \right) \le -\lambda _{3}V(t,x) \end{aligned}$$
    (3.4)
    $$\begin{aligned}&\left\| \nabla _{x}^{T}V\left( t,x \right) \right\| \le \lambda _{4}\left\| x \right\| \end{aligned}$$
    (3.5)

    for all \((t,x){\in \mathbb {R}\times \mathbb {R}}^{n}\), where \(\lambda _{1},\lambda _{2},\lambda _{3}\) and \(\lambda _{4}\) are positive scalars.

  • (A3) There exist a positive constant \(k_{\varphi }\) such that

    $$\begin{aligned}&\left\| \varphi \left( x,u \right) -\varphi \left( z,u \right) \right\| \le k_{\varphi }\left\| x-z \right\| ,\nonumber \\&\quad \forall x{{\in \mathbb {R}}}^{n}, \quad \forall z\in \mathbb {R}^{n}, \quad \forall u \in \mathbb {R}^{q}, \end{aligned}$$
    (3.6)

    where \(\left\| . \right\| \) denotes the usual Euclidean norm on \(\mathbb {R}^{n}\).

3.1 Practical stability

We propose the following state feedback law:

$$\begin{aligned} u\left( t \right) =u_{1}\left( t \right) -L(t) \end{aligned}$$
(3.7)

where \(L\left( t \right) =\frac{g^{T}\left( t,x\left( t \right) \right) \nabla _{x}V\left( t,x \right) \tilde{\psi }^{2}\left( t \right) }{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t)+\varepsilon (t)}\), with \(\tilde{\psi }(t)=\psi \left( max_{s\in [t- \tau ^*,t]}\Vert x(s)\Vert \right) \) and \(\varepsilon (t)\) is a strictly positive continuous bonded function. Denote \(\varepsilon \) is the upper bound of \(\varepsilon (t)\).

Then we state the practical exponential stability behavior of the closed-loop systems formed (3.1) and (3.7). The following theorem provides the stability result concerning the control law (3.7).

Theorem 1

Suppose that Assumptions (A1) and (A2) hold and the function \(\varphi \) satisfies (A3) with the Lipchitz constant \(k_{\varphi }\) satisfying:

$$\begin{aligned} k_{\varphi }<\frac{\lambda _{1}\lambda _{3}}{\lambda _{4}} \end{aligned}$$
(3.8)

Then the control law defined in (3.7) globally exponentially practically stabilizes system (3.1).

Proof

Using the same Lyapunov function as given in assumption (A2), we have:

$$\begin{aligned} \dot{V}\left( t,x \right)= & {} \frac{\partial V(t,x)}{\partial t}+\nabla _{x}^{T}V\left( t,x \right) \dot{x}(t)\nonumber \\= & {} \frac{\partial V(t,x)}{\partial t}+\nabla _{x}^{T}V\left( t,x \right) \left( f\left( t,x\left( t \right) \right) \right. \nonumber \\&+g\left( t,x\left( t \right) \right) \left[ h\left( t,x_{\tau \left( t \right) } \right) +u\left( t \right) \right] \nonumber \\&+\left. \varphi \left( x\left( t \right) ,u\left( t \right) \right) \right) \nonumber \\= & {} \frac{\partial V(t,x)}{\partial t}+\nabla _{x}^{T}V\left( t,x \right) \left( f\left( t,x\left( t \right) \right) \right. \nonumber \\&+g\left( t,x\left( t \right) \right) u_{1}\left( t \right) \nonumber \\&-g\left( t,x\left( t \right) \right) L\left( t \right) +g\left( t,x\left( t \right) \right) h\left( t,x_{\tau \left( t \right) } \right) \nonumber \\&+\left. \varphi \left( x\left( t \right) ,u\left( t \right) \right) \right) \\\le & {} {-\lambda }_{3}V\left( t,x \right) -\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) L\left( t \right) \nonumber \\&+\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) h\left( t,x_{\tau \left( t \right) } \right) \nonumber \\&+\nabla _{x}^{T}V\left( t,x \right) \varphi \left( x\left( t \right) ,u\left( t \right) \right) \nonumber \end{aligned}$$
(3.9)

Let

$$\begin{aligned} k\left( t \right):= & {} -\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) L\left( t \right) \\&+\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) h\left( t,x_{\tau \left( t \right) } \right) . \end{aligned}$$

\(\square \)

Using assumption (A2), we have:

$$\begin{aligned} k(t)= & {} -\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \\&\quad \frac{g^{T}\left( t,x\left( t \right) \right) \nabla _{x}V\left( t,x \right) \tilde{\psi }^{2}\left( t \right) }{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }\left( t \right) +\varepsilon \left( t \right) }\\&+\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) h\left( t,x_{\tau \left( t \right) } \right) \\= & {} -\frac{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| ^{2}\tilde{\psi }^{2}\left( t \right) }{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }\left( t \right) +\varepsilon \left( t \right) }\\&+\nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) h\left( t,x_{\tau \left( t \right) } \right) \end{aligned}$$

According to (3.2),

$$\begin{aligned} k(t)\le & {} -\frac{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| ^{2}\tilde{\psi }^{2}\left( t \right) }{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }\left( t \right) +\varepsilon \left( t \right) }\\&+\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \psi \left( \left\| x_{\tau \left( t \right) } \right\| \right) \end{aligned}$$

By the fact that \(\tilde{\psi }(t)=\psi \big (max_{s\in [t- \tau ^*,t]}\Vert x(s)\Vert \big )\), we have :

$$\begin{aligned} k(t)\le & {} -\frac{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| ^{2}\tilde{\psi }^{2}\left( t \right) }{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }\left( t \right) +\varepsilon \left( t \right) }\\&+\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t) \end{aligned}$$

Making the denominators the same, we obtain:

$$\begin{aligned} k(t)\le \frac{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t)\varepsilon (t)}{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t)+\varepsilon (t)} \end{aligned}$$
(3.10)

Therefore, from the inequality \(( 0\le \frac{ab}{a+b}\le a, \forall a,b>0 )\), we have

$$\begin{aligned} \frac{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t)\varepsilon (t)}{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t)+\varepsilon (t)}\le \varepsilon (t) \end{aligned}$$
(3.11)

So, Inequality (3.9) becomes:

$$\begin{aligned} \dot{V}\left( t,x \right)\le & {} {-\lambda }_{1}\lambda _{3}\left\| x \right\| ^{{2}}+\varepsilon (t)\nonumber \\&+\nabla _{x}^{T}V\left( t,x \right) \varphi \left( x\left( t \right) ,u\left( t \right) \right) \end{aligned}$$
(3.12)

Using assumption (A3), we have

$$\begin{aligned} \dot{V}\left( t,x \right) \le {-\lambda }_{1}\lambda _{3}\left\| x \right\| ^{{2}}+\lambda _{4}k_{\varphi }\left\| x \right\| ^{{2}}+\varepsilon (t) \end{aligned}$$
(3.13)

Yield

$$\begin{aligned} \dot{V}\left( t,x \right) \le -\delta V\left( t,x \right) +\varepsilon \end{aligned}$$
(3.14)

where \(\delta \) equals to \(\frac{\lambda _{1}\lambda _{3}-\lambda _{4}k_{\varphi }}{\lambda _{2}}.\)

Then,

$$\begin{aligned} V\left( t,x \right) \le \exp {\left( -\delta \left( t-t_{0} \right) \right) V\left( t_{0},x\left( t_{0} \right) \right) +\frac{\varepsilon }{\delta }} \end{aligned}$$
(3.15)

By inequality \(\left( \sqrt{a+b} \le \sqrt{a} +\sqrt{b}, \forall a,b>0 \right) \), we have

$$\begin{aligned}&\left\| x(t) \right\| \le \sqrt{\frac{\lambda _{2}}{\lambda _{1}}} \exp {\left( -\frac{\delta }{2}\left( t-t_{0} \right) \right) \left\| x(t_{0}) \right\| +\sqrt{\frac{\varepsilon }{\lambda _{1}\delta } } } \nonumber \\ \end{aligned}$$
(3.16)
$$\begin{aligned}&\left\| x(t) \right\| \le \sqrt{\frac{\lambda _{2}}{\lambda _{1}}} \exp {\left( -\frac{\delta }{2}\left( t-t_{0} \right) \right) \left\| \phi \right\| _{\tau }+\vartheta } \end{aligned}$$
(3.17)

where \(\vartheta =\sqrt{\frac{\varepsilon }{\lambda _{1}\delta } }\).

Hence, system (3.1) in closed loop with the law (3.7) is \(\vartheta \) globally exponentially practically stable at the origin.

3.2 Exponential stability

We propose the following state feedback law:

$$\begin{aligned} u\left( t \right) =u_{1}\left( t \right) -L(t) \end{aligned}$$
(3.18)

where \(L\left( t \right) =\frac{g^{T}\left( t,x\left( t \right) \right) \nabla _{x}V\left( t,x \right) \tilde{\psi }^{2}\left( t \right) }{\left\| \nabla _{x}^{T}V\left( t,x \right) g\left( t,x\left( t \right) \right) \right\| \tilde{\psi }(t)+\varepsilon e^{-\alpha t}}\) with \(\tilde{\psi }(t)=\psi \big (max_{s\in [t- \tau ^*,t]}\Vert x(s)\Vert \big )\) and \(\varepsilon ,\alpha \) are two positive constants.

Then we state the stability behavior of the closed-loop systems formed (3.1) and (3.18). The following theorem provides the stability result concerning the control law (3.18).

Theorem 2

Suppose that Assumptions (A1), (A2) hold and the function \(\varphi \) satisfies (A3) with the Lipchitz constant \(k_{\varphi }\) satisfying:

$$\begin{aligned} k_{\varphi }<\frac{\lambda _{1}\lambda _{3}}{\lambda _{4}} \end{aligned}$$
(3.19)

Then for \(\alpha \) strictly greater than \(\frac{\lambda _{1}\lambda _{3}-\lambda _{4}k_{\varphi }}{\lambda _{2}}\), the control law defined in (3.18) globally exponentially stabilizes the system (3.1).

Proof

Using the same Lyapunov function as given in assumption (A2), Eq. (3.13) becomes:

$$\begin{aligned} \dot{V}\left( t,x \right)\le & {} {-\lambda }_{1}\lambda _{3}\left\| x \right\| ^{2}+\varepsilon e^{-\alpha t}+\lambda _{4}k_{\varphi }\left\| x \right\| ^{2}\nonumber \\\le & {} {-(\lambda }_{1}\lambda _{3}-\lambda _{4}k_{\varphi })\left\| x \right\| ^{2}+\varepsilon e^{-\alpha t} \end{aligned}$$
(3.20)

Therefore, for

$$\begin{aligned} \alpha >\frac{\lambda _{1}\lambda _{3}-\lambda _{4}k_{\varphi }}{\lambda _{2}}, \end{aligned}$$
(3.21)

and by Lemma 1 in [28], system (3.1) in closed loop with the law (3.18) is globally exponentially stable at the origin.

As a special case of above result, we consider the nonlinear dynamical system modeled by the following state equation:

$$\begin{aligned} \dot{x}\left( t \right)= & {} Ax(t)+B\left[ h\left( t,x_{\tau \left( t \right) } \right) +u\left( t \right) \right] \nonumber \\&+\varphi \left( x\left( t \right) ,u\left( t \right) \right) \end{aligned}$$
(3.22)

where \(A \in \mathbb {R}^{n\times n}\), \(B\in \mathbb {R}^{n\times q}\) are two constant matrices.

  • (H1) Suppose that (A, B) is controllable, then there exists a matrix K such that \((A+BK)\) is Hurwitz and a Lyapunov function for the nominal linear system can be chosen as \({\frac{1}{2}x}^{T}Px\), where \(P^{T}=P>0\) is such that:

    $$\begin{aligned} P\left( A+BK \right) +\left( A+BK \right) ^{T}P=-Q, Q>0\nonumber \\ \end{aligned}$$
    (3.23)

  • (H2) There exists an increasing nonnegative continuous function \(\psi :\mathbb {R}_{+}\rightarrow \mathbb {R}\) such that:

    $$\begin{aligned}&\left\| h\left( t, x_{\tau \left( t \right) } \right) \right\| \le \psi \left( \left\| x_{\tau \left( t \right) } \right\| \right) \end{aligned}$$
    (3.24)

  • (H3) There exist a positive constant \(k_{\varphi }\) such that

    $$\begin{aligned}&\left\| \varphi \left( x,u \right) -\varphi \left( z,u \right) \right\| \le k_{\varphi }\left\| x-z \right\| ,\nonumber \\&\quad \forall x\in \mathbb {R}^{n}, \quad \forall z\in \mathbb {R}^{n}, \quad \forall u\in \mathbb {R}^{m}, \end{aligned}$$
    (3.25)

\(\square \)

Corollary 1

Suppose that (H1), (H2) hold and the function \(\varphi \) (satisfies H3) with Lipchitz constant \(k_{\varphi }\) satisfying :

$$\begin{aligned} k_{\varphi }<\frac{\lambda _\mathrm{min}(P)\lambda _\mathrm{min}(Q)}{2{\lambda _\mathrm{max}(P)}^{2}} \end{aligned}$$
(3.26)

Then, there exist \(\alpha \) such that the feedback law \(u\left( t \right) =Kx(t)-L_{1}(t)\), where \(L_{1}\left( t \right) =\frac{B^{T}Px(t)\tilde{\psi }^{2}\left( t \right) }{\left\| B^{T}Px(t) \right\| \tilde{\psi }(t)+\varepsilon e^{-\alpha t}}\) globally exponentially stabilize the system (3.1).

Proof

The Lyapunov function V(t, x) satisfies:

$$\begin{aligned}&\frac{1}{2}\lambda _\mathrm{min}\left( P \right) \left\| x \right\| ^{2}\le V(t,x)\le \frac{1}{2}\lambda _\mathrm{max}\left( P \right) \left\| x \right\| ^{2},\\&\quad \nabla V\left( t,x \right) .\left( Ax+Bu \right) =-\frac{1}{2}x^{T}Qx\\&\quad \le -{\frac{1}{2}}\lambda _\mathrm{min}\left( Q \right) \left\| x \right\| ^{2}\\&\quad \le -\frac{\lambda _\mathrm{min}\left( Q \right) }{\lambda _\mathrm{max}\left( P \right) }V\left( t,x \right) ,\\&\quad \left\| \nabla _{x}^{T}V\left( t,x \right) \right\| =\left\| x^{T}P \right\| \le \lambda _\mathrm{max}\left( P \right) \left\| x \right\| , \end{aligned}$$

where \(\lambda _\mathrm{min}\left( P \right) \) and \(\lambda _\mathrm{max}\left( P \right) \) are, respectively, the minimum and the maximum eigenvalue of the matrix P.

Therefore, using the same manipulation of Theorem 1, we have: \(\lambda _{1}=\frac{\lambda _\mathrm{min}\left( P \right) }{2},{ \lambda }_{2}=\frac{\lambda _\mathrm{max}\left( P \right) }{2}\), \(\lambda _{3}=\frac{\lambda _\mathrm{min}\left( Q \right) }{\lambda _\mathrm{max}\left( P \right) }\) and \(\lambda _{4}=\lambda _\mathrm{max}\left( P \right) \).

According to the stability analysis of the system (3.22), the design procedure for the existence of \(\alpha \) is summarized as follows:

  • Step 1: we verify that the pair (A, B) is controllable.

  • Step 2: we choose K such that \((A+BK)\) is Hurwitz.

  • Step 3: we solve the Lyapunov Eq. (3.23) to obtain P.

  • Step 4: we choose \(\alpha >0\) such that (3.21) is verified. \(\square \)

4 Example

Let us consider the nonlinear system under unknown time-variable delay:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_{1}=-x_{1}+x_{2}+u_{1}+\sin \left( x_{1,\tau \left( t \right) } \right) \\ \qquad \qquad +0.4\cos \left( u_{1} \right) {x}_{2}\\ \dot{x}_{2}=x_{2}+u_{2}+\frac{x_{2,\tau \left( t \right) }}{1+t^{2}}+0.4x_{1} \end{array}\right. } \end{aligned}$$
(4.1)

This system has the same from of (3.1) where

$$\begin{aligned}&A=\left( {\begin{array}{c@{\quad }c} -1 &{} 1\\ 0 &{} 1\\ \end{array} } \right) , B=\left( {\begin{array}{c@{\quad }c} 1 &{} 0\\ 0 &{} 1\\ \end{array} } \right) , \varphi \left( x,u \right) =0.4\\&\left( {\begin{array}{c} \cos \left( u_{1} \right) x_{2} \\ x_{1} \\ \end{array}} \right) \, \hbox {and} \\&h\left( t, x_{\tau \left( t \right) } \right) =\left( {\begin{array}{c} \sin \left( x_{1,\tau \left( t \right) } \right) \\ \frac{x_{2,\tau \left( t \right) }}{1+t^{2}} \\ \end{array}} \right) . \end{aligned}$$

The function \(\tau (t)\) is defined as follows: \(\tau \left( t \right) =\frac{{\sin }^{2}(t)}{2}\) and the initial conditions for the system are \( x\left( t \right) ={[3\cos (t) \quad 6\cos (t)]}^{T}\,\forall t\in \left[ -0.5,0 \right] .\)

The control law that stabilizes exponentially the system is defined as follows:

$$\begin{aligned} u_{1}= & {} -x_{2}-\frac{\tilde{\psi }^{2}\left( t \right) }{\sqrt{x_{1}^{2}+x_{2}^{2}} \tilde{\psi }\left( t \right) +0.1e^{-2t}}x_{1},\nonumber \\ u_{2}= & {} -{2x}_{2}-\frac{\tilde{\psi }^{2}\left( t \right) }{\sqrt{x_{1}^{2}+x_{2}^{2}} \tilde{\psi }\left( t \right) +0.1e^{-2t}}x_{2}, \end{aligned}$$
(4.2)

where \(\tilde{ \psi }\left( t \right) =\max _{s\in \left[ t-0.5,t \right] }\left\| x\left( s \right) \right\| \).

It is clear that the pair (A, B) is controllable; we choose the matrix K such that \((A+BK)\) Hurwitz, we have \(K=\left( {\begin{array}{c@{\quad }c} 0 &{} -1\\ 0 &{} -2\\ \end{array} } \right) \), we choose also the matrix Q as follows \(\hbox {Q}=\left( {\begin{array}{c@{\quad }c} 2 &{} 0\\ 0 &{} 2\\ \end{array} } \right) \) and by solving the Lyapunov equation defined in (3.17), the matrix P is given by \(P=\left( {\begin{array}{c@{\quad }c} 1 &{} 0\\ 0 &{} 1\\ \end{array} } \right) \).

It is clear that \(k_{\varphi }=0.4\) and \(\frac{\lambda _\mathrm{min}(P)\lambda _\mathrm{min}(Q)}{2{\lambda _\mathrm{max}(P)}^{2}}=1\) so, we have \(k_{\varphi }<\frac{\lambda _\mathrm{min}(P)\lambda _\mathrm{min}(Q)}{2{\lambda _\mathrm{max}(P)}^{2}}\). For this example and with according to (3.23), we choose \(\alpha =2\). Then, the assumptions of the Theorem 2 are satisfied.

Therefore, the control law that stabilizes exponentially practically the system is defined as follows:

$$\begin{aligned} u_{1}= & {} -x_{2}-\frac{\tilde{\psi }^{2}\left( t \right) }{\sqrt{x_{1}^{2}+x_{2}^{2}} \tilde{\psi }\left( t \right) +1}x_{1},\nonumber \\ u_{2}= & {} -{2x}_{2}-\frac{\tilde{\psi }^{2}\left( t \right) }{\sqrt{x_{1}^{2}+x_{2}^{2}} \tilde{\psi }\left( t \right) +1}x_{2}, \end{aligned}$$
(4.3)

For the control law defined in (3.7), we have \(\varepsilon =1\).

Fig. 1
figure 1

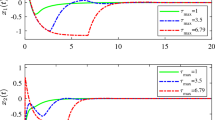
The evolution of \(x_{1}\) and \(x_{2}\) using the control law \({ u}_{1}=u_{2}={-x}_{1}-x_{2}\)

Full size image
Fig. 2
figure 2

The evolution of \(x_{1}\) and \(x_{2}\) using the control law defined in (4.2)

Full size image
Fig. 3
figure 3

The evolution of \(x_{1}\) and \(x_{2}\) using the control law defined in (4.3)

Full size image

Figure 1 shows the evolution of \(x_{1}\) and \(x_{2}\) using the control law \({ u}_{1}=u_{2}={-x}_{1}-x_{2}\). It is clear that the solutions diverge, and this is due to the bad choice of the control law, which is not in conformity with the designed one presented by Eqs. (3.7) or (3.18). Figure 2 shows the evolution of \(x_{1}\) and \(x_{2}\) using the control law defined in (4.2). It is clear that the solutions converge, and this is because of the good choice of the control feedback, which is in conformity with the designed one presented by Eq. (3.18). Then, according to Fig. 2, we point the exponential stability. Figure 3 presents the evolution of \(x_{1}\) and \(x_{2}\) using the control law defined in (4.3). Indeed, Fig. 3 shows clearly the results obtained in Theorem 1.

In accordance with the exponential stability and the practical stability presented in the proof of Theorem 1 and Theorem 2, and based on Figs. 2 and 3, it can be deduced that the proposed control law is performing.

5 Conclusion

In this paper, a new control design for a class of nonlinear systems under time-varying delay is proposed. Sufficient assumptions are given to guarantee the practical and the exponential stability of the suggested approach. Furthermore, a specific deduced class from the origin is analyzed and proved. Simulation results are shown in order to illustrate the good performances of the suggested stabilization methodology. A new control design for the same system taking into account the reduction of the number of assumptions may be a future perspective.