Impact of non-smooth threshold control on a reaction–diffusion predator–prey model with time delay

Abstract

To explore the efficacy of integrated pest management, we modify the predator–prey (pest–natural enemy) model by incorporating Holling III functional response and transform it into a non-smooth Filippov control system. Unlike conventional Filippov systems, the model takes into consideration time delay and spatial heterogeneity. Consequently, we establish and examine a delayed reaction–diffusion Filippov prey–predator model. Firstly, the dynamics of the two subsystems are analyzed, which includes the existence and stability of the equilibrium points, along with determining the adequate conditions for local Hopf bifurcation. Subsequently, we implement a detailed investigation of the sliding mode dynamics and stability of the pseudoequilibrium. Theoretical and numerical simulations indicate that on the one hand, the threshold level should be prescribed adequately to reduce the pest population equal to or below the threshold level. On the other hand, reading from the boundary node and boundary focus bifurcations, slightly varying the economic threshold may save a failure control strategy by dragging the number of the pests from a regular equilibrium above the threshold to a boundary equilibrium or a pseudoequilibrium equal to the threshold. Furthermore, the sequent appearance of global sliding bifurcations including touching, sliding switching and crossing bifurcations expound that the incorporation of time delay not only complicates the dynamics of the system, but also brings more challenge for pest control.

1 Introduction

Subsequent to the pioneering contributions of Lotka and Volterra [1, 2], numerous researchers have put forth a significant number of different models for prey–predator interactions [3,4,5,6] to investigate the complex dynamics. There are many types of mathematical models that can simulate the interactions of the prey and predator, such as ordinary differential equations, partial differential equations and discrete equations. Mokni et al. [7] applied a new approach to a special class of discrete time evolution models and established a solid mathematical foundation to analyse them. Liu et al. [8] proposed a Filippov prey–predator model with time delay to address how the threshold and time delay influence the dynamics of the model. However, the authors did not consider the spatial location variations in the model.

Traditional prey predator models generally assume that all species are spatially homogeneous [4,5,6, 9, 10]. Actually, the predators and preys are always moving in space, their distribution across different spatial locations is not uniform. Pests tend to relocate to areas with lower population density as a means of increasing their chances of survival. Therefore, many literatures [11,12,13] suggest that the reaction–diffusion prey–predator models are more suitable for studying complex spatiotemporal predator dynamics. Reaction–diffusion equations are usually used to modeling abundance of organisms and the spatiotemporal distribution [14,15,16,17,18,19,20,21,22]. Huang et al. [12] investigated a prey–predator model under Dirichlet boundary condition and showed that the synchronized steady state solution is locally asymptotically stable under equal growth and diffusion rates. In [13], the authors considered the spread of rumors into a non-smooth reaction–diffusion system, then proved the existence of non-negative solutions using the upper and lower solution method. Numerical simulations were given to illustrate various bifurcation phenomena. Considering reaction–diffusion into a prey–predator model may be more realistic from biological point of view.

Reducing the presence of crop pests and pathogens is essential for enhancing the overall performance of global agriculture and associated food systems [23,24,25]. The increasing number of pests has led to the ingestion of crops worldwide, the quality of harvest production is influenced, which may potentially result in future shortages of food. Therefore, to resist pests and deal with the losses are urgent [26]. It is usually not possible to kill pests completely, which is also economically or biologically undesirable [27, 28]. Hence, it is crucial to adopt the integrated pest management (IPM) approach that strives to maintain pest populations within acceptable or anticipated thresholds to prevent detrimental impacts of pest outbreaks. The application of IPM not only prevents financial losses but also promotes sustainable development of agricultural systems. The objective of IPM is to combine suitable tactics, such as chemical and/or biological means, to manage pests within an economically tolerable threshold level (ET). This ET serves as a tolerable limit, beyond which control measures are implemented to prevent pest populations from surpassing the acceptable level. Consequently, this study puts forth a non-smooth Filippov system with threshold control. When the pests reaches or surpasses the economic threshold, the application of insecticides and introduction of natural predators will be promptly initiated [29,30,31,32,33]. Tang et al. [34] constructed a Filippov prey–predator model incorporating threshold control strategies and time delay to examine the equilibrium points, sliding mode dynamics and different diverse branching phenomena. The results indicate that the dynamics of the system are significantly influenced by both time delay and threshold value. Jiao et al. [4, 5] and Wang et al. [6] provided a more comprehensive discussion on qualitative analysis of equilibrium points and global sliding bifurcations.

In real ecosystems, the species need a certain period of time to produce offsprings and digest food, the growth of organisms is not an instantaneous process, and the response time of system members to environmental changes cannot be disregarded [35,36,37]. Mathematically, models with delay may exhibit more complicated dynamic performances, such as changes in equilibrium stability, the emergence of Hopf bifurcation, and the possibility of various bifurcation phenomena. As pointed out by Mahmoud et al. [35], time delay has the potential to alter the stability of equilibrium in a system. It may even lead to the formation of multiple periodic motions and chaotic behaviors. Hence, it is indispensable to take account of time delay into predator–prey models to precisely reflect how the population dynamics rely on past corresponding information [38,39,40,41,42].

Therefore, we develop a Filippov reaction–diffusion predator–prey model with time delay. Usually, it is assumed that the system meets the Neumann boundary condition, which means that the prey and predator population is confined within a given domain. We are interested in how the diffusion, time delay, and threshold switching will affect the predator–prey model. Will the existence of the Laplacian term bring challenges to the proof of the existence of the sliding mode? Can the introduction of time delay result in more intricate dynamic performance, like Hopf bifurcations? Can the Filippov control strategy effectively lower the pest population below the designed tolerable threshold, thereby accomplish the control objectives? Furthermore, our research concentrates on examining the discontinuity bifurcation triggered by the right-hand discontinuity and time delay, and investigating the potential challenges posed by time delay and diffusion to Filippov control. Zhang et al. [38] considered a such model to study the dynamics of a prey–predator model with threshold harvesting, which, to our knowledge, is the few work considering both reaction–diffusion and delay in Filippov models. We will carry out more global dynamics and sliding bifurcation analysis in this work.

The manuscript is then structured as follows. We establish and elaborate the delay reaction–diffusion Filippov system in Sect. 2. Section 3 is dedicated to analyzing the existence and stability of equilibria as well as the occurrence of Hopf bifurcations. What follows are the sliding domain and sliding mode dynamics in Sect. 4. In Sect. 5, we concentrate on investigating the impacts of economic threshold and time delay on system dynamics and pest control. Local and global sliding bifurcations are investigated in Sect. 6. We conclude the work in the final section.

2 The delay reaction–diffusion Filippov prey–predator model

Based on the analysis presented above, in order to explore how the time delay and Filippov strategies will influence the reaction–diffusion prey predator model, and meanwhile, biologically investigate more complex dynamical behaviors such as Hopf bifurcations and discontinuity-induced bifurcations the time delay may bring, here, we construct a mathematical model according to the following assumptions.

$(\text{ i})$:

u(x, t) and v(x, t) represent the population density of prey (pest) and predator (natural enemy), respectively. The diffusion coefficients of prey and predator are denoted by $d_{1}$ and $d_{2}$, respectively. Filippov models with time delay have been investigated in [5, 6, 8], however, spatial heterogeneity are rarely considered. Here, we incorporate reaction–diffusion into a delay Filippov model.

$(\text{ ii})$:

r represents the intrinsic growth rate of the prey population, while k denotes the carrying capacity. The impact of the predator on the prey population is regulated by a Holling type III functional response $\frac{\alpha u^{2}v}{\beta +u^{2}}$, $\alpha$ represents the maximum capture rate of the prey, while $\beta$ denotes the search rate of the predator. $\delta$ is the mortality rate of the predator, $\eta$ is the conversion factor of prey capture. All parameters are positive. In general, there are three different functional response functions for different types of species based on experiments, Holling I, Holling II and Holling III. Holling I functional response function adapts to algae, cells and lower organisms, Holling II functional response function adapts to invertebrates, and Holling III functional response function is for vertebrates. Here, we consider Holling III functional response function other than linear rate to investigate the prey predator interactions.

$(\text{ iii})$:

$p>0$ represents the killing rate of the prey population as a result of pesticide spraying, here, assume $r>p$. $q>0$ is the release rate of natural enemies, and $q<\delta$. $\tau$ indicates the time required for the predator population to become pregnant or mature.

$(\text{ iv})$:

$\varDelta$ represents the Laplacian operator. $\varOmega$ represents a bounded domain. $\text{ n }$ is the normal vector that extends outward from the bounded domain $\varOmega$. $\partial /\partial \text{ n }$ represents the outward normal derivative on $\partial \varOmega$. The homogeneous Neumann boundary conditions imply that there is no population flux across the boundaries.

We adopt the IPM strategy, that is, once the pest population surpasses the ET, control strategies will be implemented by spraying pesticides with rate p and releasing natural enemies with rate q. The system can be then described as follows:

$$\begin{aligned} \begin{aligned} \frac{\partial u}{\partial t}&=d_{1}\varDelta u(x,t)+ru(x,t)\left( 1-\frac{u(x,t)}{k}\right) \\&\quad {-}\frac{\alpha u^{2}(x,t)v(x,t)}{\beta {+}u^{2}(x,t)}{-}\varepsilon pu(x,t), \\ \frac{\partial v}{\partial t}&=d_{2}\varDelta v(x,t)-\delta v(x,t)+\frac{\eta \alpha u^{2}(x,t-\tau )v(x,t)}{\beta +u^{2}(x,t-\tau )}\\ {}&+\varepsilon qv(x,t),\quad t>0,\quad x\in \varOmega ,\\ \end{aligned} \end{aligned}$$

(1)

with

$$\begin{aligned} \varepsilon =\left\{ \begin{array}{ll} 0,&{}\quad \text{ for }\,u(x,t)-{ ET}<0,\\ 1,&{}\quad \text{ for }\,u(x,t)-{ ET}>0, \end{array} \right. \end{aligned}$$

(2)

and the Neumann boundary conditions

$$\begin{aligned} \frac{\partial u(x,t)}{\partial \text{ n }}=0, \frac{\partial v(x,t)}{\partial \text{ n }}=0,\quad t>0,\quad x\in \partial \varOmega . \end{aligned}$$

The initial condition is $u(x,t)=\phi _{1}(x,t)\ge 0, v(x,t) =\phi _{2}(x,t)\ge 0, (x,t)\in \overline{\varOmega }\times (-\tau ,0),\overline{\varOmega }=\varOmega \cup \partial \varOmega .$ Here, we assume that $\phi _{1}, \phi _{2}\in \mathcal { C}=C([-\tau , 0], X)$, $X=\{u\in W^{2,2}(\varOmega ): \frac{\partial u(x,t)}{\partial \text{ n }}=\frac{\partial v(x,t)}{\partial \text{ n }}=0, x\in \partial \varOmega \}$ with the inner product $\langle \cdot ,\cdot \rangle$.

Remark 1

There are lots of models established to investigate the prey and predator interactions and its control [1,2,3,4,5,6,7,8]. c differentiates these existing models from the following aspects. Firstly, spatial heterogeneity is considered to explore the prey and predator interactions. The transmission of the prey and predator can be numerically provided by the analysis. Secondly, we consider a Holling type III functional response $\frac{\alpha u^{2}v}{\beta +u^{2}}$, which is different from the traditional linear rate or Holling I and II functional response functions. The delay reaction–diffusion Filippov system (1) with (2) reflects the real interactions and controls more precisely.

Let $\rho (z)=u-{ ET}$ with $z=(u,v)^{T}$, then the space $R_{+}^2=\{(u,v)^{T}|u(x,t)\ge 0, v(x,t)\ge 0\}$ is divided into three parts:

$$\begin{aligned} \varGamma _{1}= & {} \{z\in R_{+}^{2}|\rho (z)<0\},\quad \varGamma _{2}=\{z\in R_{+}^{2}|\rho (z)>0\}, \\ \varGamma= & {} \{z\in R_{+}^{2}|\rho (z)=0\}. \end{aligned}$$

The dynamics of the system (1) with (2) in $\varGamma _{1}$ and $\varGamma _{2}$ are determined by $F_{\varGamma _{1}}$ and $F_{\varGamma _{2}}$, respectively, where

$$\begin{aligned} F_{\varGamma _{1}}(z,z_{\tau })= & {} \left( \begin{array}{l} d_{1}\varDelta u+ru(1-\frac{u}{k})-\frac{\alpha u^{2}v}{\beta +u^{2}}\\ d_{2}\varDelta v-\delta v+\frac{\eta \alpha u^{2}(t-\tau )v}{\beta +u^{2}(t-\tau )} \end{array} \right) ,\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} F_{\varGamma _{2}}(z,z_{\tau })= & {} \left( \begin{array}{l} d_{1}\varDelta u+ru(1-\frac{u}{k})-\frac{\alpha u^{2}v}{\beta +u^{2}}-pu\\ d_{2}\varDelta v-\delta v+\frac{\eta \alpha u^{2}(t-\tau )v}{\beta +u^{2}(t-\tau )}+qv\\ \end{array} \right) .\nonumber \\ \end{aligned}$$

(4)

Here, denote $(z(t),z(t-\tau ))=(z,z_{\tau })$ for simplicity. In the subsequent discussion, the delay Filippov system (1) with (2) in region $\varGamma _{1}$ is designated as subsystem (3), and in region $\varGamma _{2}$ is designated as subsystem (4).

The delay reaction–diffusion Filippov system (1) with (2) could exhibit various equilibrium points, for further investigation, we first present these different types of equilibria, including regular/virtual, pseudoequilibrium and boundary/tangent points [4,5,6].

Definition 1

If an equilibrium E satisfies $F_{\varGamma _{1}}(z,z_{\tau })=0, \rho (z)<0$, or $F_{\varGamma _{2}}(z,z_{\tau })=0, \rho (z)>0$, then E is called a regular equilibrium, denoted by $E^R$; While if $F_{\varGamma _{1}}(z,z_{\tau })=0, \rho (z)>0$, or $F_{\varGamma _{2}}(z,z_{\tau })=0, \rho (z)<0$, then E is called a virtual equilibrium, denoted by $E^V$.

Definition 2

If an equilibrium E satisfies $F_{\varGamma _{1}}(z,z_{\tau })=0, \rho (z)=0$, or $F_{\varGamma _{2}}(z,z_{\tau })=0, \rho (z)=0$, then E is called a boundary equilibrium; E is called a tangent point if $\langle \nabla \rho (z),F_{\varGamma _{1}}(z,z_{\tau })\rangle =0$, $\rho (z)=0$, or $\langle \nabla \rho (z),F_{\varGamma _{2}}(z,z_{\tau })\rangle =0$, $\rho (z)=0$, where $\langle \cdot \rangle$ indicates the standard scalar product, $\nabla \rho (z)$ is the gradient of $\rho (z)$ on the discontinuity surface $\varGamma$.

Definition 3

If a point satisfies $\epsilon F_{\varGamma _{1}}(z,z_{\tau })+(1-\epsilon ) F_{\varGamma _{2}}(z,z_{\tau })=0,$ $\rho (z)=0$, $\epsilon =\frac{\langle \nabla \rho (z),F_{\varGamma _{2}}\rangle }{\langle \nabla \rho (z), F_{\varGamma _{2}}-F_{\varGamma _{1}}\rangle }$, then the point is called a pseudoequilibrium, where $\nabla \rho (z)=(1,0)^{T}$ represents the normal vector perpendicular to $\varGamma$. Accordingly, the system $F_{\varGamma _{s}}=\epsilon F_{\varGamma _{1}}+(1-\epsilon ) F_{\varGamma _{2}}$ is denoted as the sliding mode dynamics.

3 Dynamic analysis of subsystems (3) and (4)

Firstly, we will conduct a comprehensive investigation into the existence of equilibrium points of subsystems (3) and (4), and then the stability of the equilibrium points will be obtained by analyzing the corresponding characteristic equations. Finally, Hopf bifurcation will be investigated.

3.1 The equilibrium points of subsystems (3) and (4)

For subsystem (3), (0, 0) and (k, 0) are always two predator-free equilibria. The interior equilibrium satisfies

$$\begin{aligned} \begin{aligned} ru\left( 1-\frac{u}{k}\right) -\frac{\alpha u^{2}v}{\beta +u^{2}}&=0,\\ -\delta v+\frac{\eta \alpha u^{2}v}{\beta +u^{2}}&=0. \end{aligned} \end{aligned}$$

Calculation yields that if $R_{1}=\frac{k^{2}\alpha \eta }{k^{2}\delta +\beta \delta }>1,$ then subsystem (3) possesses a unique endemic equilibrium $E_{1}=(u_{1}^{*}, v_{1}^{*})=(\sqrt{\frac{\delta \beta }{\eta \alpha -\delta }}, \frac{r\eta \beta }{k(\delta -\alpha \eta )}+\frac{\eta r\sqrt{\beta }}{\sqrt{\delta (\alpha \eta -\delta )}})$.

For subsystem (4), (0, 0) and $(k(1-\frac{p}{r}),0)$ are always two predator-free equilibria. Calculation yields that if $R_{2}=\frac{k^{2}(1-\frac{p}{r})^{2}\alpha \eta }{k^{2}(1-\frac{p}{r})^{2}(\delta -q)+(\delta -q)\beta }>1$, then subsystem (4) possesses a unique endemic equilibrium $E_{2}=(u_{2}^{*}, v_{2}^{*})=(\sqrt{\frac{(\delta -q)\beta }{\eta \alpha -\delta +q}}, \frac{r\eta \beta }{k(\delta -\alpha \eta -q)}+\frac{\eta (r-p)\sqrt{\beta }}{\sqrt{(\delta -q)(\alpha \eta -\delta +q)}}).$

3.2 Stability analysis and Hopf bifurcation

Notation 31

On the basis of homogeneous Neumann boundary condition, we assume that $0=\sigma _{0}<\sigma _{1}<\sigma _{2}<\cdots<\sigma _{n}<\cdots \rightarrow \infty$ are the eigenvalues of $-\triangle$ on $\varOmega$, then the space decomposition below is true.

• (1) $S(\sigma _{n})$ is the eigenfunction space relative to $\sigma _{n}$ for $n=0,1,2,\ldots$.

• (2) $X_{ij}:=\{{{\textbf {c}}\cdot \phi _{ij},{\textbf {c}}\in R^{2}}\}$, ${\phi _{ij}}$ are orthonormal basis of $S(\sigma _{n})$ for $j=1,2,\ldots , dim[S(\sigma _{n})]$.

• (3) ${\textbf {X}}:=\{{z=(u,v)\in [C^{1}(\varOmega )]^{2}:\frac{\partial u}{\partial \text{ n }}=\frac{\partial v}{\partial \text{ n }}=0}\}$, and ${\textbf {X}}=\oplus ^{\infty }_{i=1}{} {\textbf {X}}_{i}$, where ${\textbf {X}}_{i}=\oplus ^{dim[S(\sigma _{j})]}_{j=1}{} {\textbf {X}}_{ij}$.

Linearizing system (1) at any equilibrium $E=(u^{*},v^{*})$ can yield the corresponding characteristic equation as follows,

$$\begin{aligned} \bigg | \begin{array}{cc} \varDelta _{11} &{}\quad \varDelta _{12}\\ \varDelta _{21} &{}\quad \varDelta _{22}\\ \end{array} \bigg |=0, \end{aligned}$$

(5)

where

$$\begin{aligned} \begin{aligned} \varDelta _{11}&=d_{1}\sigma _{n}+r-\frac{2ru^{*}}{k}\\ {}&-\frac{2\alpha u^{*}v^{*}\left( \beta +u^{*^{2}}\right) -2\alpha u^{*^{3}}v^{*}}{\left( \beta +u^{*^{2}}\right) ^{2}}\\&\quad -\varepsilon p-\lambda ,\\ \varDelta _{12}&=-\frac{\alpha u^{*^{2}}}{\beta +u^{*^{2}}},\\ \varDelta _{21}&=\frac{2\alpha \eta u^{*}v^{*}}{\beta +u^{*^{2}}}\left( 1-\frac{u^{*^{2}}}{\beta +u^{*^{2}}}\right) e^{-\lambda \tau },\\ \varDelta _{22}&=d_{2}\sigma _{n}-\delta +\frac{\eta \alpha u^{*^{2}}}{\beta +u^{*^{2}}}+\varepsilon q-\lambda . \end{aligned} \end{aligned}$$

Expanding (5) we can obtain the following equation,

$$\begin{aligned} \Lambda _{n}(\lambda )=\lambda ^{2}+A_{n}\lambda +B_{n}+Ce^{-\lambda \tau }=0, \end{aligned}$$

(6)

with

$$\begin{aligned} \begin{aligned} A_{n}&=d_{1}\sigma _{n}+d_{2}\sigma _{n}+\frac{ru^{*}}{k}+\frac{\alpha u^{*}v^{*}}{\beta +u^{*}}\left( 1-2u^{*^{2}}\right) ,\\ B_{n}&=\left( d_{1}\sigma _{n}+\frac{ru^{*}}{k}+\frac{\alpha u^{*}v^{*}}{\beta +u^{*}}\left( 1-2u^{*^{2}}\right) \right) d_{2}\sigma _{n},\\ C&=\frac{2\alpha ^{2}\eta u^{*^{3}}v^{*}}{\left( \beta +u^{*^{2}}\right) ^{2}}\left( 1-\frac{u^{*^{2}}}{\beta +u^{*^{2}}}\right) >0. \end{aligned} \end{aligned}$$

Obviously, the predator-free equilibria (0, 0) of subsystems (3) and (4) are always unstable for one of the eigenvalues is $\lambda =d_{1}\sigma _{n}+r-\varepsilon p>0.$ The predator-free equilibria (k, 0) and $(k(1-\frac{p}{r}),0)$ are always unstable if $R_{1}>1$ and $R_{2}>1$ for one of the eigenvalues is $\lambda =d_{2}\sigma _{n}-\delta +\frac{\eta \alpha u^{*^{2}}}{\beta +u^{*^{2}}}+\varepsilon q>0$.

When $\tau =0$, Eq. (6) can be rewritten as the following form,

$$\begin{aligned} \lambda ^{2}+A_{n}\lambda +B_{n}+C=0. \end{aligned}$$

(7)

Consequently, if condition $(\varPi _{1})$ is satisfied, the characteristic equation (7) will have roots with negative real parts, where

$(\varPi _{1}): A_{n}>0, B_{n}+C>0.$

In this case, the positive equilibria $E_{1}$ and $E_{2}$ for subsystems (3) and (4) are locally asymptotically stable.

Next, if $i\omega (\omega >0)$ is a root of Eq. (6), then $\omega$ will satisfy the following equation for some $n\in \{0,1,2,\ldots \}$, which examines the impact of time delay $\tau$ on the stability of the positive equilibrium,

$$\begin{aligned} -\omega ^{2}+iA_{n}\omega +B_{n}+C(\cos (\omega \tau )-i\sin (\omega \tau ))=0. \end{aligned}$$

(8)

By separating the real and imaginary parts, we obtain that

$$\begin{aligned} \left\{ \begin{array}{l} -\omega ^{2}+B_{n}=-C\cos (\omega \tau ),\\ A_{n}\omega =C\sin (\omega \tau ). \end{array} \right. \end{aligned}$$

(9)

Squaring both sides of Eq. (9) and adding them reads

$$\begin{aligned} \omega ^{4}+\left( A_{n}^{2}-2B_{n}\right) \omega ^{2}+B_{n}^{2}-C^{2}=0. \end{aligned}$$

(10)

Denote $Z=\omega ^{2}$, $A_{n}^{2}-2B_{n}=D_{1}, B_{n}^{2}-C^{2}=D_{2}$, Eq. (10) then can be written as

$$\begin{aligned} Z^{2}+D_{1}Z+D_{2}=0. \end{aligned}$$

(11)

The existence of positive roots of Eq. (10) can be deduced by Eq. (11), which is listed in the following lemma.

Lemma 1

• 1. If $D_{2}>0$ and $D_{1}<0$ and $D_{1}^{2}>4D_{2}$ is satisfied, Eq. (10) has two positive roots, denoted by $\omega _{n_{\pm }}$, where $\omega _{n_{\pm }}=\sqrt{\frac{-D_{1}\pm \sqrt{D_{1}^{2}-4D_{2}}}{2}}.$

• 2. If either $D_{1}<0$ and $D_{1}^{2}=4D_{2}$ or $D_{2}<0$ is satisfied, Eq. (10) has only one positive root $\omega _{n_{+}}$, $\omega _{n_{+}}=\sqrt{\frac{-D_{1}+\sqrt{D_{1}^{2}-4D_{2}}}{2}}.$

• 3. If either $D_{2}>0$ and $D_{1}>0$ or $D_{1}^{2}<4D_{2}$ is satisfied, Eq. (10) has no positive root.

Without less of generality, assume Eq. (10) has two positive roots, then from Eq. (9), we can deduce

$$\begin{aligned} \tau _{n_{\pm }}^{(j)}=\left\{ \begin{array}{ll} \frac{1}{\omega _{n_{\pm }}}\left( \arccos \frac{\omega ^{2}_{n_{\pm }}-B_{n}}{C}+2\pi j\right) ,\\ \frac{A_{n}\omega _{n_{\pm }}}{C}\ge 0,\\ \frac{1}{\omega _{n_{\pm }}}\left( 2\pi -\arccos \frac{\omega ^{2}_{n_{\pm }}-B_{n}}{C}+2\pi j\right) ,\\ \frac{A_{n}\omega _{n_{\pm }}}{C}<0, \end{array}\right. \end{aligned}$$

(12)

with $j=0,1,2,\ldots$.

The following result verifies the validity of the transversality condition.

Lemma 2

Assume $\lambda _{n}(\tau )=\alpha _{n}(\tau )\pm i\omega _{n}(\tau )$ is a root of Eq. (6) near $\tau =\tau _{n_{\pm }}^{(j)}$ satisfying $\alpha _{n}(\tau _{n_{\pm }}^{(j)})=0$ and $\omega _{n}(\tau _{n_{\pm }}^{(j)})=\omega _{n_{\pm }},$ $j=0,1,2,\ldots .$ The following transversality conditions are satisfied,

$$\begin{aligned}{} & {} Re\left( \frac{d\lambda }{d\tau }\right) _{\tau =\tau _{n_{+}}^{(j)}, \omega =\omega _{n_{+}}}>0, \\{} & {} Re\left( \frac{d\lambda }{d\tau }\right) _{\tau =\tau _{n_{-}}^{(j)}, \omega =\omega _{n_{-}}}<0. \end{aligned}$$

Proof

Differentiating Eq. (6) with respect to $\tau$ yields

$$\begin{aligned} \frac{d\lambda }{d\tau }\left( 2\lambda +A_{n}-C\tau e^{-\lambda \tau }\right) =C\lambda e^{-\lambda \tau }. \end{aligned}$$

Therefore,

$$\begin{aligned} \left( \frac{d\lambda }{d\tau }\right) ^{-1}{} & {} =\frac{2\lambda +A_{n}-C\tau e^{-\lambda \tau }}{C\lambda e^{-\lambda \tau }}=\frac{2}{C}e^{\lambda \tau }\\ {}{} & {} \quad +\frac{A_{n}}{C\lambda }e^{\lambda \tau }-\frac{\tau }{\lambda }. \end{aligned}$$

Accordingly,

$$\begin{aligned} Re\left( \frac{d\lambda }{d\tau }\right) ^{-1}_{\tau =\tau _{n_{\pm }}^{(j)}, \omega =\omega _{n_{\pm }}}{} & {} =\frac{2\cos \left( \omega _{n_{\pm }}\tau _{n_{\pm }}^{(j)}\right) }{C}\\ {}{} & {} +\frac{A_{n}\sin \left( \omega _{n_{\pm }}\tau _{n_{\pm }}^{(j)}\right) }{C\omega _{n_{\pm }}}. \end{aligned}$$

Since $C\cos (\omega _{n_{\pm }}\tau _{n_{\pm }}^{(j)})=\omega _{n_{\pm }}^{2}-B_{n}$ and $C\sin (\omega _{n_{\pm }}\tau _{n_\pm }^{(j)}) =A_{n}\omega _{n_{\pm }},$ hence, we have

$$\begin{aligned}{} & {} Re\left( \frac{d\lambda }{d\tau }\right) ^{-1}_{\tau =\tau _{n_{\pm }}^{(j)}, \omega =\omega _{n_{\pm }}}\\{} & {} =\pm \frac{\sqrt{\left( A_{n}^{2}-2B_{n}\right) ^{2}-4\left( B_{n}^{2}-C^{2}\right) }}{C^{2}}. \end{aligned}$$

The result is then followed.

The first inequality in Lemma 2 indicates that the root crosses the imaginary axis from left to right, indicating the instability of the equilibrium. While the second inequality indicates that the equilibrium is stable.

The ensuing theorem provides an analysis of the stability of the endemic equilibria $E_{1}$ and $E_{2}$.

Theorem 1

Assuming $\tau _{n_{\pm }}^{(j)}$ is described by (12), the following assertions hold true.

• (1) If $(\varPi _{1})$ does not hold, equilibria $E_{1}$ and $E_{2}$ are unstable for $\tau \in [0,+\infty )$.

• (2) If $(\varPi _{1})$ holds, equilibrium $E_i, i=1,2$, is stable when $\tau \in [0,\tau _{n_{+}}^{(0)})$ and unstable when $\tau \in (\tau _{n_+}^{(0)},+\infty )$. Furthermore, when $\tau =\tau _{n_{+}}^{(0)}$, system (1) undergoes a Hopf bifurcation at the equilibrium $E_i, i=1,2$.

Proof

Based on Theorem 2.1 in [42], if $\varPi _{1}$ does not hold, it can be concluded that $E_i, i=1,2,$ is unstable for $\tau \in [0,\tau _{n_{+}}^{(0)})$. Furthermore, due to $Re\left( \frac{d\lambda }{d\tau }\right) _{\tau =\tau _{n_{+}}^{(0)}, \omega =\omega _{n_{+}}}>0$, we have $E_i, i=1,2,$ is unstable for $\tau \ge \tau _{n_{+}}^{(0)}$, then $E_{1}, E_{2}$ are unstable for all $\tau \ge 0$.

If $\varPi _{1}$ holds, $E_i, i=1,2,$ is stable for $\tau \in [0,\tau _{n_+}^{(0)})$. $Re\left( \frac{d\lambda }{d\tau }\right) _{\tau =\tau _{n_{+}}^{(0)}, \omega =\omega _{n_{+}}}>0$ indicates that $E_i, i=1,2,$ is unstable for $\tau \in [\tau _{n_{+}}^{(0)},\tau _{n_{+}}^{(1)})$. $Re\left( \frac{d\lambda }{d\tau }\right) _{\tau =\tau _{n_{+}}^{(1)}, \omega =\omega _{n_{+}}}>0$ indicate that $E_i, i=1,2,$ is unstable for $\tau =\tau _{n_{+}}^{(1)}$, and $\tau >\tau _{n_{+}}^{(1)}$, the stability of $E_i$ is switched when $\tau =\tau _{n_{+}}^{(0)}$, and the system undergoes a Hopf bifurcation.

4 Sliding regions and sliding mode dynamics

The existence of the sliding mode is contingent on the fact that the two subsystem vectors are oriented in opposite directions towards each other on the surface of discontinuity, that is,

$$\begin{aligned} \rho (z)\frac{\partial \rho (z)}{\partial t}=\rho (x,t)\frac{\partial \rho (x,t)}{\partial t}\le 0. \end{aligned}$$

There are two methods for solving sliding mode dynamics in general, the Utkin’s equivalent control method and the Filippov convex method [4,5,6]. In this study, we will utilize the Filippov convex method to investigate the sliding mode dynamcis of delay reaction–diffusion Filippov system (1) with (2). For convenience, denote

$$\begin{aligned} \begin{aligned} f(u,v)&=(u-{ ET})f_{1}(u,v),\\ f_{1}(u,v)&=ru\left( 1-\frac{u}{k}\right) -\frac{\alpha u^{2}v}{\beta +u^{2}}+u-{ ET}-\varepsilon pu, \end{aligned} \end{aligned}$$

with $\varepsilon$ defined in (2).

Theorem 2

Suppose that $[r(1-\frac{{ ET}}{k})-p]\frac{\beta +{ ET}^{2}}{\alpha { ET}}=v_{min}<v<v_{max}=r(1-\frac{{ ET}}{k})\frac{\beta +{ ET}^{2}}{\alpha { ET}}$ and $d_{1}<1$ holds, then the sliding mode will occur on $u={ ET}$ when $v_{min}<v<v_{max}$.

Proof

First, solving two algebraic equations about v,

$$\begin{aligned} r{ ET}\left( 1-\frac{{ ET}}{k}\right) -\frac{\alpha { ET}^{2}v}{\beta +{ ET}^{2}}=0, \end{aligned}$$

and

$$\begin{aligned} r{ ET}\left( 1-\frac{{ ET}}{k}\right) -\frac{\alpha { ET}^{2}v}{\beta +{ ET}^{2}}-p{ ET}=0, \end{aligned}$$

yields two roots, $v_{min}=[r(1-\frac{{ ET}}{k})-p]\frac{\beta +{ ET}^{2}}{\alpha { ET}}$ and $v_{max}=r(1-\frac{{ ET}}{k})\frac{\beta +{ ET}^{2}}{\alpha { ET}}$. Obviously, $f(u,v)<0$ holds if $(u,v)\in \{(u,v)\mid v_{min}<v<v_{max}, { ET}-\zeta<u<{ ET}+\zeta \}$ for some sufficiently small $\zeta >0$. Then in the following, we discuss the existence of the sliding mode for the delay reaction–diffusion Filippov system (1) with (2) in region $\{(u,v)\mid v_{min}<v<v_{max}, { ET}-\zeta<{ ET}<{ ET}+\zeta \}.$ There holds

$$\begin{aligned} \rho (z)\cdot \frac{\partial \rho (z)}{\partial t}&=(u-{ ET})\frac{\partial u}{\partial t}\nonumber \\&=(u-{ ET})\left( d_{1}\varDelta u+ru\left( 1-\frac{u}{k}\right) \right. \nonumber \\&\quad \left. -\frac{\alpha u^{2}v}{\beta +u^{2}}-\varepsilon pu\right) \nonumber \\&{=}(u{-}{} { ET})d_{1}\varDelta u{-}(u{-}{} { ET})^{2}{+}f(u,v)\nonumber \\&\le \rho (x,t)d_{1}\varDelta \rho (x,t)-\rho ^{2}(x,t). \end{aligned}$$

(13)

Denote $V(x,t)=\rho (x,t)\varDelta \rho (x,t)-\rho ^{2}(x,t)$, substitute it into (13), then one can obtain

$$\begin{aligned} \rho (z)\cdot \frac{\partial \rho (z)}{\partial t}\le d_{1}V(x,t)-(1-d_{1})\rho ^{2}(x,t). \end{aligned}$$

(14)

Next, we prove that $V(x,t)\le 0$ holds for $\forall x\in \varOmega$ by contradiction [38]. If this is not true, let

$$\begin{aligned} \varOmega _{1}= & {} \{x\mid V(x,t)>0,\quad x\in \varOmega \}, \\ \varOmega _{2}= & {} \{x\mid V(x,t)\le 0,\quad x\in \varOmega \}, \end{aligned}$$

therefore, $\partial \varOmega _{1}=[\partial \varOmega \bigcap \partial \varOmega _{1}]\bigcup [\varOmega \bigcap \partial \varOmega _{1}],$ and $V(x,t)=0$ for $x\in \partial \varOmega _{1}.$ From the definition of V,  one gets

$$\begin{aligned} 0<\int _{\varOmega _{1}}V(x,t)dx&=\int _{\varOmega _{1}}\rho (x,t)\varDelta \rho (x,t)dx\nonumber \\&\quad -\int _{\varOmega _{1}}\rho ^{2}(x,t)dx\nonumber \\&=\rho (x,t)\frac{\partial \rho (x,t)}{\partial x}\bigg |_{\partial \varOmega _{1}}\nonumber \\&\quad -\int _{\varOmega _{1}}\left( \frac{\partial \rho (x,t)}{\partial x}\right) ^{2}dx\nonumber \\&\quad -\int _{\varOmega _{1}}\rho ^{2}(x,t)dx. \end{aligned}$$

(15)

We clarify with the following two cases.

• (i) if $x\in \partial \varOmega \bigcap \partial \varOmega _{1}$, then $x\in \partial \varOmega .$ Based on the homogeneous neumann boundary condition, ${ \rho (x,t)\frac{\partial \rho (x,t)}{\partial x}\bigg |_{\partial \varOmega _{1}}}$ $=0$, which contradicts with (15).

• (ii) if $x\in \varOmega \bigcap \partial \varOmega _{1},$ then $x\in \partial \varOmega _{1},$ since $V(x,t)=0$ for $x\in \partial \varOmega _{1},$ then $\rho (x,t)=\varDelta \rho (x,t)$ for $x\in \partial \varOmega _{1}.$

From (14) we have

$$\begin{aligned} \rho (z)\cdot \frac{\partial \rho (z)}{\partial t}\le -(1-d_{1})\rho ^{2}(x,t). \end{aligned}$$

Solving the above equation, there holds

$$\begin{aligned} \rho ^{2}(x,t)\le \rho ^{2}(x,0)e^{-2(1-d_{1})t}. \end{aligned}$$

This implies that if $x\in \partial \varOmega _{1}$ and t is sufficiently large, $|\rho (x,t)|$ is sufficiently small. Due to $\rho (x,t)=\varDelta \rho (x,t),x\in \partial \varOmega _{1}$, then $|\varDelta \rho (x,t)|$ is also sufficiently small when t is sufficiently large and $x\in \partial \varOmega _{1}$. Thus, $\bigg |\frac{\partial \rho (x,t)}{\partial x}\bigg |$ $(x\in \partial \varOmega _{1})$ is bounded. So $\bigg |\rho (x,t)\frac{\partial \rho (x,t)}{\partial x}\bigg |_{\partial \varOmega _{1}}$ is sufficiently small when t is sufficiently large, which contradicts with (15).

By combining with (i) and (ii), it can be concluded that for $\forall x\in \varOmega ,$ $V(x,t)\le 0$. Hence, from (13) we have

$$\begin{aligned} \begin{aligned} \rho (z)\cdot \frac{\partial \rho (z)}{\partial t}\le -(1-d_{1})(u-{ ET})^{2}<0,\quad u\ne { ET}, \end{aligned} \end{aligned}$$

which implies that a sliding mode occurs on $u={ ET}$ when $v_{min}<v<v_{max}$. The proof is completed.

Based on the analysis above, we can describe the sliding segment as follows,

$$\begin{aligned} \varGamma _{s}= & {} \{(u,v)\in \varGamma \mid u={ ET}, \max \{0,v_{min}\}\\ {}{} & {} <v<v_{max},\quad v_{max}>0\}. \end{aligned}$$

According to the relationship between ${ ET}$ and $k, \frac{k(r-p)}{r}$, the sliding segment can be clarified to three cases.

• 1. When ${ ET}>k$, then $v_{max}<0$, sliding segment is no longer present.

• 2. When $\frac{k(r-p)}{r}<{ ET}<k$, then $v_{min}<0, v_{max}>0$, the system possesses a sliding segment $\varGamma _{s}^{1}=\{(u,v)\in \varGamma |u={ ET}, 0<v<v_{max}\}.$

• 3. When ${ ET}<\frac{k(r-p)}{r}$, $v_{min}>0$, the system possesses a sliding segment $\varGamma _{s}^{2}=\{(u,v)\in \varGamma |u={ ET}, v_{min}<v<v_{max}\}.$

In the subsequent analysis, we make the assumption that ${ ET}<k$ to ensure the presence of the sliding segment.

Then, by employing the Filippov convex method, the dynamics on the sliding segment $\varGamma _{s}$ can be represented by

$$\begin{aligned} F_{\varGamma _{s}}=\epsilon F_{\varGamma _{1}}+(1-\epsilon )F_{\varGamma _{2}},\quad u={ ET}, \end{aligned}$$

with

$$\begin{aligned} \epsilon{} & {} =\frac{\langle \nabla \rho (z),F_{\varGamma _{2}}\rangle }{\langle \nabla \rho (z), F_{\varGamma _{2}}-F_{\varGamma _{1}}\rangle }=1-\frac{1}{p}\left( r\left( 1-\frac{{ ET}}{k}\right) \right. \\ {}{} & {} \quad \left. -\frac{\alpha { ET}v}{\beta +{ ET}^{2}}\right) , \end{aligned}$$

$0<\epsilon <1.$ Hence, the sliding mode dynamics on sliding segment $\varGamma _{s}$ can be listed as

$$\begin{aligned} \begin{aligned} \frac{\partial v}{\partial t}&=d_{2}\varDelta v-\delta v+\frac{\eta \alpha u^{2}(x,t-\tau )v}{\beta +u^{2}(x,t-\tau )}\\&\quad +\frac{q}{p}v\left( r\left( 1-\frac{{ ET}}{k}\right) -\frac{\alpha { ET}v}{\beta +{ ET}^{2}}\right) ,\\ {}&t>0,\quad x\in \varOmega , u={ ET},\\ \frac{\partial v}{\partial x}&=0,\quad t>0,\quad x\in \partial \varOmega .\\ \end{aligned} \end{aligned}$$

(16)

In fact, the sliding mode dynamics (16) can also be obtained by applying the Utkin’s equivalent method. From $\rho (z)=u-{ ET}$, then

$$\begin{aligned} \rho ^{\prime }= & {} u^{\prime }= ru(x,t)\left( 1-\frac{u(x,t)}{k}\right) -\frac{\alpha u^{2}(x,t)v(x,t)}{\beta +u^{2}(x,t)}\nonumber \\{} & {} -\varepsilon pu(x,t)=0, \end{aligned}$$

it follows that

$$\begin{aligned} \varepsilon =\frac{1}{p}\bigg (r\Big (1-\frac{u(x,t)}{k}\Big )-\frac{\alpha uv}{\beta +u^{2}}\bigg ). \end{aligned}$$

Substituting the above $\varepsilon$ into (1), (16) can also be obtained. Generally, the two methods are equivalent. However, when referring to discussions about some complicated phenomena, such as chattering, the Utkin’s equivalent method may have more advantages, for it is a method of forcing the trajectory of a system to move on a sliding surface.

The sliding mode dynamics (16) admits an equilibrium point $E_{p}=({ ET}, v_{p})$ with

$$\begin{aligned} v_{p}=\frac{\beta +{ ET}^{2}}{\alpha { ET}}\left( r\left( 1-\frac{{ ET}}{k}\right) -\frac{\delta p}{q}\right) +\frac{p\eta { ET}}{q}. \end{aligned}$$

The existence and stability of the pseudoequilibrium can be established by the following result.

Theorem 3

$E_{p}=({ ET}, v_{p})$ is a pseudoequilibrium for the sliding mode dynamics (16) if $v_{min}<v_{p}<v_{max}$, that is, $u_{2}^{*}<{ ET}<u_{1}^{*}$. And accordingly, $E_{p}$ is locally asymptotically stable.

Proof

$E_{p}$ is a pseudoequilibrium if it lies on the sliding segment, that is, $v_{min}<v_{p}<v_{max}$, which, by complicated but trivial calculations, is equivalent to $u_{2}^{*}<{ ET}<u_{1}^{*}$. Denote

$$\begin{aligned} \begin{aligned}W(v)&=-\delta v+\frac{\eta \alpha u^{2}(x,t-\tau )v}{\beta +u^{2}(x,t-\tau )}\\&\quad +\frac{q}{p}v\left( r\left( 1-\frac{{ ET}}{k}\right) -\frac{\alpha { ET}v}{\beta +{ ET}^{2}}\right) .\end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} W^{\prime }(v)\big |_{E_p}=-\frac{q\alpha { ET}v_{p}}{p(\beta +{ ET}^{2})}<0, \end{aligned}$$

Hence, the derivative of the sliding mode dynamics (16) at the pseudoequilibrium $E_{p}$ reads

$$\begin{aligned} W^{\prime }(v)\big |_{E_p}-d_{2}\sigma _{n}<0, \end{aligned}$$

for any $n\ge 0$. It then follows that the pseudoequilibrium point $E_{p}=({ ET}, v_{p})$ is locally asymptotically stable.

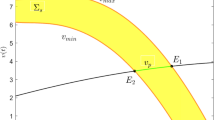
As depicted in Fig. 1, the region colored in yellow signifies the domain where the sliding mode exists, while green line denotes the presence of a sole pseudoequilibrium.

Fig. 1

Illustration of the existence of the pseudoequilibrium with $d_{1}=0.2, d_{2}=0.3, r=3, k=8, \alpha =4.5, \beta =2.26, \delta =2.7,\eta =0.833, p=0.8, q=0.2$. (Color figure online)

For further analyzing the bifurcation of the delay reaction–diffusion Filippov system (1) with (2), we introduce two distinct points referred to the boundary equilibrium and the tangent point.

Tangent points According to Definition 2, the tangent points can be calculated by the following equations,

$$\begin{aligned} ru\left( 1-\frac{u}{k}\right) -\frac{\alpha u^{2}v}{\beta +u^{2}}-\varepsilon pu=0,\quad u={ ET}, \end{aligned}$$

with $\varepsilon =0,1$. Then the two tangent points are $T_{\varGamma _{1}}=({ ET}, v_{\min })$ and $T_{\varGamma _{2}}=({ ET}, v_{\max })$ with $v_{\min }$ and $v_{\max }$ defined in Theorem 2.

Boundary equilibria According to Definition 2, let

$$\begin{aligned} \begin{aligned} ru\left( 1-\frac{u}{k}\right) -\frac{\alpha u^{2}v}{\beta +u^{2}}-\varepsilon pu&=0,\\ -\delta v+\frac{\eta \alpha u^{2}(t-\tau )}{\beta +u^{2}(t-\tau )}+\varepsilon qv&=0,\quad u={ ET},\\ \end{aligned} \end{aligned}$$

with $\varepsilon =0,1$. Then the two boundary equilibria are $E_{1}^{B}=({ ET}, \frac{r(k-{ ET})(\beta +{ ET}^{2})}{\alpha k{ ET}})$ and $E_{2}^{B}=({ ET}, \frac{(r(k-{ ET})-kp)(\beta +{ ET}^{2})}{\alpha k{ ET}})$, provided that ${ ET}=u_1^*$ or ${ ET}=u_2^*$.

5 Qualitative analysis of the delay reaction–diffusion Filippov system (1) with (2)

We will explore the global dynamics of the system with sequentially considering different values of the threshold ${ ET}$, namely, ${ ET}<u_{2}^{*}, u_{2}^{*}<{ ET}<u_{1}^{*},$ and ${ ET}>u_{1}^{*}$. Although the results are obtained numerically, here, we still state them by theorems.

5.1 Case 1: ${ ET}<u_{2}^{*}$

In this case, $E_{1}$ represents a virtual equilibrium point (referred to as $E_{1}^{V}$) and while $E_{2}$ denotes a regular equilibrium point (referred to as $E_{2}^{R}$). The dynamics of system (1) with (2) is determined by subsystem (4). According to the discussion in Sect. 3, we have the following results.

Theorem 4

Provided that ${ ET}<u_{2}^{*}$,

• (1) if condition $(\varPi _{1})$ does not hold, then the delay reaction–diffusion Filippov system (1) with (2) admits a globally asymptotically stable periodic solution which surrounds $E_{2}^{R}$ for $\tau \in [0,+\infty )$, as can be seen in Fig. 2.

• (2) if condition $(\varPi _{1})$ holds, the delay reaction–diffusion Filippov system (1) with (2) admits a globally asymptotically stable equilibrium $E_2^R$ for $\tau \in [0, \tau _{n_+}^{(0)})$, and a globally asymptotically stable periodic solution surrounding $E_2^R$ when $\tau \ge \tau _{n_+}^{(0)}$, $\tau _{n_+}^{(0)}$ is denoted by Eq. (12) with $\varepsilon =1$, as shown in Fig. 3.

Fig. 2

The phase portrait and density dynamics of system (1) with (2) if ${ ET}<u_{2}^{*}$ and ${ ET}=0.8$. $d_{1}=0.2, d_{2}=0.3, r=1, k=6, \alpha =0.8, \beta =0.6, \delta =2.1, \eta =3, p=0.2, q=0.6$. Initial values are (0.75, 1.6), (0.78, 1.8), (0.85, 1.65) and (0.9, 2), $E_1^V=(2.0493,1.9277)$, $E_2^R=(1.0000,1.2667)$

Fig. 3

The phase portrait and density dynamics of system (1) with (2) if ${ ET}<u_{2}^{*}$ and ${ ET}=2.5$. $d_{1}=0.2, d_{2}=0.3, r=3, k=8, \alpha =4, \beta =3.5, \delta =3, \eta =0.85, p=0.5, q=0.2$. Initial values are (2.37, 2.3), (2.6, 2.25), (2, 1.5) and (2.7, 1.9). $E_1^V=(5.1235,1.5659)$, $E_2^R=(4.0415,1.2078)$, $\tau _{n_+}^{(0)}=0.9987$

From Fig. 2, one can read that for any $\tau \ge 0$, the solution of the Filippov system (1) with (2) will converge to a periodic solution that surrounds $E_2^R$. Figure 2($a_{2}$)–($a_{3}$) and ($b_{2}$)–($b_{3}$) illustrates the changes of prey u and predator v over time t and space x.

Figure 3 shows the occurrence of Hopf bifurcation. By calculation, $\tau _{n_+}^{(0)}=0.9987.$ All solutions ultimately converge towards $E_2^R$ for $\tau =0<\tau _{n_+}^{(0)}=0.9987$ [Fig. 3($a_{1}$)], when $\tau =1.05>\tau _{n_+}^{(0)}$, all solutions will finally stabilize at a standard limit cycle [Fig. 3($b_{1}$)]. The variation diagrams of prey u and predator v with time t and space x are shown in Fig. 3($a_{2}$), ($a_{3}$), ($b_{2}$), ($b_{3}$), respectively.

In this condition, the strategies are unable to achieve the desired control aims as the pest population density eventually surpasses the acceptable threshold when ${ ET}<u_{2}^{*}.$

Fig. 4

The phase portrait and density dynamics of system (1) with (2) if ${ ET}>u_{1}^{*}$ and ${ ET}=3.5$. $d_{1}=0.2, d_{2}=0.3, r=3, k=8, \alpha =4.5, \beta =2.26, \delta =2.7, \eta =0.833, p=1.2, q=0.2$. Initial values are (3, 1), (3.2, 0.3), (3.8, 1.6) and (3.6, 0.8). $E_1^R=(2.4124,1.5595)$, $E_2^V=(2.1273,0.7104)$

Fig. 5

The phase portrait and density dynamics of system (1) with (2) if ${ ET}>u_{1}^{*}$ and ${ ET}=5.6$. $d_{1}=0.2, d_{2}=0.3, r=3, k=8, \alpha =4, \beta =3.5, \delta =3, \eta =0.85, p=0.5, q=0.2$. Initial values are (5.4, 0.5), (5.2, 1), (6, 1.5) and (5.8, 0.8). $E_1^R=(5.1235,1.5659)$, $E_2^V=(4.0415,1.2078)$, $\tau _{n_+}^{(0)}=1.7362$

5.2 Case 2: ${ ET}>u_{1}^{*}$

In this case, $E_{1}$ represents a regular equilibrium point (referred to as $E_{1}^{R}$) and while $E_{2}$ denotes a virtual equilibrium point (referred to as $E_{2}^{V}$). The dynamics of system (1) with (2) is determined by subsystem (3). As analyzed in Sect. 3, the following results have been obtained.

Theorem 5

Provided that ${ ET}>u_{1}^{*}$, then

• (1) If condition $(\varPi _{1})$ is not satisfied, the delay reaction–diffusion Filippov system (1) with (2) admits a globally asymptotically stable periodic solution surrounding $E_1^R$ for all $\tau \ge 0$, as can be seen in Fig. 4.

• (2) if condition $(\varPi _{1})$ is satisfied, the delay reaction–diffusion Filippov system (1) with (2) has a globally asymptotically stable equilibrium $E_1^R$ for $\tau \in [0, \tau _{n_+}^{(0)})$, and a globally asymptotically stable periodic solution around $E_1^R$ for $\tau \ge \tau _{n_+}^{(0)}$, $\tau _{n_+}^{(0)}$ is denoted as Eq. (12) with $\varepsilon =0$, as shown in Fig. 5.

Reading from Fig. 4, we can find that all solutions eventually move towards a standard limit cycle around $E_1^R$ for $\tau$=0 [Fig. 4($a_{1}$)], which is the same case when $\tau =0.2$ [Fig. 4($b_{1}$)]. Figure 4($a_{2}$), ($a_{3}$), ($b_{2}$), ($b_{3}$) illustrates the changes of prey u and predator v about time t and space x.

Figure 5 indicates that all solutions ultimately tend to $E_1^R$ for $\tau =0.7<\tau _{n_+}^{(0)}=1.7362$ [Fig. 5($a_{1}$)], when $\tau =2>\tau _{n_+}^{(0)}$, the solutions eventually move towards a standard limit cycle [Fig. 5($b_{1}$)].

Provided that ${ ET}>u_{1}^{*}$, the density of pests can ultimately reach a level that is lower than the specified threshold value. This outcome signifies the successful attainment of the integrated pest management goal.

Fig. 6

The phase portrait and density dynamics of system (1) with (2) if $u_{2}^{*}<{ ET}<u_{1}^{*}$ and ${ ET}=4.5$. $d_{1}=0.2, d_{2}=0.3, r=3, k=8, \alpha =4, \beta =3.5, \delta =3, \eta =0.85, p=0.5, q=0.2, \tau =0.2$. Initial values are (4.6, 1.3), (4.63, 1.9), (4.2, 1.6) and (4.4, 0.8)

5.3 Case 3: $u_{2}^{*}<{ ET}<u_{1}^{*}$

In this case, $E_{1}$ and $E_{2}$ are virtual equilibrium points, referred to as $E_{1}^{V}$ and $E_{2}^{V}$, respectively. The existence of a pseudoequilibrium point can also be observed. By combining Theorems 2 and 3, the following results can be obtained.

Theorem 6

If $u_{2}^{*}<{ ET}<u_{1}^{*}$, the delay reaction–diffusion Filippov system (1) with (2) admits a globally asymptotically stable equilibrium $E_{p}$ as depicted in Fig. 6.

Figure 6$(a_{1})$ illustrates that the trajectory of the solution either directly enters the sliding segment $\varGamma _{s}$ and stabilizes to $E_{p}$, or crosses from region $\varGamma _{1}(\varGamma _{2})$ to region $\varGamma _{2}(\varGamma _{1})$, and finally stabilizes to $E_{p}$. Hence, the control objective is successfully accomplished in this case.

Remark 2

In conclusion, in order to achieve the goal of IPM, the economic threshold level should be prescribed to satisfy ${ ET}>u_2^*$, which on the other hand illustrates the importance of the threshold level in designing a successful pest control.

Fig. 7

Boundary node bifurcation. $d_{1}=0.2, d_{2}=0.3, r=3,k=8,\alpha =4,\beta =3.5,\delta =3,\eta =0.85,p=0.5,q=0.2,$ $\tau =0$. a ${ ET}=3.2$, (2.3, 1.6), (2.8, 1.8), (3.4, 2.2) and (3.7, 1.7) are initial values. The stable equilibrium $E_2^R$ and $T_{\varGamma _{2}}$ coexist. b ${ ET}=4.0415$, (4.3, 1.5), (4.2, 2), (3.5, 1.3) and (3.7, 1.7) are initial values, the equilibrium $E_2^R$, pseudoequilibrium $E_{p}$ and tangent point $T_{\varGamma _{2}}$ collide together. c ${ ET}=4.6$, initial values are (4.3, 1.4), (4.2, 1), (4.8, 1.9) and (4.9, 1.4), stable pseudoequilibrium $E_{p}$ occurs

6 Sliding bifurcation analysis

6.1 Local sliding bifurcation analysis

Boundary node bifurcation occurs when a bifurcation parameter exceeds some critical value, causing a regular node equilibrium, a pseudoequilibrium, and a tangent point to collide simultaneously at the boundary equilibrium. Reading from Fig. 7a–c, firstly, a stable node equilibrium $E_2^R$ coexists with tangent point $T_{\varGamma _{2}}$ when ${ ET}=3.2<u_{2}^{*}=4.0415$. Then, with the bifurcation parameter ${ ET}$ passing through the critical value ${ ET}=u_{2}^{*}$, the regular node equilibrium $E_2^R$ disappears and is replaced by the visible tangent point $T_{\varGamma _{2}}$ , and the boundary equilibrium $E_2^B$ is an attractor. Finally, as ${ ET}$ is further increased to ${ ET}=4.6>u_{2}^{*}$, the pseudoequilibrium $E_{p}$ and tangent point $T_{\varGamma _{2}}$ appear and replace the boundary equilibrium $E_2^B$.

Fig. 8

Boundary focus bifurcation. $d_{1}=0.2, d_{2}=0.3, r=3,k=8,\alpha =4,\beta =3.5,\delta =3,\eta =0.85,p=0.5,q=0.2,$ and $\tau =1$. a The stable limit cycle and the tangent point $T_{\varGamma _{2}}$ coexist. ${ ET}=3$, initial values are (2.8, 5), (2.9, 8), (3.3, 10) and (3.4, 9). b The equilibrium $E_2^R$, pseudoequilibrium $E_{p}$ and tangent point $T_{\varGamma _{2}}$ collide together. ${ ET}=3.2274$, initial values are (2.8, 3.5), (2.95, 6), (3.3, 7) and (3.4, 5.5). c Stable pseudoequilibrium $E_{p}$ occurs. ${ ET}=3.5$, initial values are (3.2, 2.5), (3.35, 5.5), (3.7, 7) and (3.6, 5.5)

Boundary focus bifurcation occurs if a bifurcation parameter passing though some critical value leads to that a focus regular equilibrium point, a tangent point and a pseudoequilibrium collide together simultaneously. According to the analysis in Sect. 3, the stable node $E_2^R$ transits into an unstable focus with the bifurcation parameter $\tau$ increased from 0 to 1, as shown in Figs. 7a and 8a. While in Fig. 8a when ${ ET}=3<u_{2}^{*}=4.0415$, a stable limit cycle coexists with the tangent point $T_{\varGamma _{2}}$. As the parameter ${ ET}$ increased to ${ ET}=u_{2}^{*}$, the stable limit cycle disappears, resulting in the simultaneous collision of the focus regular equilibrium point $E_2^R$, tangent point $T_{\varGamma _{2}}$ and pseudoequilibrium $E_{p}$ at the boundary equilibrium $E_2^B$, as shown in Fig. 8b. With ${ ET}$ is further increased to ${ ET}=4.6>u_{2}^{*}$, the pseudoequilibrium $E_{p}$ appears and focus regular equilibrium $E_2^R$ transforms into a focus virtual equilibrium $E_2^V$, as shown in Fig. 8c.

Remark 3

The presence of these two types of local sliding bifurcations suggests that an ineffective pest control strategy may be changed by slightly varying the given threshold level to drive a stable limit cycle or a stable regular equilibrium above the threshold to a pseudoequilibrium point, so as to achieve the control aim.

6.2 Sliding mode bifurcation

According to the previous analysis, the delay reaction–diffusion Filippov system (1) with (2) may have sliding region and pseudoequilibrium, which depends on different parameters. Here, we explore the effect of $\alpha$, the maximum capture rate of the prey, and $\beta$, the search rate of the predator on the sliding region and pseudoequilibrium of the system, which leads to the appearing of the sliding mode bifurcation.

Fig. 9

Sliding mode bifurcation of the delay reaction–diffusion Filippov system (1) with (2). $d_{1}=0.2, d_{2}=0.3, r=3,k=8,\delta =3,\eta =0.85,p=0.5,q=0.2, { ET}=2.5$ and $\tau =3$. The red solid point represents $E_{P}$, and the histogram represents the sliding region. $E_{P}$ on the histogram indicates $E_{P}$ is a pseudoequilibrium. (Color figure online)

Reading from Fig. 9, if the maximum capture rate of the prey $\alpha$ is chosen to be located in interval [2.5 4.5], or the search rate of the predator $\beta$ is chosen to be located in interval [1 3], then there exists a pseudoequilibrium on the sliding region. Referring to Theorem 3, in this case, the pseudoequilibrium is stable, biologically, which indicates that the density of pests is controlled to be equal to the prescribed tolerable threshold level, the control aim is realized.

Theorem 3 shows that the density of pests should be controlled to be at a tolerable threshold level to ensure the success of the control. As we can see from Fig. 9, appropriately designing the maximum capture rate of the prey and the search rate of the predator can successfully control the pest number and maintain the balance of ecosystem.

Fig. 10

Global sliding bifurcation. $d_{1}=0.2, d_{2}=0.3, r=3, k=8,\alpha =4.5, \beta =2.26, \delta =2.7, \eta =0.833, p=0.3, q=0.2$, $T=5$. Initial values are (2.5, 1.6) and (5.5, 1.5). $E_{1}^R=(2.4124,1.5595), E_{2}^V=(2.1273,1.3484)$

6.3 Global sliding bifurcation analysis

The previous analysis show that for the system (1) with (2), there is a possibility of the existence of periodic solutions that are entirely situated within region $\varGamma _{1}$ or region $\varGamma _{2}$. In fact, the periodic solutions may also locate in both regions $\varGamma _{1}$ or $\varGamma _{2}$ or include parts of the sliding domain. In this part, we will demonstrate the global sliding bifurcation to better illustrate the critical role of delay $\tau$ in the delay reaction–diffusion Filippov system (1) with (2). We will consider $\tau$ as a bifurcation parameter and elaborate three kinds of global sliding bifurcations subsequently.

Touching bifurcation Firstly, a standard limit cycle locating totally in $\varGamma _{1}$ or $\varGamma _{2}$ may collide with the discontinuity boundary with $\tau$ varying, as shown in Fig. 10a–c. Reading from Fig. 10a with $\tau =0.08$, there exists a limit cycle that is entirely locating in $\varGamma _{1}$, which does not intersect with the discontinuity boundary. While with $\tau$ increased to $\tau =0.0945$ in Fig. 10b, the limit cycle collide with tangent point $T_{\varGamma _{1}}$ on the discontinuity boundary, which indicates that a touching bifurcation occurs. As the value of $\tau$ increased to $\tau =0.104$, part of the limit cycle slides on the sliding domain and then goes back to $\varGamma _{1}$ such that the limit cycle turns into a sliding limit cycle, seen in Fig. 10c.

Sliding switching bifurcation As the bifurcation parameter $\tau$ is further increased, a sliding limit cycle starts to intersect with the invisible quadratic tangent point $T_{\varGamma _{2}}$, shown in Fig. 10c–e. With $\tau =0.124$, the limit cycle lies in region $\varGamma _{1}$ and encompasses the entire sliding domain, see Fig. 10d. With $\tau$ further increased to $\tau =0.18$, see Fig. 10e, the limit cycle will pass through $\varGamma _{1}$ and enter into $\varGamma _{2}$, after staying a little while in $\varGamma _{2}$, then return to slide along the sliding domain and back to $\varGamma _{1}$. A sliding switching bifurcation occurs subsequently.

Crossing bifurcation As the bifurcation parameter $\tau$ varies, a stable sliding switching limit cycle will become a stable crossing limit cycle, see Fig. 10e–g. Reading from Fig. 10e with $\tau =0.18$, there is a sliding switching limit cycle that lies in regions $\varGamma _{1}$, $\varGamma _{2}$ and a portion of the sliding domain $\varGamma _{s}$. While with $\tau$ increased to $\tau =0.216$ in Fig. 10f, when the sliding switching cycle returns to the sliding domain, it is just tangent to $T_{\varGamma _{1}}$ and going back to $\varGamma _{1}$, which then becomes a sliding crossing cycle. Finally, the sliding crossing cycle transforms into a crossing cycle without containing any points of the sliding domain if $\tau =0.3$, as shown in Fig. 10g.

Remark 4

As the value of parameter $\tau$ increased, the delay reaction–diffusion Filippov system (1) with (2) exhibits a series of bifurcations, including touching bifurcation, sliding switching bifurcation and crossing bifurcation. This suggests that mathematically time delay can introduce greater complexity and richness into the system dynamics. While, on the other side, from a biological perspective, the presence of sliding switching and crossing bifurcations due to delay can pose a threat to integrated pest management, which will induce the pest population exceeding the predetermined threshold level, thereby rendering a previously effective control strategy ineffective.

7 Conclusions

We investigate the dynamic behaviors of a delay Filippov reaction–diffusion prey–predator model under the Neumann boundary conditions. The time delay corresponds to the period of gestation or maturation of predators. Following the principles of integrated pest management, if the pest population stays under the economic threshold, no control measures are implemented. However, when the pest population surpasses the economic threshold, methods such as insecticide spraying and natural enemy releases are employed to control the pest population.

Firstly, the equilibrium points of the two subsystems are examined, and their stability is assessed along with investigating the conditions for Hopf bifurcation, achieved by solving the characteristic equations. The theoretical results indicate that if delay $\tau$ surpasses a specific critical value $\tau _{n_+}^{(0)}$, Hopf bifurcation occurs. Then qualitative analysis is conducted. The results indicate that economic thresholds play a crucial role in pest control.

Too low prescribed threshold ${ ET}$ may lead to a dissipation of manpower and material resources in spraying pesticides and releasing natural enemies, as shown in Figs. 2 and 3. If the pest control is implemented when ${ ET}<u_2^*$, the number of the pests may be transiently reduced, however, finally stabilize at $E_{2}^R$ or a limit cycle around $E_{2}^R$ above the threshold level. As the prescribed threshold ${ ET}$ is increased to satisfy $u_{2}^{*}<{ ET}<u_{1}^{*}$, the number of the pests can be eventually stabilize at the pseudoequilibrium point $E_{p}$ equal to the threshold, see Fig. 6. With ${ ET}$ further increased to ${ ET}>u_{1}^{*}$, the threshold control strategy results in the quantity of pests ultimately falling under economic threshold, thus achieving the control goal as shown in Figs. 4 and 5.

Remark 5

The consequences highlight the importance of selecting a suitable economic threshold, such as ${ ET}>u_{2}^*$, in order to achieve effective pest control.

Local and global bifurcations present the crucial significance of the delay and economic threshold. Boundary node or focus bifurcations cause a transition of the equilibrium state from a stable regular equilibrium or a stable limit cycle above the economic threshold to a boundary equilibrium, and subsequently to a pseudoequilibrium equal to the economic threshold. This indicates that a failed control strategy can be made effective by a small adjustment in the threshold value. While the objective of integrated control may not always be attainable in the presence of sliding switching or crossing bifurcations, which will pose additional challenges for pest control. This further emphasizes the importance of considering delay in the control process.

In [5, 8], filippov models with time delay are established. The regular/virtual equilibrium, the sliding segment, sliding mode dynamics and pseudoequilibrium are investigated. Furthermore, the results show that the time delay plays a significant role in discontinuity-induced bifurcations. Although the delay reaction–diffusion Filippov system (1) with (2) exhibits similar dynamics, the incorporation of reaction–diffusion term does bring more challenge for the theoretical analysis, such as the existence of the sliding domain and pseudoequilibrium. Meanwhile, we can explicitly obtain the spatial transmission of the prey and predator in this case. The similar results of the delay reaction–diffusion Filippov system (1) with (2) with existing works [5, 8] indicates that the incorporation of reaction–diffusion does not bring more effects on the dynamics, but complicates the analysis. This also shows that time delay plays a more significant role than the reaction–diffusion term in resulting in complicated bifurcation phenomena and challenging the Filippov control such that a successful control becomes failure for the appearance of sliding switching and crossing bifurcations.

We here consider the delay which indicates the time required for the predator population to become pregnant or mature. In fact, pests also need some time to reproduce offsprings. Thus, the model can be improved to integrate both the delay for predator and delay for pests, which will be our future study.