Periodic solution of a pest management Gompertz model with impulsive state feedback control

Abstract

In this paper, a new model with two state impulses is proposed for pest management. According to different thresholds, an integrated strategy of pest management is considered, that is to say if the density of the pest population reaches the lower threshold $h_1$ at which pests cause slight damage to the forest, biological control (releasing natural enemy) will be taken to control pests; while if the density of the pest population reaches the higher threshold $h_2$ at which pests cause serious damage to the forest, both chemical control (spraying pesticide) and biological control (releasing natural enemy) will be taken at the same time. For the model, firstly, we qualitatively analyse its singularity. Then, we investigate the existence of periodic solution by successor functions and Poincaré-Bendixson theorem and the stability of periodic solution by the stability theorem for periodic solutions of impulsive differential equations. Lastly, we use numerical simulations to illustrate our theoretical results.

1 Introduction and model formulation

As complex ecosystems, forests play an important role in the environment for human to survive. But disease-causing organisms and insects have undesirable effects on the health of a forest [12]. For example, the mountain pine beetle, spruce budworm, gypsy moth and Dutch elm disease have led to substantial losses in Canada [10] and the Asian long-horned beetle and emerald ash borer are doing colossal damage to trees and forests in the United States [31]. On one hand, when the number of pests is very little, does not reach a certain value, as a natural part of the ecosystem, usually we do not have to worry; on the other hand, when the population and activity of pests become threatening so that they can spoil the health of a forest even kill many trees, we need to conduct interference artificially. Chemical control and biological control are two principal methods in practice. Although chemical pest control is still the main way of pest control in most of the place today, the biological control relying on predation, parasitism, herbivores or other biological mechanisms has received the welcome of people [4].

Usually, artificial interference may cause an abrupt change in pests and natural enemies populations, which very often results in difficulties in developing mathematical models to describe it. Fortunately, impulsive differential equation can accurately express this change. Driven by the desire in applications, theoretical study on impulsive differential equations attracted extra attention, please see [1–3, 5–9, 26, 27] and the references therein. Since then, numerous mathematical models governed by impulse differential equations have been established in the area. Nevertheless, most of these models are with one time impulse [15, 16, 18–25, 33–35, 41, 42] or two [32, 39, 40]. Recent research findings suggest that in the practice, according to the different density of the pest, a state feedback measure for controlling pest looks more businesslike and biological models concentrated on state impulse seem more reasonable. In this research direction, several such models have been investigated [11, 14, 28, 36, 38], where authors employed systems of impulsive differential equations with one state impulse. However, study of biological system including two state impulses is not many [28–30, 43].

Motivated by the previous work, we propose a mathematical biological system including two state feedback control in this paper. For self-contained, we first list some relevant work in the following. In references [36] and [28] models

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} \dot{x}(t)=x(t)(a-by(t)),\\ \dot{y}(t)=y(t)(cx(t)-d),\\ \end{array} \right\} x\ne ET,\\ \left. \begin{array}{l} \Delta {x}(t)=-px(t), \\ \Delta {y}(t)=\tau , \\ \end{array} \right\} x=ET, \end{array}\right. } \end{aligned}$$

(1)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} \dot{x}(t)=x(t)(a-by(t)), \\ \dot{y}(t)=y(t)\left( \frac{\lambda bx(t)}{1+bhx(t)}-d\right) ,\\ \end{array} \right\} x\ne h_1, h_2, \\ \left. \begin{array}{l} \Delta {x}(t)=0, \\ \Delta {y}(t)=\tau , \\ \end{array} \right\} x=h_1,\\ \left. \begin{array}{l} \Delta {x}(t)=-px(t), \\ \Delta {y}(t)=-qy(t), \\ \end{array} \right\} x=h_2, \end{array}\right. } \end{aligned}$$

(2)

are investigated. The authors studied the integrated pest management control strategies with the help of the Lambert $W$ function and Poincaré map. In [37], Trzcinski and Reid investigated a mountain pine beetle population dynamics governed by the Gompertz population model, where the Gompertz equation [13] is given by

$$\begin{aligned} \dot{x}(t)=rx(t)\ln \frac{K}{x(t)}, \end{aligned}$$

(3)

which describes the growth law of density dependence where the rate of increase declines linearly with the $\log e$ of population abundance.

Now we are in a position to give out our models as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} \dot{x}(t)=rx(t)\ln \frac{K}{x(t)}-\beta x(t)y(t), \\ \dot{y}(t)=\lambda \beta x(t)y(t)-dy(t),\\ \end{array} \right\} \\ x\ne h_1, h_2, \quad \text {or}\quad x=h_1, y>y^*,\\ \left. \begin{array}{l} \Delta {x}(t)=0, \\ \Delta {y}(t)=\alpha , \\ \end{array} \right\} x=h_1, y\le y^*,\\ \left. \begin{array}{l} \Delta {x}(t)=-px(t), \\ \Delta {y}(t)=-qy(t)+\tau , \\ \end{array} \right\} x=h_2, \end{array}\right. } \end{aligned}$$

(4)

where $\Delta x(t)=x(t^{+})-x(t), \Delta y(t)=y(t^{+})-y(t),\, r$ is the Gompertz intrinsic growth rate of the prey in the absence of the predator, $K$ is usually referred to the environment carrying capacity of saturation level, $\beta$ represents the predation rate of natural enemies, $\lambda$ represents the transformation rate at which ingested prey in excess of what is needed for maintenance is translated into predator population increase. $d$ is the death rate of natural enemy. $h_1$ and $h_2$ are the thresholds with slight damage and serious damage to the forest, respectively. $y^*$ is the intersection of the line $x=h_1$ and $r\ln \frac{K}{x(t)}-\beta y(t)=0;$ $\alpha , \tau$ are release quantity of natural enemy $y(t).$ $p$ represents the death rate of pests and $q$ is the death rate of natural enemies due to pesticide. For biologically meaningful, we restrict our study in the region of $R_{+}^{2}=\{(x,y)|x\ge 0,y\ge 0\}.$

Notice the fact that when pests population $x(t)$ is low enough such that the natural enemies of the natural world can control them, as a natural part of the ecosystem, there is no necessary to take any action. Our model reflects this fact and the pest control strategy mentioned above, namely we may increase the quantity of natural enemies by releasing natural enemies cultivated in the lab to control the pest instead of spraying pesticide only when the density of the pest population $x(t)$ reaches certain level, $x=h_1,$ say. The procedure goes like this:

• Release natural enemies again if the density of pests remains at the same level after releasing the previous batch of natural enemies. This step may be repeated several times;

• Stop the release if the natural enemy population $y(t)$ increases and reaches level $y^*$.

Considering the cost of cultivating natural enemies and the loss caused by pests, controlling the pest only by natural enemies in natural law is not realistic. Thus, our newly developed model should also reflect the strategy that when the density of the pest population $x(t)$ reaches certain level $x=h_2$ (usually a higher level). Hence, we not only will release the natural enemies, but also spray less pesticide to kill the pests.

The rest of the paper is organised as follows. In Sect. 2, we briefly introduce some concepts and fundamental results, which are necessary in the later discussion. Section 3 focuses on the qualitative analysis of system (4) without impulsive effect. In the Sect. 4, we investigate the periodic solution of system (4) with impulsive state feedback control. Then, we carry out numerical simulations and discussions in Sect. 5, which show all simulations agree with the theoretic results well. We finally conclude our paper in Sect. 6.

2 Preliminaries

In this section, we briefly introduce some basic concepts and fundamental theories from [3, 6, 17, 43, 44]. Consider a system of impulsive differential equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} \dot{x}(t)=P(x,y),\\ \dot{y}(t)=Q(x,y),\\ \end{array} \right\} \ \text {for}\ (x,y)\not \in M\{x,y\},\\ \left. \begin{array}{l} \Delta x=\alpha (x,y),\\ \Delta y=\beta (x,y),\\ \end{array} \right\} \ \text {for}\ (x,y)\in M\{x,y\},\\ \end{array}\right. } \end{aligned}$$

(5)

where $M$ is known as impulsive set, which can be a straight line or curve in $R^2$. Let $I: I(M) = N,$ be a continuous mapping, $I$ is called the impulse function from set $M$ to set $N$ and $N$ is called the image set. Then, from [43, 44], we have

Definition 2.1

For continuous function $f(x,t),$ if there exists a point $P_0$ and a period $T$ such that $f(P_0,T)\!=\!Q_0\in M\{x,y\}$ and $I(Q_0)\!\!=\!\!I(f(P_0,T))=P_0\in N,$ then, we call $f(P_0,[0,T])$ a periodic solution of system (5).

Definition 2.2

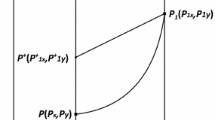
Function

$$\begin{aligned} s(x)=s(x^{+})-s(x) \end{aligned}$$

is called a successor function of point $x$ (Fig. 1).

Fig. 1

Schematic diagram of the successor function of system (5)

Theorem 2.1

(Bendixson theorem for impulsive differential equations [6]) Assume G is a Bendixson region of system (5). Then, if $G$ does not contain any critical points of it, system (5) has a closed orbit in $G.$

Theorem 2.2

Assume that in continuous dynamic system $(X,\Pi ),$ there exist two points $x_1,x_2$ in the pulse phase concentration such that the successor function $s(x_1)>0$ and $s(x_2)<0,$ then, there exists a point $P$ falling in between points $x_1$ and$x_2$ such that $s(P)=0,$ then, the system has order one periodic solution.

Theorem 2.3

(Analogue of Poincaré Criterion [3, 17]) The $T$-periodic solution $x=\phi (t), y=\varphi (t)$ of model

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} \dot{x}(t)=P(x,y), \\ \dot{y}(t)=Q(x,y),\\ \end{array} \right\} , \Phi (x,y)\ne 0, \\ \left. \begin{array}{l} \Delta x=\alpha (x,y), \\ \Delta y=\beta (x,y), \\ \end{array} \right\} , \Phi (x,y)=0, \end{array}\right. } \end{aligned}$$

(6)

is orbitally asymptotically stable if $|\mu _2|<1,$ where $\mu _2$ is the multiplier and calculated by

$$\begin{aligned} \mu _{2}&= \prod _{k=1}^{q}\Delta _{k}\exp \left[ \int _{0}^{T}\left( \frac{\partial P}{\partial x}(\phi (t),\varphi (t))\right. \right. \\&\left. \left. +\frac{\partial Q}{\partial y}(\phi (t),\varphi (t))\right) dt\right] \end{aligned}$$

with

$$\begin{aligned}&\Delta _{k}\\&=\frac{P_{+}(\frac{\partial \beta }{\partial y}\cdot \frac{\partial \Phi }{\partial x}-\frac{\partial \beta }{\partial x}\cdot \frac{\partial \Phi }{\partial y}+\frac{\partial \Phi }{\partial x})+Q_{+}(\frac{\partial \alpha }{\partial x}\cdot \frac{\partial \Phi }{\partial y}-\frac{\partial \alpha }{\partial y}\cdot \frac{\partial \Phi }{\partial x}+\frac{\partial \Phi }{\partial y})}{P\frac{\partial \Phi }{\partial x}+Q\frac{\partial \Phi }{\partial y}} \end{aligned}$$

and $P,Q,\frac{\partial \alpha }{\partial x},\frac{\partial \alpha }{\partial y},\frac{\partial \beta }{\partial x},\frac{\partial \beta }{\partial y},\frac{\partial \Phi }{\partial x},\frac{\partial \Phi }{\partial y}$ are calculated at the point $(\phi (t_{k}), \varphi (t_{k}))$ and $P_{+}=P(\phi (t_{k}^{+}),\varphi (t_{k}^{+})), Q_{+}=Q(\phi (t_{k}^{+}),\varphi (t_{k}^{+})).$

3 Qualitative analysis of system (4) without impulsive effect

We firstly consider system (4) without impulsive effect in this section. It implies that $\alpha , \tau , p, q=0.$ Then, we have a system in the form of

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(t)=rx\ln \frac{K}{x}-\beta xy,\\ y'(t)= \lambda \beta xy-dy.\\ \end{array}\right. } \end{aligned}$$

(7)

Solving equations

$$\begin{aligned} {\left\{ \begin{array}{ll} rx\ln \frac{K}{x}-\beta xy=0, \\ \lambda \beta xy-dy=0, \end{array}\right. } \end{aligned}$$

(8)

yields two equilibria: $A(K,0)$ and $E(x^\imath ,y^\imath )$ of system (7), where $x^\imath =\frac{d}{\lambda \beta }, y^\imath =\frac{r}{\beta }\ln \frac{\lambda \beta K}{d}$. Let $(H_1):\lambda \beta K>d$, then, we have the following theorem.

Theorem 3.1

System (7) has a positive equilibrium if and only if $(H_1)$ holds.

Next, we consider the stability of the equilibria. It is easy to see that system (7) has a Jacobian

$$\begin{aligned} J= \left( \begin{array}{cc} r\ln \frac{K}{x}-r-\beta y&{}-\beta x \\ \lambda \beta y&{}\lambda \beta x-d \end{array}\right) . \end{aligned}$$

At $A(K,0),$ we have

$$\begin{aligned} J(A)=\left( \begin{array}{cc} -r&{}-\beta K \\ 0&{}\lambda \beta K-d\\ \end{array}\right) , \end{aligned}$$

which implies that when $(H_1)$ holds, $A(K,0)$ is a saddle point. And at $E(x^\imath ,y^\imath ),$ we have

$$\begin{aligned} J(E)=\left( \begin{array}{cc} -r&{}-\frac{d}{\lambda }\\ \lambda r\ln \frac{K\lambda \beta }{d}&{}0\\ \end{array}\right) . \end{aligned}$$

The characteristic equation of $J(E)$ satisfies $f(\lambda )=\lambda ^2+a\lambda +b=0,$ where $a=r,b=rd\ln \frac{\lambda \beta K}{d}.$ Obviously, $\Delta =a^2-4b=r^2-4rd\ln \frac{\lambda \beta K}{d},$ then we have the following conclusions:

• (i) When $d<\lambda \beta K<de^{\frac{r}{4d}},$ $E(x^{\imath },y^{\imath })$ is a stable node;

• (ii) When $\lambda \beta K=de^{\frac{r}{4d}},$ $E(x^{\imath },y^{\imath })$ is a stable critical node; and

• (iii) when $\lambda \beta K>de^{\frac{r}{4d}},$ $E(x^{\imath },y^{\imath })$ is a stable focus.

Make an assumption $(H_2): \lambda \beta K>de^{\frac{r}{4d}}.$ Then, we have

Theorem 3.2

If condition $(H_2)$ holds true, the equilibrium $E$ of system (7) is a stable focus.

For system (7), we can prove the following.

Theorem 3.3

The solution of system (7) is bounded.

Proof

Let initial conditions of system (7) be

$$\begin{aligned} {\left\{ \begin{array}{ll} x(t_0)=x_0>0,\\ y(t_0)=y_0>0, \end{array}\right. } \end{aligned}$$

(9)

and $(x(t),y(t))$ be a solution of system (7) satisfied (9). Since point $A(K,0)$ is a saddle point, for line $\Gamma _1:x-K=0$ passing through $A,$ we have

$$\begin{aligned} \frac{{d\Gamma _1 }}{{dt}}|_{\Gamma _1=0}&= rx(t)\ln \frac{K}{x(t)}-\beta x(t)y(t)|_{\Gamma _1=0}\\&= -\beta Ky<0. \end{aligned}$$

Thus, the line $\Gamma _1$ is a segment without contact and orbit of system (7) goes across it from the right. On the other hand, define in the first quadrant:

$$\begin{aligned} \Gamma _2:y+\lambda x-M=0, \Gamma _3:y-M+\frac{d}{\beta }=0. \end{aligned}$$

Then, we have

$$\begin{aligned} \frac{{d\Gamma _2}}{{dt}}|_{\Gamma _2=0}&=y(\lambda \beta x-d)+\lambda x\left( r\ln \frac{K}{x}-\beta y\right) |_{\Gamma _2=0} \\&=\lambda x\left( r\ln \frac{K}{x}+d\right) -Md, \\ \frac{{d\Gamma _3}}{{dt}}|_{\Gamma _3=0}&= y(\lambda \beta x-d). \end{aligned}$$

Thus, we have $\frac{{d\Gamma _2}}{{dt}}<0$ for $\frac{d}{\lambda \beta }<x<K$ and $\frac{{d\Gamma _3}}{{dt}}<0$ for $0<x<\frac{d}{\lambda \beta },$ here $M$ is large enough. So there exists an area $\Omega$ with a boundary being composed of $x=0,y=0,\Gamma _1\Gamma _2$ and $\Gamma _3$ such that $(x(t),y(t))\in \Omega$ for initial point $(x(t_0),y(t_0))$ and $t>T,$ where $T>0$ is large. This completes the proof. $\square$

Theorem 3.4

If the condition $(H_2)$ is true, the positive equilibrium $E$ of system (7) is globally asymptotically stable.

Proof

Let Dulac function $B=\frac{1}{xy},$ then, we have

$$\begin{aligned} D=\frac{\partial (PB)}{\partial {x}}+\frac{\partial (QB)}{\partial {y}}=-\frac{r}{xy}<0. \end{aligned}$$

According to the Bendixson-Dulac theorem, we confirm that there is no closed orbit around $E.$ Furthermore, by theorems 3.2 and 3.3, we have that the solution of system (7) is bounded and the positive equilibrium point $E$ of system (7) is locally stable. Thus, the positive equilibrium $E$ of system (7) is globally asymptotically stable if the condition $(H_2)$ is true (Fig. 2). $\square$

Figure 7 shows that the positive equilibrium $E$ of system (7) is a stable focus.

Fig. 2

Phase diagram of system (4) with $r=1.2, K=2, \beta =0.5, \lambda =1.6, d=0.4.$

4 The order one periodic solutions of system (4) with impulsive state feedback control

4.1 The existence of order one periodic solutions of the system (4)

In this subsection, using the successor function, we study the existence of periodic solution of system (4). First setting $\dot{x}=0,\dot{y}=0$ yields: (1) the $x$-isolines, curve $L':y=\frac{r}{\beta }\ln \frac{K}{x}$ and $y$-axis and (2) the $y$-isolines, curve $L: x=\frac{d}{\lambda \beta }$ and $x$-axis. Then, by Theorem 3.4, we know that $E(x^{\imath },y^{\imath })$ is a stable focus if $(H_2)$ holds. For notation simplicity, we denote the first impulsive set by $M_{1}=\{(x,y)|x=h_{1}, 0\le y\le y^*\},$ the second by $M_{2}=\{(x,y)|x=h_{2}, y\ge 0\}$ and the image sets corresponding to them by $N_{1}=\{(x,y)|x=h_{1}, \alpha \le y\le y^*+\alpha \}$ and $N_{2}=\{(x,y)|x=(1-p)h_{2}, y\ge \tau \},$ respectively. In order to have physical meaningful, we restrict our study to the region lying in the left side of $E,$ that is $h_{1}<(1-p)h_{2}<h_{2}<\frac{d}{\lambda \beta }.$ Next, we investigate the trajectory of system (4), which passes the initial point $C_0(x_{c_0},y_{c_0})$ (Fig. 3).

Fig. 3

The structure diagram of system (4)

4.1.1 The path curve beginning from $C_0,$ a point above $P$ on $N_1$

Without loss of generality, we assume that $C_0$ satisfies $y^*<y_{C_0}\le y^*+\alpha$. In fact, if the path curve starting from $C_0$ intersects with $M_1$ at point $C_1(x_{c_1},y_{c_1}),$ and then produces pulse to point $C_1^+$ on $M_1$ such that $y_{C_1^+}<y^*,$ then from (4), we have $y_{C_1^+}=y_{C_1}+\alpha .$ Then after finite number of times impulse, point $C_1^+$ satisfies $y^*<y_{C_1^+}\le y^*+\alpha .$ Thus, in what follows, we only consider the case of $C_0$ such that $y^*<y_{C_0}\le y^*+\alpha .$ Then, we have three sub cases to be discussed.

Case I: the impulsive point $C_1^+$ overlaps with the initial point $C_0.$ Then, the curve $C_0C_1C_1^+$ constitutes a periodic path curve of system (4), please see Fig. 4.

Fig. 4

The path curve beginning from $C_0,$ a point above $P$ on $N_1$ (Case I in Sect. 4.1.1)

Case II: the impulsive point $C_1^+$ is below $C_0$ on $N_1.$ Then, we obtain $s(C_0)<0.$ Now, we choose a point $D_0$ next to $P$ on $N_1$ (that is $|D_0P|<\varepsilon$). The path curve of system (4) beginning from point $D_0$ intersects with $M_1$ at point $D_1,$ and then an impulse happens, $D_1$ jumps to point $D_1^+$ on the line $N_1.$ Because $D_0$ is near to $P,$ $D_1$ is near to $P,$ and $y_{D_1^+}=y_{D_1}+\alpha ,$ we have $s(D_0)>0.$ By Theorem 2.2, there exists an order one period solution (see Fig. 5).

Fig. 5

The path curve beginning from the point $C_0$ (Case II in Sect. 4.1.1)

Case III: the impulsive point $C_1^+$ is above $C_0$ on $N_1.$ In this case, we have $s(C_0)>0.$ Because the path curve does not produce pulse at $A(h_1,y^*+\alpha ),$ we know $s(A)<0.$ Then, the Poincaré-Bendixson theorem implies the existence of a periodic path curve of system (4) (see Fig. 6).

Fig. 6

The path curve beginning from the point $C_0$ (Case III in Sect. 4.1.1)

4.1.2 The path curve beginning from the point $Q$

Now consider a path curve starting from a point $Q$ on $N_2.$ Then, it intersects with $M_2$ at point $C_1$ and produces pulse to point $C_1^+$ on $N_2.$ According to system (4), the following is obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{C_1^+}=(1-p)h_2,\\ y_{C_1^+}=(1-q)y_{C_1}+\tau . \end{array}\right. } \end{aligned}$$

For different $\tau ,$ three cases should be discussed.

Case I: the impulsive point $C_1^+$ is exactly $Q.$ Here the curve $QC_1C_1^+$ constitutes a periodic path curve of system (4) (see Fig. 7).

Fig. 7

The path curve beginning from the point Q (Case I in Sect. 4.1.2)

Case II: the impulsive point $C_1^+$ is above $Q$ on $N_2.$ It implies that $s(Q)=y_{C_1^+}-y_{Q}>0.$ Now we choose $D_0,$ a point above $C_1^+$ on $N_2.$ The path curve starting from $D_0$ is vertical only when it intersects with $N_1$ at $P.$ Then it crosses $N_2$ from left to right, and then intersects with $M_2$ at point $D_2$ and pulses to point $D_2^+$ of the line $N_2.$ By the existence and uniqueness theorem for impulsive differential equations, $D_2$ is below $C_1$ of $M_2,$ and $D_2^+$ must below $C_1^+$ on $N_2.$ Therefore, we have $s(D_0)=y_{D_2^+}-y_{D_0}<0.$ By Theorem 2.2, there exists order one periodic solution of system (4) in region $D_0PD_1D_2C_1C_1^+D_0$ (see Fig. 8).

Fig. 8

The path curve beginning from the point Q (Case II in Sect. 4.1.2)

Case III: In this case, the impulsive point $C_1^+$ is below $Q$ on $N_2.$ Then we have $s(Q)=y_{C_1^+}-y_{Q}<0.$ Pick a point $D_0$ next to $B((1-p)h_2,0)$ on $N_2$ ($|D_0B|<<\varepsilon .$). Starting from $D_0,$ the path curve intersects with $M_2$ at point $D_1,$ and then produces pulse to point $D_1^+$ on $N_2.$ From system (4), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{D_1^+}=(1-p)h_2,\\ y_{D_1^+}=(1-q)y_{D_1}+\tau . \end{array}\right. } \end{aligned}$$

Thus, $D_1^+$ has to be above $D_0,$ and the successor function of $D_0$ satisfies $s(D_0)=y_{D_1^+}-y_{D_0}>0.$ As a result, the region $\kappa$ surrounded by the closed curve $D_0D_1C_1C_1^+$ involves a periodic solution of system (4) (see Fig. 9).

Fig. 9

The path curve beginning from the point Q (Case III in Sect. 4.1.2)

4.1.3 Initial point $C_0$ of path curve on $N_1$ falling in between the second impulsive set $M_2$ and its image set $N_2.$

In this section, we assume the path curve intersects with line $M_2$ at $C_1,$ and then jumps onto point $C_1^+$ on $N_2.$ According to values of $\tau$, we have the following cases.

Case I: Point $C_1^+$ is point $Q,$ and the path curve from point $C_1^+$ moves to point $C_2$ on $M_2.$ For point $C_2,$ we have three cases.

Case I(a): Point $C_2$ is exactly point $C_1.$ In this case, obviously the curve $C_1C_1^+C_2$ forms a periodic path curve of system (4) (see Fig.10).

Fig. 10

The path curve beginning from the point $C_0$ (Case I(a) in Sect. 4.1.3)

Case I(b): Point $C_2$ is below point $C_1.$ Then, it is easy to see the successor function of $C_1$ that is negative, namely $s({C_1})=y_{C_2}-y_{C_1}<0.$ Next, in the region between $N_2$ and $M_2$, we pick a point $D_0$ next to x-axis. Then, the path curve passing $D_0$ hits a point $D_1$ on $M_2,$ and then jumps onto $N_2$ at a point $D_1^+$, from which jumps to a point $D_2$ on $M_2.$ It is easy to verify that $D_2$ is above $D_1,$ which implies the successor function, $s({D_1})=y_{D_2}-y_{D_1}>0.$ Then, there is a point $C$ between $C_1$ and $D_1$ such that $s(C)=0,$ which implies the existence of a periodic path curve in the region enclosed by curve $C_1C_1^+D_1^+D_2$ (see Fig. 11).

Fig. 11

The path curve beginning from the point $C_0$ (Case I(b) in Sect. 4.1.3)

Case I(c): Point $C_2$ is above $C_1.$ In this case, the periodic path curve does not exist. Otherwise the curves $C_1^+C_2$ and $C_0C_1$ intersect each other, which conflict with the existence and uniqueness of solutions of impulsive differential equations.

Case II: The point $C_1^+$ is below $Q.$ In this case, using the similar argument as above yields the same conclusion (see Figs. 12 and 13).

Fig. 12

The path curve beginning from the point $C_0$ (Case II in Sect. 4.1.3)

Fig. 13

The path curve beginning from the point $C_0$ (Case II in Sect. 4.1.3)

Case III: Point $C_1^+$ on $N_2$ is above $Q.$ Then, we have two cases to be investigated.

Case III(a): the path curve starting from $C_1^+$ crosses $N_1.$ Then, it becomes vertical only for going through the line $L'.$ Using $C_2$ to denote the intersection of the path curve and $N_1,$ then same conclusion can be made as what we did in Sect. 4.1.1 (see Fig. 14).

Fig. 14

The path curve beginning from the point Q (Case III(a) in Sect. 4.1.3)

Case III(b): the path curve starting from $C_1^+$ does not touch $N_1.$ Then, the path curve becomes vertical only when it crosses $PQ.$ And then it goes back to $M_2,$ and if we denote the intersection by $C_2$, then $C_2$ is one of the three points: point $C_1,$ a point below $C_1,$ or a point above $C_1.$

If point $C_2$ is $C_1,$ then the curve $C_1C_1^+C_2$ forms a periodic path curve (see Fig. 15).

Fig. 15

The path curve beginning from the point $C_0$ (Case III(b) in Sect. 4.1.3)

If $C_2$ is below $C_1,$ the successor function $s(C_1)=y_{C_2}-y_{C_1}<0.$ Then, we can select a point $D_0$ between $N_2$ and $M_2$ near to $x$-axis such that the path curve beginning from $D_0$ hits the point $D_1$ on $M_2,$ and then jumps onto the point $D_1^+$ on $N_2,$ and then returns to the point $D_2$ on $M_2,$ and the successor function of $D_1$ is $s(D_1)=y_{D_2}-y_{D_1}>0.$ It implies that there exists a periodic path curve in the region enclosed by curves $D_1C_1C_1^+C_2$ and $C_1^+D_1^+D_2C_2$ (see Fig. 16).

Fig. 16

The path curve beginning from the point $C_0$ (Case III(b) in Sect. 4.1.3)

If $C_2$ is above $C_1,$ the periodic path curve does not exist as the Case I(c) in Sect. 4.1.3.

Now, we have proved the existence of the periodic solution, next we study the stability of it.

4.2 The stability of order one periodic solutions of the system (4)

4.2.1 The stability of order one periodic solutions on impulsive set $M_1$

Theorem 4.1

Let $(\phi (t), \varphi (t))$ be a periodic solution of system (4) with $\phi _0=\phi (0)=h_1, \varphi _0=\varphi (0), \phi _1=\phi (T), \varphi _1= \varphi (T), \phi _1^+=\phi (T^+), \varphi _1^+=\varphi (T^+).$ Then, the periodic solution is stable when $\varphi _0<\frac{r}{\beta }\ln \frac{K}{h_1}.$

Proof

Let $(\phi (t), \varphi (t))$ be a periodic solution of system (4) with $\phi _0=\phi (0)=h_1, \varphi _0=\varphi (0), \phi _1=\phi (T), \varphi _1= \varphi (T), \phi _1^+=\phi (T^+), \varphi _1^+=\varphi (T^+).$ By system (4), we have $\phi _1=\phi (T)=h_1, \varphi _1= \varphi (T)=\varphi _0-\alpha , \phi _1^+=\phi (T^+)=h_1, \varphi _1^+=\varphi (T^+)=\varphi _0.$

According to Theorem 2.3, let

$$\begin{aligned} {\left\{ \begin{array}{ll} P(x,y)=x(r\ln \frac{K}{x}-\beta y),\\ Q(x,y)=y(\lambda \beta x-d),\\ \alpha (x,y)=0,\\ \beta (x,y)=\alpha ,\\ \Phi (x,y)=x-h_1, \end{array}\right. } \end{aligned}$$

(10)

and notice that

$$\begin{aligned} \frac{\partial \alpha }{\partial x}=\frac{\partial \alpha }{\partial y}=0, \frac{\partial \beta }{\partial x}=\frac{\partial \beta }{\partial y}=0, \frac{\partial \Phi }{\partial x}=1,\frac{\partial \Phi }{\partial y}=0, \end{aligned}$$

(11)

we have

$$\begin{aligned} \int \limits _0^T\frac{\partial P}{\partial x}\mathrm{d}t&= \int \limits _0^T\left( r\ln \frac{K}{x}-\beta y-r \right) \mathrm{d}t,\\&= \int \limits _0^T\left( r\ln \frac{K}{x}-\beta y\right) \mathrm{d}t-rT,\\&= \ln \left( \frac{\phi _1}{\phi _0}\right) -rT,\\&= \ln \frac{\varphi _0-\alpha }{\varphi _0}-rT,\\ \int \limits _0^T\frac{\partial Q}{\partial y}\mathrm{d}t&= \int \limits _0^T\left( \lambda \beta x-d\right) \mathrm{d}t,\\&= \ln \left( \frac{\varphi _1}{\varphi _0}\right) . \end{aligned}$$

Using Theorem 2.3 again and some algebraic manipulations, we reach the following

$$\begin{aligned} \Delta _1\!&= \!\frac{P_+\!\cdot \left( \frac{\partial \beta }{\partial y}\cdot \frac{\partial \Phi }{\partial x}\!-\!\frac{\partial \beta }{\partial x}\cdot \frac{\partial \Phi }{\partial y}\!+\!\frac{\partial \Phi }{\partial x}\right) \!+\!Q_+\!\cdot \left( \frac{\partial \alpha }{\partial x}\cdot \frac{\partial \Phi }{\partial y}\!-\!\frac{\partial \alpha }{\partial y}\cdot \frac{\partial \Phi }{\partial x}\!+\!\frac{\partial \Phi }{\partial y}\right) }{P\frac{\partial \Phi }{\partial x}\!\!+\!\!Q\frac{\partial \Phi }{\partial y}}\\&= \frac{P(\phi (T^+),\varphi (T^+))}{P(\phi (T),\varphi (T))}\\&= \frac{P(h_1,\varphi _0)}{P(h_1,\varphi _0-\alpha )}\\&= \frac{r\ln \frac{K}{h_1}-\beta \varphi _0}{r\ln \frac{K}{h_1}-\beta (\varphi _0-\alpha )} \end{aligned}$$

and

$$\begin{aligned} \mu _2&= \Delta _1\exp \left\{ \int \limits _0^T{\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\mathrm{d}t}\right\} \\&= \frac{r\ln \frac{K}{h_1}-\beta \varphi _0}{r\ln \frac{K}{h_1} -\beta (\varphi _0-\alpha )}\exp \left\{ \ln \left( \frac{\phi _1}{\phi _0}\right) \right. \\&\left. +\ln \left( \frac{\varphi _1}{\varphi _0}\right) -rT\right\} \\&= \frac{r\ln \frac{K}{h_1}-\beta \varphi _0}{r\ln \frac{K}{h_1} -\beta (\varphi _0-\alpha )}\frac{\varphi _0-\alpha }{\varphi _0}\mathrm{e}^{-rT}. \end{aligned}$$

Obviously, if $\varphi _0<\frac{r}{\beta }\ln \frac{K}{h_1},$ we have $r\ln \frac{K}{h_1}-\beta \varphi _0>0,$ we have $|\mu _2|<1,$ which implies that the periodic solution is stable. $\square$

4.2.2 The stability of order one periodic solutions with initial point $C_0$ on $N_2$

Again, let $\Pi (C_0,t)$ be the closed path curve beginning from $C_0((1-p)h_2,\varphi _0).$ Then, by property of system (4), the path curve intersects with $M_2$ with the intersection to be denoted by $C_1(\phi (T),\varphi (T)),$ which jumps to $C_1^{+}(\phi (T^{+}),\varphi (T^{+}).$ That is to say that $\Pi (C_0,T)=C_1,C_1^{+}=I(C_1)=C_0,$ where $\phi (T^{+})=(1-p)\phi (T),\varphi (T^{+})=(1-q)\varphi (T)+\tau$ and $\phi (T)=h_2, \varphi (T)=\frac{\varphi _0-\tau }{1-q}.$ Let

$$\begin{aligned} {\left\{ \begin{array}{ll} P(x,y)=x(r\ln \frac{K}{x}-\beta y),\\ Q(x,y)=y(\lambda \beta x-d),\\ \alpha (x,y)=-px,\\ \beta (x,y)=-qx+\tau ,\\ \Phi (x,y)=x-h_2. \end{array}\right. } \end{aligned}$$

Calculating partial derivatives, one gets

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \alpha }{\partial x}=-p,\frac{\partial \alpha }{\partial y}=0,\\ \frac{\partial \beta }{\partial x}=0,\frac{\partial \beta }{\partial y}=-q,\\ \frac{\partial \Phi }{\partial x}=1,\frac{\partial \Phi }{\partial y}=0. \end{array}\right. } \end{aligned}$$

It implies

$$\begin{aligned} \Delta _1&= \frac{P_+\left( \frac{\partial \beta }{\partial y}\frac{\partial \Phi }{\partial x}-\frac{\partial \beta }{\partial x}\frac{\partial \Phi }{\partial y}+\frac{\partial \Phi }{\partial x}\right) +Q_+\left( \frac{\partial \alpha }{\partial x}\frac{\partial \Phi }{\partial y}-\frac{\partial \alpha }{\partial y}\frac{\partial \Phi }{\partial x}+\frac{\partial \Phi }{\partial y}\right) }{P\left( \frac{\partial \Phi }{\partial x}\right) +Q\left( \frac{\partial \Phi }{\partial y}\right) }\\&= \frac{P(\phi (T^+),\varphi (T^+))(1-q)}{P(\phi (T),\varphi (T))}\\&= \frac{P(\phi _0,\varphi _0)(1-q)}{P(\phi (T),\varphi (T))}\\&= \frac{(1-p)h_2\left( r\ln \frac{K}{(1-p)h_2} -\beta \varphi _0\right) (1-q)}{h_2(r\ln \frac{K}{h_2} -\beta \frac{\varphi _0-\tau }{1-q})}\\&= \frac{(1-p)(1-q)\left( r\ln \frac{K}{(1-p)h_2} -\beta \varphi _0\right) }{r\ln \frac{K}{h_2}-\beta \frac{\varphi _0-\tau }{1-q}}. \end{aligned}$$

Thus,

$$\begin{aligned} \mu _2&= \Delta _1\exp \left\{ \int \limits _0^T{\frac{\partial P}{\partial x} +\frac{\partial Q}{\partial y}\mathrm{d}t}\right\} \\&= \frac{(1-p)(1-q)\left( r\ln \frac{K}{(1-p)h_2}-\beta \varphi _0\right) }{r\ln \frac{K}{h_2}-\beta \frac{\varphi _0-\tau }{1-q}}\\&\times \exp \left\{ \ln (\frac{\phi _1}{\phi _0})+\ln (\frac{\varphi _1}{\varphi _0})-rT\right\} \\&= \frac{(1-p)(1-q)\left( r\ln \frac{K}{(1-p)h_2} -\beta \varphi _0\right) }{r\ln \frac{K}{h_2} -\beta \frac{\varphi _0-\tau }{1-q}}\\&\times \frac{\frac{\phi _0}{1-p}}{\phi _0} \frac{\frac{\varphi _0-\tau }{1-q}}{\varphi _0}\mathrm{e}^{-rT}\\&= \frac{r\ln \frac{K}{(1-p)h_2}-\beta \varphi _0}{r\ln \frac{K}{h_2} -\beta \frac{\varphi _0-\tau }{1-q}}\frac{\varphi _0-\tau }{\varphi _0}\mathrm{e}^{-rT}. \end{aligned}$$

Therefore, if $|\frac{r\ln \frac{K}{(1-p)h_2}-\beta \varphi _0}{r\ln \frac{K}{h_2} -\beta \frac{\varphi _0-\tau }{1-q}}\frac{\varphi _0-\tau }{\varphi _0}|<1,$ we have $|\mu _2|<1.$ Then, we can summarise our analysis in the following.

Theorem 4.2

If $|\frac{r\ln \frac{K}{(1-p)h_2}-\beta \varphi _0}{r\ln \frac{K}{h_2} -\beta \frac{\varphi _0-\tau }{1-q}}\frac{\varphi _0-\tau }{\varphi _0}|<1,$ the periodic solution of system (4) is stable.

5 An example and numerical simulations

In this section, we will give an example to verify the previous theoretical results. Let $r=1.2, K=2, \beta =0.5, \lambda =1.6, d=0.4, p=0.5, q=0.2, \alpha =0.5, \tau =0.2, h_1=0.2, h_2=0.45.$ By calculation, we obtain $y^*=5.5262,$ then we get $P(0.2,5.5262), Q(0.225,5.2435)$ and $E(x^\imath ,y^\imath )=(0.5,3.3271).$ Then system (4) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \left. \begin{array}{l} x'(t)=1.2x(t)\ln \frac{2}{x(t)}-0.5 x(t)y(t), \\ y'(t)=0.8 x(t)y(t)-0.4y(t),\\ \end{array} \right\} \\ x\ne 0.2, \quad \,\, 0.45, or\ \ x=0.2, y>5.5262,\\ \left. \begin{array}{l} \Delta {x}(t)=0, \\ \Delta {y}(t)=0.5, \\ \end{array} \right\} x=0.2, y\le 5.5262,\\ \left. \begin{array}{l} \Delta {x}(t)=-0.5x(t), \\ \Delta {y}(t)=-0.2y(t)+0.2, \\ \end{array} \right\} x=0.45. \end{array}\right. } \end{aligned}$$

(12)

Numerical analysis of system (12) is being done using Maple 14.0. We have the following cases.

5.1 The path curve beginning from $C_0,$ a point above $P$ on $N_1$ (corresponding to Sect. 4.1.1)

In this section, we set $C_0=(0.2,6)$ to guarantee that it is above $P(0.2,5.5262).$

Case I: The impulsive point $C_1^+$ corresponding to $C_1$ is exactly $C_0,$ thus the curve $C_0C_1C_1^+$ shall constitute a periodic path curve (Fig. 17).

Fig. 17

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case II: The impulsive point $C_1^+$ corresponding to $C_1$ is below $C_0$ (Fig. 18).

Fig. 18

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case III: The impulsive point $C_1^+$ corresponding to $C_1$ is above $C_0$ (Fig. 19).

Fig. 19

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

5.2 The path curve beginning from point $Q$ (corresponding to Sect. 4.1.2)

In this case, we let $C_0$ be $Q(0.225,5.2435).$

Case I: The impulsive point $C_1^+$ corresponding to $C_1$ is exactly $Q$ (Fig. 20).

Fig. 20

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case II: The impulsive point $C_1^+$ corresponding to $C_1$ is above $Q$ on $N_2$ (Fig. 21).

Fig. 21

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case III: The impulsive point $C_1^+$ corresponding to $C_1$ is below $Q$ on $N_2$ (Fig. 22).

Fig. 22

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

5.3 The path curve with initial point $C_0$, which is between the second impulsive set $M_2$ and its image set $N_2$ (corresponding to Sect. 4.1.3)

In this section, we choose $C_0=Q(0.225,0.9796)$.

Case I: If $C_1^+$ on $N_2$ is exactly $Q,$ the path curve from point $C_1^+$ moves to the point $C_2$ on $M_2.$

Case I(a): $C_2$ is exactly $C_1$ (Fig. 23).

Fig. 23

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case I(b): The impulsive point $C_1^+$ corresponding to $C_1$ is below $Q$ on $N_2$ (Fig. 24).

Fig. 24

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case I(c): The impulsive point $C_1^+$ corresponding to $C_1$ is above $Q$ on $N_2.$

Case II: If $C_1^+$ on $N_2$ is below $Q$ (Figs. 25 and 26).

Fig. 25

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Fig. 26

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case III: If $C_1^+$ on $N_2$ is above $Q.$

Case III(a): The path curve beginning from $C_1^+$ crosses $N_1$ from the right to the left (Fig. 27).

Fig. 27

The results of numerical simulation of system (12). (a) Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Case III(b): The path curve beginning from $C_1^+$ moves on automatically to $C_2$ on $M_2,$ which is exactly $C_1$ (28) or below $C_1$ (see Fig. 29).

Fig. 28

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

Fig. 29

The results of numerical simulation of system (12). a Phase diagram of system (12). b Time series of system (12). c Time series of system (12)

All the numerical simulation above show agreement with our theoretical results.

6 Conclusion

In this paper, we formulated a mathematical model for pest management purpose, which is with impulsive state feedback control. By feedback information of pests’ density from the monitor, we can control the pests with artificial disturbance. Firstly, we qualitatively investigated the dynamic behaviour of the system without impulsive effect, and obtained the sufficient condition for globally asymptotically stable of the positive equilibrium. And then the system with impulsive state feedback control was studied by geometric theory of impulsive differential equations. The existence and stability of order one periodic solution were proved. All the results suggested that the pest management model finally showed periodicity or steady state under impulsive state feedback control. We found that the density of the pest plays an important role in the periodic or stable state of system. When the density of the pest reaches an appropriate critical value, the state feedback measure including spraying pesticide and releasing natural enemy to control density of the pest would be taken. Theoretical derivation and numerical simulations show that the artificial intervention measures are effective. The reasonable selective feedback value can not only make the pest density in a controlled range but reduce the usage amount of pesticides for the ecological balance.