1 Introduction

One of the most important research areas in control theory is quantized control. Quantized feedback is found in many engineering systems including mechanical systems and networked systems. Since communication that need to transmit the feedback information from the sensor to the controller may become less reliable as the bandwidth is limited. Therefore, a number of significant results on this issue have been reported and different approaches have been proposed in the literature [1–11]. Recently, some fundamental approaches for quantized control systems have been developed. For example, in [12], the classical sector bound method was used to study quantized control systems with logarithmic quantizers. It should be noted that quantization errors were converted into sector bound uncertainties without conservatism. Gao et al. [13] proposed a quantization-dependent approach leading to less conservative results. The problem of robust \(H_\infty \) filtering for uncertain linear systems subject to limited communication capacity was investigated in [14]. The logarithmic quantizer considered in [15] was different from the traditional quantizer used in [12] and [13]. Liu et al. [16] studied the problem of observer-based stabilization for linear discrete-time systems with output measurement quantization. Compared with quantized feedback control, the robust synchronisation problem of chaotic systems via sampled-data control with stochastic sampling interval has been studied in [17]. In addition, the sampled data with stochastic sampling have been applied to neural networks [18]. Networked control systems with partly quantized information were investigated in [19]. The authors of [19] focused on the local and networked-link systems where only some of the inputs of the controller were quantized.

By exploring geometric properties of the logarithmic quantizer, a less conservative Tsypkin-type criterion for stability analysis of quantized feedback control system was proposed in [20]. In [21], a new necessary and sufficient condition was developed to guarantee the asymptotic stability of the closed system. The problem of \(H_\infty \) filter design for a class of discrete-time systems with quantized measurements was discussed in [22] and [23], while [24] studied the robust \(H_\infty \) dynamic output feedback control problem for networked control systems with quantized measurements. Furthermore, measurement losses of the communicated information were also considered in [24]. It should be pointed out that all of the above-mentioned works were developed in the context of the logarithmic quantizer.

Moreover, actuator saturation is present in practically all control systems. Actually, linear systems with saturating inputs will change a linear system into a nonlinear one. Saturation nonlinearity may degrade system performance and even lead a stable system into an instable one. During the past years, much attention has been drawn to the problems of stability analysis and stabilization of linear systems when subject to saturating actuator. A great number of results on this topic have been reported in the literature (see, for example, [3, 25–28]). One of the most popular ways to deal with saturation problem given in [25] was the use of polytopic differential inclusion, while in [3] the quantization was converted into a form of saturation with bounded disturbances. In the context of linear systems with saturating actuator, the problem of local uniform ultimate boundedness stabilization was solved in [26] by using modified sector conditions. Moreover, the uniform quantizer was presented in [26]. However, it seems that no results on the logarithmic quantized output feedback control for discrete-time systems with saturating actuator are available in the literature.

In this paper, we consider the quantized output feedback stabilization problem for nonlinear discrete-time systems with saturating actuator. The aim is to design quantized static output feedback controllers such that all the trajectories of the closed-loop system will converge to a minimal ellipsoid for every initial condition emanating from a large admissible domain. The nonlinearity we consider satisfies the local Lipschitz condition. However, the Lipschitz constant is not assumed to be known. Furthermore, a minimal ellipsoid, a large admissible domain and the maximum allowable Lipschitz constant are obtained by solving an optimization problem. Finally, some simulation examples are provided to demonstrate the effectiveness of the proposed method.

Notation: Throughout this brief, for symmetric matrices X and Y, the notation \(X\ge Y\) (respectively, \(X>Y\)) means that the matrix \(X-Y\) is positive semi-definite (respectively, positive definite). I is the identity matrix with appropriate dimension. \(I_n\) denotes the identity matrix of \(n\times n\) dimensions. For a square matrix \(P, P>0\) means that P is symmetric and positive definite. For a matrix \(P>0, \varepsilon (P)\) stands for \(\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1\}\). For a matrix \(H\in \mathbb {R}^{m\times n}, H^T, H_{(i)}\) and \(\mathscr {L}(H,u_0)\) represent its transpose, its ith row and \(\{x(k)\in \mathbb {R}^n: \Vert H_{(i)}x(k)\Vert \le u_{0(i)},i=1,\ldots ,m\}\), respectively. \(\star \) stands for symmetric blocks. For a vector \(\nu \in \mathbb {R}^{n}, \nu _{(j)},j=1,\ldots ,n\) denotes the jth component of \(\nu \).

2 Preliminaries and problem formulation

Consider the following class of discrete-time nonlinear systems with input saturation described by

$$\begin{aligned}&x(k+1) = Ax(k)+ B\mathrm{sat}(u(k))+ f(x(k)), \end{aligned}$$
(1)
$$\begin{aligned}&y(k) = C x(k), \end{aligned}$$
(2)

where \(x(k)\in \mathbb {R}^n\) is the system state, \(y(k)\in \mathbb {R}^s\) is the measured output, \(u(k)\in \mathbb {R}^m\) is the control input. \(f(\cdot ): \mathbb {R}^n\rightarrow \mathbb {R}^n\) is nonlinear function and assumed to be differentiable. A, B and C are known real constant matrices. In this paper, the structure of the saturation function considered here is of the form

$$\begin{aligned} \text{ sat }(u(k))=\left[ \begin{array}{ccc} \text{ sat }(u(k)_{(1)})&\ldots&\text{ sat }(u(k)_{(m)}) \end{array} \right] ^T, \end{aligned}$$
(3)

where \(\text{ sat }(u(k)_{(i)})=\text{ sign }(u(k)_{(i)})\min \{u_{0(i)},|u(k)_{(i)}|\}\) with \( u_0=\left[ \begin{array}{ccc} u_{0(1)}&\ldots&u_{0(m)} \end{array} \right] ^T,\) \(u_{0(i)}>0, i=1,\ldots , m\) being constants. Here we employ the static logarithmic quantizer. The signal is quantized by quantizer \(q(\cdot )\) which is defined as

$$\begin{aligned} {q}(\nu )=\left[ \begin{array}{cccc} {q}_1{(\nu _{(1)})}&{q}_2{(\nu _{(2)})} \ldots&{q}_l{(\nu _{(l)})} \end{array} \right] ^T. \end{aligned}$$
(4)

For each \(q_r(\nu _{(r)})(1\le r\le l)\), the associated set of quantization levels is expressed as

$$\begin{aligned}&\mathcal {Q}_r=\left\{ {\pm } \mathcal {L}_r^{(j)}\mid \mathcal {L}_r^{(j)}{=}(\rho _r)^j \mathcal {L}_r^{(0)}, j{=}{\pm } 1,{\pm } 2, \pm 3,\ldots \right\} \\&\cup \left\{ \pm \mathcal {L}_r^{(0)} \right\} \cup \left\{ 0 \right\} , 0< \rho _r < 1, \mathcal {L}_r^{(0)}>0, \end{aligned}$$

where \(\mathcal {L}_r^{(0)}\) is the initial quantization values for the rth sub-quantizer \(q_r(\nu _{(r)})\) and \(\rho _r\) is the quantizer density of the rth sub-quantizer \(q_r(\nu _{(r)})\). In this article, a characterization of the quantizer is given by

$$\begin{aligned} q_r(\nu _{(r)})= & {} \left\{ \begin{aligned} \begin{array}{l@{\quad }l} \mathcal {L}_r^{(j)}, \ \ \ &{}\text{ if } \ \frac{1}{1+\delta _r}\mathcal {L}_r^{(j)}<\nu _{(r)}\le \frac{1}{1-\delta _r}\mathcal {L}_r^{(j)}, \ \ \nu _{(r)}>0, \ \ j=\pm 1,\pm 2, \pm 3, \ldots , \\ 0, \ \ \ \ \ \ &{}\text{ if } \ \nu _{(r)}=0, \\ -q_r(-\nu _{(r)}), \ \ \ &{}\text{ if } \ \nu _{(r)}<0, \ \ r=1,2,3,\ldots ,l, \end{array} \end{aligned} \right. \end{aligned}$$
(5)

where \(\delta _r=\frac{1-\rho _r}{1+\rho _r}\). It follows from [12] and [13] that a sector bound expression can be expressed as

$$\begin{aligned} q(\nu )=(I_l+\Delta (k))\nu , \end{aligned}$$
(6)

where the uncertainty matrix \(\Delta (k)=\text{ diag }\{\Delta _1(k),\Delta _2(k),\ldots , \Delta _l(k)\}\) satisfies \(\Delta _r(k) \in [-\delta _r,\delta _r], \ r=1,2,\ldots ,l\).

Moreover, as shown in [29] and [30], we make the following assumption on the nonlinear function in system (1)–(2).

Assumption 1

We assume that the function f(x) is locally Lipschitz with respect to x in a region \(\mathscr {Q}\) containing the origin if \(\Vert f(0)\Vert =0\) and

$$\begin{aligned} \Vert f(x_1)-f(x_2)\Vert \le \eta \Vert x_1-x_2 \Vert , \ \ \ \forall x_1,x_2\in \mathscr {Q}, \end{aligned}$$

where \(\Vert \cdot \Vert \) is the induced 2-norm and \(\eta >0\) is called the Lipschitz constant.

Throughout this paper, it is worth noting that the Lipschitz constant \(\eta >0\) is not fixed. The maximum allowable Lipschitz constant \(\eta ^*\) can be determined by solving the convex optimization problem.

Now, consider two different static output feedback controllers.

  • Case 1 quantized control input

    $$\begin{aligned} u(k)= & {} q(Fy(k))=(I_m+\Delta (k))Fy(k), \nonumber \\ \Delta (k)= & {} \text{ diag }\{\Delta _1(k),\Delta _2(k),\ldots , \Delta _m(k)\}. \end{aligned}$$
    (7)

In (7), the control input is quantized. Now, applying the controller (7) to the system (1)–(2), we obtain the closed-loop system as

$$\begin{aligned} x(k+1)= & {} Ax(k)+ B \text{ sat }((I_m+\Delta (k))FCx(k))\nonumber \\&\quad + f(x(k)). \end{aligned}$$
(8)

The quantized output feedback stabilization problem being considered in this paper can be formulated as finding the quantized feedback controller in the form of (7) such that the following specification is met.

Problem 1

Design a controller (7) such that all the states of the closed-loop system will converge to a minimal ellipsoid for every initial condition emanating from a large admissible domain. The corresponding domains and the maximum allowable Lipschitz constant \(\eta ^*\) are obtained, respectively.

  • Case 2 quantized output

    $$\begin{aligned} u(k)= & {} Fq(y(k))=F(I_s+\Delta (k))y(k), \nonumber \\ \Delta (k)= & {} \text{ diag }\{\Delta _1(k),\Delta _2(k),\ldots , \Delta _s(k)\}. \end{aligned}$$
    (9)

In (9), the measured output is quantized. Then, the resulting closed-loop system from the system (1)–(2) and the controller (9) can be written as

$$\begin{aligned} x(k+1)= & {} Ax(k)+ B \text{ sat }(F(I_s+\Delta (k))Cx(k))\nonumber \\&\quad + f(x(k)). \end{aligned}$$
(10)

The quantized output feedback control problem can be formulated as finding the quantized feedback controller in the form of (9) such that the following requirement is met.

Problem 2

Determine a controller (9) such that the closed-loop system is convergent to a minimal ellipsoid for every initial condition from an admissible domain. Simultaneously, the corresponding domains and the maximum allowable Lipschitz constant \(\eta ^*\) are obtained.

3 Main results

This section begins by introducing some lemmas that will play important roles for the proof of our main results here. Firstly, let \(\mathscr {D}\) be the set of \(m\times m\) diagonal matrices whose diagonal elements are either 1 or 0. Thus, there are \(2^m\) elements in \(\mathscr {D}\). Suppose that each element of \(\mathscr {D}\) is labeled as \(D_i,i=1,2,\ldots ,2^m\). Denote \(D^-_i=I-D_i\). Clearly, \(D^-_i\) is also an element of \(\mathscr {D}\) if \(D_i\in \mathscr {D}\).

Lemma 1

([31]) For any positive definite matrix \(P\in \mathbb {R}^{n\times n}\) and vectors \(x,y\in \mathbb {R}^n\), we have

$$\begin{aligned} 2x^Ty\le x^TPx+y^TP^{-1}y. \end{aligned}$$

Lemma 2

([32]) Let \(\mathcal {A}, \mathcal {D}, \mathcal {S}, \mathcal {W}\) and F be real matrices of appropriate dimensions such that \(\mathcal {W}>0\) and \(F^TF\le I\). Then for any scalar \(\varepsilon >0\) such that \(\mathcal {W}^{-1}-\varepsilon ^{-1}\mathcal {D}\mathcal {D}^T>0\), we have

$$\begin{aligned}&(\mathcal {A}+\mathcal {D}F\mathcal {S})^T\mathcal {W} (\mathcal {A}+\mathcal {D}F\mathcal {S})\le \mathcal {A}^T\\&(\mathcal {W}^{-1}-\varepsilon ^{-1}\mathcal {D}\mathcal {D}^T)^{-1}\mathcal {A}+\varepsilon \mathcal {S}^T\mathcal {S}. \end{aligned}$$

Lemma 3

([25]) Let \(u\in \mathbb {R}^m\) and \(v\in \mathbb {R}^m\) be given. If \(\Vert v\Vert \le u_0\), then \(\text{ sat }(u)\) can be represented as \(\text{ sat }(u)=\sum \limits _{i=1}^{2^m}\eta _i(D_iu+D^-_iv)\), where \(0\le \eta _i \le 1\) and \(\sum \limits _{i=1}^{2^m}\eta _i=1\).

Now we are in a position to present a solution to Problem 1 specified above.

Theorem 1

Consider the discrete-time nonlinear system (1) and (2) and let \(\beta _2>\beta _1>0\) be given scalars. For a given matrix \(M>0\), there exists a static output feedback controller in the form of (7) such that all solutions of the closed-loop system emanating from \(S=\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1 \ \text{ and } \ x(k)^TP_2x(k)\ge 1\}\) converge to \(S_\infty =\{x(k)\in \mathbb {R}^n \mid x(k)^TP_2x(k)\le 1\}\), if there exist matrices \(P>0, P_2>0, F, H\) and scalars \(\varepsilon _1>0, \varepsilon _2>0, \alpha >0\) such that the following linear matrix inequalities (LMIs) hold for \(i=1,2,\ldots ,2^m\):

$$\begin{aligned}&\left[ \begin{array}{ccccc} -(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ A^T+C^TF^TI_mD_iB^T+H^TD_i^-B^T &{} \ C^TF^T &{} \ 0 \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ BD_i\Delta \varepsilon _2\Delta D_i B^T-2M+MPM &{} \ 0 &{} \ I \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _2I &{} \ 0 \\ \star &{} \ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _1I \end{array} \right] <0, \end{aligned}$$
(11)
$$\begin{aligned}&\left[ \begin{array}{cc} u_{0(p)}I &{} \ H_{(p)} \\ \star &{} \ u_{0(p)}P \end{array} \right] \ge 0, \ \ p=1,2,\ldots ,m, \end{aligned}$$
(12)
$$\begin{aligned}&P_2-P \ge 0. \end{aligned}$$
(13)

Proof

Choose a Lyapunov function candidate as follows: \(V(k)=x(k)^TPx(k)\). Along a similar line as in the proof of [25], \(\varepsilon (P)\subset \mathscr {L}(H,u_0)\) is equivalent to \(H_{(p)}P^{-1}H_{(p)}^T\le u_{0(p)}^2\). And also by the Schur complement equivalence, (12) can be contained. Now taking into account (13), it follows that \(\varepsilon (P)\) contains \(\varepsilon (P_2)\). Using Lemma 3, we have

$$\begin{aligned} x(k+1)= & {} Ax(k){+} B \sum \limits _{i=1}^{2^m}\eta _i(D_i(I_m{+}\Delta (k))F C x(k)\\&+D_i^{-}H x(k))+ f(x(k))\\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{(\tilde{A}{+}BD_i\Delta (k) FC)x(k){+}f(x(k)) \}, \end{aligned}$$

where \(\tilde{A}=A+BD_iI_mFC+BD^-_iH\). The forward difference in the functional V(k) along the system (1)–(2) is then given by

$$\begin{aligned}&\Delta V(k)=V(k+1)-V(k)\\&\quad =x(k+1)^TPx(k+1)-x(k)^TPx(k). \end{aligned}$$

On the other hand, we can obtain that

$$\begin{aligned}&\Delta V(k)-\beta _1(x(k)^TPx(k)-1)\nonumber \\&-\beta _2(1-x(k)^TP_2x(k)) = \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T\nonumber \\&[(\tilde{A}+BD_i\Delta (k) FC)^TP(\tilde{A}+BD_i\Delta (k) FC)\nonumber \\&\qquad -(1+\beta _1)P+\beta _2P_2]x(k) \nonumber \\&+2x(k)^T(\tilde{A}+BD_i\Delta (k) FC)^TPf(x(k))\nonumber \\&\quad +f(x(k))^TPf(x(k)) \}+\beta _1-\beta _2. \end{aligned}$$
(14)

Let \(W=\varepsilon _1I-P\). Applying Lemma 1, we obtain

$$\begin{aligned}&2x(k)^T(\tilde{A}+BD_i\Delta (k) FC)^T Pf(x(k))\\&\quad +f(x(k))^TPf(x(k))\\&= 2x(k)^T(\tilde{A}+BD_i\Delta (k) FC)^TPf(x(k))\\&\quad -f(x(k))^TWf(x(k))+\varepsilon _1f(x(k))^Tf(x(k)) \\\le & {} x(k)^T(\tilde{A}+BD_i\Delta (k) FC)^TPW^{-1}\\&\quad P(\tilde{A}+BD_i\Delta (k) FC)x(k)+\varepsilon _1\eta ^2x(k)^Tx(k). \end{aligned}$$

Next, we shall show that

$$\begin{aligned} \Pi\triangleq & {} (\tilde{A}+BD_i\Delta (k) FC)^TP(\tilde{A}+BD_i\Delta (k) FC)\nonumber \\&-\,(1+\beta _1)P+\beta _2P_2 \nonumber \\&+(\tilde{A}+BD_i\Delta (k) FC)^T\nonumber \\&\quad PW^{-1}P(\tilde{A}+BD_i\Delta (k) FC)+\,\varepsilon _1\eta ^2 \nonumber \\= & {} (P\tilde{A}+PBD_i\Delta (k) FC)^T(P^{-1}+W^{-1})\nonumber \\&\quad (P\tilde{A}+PBD_i\Delta (k) FC)-(1+\beta _1)P\nonumber \\&\qquad +\beta _2P_2+\varepsilon _1\eta ^2. \end{aligned}$$
(15)

Now, set \(\Delta =\text{ diag }\{\delta _1,\delta _2,\ldots ,\delta _m\}\) with \(\delta _r(r=1,2,\ldots ,m)\) the defined as in (6). From (6), it is easy to show that \(\Delta (k)^T\Delta (k)\le \text{ diag }\{\delta _1^2,\delta _2^2,\ldots ,\delta _m^2\}=\Delta ^2\). Using Lemma 2, it can be verified that

$$\begin{aligned}&(P\tilde{A}+PBD_i\Delta (k) FC)^T\nonumber \\&\quad (P^{-1}+W^{-1})(P\tilde{A}+PBD_i\Delta (k) FC) \nonumber \\&\le \tilde{A}^TP[(P^{-1}+W^{-1})^{-1}-\varepsilon _2PBD_i\Delta \Delta ^TD_iB^TP]^{-1}\nonumber \\&\quad P\tilde{A}+\varepsilon _2^{-1}C^TF^TFC. \end{aligned}$$
(16)

Then, by the matrix inversion lemma, it follows that

$$\begin{aligned} (P^{-1}{+}W^{-1})^{-1}{=}P{-}P(W{+}P)^{-1}P{=}P-P\varepsilon _1^{-1}P. \end{aligned}$$

By using the Schur complement equivalence to (11), one has

$$\begin{aligned} \left[ \begin{array}{cccc} -(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ A^T+C^TF^TI_mD_iB^T+H^TD_i^-B^T &{} \ C^TF^T \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ BD_i\Delta \varepsilon _2\Delta D_i B^T-2M+MPM+\varepsilon _1^{-1}I &{} \ 0 \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _2I \end{array} \right] <0. \end{aligned}$$
(17)

Noting that \(-P^{-1}\le -2M+MPM\) (see [33]), the matrix inequality (17) implies

$$\begin{aligned} \left[ \begin{array}{ccc} -(1+\beta _1)P+\beta _2P_2+C^TF^T\varepsilon _2^{-1}FC &{} \ I &{} \ \tilde{A}^T \\ \star &{} \ -\alpha I &{} \ 0 \\ \star &{} \ \star &{} \ BD_i\Delta \varepsilon _2\Delta D_i B^T-P^{-1}+\varepsilon _1^{-1}I \end{array} \right] <0. \end{aligned}$$
(18)

Pre-multiplying and post-multiplying both sides of inequality (18) by diag\(\{I,I,P\}\), respectively, and then applying the Schur complement equivalence, we can obtain

$$\begin{aligned} \left[ \begin{array}{cc} \tilde{A}^TP(P-P\varepsilon _1^{-1}P-PBD_i\Delta \varepsilon _2\Delta ^TD_iB^TP)^{-1}P\tilde{A} -(1+\beta _1)P+\beta _2P_2+C^TF^T\varepsilon _2^{-1}FC &{} \ I \\ \star &{} \ -\alpha I \end{array} \right] <0. \end{aligned}$$
(19)

Setting \(\alpha ^{-1}=\varepsilon _1\eta ^2\) and using the Schur complement equivalence again, we have

$$\begin{aligned}&\tilde{A}^TP[(P^{-1}+W^{-1})^{-1}-PBD_i\Delta \varepsilon _2\Delta ^TD_iB^TP]^{-1}\nonumber \\&\quad \quad P\tilde{A}+\varepsilon _2^{-1}C^TF^TFC -(1+\beta _1)P+\beta _2P_2\nonumber \\&\quad \quad +\,\varepsilon _1\eta ^2<0. \end{aligned}$$
(20)

It is easy to show that (20) implies that \(\Pi <0\). Noting \(\beta _1-\beta _2<0\), this together with inequality \(\Pi <0\) implies \(V(k+1)-V(k)<0\) for x(k) such that \(x(k)^TPx(k)\le 1 \ \text{ and } \ x(k)^TP_2x(k)\ge 1\). This completes the proof. \(\square \)

Inspired in the work of [26], the corresponding domains and the maximum allowable Lipschitz constant \(\eta ^*\) can be determined by solving the following convex optimization problem

$$\begin{aligned}&\inf \limits _{P, P_2, F, H, \varepsilon _1, \varepsilon _2, \alpha } \lambda (\alpha {+}\varepsilon _1){+}(1{-}\lambda )(\text{ trace }(R)+\mu ) \nonumber \\&\text{ s. } \text{ t. }\; (a) (11), (12) \ \text{ and } \ (13), \nonumber \\&(b) \left[ \begin{array}{cc} P_2 &{} \ -I \\ \star &{} \ R \end{array} \right] \ge 0 \ \text{ and } \ \left[ \begin{array}{cc} \mu I &{} \ P \\ \star &{} \ P \end{array} \right] \ge 0, \end{aligned}$$
(21)

where \(0<\lambda < 1\). Then, the maximum allowable Lipschitz constant is \(\eta ^*=\frac{1}{\sqrt{\alpha \varepsilon _1}}\).

The static output feedback reduces to a state feedback, we have the controller

$$\begin{aligned} u(k)=q(Kx(k)). \end{aligned}$$
(22)

The result on a state feedback controller design for system (1) is provided in the following corollary.

Corollary 1

Given scalars \(\beta _1\) and \(\beta _2\) satisfying \(\beta _2>\beta _1>0\). Suppose there exist matrices \(Q>0, \bar{P}_2>0, \bar{K}, \bar{H}\) and scalars \(\varepsilon _1>0, \varepsilon _3>0, \alpha >0\) such that the following LMIs hold for \(i=1,2,\ldots ,2^m\):

$$\begin{aligned}&\left[ \begin{array}{ccccc} -(1+\beta _1)Q+\beta _2\bar{P}_2 &{} \ Q &{} \ QA^T+\bar{K}^TI_mD_iB^T+\bar{H}^TD_i^-B^T &{} \ \bar{K}^T &{} \ 0 \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ BD_i\Delta \varepsilon _3\Delta D_i B^T-Q &{} \ 0 &{} \ I \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _3I &{} \ 0 \\ \star &{} \ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _1I \end{array} \right] <0, \end{aligned}$$
(23)
$$\begin{aligned}&\left[ \begin{array}{cc} u_{0(p)}I &{} \ \bar{H}_{(p)} \\ \star &{} \ u_{0(p)}Q \end{array} \right] \ge 0, \ \ p=1,2,\ldots ,m, \end{aligned}$$
(24)
$$\begin{aligned}&\bar{P}_2-Q \ge 0. \end{aligned}$$
(25)

Then, all solutions of the closed-loop system are convergent to \(S_\infty =\{x(k)\in \mathbb {R}^n \mid x(k)^TQ^{-1}\bar{P}_2Q^{-1}x(k)\le 1\}\) for every initial condition from \(S=\{x(k)\in \mathbb {R}^n \mid x(k)^TQ^{-1}x(k)\le 1 \ \text{ and } \ x(k)^TQ^{-1}\bar{P}_2Q^{-1}x(k)\ge 1\}\). Moreover, a suitable state feedback controller can be chosen as \(u(k)=q(Kx(k))\) with \(K=\bar{K}Q^{-1}\).

Proof

Applying the controller \(u(k)=q(Kx(k))\) to the system (1) and then using Lemma 3, the resulting closed-loop system can be written as

$$\begin{aligned} x(k+1) {=} \sum \limits _{i=1}^{2^m}\eta _i\{(\tilde{A}{+}BD_i\Delta (k) K)x(k){+}f(x(k))\},\nonumber \\ \end{aligned}$$
(26)

where \(\tilde{A}=A+BD_iI_mK+BD^-_iH\). Now, define the Lyapunov functional cadidate as \(V(k)=x(k)^TPx(k)\), where \(P>0\). The forward difference in the functional V(k) along the system (26) is then given by

$$\begin{aligned} \Delta V(k)= & {} V(k+1)-V(k) \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{[(\tilde{A}{+}BD_i\Delta (k) K)x(k){+}f(x(k))]^TP \\&\times [(\tilde{A}+BD_i\Delta (k) K)x(k)+f(x(k))]\\&-x(k)^TPx(k)\}. \end{aligned}$$

Let \(Q=P^{-1}, P_2=Q^{-1}\bar{P}_2Q^{-1}, K=\bar{K}Q^{-1}, H=\bar{H}Q^{-1}, W=\varepsilon _1I-P, \Delta =\text{ diag }\{\delta _1,\delta _2,\ldots ,\delta _m\}\). Following the same argument as in the proof of Theorem 1, we assert that

$$\begin{aligned}&\Delta V(k){-}\beta _1(x(k)^TPx(k){-}1){-}\beta _2(1{-}x(k)^TP_2x(k)) \nonumber \\&= \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(\tilde{A}{+}BD_i\Delta (k) K)^TP\nonumber \\&\quad \times (\tilde{A}+\,BD_i\Delta (k) K)-(1+\beta _1)P+\beta _2P_2]x(k) \nonumber \\&\quad +\,2x(k)^T(\tilde{A}+BD_i\Delta (k) K)^TPf(x(k))\}\nonumber \\&\quad +\,f(x(k))^TPf(x(k))+\beta _1-\beta _2 \nonumber \\&\le \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(\tilde{A}+BD_i\Delta (k) K)^T(P+PW^{-1}P)\nonumber \\&\quad \times (\tilde{A}+BD_i\Delta (k) K) -(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]\nonumber \\&\quad \times x(k) \}+\beta _1-\beta _2 \nonumber \\&\le \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[\tilde{A}^TP((P^{-1}+W^{-1})^{-1}\nonumber \\&\quad -\varepsilon _3PBD_i\Delta \Delta D_iB^TP)^{-1}P\tilde{A}+\varepsilon _3^{-1}K^TK \nonumber \\&\quad -(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]x(k) \}+\beta _1-\beta _2 \nonumber \\&= \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T\Xi x(k)+\beta _1-\beta _2 \}, \end{aligned}$$
(27)

where \(\Xi =\tilde{A}^TP((P^{-1}+W^{-1})^{-1} -\varepsilon _3PBD_i\Delta \Delta D_iB^TP)^{-1}P\tilde{A}+\varepsilon _3^{-1}K^TK-(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2\). By using the Schur complement equivalence to (23), it follows that

$$\begin{aligned} \left[ \begin{array}{cccc} -(1+\beta _1)Q+\beta _2\bar{P}_2 &{} \ Q &{} \ QA^T+\bar{K}^TI_mD_iB^T+\bar{H}^TD_i^-B^T &{} \ \bar{K}^T \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ BD_i\Delta \varepsilon _3\Delta D_i B^T-Q+\varepsilon _1^{-1}I &{} \ 0 \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _3I \end{array} \right] <0. \end{aligned}$$
(28)

Pre-multiplying and post-multiplying both sides of inequality (28) by diag\(\{P,I,P,I\}\), we obtain

$$\begin{aligned} \left[ \begin{array}{ccc} \varepsilon _3^{-1}K^TK-(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ \tilde{A}^TP \\ \star &{} \ -\alpha I &{} \ 0 \\ \star &{} \ \star &{} \ PBD_i\Delta \varepsilon _3\Delta D_i B^TP-P+P\varepsilon _1^{-1}P \end{array} \right] <0. \end{aligned}$$
(29)

Next, setting \(\alpha ^{-1}=\varepsilon _1\eta ^2\), it follows from the matrix inequality (29) and the Schur complement equivalence that \(\Xi <0\). The rest of the proof is similar to Theorem 1 and thus omitted. This completes the proof of the corollary. \(\square \)

Moreover, it is desired to make \(S_\infty =\{x(k)\in \mathbb {R}^n \mid x(k)^TQ^{-1}\bar{P}_2Q^{-1}x(k)\le 1\}\) as small as possible and \(S=\{x(k)\in \mathbb {R}^n \mid x(k)^TQ^{-1}x(k)\le 1 \}\) as large as possible when designing state feedback controllers. Therefore, the corresponding domains and the maximum allowable Lipschitz constant \(\eta ^*\) can be determined by solving the following convex optimization problem

$$\begin{aligned}&\inf \limits _{Q, \bar{P}_2, \bar{K}, \bar{H}, \varepsilon _1, \varepsilon _3, \alpha } \lambda (\alpha +\varepsilon _1)+(1-\lambda )(\text{ trace }(R)+\mu ) \nonumber \\&\text{ s. } \text{ t. } \; (a) (23), (24) \ \text{ and } \ (25), \nonumber \\&\qquad \quad (b) \left[ \begin{array}{cc} \bar{P}_2 &{} \ -Q \\ \star &{} \ R \end{array} \right] \ge 0 \ \text{ and } \ \left[ \begin{array}{cc} \mu I &{} \ I \\ \star &{} \ Q \end{array} \right] \ge 0, \end{aligned}$$
(30)

where \(0<\lambda < 1\) and \(\eta ^*=\frac{1}{\sqrt{\alpha \varepsilon _1}}\).

Now, we are in a position to present the output quantization result for discrete-time nonlinear systems. In this sense, we obtain the sufficient condition for the solvability of Problem 2 in the following theorem.

Theorem 2

Consider the discrete-time nonlinear system (1) and (2). For given scalars \(\beta _2>\beta _1>0\) and a matrix \(M>0\), if there exist matrices \(P>0, P_2>0, F, H\) and scalars \(\varepsilon _1>0, \varepsilon _4>0, \alpha >0\) such that the following LMIs hold for \(i=1,2,\ldots ,2^m\):

$$\begin{aligned}&\left[ \begin{array}{ccccc} \varepsilon _4C^T\Delta \Delta C-(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ A^T+C^TI_rF^TD_iB^T+H^TD_i^-B^T &{} \ 0 &{} \ 0 \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ -2M+MPM &{} \ BD_iF &{} \ I \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _4I &{} \ 0 \\ \star &{} \ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _1I \end{array} \right] <0, \end{aligned}$$
(31)
$$\begin{aligned}&\left[ \begin{array}{cc} u_{0(p)}I &{} \ H_{(p)} \\ \star &{} \ u_{0(p)}P \end{array} \right] \ge 0, \ \ p=1,2,\ldots ,m, \end{aligned}$$
(32)
$$\begin{aligned}&P_2-P \ge 0. \end{aligned}$$
(33)

Then there exists a static output feedback controller in the form of (9) such that all solutions of the closed-loop system emanating from \(S=\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1 \ \text{ and } \ x(k)^TP_2x(k)\ge 1\}\) converge to \(S_\infty =\{x(k)\in \mathbb {R}^n \mid x(k)^TP_2x(k)\le 1\}\).

Proof

Applying the controller (9) to the system (1)–(2), we obtain the resulting closed-loop system as

$$\begin{aligned} x(k+1)= & {} \sum \limits _{i=1}^{2^m}\eta _i\{(\hat{A}+BD_iF\Delta (k) C)x(k)\nonumber \\&+f(x(k)) \}, \end{aligned}$$
(34)

where \(\hat{A}=A+BD_iFI_sC+BD^-_iH\). Let \(\Delta =\text{ diag }\{\delta _1,\delta _2,\ldots ,\delta _s\}\) and \(W=\varepsilon _1I-P\). Now, define the following Lyapunov function candidate for the system in (34): \(V(k)=x(k)^TPx(k)\). By Lemma 1 and Lemma 2, it can be shown that

$$\begin{aligned}&V(k+1)-V(k)-\beta _1(x(k)^TPx(k)-1)\nonumber \\&-\beta _2(1-x(k)^TP_2x(k)) \nonumber \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(\hat{A}+BD_iF\Delta (k) C)^T \nonumber \\&\times P(\hat{A}+BD_iF\Delta (k) C)-(1+\beta _1)P+\beta _2P_2]x(k) \nonumber \\&+\,2x(k)^T(\hat{A}+BD_iF\Delta (k) C)^TPf(x(k))\nonumber \\&+\,f(x(k))^TPf(x(k)) \}+\beta _1-\beta _2 \nonumber \\\le & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(P\hat{A}+PBD_iF\Delta (k) C)^T\nonumber \\&\times (P^{-1}+W^{-1})(P\hat{A}+PBD_iF\Delta (k) C) \nonumber \\&-(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]x(k) \}+\beta _1-\beta _2 \nonumber \\\le & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[\hat{A}^TP((P^{-1}+W^{-1})^{-1}\nonumber \\&-\varepsilon _4^{-1}PBD_iFF^T D_iB^TP)^{-1}P\hat{A}+\varepsilon _4C^T\Delta \Delta C \nonumber \\&-(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]x(k) \}+\beta _1-\beta _2 \nonumber \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[\hat{A}^TP(P-P\varepsilon _1^{-1}P\nonumber \\&-\varepsilon _4^{-1}PBD_iFF^T D_iB^TP)^{-1}P\hat{A}+\varepsilon _4C^T\Delta \Delta C \nonumber \\&-(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]x(k) \}+\beta _1-\beta _2 \nonumber \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T\Pi x(k)+\beta _1-\beta _2 \}, \end{aligned}$$
(35)

where \(\Pi =\hat{A}^TP(P-P\varepsilon _1^{-1}P -\varepsilon _4^{-1}PBD_iFF^T D_iB^TP)^{-1}P\hat{A}+\varepsilon _4C^T\Delta \Delta C -(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2\). Noting \(-P^{-1}\le -2M+MPM\) and using the Schur complement equivalence to (31), it is easy to see that

$$\begin{aligned} \left[ \begin{array}{cccc} \varepsilon _4C^T\Delta \Delta C-(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ \hat{A}^T &{} \ 0 \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ -P^{-1}+\varepsilon _1^{-1}I &{} \ BD_iF \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _4I \end{array} \right] <0. \end{aligned}$$
(36)

On the other hand, pre-multiplying and post-multiplying (36) by diag\(\{I,I,P,I\}\) result in

$$\begin{aligned} \left[ \begin{array}{ccc} \varepsilon _4C^T\Delta \Delta C-(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ \hat{A}^TP \\ \star &{} \ -\alpha I &{} \ 0 \\ \star &{} \ \star &{} \ -P+P\varepsilon _1^{-1}P+\varepsilon _4^{-1}PBD_iFF^TD_iB^TP \end{array} \right] <0, \end{aligned}$$
(37)

which, by the Schur complement equivalence, implies that \(\Pi <0\) with \(\alpha ^{-1}=\varepsilon _1\eta ^2\). This together with \(\beta _1-\beta _2<0\) implies that for all x(k) such that \(x(k)^TPx(k)\le 1 \ \text{ and } \ x(k)^TP_2x(k)\ge 1\), we have \(V(k+1)-V(k)<0\). Moreover, by (32) and [25], it can be seen that \(\varepsilon (P)\subset \mathscr {L}(H,u_0)\). Then taking into account (33), it follows that \(\varepsilon (P)\) contains \(\varepsilon (P_2)\). This completes the proof. \(\square \)

Similar to (21), we can obtain the corresponding domains and the maximum allowable Lipschitz constant \(\eta ^*\) by solving an optimization problem

$$\begin{aligned}&\inf \limits _{P, P_2, F, H, \varepsilon _1, \varepsilon _4, \alpha } \lambda (\alpha +\varepsilon _1)+(1-\lambda )(\text{ trace }(R)+\mu ) \nonumber \\&\text{ s. } \text{ t. } \; (a) (31), (32) \ \text{ and } \ (33), \nonumber \\&\qquad \quad (b) \left[ \begin{array}{cc} P_2 &{} \ -I \\ \star &{} \ R \end{array} \right] \ge 0 \ \text{ and } \ \left[ \begin{array}{cc} \mu I &{} \ P \\ \star &{} \ P \end{array} \right] \ge 0, \end{aligned}$$
(38)

where \(0<\lambda < 1\). The maximum allowable Lipschitz constant is \(\eta ^*=\frac{1}{\sqrt{\alpha \varepsilon _1}}\).

The results in Theorem 2 are now employed to design a state feedback control law for the system (1). We represent a state feedback controller in the following form:

$$\begin{aligned} u(k)=Kq(x(k)). \end{aligned}$$
(39)

Then, from Theorem 2, we have the following quantized state feedback controller design result for the discrete-time nonlinear system (1).

Corollary 2

Given scalars \(\beta _1\) and \(\beta _2\) satisfying \(\beta _2>\beta _1>0\). Suppose there exist matrices \(P>0, P_2>0, K, H\) and scalars \(\varepsilon _1>0, \varepsilon _5>0, \alpha >0\) such that the following LMIs hold for \(i=1,2,\ldots ,2^m\):

$$\begin{aligned}&\left[ \begin{array}{ccccc} \varepsilon _5\Delta \Delta -(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ A^T+K^TD_iB^T+H^TD_i^-B^T &{} \ 0 &{} \ 0 \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ -2M+MPM &{} \ BD_iK &{} \ I \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _5I &{} \ 0 \\ \star &{} \ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _1I \end{array} \right] <0, \end{aligned}$$
(40)
$$\begin{aligned}&\left[ \begin{array}{cc} u_{0(p)}I &{} \ H_{(p)} \\ \star &{} \ u_{0(p)}P \end{array} \right] \ge 0, \ \ p=1,2,\ldots ,m, \end{aligned}$$
(41)
$$\begin{aligned}&P_2-P \ge 0. \end{aligned}$$
(42)

Then, the closed-loop system obtained by applying the quantized state feedback controller in (39) to system (1) is convergent to \(S_\infty =\{x(k)\in \mathbb {R}^n \mid x(k)^TP_2x(k)\le 1\}\) for all initial condition from \(S=\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1 \ \text{ and } \ x(k)^TP_2x(k)\ge 1\}\).

Proof

Applying the controller (39) to the system (1), we obtain the following closed-loop system

$$\begin{aligned} x(k+1)= & {} \sum \limits _{i=1}^{2^m}\eta _i\{(\hat{A}+BD_iK\Delta (k))x(k)\nonumber \\&\quad +f(x(k)) \}, \end{aligned}$$
(43)

where \(\hat{A}=A+BD_iKI_n+BD^-_iH=A+BD_iK+BD^-_iH\). Firstly, we set \(\Delta =\text{ diag }\{\delta _1,\delta _2,\ldots ,\delta _n\}\) and \(W=\varepsilon _1I-P\). Next, we define the Lyapunov function candidate as \(V(k)=x(k)^TPx(k)\). Taking the difference between the Lyapunov function candidates for two consecutive time instants yields

$$\begin{aligned} \Delta V(k)= & {} V(k+1)-V(k) \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(\hat{A}+BD_iK\Delta (k) )^T\\&\times P(\hat{A}+BD_iK\Delta (k) )-P]x(k) \\&+ 2x(k)^T(\hat{A}+BD_iK\Delta (k) )^TPf(x(k))\\&+f(x(k))^TPf(x(k)) \}. \end{aligned}$$

Then, similar to the proof of Theorem 2, we can obtain

$$\begin{aligned}&\Delta V(k)-\beta _1(x(k)^TPx(k)-1)-\beta _2(1-x(k)^TP_2x(k)) \nonumber \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(\hat{A}+BD_iK\Delta (k))^T\nonumber \\&\times P(\hat{A}+BD_iK\Delta (k))-(1+\beta _1)P+\beta _2P_2]x(k) \nonumber \\&+2x(k)^T(\hat{A}+BD_iK\Delta (k))^TPf(x(k))+f(x(k))^T\nonumber \\&\times Pf(x(k)) \}+\beta _1-\beta _2 \nonumber \\\le & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[(P\hat{A}+PBD_iK\Delta (k))^T(P^{-1}+W^{-1})\nonumber \\&\times (P\hat{A}+PBD_iK\Delta (k)) \nonumber \\&-(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]x(k) \}+\beta _1-\beta _2 \nonumber \\\le & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T[\hat{A}^TP((P^{-1}+W^{-1})^{-1}\nonumber \\&-\varepsilon _5^{-1}PBD_iKK^T D_iB^TP)^{-1}P\hat{A}+\varepsilon _5\Delta \Delta \nonumber \\&-(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2]x(k) \}+\beta _1-\beta _2 \nonumber \\= & {} \sum \limits _{i=1}^{2^m}\eta _i\{x(k)^T\Theta x(k)+\beta _1-\beta _2 \}, \end{aligned}$$
(44)

where \(\Theta =\hat{A}^TP((P^{-1}+W^{-1})^{-1}-\varepsilon _5^{-1}PBD_iKK^T\) \( D_iB^TP)^{-1}P\hat{A} +\varepsilon _5\Delta \Delta -(1+\beta _1)P+\beta _2P_2+\varepsilon _1\eta ^2\). Then, by the Schur complement equivalence it follows from (40) that

$$\begin{aligned} \left[ \begin{array}{cccc} \varepsilon _5\Delta \Delta -(1+\beta _1)P+\beta _2P_2 &{} \ I &{} \ \hat{A}^TP &{} \ 0 \\ \star &{} \ -\alpha I &{} \ 0 &{} \ 0 \\ \star &{} \ \star &{} \ P\varepsilon _1^{-1}P-P &{} \ PBD_iK \\ \star &{} \ \star &{} \ \star &{} \ -\varepsilon _5I \end{array} \right] <0,\nonumber \\ \end{aligned}$$
(45)

Noting \((P^{-1}+W^{-1})^{-1}=P-P\varepsilon _1^{-1}P\), the matrix inequality (45) implies that \(\Theta <0\) with \(\alpha ^{-1}=\varepsilon _1\eta ^2\). The rest of the proof can be carried out by following a similar line as in the proof of Theorem 2 and thus is omitted. This completes the proof. \(\square \)

Similar to (21), the corresponding domains and the maximum allowable Lipschitz constant \(\eta ^*\) can be obtained by solving the following optimization problem

$$\begin{aligned}&\inf \limits _{P, P_2, K, H, \varepsilon _1, \varepsilon _5, \alpha } \lambda (\alpha +\varepsilon _1)+(1-\lambda )(\text{ trace }(R)+\mu ) \nonumber \\&\text{ s. } \text{ t. } \; (a) (40), (41) \ \text{ and } \ (42), \nonumber \\&\qquad \quad (b) \left[ \begin{array}{cc} P_2 &{} \ -I \\ \star &{} \ R \end{array} \right] \ge 0 \ \text{ and } \ \left[ \begin{array}{cc} \mu I &{} \ P \\ \star &{} \ P \end{array} \right] \ge 0, \end{aligned}$$
(46)

where \(0<\lambda < 1\). The maximum allowable Lipschitz constant is \(\eta ^*=\frac{1}{\sqrt{\alpha \varepsilon _1}}\).

4 Simulation examples

In this section, we present some examples to demonstrate the applicability and effectiveness of the proposed method. Example 1 and Example 2 are provided to check the static logarithmic quantizer of one dimension, while Example 3 and Example 4 are given to show the static logarithmic quantizer of two dimensions.

Example 1

Consider the following discrete-time nonlinear system with parameters as

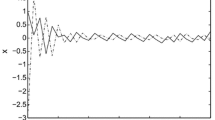
$$\begin{aligned} A= & {} \left[ \begin{array}{cc} -0.8 &{} 0.9 \\ 0.2 &{} 1.3 \end{array} \right] ,\quad B=\left[ \begin{array}{c} 0.5 \\ 2 \end{array} \right] , \quad C=\left[ \begin{array}{cc} 1.2 &{} 1 \\ 0.5 &{} 0 \end{array} \right] . \end{aligned}$$

The tuning parameters are \(\beta _1=10^{-3}\) and \(\beta _2=0.1\). Moreover, we consider that the saturation level is fixed as \(u_0=5\). In this example, we choose \(M=(A^TA+I)^{-1}, \rho _1=0.6, \lambda =0.3\) and \(\mathcal {L}_1^{(0)}=30\). Solving the convex optimization problem (21) by the standard convex optimization numerical software, we can obtain the maximum allowable Lipschitz constant \(\eta ^*=0.09\) and the controller gain \(F=\left[ \begin{array}{cc} -0.5930 \&1.0545 \end{array} \right] \). The nonlinear function is selected as \(f(x(k))=\left[ \begin{array}{c} 0.08\text{ sin }(e^{-x_2(k)})+0.06\text{ cos }(x_1(k)) \\ 0.09\text{ sin }(e^{-x_1(k)}) \end{array} \right] \). The state trajectories of the closed-loop system are shown in Fig. 1. As shown in Fig. 1, the outer ellipsoid is \(\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1 \}\) with \(P=\left[ \begin{array}{cc} 1.6158 \ &{} -0.8927 \\ -0.8927 \ &{} 1.4416 \end{array} \right] \) and the inner ellipsoid is \(\{x(k)\in \mathbb {R}^n \mid x(k)^TP_2x(k)\le 1\}\) with \(P_2=\left[ \begin{array}{cc} 1.6273 \ &{} -0.6880 \\ -0.6880 \ &{} 5.0837 \end{array} \right] \). It is clearly observed from Fig. 1 that some trajectories of plant states emanating from the outer ellipsoid converge to the inner ellipsoid. Figure 2 shows the input trajectory of the closed-loop system for initial condition given by \(x(0)=\left[ \begin{array}{c} -0.2 \\ -0.94 \end{array} \right] \).

Fig. 1
figure 1

State trajectories (Example 1)

Full size image
Fig. 2
figure 2

Trajectory of input (Example 1)

Full size image

Example 2

Consider the system described in Example 1. Furthermore, the saturation level and the parameters \(\beta _1, \beta _2, \rho _1, \mathcal {L}_1^{(0)}\) are the same as those presented in Example 1. Then, by solving the optimization problem (30) with \(\lambda =0.1\), we can obtain \(\eta ^*=0.13\) and the state feedback gain \(K=\left[ \begin{array}{cc} -0.3609 \&-0.4735 \end{array} \right] \). The nonlinear function is chosen as \(f(x(k))=\left[ \begin{array}{c} 0.1\text{ sin }(e^{-x_2(k)})+0.125\text{ cos }(x_1(k)) \\ 0.13\text{ sin }(e^{-x_1(k)}) \end{array} \right] \). Figure 3 shows the state trajectories of the closed-loop system and two ellipsoids. For this example, the outer ellipsoid is \(\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1 \}\) with \(P=\left[ \begin{array}{cc} 1.0201 \ &{} -0.5317 \\ -0.5317 \ &{} 0.7665 \end{array} \right] \) and the inner ellipsoid is \(\{x(k)\in \mathbb {R}^n \mid x(k)^TP_2x(k)\le 1\}\) with \(P_2=\left[ \begin{array}{cc} 1.3669 \ &{} -0.5430 \\ -0.5430 \ &{} 2.7315 \end{array} \right] \). The control input of the closed-loop system for initial condition given by \(x(0)=\left[ \begin{array}{c} 1.2 \\ 1.12 \end{array} \right] \) is recorded in Fig. 4.

Fig. 3
figure 3

State trajectories (Example 2)

Full size image
Fig. 4
figure 4

Trajectory of input (Example 2)

Full size image

Example 3

Consider the discrete-time nonlinear system (1)–(2) with parameters as follows:

$$\begin{aligned} A= & {} \left[ \begin{array}{cc} -0.3 &{} 0.1 \\ 0.2 &{} 1.2 \end{array} \right] ,\quad B=\left[ \begin{array}{cc} 0.5 &{} 0.2 \\ 1.2 &{} 0.6 \end{array} \right] , \quad C=\left[ \begin{array}{cc} 0.2 &{} 1 \\ 0.5 &{} 2.5 \end{array} \right] . \end{aligned}$$

Now, we choose \(\beta _1=10^{-2}\) and \(\beta =0.1\), respectively. The saturation level is selected as \(u_0=5\). In this case, we choose \(M=10(A^TA+I)^{-1}, \rho _1=0.2, \rho _2=0.5, \lambda =0.2\) and \(\mathcal {L}_1^{(0)}=\mathcal {L}_2^{(0)}=30\). Then, solving the convex optimization problem (38), we can obtain the maximum allowable Lipschitz constant \(\eta ^*=0.18\) and the controller gain \(F=\left[ \begin{array}{cc} -0.1452 \ &{} 0.0774 \\ 0.0774 \ &{} -0.7221 \end{array} \right] \). The nonlinear function is supposed to be \(f(x(k))=\left[ \begin{array}{c} 0.15\text{ sin }(e^{-x_2(k)}) \\ 0.17\text{ cos }(x_1(k))+0.12\text{ sin }(e^{-x_1(k)}) \end{array} \right] \). The state trajectories of the closed-loop system with the controller (9) are shown in Fig. 5, and the control input of the closed-loop system for initial condition given by \(x(0)=\left[ \begin{array}{c} 1.5 \\ -1.5 \end{array} \right] \) is shown in Fig. 6. As shown in these figures (Figures 1,3,5), in the quantized feedback controller, the states cannot converge to the origin; however, they remain around a certain area. Furthermore, we can obtain that the outer ellipsoid is \(\{x(k)\in \mathbb {R}^n \mid x(k)^TPx(k)\le 1 \}\) with \(P=\left[ \begin{array}{cc} 0.1707 \ &{} 0.0224 \\ 0.0224 \ &{} 0.3104 \end{array} \right] \) and the inner ellipsoid is \(\{x(k)\in \mathbb {R}^n \mid x(k)^TP_2x(k)\le 1\}\) with \(P_2=\left[ \begin{array}{cc} 0.5374 \ &{} -0.0410 \\ -0.0410 \ &{} 0.9256 \end{array} \right] \).

Fig. 5
figure 5

State trajectories (Example 3)

Full size image
Fig. 6
figure 6

Trajectory of input (Example 3)

Full size image

Example 4

Consider the system described in Example 3. In this case, the parameters \(u_0, \beta _1, \beta _2, \rho _1, \rho _2, \mathcal {L}_1^{(0)}, \mathcal {L}_2^{(0)}\) are the same as those presented in Example 3. Similarly, by solving the optimization problem (46) with \(\lambda =0.1\) and \(M=(A^TA+I)^{-1}\), we can obtain the following solutions \(\eta ^*=0.13, K=\left[ \begin{array}{cc} 0.3337 \ &{} -0.7061 \\ -0.7061 \ &{} -0.0879 \end{array} \right] , P=\left[ \begin{array}{cc} 1.6642 \ &{} 0.1904 \\ 0.1904 \ &{} 1.2179 \end{array} \right] \) and \(P_2=\left[ \begin{array}{cc} 1.9512 \ &{} -0.3058 \\ -0.3058 \ &{} 2.7214 \end{array} \right] \). The nonlinear function is fixed as \(f(x(k))=\left[ \begin{array}{c} 0.13\text{ sin }(e^{-x_2(k)}) \\ 0.13\text{ cos }(x_1(k))+0.12\text{ sin }(e^{-x_1(k)}) \end{array} \right] \).

Figure 7 illustrates the trajectory of the states, and Fig. 8 shows the control input of the closed-loop system for initial condition given by \(x(0)=\left[ \begin{array}{c} 0.7 \\ -0.5 \end{array} \right] \).

Fig. 7
figure 7

State trajectories (Example 4)

Full size image
Fig. 8
figure 8

Trajectory of input (Example 4)

Full size image

5 Conclusions

The problems of quantized output feedback stabilization for nonlinear discrete-time systems with saturating actuator have been studied. Two cases of quantized control laws are considered. The first case is the input quantization, and the other is the output quantization. Attention has been paid to the design of static output feedback controllers such that all the trajectories of the closed-loop system will converge to a minimal ellipsoid for every initial condition emanating from a large admissible domain. Finally, some examples have shown the effectiveness of the proposed approach.