${\mathcal {H}}_\infty$ control of continuous-time uncertain linear systems with quantized-input saturation and external disturbances

Abstract

This paper introduces an ${\mathcal {H}}_\infty$ state- feedback controller for uncertain linear systems with quantized-input saturation and external disturbances. The proposed controller comprises two parts: a linear control part to achieve an ${\mathcal {H}}_\infty$ performance against model uncertainties and the mismatched part of the disturbances and a nonlinear control part to eliminate the effect of input quantization and the matched part of the disturbances, which provides the better disturbance attenuation performance than a controller that deals with a unified disturbance regardless of the presence of matched and mismatched parts. Simulation results confirm the effectiveness of the proposed controller.

1 Introduction

Quantization caused by analog-to-digital and digital-to-analog converters in sensors and actuators [17, 18, 25] or by encoders and decoders in network-based control systems (NCSs) [15, 20, 23, 28, 35] is a peculiar feature of many systems. Since quantization has adverse effects on the general performance of systems, such as a transient response, a steady-state response, and the stability of the system, many studies on this subject have received considerable attention. Early studies on quantization were conducted by [9] and [16], which investigated the effect of quantization in a sampled data system and least mean-squares state estimation in the presence of quantized outputs, respectively. Recently, many researches have considered the stabilization problem of quantized feedback systems. There are mainly two approaches in the existing literatures on this subject. The first approach handles the dynamic quantizers [2, 5, 6, 19, 23, 34]. In order to improve the steady-state performance, this approach varies the quantization levels dynamically. The second approach considers the static quantizers such as uniform and logarithmic quantizers [7, 8, 10–13, 22, 24, 27–33]. The second approach quantizes data using the static quantization levels so that the static quantizers have relatively simple structures compared with the dynamic quantizers.

To the best of the authors’ knowledge, in the framework of the second approach, intensive studies on ${\mathcal {H}}_\infty$ control of uncertain systems with quantized-input saturation and external disturbances have not been carried out thus far. Although [5, 6] handled the problems of dynamic output-feedback and state-feedback ${\mathcal {H}}_\infty$ control for quantized discrete-time linear time-invariant (LTI) systems, they employed the dynamic quantizers proposed by [2, 19]. Peng and Tian [23] addressed the problem of ${\mathcal {H}}_\infty$ controller design for linear systems over digital communication networks, and they also used the dynamic quantizers of [2, 19]. Further, [29] proposed an ${\mathcal {H}}_2$ state-feedback controller for uncertain linear systems with input quantization and matched disturbances; however, it did not consider the saturation level of the uniform quantizers.

This paper introduces an ${\mathcal {H}}_\infty$ state-feedback controller for uncertain linear systems with quantized-input saturation and external disturbances. The proposed ${\mathcal {H}}_\infty$ controller comprises linear and nonlinear parts: a linear control part to achieve an ${\mathcal {H}}_\infty$ performance against model uncertainties and the mismatched part of the disturbances and a nonlinear control part to eliminate the effect of input quantization and the matched part of the disturbances. In other words, each component of the nonlinear control part is designed as an integer multiple of the quantization level, which enables us to remove the energy in the sense of Lyapunov caused by quantization errors and the matched part of the disturbances. The main contributions of this paper are (1) the design of a state-feedback controller to achieve asymptotic stability and ${\mathcal {H}}_\infty$ performance for uncertain linear systems with quantized-input saturation and external disturbances, where such systems with the uniform quantizer have not been introduced thus far and (2) the separation of external disturbances into the matched and the mismatched part of the disturbances using the projection matrix, where this method improves an ${\mathcal {H}}_\infty$ performance.

This paper is organized as follows. Section 2 provides a system description and some preliminary results. Section 3 introduces an $\mathcal {H}_\infty$ state-feedback controller for uncertain linear systems with quantized-input saturation and external disturbances. Section 4 presents some simulation results for validating the proposed controller. Finally, Sect. 5 concludes the paper with a summarization.

Notation: The notations in this paper are fairly standard. For $x \in \mathbf {R}^n,\, x^T$ means the transpose of $x$ and $x_i$ denotes the $i$th element of $x$. The notation $e_i$ means a unit vector with a single nonzero entry at the $i$th position, i.e., $e_i \mathop {=}\limits ^{\triangle }[0\,\cdots \,\underbrace{1}_{i{th}}\,\cdots \,0]^T$. The notation $X \ge Y$ or $X > Y$, where $X$ and $Y$ are symmetric matrices, denotes that $X-Y$ is positive semi-definite or positive definite, respectively. $I$ is an identity matrix with appropriate dimensions. We use $||x||_p$ to indicate the $p$-norm of $x$, i.e., $||x||_p \mathop {=}\limits ^{\triangle }(|x_1|^p + \cdots +|x_n|^p)^{\frac{1}{p}},\,p\ge 1$. When $p = \infty ,\, ||x||_{\infty } \mathop {=}\limits ^{\triangle }\max _{1\le i \le n}|x_i|$. For $X \in \mathbf {R}^{m \times n},\, ||X||_{p}$ denotes the matrix $p$-norm, i.e., $||X||_{p} \mathop {=}\limits ^{\triangle }\sup _{x \ne 0} \frac{||Xx||_{p}}{||x||_{p}}$. The space of square-integrable functions is denoted by $\mathcal {L}_2$, that is, for any $x \in \mathcal {L}_2$,

$$\begin{aligned} ||x||_2 \mathop {=}\limits ^{\triangle }\left( \int _0^\infty x^T(t)x(t)dt \right) ^{\!\!1/2} < \infty . \end{aligned}$$

Furthermore, $\mathbf {Sym}(X)=X+X^T$ stands for any matrix $X$.

2 System description and preliminaries

Consider the following continuous-time uncertain linear system with quantized-input saturation and external disturbances:

$$\begin{aligned} \dot{x}(t)&= (A+{\Delta } A(t))x(t)+B(I+{\Delta } B(t))sat( Q(u(t)) ) \nonumber \\&+\,Dw(t), \end{aligned}$$

(1)

$$\begin{aligned} z(t)&= Cx(t), \end{aligned}$$

(2)

where $x(t) \in \mathbf {R}^n$, $u(t) \in \mathbf {R}^m$, $w(t)\in \mathbf {R}^m$, and $z(t)\in \mathbf {R}^q$ are the state, the control input, the external disturbance, and the controlled output, respectively. ${\Delta } A(t),\, {\Delta } B(t),\, Q(\cdot )$, and $sat(\cdot )$ are the system characteristic matrix uncertainty, input matrix uncertainty, quantization operator, and saturation operator, respectively. System (1 2) yields to

$$\begin{aligned} \dot{x}(t)&= (A+{\Delta } A(t))x(t)+ B \left\{ (I+\right. \nonumber \\&\quad \left. {\Delta } B(t))sat(Q(u(t))) + \tilde{B}w(t) \right\} +\bar{B}w(t),\!\! \end{aligned}$$

(3)

where $\tilde{B} \!=\! (B^TB)^{-1}B^TD$ and $\bar{B} = (I - B(B^T\!B)^{-1}\!B^T) D$. That is, the external disturbances, $Dw(t)$, can be separated into the matched part, $B(B^TB)^{-1}B^TDw(t)$, and the mismatched part, $(I - B(B^TB)^{-1}B^T)Dw(t)$, using the projection matrix. Here, we define $\Vert \tilde{B}\Vert _\infty \triangleq \varphi$. For ${\Delta } A(t),\, {\Delta } B(t),\, w(t), Q(\cdot )$, and $sat(\cdot )$, it is assumed that the following assumptions are valid:

• (${\mathcal {A}}1$) Each component of the disturbance $w(\cdot ) \in {\mathcal {L}}_2$ is bounded by $\varepsilon _w (> 0)$, i.e.,

  $$\begin{aligned} \Vert w(t)\Vert _{\infty } \le \varepsilon _w. \end{aligned}$$

  (4)

• (${\mathcal {A}}2$) The operator $Q(\cdot )$ is defined by a function $round(\cdot )$ that rounds toward the nearest integer, i.e.,

  $$\begin{aligned} Q(u(t)) \mathop {=}\limits ^{\triangle }\varepsilon _u \, round\;( u(t)/\varepsilon _u), \end{aligned}$$

  (5)

  where $\varepsilon _u (> 0)$ is called a quantizing level and $Q(\cdot )$ is the uniform quantizer with the fixed $\varepsilon _u$. We note that the quantization error $\nabla u(t)$ is defined as $\nabla u(t)$ $\triangleq Q(u(t)) - u(t)$. Based on the condition (5) and the definition of $\nabla u(t)$, each component of $\nabla u(t)$ at time $t$ is bounded by the half of the quantizing level $\varepsilon _u$, i.e.,

  $$\begin{aligned} \Vert \nabla u(t)\Vert _{\infty } \le \varepsilon _u/2. \end{aligned}$$

  (6)

• (${\mathcal {A}}3$) For a saturation level $\mu ~(>\varepsilon _w)$, the saturation operator $sat(\cdot )$ is defined as

  $$\begin{aligned}{}[sat(\sigma )]_i \mathop {=}\limits ^{\triangle }\left\{ \begin{array}{lll} \sigma _i &{}\quad \text{ if } &{}\quad |\sigma _i| < \mu \\ \mu &{} \quad \text{ if } &{}\quad \sigma _i \ge \mu \\ -\mu &{}\quad \text{ if } &{}\quad \sigma _i \le -\mu \end{array} \right. . \end{aligned}$$

  (7)

  where $[sat(\sigma )]_i$ denotes the $i$th element of $sat(\sigma )$.

• (${\mathcal {A}}4$) ${\Delta } A(t)$ and ${\Delta } B(t)$ are unknown time-varying uncertainties satisfying

  $$\begin{aligned}&{\Delta } A(t) = F_1 {\Delta }_1(t) G_1,\;{\Delta }_1(t){\Delta }^T_1(t) \le I,\end{aligned}$$

  (8)
  $$\begin{aligned}&{\Delta } B(t) = F_2 {\Delta }_2(t) G_2,\nonumber \\&{\Delta }_2(t){\Delta }^T_2(t)\le I,\; \Vert {\Delta } B(t) \Vert _{\infty } \le \psi < 1, \end{aligned}$$

  (9)

  where $F_1, G_1, F_2$, and $G_2$ are known real constant matrices with appropriate dimensions, ${\Delta }_1(t)$ and ${\Delta }_2(t)$ are unknown matrix functions, and $\psi$ is a known nonnegative constant.

We introduce the following lemmas that are required to prove a theorem in the next section.

Lemma 1

(Hölder’s inequality) For $\alpha , \beta \in \mathbf {R}^n, p \ge 1$, and $q \ge 1$, the following inequality holds:

$$\begin{aligned} |\alpha ^T \beta | \le ||\alpha ||_p||\beta ||_q, \quad p^{-1} + q^{-1} = 1. \end{aligned}$$

(10)

Lemma 2

([3, 26]) Assume that X and Y are matrices with appropriate dimensions. For any scalar $\eta >0$, if a matrix ${\Delta }$ with appropriate dimensions satisfies ${\Delta }{\Delta }^T \le I$, then the following inequality holds:

$$\begin{aligned} X {\Delta } Y + Y^T{\Delta }^T X^T \le \eta X X^T + \eta ^{-1}Y^T Y. \end{aligned}$$

(11)

Lemma 3

([4, 14]) Let $u, v\,\in \,\mathbf {R}^m$,

$$\begin{aligned} u = \begin{bmatrix} u_1&u_2&\ldots&u_m \end{bmatrix}^T,\, v = \begin{bmatrix} v_1&v_2&\ldots&v_m \end{bmatrix}^T. \end{aligned}$$

Suppose that $|e_i^Tv| \le \mu$ for all $i \in [1,m]$ and a real number $\mu >0$, then

$$\begin{aligned} sat(u) \in \mathbf {Co}\left\{ \begin{array}{l|l} E_ju + E^-_jv&j \in [1,2^m] \end{array}\right\} , \end{aligned}$$

(12)

where $\mathbf {Co}$ is a convex hull, $E_j$ denotes a diagonal matrix whose diagonal elements are either 1 or 0, and $E_j^- \mathop {=}\limits ^{\triangle }I-E_j$. Further, for given two matrices $F,H \in \mathbf {R}^{m \times n}$ and the relations that $\sum _{j = 1}^{2^m} \xi _j = 1$ and $\xi _j \ge 0$, suppose that $|e_i^T Hx(t)| \le \mu$ for all $i \in [1,m]$, then we have

$$\begin{aligned} sat(Fx) = \sum _{j = 1}^{2^m} \xi _j \{ E_jFx + E^-_jHx \}. \end{aligned}$$

(13)

Lemma 4

(Set invariance condition) For a given positive definite matrix ${\varOmega }$, let us define an ellipsoid $\mathcal {E}({\varOmega })$ as

$$\begin{aligned} \mathcal {E}({\varOmega }) \triangleq \{ x(t) \in \mathcal {R}^n\,|\,x^T(t){\varOmega } x(t) \le 1 \}. \end{aligned}$$

(14)

For system (3), it is assumed that $V(x(t)){=}x^T(t)P x(t)$ where $P$ is a positive definite matrix. For a given ellipsoid $\mathcal {E}(P)$ and a given state-feedback gain matrix $K$, if there exist a matrix $H \in {\mathcal {R}}^{m \times n}$ and a positive scalar $\lambda$ such that

$$\begin{aligned}&\dot{V}(x(t)) < \lambda (\,1 - x^T(t)P x(t)\,), \end{aligned}$$

(15)

$$\begin{aligned}&|e_i^T Hx(t)| \le \mu , \quad \forall x(t) \in \mathcal {E}(P), \quad \forall i \in [1,m] \end{aligned}$$

(16)

subject to (4), then $\mathcal {E}(P)$ is a (strictly) invariant set for the closed-loop system under the state-feedback controller.

Proof

In (15 16), it is obvious that $\dot{V}(x(t)) < 0$ for $x(t) \notin \mathcal {E}(P )$, i.e., $x^T(t)P x(t) > 1$. Further, on the boundary of $\mathcal {E}(P)$, i.e., $x^T(t)Px(t)=1$, the relation $\dot{V}(x(t)) < 0$ is also satisfied. This implies that the ellipsoid $\mathcal {E}(P)$ is a (strictly) invariant ellipsoid. $\square$

3 Main results

Firstly, consider the system (3) with ${\Delta } A(t) = 0$ and ${\Delta } B(t) = 0$, i.e.,

$$\begin{aligned} \dot{x}(t)&= Ax(t)+B \{ sat( Q(u(t)) ) + \tilde{B}w(t) \} + \bar{B}w(t). \end{aligned}$$

(17)

The following theorem can be obtained for the system (17).

Theorem 1

For all $x(t) \in \mathcal {E}(\bar{P}^{-1}),\, i \in [1, m],\, j \in [1,2^m]$, and a given positive scalar $\lambda$, the proposed system (17) with assumptions $({\mathcal {A}}1),\, ({\mathcal {A}}2)$, and (${\mathcal {A}}3$) is locally asymptotically stable with the $\mathcal {H}_\infty$ performance $\gamma$ if there exist a symmetric positive definite matrix $\bar{P}$, matrices $\bar{K}$ and $\bar{H}$, a positive definite diagonal matrix $M$, and positive scalars $\gamma$ such that

$$\begin{aligned} 0&< \begin{bmatrix} (\mu - (N + \frac{1}{2})\varepsilon _u )^2&\, e_i^T\bar{H} \\ \bar{H}^T e_i&\bar{P} \end{bmatrix},\end{aligned}$$

(18)

$$\begin{aligned} 0&> \epsilon _w^2 \mathbf {1}_m^TM\mathbf {1}_m - \lambda , \end{aligned}$$

(19)

$$\begin{aligned} 0&> \begin{bmatrix} {\varGamma }_j + \lambda \bar{P}&\bar{B} \\ \bar{B}^T&-M \end{bmatrix},\end{aligned}$$

(20)

$$\begin{aligned} 0&> \begin{bmatrix} {\varGamma }_j&\bar{P} C^T \!&\! \bar{B} \\ \!C\bar{P}&-\gamma I \!&\! 0 \\ \!\bar{B}^T&0 \!&\! -\gamma I \end{bmatrix}, \end{aligned}$$

(21)

where ${\varGamma }_j \mathop {=}\limits ^{\triangle }A\bar{P} + \bar{P} A^T + B E_j \bar{K} + \bar{K}^T E_j^T B^T + B E_j^{-} \bar{H} + \bar{H}^T E_j^{-T} B^T$, $\mathbf {1}_m \mathop {=}\limits ^{\triangle }\begin{bmatrix} 1&1&\cdots&1&1\end{bmatrix}^T \in \mathbf {R}^m$. In this case, the control input is constructed as $u(t) = Kx(t) + \bar{u}(x(t))$, where $K = \bar{K} \bar{P}^{-1}$ and each component of $\bar{u}(x(t))$ is defined as

$$\begin{aligned} \bar{u}_i(x(t)) \mathop {=}\limits ^{\triangle }- \varepsilon _u N sgn(\; \sigma _i(x(t)) \;), \end{aligned}$$

(22)

where $\sigma _i(x(t))$ is the $ith$ component of $\sigma (x(t))$, $\sigma (x(t)) \mathop {=}\limits ^{\triangle }B^TPx(t)$, $P \triangleq \bar{P}^{-1}$, $sgn(\varrho )$ is the sign of $\varrho$, $N = \left\lceil \frac{\varepsilon _u + \varphi \varepsilon _w}{ \varepsilon _u} \right\rceil$, and the operator $\lceil \rho \rceil$ denotes the nearest integer greater than or equal to a scalar $\rho$. Moreover, the $\gamma$-performance bound can be reduced by solving the following minimization problem: for all $j \in [1, 2^m]$ and $i \in [1,m]$, $\min {\gamma }$ subject to (18), (19), (20), and (21).

Proof

We first construct an input $u(t)$ and an auxiliary input $v(t)$ such that

$$\begin{aligned} u(t)&= K x(t) + \bar{u}(x(t) ), \end{aligned}$$

(23)

$$\begin{aligned} v(t)&= H x(t) + \bar{u}(x(t) ), \end{aligned}$$

(24)

where $v(t)$ is employed to utilize Lemma 3 for handling the input saturation in (7).

In order to use the polytopic representation method in Lemma 3, the following relation should be satisfied: for all $i \in [1,m]$, $\mu \ge |e^T_i Q(v(t))| = |e^T_i v(t) + e^T_i\nabla v(t) |$, or equivalently,

$$\begin{aligned} \mu&\ge |\;e_i^T H x(t) + e_i^T \bar{u}(x(t)) + e_i^T \nabla v(t) \;|. \end{aligned}$$

(25)

Using the nonlinear control part in (22), the right side of inequality (25) can be represented as follows:

$$\begin{aligned}&|e_i^T H x(t) + e_i^T \bar{u}(x(t)) + e_i^T \nabla v(t)| \\&\quad =| e_i^THx(t) -\varepsilon _u N sgn( \sigma _i(x(t)) ) + e_i^T \nabla v(t) | \\&\quad \le |e_i^TH x(t)| + \varepsilon _uN + \varepsilon _u/2. \end{aligned}$$

Then, inequality (25) is satisfied if it holds that for $i \in [1,m]$,

$$\begin{aligned} |e_i^TH x(t)| \le \mu - (N+\frac{1}{2})\varepsilon _u. \end{aligned}$$

(26)

Using (26), the polytopic representation of the input saturation in Lemma 3 is guaranteed if it holds that

$$\begin{aligned} e_i^T HP^{-1}H^T e_i \le \left( \mu - \left( N+\frac{1}{2}\right) \varepsilon _u\right) ^2, \end{aligned}$$

(27)

or equivalently,

$$\begin{aligned} 0 \le \begin{bmatrix} \left( \mu - \left( N+\frac{1}{2}\right) \varepsilon _u\right) ^2&e_i^T H \\ H^T e_i&P \end{bmatrix} . \end{aligned}$$

(28)

Then, pre- and post-multiplying both sides of (28) by $diag\{I,~ P^{-1}\}$ yield (18), i.e.,

$$\begin{aligned} 0 \le \begin{bmatrix} \left( \mu - \left( N+\frac{1}{2}\right) \varepsilon _u\right) ^2&e_i^T \bar{H} \\ \bar{H}^T e_i&\bar{P} \end{bmatrix}, \end{aligned}$$

(29)

where $\bar{H} \triangleq {H} \bar{P}$.

If the above linear matrix inequality (LMI) condition is satisfied, it is ensured that there exists a weighting factor $\xi _j$ such that

$$\begin{aligned} sat( Q(u(t)))&= \sum _{j = 1}^{2^m} \xi _j \{ \;E_j Q(u(t)) \;+\; E^-_j Q(v(t)) \;\} \nonumber \\&= \sum _{j = 1}^{2^m} \xi _j \{ E_j u(t) \nonumber \\&+\, E_j^- v(t) + E_j \nabla u(t) + E_j^- \nabla v(t)\}\nonumber \\&= \sum _{j = 1}^{2^m} \xi _j F x(t) + \sum _{j = 1}^{2^m} \xi _j \nabla F(t). \end{aligned}$$

(30)

where $F \triangleq E_jK + E_j^-H$ and $\nabla F(t) \triangleq E_j \nabla u(t) + E_j^- \nabla v(t) + \bar{u}(x(t))$.

Using (30) and the relation $\sum _{j = 1}^{2^m} \xi _j = 1$ in Lemma 3, the resultant closed-loop system is given as follows:

$$\begin{aligned} \dot{x}(t)&= \sum _{j = 1}^{2^m} \xi _j \left\{ A + BF \right\} x(t)\nonumber \\&+ \sum _{j = 1}^{2^m} \!\xi _j\! B\!\left\{ \! \nabla F(t) + \tilde{B}w(t) \right\} \nonumber \\&+ \bar{B}w(t). \end{aligned}$$

(31)

Then, the derivative of $V(x(t))$ is

$$\begin{aligned} \dot{V}(x(t)) =\,&2x^T(t)\sum _{j = 1}^{2^m} \xi _j P \left\{ A + B F \right\} x(t) \nonumber \\&+ 2\sigma ^T(x(t)) \!\sum _{j = 1}^{2^m} \xi _j \left\{ \nabla F(t) + \tilde{B}w(t)\right\} \nonumber \\&+ 2x^T(t)P \bar{B} w(t). \end{aligned}$$

(32)

Using the conditions (4) and (6), the relations $|\alpha ^T \beta |$ $\le \Vert \alpha \Vert _{1} \Vert \beta \Vert _{\infty }$ and $||X \alpha ||_{\infty } \le ||X||_{\infty }||\alpha ||_{\infty }$ from Lemma 1 and the definition of the matrix $p$-norm, respectively, it is shown that $\bar{u} (x(t))$ in (22) ensures that the second term of $\dot{V}(x(t))$ is negative, i.e., for all $j \in [1,2^m]$,

$$\begin{aligned}&2\sigma ^T(x(t))\nabla F(t) + 2\sigma ^T(x(t)) \tilde{B}w(t)\\&\quad =2\sigma ^T(x(t))\bar{u}(x(t)) + 2\sigma ^T(x(t))E_j \nabla u(t)\\&\quad ~~+ 2\sigma ^T(x(t))E_j^- \nabla v(t) + 2\sigma ^T(x(t)) \tilde{B}w(t) \\&\quad \le 2\sigma ^T(x(t))\bar{u}(x(t))\\&\quad ~~+ 2\Vert \sigma (x(t))\Vert _{1} \Vert E_j\Vert _{\infty } \Vert \nabla u(t)\Vert _{\infty }\\&\quad ~~+ 2\Vert \sigma (x(t))\Vert _{1} \Vert E_j^-\Vert _{\infty } \Vert \nabla v(t)\Vert _{\infty }\\&\quad ~~+ 2\Vert \sigma (x(t))\Vert _{1}\Vert \tilde{B}\Vert _{\infty } \Vert w(t)\Vert _{\infty } \\&\quad \le -2\varepsilon _uN\Vert \sigma (x(t))\Vert _{1} + 2\varepsilon _u \Vert \sigma (x(t))\Vert _{1}\\&\qquad +\, 2\varphi \varepsilon _w \Vert \sigma (x(t))\Vert _{1}\\&\quad = 2 \{ -\varepsilon _u N + \varepsilon _u + \varphi \varepsilon _w\}\Vert \sigma (x(t))\Vert _1\\&\quad \le 2 \left\{ \begin{array}{c} - \varepsilon _u \left( \frac{\varepsilon _u + \varphi \varepsilon _w}{ \varepsilon _u}\right) + \varepsilon _u + \varphi \varepsilon _w \end{array}\right\} \Vert \sigma (x(t))\Vert _1 = 0, \end{aligned}$$

where, by choosing $N$ as $\left\lceil \frac{\varepsilon _u + \varphi \varepsilon _w}{ \varepsilon _u} \right\rceil$ and using the relation $-\lceil \varrho \rceil \le -\varrho \,$ for a scalar $\varrho \ge 0$, we can make the second term of $\dot{V}(x(t))$ negative. Then, $\dot{V}(x(t))$ can be rewritten as

$$\begin{aligned} \dot{V}(x(t)) \le \sum _{j = 1}^{2^m}\xi _j x^T(t) \mathbb {A}_j x(t) + 2x^T(t)P \bar{B} w(t), \end{aligned}$$

(33)

where

$$\begin{aligned} \mathbb {A}_j&= \mathbf {Sym}(PA + PBE_jK + PBE_j^-H). \end{aligned}$$

Next, we shall derive a set invariance condition for (15 16). To this end, we use the following constraint that comes from (4):

$$\begin{aligned} w^T(t)Mw(t) \le \epsilon _w^2Tr(M), \end{aligned}$$

(34)

where $M\in {\mathcal {R}}^{m\times m}$ is a positive definite diagonal matrix and $Tr(M)$ is a trace of $M$. Combining (15 16) and (34) with the S-procedure [1] yields the following relation:

$$\begin{aligned} 0 >&\dot{V}(x(t))-\lambda (\,1 - x^T(t)Px(t)\,) + \epsilon _w^2Tr(M) \nonumber \\&- w^T(t)Mw(t). \end{aligned}$$

(35)

Relation (35) is ensured if it holds that

$$\begin{aligned} 0 >\,&x^T(t)\!\sum _{j = 1}^{2^m} \xi _j \mathbb {A}_j x(t) + 2x^T(t)P \bar{B} w(t) \nonumber \\&- \lambda \left( 1 - x^T(t) P x(t) \right) + \epsilon _w^2Tr(M)\nonumber \\&- w^T(t)Mw(t), \end{aligned}$$

(36)

which is obtained by using (33) and can be represented as the following matrix inequality: for all $j \in [1,2^m]$,

$$\begin{aligned} 0 > \begin{bmatrix} x^T(t)&w^T(t)&1 \end{bmatrix} \mathcal {M}_{1,j} \begin{bmatrix} x^T(t)&w^T(t)&1 \end{bmatrix}^T, \end{aligned}$$

(37)

where

$$\begin{aligned} \mathcal {M}_{1,j}&\mathop {=}\limits ^{\triangle }\begin{bmatrix} \mathbb {A}_j + \lambda {P}&~~~{P} \bar{B}&~0 \\ \bar{B}^T {P}&~-M&~0 \\ 0&0&\,\epsilon _w^2Tr(M) - \lambda \end{bmatrix}. \nonumber \\ \end{aligned}$$

(38)

We remark that (37) is ensured if it holds that $\mathcal {M}_{1,j} <0$. Pre- and post-multiplying both sides of $\mathcal {M}_{1,j}$ by $diag\{\bar{P} ,\;I,\;I\}$ yield (19) and (20).

Further, we derive an $\mathcal {H}_\infty$ performance condition. As is well known, the condition can be derived by

$$\begin{aligned} 0 > \dot{V}(x(t)) + \gamma ^{-1}z^T(t)z(t) - \gamma w^T(t)w(t). \end{aligned}$$

(39)

Using (33), relation (39) is ensured if it holds that

$$\begin{aligned} 0 >&x^T(t)\sum _{j = 1}^{2^m} \xi _j \mathbb {A}_j x(t)+ 2x^T(t)P \bar{B} w(t) \nonumber \\&+\gamma ^{-1}z^T(t)z(t) - \gamma w^T(t)w(t), \end{aligned}$$

(40)

which is represented as the following matrix inequality: for all $j \in [1,2^m]$,

$$\begin{aligned} 0 > \begin{bmatrix} x^T(t)&w^T (t) \end{bmatrix} {\mathcal {M}}_{2,j} \begin{bmatrix} x^T(t)&w^T (t) \end{bmatrix}^T, \end{aligned}$$

(41)

where

$$\begin{aligned} {\mathcal {M}}_{2,j}&=\begin{bmatrix} \mathbb {A}_j + \gamma ^{-1} C^TC&~~{P} \bar{B} \\ \bar{B}^T {P}&\,\,-\gamma I \end{bmatrix}. \end{aligned}$$

Relation (41) is satisfied if ${\mathcal {M}}_{2,j} < 0$. Thus, pre- and post-multiplying both sides of ${\mathcal {M}}_{2,j}$ by $diag\{\bar{P} ,\;I\}$ and using the Schur complement technique [1] afford the resultant $\mathcal {H}_\infty$ performance condition (21). $\square$

Using the method in Theorem 1 and the approach for the analysis of the uncertainties, the following result is obtained.

Theorem 2

For all $x(t) \in \mathcal {E}(\bar{P}^{-1}), i \in [1, m], j \in [1,2^m]$, and a given positive scalar $\lambda$, the proposed system (3) with assumptions $({\mathcal {A}}1), ({\mathcal {A}}2), ({\mathcal {A}}3)$, and (${\mathcal {A}}4$) is locally asymptotically stable with the $\mathcal {H}_\infty$ performance $\gamma$ if there exist a symmetric positive definite matrix $\bar{P}$, matrices $\bar{K}$ and $\bar{H}$, a positive definite diagonal matrix $M$, and positive scalars $\eta _1$, $\eta _2$, $\eta _3$, and $\gamma$ such that (18), (19),

$$\begin{aligned} 0&> \begin{bmatrix} {\varGamma }_j + \lambda \bar{P}&\bar{P}G_1^T&\bar{K}^T E_j^T G_2^T&\bar{H}^T E_j^{-T} G_2^T&\bar{B} \\ G_1\bar{P}&-\eta _1 I&0&0&0 \\ G_2E_j \bar{K}&0&-\eta _2 I&0&0 \\ G_2E_j^{-} \bar{H}&0&0&-\eta _3 I&0 \\ \bar{B}^T&0&0&0&-M \end{bmatrix},\nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned} 0&> \!\begin{bmatrix} \!{\varGamma }_j \!&\bar{P}G_1^T&\bar{K}^T E_j^T G_2^T&\bar{H}^T E_j^{-T} G_2^T&\bar{P} C^T \!&\! \bar{B} \\ \!G_1\bar{P} \!&-\eta _1 I&0&0&0 \!&\! 0 \\ \!G_2E_j \bar{K} \!&0&-\eta _2 I&0&0 \!&\! 0 \\ \!G_2E_j^{-} \bar{H} \!&0&0&-\eta _3 I&0 \!&\! 0 \\ \!C\bar{P} \!&0&0&0&-\gamma I \!&\! 0 \\ \!\bar{B}^T \!&0&0&0&0 \!&\! -\gamma I \end{bmatrix},\nonumber \\ \end{aligned}$$

(43)

where ${\varGamma }_j \mathop {=}\limits ^{\triangle }A\bar{P} + \bar{P} A^T + B E_j \bar{K} + \bar{K}^T E_j^T B^T + B E_j^{-} \bar{H} + \bar{H}^T E_j^{-T} B^T + \eta _1 F_1F_1^T + \eta _2 BF_2F_2^TB^T + \eta _3 BF_2F_2^TB^T$. In this case, the control input is constructed as $u(t) = Kx(t) + \bar{u}(x(t))$, where $K = \bar{K} \bar{P}^{-1}$ and each component of $\bar{u}(x(t))$ is defined as

$$\begin{aligned} \bar{u}_i(x(t)) \mathop {=}\limits ^{\triangle }- \varepsilon _u N sgn(\; \sigma _i(x(t)) \;), \end{aligned}$$

(44)

where $\sigma _i(x(t))$ is the $i$th component of $\sigma (x(t)), \sigma (x(t)) \mathop {=}\limits ^{\triangle }B^TPx(t), P \triangleq \bar{P}^{-1}, sgn(\varrho )$ is the sign of $\varrho , N = \left\lceil \frac{(1+\psi )\varepsilon _u + \varphi \varepsilon _w}{(1-\psi )\varepsilon _u} \right\rceil$, and the operator $\lceil \rho \rceil$ denotes the nearest integer greater than or equal to a scalar $\rho$. Moreover, the $\gamma$-performance bound can be reduced by solving the following minimization problem: for all $j \in [1, 2^m]$ and $i \in [1,m]$, $\min {\gamma }$ subject to (18), (19), (42), and (43).

Proof

For the system with uncertainties, the derivative of $V(x(t))$ is rewritten as

$$\begin{aligned}&\dot{V}(x(t))\nonumber \\&= 2x^T(t)\sum _{j = 1}^{2^m} \xi _j P \left\{ (A \!+\! {\Delta } A(t)) + B(I \!+\! {{\Delta } B(t)})F \right\} x(t) \nonumber \\&\quad +\, 2\sigma ^T(x(t) ) \!\sum _{j = 1}^{2^m} \xi _j \left\{ (I \!+\! {{\Delta } B(t)})\nabla F(t) + \tilde{B}w(t)\right\} \nonumber \\&\quad +\, 2x^T(t)P \bar{B} w(t). \end{aligned}$$

(45)

Using the conditions (4) and (6), the relations $|\alpha ^T \beta | \le \Vert \alpha \Vert _{1} \Vert \beta \Vert _{\infty }$ and $||X \alpha ||_{\infty } \le ||X||_{\infty }||\alpha ||_{\infty }$ from Lemma 1 and the definition of the matrix $p$-norm, respectively, it is shown that $\bar{u} (x(t))$ in (44) ensures that the second term of $\dot{V}(x(t))$ is negative, i.e., for all $j \in [1,2^m]$,

$$\begin{aligned}&2\sigma ^T(x(t))(I+{{\Delta } B(t)})\nabla F(t) + 2\sigma ^T(x(t)) \tilde{B}w(t)\\&\quad =2\sigma ^T(x(t))\bar{u}(x(t)) + 2\sigma ^T(x(t)) {{\Delta } B(t)} \bar{u}(x(t))\\&\qquad + 2\sigma ^T(x(t))(I+{\Delta } B(t))E_j \nabla u(t)\\&\qquad + 2\sigma ^T(x(t))(I+{\Delta } B(t))E_j^- \nabla v(t)\\&\qquad + 2\sigma ^T(x(t)) \tilde{B}w(t) \\&\quad \le 2\sigma ^T(x(t))\bar{u}(x(t))\\&\qquad + 2\Vert \sigma (x(t))\Vert _{1} \Vert { {\Delta } B(t)}\Vert _{\infty } \Vert \bar{u}(x(t))\Vert _{\infty }\\&\qquad + 2\Vert \sigma (x(t))\Vert _{1}\Vert I+{ {\Delta } B(t)} \Vert _{\infty } \Vert E_j\Vert _{\infty } \Vert \nabla u(t)\Vert _{\infty }\\&\qquad + 2\Vert \sigma (x(t))\Vert _{1}\Vert I+{ {\Delta } B(t)} \Vert _{\infty } \Vert E_j^-\Vert _{\infty } \Vert \nabla v(t)\Vert _{\infty }\\&\qquad + 2\Vert \sigma (x(t))\Vert _{1}\Vert \tilde{B}\Vert _{\infty } \Vert w(t)\Vert _{\infty } \\&\quad \le -2\varepsilon _uN\Vert \sigma (x(t))\Vert _{1} + 2\psi \varepsilon _u N\Vert \sigma (x(t))\Vert _{1} \\&\qquad + 2(1+\psi )\varepsilon _u \Vert \sigma (x(t))\Vert _{1} + 2\varphi \varepsilon _w \Vert \sigma (x(t))\Vert _{1}\\&\quad = 2 \{ -(1-\psi )\varepsilon _u N + (1+\psi )\varepsilon _u + \varphi \varepsilon _w\}\Vert \sigma (x(t))\Vert _1\\&\quad \le 2 \left\{ - (1-\psi )\varepsilon _u \left( \frac{(1+\psi )\varepsilon _u{+}\varphi \varepsilon _w}{ (1-\psi )\varepsilon _u}\right) \right. \\&\qquad \left. {+}(1+\psi )\varepsilon _u{+}\varphi \varepsilon _w \right\} \Vert \sigma (x(t))\Vert _1 \!=\! 0, \end{aligned}$$

where, by choosing $N$ as $\left\lceil \frac{(1+\psi )\varepsilon _u + \varphi \varepsilon _w}{ (1-\psi )\varepsilon _u} \right\rceil$ and using the relation $-\lceil \varrho \rceil \le -\varrho \,$ for a scalar $\varrho \ge 0$, we can make the second term of $\dot{V}(x(t))$ negative. Then, $\dot{V}(x(t))$ can be rewritten as

$$\begin{aligned}&\dot{V}(x(t)) \le 2x^T(t)\sum _{j = 1}^{2^m} \xi _j P \left\{ (A \!+\! {\Delta } A(t))\right. \nonumber \\&\quad \left. +\, B(I \!+\! {{\Delta } B(t)})F \right\} x(t) + 2x^T(t)P \bar{B} w(t). \end{aligned}$$

(46)

This inequality is relaxed by Lemma 2 as

$$\begin{aligned} \dot{V}(x(t))&\le \sum _{j = 1}^{2^m}\xi _j x^T(t) \mathcal {A}_j x(t) + 2x^T(t)P \bar{B} w(t), \end{aligned}$$

(47)

where

$$\begin{aligned} \mathcal {A}_j&= \mathbf {Sym}(PA{+}PBE_jK{+}PBE_j^-H){+}\eta _1 PF_1F_1^TP\\&\quad + \eta _2 PBF_2F_2^TB^TP + \eta _2^{-1} K^TE_j^TG_2^T G_2 E_j K \\&\quad + \eta _3 PBF_2F_2^TB^TP + \eta _3^{-1} H^TE_j^{-T}G_2^T G_2 E_j^- H \\&\quad + \eta _1^{-1}G_1^TG_1, \end{aligned}$$

since

$$\begin{aligned}&PF_1{\Delta }_1(t)G_1 + G_1^T{\Delta }_1^T(t)F_1^TP \nonumber \\&\qquad \le \eta _1 PF_1F_1^TP + \eta _1^{-1}G_1^TG_1, \end{aligned}$$

(48)

$$\begin{aligned}&PBF_2{\Delta }_2(t)G_2 E_j K+ K^TE_j^TG_2^T{\Delta }_2^T(t)F_2^TB^TP \nonumber \\&\,\qquad \le \eta _2 PBF_2F_2^TB^TP + \eta _2^{-1}K^T E_j^T G_2^T G_2 E_j K,\nonumber \\ \end{aligned}$$

(49)

$$\begin{aligned}&PBF_2{\Delta }_2(t)G_2 E_j^- H+ H^TE_j^{-T}G_2^T{\Delta }_2^T(t)F_2^TB^TP \nonumber \\&\,\quad \le \eta _3 PBF_2F_2^TB^TP + \eta _3^{-1}H^T E_j^{-T} G_2^T G_2 E_j^- H.\nonumber \\ \end{aligned}$$

(50)

By applying (47) to (36) and (40), (42) and (43) are derived using the same procedure of the proof in Theorem 1. $\square$

Remark 1

The matrix inequalities (20) in Theorem 1 and (42) in Theorem 2 are nonconvex with respect to $\lambda$ and $\bar{P}$. If $\lambda$ is fixed, then (20) and (42) become an LMI. In order to obtain the global infimum, we minimize $\gamma$ by varying $\lambda$ from $0$ to sufficiently large value $(< \infty )$.

Remark 2

For perfectly rejecting the effect of $\nabla u(t), \nabla v(t)$, and $w(t)$ that have known bounds and satisfy matched conditions, $\bar{u}(x(t))$ is designed as (22) and (44) by employing variable structure control (VSC) technique, which provides an effective and robust means of controlling dynamic systems with bounded and matched uncertainties [21]. That is, adding $\bar{u}(x(t))$ to $Kx(t)$ enables us to eliminate the energy in the sense of Lyapunov caused by $\nabla u(t), \nabla v(t)$, and $w(t)$.

4 Numerical examples

In this section, we discuss the performance of the following two types of controllers: the Type-1 controller for system (1 2) is designed as (23) with

$$\begin{aligned}&\bar{u}_i(x(t)) = - \varepsilon _u N sgn(\sigma _i(x(t))), \\&\sigma (x(t)) \mathop {=}\limits ^{\triangle }B^T P x(t),\, N = \left\lceil \frac{(1+\psi )}{(1-\psi )} \right\rceil , \end{aligned}$$

and the Type-2 controller for system (3), the proposed controller, is constructed as (23) with

$$\begin{aligned} \bar{u}_i(x(t))&= - \varepsilon _u N sgn(\sigma _i(x(t))), \\ \sigma (x(t))&\mathop {=}\limits ^{\triangle }B^T P x(t),\, N = \left\lceil \frac{(1+\psi )\varepsilon _u + \varphi \varepsilon _w}{ (1-\psi )\varepsilon _u} \right\rceil . \end{aligned}$$

In particular, in the case of the Type-1 controller, the linear control part can be designed by Theorem 2 except that $\bar{B}$ in (42) and (43) is replaced with $D$.

4.1 Example 1

Consider the following system: for $x(0)= \begin{bmatrix} 0.9&0.5 \end{bmatrix}^T$,

$$\begin{aligned}&A = \begin{bmatrix} 0&1\\ -5&3 \\ \end{bmatrix},\, {\Delta } A(t) = \begin{bmatrix} r(t)&0 \\ 0&0 \end{bmatrix},\\&B = \begin{bmatrix} -1&1 \end{bmatrix}^T,\,C = \begin{bmatrix} 1&1 \end{bmatrix},\, D = \begin{bmatrix} 1&-2 \end{bmatrix}^T, \\&{\Delta } B(t) = 0.2 r(t),\,r(t) = cos(2\pi t),\\&w(t) = 0.3 \exp (-t) r(t),\,\varepsilon _u=0.2,\, \mu = 4. \end{aligned}$$

From the above data, we obtain the following additional information:

$$\begin{aligned}&F_1 = G_1 {=} I, \!{\Delta }_1(t) {=} {\Delta } A(t), \!F_2 {=} 0.2, \!G_2 {=} 1,\nonumber \\&{\Delta }_2(t) = r(t), \psi {=} 0.2,\, \varepsilon _w {=} 0.3. \end{aligned}$$

(51)

In Theorem 2, the solutions are as follows:

• Type-1 controller

  $$\begin{aligned} K&= \begin{bmatrix} 9.7701&-15.2312 \end{bmatrix}, \\ P&= \begin{bmatrix} 3.7841&-2.3557 \\ -2.3557&7.2160 \end{bmatrix}, \end{aligned}$$

• Type-2 controller

  $$\begin{aligned} K&= \begin{bmatrix} 9.1329&-39.0831 \end{bmatrix}, \\ P&= \begin{bmatrix} 3.0951&-1.2231 \\ -1.2231&17.2548 \end{bmatrix}, \end{aligned}$$

and an ${\mathcal {H}}_\infty$ performance $\gamma$ is 4.1893 for Type-1 controller and 0.6810 for Type-2 controller.

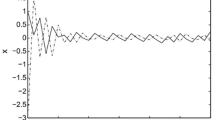
Table 1 presents the ${\mathcal {H}}_\infty$ performance $\gamma$ of the Type-1 controller in comparison with that of the Type-2 controller for different values of $\mu$. In this table, for a certain saturation level $\mu$, the Type-2 controller gives a smaller ${\mathcal {H}}_\infty$ performance $\gamma$ than the Type-1 controller. Further, for a small saturation level $\mu$, the Type-2 controller is feasible but the Type-1 controller is infeasible. This is because the nonlinear part of the Type-2 controller perfectly rejects the effect of input quantization and matched part, simultaneously; on the other hand, the nonlinear part of the Type-1 controller only eliminates the effect of input quantization. That is, the Type-1 controller considers the unified disturbance despite the presence of matched and mismatched disturbances, which results in the deterioration of the performance. Figure 1 presents the trajectories of the states for each controller. In this figure, the states in the Type-1 controller and the Type-2 controller asymptotically converge to the origin regardless of model uncertainties, quantization error, and external disturbances.

Fig. 1

Trajectories of the states for each controller ($\mu =4$)

Table 1 Comparison of ${\mathcal {H}}_\infty$ performance $\gamma$ for different values of $\mu$

4.2 Example 2

The system parameters are as follows: for $x(0)=\begin{bmatrix} 1&-1&0.5 \end{bmatrix}^T$,

$$\begin{aligned}&A = \begin{bmatrix} -3&0&1\\ 1&2&0 \\ 0&1&-2 \end{bmatrix}, {\Delta } A(t) = \begin{bmatrix} r(t)&0&0 \\ 0&0&r(t) \\ 0&r(t)&0 \end{bmatrix},\\&B = \begin{bmatrix} 0&1\;&0 \end{bmatrix}^T,\,C = \begin{bmatrix} 1&0&0 \end{bmatrix},\, D = \begin{bmatrix} 1&2&1 \end{bmatrix}^T,\\&{\Delta } B(t) = 0.5 r(t),\,r(t) = sin(2\pi t),\\&w(t) = 0.2 \exp (-0.5t) r(t),\,\varepsilon _u=0.1,\,\mu =5. \end{aligned}$$

From the above data, we obtain the following additional information:

$$\begin{aligned}&F_1 = G_1 = I,\, {\Delta }_1(t) = {\Delta } A(t),\, F_2 = 1,\, G_2 = 0.5,\nonumber \\&{\Delta }_2(t) = r(t),\, \psi = 0.5,\, \varepsilon _w = 0.2. \end{aligned}$$

(52)

In Theorem 2, the solutions are as follows:

• Type-1 controller

  $$\begin{aligned} K&= \begin{bmatrix} -6.1837&-27.0341&-4.8357 \end{bmatrix}, \\ P&= \begin{bmatrix} 3.6622&3.6695&0.6798 \\ 3.6695&16.0424&2.8695 \\ 0.6798&2.8695&5.7545 \end{bmatrix}, \end{aligned}$$

• Type-2 controller

  $$\begin{aligned} K&= \begin{bmatrix} -5.4592&-22.6638&-3.6457 \end{bmatrix}, \\ P&= \begin{bmatrix} 2.0844&4.0708&0.8502 \\ 4.0708&16.9002&2.7187 \\ 0.8502&2.7187&2.5094 \end{bmatrix}, \end{aligned}$$

and an ${\mathcal {H}}_\infty$ performance $\gamma$ is 19.4070 for Type-1 controller and 2.6932 for Type-2 controller.

Figure 2 presents the trajectories of the states for each controller. In this figure, the states in the Type-1 controller and the Type-2 controller asymptotically converge to the origin regardless of model uncertainties, quantization error, and external disturbances. Table 2 describes the ${\mathcal {H}}_\infty$ performance $\gamma$ of the Type-1 controller in comparison with that of the Type-2 controller for different values of $\mu$. In this table, we can clearly show that the performance of the Type-2 controller outperforms that of the Type-1 controller.

Fig. 2

Trajectories of the states for each controller ($\mu = 5$)

Table 2 Comparison of ${\mathcal {H}}_\infty$ performance $\gamma$ for different values of $\mu$

Tables 3 and 4 show the ${\mathcal {H}}_\infty$ performance $\gamma$ for the Type-1 controller and the Type-2 controller for different $D$. Table 3 presents the ${\mathcal {H}}_\infty$ performance $\gamma$ under external disturbances, $Dw(t)$, in the direction of $Bw(t)$. In this table, the Type-2 controller gives a very small ${\mathcal {H}}_\infty$ performance $\gamma$ that is almost zero. This is due to that the nonlinear part of the Type-2 controller perfectly removes external disturbances, $Dw(t)$, because the external disturbances only exist as the matched part for system (3). However, the nonlinear part of the Type-1 controller only rejects the effect of input quantization and the linear part of that handles both stability of system and the ${\mathcal {H}}_\infty$ performance because the external disturbances only exist as the mismatched part for system (1).

Table 3 Comparison of ${\mathcal {H}}_\infty$ performance $\gamma$ under matched disturbance $(D=[0 \,2 \,0]^T,\, \mu = 5)$

Table 4 Comparison of ${\mathcal {H}}_\infty$ performance $\gamma$ for different values of external disturbances $(D=[1 \,\alpha \,1]^T, \,\mu = 5)$

Table 4 illustrates the ${\mathcal {H}}_\infty$ performance $\gamma$ of the Type-1 controller in comparison with that of the Type-2 controller for different values of $\alpha$. In this table, the component of $Dw(t)$ in the direction of $Bw(t)$ that is the matched part is varied by different values of $\alpha$. In this table, the Type-2 controller gives a smaller ${\mathcal {H}}_\infty$ performance $\gamma$ than the Type-1 controller. In addition, for a large $\alpha$, the Type-2 controller is feasible but the Type-1 controller is infeasible. This is due to that the nonlinear part of the Type-2 controller successfully banishes the effect of matched part and quantization error so as the ${\mathcal {H}}_\infty$ performance. Therefore, the proposed controller, Type-2 controller, guarantees ${\mathcal {H}}_\infty$ performance under large external disturbance that has a large component of $Dw(t)$ in the direction of $Bw(t)$.

5 Conclusion

In this paper, based on a uniform quantizer with a saturation nonlinearity, we introduced an ${\mathcal {H}}_\infty$ state-feedback controller for uncertain linear systems with quantized-input saturation and external disturbances. The proposed controller consisted of two control parts: a linear part to achieve the $\mathcal {H}_\infty$ performance against model uncertainties and the mismatched part of the disturbances and a nonlinear part to eliminate the effect of input quantization and the matched part of the disturbances. In the simulation, we compared two controllers: the Type-1 controller for system (1 2) and the Type-2 controller for system (3). As shown in the simulation results, the Type-2 controller outperformed the Type-1 controller because the Type-1 controller considered the unified disturbance regardless of the presence of matched and mismatched disturbances.