Decentralized sliding mode quantized feedback control for a class of uncertain large-scale systems with dead-zone input

Abstract

This paper is concerned with the robust quantized feedback stabilization problem for a class of uncertain nonlinear large-scale systems with dead-zone nonlinearity in actuator devices. It is assumed that state signals of each subsystem are quantized and the quantized state signals are transmitted over a digital channel to the controller side. Combined with a proposed discrete on-line adjustment policy of quantization parameters, a decentralized sliding mode quantized feedback control scheme is developed to tackle parameter uncertainties and dead-zone input nonlinearity simultaneously, and ensure that the system trajectory of each subsystem converges to the corresponding desired sliding manifold. Finally, an example is given to verify the validity of the theoretical result.

1 Introduction

Decentralized control design for large-scale systems has been paid much more attention in the control community for a long time and many valuable results have been published, such as, see [1–10] and the references therein. On the other hand, the effect of dead-zone input nonlinearity should be taken into consideration in the design of control systems. As shown in many research papers, dead-zone phenomenon is a very important nonsmooth nonlinear characteristic, which is frequently encountered in various practical engineering systems, such as mechanical connections, hydraulic servo valves, piezoelectric translators, and electric servomotors. The existence of dead-zone nonlinearity usually causes severe deterioration of system performances and even induces instability of the system. Some interesting results for large-scale interconnected systems with respect to dead-zone input nonlinearity can be seen in [11, 12]. As well known, sliding mode control is an effective method to cope with uncertain systems since it has several advantages, such as, disturbance rejection and insensitivity to plant parameter variation and so on [13, 14]. Related researches on decentralized sliding mode control for uncertain large-scale interconnected systems in the presence of dead-zone input nonlinearity have been proposed; see [15, 16] for details. It is worthy noting that the uncertainty in each subsystem was assumed to satisfy the so-called matching condition, and signal quantization is neglected.

In modern engineering, due to the widespread application of analog-to-digital and digital-to-analog converters in sensors and actuators, quantization has become one of important aspects that should be taken into consideration in the control design. Many results have been published, see, e.g., [17–20], and [21]. However, no results have been reported on the robust stabilization of uncertain large-scale interconnected nonlinear systems with dead-zone input nonlinearity by utilizing the decentralized quantized state feedback sliding mode control schemes. For the design of the quantized feedback sliding mode control, how to form a quantized feedback control law to ensure the reachability of the sliding surface is the main question. When a quantized feedback sliding mode control policy is designed with a static uniform quantizer, the system trajectory cannot ensure to reach the desired sliding surface, thus the sliding motion cannot be well implemented. In fact, the system trajectory can only be driven to some neighbor of the sliding surface and as a result, further convergence of the system cannot be obtained [22].

Motivated by the above discussion, for a class of uncertain large-scale interconnected systems with dead-zone input nonlinearity, the decentralized quantized feedback sliding mode control design is addressed. The main contribution of this paper is that based on the proposed static adjustment policy of quantization parameters for dynamic quantizers, the reaching condition of the sliding mode for each subsystem is established via a decentralized sliding mode quantized feedback control law. It is shown that the proposed control strategy can effectively eliminate the effects of matched/mismatched uncertainties and dead-zone input nonlinearity simultaneously, and as a result, the state trajectory of each subsystem can be driven onto the corresponding sliding surface, then a stable sliding motion is maintained thereafter.

The rest of this paper is organized as follows. The problem statement and preliminaries are presented in Sect. 2. A robust decentralized sliding mode quantized feedback control design method is given in Sect. 3. In Sect. 4, an example is provided to illustrate the effectiveness of the proposed method and the conclusions are drawn in Sect. 5.

Throughout this paper, the following notations are used. Notation |a| denotes the absolute value of a scalar a and we will denote by ∥x∥ the standard Euclidean norm of a vector x∈ℝⁿ and by ∥A∥ the induced norm of a matrix A∈ℝ^n×n. Let ⌊x⌋ denote the function which rounds the element of x to the nearest integer toward minus infinity.

2 Problem statement and preliminaries

Consider a class of uncertain nonlinear large-scale interconnected systems with dead-zone nonlinear input described as follows:

(1)

where $x_{i}\in \mathbb{R}^{n_{i}}$, u _i ∈ℝ are the state and the control input of the ith subsystem, respectively. $\varDelta A_{i} (t)\in\mathbb{R}^{n_{i}\times n_{i}}$ is the unknown mismatched bounded matrix denoting the parameter uncertainty, which satisfies $\Vert \varDelta A_{i}(t)\Vert\leq \bar{A}_{i}$, where $\bar{A}_{i}$ is a known constant. f _i (t,x,p)∈ℝ describes the nonlinear interconnection term affecting the ith subsystem, and Φ _i (u _i ):ℝ→ℝ denotes the input nonlinearity in the ith subsystem. Let us denote $x^{T}=[x_{1}^{T}, x_{2}^{T}, \ldots, x_{N}^{T}]$. Throughout this paper, some necessary assumptions are made as follows.

Assumption 1

For each uncertain subsystem in (1), the pair (A _i ,B _i ) is controllable.

Assumption 2

There exist known positive scalars $k_{i}^{0}$, $k_{ij}^{1}$ and $k_{ij}^{2}$ for the nonlinear interconnected uncertain term f _i (t,x,p) such that

(2)

Remark 1

Compared with [15], more complicated interconnected structure is considered under Assumption 2 since the presence of the term $\sum_{j= 1}^{N}k_{ij}^{2}\Vert x_{i}\Vert\*\Vert x_{j}\Vert$. Thus, more general interconnected cases can be dealt with the proposed method in this paper.

The dead-zone nonlinear input is described as follows:

(3)

where ϕ _i+>0 and ϕ _i− are nonlinear functions of u _i , and u _i0+>0, u _i0−>0 are two known constants.

Assumption 3

[16]

The dead-zone nonlinear input function Φ _i (u _i ) satisfies the following property:

where m _i+≤ϕ _i+ and m _i−≤ϕ _i− are two known positive constants for i=1,2,…,N.

To simplify the complexity of derivation, it is assumed that u _i0+=u _i0−=u _i0 and m _i+=m _i−=m _i .

2.1 Sliding surface design

In general, sliding mode control design includes two procedures, the first is the development of a sliding surface and the second is the establishment of a sliding mode control law for driving the system to the sliding surface and maintaining a stable sliding motion thereafter. How to design the sliding surface is an interesting question in its own but is not pursued here, it is just assumed that the sliding surface is well designed by existing methods, e.g., see [23].

In this paper, suppose that the following linear sliding surface

$$s_{i}(t)=C_{i}x_{i}=0 $$

is well designed for the ith subsystem such that a stable sliding motion is maintained on it, where $C_{i}\in R^{1\times n_{i}}$. Without loss of generality, it is assumed that C _i is designed such that C _i B _i ≥1.

2.2 Quantization

In this paper, it is assumed that state signals are quantized before they are sent to the controller side over a digital communication channel. A quantizer can be treated to be a device that converts a real-valued signal into piecewise constant ones in the control systems [24]. It can be usually considered to be a mathematical operator defined by the function $\operatorname{round}(\cdot)$ that rounds toward the nearest integer, i.e.,

(4)

where the quantization parameter μ is called the quantization sensitivity of the quantizer. Let us define the quantization error e _μ =q _μ (z)−z, since each component of the quantization error e _μ is bounded by the half of the quantization parameter μ, we have

(5)

where $\varDelta =\frac{\sqrt{p}}{2}$ and p is the dimension of the vector z.

A quantizing level μ=0 is added to handle the case that the system trajectory maintains on the sliding surface. The additional definition of the quantizer in this level is presented as follows:

(6)

The quantization parameter μ=0 expresses the case that the system trajectory are on the sliding surface. In other words, when the system trajectory are kept on the sliding surface, one has μ=0 and q _μ (z)=0. In addition, though the relation in (3) does not maintain in such case because of μ=0, it has no effect on the reachability of the sliding surface with the proposed quantized feedback controller in this paper.

The main objective of this paper is to present a decentralized sliding mode quantized control law for system (1) such that the system trajectory of each subsystem can be driven to the corresponding subsystem sliding manifold in spite of the effects of matched/mismatched uncertainties and dead-zone input nonlinearity.

3 Main results

To obtain the main result, two lemmas will be used, where the Lemma 2 has been given in [25]; we present it here for completeness. Its proof is given in the Appendix.

Lemma 1

[26]

If the following condition holds:

(7)

then the motion of the sliding manifold s _i (t)=C _i x _i (t)=0 is asymptotically stable.

Lemma 2

Fix an arbitrary constant β _i >1, and suppose that the parameter μ _i ≥0 satisfies

(8)

then the following inequality

(9)

holds.

Remark 2

From Lemma 2, one can see that the relation in (9) is established by the condition in (8). In other words, as long as the quantization parameter μ _i is adjusted to satisfy (8), the relation in (9) will be ensured. It will be observed that the inequality (9) plays a very important role in the proof of Theorem 1.

In the following, we first present the reaching controller design under the relation in (9), then by virtue of (8), an adjustment policy of the parameter μ _i will be provided for ensuring the establishment of (9) after the proof of Theorem 1.

Theorem 1

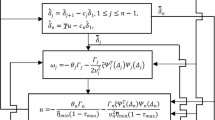
Consider the uncertain large-scale system (1) subject to Assumptions 1–3, then the global reaching condition (7) is guaranteed when the decentralized sliding mode quantized feedback controller is designed as

(10)

where

Proof

Select V _i =|s _i (t)| and let $V(t)=\sum_{i=1}^{N}|s_{i}(t)|$ be the Lyapunov function candidate, then differentiating the function V(t) with respect to time t along the solutions of system (1) yields

By virtue of $q_{\mu_{i}}(x_{i})-x_{i}=e_{\mu_{i}}$, one can see that

It follows from (9) that

(11)

First, we prove that

(12)

It is obviously that (12) is right when $C_{i}q_{\mu_{i}}(x_{i})=0$. When $C_{i}q_{\mu_{i}}(x_{i})<0$, according to (10) and (3), we have Φ _i (u _i )=ϕ _i+ h _i . Combining with C _i B _i ≥1, one can see that

Similarly, when $C_{i}q_{\mu_{i}}(x_{i})>0$, we have

Thus (12) is right. It then follows from (11), (12), and (2) that

(13)

Using the basic inequality $ab\leq\frac{1}{2}a^{2}+\frac{1}{2}b^{2}$ for ∀a∈ℝ, b∈ℝ, and $\Vert x_{i}\Vert\leq\Vert q_{\mu_{i}}(x_{i})\Vert+\varDelta _{i}\mu_{i}$, one can obtain that

(14)

Furthermore, by the utilization of $q_{\mu_{i}}(x_{i})-x_{i}=e_{\mu_{i}}$ and (9), one can see that

so

(15)

Noticing that

$$\sum_{i=1}^{N}\sum _{j=1}^{N}a_{i}b_{ij}c_{i}= \sum_{i=1}^{N}\sum _{j=1}^{N}a_{j}b_{ji}c_{j}, $$

one can see that

(16)

Substituting (16) into (15), we have

(17)

Since

we have

(18)

In the following, we will show that

(19)

It is obvious that (19) holds when $C_{i}q_{\mu_{i}}(x_{i})=0$. From (10), it can be observed that u _i >u _i0 when $C_{i}q_{\mu_{i}}(x_{i})<0$, and then

(20)

On the other hand, according to Assumption 3, one can see that

(21)

From (20), (21), and C _i B _i ≥1, we have

$$C_{i}q_{\mu_{i}}(x_{i})C_{i}B_{i} \varPhi_{i}(u_{i})\leq-m_{i}h_{i}C_{i}B_{i}\bigl|C_{i}q_{\mu_{i}}(x_{i})\bigr|. $$

Similarly, one can achieve that

$$C_{i}q_{\mu_{i}}(x_{i})C_{i}B_{i} \varPhi_{i}(u_{i})\leq-m_{i}h_{i}C_{i}B_{i}\bigl|C_{i}q_{\mu_{i}}(x_{i})\bigr| $$

when $C_{i}q_{\mu_{i}}(x_{i})>0$. Thus, (19) is guaranteed.

In terms of (18), (19) and $h_{i}=\eta_{i}\frac{\beta_{i}+1}{(\beta_{i}-1)C_{i}B_{i}m_{i}}\rho_{i}$, it can be observed that

Since

one can see that

by virtue of η _i >1. According to Lemma 1, the reaching condition is established. Thus, the proof is completed. □

During the proof of Theorem 1, the relation in (9) is utilized, then an adjustment strategy for the quantization parameter μ _i is required to ensure its establishment. In this paper, a simple and effective design of the adjustment law is developed based on Lemma 2.

The adjustment law of the quantization parameter μ _i

• If |C _i x _i |≥1, then we can take $\mu_{i}=\frac{\lfloor|C_{i}x_{i}|\rfloor}{(\beta_{i}+1)|C_{i}|\varDelta _{i}}$;

• If 0<|C _i x _i |<1, fix a positive constant θ _i , (0<θ _i <1) a prior, thus there exists a positive integer l _i such that $\theta_{i}^{l_{i}}\leq|C_{i}x_{i}|<\theta_{i}^{l_{i}-1}$, then we take $\mu_{i}=\frac{\theta_{i}^{l_{i}}}{(\beta_{i}+1)|C_{i}|\varDelta _{i}}$;

• If |C _i x _i |=0, it means the state trajectory of the ith subsystem stays on the sliding surface s _i (t)=0, one can choose μ _i =0 in this case.

From the design above, it is easy to see that it is a static adjustment law.

Remark 3

According to the adjustment law of the quantization parameters, it requires to obtain the information of parameters ⌊|C _i x _i |⌋, β _i , C _i , Δ _i , θ _i , and l _i at the controller side. Parameters C _i , θ _i , and β _i are all given in advance by the designer, and $\varDelta _{i}=\frac{\sqrt{n_{i}}}{2}$ depends only on the dimension of the ith subsystem, then they all can be known on both sides of the digital channel. The rest parameters, l _i and ⌊|C _i x _i |⌋ are integers, then they can be easily transmitted from the coder side to the decoder side over the digital channel. Hence, the quantization parameter μ _i can be achieved perfectly on the decoder side. As a result, the quantization state signal $q_{\mu_{i}}(x_{i})$ can be obtained at the controller side since it is the integer multiple of the parameter μ _i by the definition of quantizers.

Remark 4

In this paper, the term “decentralized” means that the controller design of the ith subsystem only evolves the signals of the ith subsystem, that is, the quantized state signals used in the ith subsystem are $q_{\mu_{i}}(x_{i})$ while without utilizing $q_{\mu_{j}}(x_{j})$, j=1,2,…,N, j≠i. It is consistent with the notion of decentralized control, please see [2] for details.

4 Simulation results

Consider a large-scale interconnected system composed of two subsystems with the system parameters:

$$\varPhi_{1}(u_{1})= \left \{ \begin{array}{l@{\quad}l} 1.2e^{-0.1\sin(t)}(u_{1}-u_{10}),& u_{1}>u_{10}, \\ 0,& |u_{1}|\leq u_{10}, \\ 1.2e^{-0.1\sin(t)}(u_{1}+u_{10}),& u_{1}<-u_{10}, \end{array} \right . $$

and

$$\varPhi_{2}(u_{2})= \left \{ \begin{array}{l@{\quad}l} 1.3e^{-0.5\cos(t)}(u_{2}-u_{20}),& u_{2}>u_{20}, \\ 0,& |u_{2}|\leq u_{20}, \\ 1.3e^{-0.5\cos(t)}(u_{2}+u_{20}),& u_{1}<-u_{20}. \end{array} \right . $$

It is easy to check that ∥ΔA ₁(t)∥≤0.5 and ∥ΔA ₂(t)∥≤0.5, the interconnected terms f ₁(t,x,p) and f ₂(t,x,p) satisfy Assumption 2 with k ₁₀=0.1, k ₂₀=0.1, $k_{12}^{2}=0.2$, $k_{21}^{2}=0.2$, $k_{21}^{1}=0.3$, and $k_{12}^{1}=0.3$, and he dead-zone input nonlinearity satisfies Assumption 3 with m ₁=1 and m ₂=1.

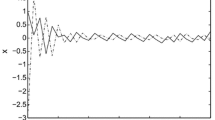
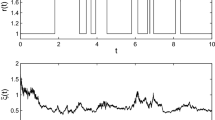
In the simulation, the linear switching surfaces of the two subsystems are selected to be s ₁(t)=1.5x ₁₁+x ₁₂=0 and s ₂(t)=3x ₂₁+x ₂₂=0. For simulation, let us choose the initial values of the two subsystems are x ₁(0)=[1 2]^T and x ₂(0)=[1 1]^T, respectively. The related parameters required for the simulation are selected as u ₁₀=1, u ₂₀=1, η ₁=1.5, η ₂=1.5, β ₁=5, β ₂=5, θ ₁=0.5, and θ ₂=0.5. The simulation results with the proposed method are shown in Figs. 1–6.

Fig. 1

Evolution of state variables x ₁

Fig. 2

Evolution of state variables x ₂

Fig. 3

Evolution of the sliding surface s ₁(t)

Fig. 4

Evolution of the sliding surface s ₂(t)

Fig. 5

Evolution of the quantization parameter μ ₁

Fig. 6

Evolution of the quantization parameter μ ₂

For comparison, the corresponding results with static uniform quantizers are presented in Figs. 7, 8, 9 and 10, with μ ₁=0.4 and μ ₂=0.4. It can be observed that with the proposed adjustment policy for the quantizer parameters, the state trajectories of each subsystem can be driven to the desired sliding surface and then better convergence performance of the state trajectories is achieved.

Fig. 7

Evolution of state variables x ₁

Fig. 8

Evolution of state variables x ₂

Fig. 9

Evolution of the sliding surface s ₁(t)

Fig. 10

Evolution of the sliding surface s ₂(t)

5 Conclusions

In this paper, the robust quantized feedback stabilization problem for a class of uncertain large-scale systems has been addressed. With the proposed static adjustment law of the quantizer parameters, a decentralized sliding mode quantized feedback control strategy is developed to tackle dead-zone input nonlinearity, interconnected nonlinearities, and matched/mismatched uncertainties simultaneously. It ensures that the state trajectories of each subsystem can converge to the corresponding subsystem sliding manifold. Finally, simulation results demonstrate the effectiveness of the proposed method.

Appendix: Proof of the technical lemma

Proof of Lemma 2

First, it is obvious that the inequality

(22)

is satisfied by virtue of (5). Next, we will illustrate that the inequality $|C_{i}|\varDelta _{i}\mu_{i}\leq\frac{1}{\beta_{i}}|C_{i}q_{\mu_{i}}(x_{i})|$ holds when the parameter μ _i satisfies $0<\mu_{i}\leq\frac{|C_{i}x_{i}|}{(\beta_{i}+1)|C_{i}|\varDelta _{i}}$.

Multiplying (β _i +1)|C _i |Δ _i from both sides of (8), we have

(23)

Subtracting |C _i |Δ _i μ _i from both sides of the above inequality (23), one can obtain

Furthermore, combined with inequality (22), it is easy to check that

Owing to the triangle basic inequality |a−b|≥|a|−|b|,∀a∈ℝ,b∈ℝ, it follows that

Utilizing the relationship $q_{\mu_{i}}(x_{i})=x_{i}+e_{\mu_{i}}$, one can see that

(24)

Therefore, by virtue of (22) and (24), it can be seen that (9) is obtained. Thus, the proof is completed. □