Anti-windup strategy for interval positive linear systems with input saturation

Abstract

This article discusses an approach to designing an anti-windup gain for an interval positive linear system (PLS) with input saturation in a continuous time framework. The suggested approach demonstrates that the closed-loop system with a controller and the anti-windup gain can be described by a PLS with a dead-zone nonlinearity. The stability analysis for a region of admissible initial states is shown using the Lyapunov function wherein a sector condition is used. Also, a linear matrix inequality (LMI)-based optimization is proposed for maximizing the domain of stability associated with the closed-loop system. For ease of synthesis, the methodology is proposed through conditions incorporated in LMIs. The viability of the proposed method is illustrated through simulation studies.

1 Introduction

Dynamical systems whose state trajectories initiate from non-negative initial conditions and consistently remain within the positive orthant for all non-negative inputs are referred to as positive systems. It is noteworthy that, in these systems, all state variables are invariably constrained to be non-negative throughout their evolution [1, 2]. Positive systems find application in various domains, including bio-medicine [3, 4], industrial engineering [5], pharmacokinetics [6], chemical engineering [7], ecology [8], and numerous other fields. The diverse range of applications underscores the significance of exploring various facets of positive systems.

One distinctive characteristic of positive systems is their inherent complexity when compared to conventional linear systems. Positive systems are defined within cones, as opposed to linear systems, which are defined within linear spaces. This distinction has led to substantial research on the stability domain, control and stabilization of PLSs [9,10,11]. Furthermore, research efforts have been dedicated to the study of PLSs with uncertainties [12, 13], as uncertainties in system parameters are inevitable due to factors such as data acquisition limitations [14], plant variability [3], measurement errors, stochastic environmental disturbances [15], and more. Numerous controller design approaches have been proposed to address interval uncertainties in PLSs [16, 17].

Many engineering applications evolving in the positive orthant are influenced by input saturation. For instance, biomedical control systems regulate physiological variables that remain in the positive orthant. In this context, control input, typically administered through drug delivery, is implemented using pumps. Likewise, in process control systems, variables such as level, flow, and pressure are consistently positive. In all these scenarios, system-level constraints and the operational range of physical actuators introduce the effects of saturation. Input saturation, where the input signal to a system is confined within specific limits, is a common phenomenon in practical systems [18]. This limitation can result from physical constraints, actuator limitations, or design specifications. The presence of actuator saturation can compromise system performance, leading to reduced tracking accuracy, slower response times, and increased steady-state errors. Consequently, the analysis and design of control systems to address these challenges become imperative.

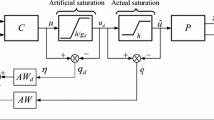
Traditionally, two main approaches have been documented in the literature for addressing the saturation issue: (i) Initially designing a controller to meet performance requirements without considering saturation and subsequently modifying the controller using an anti-windup compensator to mitigate the undesirable effects of actuator saturation [19,20,21]. (ii) Developing a controller while accounting for actuator saturation from the outset. The first approach, known as anti-windup design, is often favored because it allows for the design of controllers using standard techniques suited to the specific system and later modifies them to handle the effects of saturation. These anti-windup compensators operate specifically during saturation periods, ensuring both the maintenance of internal stability within the closed-loop system and the mitigation of performance degradation caused by actuator saturation. During the earlier stages of anti-windup research, it was commonly believed that windup phenomena were solely attributable to the integral part of the controller. The ‘anti-reset windup’ concept which involved modifying the integral part of the controller to circumvent actuator saturation is introduced in [22]. A similar method, known as the conventional anti-windup technique, was presented in [23], focusing on modifying the control input instead of altering the integral part of the controller. Subsequently, in [24], a linear conditioning technique was introduced as an extension of the ‘back-calculation strategy’ originally outlined in [22]. This approach involves shaping the reference input through an additional feedback loop triggered at the moment of actuator saturation. A block diagram illustrating a conventional anti-windup scheme for managing actuator saturation is depicted in Fig. 1.

Fig. 1

Block diagram of a system with actuator saturation and anti-windup

Numerous noteworthy control methodologies are discussed in the literature, including proportional (P) [11], proportional-integral (PI) [25], proportional-derivative (PD) [26], and proportional-integral-derivative (PID) controllers [27]. The PID controller finds extensive application in diverse industrial processes, due to its comprehensible structure in comparison with more complex controllers. However, saturation is a significant consideration in PID control systems because it can impact the system’s performance and stability. When a controller output saturates, it may lead to issues such as integral windup and reduced responsiveness. Integral windup can occur when the integral term of the PID controller continues to accumulate error even when the system is at its limits, leading to overshooting or oscillations when the saturation is lifted. To mitigate saturation-related challenges, anti-windup mechanisms are often employed in PID controllers. Anti-windup techniques are essential in positive systems to effectively manage integrator windup, ensuring system stability, performance optimization, and actuator protection. By carefully limiting the accumulation of error in the integral term and resetting it appropriately when control saturation occurs, these techniques prevent overshooting, maintain steady-state accuracy, and minimize actuator stress. In positive systems, the linearity and time-invariance properties facilitate the analysis and implementation of anti-windup mechanisms, allowing for efficient and reliable control of complex systems while extending the operational lifespan of critical components.

The study of controller design for PLSs with saturating inputs has been a subject of investigation, as evidenced by reference [28] and other related works [19,20,21, 29], primarily focused on linear systems. Actuator saturation has been a prominent concern in these studies, exerting a substantial impact on PLSs behavior. This effect introduces nonlinearity, compromises system performance, complicates stability analysis, and necessitates special considerations in control design. Consequently, comprehending and accommodating input saturation effects are indispensable for effectively modeling, analyzing, and controlling PLSs in real-world applications. However, it is worth noting that the existing literature has shown a gap in addressing PLSs with interval uncertainties and actuator saturation. This particular gap in research has motivated the current study.

In this proposed work, the author seeks to employ an anti-windup design procedure to alleviate the influence of input saturation on a positive system when it is subjected to interval uncertainties. The major contributions of the proposed work are outlined as follows:

• 1. Addresses actuator saturation in PLSs with interval uncertainties by incorporating an anti-windup gain to guarantee stability in the presence of actuator saturation.

• 2. Determines the stability region of the closed-loop systems using a quadratic Lyapunov function and a modified sector condition.

• 3. Identifies initial states ensuring asymptotic convergence toward the origin.

• 4. Establishes sufficient conditions in the form of LMIs for theoretical validation.

• 5. The article upholds the use of convex optimization to maximize the area of asymptotic convergence while ensuring closed-loop system stability.

The subsequent section of the manuscript is organized as follows. Section 2 presents the problem statement and provides a description of the system. Theoretical aspects pertaining to stability analysis and computation of anti-windup gain are elaborated in Sect. 3 using a convex optimization problem. The effectiveness of the proposed approach is demonstrated through simulation results in Sect. 4, followed by the conclusion in 5, which concludes the paper.

Notations: Let $\mathbb {R}$ represent the set of real numbers, $\mathbb {R}^{m\times n}$ represents the set of $m\times n$ matrices with elements from $\mathbb {R}$, $\mathbb {R}^n$ denotes the Euclidean space of n dimensions and $\mathbb {R}_+^n$ refers to the non-negative orthant in $\mathbb {R}^n$. $A_1\in [\underline{A_1},\overline{A_1}]$ means $\underline{A_1} \le {A_1} \le \overline{A_1}$ (entrywise) for any matrices $A_1$, $\underline{ A_1}$, and $\overline{A_1}$. The $i^{th}$ row of matrix X is denoted by $X_{(i)}$. $I_n$ denotes the $n^{th}$- order identity matrix. $X^T$ represents the transpose of matrix X. The minimum and maximum eigenvalues of matrix X are denoted by $\lambda _{min} (X)$ and $\lambda _{max} (X)$, respectively. $\hbox {Co}\{\cdot \}$ denotes the convex hull of a set.

2 Problem formulation

Considering the continuous time interval PLS as:

$$\begin{aligned} \begin{aligned} \dot{x_s}(t)&=A_sx_s(t)+B_su_s(t)\\ y_s(t)&=C_sx_s(t) \end{aligned} \end{aligned}$$

(1)

with initial conditions described as:

$$\begin{aligned} x_s(t_0)=\sigma _{x} \ge 0, \quad \forall ~t \in \mathbb {R}_{+}. \end{aligned}$$

where system state $x_s(t)=x_s\in \mathbb {R}_+^n$, control input $u_s(t)=u_s\in \mathbb {R}_+^m$ and measured output $y_s(t)=y_s\in \mathbb {R}_+^r$, $A_s \in [\underline{A_s}$, $\overline{A_s}]$, $B_s \in [\underline{B_s}$, $\overline{B_s}]$, $C_s \in [\underline{C_s}$, $\overline{C_s}]$ are constant matrices with known bound. Also, $A_s\in \mathbb {R}^{n \times m}$ is Metzler (its off-diagonal entries are all non-negative, i.e., for all (i, j) such that $i\ne j$, $[A_s]_{ij}\ge 0$ entrywise), ${B_s} \ge 0 \in \mathbb {R}^{n \times m}$, ${C_s} \ge 0 \in \mathbb {R}^{r \times n}$.

Definition 1

( [16]): The system defined by equation (1) is a positive system if for any given non-negative initial condition $x_s(t_0)=\sigma _x\ge 0,~\forall ~t \ge 0$ and input $u_s \ge 0$ its state trajectory never becomes negative, i.e., $x_s\in \mathbb {R}_{+}^n, ~\forall ~ t \ge 0$.

A positive dynamic output-feedback stabilizing controller (in this case observer-based controller) has been formulated guaranteeing performance requirements and closed-loop system stability without control saturation as:

$$\begin{aligned} \begin{aligned} \dot{\vartheta _c}&=A_c\vartheta _c+B_c y_s\\ \Phi _c&=C_c\vartheta _c+D_c y_s \end{aligned} \end{aligned}$$

(2)

where controller state $\vartheta _c\in \mathbb {R}_+^n$, controller output $\Phi _c\in \mathbb {R}_+^{m}$ and $A_c$, $B_c$, $C_c$, $D_c$ are real matrices of well-suited dimensions, with $A_c$ being a Metzler matrix. These matrices can be obtained based on (Theorem 5 and Theorem 7, ( [16])).

Now taking actuator saturation into effect, the control input to the system (2) is described as:

$$\begin{aligned} u_s=sat(\Phi _c)=sat(C_c\vartheta _c+D_c y_s) \end{aligned}$$

(3)

where $sat(\Phi _{c(i)})=\hbox {sgn}(\Phi _{c(i)})\hbox {min}\left[ u_{0(i)}, |\Phi _{c(i)}|\right]$ with $u_{0(i)}>0$ for $i=\{1, 2, \cdots m\}$ and the input vector $u_s$ has the amplitude limitation of $0\le u_{s(i)}\le u_{0(i)}$.

To mitigate the adverse impacts of actuator saturation, the controller design has been updated with an anti-windup term $E_0 (sat(\Phi _c)-\Phi _c)$, where $E_0 \in \mathbb {R}^{n\times m}$ is an anti-windup gain. The modified controller design is:

$$\begin{aligned} \begin{aligned} \dot{\vartheta _c}&=A_c\vartheta _c+B_c y_s+E_0(sat\left( \Phi _c\right) -\Phi _c) \\ \Phi _c&=C_c\vartheta _c+D_c y_s. \end{aligned} \end{aligned}$$

(4)

Defining the error of the system and proceeding further,

$$\begin{aligned} \begin{aligned} e_r&=x_s-\vartheta _c \\ \dot{e_r}&=\dot{x_s}-\dot{\vartheta _c} \end{aligned} \end{aligned}$$

(5)

The compensated closed-loop system is described with an augmented vector, $\rho =\begin{bmatrix} x_s&e_r\end{bmatrix}^{T}\in \mathbb {R}_+^{2n}$ and a dead-zone nonlinearity function, $\psi (\Phi _c)= \Phi _c-sat(\Phi _c)$ as follows:

$$\begin{aligned} \dot{\rho }=A_1\rho -(B_1+RE_0)\psi (\Phi _c) \end{aligned}$$

(6)

where $\Phi _c=K \rho ~ \hbox {with} ~K=\begin{bmatrix}(D_c C_s+C_c)&- C_c \end{bmatrix}$ and

$$\begin{aligned} A_1&= \begin{bmatrix} A_s+B_s C_c+B_sD_c C_s &{} -B_s C_c\\ A_s-A_c-B_c C_s+B_s C_c+B_sD_c C_s &{} A_c-B_sC_c \end{bmatrix},\\ B_1&=\begin{bmatrix} B_s&B_s\end{bmatrix}^{T}, \quad R=\begin{bmatrix} 0&I_{n}\end{bmatrix}^{T}. \end{aligned}$$

In general, $\psi (\Phi _c)$ corresponds to a dead-zone nonlinearity

$$\begin{aligned} \psi (\Phi _c)=[\psi (\Phi _{c(1)}) \cdots \psi (\Phi _{c(m)}) ]^T, \hspace{0.3cm} \text {where} \hspace{0.3cm} \forall i=1,\cdots ,m \\ \psi (\Phi _{c(i)})={\left\{ \begin{array}{ll} \Phi _{c(i)} -u_{0(i)} &{}\text {if} \quad \Phi _{c(i)} >u_{0(i)} \\ 0 &{}\text {if} \quad -u_{0(i)}\le \Phi _{c(i)} \le u_{0(i)}\\ \Phi _{c(i)} +u_{0(i)} &{}\text {if} \quad \Phi _{c(i)} <-u_{0(i)} \end{array}\right. } \end{aligned}$$

In this case, the input vector $u_s$ has the amplitude limitation of $0\le u_{s(i)}\le u_{0(i)}$ with $u_{0(i)}>0$ for $i=\{1, 2, \cdots m\}$ so, a dead-zone nonlinearity function, $\psi (\Phi _c)= \Phi _c-sat(\Phi _c)$ is considered. The augmented system (6) acknowledges an augmented initial condition as:

$$\begin{aligned} \rho (t_0)=\sigma _\rho =\begin{bmatrix}x_s(t_0) \\ e_r(t_0) \end{bmatrix}=\begin{bmatrix}\sigma _x \\ \sigma _e \end{bmatrix}\ge 0, \quad \forall ~t\in \mathbb {R}_+. \end{aligned}$$

The global asymptotic stability of the system described in equation (6) is ensured when the initial condition satisfies $\sigma _{\rho }\ge 0 \in \varepsilon (P)$, where $\varepsilon (P)$ represents an ellipsoidal cone defined as: $\varepsilon (P)=\{\rho \in \mathbb {R}_+^{2n}: \rho ^TP\rho \le 1\}$. This stability condition guarantees that the system trajectories converge toward the origin.

In this note, the aim is to search for a solution to the summarized problem.

Remark 1

The problem at hand is to design an anti-windup gain $E_0$ for the augmented system such that a large domain of asymptotic stability can be determined. This task involves careful consideration of the system’s behavior under windup conditions, and finding a gain that can effectively prevent windup while ensuring stability. Thus, the objective is to design an anti-windup gain minimizing the impact of input saturation.

3 Main results

3.1 Stability analysis

• 1. The augmented system (6) without the control bound is globally stable if matrix $A_1$ is Hurwitz Metzler matrix.

• 2. With matrices $J, K\in \mathbb {R}_+^{m\times 2n}$, a polyhedral set Q is defined as:

  $$\begin{aligned} Q(K,J,u_0)\cong \{\rho \in \mathbb {R}_+^{2n};~|{(K_{(i)}-J_{(i)})\rho |\le u_{0(i)}}\} \end{aligned}$$

  (7)

  where, $i=\{1, 2, \cdots m\}$ with $u_{0(i)}>0$ and $J_{(i)},K_{(i)}$ are the $i^{th}$ row of matrix J and K, respectively.

Lemma 1

Considering the nonlinearity $\psi (\Phi _c)$, if $\rho \in Q(K,J,u_0)$ then for any diagonal and positive definite matrix $T\in \mathbb {R}_+^{m\times m}$, the following relation holds good:

$$\begin{aligned} \psi (\Phi _c)^T T[\psi (\Phi _c)-J\rho ]\le 0. \end{aligned}$$

(8)

Proof

Proof of this Lemma 1 is similar to the proof of Lemma 1,( [20]). $\square$

The domain of stability of the closed-loop system (6) using the Lyapunov function is evaluated as follows.

A Lyapunov function is chosen as:

$$\begin{aligned} V(\rho )={\rho }^TP\rho ~\hbox {where} ~P=P^T>0. \end{aligned}$$

(9)

For the augmented system described by equation (6) to be asymptotically stable certain conditions are derived using the Lyapunov function and accordingly anti-windup gain, $E_0$ matrix is to be computed.

Theorem 1

For the asymptotic stability of the augmented system (6) there should exists a positive definite symmetric-matrix $X\in \mathbb {R}^{2n\times 2n}$, a matrix $Y\in \mathbb {R}^{m\times 2n}$, a matrix $Z\in \mathbb {R}^{n\times m}$ and a diagonal positive definite matrix $W\in \mathbb {R}^{m\times m}$ which satisfies:

$$\begin{aligned} \begin{bmatrix} XA_1+(A_1)^TX &{} B_1W+RZ-Y^T \\ W{B_1}^T+Z^TR^T-Y &{} -2W \end{bmatrix}<0 \end{aligned}$$

(10)

$$\begin{aligned} \begin{bmatrix} X &{} X{K_{(i)}}^T-{Y_{(i)}}^T\\ K_{(i)}X-Y_{(i)} &{} u^2_{0(i)} \end{bmatrix}\ge 0, \end{aligned}$$

(11)

Then gain matrix is found as $E_0=ZW^{-1}$, such that the ellipsoidal cone $\varepsilon (P)=\{\rho \in \mathbb {R}_+^{2n};~\rho ^TP\rho \le 1\}$, with $P=X^{-1}$, is an asymptotic stability region of system (6).

Proof

Considering $J=YX^{-1}$ to satisfy relation (11), indicates that the polyhedral set Q defined above includes the ellipsoidal cone $\varepsilon (P)$. From Lemma 1, it can be inferred that $\forall \rho \in \varepsilon (P)$, $\psi (\Phi _c)= \Phi _c-sat(\Phi _c)$ satisfies the sector condition (8). Computing time derivative of Lyapunov function along trajectories of the augmented system.

(12)

(13)

Using sector condition (8),

$$\begin{aligned} \dot{V}(\rho )&\le \dot{V}(\rho )-2\psi (K\rho )^TT\psi (K\rho )\nonumber \\&\quad +2\psi (K\rho )^TTJ\rho ~~~\forall \rho \in \varepsilon (P) \end{aligned}$$

(14)

$$\begin{aligned} \dot{V}(\rho )&=\begin{bmatrix} \rho ^T&-\psi (K\rho )^T\end{bmatrix}\\&\quad \begin{bmatrix} PA_1+A_1^TP &{} P(B_1+RE_0)-J^TT^T\\ (B_1+RE_0)^TP-TJ &{} -2T\end{bmatrix}\\&\quad \begin{bmatrix} \rho \\ -\psi (K\rho )\end{bmatrix} \end{aligned}$$

For the system to be stable, the below inequality should be satisfied.

$$\begin{aligned} \begin{bmatrix}PA_1+A_1^TP &{} P(B_1+RE_0)-J^TT^T\\ (B_1+RE_0)^TP-TJ &{} -2T\end{bmatrix}<0\nonumber \\ \end{aligned}$$

(15)

Also, equation (15) is pre- and post-multiplied by

$$\begin{aligned} \begin{bmatrix}P^{-1} &{} 0\\ 0 &{} T^{-1}\end{bmatrix}\end{aligned}$$

and taking $P^{-1}=X$, $T^{-1}=W$, $Y=JX$, $E_0=ZW^{-1}$ equation (15) is equivalent to

$$\begin{aligned} \begin{bmatrix} A_1X+XA_1^T &{} B_1W+RZ-Y^T\\ W{B_1}^T+Z^TR^T-Y &{} -2W\end{bmatrix}<0. \end{aligned}$$

(16)

Now, when equation (10) is satisfied $\forall {\rho }\in \varepsilon (P)$, where $\rho \ne 0$ then, $\dot{V}(\rho )<0$. Hence, it can be concluded that $\varepsilon (P)$ is a positively invariant and contractive region for the closed-loop system (6) which implies that for any $\rho (0)\in \varepsilon (P)$, the corresponding trajectories of the system converges asymptotically to the origin, i.e., $\varepsilon (P)$ is the domain of asymptotic stability for the augmented system (6). $\square$

3.2 Estimation of basin of attraction

The asymptotic stability of the system, defined by Eq. (6), is affirmed for all admissible initial conditions given by a polyhedral set formed by the convex hull of its vertices as $\Pi \cong \hbox {Co}\{\nu _1,\nu _2,\cdots \nu _{n_r}\},~\nu _r\in \mathbb {R}^{2n} ~(\text {where} ~r=1,2,\cdots n_r)$. In this Section, a convex optimization technique is presented where optimization implicitly implies the maximization of the approximation of the basin of attraction linked to it (i.e., $\beta \Pi \subset \varepsilon (P)$) where $\beta$ is a scaling factor. So, for obtaining a set $\varepsilon (P)$ with significant size, the optimization problem (eigenvalue problem [30]) is given as:

$$\begin{aligned} \begin{aligned}&\min \limits _{X,Y,Z,W}\{\alpha \gamma \} \\&\hbox {subject to}\\&\hbox {relation (10) and (11) with}\\&\begin{bmatrix}\gamma &{} \nu _{r}^T\\ \nu _{r} &{} X\end{bmatrix}\ge 0. \end{aligned} \end{aligned}$$

(17)

where $\alpha$ is the tuning parameter, $\gamma =\lambda _{max} (X^{-1})$ and $\frac{1}{\beta ^2}=\gamma$.

Also, $\beta =\frac{1}{\sqrt{\lambda _{max} (X^{-1})}}$, the minimization of $\lambda _{max} (X^{-1})$ infers maximization of $\beta$. The relation, $\beta \Pi \subset \varepsilon (P)$ is satisfied by LMI condition (17).

This optimization is useful for illustrating the anti-windup benefit, across broad asymptotic stability domains. With the new $E_0$ design, an estimate of the basin of attraction of the improved closed-loop system can be made larger, guaranteeing the stability of the system under interval uncertainties and input saturation.

4 Illustrative examples

Example 1: Consider a two compartment mammillary model as depicted in Fig. 2 where $m_{ij}$ represent flow rate constants. Such model has wide range of applicability in the area of pharmacokinetics for analysis of certain body metabolism.

Fig. 2

Mammillary model with two compartments

The system parameters for the compartmental system (borrowed from [17]) are:

$$\begin{aligned} A_s&=\begin{bmatrix}-(m_{11}+m_{21})&{} m_{12}\\ m_{21} &{} -(m_{22}+m_{12}) \end{bmatrix}; \\ B_s&=\begin{bmatrix} b_1 &{} 0\\ 0 &{} b_2 \end{bmatrix}; ~~C_s=\begin{bmatrix} n_{11}&0 \end{bmatrix} \end{aligned}$$

The elements of the bounded matrices $\underline{A_s}, \overline{A_s}, \underline{C_s}, \overline{C_s}$ are derived from:

$$\begin{aligned}&m_{11}=1.2\pm 0.042,~ m_{12}=0.3\pm 0.061, ~m_{21}=0.5\pm 0.045,\\ {}&m_{22}=0.6\pm 0.140, ~n_{11}=1\pm 0.1, ~b_1=1,~b_2=1. \end{aligned}$$

Fig. 3

Plot of $x_{s_1}(t)$ state without saturation compensation

Now, considering the observer-based controller design approach [16] for the interval positive system in the above-mentioned compartmental system, the following state observer matrices G, L, and controller matrix K are obtained.

$$\begin{aligned} G&=\begin{bmatrix} -11.0313 &{} 6.1204\\ 8.0419 &{} -13.6149\end{bmatrix}; \quad L=\begin{bmatrix} 5.8297 \\ 17.8711\end{bmatrix};\\ K&=\begin{bmatrix}-0.4214 &{} -0.1212\\ -2.0942 &{} -0.8231\end{bmatrix}. \end{aligned}$$

Further, the above-designed observer-based controller for the interval positive system without saturation is compared with Eq. (2) and then considering input saturation in the system, the procedure for anti-windup gain design is followed with random control bounds $u_{0(i)}=\begin{bmatrix}1&1\end{bmatrix}^T$ and tuning parameters $\alpha =1$. Now, solving the LMI conditions in (17) following results are obtained.

Fig. 4

Plot of $x_{s_2}(t)$ state without saturation compensation

Fig. 5

Plot of control inputs without saturation compensation

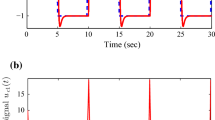
Figure   3 and 4 depict the states of the plant with (dashed curve) and without (solid curve) controller action with $E_0=0$ by taking three random sample of the uncertain system matrices A and C. It can be observed that the multiple trajectories evident the uncertain system and due to the saturation effect the trajectories of the system do not converge asymptotically to zero. Figure  5 shows the control signal for $E_0=0$ where saturated control input can easily be depicted. Furthermore, Figs. 6 and 7 depict the states of the plant with and without controller action with designed $E_0$ and it can be mentioned that the anti-windup greatly improved the time response and lead the system’s trajectories asymptotically to zero. Figure  8 shows that the control signal for the designed $E_0$ remained saturated for a small duration of time. Table 1 illustrates certain system parameters for comparison of performance with $E_0=0$ and with designed $E_0$. It is evident that with designed $E_0$, the system performance is improved, particularly in relation to settling time and steady-state error.

Fig. 6

Plot of $x_{s_1}(t)$ state with saturation compensation

Fig. 7

Plot of $x_{s_2}(t)$ state with saturation compensation

Fig. 8

Plot of control inputs with saturation compensation

Figure 9 illustrates the domain of stability projected onto the plane $(x_1,x_2)$, which corresponds to the states $x_{s_1}$ and $x_{s_2}$ of the plant with unstable equilibrium points $\pm [0.8709 ~~1.6015]^{T}$; which are very close to the edge of the obtained domain of stability. Being positive system, the equilibrium point lying in the positive orthant has to be taken into account in this context. Thus, proving the efficiency of the proposed approach in providing potentially a good approximation of the basin of attraction.

Table 1 Comparison of system parameters

Fig. 9

Stability domain

5 Conclusions and future works

An approach of anti-windup design to mitigate the saturation effect in a PLS with interval uncertainty in system parameters has been proposed with conditions solvable in LMI framework. The demonstrated controller shows its effectiveness with guaranteeing the positivity of the system. While designing the anti-windup gain to investigate the stability aspects of the closed-loop system (6), a Lyapunov function is taken into consideration, and then the condition for anti-windup gain $E_0$ calculation is given with defined region of asymptotic stability. The Lyapunov stability utilizing convex optimization enables the design of $E_0$, resulting in a wider domain of asymptotic stability. The proposed control scheme is believed to be widely applicable in practical systems where a range of operations of the physical actuator involves the saturation effect. As a result, new avenues for investigation into more realistic scenarios involving delayed positive systems have opened up. This is viewed as one of the potential opportunities for developing this work further. Additionally, this paper is framed as an instance of applying a single proportional control in the controller design to address saturation effects. It would be valuable to investigate comprehensive PID controllers in future studies.