1 Introduction

Fractional systems are characterized by that each state described by a differential equation in systems is allowed to have an non-integer order. It has been found that fractional systems are fit for simulating many physical systems with memory hysteresis and diffusion dynamics [1,2,3], and can be successfully used in all kinds of fields on engineering and science such as viscous-elastic material, electronic device, colored noise, and so forth [4,5,6,7,8,9]. To this end, fractional systems have been received increasing attention in the past few years.

In some scenarios, the fractional systems may be with multi-order, which means that each differential equation of state has its own derivative order which may differ from the others. Compared with fractional systems with the identical order, multi-order fractional systems are more flexible in terms of order and may be more accurate in portraying some phenomena. Consequently, the attention of dynamic behavior analysis towards multi-order fractional systems has increased in recent years [10,11,12,13,14,15]. In [10], underpinning the theory of positive system, the asymptotic stability on multi-order fractional time-varying delayed system was addressed. In [13], the global boundedness of solution and asymptotic stability for nonlinear multi-order fractional systems were investigated. In [14], by proposing a multi-order comparison principle, the issue of asymptotic stability on the multi-order fractional system was discussed in detail.

Fractional neural networks are typical fractional systems. It has been substantiated that fractional neural networks with different dynamical behaviors can be successfully utilized in many applications [7,8,9, 16,17,18]. In particular, fractional neural networks with synchronization can effectively depict a number of physical phenomena and can be utilized in communication science, associative memory, combinational optimization, etc [19,20,21,22,23]. In view of this, plenty of efforts have been dedicated to investigate the synchronization on various fractional neural networks in current years [24,25,26,27,28,29,30]. For instance, the synchronization of fractional neural networks with unbounded time-varying delays was discussed in [26]. Some interesting results concerning the synchronization of fractional recurrent neural networks are presented in [27]. The cluster synchronization for fractional time delayed neural networks in finite-time sense and asymptotic sense were reported in [28]. Note that the current works about the synchronization of fractional neural networks are with identical derivative order.

In view that multi-order fractional neural networks are valuable generalizations of fractional neural networks with identical derivative order, they have widespread application potentials. However, in comparison with numerous results for the dynamic characteristics of fractional neural networks with identical derivative order, there are few works on the dynamical behavior analysis of multi-order fractional neural networks. Just in [15], the global stabilization for multi-order fractional neural networks based on memristor with multiple time-varying delays was reported. As far as authors know, there has been no report concerning the synchronization of multi-order fractional neural networks, in spite of their widespread application potentials.

In addition, the existence of time delays is ineluctability in designing neural networks owing to large-scale networks and limited channels of information transmission between neurons [31, 32]. In some scenarios, the time delays actually may be changed with regard to time and even unbounded. In the existing research results of multi-order fractional systems, the networks considered are with no delays or bounded time delays [10,11,12,13,14]. This stimulates us to discuss the synchronization of multi-order fractional systems with time-varying delays, wherein the delays considered are not assumed to be bounded.

Inspired by the above discussions, the synchronization of MoFNNs with time-varying delays is investigated in this paper. The main contributions of this paper include the following aspects: Firstly, by virtue of an inequality for multi-order fractional systems with time-varying delays, a vector Lyapunov function is introduced to investigate the synchronization of MoFNNs with time-varying delays. Secondly, in addition to the continuous control, a quantized control is introduced to realize the synchronization of MoFNNs, which effectively reduces the transmission pressure in the control. Finally, the systems investigated in this paper are of multiple order, which can be viewed as extensions of fractional systems investigated in [24,25,26,27,28,29,30]. And the criteria herein are also applicable to the synchronization of fractional systems with identical derivative order.

The remaining part of this paper is outlined as follows: Several definitions and lemmas about fractional calculus are introduced and the model description of MoFNNs is provided in Sect. 2. Sufficient criteria are deduced to guarantee the realization of synchronization on MoFNNs with time-varying delays in Sect. 3. Moreover, an example for verifying the validity and correctness of the results is given in Sect. 4. Finally, the conclusion is made in Sect. 5.

Notation: \(\mathbb {R}^{n\times n}\) and \(\mathbb {R}^{n}\) respectively represent the sets of \(n\times n\)-dimensional real matrices and n-dimensional real column vectors. \(B>0\) \((\in \mathbb {R}^{n\times n})\) signifies that B is positive definite. For \(z=(z_1,\cdots ,z_n)^{T}\in \mathbb {R}^{n}\), \(z>0\) \((<0)\) means that \(z_{i}>0\) \((<0)\) for \(i=1,2,\cdots ,n\). \(\mathbb {N}\) is the set of integers.

2 Preliminaries

In this section, several definitions and lemmas for the fractional calculus are introduced. Moreover, the model description of MoFNNs with time-varying delays is provided.

2.1 Definitions and Lemmas of Fractional Calculus

Definition 1

[33] The fractional integral of a vector function \(h(t)=(h_1(t),\cdots ,h_n(t))^T\) is denoted by \(D^{-\beta }_{t_{0}+}h(t)=(D^{-\beta _1}_{t_{0}+}h_1(t),\cdots ,D^{-\beta _n}_{t_{0}+}h_n(t))^T\), where

$$\begin{aligned} D^{-\beta _i}_{t_{0}+}h_i(t)=\frac{1}{\Gamma (\beta _i)}\int ^{t}_{t_{0}}(t-\iota )^{\beta _i-1}h_i(\iota ) d\iota ,~t\ge t_{0}, \end{aligned}$$

\(\beta =(\beta _1,\cdots ,\beta _n)^T\) with \(\beta _i>0\) for \(i=1,2,\cdots ,n\), \(\Gamma (z)=\int ^{\infty }_{0} \iota ^{z-1}e^{-\iota }d\iota \).

Definition 2

[33] The Caputo fractional derivative of a vector function \(h_i(t)\) is denoted by \(^{C}D^{\beta }_{t_{0}+}h(t)=(^{C}D^{\beta _1}_{t_{0}+}h_1(t),\cdots ,^{C}D^{\beta _n}_{t_{0}+}h_n(t))^T\), where

$$\begin{aligned} ^{C}D^{\beta _i}_{t_{0}+}h_i(t)=\frac{1}{\Gamma (1-\beta _i)}\int ^{t}_{t_{0}}(t-\iota )^{-\beta _i}\dot{h}_i(\iota ) d\iota ,~t\ge t_{0}, \end{aligned}$$

\(\beta =(\beta _1,\cdots ,\beta _n)^T\) with \(\beta _i\in (0, 1)\) for \(i=1,2,\cdots ,n\), \(\dot{h}_i(\iota )\) stands for the first-order derivative of \(h_i(\iota )\).

Lemma 1

[34] The fractional calculus of a continuously differentiable function \(z(t)\in \mathbb {R}\) obeys the following derivative rule:

$$\begin{aligned} ^{C}D^{\bar{\beta }}_{t_{0}+}z^{2}(t)\le 2z(t){^{C}D^{\bar{\beta }}_{t_{0}+}}z(t), \end{aligned}$$

where \(\bar{\beta }\in (0, 1)\) is a constant.

Definition 3

A matrix is called Metlzer matrix if its non-diagonal elements are non-negative; a matrix is called nonnegative matrix if its elements are non-negative; a matrix is Hurwitz matrix if all the eigenvalues have negative real parts.

The following lemma refers to the comparison principle for multi-order fractional time-varying delayed systems.

Lemma 2

[15] Assume that there exists a Metlzer matrix \(\beth \in \mathbb {R}^{n\times n}\) and a nonnegative matrix \(\daleth \in \mathbb {R}^{n\times n}\) such that the nonnegative vector \(y(t)=(y_{1}(t), \cdots , y_{n}(t))^{T}\in \mathbb {R}^{n}\) satisfies:

$$\begin{aligned} \left\{ \begin{array}{lll} ^{C}D_{t_{0}+}^{\beta }y(t)\le \beth y(t)+\daleth y(t-\tau (t)),\\ y(\iota )=\phi (\iota )\ge 0,~\iota \in [t_{0}-\vartheta , t_{0}]. \end{array} \right. \end{aligned}$$

where \(\beta =(\beta _1,\cdots ,\beta _n)^T\) with \(\beta _i\in (0, 1]\) for \(i=1,2,\cdots ,n\) and \(^{C}D^{\beta }_{t_{0}+}y(t)=(^{C}D^{\beta _1}_{t_{0}+}y_1(t),\cdots ,{^{C}D^{\beta _n}_{t_{0}+}y_n(t)})^T\); \(\tau (t)=(\tau _1(t),\cdots ,\tau _n(t))^T\) \((\in \mathbb {R}^{n})\) stands for the term of time delays which satisfies \(\tau _i(t)\le t+\vartheta \) (\(\vartheta >0\)) and \(\lim _{t\rightarrow +\infty }t-\tau _i(t)=+\infty \) for \(i=1,2,\cdots ,n\). If \(\beth +\daleth \) is a Hurwitz matrix, one has \(\lim _{t\rightarrow +\infty }y(t)=0\).

2.2 Model Description

Consider a multi-order fractional system consisting of N MoFNNs with time-varying delays, and the i-th MoFNN is introduced by

$$\begin{aligned} ^{C}D^{\beta }_{t_{0}+}x_{i}(t)=&-Ax_{i}(t)+Bh(x_{i}(t))+Fh(x_{i}(t-\tau (t)))\nonumber \\&+c\sum _{j=1}^{N}g_{ij}\Gamma x_{j}(t)+E+u_{i}(t), ~i=1,2,\cdots , N, \end{aligned}$$
(1)

where \(\beta =(\beta _{1},\cdots , \beta _{n})^{T}\) with \(\beta _{i}\in (0,1)\) (\(i=1,2,\cdots ,n\)) represents the multi-order vector; \(x_{i}(t)=(x_{i1}(t), \cdots , x_{in}(t))^{T}\in \mathbb {R}^{n}\) stands for the state vector and \(^{C}D^{\beta }_{t_{0}+}x_{i}(t)=({^{C}D^{\beta _{1}}_{t_{0}+}x_{i1}(t)},\cdots ,{^{C}D^{\beta _{n}}_{t_{0}+}x_{in}(t)})^{T}\); \(h(x_{i})=(h_{1}(x_{i1}), \cdots , h_{n}(x_{in}))^{T}: \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}\) stands for the activation function vector, which is continuously differentiable; \(\tau (t)=(\tau _{1}(t), \cdots , \tau _{n}(t))^{T}\) is the vector of time delays, which satisfies \(\tau _i(t)\le t+\vartheta \) (\(\vartheta >0\)) and \(\lim _{t\rightarrow +\infty }t-\tau _i(t)=+\infty \) for \(i=1,2,\cdots ,n\); constant c \(>0\) represents the coupling strength; \(A=\text {diag}(a_{1},\cdots ,a_{n})>0\) is the self-feedback matrix; \(B=(b_{pq})_{n\times n}\in \mathbb {R}^{n\times n}\) and \(F=(f_{pq})_{n\times n}\in \mathbb {R}^{n\times n}\) signify the connection and delayed connection weight matrices respectively; \(g_{ij}\) stand for the elements of coupling configuration matrix \(G=(g_{ij})_{N\times N}\) and obey the following rule: \(g_{ij}>0\) when there exist directed links from node j to i \((i\ne j)\), or else, \(g_{ij}=0\), and \(g_{ii}=-\sum _{j=1, j\ne i}^{N}g_{ij}\) \((i=1,2,\cdots ,N)\); \(\Gamma =\text {diag}(\gamma _{1},\cdots ,\gamma _{n})>0\) and \(E\in \mathbb {R}^{n}\) represents the inner coupling matrix and external input vector respectively. \(u_{i}(t)=(u_{i1}(t), \cdots , u_{in}(t))^T\in \mathbb {R}^n\) stands for the feedback control.

Remark 1

Due to the combination of the characteristics of fractional calculus and neural networks, fractional neural networks have been widely applied in many fields, such as system identification [8, 9], associative memory [7, 18, 19], secure communication [22], parameter estimation [23], and so forth. Particularly, as valuable generalizations for traditional fractional neural networks and with greater flexibility in fractional differential order, it is foreseeable that the MoFNNs will have a wide range of applications.

Let \(C([t_{0}-\vartheta , t_{0}], \mathbb {R}^{n})\) be the set of continuous function mapping \([t_{0}-\vartheta , t_{0}]\rightarrow \mathbb {R}^{n}\). The initial condition of MoFNN (1) has the form of

$$\begin{aligned} x_{ik}(\iota )=\phi _{ik}(\iota ),~\iota \in [t_{0}-\vartheta , t_{0}],~k=1,2,\cdots ,n, \end{aligned}$$

where \(\phi _i\in C([t_{0}-\vartheta , t_{0}], \mathbb {R}^{n})\).

In addition, the desired state of the multi-order fractional system is denoted by s(t), which satisfies

$$\begin{aligned} ^{C}D^{\beta }_{t_{0}+}s(t)=&-As(t)+Bh(s(t))+Fh(s(t-\tau (t)))+E, \end{aligned}$$
(2)

where \(^{C}D^{\beta }_{t_{0}+}s(t)=({^{C}D^{\beta _{1}}_{t_{0}+}s_{1}(t)},\cdots ,{^{C}D^{\beta _{n}}_{t_{0}+}s_{n}(t)})^{T}\), and s(t) could be viewed as a cycle orbit, an equilibrium point or even a chaos. The main objective in the following is to devise suitable controls \(u_i(t)\) so that the solutions in (1) could be synchronized with desired state s(t) in (2) as \(t\rightarrow +\infty \), i.e., \(\lim _{t\rightarrow +\infty }\Vert x_{i}(t)-s(t)\Vert =0\) for \(i=1,2,\cdots ,N\).

A necessary assumption is provided as follows:

Assumption 1

There exists positive constant \(w_{p}\) such that

$$\begin{aligned} \mid h_{p}(x)-h_{p}(y)\mid \le w_p \mid x-y\mid , ~\forall x,y\in \mathbb {R},~p=1,2,\cdots ,n. \end{aligned}$$
(3)

3 Main Results

In this section, the continuous control and quantized control are introduced respectively for achieving the synchronization of MoFNNs.

Without loss of generality, assume that the first \(l\in \mathbb {N}\) \((1\le l\le N)\) MoFNNs are picked to be pinned. Denote node 0 as a virtual node and \(d_{i}\) \((\ge 0)\) as the link weight from node 0 to i \((i=1, 2,\cdots , N)\), which meets that \(d_{i}>0\) for \(1\le i\le l\), otherwise, \(d_{i}=0\). Correspondingly, a graph \(\mathcal {G}\) is gained by combining original graph G, virtual node 0 along with the links from it to the first l nodes. The assumption on the graph \(\mathcal {G}\) is as follows:

Assumption 2

\(\mathcal {G}\) contains a direct spanning tree.

From Assumption 2, the following lemma is given.

Lemma 3

[35] Under Assumption 2, there exists a diagonal matrix \(\Omega =\text {diag}(\omega _{1},, \cdots , \omega _{N})\) \((>0)\) such that

$$\begin{aligned} (L+D)^{T}\Omega +\Omega (L+D)\ge \kappa \Omega , \end{aligned}$$
(4)

where \(L=(l_{ij})_{N\times N}\) is the Laplacian matrix of graph G, whose elements satisfy \(l_{ij}=-g_{ij}\) \((i,j=1,2,\cdots ,N)\); \(D=\text {diag}(d_1, \cdots , d_{N})\); \(\kappa =\lambda _{\min }((L+D)^{T}\Omega +\Omega (L+D))/\lambda _{\max }(\Omega )\) is a positive constant.

Denoting \(e_{i}(t)=x_{i}(t)-s(t)=(x_{i1}(t)-s_{1}(t),\cdots ,x_{in}(t)-s_{n}(t))^{T}\) as the error vector, the following error equation is obtained,

$$\begin{aligned} ^{C}D^{\beta }_{t_{0}+}e_{i}(t)=&-Ae_{i}(t)+B\bar{h}(e_{i}(t))+F\bar{h}(e_{i}(t-\tau (t)))\nonumber \\&+c\sum _{j=1}^{N}g_{ij}\Gamma x_{j}(t)+u_{i}(t), ~i=1, 2,\cdots , N, \end{aligned}$$
(5)

where \(\bar{h}(e_{i}(t))=h(x_{i}(t))-h(s(t))\) and \(\bar{h}(e_{i}(t-\tau (t)))=h(x_{i}(t-\tau (t)))-h(s(t-\tau (t)))\).

Due to the existence of different differential orders in the MoFNNs, it is not feasible to analyze the errors by using methods provided in [28, 29, 36, 37], which analyzes the error of each network as a whole. Instead, for i-th \((i=1,2,\cdots ,N)\) MoFNN, the error function of p-th \((p=1, 2,\cdots , n)\) neuron is introduced as follows:

$$\begin{aligned} ^{C}D^{\beta _{p}}_{t_{0}+}e_{ip}(t)=&-a_{p}e_{ip}(t)+\sum _{q=1}^{n}b_{pq}\bar{h}_{q}(e_{iq}(t))+\sum _{q=1}^{n}f_{pq}\bar{h}_{q}(e_{iq}(t-\tau _{q}(t)))\nonumber \\&+c\sum _{j=1}^{N}g_{ij}\gamma _{p} x_{jp}(t)-u_{ip}(t). \end{aligned}$$
(6)

3.1 The Synchronization of MoFNNs with Time-varying Delays Under a Continuous Control

Introduce a continuous control as follows:

$$\begin{aligned} u_{i}(t)=-cd_{i}\Gamma e_{i}(t), \end{aligned}$$
(7)

where constant \(d_{i}\) stands for the feedback gain with \(d_{i}>0\) if \(1\le i\le l\), otherwise, \(d_{i}=0\).

Denote \(\beth =-\text {diag}(2a_{1}-2n+c\kappa \gamma _{1}, 2a_{2}-2n+c\kappa \gamma _{2}, \cdots , 2a_{n}-2n+c\kappa \gamma _{n})+(b_{pq}^{2}w_{q}^{2})_{n\times n}\) and \(\daleth =(f_{pq}^{2}w_{q}^{2})_{n\times n}\), where \(\kappa =\lambda _{\min }((L+D)^{T}\Omega +\Omega (L+D))/\lambda _{\max }(\Omega )>0\) and \(D=\text {diag}(\overbrace{d_{1}, \cdots , d_{l}}^{l}, \overbrace{0, \cdots , 0}^{N-l})\). It can be observed that \(\beth \) is a Metlzer matrix and \(\daleth \) is nonnegative. Then, the following theorem about the synchronization of MoFNNs with time-varying delays under continuous control (7) is obtained.

Theorem 1

Under Assumptions 1 and 2, the synchronization of MoFNNs (1) can be realized via continuous control (7) if \(\beth +\daleth \) is a Hurwitz matrix.

Proof

Consider a vector Lyapunov function \(V(t)=(V_{1}(t), \cdots , V_{n}(t))^{T}\), and

$$\begin{aligned} V_{p}(t)=\frac{1}{2}\sum _{i=1}^{N}\omega _{i}e_{ip}^{2}(t)=\frac{1}{2}\epsilon _{p}^{T}(t)\Omega \epsilon _{p}(t), ~p=1,2,\cdots ,n, \end{aligned}$$
(8)

where \(\epsilon _{p}(t)=(e_{1p}(t), \cdots , e_{Np}(t))^{T}\), \(\Omega \) is defined in Lemma 3.

From Lemma 1 and (8), one has

$$\begin{aligned} ^{C}D_{t_{0}+}^{\beta _{p}}V_{p}(t)\le&\sum _{i=1}^{N}\omega _{i}e_{ip}(t)^{C}D_{t_{0}+}^{\beta _{p}}e_{ip}(t)\\ =&\sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (-a_{p}e_{ip}(t)+\sum _{q=1}^{n}b_{pq}\bar{h}_{q}(e_{iq}(t))\\&+\sum _{q=1}^{n}f_{pq}\bar{h}_{q}(e_{iq}(t-\tau _{q}(t)))+c\sum _{j=1}^{N}g_{ij}\gamma _{p} x_{jp}(t)-cd_{i}\gamma _{p}e_{ip}(t)\Big ). \end{aligned}$$

With Assumption 1, one arrives at

$$\begin{aligned} \sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (\sum _{q=1}^{n}b_{pq}\bar{h}_{q}(e_{iq}(t))\Big )\le&\frac{1}{2}\sum _{i=1}^{N}\omega _{i}\Big (ne_{ip}^{2}(t)+\sum _{q=1}^{n}b_{pq}^{2}w_{q}^{2}e_{iq}^{2}(t)\Big )\\ =&nV_{p}(t)+\sum _{q=1}^{n}b_{pq}^{2}w_{q}^{2}V_{q}(t). \end{aligned}$$

Similarly,

$$\begin{aligned} \sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (\sum _{q=1}^{n}f_{pq}\bar{h}_{q}(e_{iq}(t-\tau _{q}(t)))\Big )\le&\,\frac{1}{2}\sum _{i=1}^{N}\omega _{i}\Big (ne_{ip}^{2}(t)+\sum _{q=1}^{n}f_{pq}^{2}w_{q}^{2}e_{iq}^{2}(t-\tau _{q}(t))\Big )\\ =&\,nV_{p}(t)+\sum _{q=1}^{n}f_{pq}^{2}w_{q}^{2}V_{q}(t-\tau _{q}(t)). \end{aligned}$$

Moreover, it follows from Lemma 3 that

$$\begin{aligned} \sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (c\sum _{j=1}^{N}g_{ij}\gamma _{p} x_{jp}(t)-cd_{i}\gamma _{p}e_{ip}(t)\Big )=&\,c\gamma _{p}\epsilon _{p}^{T}(t)\Omega G\epsilon _{p}(t)-c\gamma _{p}\epsilon _{p}^{T}(t)\Omega D\epsilon _{p}(t)\\ =&\,-c\gamma _{p}\epsilon _{p}^{T}(t)\Omega (L+D)\epsilon _{p}(t)\\ =&\,-\frac{1}{2}c\gamma _{p}\epsilon _{p}^{T}(t)\big ((L+D)^{T}\Omega \\&\,+\Omega (L+D)^{T}\big )\epsilon _{p}(t)\\ \le&\,-\frac{1}{2}c\gamma _{p}\epsilon _{p}^{T}(t)\kappa \Omega \epsilon _{p}(t)\\ =&\,-c\kappa \gamma _{p}V_{p}(t). \end{aligned}$$

Combining the above inequalities yields to

$$\begin{aligned} ^{C}D_{t_{0}+}^{\beta _{p}}V_{p}(t)\le -(2a_{p}-2n+c\kappa \gamma _{p})V_{p}(t)+\sum _{q=1}^{n}b_{pq}^{2}w_{q}^{2}V_{q}(t)+\sum _{q=1}^{n}f_{pq}^{2}w_{q}^{2}V_{q}(t-\tau _{q}(t)). \end{aligned}$$

According to the definitions of \(\beth \) and \(\daleth \),

$$\begin{aligned} ^{C}D_{t_{0}+}^{\beta }V(t)\le&\beth V(t)+\daleth V(t-\tau (t)), \end{aligned}$$

where \(^{C}D_{t_{0}+}^{\beta }V(t)=(^{C}D_{t_{0}+}^{\beta _{1}}V_{1}(t),\cdots ,{^{C}D_{t_{0}+}^{\beta _{n}}}V_{n}(t))\). Since \(\beth +\daleth \) is a Hurwitz matrix, from Lemma 2, one arrives at \(\lim _{t\rightarrow +\infty }V(t)=0\), implying \(\lim _{t\rightarrow +\infty }\epsilon _{p}(t)=0\) for all \(p=1,2,\cdots ,n\). As a consequence, the synchronization of MoFNNs (1) is achieved via continuous control (7). \(\square \)

Remark 2

The vector Lyapunov function introduced in this paper can be seen as an extension of the scalar Lyapunov function in terms of dimensionality. In view of this, the vector Lyapunov function may be more advantageous than the scalar Lyapunov function in analyzing the dynamical behaviors of systems in certain situations. In [28, 29, 36, 37], the scalar Lyapunov function is utilized to investigate the dynamic behaviors of fractional systems with identical derivative order. Due to that the fractional systems of this paper are with different derivative orders, the scalar Lyapunov function cannot be directly utilized herein, and the vector Lyapunov function is introduced in Theorem 1 analyze the synchronization of MoFNNs.

Especially, if \(\beta _i\equiv \beta _0\) \((0<\beta _0<1)\) for \(i=1,2,\cdots ,n\), the MoFNN (1) and error system (5) can be respectively rewritten as

$$\begin{aligned} {^{C}D^{\beta _0}_{t_{0}+}x_{i}(t)}=&-Ax_{i}(t)+Bh(x_{i}(t))+Fh(x_{i}(t-\tau (t)))\nonumber \\&+c\sum _{j=1}^{N}g_{ij}\Gamma x_{j}(t)+u_{i}(t), ~i=1, 2,\cdots , N, \end{aligned}$$
(9)

and

$$\begin{aligned} ^{C}D^{\beta _0}_{t_{0}+}e_{i}(t)=&-Ae_{i}(t)+B\bar{h}(e_{i}(t))+F\bar{h}(e_{i}(t-\tau (t)))\nonumber \\&+c\sum _{j=1}^{N}g_{ij}\Gamma x_{j}(t)+u_{i}(t), ~i=1, 2,\cdots , N, \end{aligned}$$
(10)

where \(^{C}D^{\beta _0}_{t_{0}+}x_{i}(t)=(^{C}D^{\beta _0}_{t_{0}+}x_{i1}(t),\cdots ,{^{C}D^{\beta _0}_{t_{0}+}x_{in}(t)})^T\).

One can see that Theorem 1 still holds for \(\beta _i\equiv \beta _0\) \((i=1,2,\cdots ,n)\). That is, by virtue of vector Lyapunov function (8), the following corollary about the synchronization on fractional neural networks (9) with identical derivative order can be obtained.

Corollary 1

Under Assumptions 1 and 2, the synchronization of fractional neural networks (9) with identical derivative order can be realized via continuous control (7) if \(\beth +\daleth \) is a Hurwitz matrix, where matrices \(\beth \) and \(\daleth \) are the same as defined above.

It should be noted that if the scalar Lyapunov function is used to investigate the synchronization of fractional neural networks (9) with identical derivative order, a corollary with another form of synchronization criteria is obtained.

Corollary 2

Under Assumptions 1 and 2, the synchronization of fractional neural networks (9) with identical derivative order can be realized via continuous control (7) if the following inequality can be satisfied

$$\begin{aligned} c>\max \left\{ \frac{\lambda _{\max }(\mu _1BB^{T}+W/\mu _1+\mu _1I_{n}+\mu _2FF^{T}-2A)}{\kappa \lambda _{\min }(\Gamma )}, 0\right\} , \end{aligned}$$
(11)

where \(\mu _1\) and \(\mu _2\) are positive constants with \(\mu _1>\mu _2>\max _{1\le p\le n}\{w_{p}\}\), \(\kappa \) is defined in Lemma 3, and \(W=\text {diag}(w_{1}^{2}, \cdots , w_{n}^{2})\).

Proof

Consider a scalar Lyapunov function as

$$\begin{aligned} \tilde{V}(t)=\frac{1}{2}\tilde{\epsilon }^{T}(t)(\Omega \otimes I_{n})\tilde{\epsilon }(t), \end{aligned}$$
(12)

where \(\Omega \) is as defined in Lemma 3, and \(\tilde{\epsilon }(t)=(e_{1}^{T}(t), \cdots , e_{N}^{T}(t))^{T}\). In light of error system (6) and the analysis in [26], one can get

$$\begin{aligned}&^{C}D^{\beta _0}_{t_{0}+}\tilde{V}(t)+\mu _1\tilde{V}(t)-\mu _2\sup _{-\tau (t)\le \varpi \le 0}\tilde{V}(t+\varpi )\\ \le&-\frac{1}{2}(c-\frac{\lambda _{\max }(M)}{\kappa \lambda _{\min }(\Gamma )})\tilde{\epsilon }^{T}(t)(\Omega \otimes I_{n})\tilde{\epsilon }(t)+\tilde{\epsilon }^{T}(t-\tau (t))(\Omega \otimes (-\frac{\mu _2I_{n}-W/\mu _2}{2}))\tilde{\epsilon }(t-\tau (t)), \end{aligned}$$

where \(M=\mu _1BB^{T}+W/\mu _1+\mu _1I_{n}+\mu _2FF^{T}-2A\). According to (11) and the definition of \(\mu _2\), one has

$$\begin{aligned} ^{C}D^{\beta _0}_{t_{0}+}\tilde{V}(t)+\mu _1\tilde{V}(t)-\mu _2\sup _{-\tau (t)\le \varpi \le 0}\tilde{V}(t+\varpi )\le 0, \end{aligned}$$

which follows from the results in [26] that \(\lim _{t\rightarrow +\infty }\tilde{V}(t)=0\), implying that \(\lim _{t\rightarrow +\infty }||\tilde{\epsilon }(t)||=0\). Hence, the synchronization of fractional neural networks (9) with identical derivative order can be realized via continuous control (7). \(\square \)

Remark 3

Compared with the results about the synchronization of fractional systems in [27,28,29,30], where the fractional systems are with identical derivative order, the synchronization of multi-order fractional systems is discussed in Theorem 1. What is more, as a special case, the synchronization of fractional time-varying delayed neural networks with identical derivative order is considered in Corollary 2. In view of this, the obtained results in Theorem 1 are more general.

3.2 The Synchronization of MoFNNs with Time-varying Delays Under a Quantized Control

Consider the following function:

$$\begin{aligned} \xi (\iota )= \left\{ \begin{array}{lll} \chi _i,~&{}\displaystyle {\frac{1}{1+\theta }}\chi _i<\iota \le \frac{1}{1-\theta }\chi _i\\ 0,~&{}\iota =0\\ -\xi (-\iota ),~&{}\iota <0 \end{array}, \right. \end{aligned}$$
(13)

where \(\xi (\cdot ):\mathbb {R}\rightarrow \mathcal {Q}\) signifies the quantizer and \(\mathcal {Q}=\{\pm \chi _i: \chi _i=\varrho ^i\chi _0, i=0,\pm 1,\pm 2,\cdots ,\}\cup \{0\}\) with \(\chi _0>0\); \(\theta =\frac{1-\varrho }{1+\varrho }\) with \(0<\varrho <1\). According to the analysis of [40], there exists a Filippov solution \(\delta \in [-\theta ,\theta )\) satisfying \( \xi (\iota )=(1+\delta )\iota \).

Based on (13), introduce the following quantized control:

$$\begin{aligned} u_{i}(t)=-cd_{i}\Gamma \bar{\xi }(e_i(t)), \end{aligned}$$
(14)

where \(d_i\) as defined in control (7), and \(\bar{\xi }(e_i(t))=(\xi (e_{i1}(t)),\cdots ,\xi (e_{in}(t)))^T\).

Denote \(\tilde{\beth }=-\text {diag}(2a_{1}-2n+c\tilde{\kappa }\gamma _{1}, 2a_{2}-2n+c\tilde{\kappa }\gamma _{2}, \cdots , 2a_{n}-2n+c\tilde{\kappa }\gamma _{n})+(b_{pq}^{2}w_{q}^{2})_{n\times n}\) and \(\daleth =(f_{pq}^{2}w_{q}^{2})_{n\times n}\), where \(\tilde{\kappa }=\lambda _{\min }((L+\tilde{D})^{T}\Omega +\Omega (L+\tilde{D}))/\lambda _{\max }(\Omega )>0\) and \(\tilde{D}=(1-\theta )\text {diag}(\overbrace{d_{1}, \cdots , d_{l}}^{l}, \overbrace{0, \cdots , 0}^{N-l})\). It can be observed that \(\tilde{\beth }\) is a Metlzer matrix and \(\daleth \) is nonnegative. The following theorem about the synchronization on MoFNNs with time-varying delays under quantized control (14) is obtained.

Theorem 2

Under Assumptions 1 and 2, the synchronization of MoFNNs (1) can be realized via quantized control (14) if \(\tilde{\beth }+\daleth \) is a Hurwitz matrix.

Proof

It follows from the vector Lyapunov function (8) and Lemma 1 that

$$\begin{aligned} ^{C}D_{t_{0}+}^{\beta _{p}}V_{p}(t)\le&\sum _{i=1}^{N}\omega _{i}e_{ip}(t)^{C}D_{t_{0}+}^{\beta _{p}}e_{ip}(t)\\ =&\sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (-a_{p}e_{ip}(t)+\sum _{q=1}^{n}b_{pq}\bar{h}_{q}(e_{iq}(t))\\&+\sum _{q=1}^{n}f_{pq}\bar{h}_{q}(e_{iq}(t-\tau _{q}(t)))+c\sum _{j=1}^{N}g_{ij}\gamma _{p} x_{jp}(t)-cd_{i}\gamma _{p}\xi (e_{ip}(t))\Big ). \end{aligned}$$

Similar to the proofs in Theorem 1, one arrives at

$$\begin{aligned} \sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (\sum _{q=1}^{n}b_{pq}\bar{h}_{q}(e_{iq}(t))\Big )\le nV_{p}(t)+\sum _{q=1}^{n}b_{pq}^{2}w_{q}^{2}V_{q}(t), \end{aligned}$$

and

$$\begin{aligned} \sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (\sum _{q=1}^{n}f_{pq}\bar{h}_{q}(e_{iq}(t-\tau _{q}(t)))\Big )\le nV_{p}(t)+\sum _{q=1}^{n}f_{pq}^{2}w_{q}^{2}V_{q}(t-\tau _{q}(t)). \end{aligned}$$

Moreover, it follows from Lemma 3 that

$$\begin{aligned}&\sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (c\sum _{j=1}^{N}g_{ij}\gamma _{p} x_{jp}(t)-cd_{i}\gamma _{p}\xi (e_{ip}(t))\Big )\\ \le&\sum _{i=1}^{N}\omega _{i}e_{ip}(t)\Big (c\sum _{j=1}^{N}g_{ij}\gamma _{p} x_{jp}(t)-cd_{i}\gamma _{p}(1-\theta )e_{ip}(t)\Big )\\ =&c\gamma _{p}\epsilon _{p}^{T}(t)\Omega G\epsilon _{p}(t)-c\gamma _{p}\epsilon _{p}^{T}(t)\Omega \tilde{D}\epsilon _{p}(t)\\ =&-\frac{1}{2}c\gamma _{p}\epsilon _{p}^{T}(t)\big ((L+\tilde{D})^{T}\Omega +\Omega (L+\tilde{D})^{T}\big )\epsilon _{p}(t)\\ \le&-\frac{1}{2}c\gamma _{p}\epsilon _{p}^{T}(t)\tilde{\kappa }\Omega \epsilon _{p}(t)\\ =&-c\tilde{\kappa }\gamma _{p}V_{p}(t). \end{aligned}$$

Combining the above inequalities yields to

$$\begin{aligned} ^{C}D_{t_{0}+}^{\beta _{p}}V_{p}(t)\le -(2a_{p}-2n+c\tilde{\kappa }\gamma _{p})V_{p}(t)+\sum _{q=1}^{n}b_{pq}^{2}w_{q}^{2}V_{q}(t)+\sum _{q=1}^{n}f_{pq}^{2}w_{q}^{2}V_{q}(t-\tau _{q}(t)). \end{aligned}$$

Hence, one obtains

$$\begin{aligned} ^{C}D_{t_{0}+}^{\beta }V(t)\le&\tilde{\beth } V(t)+\daleth V(t-\tau (t)), \end{aligned}$$

where \(^{C}D_{t_{0}+}^{\beta }V(t)=(^{C}D_{t_{0}+}^{\beta _{1}}V_{1}(t),\cdots ,{^{C}D_{t_{0}+}^{\beta _{n}}}V_{n}(t))\). As \(\tilde{\beth }+\daleth \) is a Hurwitz matrix, in virtue of Lemma 2, we have \(\lim _{t\rightarrow +\infty }V(t)=0\), implying that \(\lim _{t\rightarrow +\infty }\epsilon _{p}(t)=0\) for \(p=1,2,\cdots ,n\). Therefore, the synchronization of MoFNNs (1) can be achieved via quantized control (14). \(\square \)

Remark 4

In Theorem 1, the continuous control is proposed to investigate the synchronization on MoFNNs with time-varying delays. In contrast in Theorem 2, the quantized control is proposed to realize the synchronization of MoFNNs with time-varying, which can reduce the transmission pressure effectively.

Similar to Corollaries 1 and 2, the following two corollaries about the synchronization of fractional neural networks (9) with identical derivative order under quantized control (14) are presented.

Corollary 3

Under Assumptions 1 and 2, the synchronization of fractional neural networks (9) with identical derivative order can be realized via quantized control (14) if \(\tilde{\beth }+\daleth \) is a Hurwitz matrix.

Corollary 4

Under Assumptions 1 and 2, the synchronization of fractional neural networks (9) with identical derivative order can be realized via quantized control (14) if the following inequality can be satisfied

$$\begin{aligned} c>\max \left\{ \frac{\lambda _{\max }(\mu _1BB^{T}+W/\mu _1+\mu _1I_{n}+\mu _2FF^{T}-2A)}{\tilde{\kappa }\lambda _{\min }(\Gamma )}, 0\right\} , \end{aligned}$$
(15)

where \(\mu _1\) and \(\mu _2\) are positive constants with \(\mu _1>\mu _2>\max _{1\le p\le n}\{w_{p}\}\), \(\tilde{\kappa }\) as denoted above, and \(W=\text {diag}(w_{1}^{2}, \cdots , w_{n}^{2})\).

Proof

It following from Lyapunov function (12) and error system (10) that

$$\begin{aligned}&^{C}D^{\beta _0}_{t_{0}+}\tilde{V}(t)+\mu _1\tilde{V}(t)-\mu _2\sup _{-\tau (t)\le \varpi \le 0}\tilde{V}(t+\varpi )\\ \le&-\frac{1}{2}(c-\frac{\lambda _{\max }(M)}{\tilde{\kappa }\lambda _{\min }(\Gamma )})\varepsilon ^{T}(t)(\Omega \otimes I_{n})\varepsilon (t)+\varepsilon ^{T}(t-\tau (t))(\Omega \otimes (-\frac{\mu _2I_{n}-W/\mu _2}{2}))\varepsilon (t-\tau (t)), \end{aligned}$$

where \(M=\mu _1BB^{T}+W/\mu _1+\mu _1I_{n}+\mu _2FF^{T}-2A\). Similar to the arguments in Corollary 2, we know that the synchronization of fractional neural networks (9) with identical derivative order can be realized via quantized control (14). \(\square \)

Remark 5

In previous works [24, 27,28,29,30, 41], the continuous control or quantized control was utilized to realize the synchronization of fractional neural networks that are with identical derivative order. In contrast, the two kinds of controls are introduced to implement the synchronization of MoFNNs in Theorem 1 and Theorem 2 respectively. Therefore, the results of this paper can be viewed as extensions for the existing works.

4 A Numerical Example

In this section, an example is provided to demonstrate the effectiveness of results.

Consider a three-dimensional \((n=3)\) isolated MoFNN with time-varying delays, where \(\beta =(0.92, 0.95, 0.98)^T\); \(\tau _1(t)=\tau _2(t)=\tau _3(t)=\lg (1+t)/10\); \(h_1(\cdot )=h_2(\cdot )=h_3(\cdot )=\tanh (\cdot )\); \(E=(0,0,0)^T\); \(A=\text {diag}(1,1,1)\), and

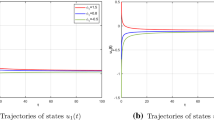
$$\begin{aligned} B= \left( \begin{array}{ccc} 1.99 &{} -1.59 &{} 0 \\ 2.11 &{} 1.77 &{} 1.21 \\ -4.85 &{} 0.5 &{} 0.85 \end{array} \right) ,~ F= \left( \begin{array}{ccc} -0.1 &{} 0.2 &{} 0\\ -0.2 &{} -0.05 &{} -0.2\\ 0 &{} 0 &{} 0.2\\ \end{array} \right) . \end{aligned}$$

The orbits of network (2) with initial values \(\phi (t_0)=(1.1,0.01,-1)^T\) \((t_0=0)\) are depicted in Fig. 1.

Fig. 1
figure 1

The graph of orbits for the network (2)

Full size image

In the following, a multi-order fractional system composed of 9 \((N=9)\) MoFNNs (1) with time-varying delays is considered, in which matrix \(\Gamma =\text {diag}(1, 1, 1)\). Moreover, the initial conditions of those networks are chosen randomly and the topology is shown in Fig. 2, whose weights of all directed connections are equal 1. According to the given activation function \(\tanh (\cdot )\), it can be verified that there exist \(w_p=1\) \((p=1,2,3)\) such that Assumption 1 holds. In addition, by virtue of the introduced pinning control, the first three \((l=3)\) nodes are selected to be controlled so that the graph of this system has a spanning tree, as shown in Fig. 2, which means that Assumption 2 holds.

Fig. 2
figure 2

The topology of MoFNNs (1) with a virtual node 0

Full size image

Case 1. By utilizing continuous control (7), pick up \(d_1=d_2=d_3=5\), i.e., \(D=\text {diag}(5, 5, 5, 0,0,0,0,0,0,0)\). By virtue of Lemma 3, there exists \(\Omega =\text {diag}(1,1,1,1,1,1,1,1,1)\) such that (4) holds with \(\kappa =1.5667\). When choosing coupling strength \(c=8\), one obtains

$$\begin{aligned} \beth +\daleth = \left( \begin{array}{ccc} -4.5635 &{} 2.5681 &{} 0 \\ 4.4921 &{} -5.3982 &{} 1.5041 \\ 23.5225 &{} 0.25 &{} -7.7711 \end{array} \right) . \end{aligned}$$

It can be verified that all eigenvalues of matrix \(\beth +\daleth \) have negative real parts, showing that \(\beth +\daleth \) is a Hurwitz matrix. According to Theorem 1, the synchronization of MoFNNs (1) can be achieved via continuous control (7).

Finally, denote \(\mathcal {E}(t)=\max _{1\le i\le 9}\Vert x_{i}(t)-s(t)\Vert \) as synchronized error to illustrate the viability of the above results. Figure 3 shows the transient behaviors of \(\mathcal {E}(t)\) with regard to t, which indicates that the realization of synchronization on MoFNNs via continuous control (7).

Fig. 3
figure 3

The transient behaviors of synchronized error \(\mathcal {E}(t)\) under continuous control (7)

Full size image

Case 2. Choose \(\theta =0.8\) and \(\chi _0=2\) as the parameters of quantizer (13). By applying quantized control (14), take \(d_1=d_2=d_3=10\), i.e., \(D=\text {diag}(10, 10, 10, 0,0,0,0,0,0,0)\) and \(\tilde{D}=\text {diag}(2, 2, 2, 0,0,0,0,0,0,0)\). Similarly, according to Lemma 3, there exists \(\Omega =\text {diag}(1,1,1,1,1,1,1,1,1)\) such that (4) holds with \(\tilde{\kappa }=1.5056\). When choosing \(c=8.3\), one has

$$\begin{aligned} \tilde{\beth }+\daleth = \left( \begin{array}{ccc} -4.5264 &{} 2.5681 &{} 0 \\ 4.4921 &{} -5.3611 &{} 1.5041 \\ 23.5225 &{} 0.25 &{} -7.7340 \end{array} \right) . \end{aligned}$$

We can verify that \(\tilde{\beth }+\daleth \) is a Hurwitz matrix. Hence, in view of Theorem 2, the synchronization of MoFNNs (1) can be realized via quantized control (14). Figure 4 depicts the transient behaviors of \(\mathcal {E}(t)\) with regard to t, which indicates that the realization of synchronization on MoFNNs via quantized control (14).

Fig. 4
figure 4

The transient behaviors of synchronized error \(\mathcal {E}(t)\) under quantized control (14)

Full size image

Figures 5 and 6 illustrate the time evolutions of controls utilized in Case 1 and Case 2, respectively. In view that the control in Case 2 is the quantized control, it can reduce the transmission pressure compared with the continuous control utilized in Case 1.

Fig. 5
figure 5

The time evolutions of linear control \(u_{ij}(t)\) \((i,j=1,2,3)\) in Case 1

Full size image
Fig. 6
figure 6

The time evolutions of quantized control \(u_{ij}(t)\) \((i,j=1,2,3)\) in Case 2

Full size image

5 Conclusion

The synchronization on MoFNNs with time-varying delays has been discussed in this paper. By means of the vector Lyapunov function, the synchronized criteria of MoFNNs with time-varying delays under continuous control and quantized control have been derived respectively. Compared with traditional fractional neural networks with identical derivative order, the systems investigated in this paper are general and with multiple derivative orders. An example for demonstrating the effectiveness of theoretical results has been presented. Future research efforts may aim to extend the results to other types of synchronization on MoFNNs with time-varying delays, such as cluster synchronization, finite-time synchronization, etc.