The Optimization of Synchronization Control Parameters for Fractional-Order Delayed Memristive Neural Networks Using SIWPSO

Abstract

The paper mainly deals with the optimization of synchronization for fractional-order memristive neural networks (FOMNNs) with a time delay. Based on synchronization conditions, an optimization model for control parameters is designed and computed. It’s significative to design an appropriate controller which can synchronize the drive FOMNNs and response FOMNNs. Based on the proposed controller, some synchronization conditions of FOMNNS can be obtained with the help of the linear matrix inequality, along with fractional-order Lyapunov methods and matrix analysis. The optimal model of control parameters includes a target function and some constraints. The target function is the minimal sum of control energy and integral square error index. The constraint conditions choose the sufficient conditions for synchronization of FOMNNs. The optimization model is difficult to compute but can be solved by means of the stochastic inertia weight particle swarm optimization algorithm. A simulation is provided to verify the validity of the proposed theoretical results.

1 Introduction

As the extension of the integer-order calculus,the basic theory of fractional differential and integral calculus were studied in early period. With the improvement of computing technology and the realization of the analog circuit, the fractional calculus has been widely applied in physics and engineering in recent years. One of the advantages of fractional calculus is that it’s an excellent mathematical tool for describing the memory and genetic characteristic of many novel materials and special processes. Furthermore, compared to the integer-order model, the fractional-order model has more degrees of freedom and infinite memories. Based on the salient properties of fractional calculus, many practical systems described by fractional order models could reflect the characteristics of the system more accurately than integer order models. As a result, fractional calculus has been applied in many territories, such as quantum mechanics [1], viscoelasticity [2], control engineering, robotics and chaotic synchronization [3].

Neural network is an intricate system formed by high interconnection of a large number of neurons originally. Scientists have constructed artificial neural networks (neural networks for short) after understanding the biological neural networks. Neural networks [4,5,6,7] have attracted wide interest in many domains, such as pattern recognition, artificial intelligence and signal processing. Since the discovery of physical devices with memristive characteristics in HP LABS in 2008, the memristive neural networks (MNNs) model has become a new hot topic [8, 9]. A neural network consists of neurons (nodes) and synapses (connections between nodes). In order to train the neural network to complete a task, it needs to be “fed” a large number of questions and corresponding answers. Once trained, neural networks can be tested without knowing the answer. The training process requires a lot of manpower, resources and time. It is also very expensive. However, by using memristors, most of the expensive training processes can be avoided. The memristors can provide memory ability to the networks as well. The memory storage capacity will be significantly improved due to the application of memrisive neural networks in associative memories. The memristors which have different history-dependent resistors, make the memrisive neural networks have more complicated and fruitful dynamics than traditional neural networks.

Synchronization is a significative research subject of chaotic systems. MNN is one kind of chaotic systems. Hence, many scholars from in and abroad pay attentions to the synchronization of MNNs. Global anti-synchronization of MNNs was analyzed by Zhang et al. [10]. Exponential synchronization of Cohen−Grossberg neural networks with memristors was analyzed by Yang et al. [11]. Robust synchronization of multiple MNNs was analyzed by Yang et al. [12]. The MNNs cannot be spontaneously synchronized upon most occasions. Thus, control schemes play an important role. There are many control strategies, such as adaptive control [13], intermittent control [14], sampled-data control [15], event-trigger [16] control and so on.

More and more attentions have been paid to the parameter optimization of synchronization controller [17, 18]. A particle swarm optimization (PSO) algorithm was exploited by Kennedy and Eberhart. It is an evolutionary algorithm. The algorithm begins with some random solutions, then searches the optimum solution through iterations, and estimates the solution’s quality according to the fitness function in the PSO algorithm. The PSO algorithm has more simply rule compared with the rule of a genetic algorithm (GA). The crossover and mutation operation are needed in the GA, nevertheless, the PSO algorithm can do without them. The PSO algorithm is based on the current optimal solution to find the location of the global optimal solution. The algorithm has gained the attention of academia due to its advantages such as easy implementation, high precision computation and rapid convergence, which has already confirmed its advantages in dealing with real issues. The improved particle swarm optimization algorithms [19, 20] have attracted much interest in the area of artificial intelligence. Stochastic inertia weight particle swarm optimization (SIWPSO) algorithm [21] is one of them which can find optimal solutions effectively.

A time delay [22] is inevitable in practical application. However, its existence will affect the networks to become unstable. Therefore, the discussion on the time delay is necessary when the synchronization of FOMNNs is studied. Many articles have analyzed the synchronization of FOMNNs [23, 24]. However, the optimization of controller parameters is not considered in these articles. Many articles about PID controller have applied the PSO algorithm to deal with the optimization problem [25, 26]. The authors in [27] have analyzed the optimal synchronization of complex networks via PSO algorithm. Try the best of the authors’ ablity, there is no literature investigating the optimization of the FOMNNs by the SIWPSO algorithm before. In summary, the paper investigates the optimal synchronization of fractional-order delayed memristive neural networks along with SIWPSO.

The main contributions of this paper include three aspects. (1) The drive-response synchronization for fractional-order memristive neural networks with time delay is studied in this paper. For convenience, the model is described in compact forms. (2) Based on fractional-order Lyapunov methods and some inequations, synchronization conditions are shown in linear matrix inequality’s (LMIs) form. The proposed methods apply equally to the synchronization problem for fractional-order delayed neural networks and fractional-order memristive neural networks. (3) To get a better controller with low control energy and integral square error (ISE) index, an optimization model is established to solve the optimal control parameters. The complicated model is solved by SIWPSO algorithm, which is an improved intelligent algorithm.

The rest of this paper is arranged as follows: some definitions, lemmas and assumptions are introduced in Sect. 2. The models of the FOMNNs are described comprehensively and distinctly in this section as well. Section 3 presents some achievements about the synchronization of the FOMNNs with a constant time delay. Simultaneously, two corollaries are also given in this section. One is the synchronization without memristor, and the other is without the time delay. Then, a parameter optimization of the controller is specifically designed in Sect. 4, which includes the optimization model and the SIWPSO algorithm. Finally, numerical examples and the conclusions are provided in Sects. 5 and 6 respectively.

Notations Let $I_{n}$ represent the $n\times n$ identity matrix. Let T stand for matrix transposition. Let R, ${\mathbb {R}}^{n}$ and ${\mathbb {R}}^{m\times n}$ respectively denote the set of real numbers, n-dimensional vectors and $m\times n$ real matrices. $\Vert x\Vert$ is the Euclidean norm for a vector $x\in {\mathbb {R}}^{n}$. $\Vert \Gamma \Vert$ represents the 2-norm of $\Gamma$ for a matrix $\Gamma \in {\mathbb {R}}^{n\times n}$. A diagonal matrix can be expressed by $diag\{...\}$. If a matrix P is a symmetric positive (semi-positive) definite matrix, it will be expressed in terms of $P>0(\ge 0)$. Finally, “$\star$” are used to represent the omitted symmetry parts of the symmetric block matrix.

2 Preliminary Knowledge and Model Description

This section gives some lemmas and definitions of fractional calculus which play important roles in next parts. Besides, the mathematical models of FOMNNs with a time delay are introduced.

2.1 Fractional Calculus

Definition 1

[28] When fractional order $\alpha \in {\mathbb {R}}^{+}$, the Caputo derivative with function $\omega (s)$ is defined as:

$$\begin{aligned} D_{t_{0},t}^{\alpha }\omega (s)=D_{t_{0},t}^{-(n-\alpha )}\frac{d^{n}}{dt^{n}}\omega (s)=\frac{1}{\Gamma (n-\alpha )}\int _{t_{0}}^{t}(s-\tau )^{n-\alpha -1}\omega ^{(n)}(\tau )d\tau , \end{aligned}$$

where $t\ge t_{0}$ and $n-1<\alpha <n\in {\mathbb {Z}}^{+}$, and $\Gamma (\cdot )$ is the Gamma function and $\Gamma (\alpha )=\int _{0}^{\infty }t^{\alpha -1}e^{-t}dt, t\ge t_{0}.$ Specifically, $D_{t_{0},t}^{\alpha }\omega (s)=\frac{1}{\Gamma (1-\alpha )}\int _{t_{0}}^{t}(s-\tau )^{-\alpha }\omega '(\tau )d\tau$, when $0<\alpha <1$.

Remark 1

The Caputo derivative of constant functions is zero. Besides, the initial condition of Caputo differential operator is in the same form as that of integer order differential equations [29].The Caputo derivative is more appropriate for a realistic model and is chosen in this paper.

Lemma 1

[30] Let $f(t)\in {\mathbb {R}}^{n}$ is a vector of differentiable function, for any time instant $t\ge t_{0},$ the inequality holds

$$\begin{aligned} D^{\alpha }[f^{T}(t)Pf(t)]\le 2f^{T}(t)PD^{\alpha }f(t), \forall \alpha \in (0,1], \end{aligned}$$

where P is a symmetric positive definite constant matrix.

Lemma 2

[31] Let $X,Z\in {\mathbb {R}}^{n},$$\epsilon >0$ is a constant, then

$$\begin{aligned} X^{T}Z+Z^{T}X\le \epsilon ^{-1} X^{T}X+\epsilon Z^{T}Z. \end{aligned}$$

Lemma 3

[32] The linear matrix inequality

$$\begin{aligned} S=\left( \begin{array}{cc} S_{11} &{}S_{12}\\ S^{T}_{12} &{}S_{22}\\ \end{array} \right) <0, \end{aligned}$$

if and only if conditions (i) or (ii) holds:

$$\begin{aligned} \mathrm{(i)} S_{11}< & {} 0,S_{22}-S_{12}^{T}S_{11}^{-1}S_{12}<0, \\ \mathrm{(ii)} S_{22}< & {} 0,S_{11}-S_{12}^{T}S_{22}^{-1}S_{12}<0, \end{aligned}$$

where $S_{11}=S^{T}_{11}$ and $S_{22}=S^{T}_{22}.$

Lemma 4

[33] Suppose that $\omega _{1}, \omega _{2}: R\rightarrow R$ are continuous and strictly increasing. $\omega _{1}(s)$ and $\omega _{2}(s)$ are positive for $s>0$, and $\omega _{1}(0)=\omega _{2}(0)=0,$$\omega _{1}, \omega _{2}$ strictly increasing. If there exists a continuous and differentiable function $V: R\times {\mathbb {R}}^{n}\rightarrow R$ so that $\omega _{1}(\Vert x(t)\Vert )\le V(t,x(t))\le \omega _{2}(\Vert x(t)\Vert )$ holds, and there exist two constants $\kappa> \beta > 0$ so that for any given $t_{0}\in R$ the Caputo system $D^{\alpha }x(t)=f(t,x(t),x(t-\tau ))$ satisfies

$$\begin{aligned} D^{\alpha }V(t,x(t))\le -\kappa V(t,x(t))+ \beta \sup _{-\tau \le \theta \le 0} V(t+\theta ,x(t+\theta )) \end{aligned}$$

for $t\ge t_{0}$, then the Caputo system $D^{\alpha }x(t)=f(t,x(t),x(t-\tau ))$ will achieve global asymptotical stability.

Remark 2

It’s difficult to directly synchronize fractional-order neural networks(FONNs) through common integer-order Lyapunov methods. However, Lemmas 1 and 4 are adopted to synchronize the fractional-order ones.

2.2 Model Description

The FOMNNs with a constant time delay is considered as follows:

$$\begin{aligned} D^{\alpha }x(t)=-Dx(t)+A(x(t))f(x(t))+B^{\tau }(x(t))f(x(t-\tau ))+I \end{aligned}$$

(1)

where $0<\alpha <1$, $x(t)=(x_{1}(t), x_{2}(t), \ldots , x_{n}(t))^{T} \in {\mathbb {R}}^{n}$ is the neuron’s state variable, $D=diag\{d_{1}, d_{2}, \ldots , d_{n}\}$, $d_{i}>0 (i=1,2,\ldots ,n)$ stands for the rate at which the ith neuron returns to the resting state, $f(x(t))=(f_{1}(x_{1}(t)), f_{2}(x_{2}(t)),\ldots , f_{n}(x_{n}(t)))^{T}$ is the activation function of neurons without the time delay. $f(x(t-\tau ))$ is the activation function with the time delay, $\tau$ represents the constant time delay. $I=(I_{1}(t), I_{2}(t),\ldots , I_{n}(t))^{T}\in {\mathbb {R}}^{n}$ denotes an external input vector. $A(x(t))=[a_{ij}(x_{i}(t))]_{n\times n}, B^{\tau }(x(t))=[b^{\tau }_{ij}(x_{i}(t))]_{n\times n}$ are the connection memristive weight matrices at time t and $t-\tau$:

$$\begin{aligned} a_{ij}(x_{i}(t))= & {} \frac{{\widetilde{R}}^{1}_{ij}}{C_{i}}sgn_{ij},\ \ \ \ \ \ \ b^{\tau }_{ij}(x_{i}(t))=\frac{{\widetilde{R}}^{2}_{ij}}{C_{i}}sgn_{ij}, \\ sgn_{ij}= & {} \left\{ \begin{aligned} 1,&i\ne j, \\ -1,&i= j. \end{aligned} \right. \end{aligned}$$

where ${\widetilde{R}}^{1}_{ij}$ and ${\widetilde{R}}^{2}_{ij}$ denote the memductance of memristors $R^{1}_{ij}$ and $R^{2}_{ij}$, respectively. $R^{1}_{ij}$ donates the memristor between $f_{j}(x_{j}(t))$ and $x_{i}(t)$, and $R^{2}_{ij}$ donates the memristor between $f_{j}(x_{j}(t-\tau ))$ and $x_{i}(t-\tau )$. On account of the current and voltage feature and the characteristics of memristor, a general mathematical model with the memristance is established as follows [34]:

$$\begin{aligned} a_{ij}(x_{i}(t))=\left\{ \begin{aligned} \acute{a}_{ij},&|x_{i}(t)|\le T_{i}, \\ \grave{a}_{ij},&|x_{i}(t)|> T_{i}, \end{aligned} \right. \ \ \ \ \ \ \ b^{\tau }_{ij}(x_{i}(t))=\left\{ \begin{aligned} \acute{b}^{\tau }_{ij},&|x_{i}(t)|\le T_{i}, \\ \grave{b}^{\tau }_{ij},&|x_{i}(t)|> T_{i}, \end{aligned} \right. \end{aligned}$$

where $T_{i}>0$ are switching jumps, weights $\acute{a}_{ij}, \grave{a}_{ij}, \acute{b}^{\tau }_{ij}$ and $\grave{b}^{\tau }_{ij}$ are all constants for $1\le i, j\le n$.

The Filippov solution [35] for all systems is considered on account of the discontinuity of $a_{ij}(x_{i}(t))$ and $b^{\tau }_{ij}(x_{i}(t))$ in this paper. Denote ${\overline{a}}_{ij} = \max \{\acute{a}_{ij}, \grave{a}_{ij}\}$, ${\underline{a}}_{ij} = \min \{\acute{a}_{ij}, \grave{a}_{ij}\}$, ${\overline{b}}^{\tau }_{ij} = \max \{\acute{b}^{\tau }_{ij}, \grave{b}^{\tau }_{ij}\}$, ${\underline{b}}^{\tau }_{ij} = \min \{\acute{b}^{\tau }_{ij}, \grave{b}^{\tau }_{ij}\}$, $a_{ij}=\frac{1}{2}({\overline{a}}_{ij} + {\underline{a}}_{ij})$, $b^{\tau }_{ij}=\frac{1}{2}({\overline{b}}^{\tau }_{ij} + {\underline{b}}^{\tau }_{ij})$, ${\widetilde{a}}_{ij}=\frac{1}{2}({\overline{a}}_{ij} - {\underline{a}}_{ij})$ and ${\widetilde{b}}^{\tau }_{ij}=\frac{1}{2}({\overline{b}}^{\tau }_{ij} - {\underline{b}}^{\tau }_{ij})$. According to some equation transformations [36, 37] and the fractional differential methods [38], the FOMNNs (1) can be rewritten to the following system:

$$\begin{aligned} D^{\alpha }x(t)=-Dx(t)+(A+M\Lambda _{1}(t)E)f(x(t))+(B^{\tau }+{\widehat{M}}\Lambda _{2}(t){\widehat{E}})f(x(t-\tau ))+I. \end{aligned}$$

(2)

Throughout this paper, the FOMNNs (2) is considered as the drive FOMNNs, the response FOMNNs with control is as described by:

$$\begin{aligned} D^{\alpha }y(t)= & {} -Dy(t)+(A+M\Lambda _{3}(t)E)f(y(t))\nonumber \\&+(B^{\tau }+{\widehat{M}}\Lambda _{4}(t){\widehat{E}})f(y(t-\tau ))+u(t)+I \end{aligned}$$

(3)

where $u(t)=(u_{1}(t), u_{2}(t),\ldots , u_{n}(t))^{T}$ is the controller to be designed. $A=(a_{ij})_{n\times n}$, $B^{\tau }=(b^{\tau }_{ij})_{n\times n}$ , $M = (\sqrt{\;{\widetilde{a}}_{11}}\xi _{1},\ldots , \sqrt{{\widetilde{a}}_{1n}}\xi _{1},\ldots , \sqrt{{\widetilde{a}}_{n1}}\xi _{n},\ldots , \sqrt{{\widetilde{a}}_{nn}}\xi _{n})_{n\times n^{2}}$, $E = (\sqrt{{\widetilde{a}}_{11}}\xi _{1},\ldots , \sqrt{{\widetilde{a}}_{1n}}\xi _{n},\ldots , \sqrt{{\widetilde{a}}_{n1}}\xi _{1},\ldots , \sqrt{{\widetilde{a}}_{nn}}\xi _{n})_{n^{2}\times n}$, ${\widehat{M}} = (\sqrt{{\widetilde{b}}^{\tau }_{11}}\xi _{1},\ldots , \sqrt{{\widetilde{b}}^{\tau }_{1n}}\xi _{1},\ldots , \sqrt{{\widetilde{b}}^{\tau }_{n1}}\xi _{n},\ldots , \sqrt{{\widetilde{b}}^{\tau }_{nn}}\xi _{n})_{n\times n^{2}}$, ${\widehat{E}} = (\sqrt{{\widetilde{b}}^{\tau }_{11}}\xi _{1},\ldots , \sqrt{{\widetilde{b}}^{\tau }_{1n}}\xi _{n},\ldots , \sqrt{{\widetilde{b}}^{\tau }_{n1}}\xi _{1},\ldots , \sqrt{{\widetilde{b}}^{\tau }_{nn}}\xi _{n})_{n^{2}\times n}$, $\xi _{i}\in {\mathbb {R}}^{n}$ is the column vector which the ith element is 1 and others are all 0, $\{[\Lambda _{k}(t)]_{n^{2}\times n^{2}}= diag\{\theta _{11}^{k}(t),\ldots , \theta _{1n}^{k}(t),\ldots , \theta _{n1}^{k}(t),\ldots , \theta _{nn}^{k}(t)\}: |\theta _{ij}^{k}|\le 1, 1\le i, j \le n, k=1,2,3,4\}$. It’s easy to obtain that $\Lambda _{k}^{T}(t)\Lambda _{k}(t)\le I (k=1,2,3,4)$.

Let $e(t)= y(t)-x(t)$, the error dynamical system is derived from (2) and (3):

$$\begin{aligned} D^{\alpha }e(t)=-De(t)+(A+\triangle A)g(e(t))+(B^{\tau }+\triangle B^{\tau })g(e(t-\tau ))+\Sigma (t)+u(t) \end{aligned}$$

(4)

where $\triangle A= M \Lambda _{3}(t) E$, $\triangle B= {\widehat{M}} \Lambda _{4}(t){\widehat{E}}$, $g(e(t))=f(y(t))-f(x(t))$, $g(e(t-\tau ))=f(y(t-\tau ))-f(x(t-\tau ))$, $\Sigma (t)= [M(\Lambda _{3}(t)-\Lambda _{1}(t))E]f(x(t))+[{\widehat{M}}(\Lambda _{4}(t)-\Lambda _{2}(t)){\widehat{E}}]f(x(t-\tau ))$. The initialization of (4) is $e(s)=\Psi (s)\in {\mathcal {C}}([-\tau ,0], {\mathbb {R}}^{n})$.

There are some assumptions required for the following research:

Assumption 1

The activation functions $f_{j}$ are Lipschitz continuous on R, i.e.,

$$\begin{aligned} |f_{j}(u)-f_{j}(v)|\le L_{j}|u-v| \end{aligned}$$

where $u,v\in R$, $j=1,2,\ldots ,n$ and constant $L_{j}>0$.

Assumption 2

Constants $M_{j}$ exist so that $|f_{j}(z)|\le M_{j}$ for $\forall z\in {\mathbb {R}}$ and $j=1,2,\ldots ,n$.

When $|x_{i}(t)|\le T_{i}$ at time t, the state $y_{i}(t)$ will not be confirmed whether $|y_{i}(t)|\le T_{i}$ or $|y_{i}(t)|\ge T_{i}$ due to their different initial value. As a result, it’s easy to realize that $\Lambda _{3}(t) \ne \Lambda _{1}(t)$, $\Lambda _{4}(t) \ne \Lambda _{2}(t)$. Hence, the linear feedback controller such as those in [39, 40] can not be used to synchronize the FOMNNs firsthand. In addition, the term $\Sigma (t)$ of error system (4) can be treated as an external perturbation under some assumption conditions. Based on these, the following controller is designed:

$$\begin{aligned} u(t)=-Ke(t)-\Gamma sgn(e(t)), \end{aligned}$$

(5)

where K is a real matrix, $\Gamma =diag\{\gamma _{1}, \gamma _{2},\ldots , \gamma _{n}\}$, K and $\Gamma$ are gain matrices to be confirmed. $e(t)=(e_{1}(t), e_{2}(t),\ldots , e_{n}(t))^{T}$, $sgn(\cdot )$ is the standard sign function.

3 Main Result: Synchronization Criteria

Based on the proposed controller (5), some novel sufficient criteria are obtained to synchronize the FOMNNs (2) and (3). The definition and theorems of synchronization are present for FOMNNs in this section. Some corollaries are given as well.

Definition 2

The drive-response synchronization of the two FOMNNs (2) and (3) is said to be achieved, if a suitable controller u(t) is designed,

$$\begin{aligned} \lim _{t\rightarrow \infty } \parallel y(t)-x(t)\parallel =0 \end{aligned}$$

holds for any initial values.

Theorem 1

Suppose that Assumptions 1 and 2 hold, for given constants $0<\beta <\kappa$, under the proposed controller (5), with $\gamma _{i}=\sum _{j=1}^{n}(|\acute{a}_{ij}-\grave{a}_{ij}|+|\acute{b}^{\tau }_{ij}-\grave{b}^{\tau }_{ij}|)M_{j}$, the FOMNNs (2) and (3) can reach global asymptotical synchronization, if there exists a matrix Y, some positive constants $\epsilon$, $\rho _{1}$, $\rho _{2}$ and a positive definite matrix Q so that the following LMIs (6) and (7) are satisfied:

$$\begin{aligned} \Pi= & {} \left( \begin{array}{cccc} \Pi _{11} &{}\quad QB &{}\quad QM &{}\quad 0\\ * &{}\quad -\epsilon I_{n} &{}\quad 0 &{}\quad QE{\widehat{M}} \\ * &{}\quad * &{}\quad -\rho _{1}I_{n^{2}\times n^{2}} &{}\quad 0\\ * &{}\quad * &{}\quad * &{}\quad -\rho _{2}I_{n^{2}\times n^{2}} \\ \end{array} \right) <0, \end{aligned}$$

(6)

$$\begin{aligned}&\epsilon L^{T}L-\beta Q<0 \end{aligned}$$

(7)

where $\Pi _{11}=-QD-D^{T}Q-Y-Y^{T}+QAL+L^{T}A^{T}Q+\kappa Q + \rho _{1}L^{T}E^{T}EL+ \rho _{2}{\widehat{E}}^{T}{\widehat{E}}$, $K=Q^{-1}Y$.

Proof

Construct the Lyapunov function as follows:

$$\begin{aligned} V(t)=e^{T}(t)Qe(t) \end{aligned}$$

where $Q=diag\{q_{1}, q_{2},\ldots , q_{n}\}$.

Taking the time derivative of V(t) along the error system and applying Lemma 1 and Assumption 1, one can get

$$\begin{aligned} \begin{aligned} D^{\alpha }V(t)&\le 2e^{T}(t)QD^{\alpha }e(t) \\&= 2e^{T}(t)Q[-De(t)+(A+\triangle A)g(e(t)) + (B^{\tau }+\triangle B^{\tau })g(e(t-\tau ))\\&\quad +\Sigma (t)-Ke(t)-\Gamma \omega (t)]\\&\le e^{T}(t)[-QD-D^{T}Q-QK-K^{T}Q]e(t) + 2e^{T}(t)Q(A+\triangle A)g(e(t))\\&\quad +\Vert 2e^{T}(t)Q(B^{\tau }+\triangle B^{\tau })g(e(t-\tau ))\Vert + 2e^{T}(t)Q[\Sigma (t)-\Gamma \omega (t)] \\&\le e^{T}(t)[-QD-D^{T}Q-QK-K^{T}Q]e(t)\\&\quad + e^{T}(t)[Q(A+\triangle A)L+L^{T}(A+\triangle A)^{T}Q]e(t)\\&\quad + \Vert e^{T}(t)Q(B^{\tau }+\triangle B^{\tau })Le(t-\tau ) + e^{T}(t-\tau )L^{T}(B^{\tau }+\triangle B^{\tau })^{T}Qe(t)\Vert \\&\quad + 2e^{T}(t)Q[\Sigma (t)-\Gamma \omega (t)]\\ \end{aligned} \end{aligned}$$

where $A+\triangle A>0$, $L=diag\{L_{1}, L_{2}, \ldots ,L_{n}\}$, $\omega (t)=(\omega _{1}(t), \omega _{2}(t), \ldots , \omega _{n}(t))^{T}$,$i=1,2,\ldots , n$,

$$\begin{aligned} \omega _{i}(t)=\left\{ \begin{aligned} sgn(e_{i}(t)),&if ~~e_{i}(t)\ne 0, \\ 0,&if ~~e_{i}(t)=0. \end{aligned} \right. \end{aligned}$$

According to Lemma 2, it holds for any $t\in [0,\infty )$ that

$$\begin{aligned} \begin{aligned}&\Vert e^{T}(t)Q(B^{\tau }+\triangle B^{\tau })Le(t-\tau ) + e^{T}(t-\tau )L^{T}(B^{\tau }+\triangle B^{\tau })^{T}Qe(t)\Vert \\&\quad \le \frac{1}{\epsilon }e^{T}(t)Q(B^{\tau }+\triangle B^{\tau })(B^{\tau }+\triangle B^{\tau })^{T}Qe(t)+\epsilon e^{T}(t-\tau )L^{T}Le(t-\tau ). \end{aligned} \end{aligned}$$

Noticing that $2{\widetilde{a}}_{ij}=|\acute{a}_{ij}-\grave{a}_{ij}|$, $2{\widetilde{b}}^{\tau }_{ij}=|\acute{b}^{\tau }_{ij}-\grave{b}_{ij}^{\tau }|$, $\gamma _{i}=\sum _{j=1}^{n}(|\acute{a}_{ij}-\grave{a}_{ij}|+|\acute{b}^{\tau }_{ij}-\grave{b}^{\tau }_{ij}|)M_{j}=\varphi _{i}$, along with the Assumption 2, one can get that

$$\begin{aligned} 2e^{T}(t)Q[\Sigma (t)-\Gamma \omega (t)] \le 2\sum _{i=1}^{n}|e_{i}(t)|q_{i}(\varphi _{i}-\gamma _{i})=0. \end{aligned}$$

From the above, differentiating V(t) along the solutions of (4) becomes

$$\begin{aligned} \begin{aligned} D^{\alpha }V(t)&\le e^{T}(t)[-QD-D^{T}Q-QK-K^{T}Q+Q(A+\triangle A)L+L^{T}(A+\triangle A)^{T}Q\\&~~~+\frac{1}{\epsilon }Q(B^{\tau }+\triangle B^{\tau })(B^{\tau }+\triangle B^{\tau })^{T}Q]e(t)+\epsilon e^{T}(t-\tau )L^{T}Le(t-\tau )\\&= e^{T}(t)\Xi e(t)+\epsilon e^{T}(t-\tau )L^{T}Le(t-\tau ), \end{aligned} \end{aligned}$$

(8)

where $\Xi = -QD-D^{T}Q-QK-K^{T}Q+Q(A+\triangle A)L+L^{T}(A+\triangle A)^{T}Q+\frac{1}{\epsilon }Q(B^{\tau }+\triangle B^{\tau })(B^{\tau }+\triangle B^{\tau })^{T}Q$.

Let

$$\begin{aligned} \Omega =\left( \begin{array}{cc} \Omega _{11} &{} Q(B^{\tau }+\triangle B^{\tau }) \\ * &{}-\epsilon I_{n} \end{array} \right) ,\ \ \ \Phi _{1}=\left( \begin{array}{cc} \Phi _{11} &{} QB^{\tau } \\ * &{}-\epsilon I_{n} \end{array} \right) ,\ \ \ \Phi _{2}=\left( \begin{array}{cc} \Phi _{11}^{'} &{} Q\triangle B^{\tau } \\ * &{} 0_{n\times n} \end{array} \right) , \end{aligned}$$

where $\Omega _{11}=-QD-D^{T}Q-QK-K^{T}Q+Q(A+\triangle A)L+L^{T}(A+\triangle A)^{T}Q+\kappa Q$, $\Phi _{11}=-QD-D^{T}Q-QK-K^{T}Q+QAL+L^{T}A^{T}Q+\kappa Q$, $\Phi _{11}^{'}= Q \Vert \triangle A\Vert L+L^{T}\Vert \triangle A^{T}\Vert Q$. It’s easy to see that $\Omega \le \Phi _{1}+\Phi _{2}$.

$$\begin{aligned} \Phi _{2}= & {} \left( \begin{array}{cc} Q \Vert \triangle A\Vert L+L^{T}\Vert \triangle A^{T}\Vert Q &{} Q\triangle B^{\tau } \\ * &{}0 _{n\times n} \end{array} \right) \\= & {} \left( \begin{array}{cc} QM\Vert \Lambda _{3}(t)\Vert EL+L^{T}E^{T}\Vert \Lambda _{3}^{T}(t)\Vert M^{T}Q &{} Q{\widehat{M}}\Vert \Lambda _{4}(t)\Vert {\widehat{E}} \\ * &{} 0_{n\times n} \end{array} \right) , \end{aligned}$$

Let

$$\begin{aligned} N_{1}=(QM, 0_{n\times n^{2}})^{T}, N_{2}=( 0_{n\times n^{2}},Q{\widehat{M}})^{T}, F_{1}=(EL,0_{n^{2}\times n}), F_{2}=({\widehat{E}},0_{n^{2}\times n}), \end{aligned}$$

and according to Lemma 2, $\Phi _{2}$ can be rewritten as follows:

$$\begin{aligned} \begin{aligned} \Phi _{2}&=N_{1}\Vert \Lambda _{3}(t)\Vert F_{1}+F_{1}^{T}\Vert \Lambda _{3}^{T}(t)\Vert N_{1}^{T}+N_{2}\Vert \Lambda _{4}(t)\Vert F_{2}+F_{2}^{T}\Vert \Lambda _{4}^{T}(t)\Vert N_{2}^{T}\\&\le \rho _{1}^{-1}N_{1}N_{1}^{T}+\rho _{1}F_{1}^{T}F_{1}+\rho _{2}^{-1}N_{2}N_{2}^{T}+\rho _{2}F_{2}^{T}F_{2}. \end{aligned} \end{aligned}$$

By Lemma 3, the Theorem’s condition (6) $\Pi <0$ is equivalent to

$$\begin{aligned} \Phi _{1}+\rho _{1}F_{1}^{T}F_{1}+\rho _{2}F_{2}^{T}F_{2}+\rho _{1}^{-1}N_{1}N_{1}^{T}+\rho _{2}^{-1}N_{2}N_{2}^{T}<0, \end{aligned}$$

which means $\Omega <0$. Based on Lemma 3 again, $\Omega <0$ means that

$$\begin{aligned}&-QD-D^{T}Q-QK-K^{T}Q+Q(A+\triangle A)L+L^{T}(A+\triangle A)^{T}Q\\&\quad +\frac{1}{\epsilon }Q(B^{\tau }+\triangle B^{\tau })(B^{\tau }+\triangle B^{\tau })^{T}Q+\kappa Q<0, \end{aligned}$$

that is

$$\begin{aligned} \Xi <-\kappa Q. \end{aligned}$$

(9)

Using (7) and (9), the derivative of V(t) (8) can be rewritten as:

$$\begin{aligned} D^{\alpha } \le -\kappa V(t)+ \beta V(t-\tau ). \end{aligned}$$

If the condition $\kappa> \beta >0$ is combined, then the conditions of the Lemma 4 are all satisfied. As a consequence, error system (4) is asymptotically stable. It’s not complicated to get that $e(t)\rightarrow 0$, when $t\rightarrow \infty$, that is to say, $\lim _{t\rightarrow \infty }\Vert y(t)-x(t)\Vert =0$. On the basis of Definition 3, the drive FOMNNs (2) and response FOMNNs (3) can synchronize via the designed controller (5). This completes the proof. $\square$

Remark 3

The drive-response FOMNNs (2) and (3) can achieve synchronization by ingeniously designed controller (5) with $\gamma _{i}=\sum _{j=1}^{n}(|\acute{a}_{ij}-\grave{a}_{ij}|+|\acute{b}^{\tau }_{ij}-\grave{b}^{\tau }_{ij}|)M_{j}$. Underlying given constants $\kappa$, $\beta$ and defined $Y=QK$, the synchronization criteria LMIs (6) and (7) are easy to be solved by the matlab toolbox.

A fractional-order drive-response neural networks with a constant time delay is established as follows:

$$\begin{aligned} D^{\alpha }x(t)= & {} -Dx(t)+Af(x(t))+B^{\tau }f(x(t-\tau ))+I \end{aligned}$$

(10)

$$\begin{aligned} D^{\alpha }y(t)= & {} -Dy(t)+Af(y(t))+B^{\tau }f(y(t-\tau ))+u^{'}(t)+I \end{aligned}$$

(11)

The controller is reduced to

$$\begin{aligned} u^{'}(t)=-Ke(t), \end{aligned}$$

(12)

then the error system is taken as follows:

$$\begin{aligned} D^{\alpha }e(t)=-(D+K)e(t)+Ag(e(t))+B^{\tau }g(e(t-\tau )) \end{aligned}$$

(13)

Based on controller (13), the synchronization criteria for fractional neural networks(FNNs) is obtained in Corollary 1.

Corollary 1

Suppose that Assumption 1 holds, for given constants $0<\beta <\kappa$, under the proposed controller (12), the FNNs (10) and (11) can globally and asymptotically synchronize, if there exists a matrix Y, a positive constant $\epsilon$ and a positive definite matrix $Q=diag\{q_{1}, q_{2},\ldots , q_{n}\}$ so that the following LMIs (14) and (15) are satisfied:

$$\begin{aligned} \Pi ^{'}= & {} \left( \begin{array}{cc} \Pi _{11}^{'} &{} QB^{\tau } \\ * &{}-\epsilon I_{n} \\ \end{array} \right) <0, \end{aligned}$$

(14)

$$\begin{aligned}&\epsilon L^{T}L-\beta Q<0 \end{aligned}$$

(15)

where $\Pi _{11}^{'}=-QD-D^{T}Q-Y-Y^{T}+QAL+L^{T}A^{T}Q+\kappa Q$, $K=Q^{-1}Y$.

Remark 4

The model in Theorem 1 is FOMNNs, the memristive connection weights $\acute{a}_{ij}, \grave{a}_{ij}, \acute{b}^{\tau }_{ij}, \grave{b}^{\tau }_{ij}$ of (2) and (3) switch their values when their states change. If the connection values are not changed, the model will become traditional FNNs. Then, the synchronization criteria for FNNs can be obtained facilely.

Consider the following FOMNNs without time delays:

$$\begin{aligned} D^{\alpha }x(t)= & {} -Dx(t)+(A+M\Lambda _{1}(t)E)f(x(t))+I \end{aligned}$$

(16)

$$\begin{aligned} D^{\alpha }y(t)= & {} -Dy(t)+(A+M\Lambda _{3}(t)E)f(y(t))+u(t)+I \end{aligned}$$

(17)

Based on the controller (5), the error system is gotten as follows:

$$\begin{aligned} D^{\alpha }e(t)=-(D+K)e(t)+(A+\triangle A)g(e(t))+\Sigma ^{'}(t)-\Gamma sgn(e(t)) \end{aligned}$$

(18)

where $\triangle A= M \Lambda _{3}(t) E$, $\Sigma ^{'}(t)= [M(\Lambda _{3}(t)-\Lambda _{1}(t))E]f(x(t))$. Based on controller (5), the synchronization criteria for FOMNNs without time delays are obtained in Corollary 2.

Corollary 2

Suppose that Assumptions 1 and 2 hold, under the proposed controller (5) with $\gamma _{i}=\sum _{i=1}^{n}(|\acute{a}_{ij}-\grave{a}_{ij}|)M_{j}$, the FOMNNs (16) and (17) can reach global asymptotical synchronization, if there exists a matrix Y, a positive constant $\rho _{1}$ and a positive definite matrix $Q=diag\{q_{1}, q_{2},\ldots , q_{n}\}$ so that the following LMI (19) is satisfied:

$$\begin{aligned} \Pi ^{''}=\left( \begin{array}{cc} \Pi _{11}^{''} &{} QM \\ * &{}-\rho _{1} I_{n} \\ \end{array} \right) <0, \end{aligned}$$

(19)

where $\Pi _{11}^{''}=-QD-D^{T}Q-Y-Y^{T}+QAL+L^{T}A^{T}Q + \rho _{1}L^{T}E^{T}EL$, $K=Q^{-1}Y$.

Remark 5

If the communications among neural cells are without time delays, the model of drive-response FOMNNs will be reduced to (16) and (17). Then, the synchronization criteria for FMNNs with no delay can be obtained effortlessly.

4 Parameters Optimization by SIWPSO

The optimization model of the controller parameters is provided in this section. In order to get the optimal controller, the target function of the model is the sum of the control energy index and the ISE index. To achieve the synchronization of the FOMNNs (2) and (3), the criteria in Theorem 1 are chosen as the constraint conditions. However, the proposed optimization model is not easy to solve. The SIWPSO algorithm is applied to find out the optimal parameters.

4.1 The Optimization Model

The following target function is chosen to obtain the optimal parameters of the controller.

$$\begin{aligned} \ J=\int _{0}^{\infty }(u^{T}(t)u(t)+e^{T}(t)e(t))dt. \end{aligned}$$

(20)

where $\int _{0}^{\infty }(u^{T}(t)u(t))dt$ is the control energy index, $\int _{0}^{\infty }(e^{T}(t)e(t))dt$ is the ISE index. Moreover, the synchronization conditions of the FOMNNs need to be achieved, which means that the proposed Theorem 1 needs to be reached. This suggests that for given constants $0<\beta <\kappa$, there exists a matrix Y, some positive constants $\epsilon$, $\rho _{1}$, $\rho _{2}$ and a positive definite matrix Q so that the LMIs (6) and (7) are satisfied:

$$\begin{aligned} \Pi= & {} \left( \begin{array}{cccc} \Pi _{11} &{}\quad QB^{\tau } &{}\quad QM &{}\quad 0\\ * &{}\quad -\epsilon I_{n} &{}\quad 0 &{}\quad Q{\widehat{M}} \\ * &{}\quad * &{}\quad -\rho _{1}I_{n^{2}\times n^{2}} &{}\quad 0\\ * &{}\quad * &{}\quad * &{}\quad -\rho _{2}I_{n^{2}\times n^{2}} \\ \end{array} \right)<0, \\&\epsilon L^{T}L-\beta Q<0 \end{aligned}$$

where $\Pi _{11}=-QD-D^{T}Q-Y-Y^{T}+QAL+L^{T}A^{T}Q+\kappa Q + \rho _{1}L^{T}E^{T}EL+ \rho _{2}{\widehat{E}}^{T}{\widehat{E}}$, $K=Q^{-1}Y$.

In brief, the parameter optimization of the controller is as follows:

$$\begin{aligned}&\min J=\int _{0}^{\infty }(u^{T}(t)u(t)+e^{T}(t)e(t))dt,\nonumber \\&\begin{aligned} s.t.\left\{ \begin{array}{l} \Pi<0,\\ \epsilon L^{T}L-\beta Q<0,\\ Q>0,\\ \epsilon>0,\\ \rho _{j}>0(j=1,2). \end{array} \right. \end{aligned} \end{aligned}$$

(21)

where $\Pi _{11}=-QD-D^{T}Q-Y-Y^{T}+QAL+L^{T}A^{T}Q+\kappa Q + \rho _{1}L^{T}E^{T}EL+ \rho _{2}{\widehat{E}}^{T}{\widehat{E}}$, $K=Q^{-1}Y$.

The parameter optimization of the controller is essentially to optimize the control gain matrix K. The optimal gain matrix can minimize the target function which includes the control energy index and ISE index. To solve the complicated calculation (21), the SIWPSO algorithm is put into use.

Remark 6

The target function (20) cannot be directly evaluated. In order to facilitate calculation, the Riemann sum definition of integral $\int _{a}^{b}F(x)dx \cong (b-a)F(c), c\in [a,b]$ is used to obtain an approximated value of the target function. The SIWPSO algorithm is an improved intelligent algorithm to solve the optimization model (21). The better performance will be presented in simulation part.

4.2 SIWPSO for the Optimization Model

The SIWPSO algorithm requires each individual (particle) to maintain two vectors during evolution, namely the velocity vector ${\mathbf {v}}_{i}=(v_{i1}, v_{i2}, \ldots , v_{iDm})$ and the position vector ${\mathbf {x}}_{i}=(x_{i1}, x_{i2}, \ldots , x_{iDm})$, where i represents the number of particles, and Dm is the dimension of solutions. The velocity of a particle determines the direction and speed. The position reflects the position in the solution space. Both are the basis of evaluating the solution. The algorithm also requires each particle to maintain its own historical optimal position vector (represented by $\mathbf {pBest}=(pBest_{i}^{1}, pBest_{i}^{2}, \ldots , pBest_{i}^{Dm})$) and a global optimal vector (represented by $\mathbf {gBest}=(gBest_{i}^{1}, gBest_{i}^{2}, \ldots , gBest_{i}^{Dm})$), which guides particles to approach the global optimal region. The following are steps of the SIWPSO algorithm:

Step 1 Assign values to the parameters in the algorithm. For example, the particle swarm size m, maximum number of iterations N, and acceleration coefficient $ac_{1}$, $ac_{2}$.

Step 2 Randomly initialize each particle.

Step 3 Evaluate each particle and get the global optimum.

Step 4 Evaluate the current solution with the consistent conditions (21). If they can synchronize the FOMNNs, go to the next step, whereas, go to the Step 7.

Step 5 Update (22) the velocity and position of every particle.

Step 6 Evaluate the fitness function (20) of each particle.

Step 7 Recalculate the historical optimum position $pBest_{i}$ of each particle.

Step 8 Recalculate the global optimal position $gBest_{g}$ of the group.

Step 9 Repeat steps 4-8 before reaching the maximum number of iterations.

Step 10 The optimal control gain is the latest $gBest_{g}$.

The update rules of position and velocity are as follows:

$$\begin{aligned} \begin{aligned}&{\mathbf {v}}_{id}(t+1)=\varpi (t) {\mathbf {v}}_{id}(t)+ac_{1}\gamma _{1}(\mathbf {pBest}_{id}(t)-{\mathbf {x}}_{id}(t))+ac_{2}\gamma _{2}(\mathbf {gBest}_{gd}(t)-{\mathbf {x}}_{id}(t)),\\&{\mathbf {x}}_{id}(t+1)={\mathbf {x}}_{id}(t)+{\mathbf {v}}_{id}(t+1), \end{aligned} \end{aligned}$$

(22)

where i represents the ith particle and d is on behalf of the dth dimension in the search space. Usually, the inertia weight $\varpi (t)$ is chosen in (0.5, 1) randomly. Let $ac_{1}=ac_{2}=2$. $\gamma _{1}$ and $\gamma _{2}$ are random numbers which are uniformly distributed at (0, 1).

Remark 7

The main difference between PSO and SIWPSO algorithm is the inertia weight. In PSO algorithm, the value of the inertia weight is usually set as 0.9, while in SIWPSO algorithm, it is randomly selected in (0.5, 1).

5 Simulation

A complete simulation is presented to exhibit the proposed theoretical approach and the optimization.

Consider the FOMNNs(1) with the following parameters: $\alpha =0.98$, $\tau =1$, $I=(0,0)^{T}$, $f_{i}(x_{i})=tanh(x_{i})(i=1,2)$, $D=diag\{1,1\}$,

$$\begin{aligned} A(x(t))=\left( \begin{array}{cc} a_{11}(x_{1}(t)) &{} a_{12}(x_{1}(t)) \\ a_{21}(x_{2}(t)) &{} a_{22}(x_{2}(t)) \\ \end{array} \right) ,\ \ \ \ \ B^{\tau }(x(t)) =\left( \begin{array}{cc} b^{\tau }_{11}(x_{1}(t)) &{} b^{\tau }_{12}(x_{1}(t)) \\ b^{\tau }_{21}(x_{2}(t)) &{} b^{\tau }_{22}(x_{2}(t)) \\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} a_{11}(x_{1})= & {} \left\{ \begin{aligned} 1.75,&|x_{1}|\le 3, \\ 2.1,&|x_{1}|> 3, \end{aligned} \right. \ \ \ \ \ \ \ a_{12}(x_{1})=\left\{ \begin{aligned} -0.1,&|x_{1}|\le 3, \\ -0.12,&|x_{1}|> 3, \end{aligned} \right. \\ a_{21}(x_{2})= & {} \left\{ \begin{aligned} -4.7,&|x_{2}|\le 3, \\ -5.1,&|x_{2}|> 3, \end{aligned} \right. \ \ \ \ \ \ \ a_{22}(x_{2})=\left\{ \begin{aligned} 2.85,&|x_{2}|\le 3, \\ 3.2,&|x_{2}|> 3, \end{aligned} \right. \\ b^{\tau }_{11}(x_{1})= & {} \left\{ \begin{aligned} -1.7,&|x_{1}|\le 3, \\ -1.6,&|x_{1}|> 3, \end{aligned} \right. \ \ \ \ \ \ \ b^{\tau }_{12}(x_{1})=\left\{ \begin{aligned} -0.08,&|x_{1}|\le 3, \\ -0.11,&|x_{1}|> 3, \end{aligned} \right. \\ b^{\tau }_{21}(x_{2})= & {} \left\{ \begin{aligned} -0.3,&|x_{2}|\le 3, \\ -0.2,&|x_{2}|> 3, \end{aligned} \right. \ \ \ \ \ \ \ b^{\tau }_{22}(x_{2})=\left\{ \begin{aligned} -2.5,&|x_{2}|\le 3, \\ -2.38,&|x_{2}|> 3. \end{aligned} \right. \end{aligned}$$

It’s easy to verify that $L_{1}=L_{2}=1$, $M_{1}=M_{2}=1$, $\gamma _{1}=0.5$, $\gamma _{2}=0.97$,

$$\begin{aligned} A= & {} \left( \begin{array}{cc} 1.925 &{}\quad -\,0.11 \\ -\,4.9 &{}\quad 3.025 \\ \end{array} \right) ,\ \ \ \ \ B^{\tau } =\left( \begin{array}{cc} -\,1.65 &{}\quad -\,0.095 \\ -\,0.25 &{}\quad -\,2.44 \\ \end{array} \right) , \\ M= & {} \left( \begin{array}{cccc} \sqrt{0.175} &{}\quad \sqrt{0.01} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \sqrt{0.2}&{}\quad \sqrt{0.175}\\ \end{array} \right) ,\ \ \ E=\left( \begin{array}{cccc} \sqrt{0.175} &{}\quad 0 &{}\quad \sqrt{0.2} &{}\quad 0 \\ 0 &{}\quad \sqrt{0.01} &{}\quad 0 &{}\quad \sqrt{0.175} \\ \end{array} \right) ^T, \\ {\widehat{M}}= & {} \left( \begin{array}{cccc} \sqrt{0.05} &{}\quad \sqrt{0.015} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \sqrt{0.05}&{}\quad \sqrt{0.06}\\ \end{array} \right) ,\ \ \ {\widehat{E}}=\left( \begin{array}{cccc} \sqrt{0.05} &{}\quad 0 &{}\quad \sqrt{0.05} &{}\quad 0\\ 0 &{}\quad \sqrt{0.015} &{}\quad 0 &{}\quad \sqrt{0.06} \\ \end{array} \right) ^T. \end{aligned}$$

The phase portrait of the drive-FOMNNs is shown in Fig. 1 with initial conditions $x=(-0.5,0.4)^{T}$ for $t \in [-1,0].$

Fig. 1

Phase portrait of the drive-FOMNNs

Take $\kappa =1.5$, $\beta =0.8$. By solving the LMIs (6) and (7) via the matlab toolbox, the feasible solutions are $\epsilon =0.1494$, $\rho _{1}=1.1800$, $\rho _{2}=1.2099$, $Q=diag\{ 0.2541, 0.2541\}$,

$$\begin{aligned} Y=\left( \begin{array}{cc} 1.6864 &{}\quad -\,0.6069\\ -\,0.6069 &{}\quad 2.2883 \end{array} \right) ,\ \ \ \ \ K=Q^{-1}Y =\left( \begin{array}{cc} 6.6358 &{}\quad -\,2.3883\\ -\,2.3883 &{}\quad 9.0042 \end{array} \right) . \end{aligned}$$

Fig. 2

State trajectories of the drive-response FOMNNs under the controller

Fig. 3

State trajectories of the drive-response FOMNNs without controller

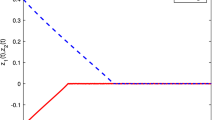
Based on Theorem 1, the driven-FOMNNs (2) can synchronize the response-FOMNNs (3) under the controller (5) for any initial values, which is verified by Figs. 2, 3 and 4. Figure 2 presents the state trajectories of the drive-response FOMNNs under the controller with initial values $x=(-\,0.5,0.4)^{T}$, $y=(1,0.5)^{T}$ for $t \in [-1,0].$ Figure 3 presents the state trajectories of the drive-response FOMNNs without controller and the initial values are same with the Fig. 2. In Fig. 4, the left one describes the error trajectories of the FOMNNs with the controller and the right one without controller. It’s obvious that the drive-response FOMNNs can be synchronized by the proposed controller. As time approaches infinity, the error system tends to zero.

Fig. 4

Error trajectories with (left) and without (right) the controller

The scale of the particle swarm is chosen as $m=20$. The maximum iterations is chosen as $N=30$. The unknown matrix

$$\begin{aligned} K=\left( \begin{array}{cc} k_{11} &{}\quad k_{12} \\ k_{21} &{}\quad k_{22}\\ \end{array} \right) , \end{aligned}$$

Table 1 Fitness function values for different values with K

the initial values of position are selected in $[-\,20,20]$ randomly. The initial values of velocity are selected in $[-\,0.1,0.1]$ randomly. After the performance of SIWPSO algorithm, the optimal solutions are presented in Table 1. As comparison groups, the optimal solutions by PSO and the solutions without optimizing process are presented in Table 1 as well. It’s evident that the solutions searched by SIWPSO algorithm can realize the minimum of the fitness function . The solutions searched by PSO algorithm are also feasible, but they are not better than those searched by the SIWPSO algorithm.

Figure 5 illustrates the evolution process of the fitness function via SIWPSO algorithm. The conclusion can be drawn from the Fig. 5 that when the number of iterations increases, the value of J decreases from near 7400 to 5552.3, and at last, it does not change any more. In other word, the solutions which can minimize the value of J and let the value stable are the optimal control gains. The stable solution that minimizes the J value is the desirable optimization gain matrix of the controller.

Fig. 5

The evolution of SIWPSO algorithm

6 Conclusion

In the paper, the synchronization of delayed memristive neural networks via optimal control using SIWPSO is studied. The networks are in fractional-order. First, a valid controller is designed, then based on some analytical methods, the drive-response synchronization results are received. Two corollaries without memristor and without time delays are provided at the same time. Second, this paper describes the optimization model of control paraments and the optimization process according to the SIWPSO algorithm. The optimization solutions can achieve the minimum target function, meanwhile, synchronize the drive-response FOMNNs. Finally, the proposed results can be confirmed by the simulations. Notably, a constant time delay is considered in this paper. If time delays are variant, maybe the delay partitioning approach can solve this problem. Besides, only the SIWPSO algorithm is considered in this paper. The genetic algorithm possibly has better effect, which will be studied in the future study.