1 Introduction

Recently, the fractional-order systems and fractional calculus have attracted many researchers’ attention. Due to its infinite memory, the fractional-order model can better depict the dynamical behaviors for some systems [1–5], and the fractional-order calculus can offer an effective tool to describe the memory properties for these systems. Therefore, the fractional-order systems and fractional calculus have been applied to neural networks recently to establish the fractional-order neural networks system (FNNs). The dynamic characteristics for FNNs attracted some researchers, see, e.g., [6–11], and in particular the synchronization, which is one of the most important dynamic characteristics for these systems, has seen more and more interesting applications in information fields. Some excellent results on synchronization were listed in [6–10, 12–14]. In last years, researchers were devoted to the adaptive synchronization, in which the drive and response systems synchronize up to a scalar factor, since it is an important branch of synchronization. Most recently the authors of [15–18] have studied the adaptive synchronization for fractional-order NNs under the assumption that the activation functions are generally Lipschitz continuous. The synchronization criteria of neural systems mainly take into account the Lyapunov stability theory, picking the L–K functional, and investigating its derivative with the appropriate methodologies. Different sorts of L–K functional have been developed for the NNs [6, 7, 19]. However, it is a challenge to pick an appropriate L–K functional for a fractional-order system.

Meanwhile, when signals between neurons are transmitted, the time delays always appear because the propagation’s speed is finite and the switching speed on the amplifiers is limited. It is a difficult problem and the time delays importantly affect the characteristics of NNs. Up to date, more and more papers have considered the problem, see [6–14, 20–22]. The authors in [11] considered the sampled-data stabilization for fuzzy genetic regulatory networks including leakage delay signals. The authors in [6] gave sufficient conditions to ensure projective synchronization of fractional-order neural networks with delays. The authors in [12] dealt with the synchronization analysis for fractional-order BAM neural networks with time delays. The authors in [23] examined \(H_{\infty }\) state estimation of generalized neural networks with interval time-varying delays. The authors in [19, 24] considered stability of neural networks with discrete and distributed time-varying delays. Thus, the impact of the delay in NNs cannot be ignored.

As is well known, the external uncertainty perturbations usually influence the system. Since the external uncertainty perturbations are treated as a stochastic process by [25], it is significant to investigate the dynamic properties for neural networks under stochastic effects. In general, Brownian motion is often used to describe the stochastic effects in some mathematic models (see [20, 21, 26–29]).

However, the high-gain activations are discontinuous [30] as neuron amplifiers meet accidently with high gain, thus NNs with discontinuous activations are considered ideal [31]. In 2017, the authors in [18] studied the existence of a solution and synchronization for bidirectional associative memory NNs under discontinuous activations.

Motivated by the above discussion, we mainly investigate the adaptive synchronization for the fractional-order NNs with time delays and discontinuous activation functions under the Brownian motion environment in this paper. Firstly, using the definition of Filippov solution, the condensing map is defined for fractional-order stochastic NNs to prove the solution’s existence by using the fixed-point theory. Secondly, the controller is expressed to guarantee the synchronization between FNNs and FSNNs. Our main goal is to establish the stochastic delay-dependent synchronization criteria for FNNs under discontinuous activations. Some new synchronization criteria are displayed in the form of linear matrix in equalities (LMIs) by using Lyapunov–Krasovskii functional method. The main advantage of the LMI-based approach is that the LMI synchronization conditions can be checked numerically using MATLAB LMI toolbox.

The contributions of this paper are summarized as follows:

(1) Under the Brownian motion environment, adaptive synchronization is mainly studied for fractional-order stochastic neural networks (FSNNs) with time delays and discontinuous activation functions, which is innovative.

(2) An appropriate Lyapunov functional is constructed, the main results are expressed in LMIs, by using Itô formula, as well as fractional integral and derivative techniques.

(3) Finally, a numerical example is provided to illustrate the given results.

2 System description and preliminaries

The fractional-order delayed NNs without noise disturbance are considered as follows:

$$ \begin{aligned} &du_{k}(s)+dI_{0^{+}}^{1-\alpha } \Biggl(\sum_{i=1}^{m} d_{ki}u_{i}(s)-u_{i0} \Biggr) \\ &\quad =\Biggl[-a_{k}u_{k}(s)+\sum _{i=1}^{m}b_{ki}h_{i} \bigl(u_{i}(s)\bigr) + \sum_{i=1}^{m}c_{ki}l_{i} \bigl(u_{i}(s-\tau )\bigr) +J_{k}(s)\Biggr]\,dt, \\ &u(s)=u_{0}(s),\quad s\in [-\tau,0], \end{aligned} $$
(1)

where \(I_{0^{+}}^{1-\alpha }\) is the Riemann–Liouville fractional integral operator with \(\frac{1}{2}<\alpha \leq 1\). At time s, \(u_{k}(s)\) is the state variable of the kth neuron; \(a_{k}>0\) are the self-inhibitions, \(d_{ki}>0\) are the strengths for fractional parts; \(b_{ki}\) are the connection strengths between the kth and ith neuron; \(c_{ki}\) are the time delay connection strengths between the kth and ith neuron; \(h_{i}(u_{i}(s))\) and \(l_{i}(u_{i}(s))\) are the activation functions, which are discontinuous; τ is the time delay; \(J_{k}\) is the input, where \(k=1,2,\dots, m; i=1,2,\dots,m\).

Letting \(u(s)=(u_{1}(s),u_{2}(s),\dots,u_{m}(s))^{T}\), \(h(s)=(h_{1}(s),h_{2}(s),\dots,h_{m}(s))^{T}\), \(l(s)=(l_{1}(s),l_{2}(s), \dots, l_{m}(s))^{T}\), \(A=\operatorname{diag}\{a_{1},a_{2},\dots,a_{m}\}>0\), \(B=(b_{ki})_{m\times m}\), \(C=(c_{ki})_{m\times m}\), and \(D=(d_{ki})_{m\times m}\), we rewrite system (1) in the following matrix form:

$$ du(s)-dI_{0^{+}}^{1-\alpha }\bigl(Du(s)-u_{0} \bigr) =\bigl[-Au(s)+Bh\bigl(u(s)\bigr)+Cl\bigl(u(s- \tau )\bigr)+J(s)\bigr]\,ds. $$
(2)

In what follows the Filippov solution will be considered for fractional NNs (1). Some definitions on the Filippov solutions [18, 32] will be introduced firstly.

Definition 1

(Filippov set-valued map, [32])

Define the map \(K[h(u)]: \mathbb{R}^{n}\rightarrow 2^{\mathbb{R}^{n}}\) of \(h(u)\) at \(u\in \mathbb{R}^{n}\) as follows:

$$ K\bigl[h\bigl(u(t)\bigr)\bigr]=\bigcap_{\rho >0}\bigcap _{\mu (Q)=0}\bar{co}\bigl[h\bigl(A(u,\rho ) \setminus Q \bigr)\bigr], $$

where \(A(u,\rho )\) is the open ball of radius ρ whose center is at \(u\in \mathbb{R}^{n}\), \(Q\subset \mathbb{R}^{n}\), \(\mu (\cdot )\) is the Lebeague measure. The map is called a Filippov set-valued map.

Definition 2

(Filippov solution for fractional NNs)

If the function \(u(s)^{T}:[-\tau,t]\rightarrow \mathbb{R}^{n}, t>0\) satisfies:

  1. (1)

    \(u(s)^{T}\) is continuous on \([-\tau,t]\), and absolutely continuous on any compact time subinterval of \([t_{1},t_{2})\);

  2. (2)

    \(u(s)^{T}\) satisfies the following differential system on \(s\in (0,t]\),

    $$\begin{aligned} &du(s)+dI_{0^{+}}^{1-\alpha }\bigl(Du(s)-u_{0}\bigr)\\ &\quad \in \bigl[-Au(s)+Bh\bigl(u(s)\bigr)+Cl\bigl(u(s- \tau )\bigr)+J(s)\bigr]\,ds, \end{aligned}$$

    or equivalently, the following equation is satisfied [33]:

  3. (2’)

    There are measurable functions \(f(s)=(f_{1},\dots,f_{n})^{T}: [-\tau,t]\rightarrow \mathbb{R}^{n}\) and \(g(s)=(g_{1},\dots,g_{n})^{T}: [-\tau,t]\rightarrow \mathbb{R}^{n}\) such that \(f(s)\in K[h(x(s))],g(t)\in K[l(x(s))]\) for a.a. \(s\in [-\tau,t]\), and \(u(s)\) satisfies

    $$ du(s)+dI_{0^{+}}^{1-\alpha }\bigl(Du(s)-u_{0}\bigr) \in \bigl[-Au(s)+Bf(s)+Bg(s)+J(s)\bigr]\,ds, \quad s\in (0,T], $$

    then \(u(s)\) is called the Filippov solution for the fractional NNs (1).

It is well known that the uncertainties are unavoidable in many situations, so we will consider the stochastic effect in the fractional NNs (2), the corresponding stochastic NNs with Brownian motion are given as follows:

$$ \begin{aligned} &dv(s)+dI_{0^{+}}^{1-\alpha } \bigl(Dv(s)-v_{0}\bigr) \\ &\quad=\bigl[-Av(s)+Bh\bigl(v(s)\bigr)+Cl\bigl(v(s- \tau )\bigr) +J(s)+\delta (s)\bigr]\,ds+\sigma (s)\,dB(s), \\ &v(s)=v_{0}(s),\quad s\in [-\tau,0], \end{aligned} $$
(3)

where \(v(s)=(v_{1}(s),\dots,v_{m}(s))^{T}\) is the state vector of the stochastic NNs, \(\delta (s)=(\delta _{1}(s),\dots, \delta _{m}(s))^{T}\) is a controller, which need to be designed to ensure the synchronization, and other parameters are the same as those in fractional NNs (2); \(\sigma (s)\) is the matrix representing the power of the perturbation, \(B(s)\) is Brownian motion on \([0,t]\), and \(v_{0}\) is a real-valued random variable on a complete probability space \((\Omega,\mathscr{F},P)\).

Similar to the fractional NNs (2), if \(v(s)^{T}\) is a solution of stochastic fractional NNs (3), then there exist bounded measurable functions \(\hat{f}(s)\in K[h(y(s))],\hat{g}(s)\in K[l(y(s))]\) such that

$$ \begin{aligned} &dv(s)+dI_{0^{+}}^{1-\alpha }\bigl(Dv(s)-v_{0}\bigr)\\ &\quad \in \bigl[-Av(s)+B\hat{f}(s)+C \hat{g}(s) +J(s)+\delta (s)\bigr]\,ds+\pi (s)\,dB(s),\quad s \in (0,t]. \end{aligned}$$

Let \(\varepsilon _{i}(s)=v_{i}(s)-u_{i}(s)\) and \(\varepsilon (s)=v(s)-u(s)=[\varepsilon _{1}(s), \varepsilon _{2}(s), \dots, \varepsilon _{m}(s)]^{T} \). We aim to design a controller δ which can ensure the synchronization between the fractional NNs (3) with initial condition \(v(0)\) and the fractional NNs (1) with initial condition \(u(0)\), i.e.,

$$ \lim_{t\rightarrow \infty }E \Vert \varepsilon \Vert =\lim _{t \rightarrow \infty }E \bigl\Vert v(s)-u(s) \bigr\Vert =0, $$

where \(\Vert \cdot \Vert \) denotes the Euclidean norm, E is the expectation with respect to P.

Subtracting (3) from (2), the error satisfies the following system:

$$ \begin{aligned} &d\varepsilon (s)+dI_{0^{+}}^{1-\alpha }\bigl(D\varepsilon (s)-\varepsilon _{0}\bigr) \\ &\quad\in \bigl[-A\varepsilon (s)+B\bigl( \hat{f}(s)-f(s)\bigr)+B\bigl(\hat{g}(s)-g(s)\bigr) +\delta (s)\bigr]\,ds+ \pi (s) \,dB(s),\quad s\in (0,t], \end{aligned} $$
(4)

and the initial condition is

$$ \varepsilon (s)=v(s)-u(s),\quad s\in [-\tau,0]. $$
(5)

In order to establish the expected results, several assumptions are given in the following.

Assumption 1

Assume that \(h_{j}, l_{j}: \mathbb{R}\rightarrow \mathbb{R},j=1,2,\dots,m\) are globally bounded and continuous excluding the finite bounded intervals \(\{\mu _{k}\}\) and \(\{\nu _{k}\}\), and \(h_{j}, l_{j}\) have the finite left and right limits on \(\{\mu _{k}\}\) and \(\{\nu _{k}\}\) denoted by \(h_{j}(\mu _{k}^{-}),h_{j}(\mu _{k}^{+}),l_{j}(\nu _{k}^{-}),l_{j}( \nu _{k}^{+})\), respectively.

Assumption 2

Assume that there exist constants \(l_{j}^{h}>0,l_{j}^{l}>0\) and \(m_{j}>0, n_{j}>0,j=1,2,\dots,m\) such that the following two inequalities hold:

$$ \begin{aligned}& \bigl\vert \hat{f}(s)-f(s) \bigr\vert \leq l_{j}^{g} \bigl\vert v_{j}(s)-u_{j}(s) \bigr\vert +m_{j}, \\ &\hat{g}(s)-g(s) \vert \leq l_{j}^{l} \bigl\vert v_{j}(s)-u_{j}(s) \bigr\vert +n_{j}, \end{aligned} $$

for any \(f(s)\in K[h(x(s))],g(s)\in K[l(x(s))],\hat{f(s)}\in K[h(y(s))], \hat{g}(s)\in K[l(y(s))]\).

In the following, a fixed-point theorem for a condensing map will be introduced to obtain the solution for the fractional NNs (2).

Lemma 1

([34])

Let \(\mathcal{H}\) be a Banach space and denote by \(S(\mathcal{H})\) the set of all nonempty, bounded, closed, and convex subsets of \(\mathcal{H}\). For the map \(f:\mathcal{H}\rightarrow S(\mathcal{H})\), if the set \(\Lambda =\{y\in \mathcal{H}: \lambda y \in f(\mathcal{H}),\lambda >1 \}\) is bounded, then f is a condensing map and has a fixed point on \(\mathcal{H}\).

The following basic definitions and lemmas will be used in the following.

Definition 3

Given \(\alpha >0\), for \(h:(0,\infty )\rightarrow \mathbb{R,}\) the Riemann–Liouville fractional integral is defined as

$$ I_{0^{+}}^{\alpha }h(s)=\frac{1}{\Gamma (\alpha )} \int _{0}^{s}(s-t)^{ \alpha -1}h(t)\,dt,\quad s>0, $$

where \(\Gamma (\cdot )\) represents the Gamma function.

The main properties for the Riemann–Liouville fractional integral operators [22, 35] are recalled:

  1. (i)

    \(I_{0^{+}}^{\alpha }h(t)\) is nondecreasing with h;

  2. (ii)

    \(I_{0^{+}}^{\alpha }\) is compact, and \(\rho I_{0^{+}}^{\alpha }=\{0\}\), where ρ is the spectral set of the operator \(I_{0^{+}}^{\alpha }\);

  3. (iii)

    \(I_{0^{+}}^{\alpha }I_{0^{+}}^{\beta }=I_{0^{+}}^{\beta }I_{0^{+}}^{\alpha }=I_{0^{+}}^{ \alpha +\beta }\);

  4. (iv)

    For the real-valued continuous function h, \(\Vert I_{0^{+}}^{\alpha }h\Vert \prec I_{0^{+}}^{\alpha }\Vert h\Vert \), where \(\alpha,\beta >0\) and \(\Vert \cdot \Vert \) is an arbitrary norm.

Definition 4

Given α, if \(\alpha \in (n-1,n],n\in \mathbb{N}^{+}\), the Riemann–Liouville fractional derivative of order α of a function \(h\in C([0,T])\) is defined as

$$ D_{0^{+}}^{\alpha }h(s)=\frac{1}{\Gamma (n-\alpha )} \frac{d^{n}}{ds^{n}} \int _{0}^{s}(s-t)^{n-\alpha -1}h(t)\,dt,\quad s>0, $$

and the Caputo fractional derivative of order \(\alpha >0\) is defined as

Especially, if \(h^{(j)}(0)=0, j=0,1,\dots,m-1\), then coincides with \(D_{0^{+}}^{\alpha }h(s)\).

Meanwhile, if h has continuous order m derivative, then the Caputo fractional derivative can be written as

Property 1

If \(m-1<\alpha \leq m\), where \(m\in \mathbb{N}^{+}\), we have that

$$ \begin{aligned} &\bigl(D_{0^{+}}^{\alpha }I_{0^{+}}^{\alpha }h \bigr) (s)=h(s), \\ &\bigl(I_{0^{+}}^{\alpha }D_{0^{+}}^{\alpha }h\bigr) (s)=h(s)-\sum_{j=1}^{m} \frac{(I_{0^{+}}^{m-\alpha } f)^{(m-j)}(0^{+})}{\Gamma (\alpha -j+1)}t^{ \alpha -j},\quad s>0 \end{aligned} $$

hold.

We now present the Itô formula for the Brownian motion.

Lemma 2

([5])

Given \(\frac{1}{2}<\alpha <1\), suppose \(\xi (s)\) satisfies

$$ d\xi (s)=b(s,\xi )\,ds+\sigma _{1}(s,\xi )\,dB(s)+\sigma _{2}(ds)^{\alpha }. $$

If \(F\in C(\mathbb{R}^{+} \times \mathbb{R}^{n},\mathbb{R}^{m})\) is once differentiable with respect to s, and twice continuously differentiable with respect to ξ, the derivatives are denoted by \(F_{s}, F_{\xi }\), and \(F_{\xi \xi }\), respectively, then

$$ \begin{aligned} dF(s,\xi ) ={}&\biggl(F_{s}(s,\xi )+F_{\xi }(s,\xi )b(s,\xi ) +\frac{1}{2} \sigma _{1}(s, \xi )^{T}F_{\xi }\xi (s,\xi )\sigma _{1}(s,\xi ) \biggr)\,ds \\ &{}+F_{\xi }(s,\xi )\sigma _{1}(s,\xi )\,dB(s)+F_{\xi }(s, \xi )\sigma _{2}(s, \xi ) (ds)^{\alpha }. \end{aligned} $$

Lemma 3

([5])

If \(z(s)\) is nonnegative and locally integrable on \([0,t)\) and satisfies

$$ z(s)\leq c(s)+a(s) \int _{0}^{s}z(t)\,dt+b(s) \int _{0}^{s}(s-t)^{\gamma -1}z(t)\,dt, $$

then

$$ z(s)\leq c(s)+\sum_{m=1}^{\infty }\sum _{k=0}^{m} c^{k}_{m} a^{m-k}(t)c_{k}(s) \frac{(\Gamma (\beta ))^{\beta }}{\Gamma (k\beta +m-i)} \times \int _{0}^{s}(s-t)^{k \beta -(k+1-m)}b(t)\,dt, $$

where \(0<\gamma <1\), assuming that \(c(s)\) is nonnegative and locally integrable on \([0,t),t<\infty \), and \(a(s),b(s)\) are nonnegative and nondecreasing continuous with bound \(C>0\) on \([0,T)\).

3 Main results

In this section the existence of the Filippov solution will be considered for the fractional NNs (3) with discontinuous activations functions by using the fixed point theory for the condensing map. Then the adaptive controller \(\delta (t)\) is designed to ensure the synchronization between the stochastic NNs (2) and the fractional NNs (3).

3.1 Existence of solutions for FNNs

The following theorem gives the existence of the Filippov solutions for the fractional NNs (2).

Theorem 1

Under Assumptions 1–2, if the coefficient matrix of the fractional NNs (2) satisfies \(\Vert B \Vert L- \Vert A \Vert + \Vert C \Vert \tilde{L}\geq 0\), then there exists at least one Filippov solution \((u(s))^{T}\) for the fractional NNs (2) on \([0,+\infty )\).

Proof

Write the fractional NNs (2) as the integral system

$$ \begin{aligned} u(s)={}&u_{0}\biggl(1+ \frac{t^{1-\alpha }}{\Gamma (1-\alpha )}\biggr)- \frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha }Du(h)\,dh \\ &{}+ \int _{0}^{s}\bigl(-Au(h)+Bf\bigl(u(h)\bigr)+Cg \bigl(u(h-\tau )\bigr)+J\bigr)\,dh, \quad s\in [0,t]. \end{aligned} $$
(6)

Equivalently, we should prove that equation (6) has a unique solution.

Consider the map \(F: C([-\tau,t],\mathbb{R}^{n})\rightarrow S(C([-\tau,t],\mathbb{R}^{n}))\) given as follows:

$$ \begin{aligned} &F(\varpi ) (s)=w_{0} \biggl(1+\frac{s^{1-\alpha }}{\Gamma (1-\alpha )}\biggr) - \frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha }D\varpi (h)\,dh \\ &\phantom{F(\varpi ) (s)=}{}+ \int _{0}^{s}\bigl(-A\varpi (h)+Bh\bigl(\varpi (h) \bigr)+Cl\bigl(\varpi (h-\tau )\bigr)+J\bigr)\,dh,\quad t\in [0,T], \\ &F(\varpi ) (s)=\Phi (s),\quad s\in [-\tau,0], \end{aligned} $$
(7)

for \(\varpi \in C([-\tau,t], \mathbb{R}^{n})\), and define the norm as \(\Vert \varpi \Vert _{\infty }=\sup { \Vert \varpi (s) \Vert , s\in [-\tau, t]}\). It is easy to see that the fixed points of F are the solutions of (6) by using Property 1.

Similarly, following the proof Theorem 3.2 in [36], and using Assumptions 1–2, we conclude that F is completely continuous with convex closed values [33].

Now, we obtain the boundary of the set \(\Upsilon =\{\varpi \in C([-\tau, t], \mathbb{R}^{n}):\gamma \varpi \in F(\varpi ), \gamma >1\}\).

Given \(\varpi \in \Upsilon \), using the definition of ϒ, we have \(\gamma \varpi \in F(\varpi )\) for some \(\gamma >1\). Then, there exists \(\tilde{h}(s\varpi )\in F(\varpi (s)), \tilde{l}(s)\in F(\varpi (s))\) such that

$$ \begin{aligned} \varpi (s)={}&\frac{1}{\gamma } \biggl[w_{0}\biggl(1+ \frac{s^{1-\alpha }}{\Gamma (1-\alpha )}\biggr)-\frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha }D\varpi (h)\,dh \\ &{} + \int _{0}^{t}\bigl(-A\varpi (h)+B\tilde{h}\bigl( \varpi (h)\bigr)+C\tilde{l}\bigl( \varpi (h-\tau )\bigr)+J\bigr)\,dh\biggr],\quad t\in [0,T]. \end{aligned} $$
(8)

Let \(L=\max_{k}\{l_{k}^{h}\}\), \(M=\sum_{k=1}^{m}(m_{k}+n_{k})\), \(\tilde{L}=\max_{k}\{l_{k}^{l}\}\), \(\tilde{M}=\sum_{k=1}^{m}(n_{k})\). Then, by using Assumption 2 and the definition of \(\varpi (s)\), we obtain

$$ \begin{aligned}& \bigl\Vert \tilde{h}(s) \bigr\Vert \leq \sum_{k=1}^{m}\bigl(l_{k}^{h} \bigl\vert u_{k}(s) \bigr\vert +m_{k}\bigr)\leq L \bigl\Vert \varpi (s) \bigr\Vert +M, \\ &\bigl\Vert \tilde{l}(t) \bigr\Vert \leq \sum_{k=1}^{n} \bigl(l_{k}^{l} \bigl\vert u_{k}(t) \bigr\vert +n_{k}\bigr)\leq \tilde{L} \bigl\Vert \varpi (s) \bigr\Vert +\tilde{M}. \end{aligned} $$
(9)

By the above (9), we have

$$ \begin{aligned} \bigl\Vert \varpi (s) \bigr\Vert \leq{}& \biggl\Vert \varpi _{0}\biggl(1+ \frac{s^{1-\alpha }}{\Gamma (1-\alpha )}\biggr) \biggr\Vert - \frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha } \Vert D \Vert \bigl\Vert \varpi (h) \bigr\Vert \,dh \\ &{} + \int _{0}^{s}\bigl(- \Vert A \Vert \bigl\Vert \varpi (h) \bigr\Vert + \Vert B \Vert \bigl\Vert \tilde{l}\bigl(\varpi (h)\bigr) \bigr\Vert + \Vert C \Vert \bigl\Vert \tilde{l}\bigl(\varpi (h- \tau )\bigr) \bigr\Vert + \Vert J \Vert \bigr)\,dh] \\ \leq{} &\biggl(1+\frac{s^{1-\alpha }}{\Gamma (1-\alpha )}\biggr) \Vert \varpi _{0} \Vert - \frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha } \Vert D \Vert \bigl\Vert \varpi (h) \bigr\Vert \,dh \\ &{} +\bigl( \Vert A \Vert L- \Vert B \Vert \bigr) \int _{0}^{s} \bigl\Vert \varpi (h) \bigr\Vert \,dh + \Vert C \Vert \tilde{L} \int _{0}^{s} \bigl\Vert \varpi (h-\tau ) \bigr\Vert \,dh+ \Vert I \Vert s. \end{aligned} $$

Note that

$$ \int _{0}^{s} \bigl\Vert \varpi (s-\tau ) \bigr\Vert \,dh\leq \int _{-\tau }^{0} \bigl\Vert \varpi (h) \bigr\Vert \,dh+ \int _{0}^{s} \bigl\Vert \varpi (h) \bigr\Vert \,dh. $$

So, we can get

$$ \begin{aligned} \bigl\Vert \varpi (s) \bigr\Vert \leq{}& \biggl(1+ \frac{s^{1-\alpha }}{\Gamma (1-\alpha )}\biggr) \Vert \varpi _{0} \Vert + \Vert J \Vert s + \Vert C \Vert \tilde{L} \int _{-\tau }^{0} \bigl\Vert \varpi (h) \bigr\Vert \,dh \\ &{} +\bigl( \Vert B \Vert L- \Vert A \Vert + \Vert C \Vert \tilde{L} \bigr) \int _{0}^{s} \bigl\Vert \varpi (h) \bigr\Vert \,dh \\ &{}+ \Vert D \Vert \frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha } \bigl\Vert \varpi (h) \bigr\Vert \,dh, \end{aligned} $$

where \(c(s)=(1+\frac{t^{1-\alpha }}{\Gamma (1-\alpha )}) \Vert \varpi _{0} \Vert + \Vert J \Vert s+ \Vert C \Vert \tilde{L}\int _{-\tau }^{0} \Vert \varpi (h) \Vert \,dh\) is a nonnegative locally integrable function on \([0,t)\), \(a(s)= \Vert B \Vert L- \Vert A \Vert + \Vert C \Vert \tilde{L}\) and \(\Vert D \Vert \frac{1}{\Gamma (1-\alpha )}\) are nonnegative constants on \([0,T)\). By Lemma 3, \(\varpi (t)\) is bounded on any positive time interval, which implies that the set ϒ is bounded on \([0,+\infty ]\). Then, from Lemma 1, F has a fixed point, which is the solution of (7) on \([0, t ]\). That is, there exists a solution \(u^{T}(t)\) for the fractional NNs (2) on \([-\tau,+\infty )\). This completes the proof. □

3.2 Controller for fractional stochastic NNs

A controller for synchronization is designed in this subsection by using the adaptive control theory.

Theorem 2

The fractional NNs (2) and the corresponding stochastic NNs (3) can achieve synchronization, if the controller is designed as

$$ \delta (s)=-BLe(s)-C\tilde{l}e(s-\tau )-BM-C\tilde{M}- \frac{1}{2}\pi ^{T}(s) \pi (s) $$

and \(Ev_{0}=u_{0}\).

Proof

For the solution of system (4), \(\varepsilon (t)\), define the Lyapunov function

$$ F\bigl(s,\varepsilon (s)\bigr) =\frac{1}{2}\varepsilon ^{T}(s) \varepsilon (s)+ \frac{2}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha }\varepsilon ^{T}(h)D \varepsilon (h)\,dh. $$

Obviously, F is nonnegative.

By using Itô formula for F, we have

$$ \begin{aligned} DF\bigl(s,\varepsilon (s)\bigr)={}&\varepsilon ^{T}(s)\bigl[-A\varepsilon (s)+B\bigl( \hat{h}(s)-f(s)\bigr) +C\bigl( \hat{l}(t)-l(t)\bigr)+\delta (s)\bigr]\,ds+\varepsilon ^{T}(s) \pi (s) \,dB(s) \\ & {}-\frac{2\alpha }{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-1- \alpha }\varepsilon ^{T}(h)D\varepsilon (h)\,dh +\frac{1}{2}\pi ^{T}(s) \pi (s)\,ds \\ &{} +\frac{1}{\Gamma (2-\alpha )}\varepsilon ^{T}(s)D\varepsilon (s) (ds)^{1- \alpha }. \end{aligned} $$

Furthermore, we have

$$ \begin{aligned} &F\bigl(s,\varepsilon (s)\bigr)\\ &\quad=F(0, \varepsilon _{0})+ \int _{0}^{s} \varepsilon ^{T}(h)\bigl[-A \varepsilon (h)+B\bigl(\hat{h}(h)-h(h)\bigr) +C\bigl(\hat{l}(h)-l(h)\bigr)+ \delta (h)\bigr]\,dh \\ &\qquad{} + \int _{0}^{s}\varepsilon ^{T}(h)\pi (h) \,dB(h) + \frac{2}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha }\varepsilon ^{T}(h)D \varepsilon (h)\,dh \\ &\qquad{} +\frac{1}{\Gamma (1-\alpha )} \int _{0}^{s}(s-h)^{-\alpha } \varepsilon ^{T}(h)D\varepsilon (h)\,dh +\frac{1}{2} \int _{0}^{s}\pi ^{T}(s) \pi (h)\,dh \\ &\quad=F(0,\varepsilon _{0})+ \int _{0}^{s}\varepsilon ^{T}(h)\bigl[-A \varepsilon (h)+B\bigl(\hat{h}(h)-h(h)\bigr) +C\bigl(\hat{l}(h)-l(h)\bigr)+\delta (h)\bigr]\,dh \\ &\qquad{} + \int _{0}^{s}\varepsilon ^{T}(h)\pi (h) \,dB(h)+\frac{1}{2} \int _{0}^{s}\pi ^{T}(h)\pi (h)\,dh \\ &\quad\leq F(0,\varepsilon _{0})+ \int _{0}^{s}\varepsilon ^{T}(h)\bigl[-A \varepsilon (h)+BL\varepsilon (h)+BM +C\tilde{L}\varepsilon (h)+C \tilde{M}+\delta (h)\bigr]\,dh \\ &\qquad{} +\frac{1}{2} \int _{0}^{s}\pi ^{T}(h)\pi (h)\,dh+ \int _{0}^{s} \varepsilon ^{T}(h)\pi (h) \,dB(h) \\ &\quad\leq F(0,\varepsilon _{0})- \int _{0}^{s}\varepsilon ^{T}(h)A \varepsilon (h)\,dh+ \int _{0}^{s}\varepsilon ^{T}(h)\pi (h) \,dB(h). \end{aligned} $$
(10)

For (10), taking the expectation with respect to the probability P, we have

$$ E\bigl[F\bigl(s,\varepsilon (s)\bigr)\bigr]\leq E\bigl[F(0,\varepsilon _{0})\bigr]-E\biggl[ \int _{0}^{s} \varepsilon ^{T}(h)A \varepsilon (h)\,dh\biggr]. $$

So, we obtain

$$ E\biggl[ \int _{0}^{t}\varepsilon ^{T}(h) \varepsilon (h)\,dh\biggr]\leq \frac{E[F(0,\varepsilon _{0})]-E[F(t,\varepsilon (t))]}{\lambda _{\min }(A)} \leq \frac{E[F(0,\varepsilon _{0})]}{\lambda _{\min }(A)} $$

From the condition of Theorem 2, system (4) is adaptively synchronized. The proof is finished. □

Corollary 1

The driven complex networks (2) and the response complex networks

$$ \begin{aligned} &dv(s)-dI_{0^{+}}^{1-\alpha } \bigl(Dv(s)-v_{0}\bigr) =\bigl[-Av(s)+Bh\bigl(v(s)\bigr)+Cl\bigl(v(s- \tau )\bigr)+J(s)+\delta (s)\bigr]\,ds, \\ &v(s)=v_{0}(s),\quad s\in [-\tau,0] \end{aligned} $$
(11)

can achieve synchronization, if the controller satisfies

$$ \delta (s)=-BL\varepsilon (s)-C\tilde{l}\varepsilon (s-\tau )-BM-C \tilde{M} $$

and \(v_{0}=u_{0}\).

Remark 1

The Lyapunov function is very skillfully constructed in Theorem 1, whose second term successfully eliminates the fractional-order integral in the process of integrating to DF.

Remark 2

Ding et al. [5] have investigated the stability of solutions of the fractional-order equations with continuous activations. The FNNs with delays have been presented in [18], and that research has considered the Mittag-Leffler synchronization with discontinuous activations, but without considering the stochastic effect. Thus, the results obtained in this paper improve those in [18].

4 Numerical simulations

An example is presented in this section to illustrate the synchronization result obtained in this paper.

Example 1

The two-neuron fractional stochastic NNs are considered with the following parameters: D= [ 1 1 1 3 ] , A= [ 0.2 0 0 0.1 ] , B= [ 0.33 0.12 0.18 0.11 ] , C= [ 0.38 − 0.32 0.45 0.45 ] , σ(t)= [ 3 2 − 1 2 1 2 3 2 ] [ e − t e − t ] . The activation functions are \(h_{1}(u)=h_{2}(u)=-0.8\tanh (u)+\operatorname{sign}(u),l_{1}(u)=l_{2}(u)=0.8 \tanh (u)+\operatorname{sign}(u)\) for all \(u\in \mathbb{R}\), and \(\alpha =0.88\), \(J=(0,0)^{T},\tau =0.2\).

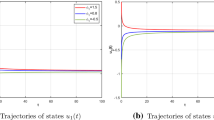
It is easily found that the activation functions \(h_{k},l_{k},k=1,2\) are discontinuous and satisfy Assumptions 1–2. Computations show that \(l_{k}^{h}=l_{k}^{l}=0.8,m_{k}=1,n_{k}=1,k=1,2\). Thus, the conditions of Theorem 1 are satisfied. And so there is a solution for fractional NNs. For illustrating the presented synchronization result, Fig. 1 presents a plot of a trajectory of the Brownian motion, while Fig. 2 shows a plot of the results with the initial conditions of the drive-response system taken as \(u(s)=(0,0)^{T}\) for \(s\in [-0.2,0]\). From Fig. 1, we can observe that the numerical curve agrees with the obtained synchronization result.

Figure 1
figure 1

A trajectory of Brownian motion

Full size image
Figure 2
figure 2

Adaptive synchronization result

Full size image

5 Conclusions

The paper has been devoted to the study of the adaptive synchronization for FNNs with time delays and discontinuous activations under Brownian motion environment. Firstly, an existence theorem of Filipov solutions for the given NNs was established by using the fixed point theorem of condensing map in the Filippov’s framework. Secondly, a feedback controller was designed for the response systems to get the adaptive synchronization. Finally, a numerical example was presented to illustrate the presented results. It is concluded that the criteria for adaptive synchronization can be easily realized. In the future, more fractional-order stochastic systems with different time delays can be explored.