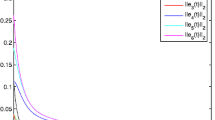1 Introduction

Very recently, due to their future real-life uses in neural networks, social networks, ecological networks, communications networks, information technology, and smart power grids, etc., complex dynamical networks have now become an interesting area of study for different fields such as mathematics, biology, and sociology. These networks contain several nodes that on some connections interact with each other. It is increasingly clear that it is possible to view some aspects of our culture as a networked world. Through information networks itself (internet, cable networks, telecommunications networks, etc.) to the global ecosystem, from road transportation systems to financial exchanges, from biological and evolutionary systems, which are massively interconnected and dynamic components, make up fairly important processes in the world. A series of interconnected nodes comprises complex dynamic networks, where each node is a specific dynamic system and connects to its neighbors through a certain topological connection. CDN’s are fundamentally difficult to analyse and synthesize compound networks. In recent decades, the interest in control and system sciences has been highly inspired and special emphasis was placed on the question of synchronization analyses for complex dynamic networks and numerous findings were published in the literature.

In comparison to the traditional integer order systems, the fractional model provides excellent methods for describing the memory and properties of different materials and procedures. If more functional challenges were specified by fractional-order dynamic systems rather than integral-order ones, it would have been much safer. In addition, over the past few decades, dynamics of delayed systems have become a very popular research subject, and various applications have been found in different fields, including artificial neural networks [30], signal processing [11], image recognition, physics engineering, secure communications [15, 18], or computer systems. Nowadays, the research on fractional-order delayed dynamical systems brought about numerous fruitful achievements due to the fact a few scholars and researchers were contributed to this area. In the application perspective, fractional order calculus is applied in many fields [1], The resulting rapid data transfer rates make the time delay unavoidable in the digital application of biological neural network complex behaviors. Time delays of different kinds have also been established, such as persistent time delays, time-varying delays [27], random coupling dealy [25], scattered delays, and leakage delays, which may also influence the overall degradation of dynamic service in the sense of fractional order in a complex network. One of its most common and crucial collaborative processes in complex dynamic networks has been synchronization. Due to this importance in the field of analysis, numerous forms of synchronization have been developed by researchers, including adaptive impulsive synchronization [5], lag synchronization, exponential synchronization [32] asymptotic synchronization, fixed-time synchronization [13, 14], projective synchronization [6], quasi synchronization [3], composite synchronization [8], synchronization of finite time [4], etc. In addition, in everyday life, control systems play a crucial function. The basic aim of control is to establish engineering process planning concepts and techniques that naturally respond to ecological changes in order to safeguard attractive productivity. It should be recalled that it is not feasible to organize any networks directly. For synchronizing complex networks, efficient control systems, such as sample data control [31], delayed feedback control [41], impulsive control [24], pinning control, adaptive control, hybrid control or bifurcation control, non-fragile control, have been programmed.

There are some results reported regarding the fractional order multi-weighted complex dynamical networks. In [26] investigates the observer based synchronization for FMCDN with time varying delays. In [2] studied the multi-weighted complex structure on fractional order neural network with linear coupling delays. In [40] addressed the finite time synchronization for fractional order multi-weighted complex dynamical network via non-fragile control with uncertain inner couplings. In [38] investigated the new complex network model for synchronization control of fractional order with time delays. In [29] studied the finite time synchronization for multi-weighted complex networks with and without coupling delays. In [38] discussed the passivity analysis of multi-weighted complex networks with fixed switching topologies. In [12] investigated the \(H_{\infty }\) synchronization for multi-weighted complex delayed dynamical networks with fixed switching topologies and time delays. In [39] discussed the anti lag synchronization for delayed coupled neural networks in reaction-diffusion terms with multi-weights. In [23] studied the event triggered multi-weighted networks with delays using distributed dynamic output dissipative control. In [9] studied the exponential synchronization for stochastic complex networks using graph theoretic approach with multi-weights.

Lag synchronization is of major interest, in which the coupled systems have identical state space trajectories but are time shifted relative to each other. It is simple to achieve by coupling the response system to a previous state of the drive system or by mismatching the system parameters. It has been observed in lasers, neuronal models, and electronic circuits, it may hold fascinating potential for technological applications. In [33] the author studied and investigated the lag synchronization in complex networks by using the pinning control without considering the delays. In [10], the author investigated chaotic lag synchronization of coupled time delayed systems and gives application to secure communications without considering any external disturbances. In [34] the author studied the lag and adaptive synchronization of time delayed uncertain dynamical system based on parameter identification. Since most of the existing results on complex networks, by investigating lag synchronization criteria are discussed on integer order only. To fill this gap, we considered the more general fractional order multi-weighted complex network with external disturbances and derive its lag synching criteria by algebraic method under the suitable controller.

The key contributions of our proposed work are described as below:

  1. (1)

    We established a more general model for FMCDN with external disturbances. As there are no works done while considering this type of model in a previous literature.

  2. (2)

    Next, we analyze by adding constant delays in both internal and coupling terms for the multi-weighted complex network and for the first time evaluating its lag synchronization criteria by using non-fragile controller.

  3. (3)

    The theory of fractional order differential equations and several modern analytical methods are used to achieve adequate novel conditions.

  4. (4)

    We present numerical example of our proposed model in order to demonstrate efficiency.

The paper is relaxed in the following way. The preliminaries, definition, lemmas and problem formulation are presented in Section 2 for the considered FMCDN. The analysis of lag synchronization for FMCDN was examined in Sect. 3. Section 4 reveals the example with numerical simulations to demonstrate the performance regarding our proposal.The paper ends with conclusion in Sect. 5.

Notations. \({\mathbb {R}}^{n}\) denotes the n-dimensional Euclidean space throughout this paper, and \({\mathbb {R}}^{n\times m}\) be set of real \(n\times m\) matrices. \(\lambda _{max}\) and \(\lambda _{min}\) denotes the maximum and minimum eigen values respectively.

2 Problem Statement and Description

In general, it is possible to consider the multi-weighted complex dynamical network composed of K identical nodes in a general fractional order where each node is n-dimensional system can be given as:

$$\begin{aligned} D^{\zeta }_{t} \varsigma _{p}(t)= & {} A\varsigma _{p}(t)+B f(\varsigma _{p}(t))+ Cf(\varsigma _{p}(t-\chi _{1}))+\sum _{q=1}^{K}\varpi _{pq}^{1}\Gamma _{1} \varsigma _{q}(t)\nonumber \\ \quad&+\sum _{q=1}^{K}\varpi _{pq}^{2}\Gamma _{2} \varsigma _{q}(t)+...+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varsigma _{q}(t) \nonumber \\ \quad&+\sum _{q=1}^{K}\pi _{pq}^{1}\Lambda _{1}\varsigma _{q}(t-\chi _{2})+\sum _{q=1}^{K}\pi _{pq}^{2}\Lambda _{2}\varsigma _{q}(t-\chi _{2})+...\nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varsigma _{q}(t-\chi _{2}). ~~~~~ p = 1,2,3,...,K. \end{aligned}$$
(1)

Where \(0< \zeta < 1\). \(\varsigma _{p}(t) = [\varsigma _{p1},\varsigma _{p2},...,\varsigma _{pn}]^{T}\) be the state variables of the \(p^{th}\) node. Let A, B, C be the known matrices with appropriate dimension of the state vectors. \(\chi _{1}\) and \(\chi _{2}\) are the different delays representing the internal and coupling delays respectively. \( \Gamma _{h}\) and \(\Lambda _{h}\) are the inner coupling matrices which interconnect the subsystems of the network. \(( \varpi ^{h}_{pq})_{N\times N}\), and \(( \pi ^{h}_{pq})_{N\times N}\) are the non-delayed and delayed outer coupling structure matrix expressing the coupling strength and topological structure of complex dynamic networks with different weights in the \(h^{th}\) coupling form in which \(\varpi _{pq}>0\), and \(\pi _{pq}>0\), if there is connection between node p to node q, and \((p \ne q)\), \(\varpi _{pq}=0\), \(\pi _{pq}=0\) otherwise. The diagonal elements of \(\varpi _{pq}\) and \(\pi _{pq}\) are given by \(\varpi _{pp} +\sum _{q=1,q\ne p}^{K} \varpi _{pq} = 0\), and \(\pi _{pp} +\sum _{q=1,q\ne p}^{K} \pi _{pq} = 0\). Let \(f:{\mathbb {R}}^{n} \times {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}\) is a nonlinear vector function.

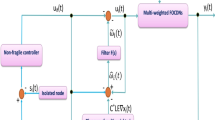
Now the controlled response system can be given by

$$\begin{aligned} D^{\zeta }_{t} \phi _{p}(t)= & {} A\phi _{p}(t)+B f(\phi _{p}(t))+ Cf(\phi _{p}(t-\chi _{1}))+\sum _{q=1}^{K}\varpi _{pq}^{1}\Gamma _{1} \phi _{q}(t)\nonumber \\ \quad&+\sum _{q=1}^{K}\varpi _{pq}^{2}\Gamma _{2} \phi _{q}(t)+...+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \phi _{q}(t) \nonumber \\ \quad&+\sum _{q=1}^{K}\pi _{pq}^{1}\Lambda _{1}\phi _{q}(t-\chi _{2})+\sum _{q=1}^{K}\pi _{pq}^{2}\Lambda _{2}\phi _{q}(t-\chi _{2})+...\nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\phi _{q}(t-\chi _{2})+\vartheta _{p}(t) +u_{p}(t) ~~~~ p = 1,2,3,...,K, \end{aligned}$$
(2)

where \(\vartheta _{p}(t)\)is the external disturbances which satisfy some bounded condition which to be designed later and \(u_{p}(t)\) is the control input. The remaining parameters are all same as the drive system which was mentioned earlier.

Remark 2.1

In [17] the author studied the Mittag-Leffler lag quasi synchronization for memristor-based neural networks via linear feedback pinning control in a fractional order case. In [21], the author studied the projective lag synchronization in fractional order chaotic(hyperchaotic) systems and in [22] investigated the lag synchronization for fractional order memristive neural networks considering the time delays via switching jumps. In [35] investigated the lag projective synchronization of fractional order delayed chaotic systems. In [10], the author investigated chaotic lag synchronization of coupled time delayed systems and gives application to secure communications without considering any external disturbances. In [34] the author studied the lag and adaptive synchronization of time delayed uncertain dynamical system based on parameter identification. By comparing with the existing results, most of the researchers investigated the lag synchronization criteria in integer order cases and few in fractional order cases. But while we consider in a fractional order cases, its a new challenging task to investigate the lag synchronization for complex networks. Also, we incorporate the external disturbances and constant delays in both internal and coupling terms which will become more complicated in a fractional order cases. To fill this gap, we considered the more general fractional order multi-weighted complex network with external disturbances and derive its lag synching criteria by algebraic method under the Non-Fragile controller.

3 Preliminaries

Some fundamental knowledge of fractional calculus, model formulation and lemmas have been illustrated in this part.

3.1 Basic Tools

Definition 3.1

[19] The fractional order integral of order \(\alpha \) for an integral function \(h(t): [0, +\infty )\longrightarrow {\mathbb {R}} \) is defined as

$$\begin{aligned} I^{\alpha } h(t)=\frac{1}{\Gamma (\alpha )}\int _{0}^{t}(t-\nu )^{\alpha -1}h(\nu )\,\mathrm{d}\nu , \end{aligned}$$

where \(\alpha \in (0,1)\) and \(\Gamma (\cdot )\) is the gamma function,is defined by

$$\begin{aligned} \Gamma (z)= \int _{0}^{+\infty }\exp {(-s)}t^{z-1}\,\mathrm{d}s, \end{aligned}$$

Definition 3.2

[19] The Caputo fractional order derivative \(\alpha \) for a function \(h(t)\in {\mathbb {C}}^{n}([t_{0}, +\infty ))\) is defined as

$$\begin{aligned} D^{\alpha }h(t)=\frac{1}{\Gamma (n-\alpha )}\int _{0}^{t}\frac{h^{(n)}(\tau )}{(t-\tau )^{{\alpha -n+1}}}\,\mathrm{d}\tau , \end{aligned}$$

where \(t\ge 0\) and n is the positive integer such that \(n-1<\alpha <n\). Particularly, when \(0<\alpha <1,\)

$$\begin{aligned} D^{\alpha }h(t)=\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}\frac{h'(\tau )}{(t-\tau )^{{\alpha }}}\,\mathrm{d}\tau . \end{aligned}$$

To go further, we need the following helpful assumptions and lemmas to solve the problem theoretically.

Lemma 3.3

[7] If M is a an \(x\times y\) matrix with \(ij^{th}\) element \(m_{ij}\) for i = 1, 2, ..., x and j = 1, 2, ..., y and N is any \(t \times x\) matrix, then the Kronecker product of M and N, denoted by \(M\otimes B\) is the \(xt \times yv\) matrix formed by multiplying each \(m_{ij}\) denoted by the entire matrix N. That is

$$\begin{aligned} M \otimes N= & {} \left( \begin{array}{cccc} m_{11}N &{} m_{12}N &{} ... &{} m_{1y}N \\ m_{21}N &{} m_{22}N &{} ... &{} m_{2y}N \\ . . . &{} . . . &{} . . . &{} . . . \\ m_{x1}N &{} m_{x2}N &{} ... &{} m_{xy}N \\ \end{array} \right) \end{aligned}$$

Lemma 3.4

[20] Let \(\varepsilon \in {\mathbb {R}}, L,N,M,P\) be the matrices that have the appropriate dimensions. Then the characteristics of Kronecker product come up with:

  1. (1)

    \((\varepsilon M)\otimes P= M \otimes (\varepsilon P)\);

  2. (2)

    \((M+P)\otimes L=(M \otimes L) + (P\otimes L)\);

  3. (3)

    \((M \otimes P)^{T} =(M^{T} \otimes P^{T})\);

  4. (4)

    \((M \otimes P)(L\otimes N) =(M L \otimes P N)\).

Lemma 3.5

[16] Let \(a,b \in {\mathbb {R}}^{n}\), then for any \(\epsilon >0\)

$$\begin{aligned} 2 a^{T}b \le \epsilon a^{T}a+\frac{1}{\epsilon }b^{T}b. \end{aligned}$$

Lemma 3.6

[37] Let U, V, W and the M be the real matrices of appropriate dimensions with M satisfying \(M = M^{T}\), then

$$\begin{aligned} M + U V W + W^{T} V^{T} U^{T}< & {} 0 \end{aligned}$$

if and only if there exists \(\epsilon > 0\),

$$\begin{aligned} M + \epsilon ^{-1} U U^{T}+\epsilon W W^{T}< & {} 0 \end{aligned}$$

Lemma 3.7

[28] Let us consider the following fractional order delayed systems

and

where x(t) and y(t) \(\in \) \({\mathbb {R}}^{n}\), \(\tau = max\{\tau _{1}, \tau _{2},..., \tau _{n}\}\), \(v(x(t))\in {\mathbb {R}}\) and \(v(y(t)) \in {\mathbb {R}}\) are the functions of x(t) and y(t). x(t) and y(t) are continuous in \((0, \infty )\) and h(t) is continuous in \([-\tau , 0]\), respectively. If \(b > 0\), \(c_{j}>0\), and \(\tau _{j} >0\), then \(v(x(t)) \le v(y(t))\), for all \(t\in [0, \infty )\).

The following assumption is mainly needed in this paper,

\(\mathbf {Assumption \;[{\mathcal {A}}_{1}]}\): There exists matrices \(0< W_{i} = diag\{w_{i1}, w_{i2},...,w_{in_{i}}\} \in {\mathbb {R}}^{n\times n}\) and \(\Gamma _{i}= diag\{ \lambda _{i1}, \lambda _{i2},...,\lambda _{in}\} \in {\mathbb {R}}^{n \times n}\)such that \(g_{i}(.)\) satisfies the following inequality

$$\begin{aligned} (\xi _{1}-\xi _{2})^{T}W_{i}[g_{i}(\xi _{1})-g_{i}(\xi _{2})-\Gamma _{i}(\xi _{1}-\xi _{2})]\le & {} -\rho _{i}(\xi _{1}-\xi _{2})^{T}(\xi _{1}-\xi _{2}) \end{aligned}$$

for some \(0< \rho _{i}\in {\mathbb {R}}\) and any \(\xi _{1}\) and \(\xi _{2} \in {\mathbb {R}}^{n}\).

\(\mathbf {Assumption \;[\mathcal {A}_{2}]}\): The non linear activation function \(g_{k}(\cdot )\) satisfies the Lipschitz continuous if there exists a constants \(K_{k}>0\) such that

$$\begin{aligned} \big |g_{k}(\chi _{1})-g_{k}(\chi _{2})\big |\le & {} K_{k}\big |\chi _{1}-\chi _{2}\big |, \;k=1,2,....,n,\;\chi _{1},\;\chi _{2}\in \mathbb {R}. \end{aligned}$$

where \(\big |(\cdot )\big |\) is the absolute value.

\(\mathbf {Assumption \;[\mathcal {A}_{3}]}\):Let us assume that the external disturbances is bounded and there exists a positive constant \(d_{p} > 0\) such that \(|\vartheta _{p}| \le d_{p}sign(\varphi (t))\),    p = 1, 2,..., K.

Remark 3.8

A synchronization network is a network of connected dynamical systems. It is made up of a network that connects oscillators, where oscillators are nodes that generate a signal with a somewhat in a regular frequency which it be in a same state and may also receive a signal. while the Lag synchronization refers to the coincidence of the states between two coupled dynamical networks (systems)i.e (Drive and Response system), where one dynamical network is delayed by a finite time. Lag synchronization normally appears as a convergence of shifted-in-time states of two systems, i.e \(y(t) \approx x_{\tau }(t) \equiv x(t-\tau )\) with positive \(\tau \), here \(\tau \) is the positive finite delay.

The error vector can be defined by

$$\begin{aligned} \varphi _{p}(t)= \phi (t)-\varsigma (t-\rho ) \end{aligned}$$
(3)

where \(\rho \) is the propagation delay.

$$\begin{aligned} \varphi _{p}(t)= & {} A\phi _{p}(t)+B f(\phi _{p}(t))+ Cf(\phi _{p}(t-\chi _{1}))+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \phi _{h}(t)\nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\phi _{h}(t-\chi _{2})+\vartheta _{p}(t) +u_{p}(t)\nonumber \\ \quad&-\Bigg \{ A\varsigma _{p}(t-\rho )+B f(\varsigma _{p}(t-\rho ))+ Cf(\varsigma _{p}(t-\chi _{1}-\rho ))\nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h}\varsigma _{h}(t-\rho )\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varsigma _{h}(t-\chi _{2}-\rho )\Bigg \}\\ D^{\zeta }\varphi _{p}(t)= & {} A\varphi _{p}(t)+B f(\phi _{p}(t))-B f(\varsigma _{p}(t-\rho ))+ Cf(\phi _{p}(t-\chi _{1}))\nonumber \\ \quad&-Cf(\varsigma _{p}(t-\chi _{1}-\rho )) \nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})+\vartheta _{p}(t) +u_{p}(t).\\ D^{\zeta }\varphi _{p}(t)= & {} A\varphi _{p}(t)+B (f(\phi _{p}(t))-f(\varsigma _{p}(t-\rho )))+ C(f(\phi _{p}(t-\chi _{1}))\nonumber \\ \quad&-f(\varsigma _{p}(t-\chi _{1}-\rho ))) \nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})+\vartheta _{p}(t) +u_{p}(t). \end{aligned}$$

The non-fragile controller can be chosen as follows,

$$\begin{aligned} u_{p}(t) = -(Y+\Delta Y)(\phi _{p}(t)-\varsigma _{p}(t-\rho ))-\sum _{p=1}^{K}d_{p}\varphi _{p}^{T}(t)\varphi _{p}(t); \end{aligned}$$
(4)

where \(\Delta Y = H_{1}\Xi _{1}(t)T_{1}\); \(Y = diag\{\theta _{1},\theta _{2},...,\theta _{n}\}\in {\mathbb {R}}^{n}\) represents the control gain matrix which is to be defined. Therefore , the controlled error system can be given by,

$$\begin{aligned} D^{\zeta }\varphi _{p}(t)= & {} A\varphi _{p}(t)+B (f(\phi _{p}(t))-f(\varsigma _{p}(t-\rho )))+ C(f(\phi _{p}(t-\chi _{1}))\nonumber \\ \quad&-f(\varsigma _{p}(t-\chi _{1}-\rho ))) \nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})+\vartheta _{p}(t)\nonumber \\ \quad&-(Y+\Delta Y)(\phi _{p}(t)-\varsigma _{p}(t-\rho ))-\sum _{p=1}^{K}d_{p}(t)\varphi _{p}(t). \end{aligned}$$
$$\begin{aligned} D^{\zeta }\varphi _{p}(t)= & {} A\varphi _{p}(t)+B (f(\phi _{p}(t))-f(\varsigma _{p}(t-\rho )))+ C(f(\phi _{p}(t-\chi _{1}))\nonumber \\ \quad&-f(\varsigma _{p}(t-\chi _{1}-\rho ))) \nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})\nonumber \\ \quad&+\vartheta _{p}(t) -(Y+\Delta Y)\varphi _{p}(t)-\sum _{p=1}^{K}d_{p}\varphi _{p}(t) \end{aligned}$$
(5)

Remark 3.9

As we know, for example, a satellite transmission system is an example of the dynamic complexity of multi-weighted systems. Propagation delay (lag) thus plays a critical role in the interaction between the different satellites. The time it takes for the signal to travel from the transmitter node to the receiver node on Earth, where the signal follows an uplink and downlink phase, is considered to be the propagation delay. And also, many real-life systems have a delay in propagation, such as electronic networks, laser networks, etc. Hence, it is necessary and important to analyze about the propagation delay in multi-weighted complex network systems

4 Main Results

Theorem 4.1

Under the assumptions \([\mathcal {A}_{1}]\), \([\mathcal {A}_{2}]\) and \([\mathcal {A}_{3}]\) holds, and for a given \(Y > 0\) the drive system is synchronized with the response system, if the following condition is satisfied

$$\begin{aligned} \Phi > C\frac{K_{1}}{\epsilon }+\frac{1}{2\epsilon }, \end{aligned}$$
(6)

where \(-\Phi = \lambda _{max}(p)\), where \(\eta = \lambda _{min}(\frac{W_{\Gamma }+W_{\Gamma }^{T}}{2})\), \(W_{\Gamma } = \sum _{h=1}^{Z}\Gamma _{h}\), \(\eta _{o}= \sum _{h=1}^{Z}\Vert \Gamma _{h}\Vert \), \(\tilde{P} =\sum _{h=1}^{Z}\sum _{p=1}^{K} diag\{\varpi _{11}^{h}, \varpi _{22}^{h},...,\varpi _{NN}^{h}\}\), \(P_{i} = \sum _{h=1}^{Z}\sum _{q=1, q\ne p}^{K}\varpi _{pq}^{h}\),\(E = \sum _{p=1}^{K}\sum _{h=1}^{Z}\pi _{pq}^{h},\) \(\tilde{E} = \sum _{h=1}^{Z}\Lambda _{h}\), \(P=2 A+2B(W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}})+2((\eta -\eta _{o}) \tilde{P} +\eta _{o}\frac{P_{i}+P_{i}^{T}}{2})-4Y-4Z_{1}-4Z_{2}+2(\frac{\epsilon }{2}\lambda _{max}(EE^{T})\lambda _{max}(\tilde{E}\tilde{E}^{T}))\), \(Z_{1}=\frac{\epsilon _{1}}{2} H_{1}H_{1}^{T}\);\(Z_{2}=\frac{\epsilon _{1}^{-1}}{2} T_{1}T_{1}^{T}\); p = 1,2,...,K.

Proof

According to the error system, Lyapunov function can be designed by

$$\begin{aligned} V(\varphi (t))= & {} \frac{1}{2}\varphi _{p}^{T}(t)\varphi _{p}(t)\\ D^{\zeta }V(\varphi _{p}(t))= & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t)D^{\zeta } \varphi _{p}(t)\nonumber \\= & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t)[A\varphi _{p}(t)+B (f(\phi _{p}(t))-f(\varsigma _{p}(t-\rho )))\nonumber \\&+C(f(\phi _{p}(t-\chi _{1}))-f(\varsigma _{p}(t-\chi _{1}-\rho ))) \nonumber \\&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})+\vartheta _{p}(t)\nonumber \\&-(Y+\Delta Y)\varphi _{p}(t)-\sum _{p=1}^{K}d_{p}\varphi _{p}^{T}(t)\varphi _{p}(t)]. \end{aligned}$$
$$\begin{aligned} D^{\zeta }V(\varphi _{p}(t))= & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t)A \varphi _{p}(t)+\sum _{p=1}^{K}\varphi _{p}^{T}(t) B (f(\phi _{p}(t))\nonumber \\&-f(\varsigma _{p}(t-\rho )))+\sum _{p=1}^{K}\varphi _{p}^{T}(t)C(f(\phi _{p}(t-\chi _{1}))\nonumber \\&-f(\varsigma _{p}(t-\chi _{1}-\rho )))+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)\nonumber \\&+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\vartheta _{p}(t)\nonumber \\&-\sum _{p=1}^{K}\varphi _{p}^{T}(t)(Y+\Delta Y)\varphi _{p}(t)-\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{p=1}^{K}d_{p}\varphi _{p}^{T}(t)\varphi _{p}(t) \end{aligned}$$
(7)

Applying Assumption \([{\mathcal {A}}_{1}]\) to the (7), we can deduce as follows,

$$\begin{aligned} B \sum _{p=1}^{K}\varphi _{p}^{T}(t) (f(\phi _{p}(t))-f(\varsigma _{p}(t-\rho )))\le & {} \sum _{p=1}^{K}(\phi (t)-\varsigma (t-\rho ))^{T}B(f(\phi _{p}(t))\nonumber \\&-f(\varsigma _{p}(t-\rho )))\nonumber \\\le & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t) (W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}})\varphi _{p}(t) \end{aligned}$$
(8)

By using \([{\mathcal {A}}_{2}]\) and Lemma (3.4) we have,

$$\begin{aligned}&\sum _{p=1}^{K}\varphi _{p}^{T}(t)C(f(\phi _{p}(t-\chi _{1}))-f(\varsigma _{p}(t-\chi _{1}-\rho )))\nonumber \\&\quad \le \sum _{p=1}^{K}K_{1}C\varphi _{p}^{T}(t)\varphi _{p}(t-\chi _{1}) = \sum _{p=1}^{K}\frac{\epsilon }{2}\varphi _{p}^{T}(t) K_{1}C\varphi _{p}(t) \nonumber \\&\qquad + \sum _{p=1}^{K}\frac{1}{2\epsilon }K_{1}C \varphi _{p}^{T}(t-\chi _{1})\varphi _{p}(t-\chi _{1}) \end{aligned}$$
(9)
$$\begin{aligned} D^{\zeta }V(\varphi _{p}(t))= & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t)A \varphi _{p}(t)\nonumber \\&+\sum _{p=1}^{K}\varphi _{p}^{T}(t) B (W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}})\varphi _{p}(t)\nonumber \\&+\sum _{p=1}^{K}\frac{1}{2\epsilon }K_{1}C\varphi _{p}^{T}(t-\chi _{1})\varphi _{p}(t-\chi _{1})\nonumber \\&+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)\nonumber \\&+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})\nonumber \\&+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\vartheta _{p}(t)-\sum _{p=1}^{K}\varphi _{p}^{T}(t)(Y+\Delta Y)\varphi _{p}(t)\nonumber \\&-\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{p=1}^{K}d_{p}\varphi _{p}^{T}(t)\varphi _{p}(t) \end{aligned}$$
(10)

Now from (10),

$$\begin{aligned} \sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)= & {} \sum _{p=1}^{K} \sum _{h=1}^{Z}\varpi _{pp}^{h}\Gamma _{h} \varphi _{h}^{T}(t)\varphi _{h}(t)\nonumber \\&+\sum _{p=1}^{K} \sum _{h=1}^{Z}\sum _{q=1, q\ne p}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}^{T}(t)\varphi _{h}(t)\\= & {} \sum _{p=1}^{K}\eta \tilde{P}\varphi _{h}^{T}(t)\varphi _{h}(t)\nonumber \\&+\sum _{p=1}^{K}\eta _{o}P_{j}\Vert \varphi _{h}^{T}(t) \Vert \Vert \varphi _{h}(t) \Vert \\= & {} \sum _{p=1}^{K}\varphi _{h}^{T}(t)\Bigg \{(\eta - \eta _{o}) \tilde{P}\nonumber \\&+\eta _{o}\frac{P_{i}+P_{i}^{T}}{2}\Bigg \} \varphi _{h}(t) \end{aligned}$$

Similarly,

$$\begin{aligned} \sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varphi _{h}(t-\chi _{2})\le & {} \frac{\epsilon }{2}\varphi _{p}^{T}(t)(E\otimes \tilde{E})(E\otimes \tilde{E})^{T}\varphi _{h}(t)\nonumber \\&+\frac{1}{2\epsilon }\varphi _{h}(t-\chi _{2}) (I_{K}\otimes I_{n})\varphi _{h}(t-\chi _{2})\nonumber \\\le & {} \frac{\epsilon }{2}\varphi _{p}^{T}(t)\lambda _{max}(EE^{T})\lambda _{max}(\tilde{E}\tilde{E}^{T})\varphi _{p}(t)\nonumber \\ \quad&+\frac{1}{2\epsilon }\varphi _{h}(t-\chi _{2})^{T} \varphi _{h}(t-\chi _{2}) \end{aligned}$$
(11)
$$\begin{aligned} -2\sum _{p=1}^{N}\varphi ^{T}_{p}(t)M(Y+\Delta Y)\varphi _{p}(t)\le & {} -2\sum _{p=1}^{N}\varphi ^{T}_{p}(t) Y \varphi _{p}(t) -2\sum _{p=1}^{N}\varphi ^{T}_{p}(t)\Delta Y\varphi _{p}(t)\nonumber \\\le & {} -2\sum _{p=1}^{N}\varphi ^{T}_{p}(t)Y \varphi _{p}(t)-2\sum _{p=1}^{N}\varphi ^{T}_{p}(t) (H_{1}\Xi _{1}(t)T_{1}))\varphi _{p}(t)\nonumber \\ -2\sum _{p=1}^{N}\varphi ^{T}_{p}(t)(Y+\Delta Y)\varphi _{p}(t)\le & {} -2\sum _{p=1}^{N}\varphi ^{T}_{p}(t)Y \varphi _{p}(t)-2\sum _{p=1}^{N}\varphi ^{T}_{p}(t) Z_{1} \varphi _{p}(t)\nonumber \\ \quad&-2\sum _{p=1}^{N}\varphi ^{T}_{p}(t) Z_{2}\varphi _{p}(t) \end{aligned}$$
(12)

Combining the equations (8)-(12) and substitute in (7), we can write

$$\begin{aligned} D^{\zeta }V(\varphi _{p}(t))= & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t)A \varphi _{p}(t)+\sum _{p=1}^{K}\varphi _{p}^{T}(t) (W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}}) \varphi _{p}(t)\nonumber \\&+\sum _{p=1}^{K}\frac{1}{2\epsilon }K_{1}C \varphi _{p}^{T}(t-\chi _{1})\varphi _{p}(t-\chi _{1})\nonumber \\ \quad&\sum _{p=1}^{K}\varphi _{h}^{T}(t)\Bigg \{(\varphi - \varphi _{o}) \tilde{P} +\varphi _{o}\frac{P_{i}+P_{i}^{T}}{2}\Bigg \} \varphi _{h}(t)\nonumber \\&+\frac{\epsilon }{2}\varphi _{p}^{T}(t)\lambda _{max}(EE^{T})\lambda _{max}(\tilde{E}\tilde{E}^{T})\varphi _{p}(t)\nonumber \\ \quad&+\frac{1}{2\epsilon }\varphi _{p}(t-\chi _{2})^{T} \varphi _{p}(t-\chi _{2})-2\sum _{p=1}^{N}\varphi ^{T}_{p}(t)Y \varphi _{p}(t)-2\sum _{p=1}^{N}\varphi ^{T}_{p}(t) Z_{1} \varphi _{p}(t)\nonumber \\ \quad&-2\sum _{p=1}^{N}\varphi ^{T}_{p}(t) Z_{2}\varphi _{p}(t)+\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{p=1}^{K}d_{p}(t)\varphi _{p}(t)-\sum _{p=1}^{K}\varphi _{p}^{T}(t)\sum _{p=1}^{K}d_{p}\varphi _{p}(t)\\ D^{\zeta }V(\varphi _{p}(t))\le & {} \sum _{p=1}^{K}\varphi _{p}^{T}(t)\bigg \{A+(W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}})+(\eta -\eta _{o}) \tilde{P}\nonumber \\&+\eta _{o}\frac{P_{i}+P_{i}^{T}}{2}-Y-2Z_{1}-2Z_{2}+\frac{\epsilon }{2}\lambda _{max}(EE^{T})\nonumber \\ \quad&\times \lambda _{max}(\tilde{E}\tilde{E}^{T})\Bigg \} \varphi _{p}(t)\nonumber \\&+\sum _{p=1}^{K}C\frac{K_{1}}{2\epsilon }\varphi _{p}^{T}(t-\chi _{1})\varphi _{p}(t-\chi _{1})\nonumber \\&+\frac{1}{2\epsilon }\sum _{p=1}^{K}\varphi _{p}(t-\chi _{2})^{T} \varphi _{p}(t-\chi _{2})\\ D^{\zeta }V(\varphi _{p}(t))\le & {} \frac{1}{2} \lambda _{max}\bigg \{2 A+2(W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}})+2((\eta -\eta _{o}) \tilde{P}\nonumber \\&+\eta _{o}\frac{P_{i}+P_{i}^{T}}{2})-4Y-4Z_{1}-4Z_{2}\nonumber \\ \quad&+2(\frac{\epsilon }{2}\lambda _{max}(EE^{T})\lambda _{max}(\tilde{E}\tilde{E}^{T})) \bigg \}\varphi _{p}^{T}(t)\varphi _{p}(t)\nonumber \\&+\sum _{p=1}^{K}C\frac{K_{1}}{\epsilon }\frac{1}{2}\varphi _{p}^{T}(t-\chi _{1})\varphi _{p}(t-\chi _{1})\nonumber \\ \quad&+\frac{1}{2\epsilon }\sum _{p=1}^{K}\varphi _{p}(t-\chi _{2})^{T} \varphi _{p}(t-\chi _{2}) \end{aligned}$$
$$\begin{aligned} D^{\zeta }V(\varphi _{p}(t))= & {} -\Phi V(\varphi _{p}(t))+C\frac{K_{1}}{\epsilon }V(\varphi _{p}(t-\chi _{1}))+\frac{1}{2\epsilon }V(\varphi _{p}(t-\chi _{2})) \end{aligned}$$
(13)

Now, let us consider the linear fractional differential equation can be given by

$$\begin{aligned} D^{\zeta }V(\psi (t))= & {} -\Phi V(\psi _{p}(t))+C\frac{K_{1}}{\epsilon }V(\psi _{p}(t-\chi _{1}))+\frac{1}{\epsilon }V(\psi _{p}(t-\chi _{2}))\nonumber \\ V(\psi (t))= & {} h(t)\ge 0. \end{aligned}$$
(14)

As we can write a characteristic equation of the above term as,

$$\begin{aligned} s^{\zeta }+\Phi -C\frac{K_{1}}{\epsilon }e^{-s\chi _{1}}-\frac{1}{2\epsilon }e^{-s\chi _{2}}=0. \end{aligned}$$
(15)

which has no purely imaginary roots and \(\Phi > C\frac{K_{1}}{\epsilon }+\frac{1}{2\epsilon }\), then we can get the zero solution of (above equation) is asymptotical stable. Suppose in the case of pure imaginary \(s = \omega i = |\omega ||cos(\frac{\pi }{2})+i sin(\pm \frac{\pi }{2})|\). Where \(\omega \) is the real number. Hence substitute the value of s in (15), we have

$$\begin{aligned} (\omega i)^{\zeta }+\Phi -C\frac{K_{1}}{\epsilon }e^{-\omega i\chi _{1}}-\frac{1}{2\epsilon }e^{-\omega i\chi _{2}}=0. \end{aligned}$$

Here,

$$\begin{aligned} \omega> & {} 0, ~~~~~~ s = |\omega ||cos(\frac{\pi }{2})+i sin(\pm \frac{\pi }{2})|,\\ \omega< & {} 0, ~~~~~~ s = |\omega ||cos(\frac{\pi }{2})-i sin(\pm \frac{\pi }{2})|, \end{aligned}$$

which can be written as,

$$\begin{aligned} (\omega i)^{\zeta }+\Phi = C\frac{K_{1}}{\epsilon }e^{-\omega i\chi _{1}}+\frac{1}{\epsilon }e^{-\omega i\chi _{2}}=0. \end{aligned}$$

Squaring on both sides

$$\begin{aligned} |\omega i^{\zeta }+\Phi |^{2}= & {} \Big (C\frac{K_{1}}{\epsilon }cos\omega \chi _{1} + C\frac{K_{1}}{\epsilon }cos\omega \chi _{1}\Big )^{2}\\&+\Big (\frac{1}{2\epsilon }sin\omega \chi _{1}+\frac{1}{2\epsilon }sin\omega \chi _{1}\Big )^{2}\\ |\omega |^{2\zeta }+C\frac{K_{1}}{\epsilon }cos\Big (\frac{\zeta \pi }{2}\Big )|\omega |^{\zeta }+\Phi ^{2}= & {} C^{2}\frac{K_{1}^{2}}{\epsilon ^{2}}+\Big (\frac{1}{4\epsilon ^{2}}\Big )^{2}+ \frac{2CK_{1}}{2\epsilon ^{2}}cos\omega \Big (\chi _{1}-\chi _{2}\Big )\\\le & {} \Big (C\frac{K_{1}}{\epsilon }+\frac{1}{2\epsilon }\Big )^{2}. \end{aligned}$$

Hence we have \(\Phi >0\), if \(\Phi > C\frac{K_{1}}{\epsilon }+\frac{1}{2\epsilon }\), has no real roots. By lemma (3.7), we can get \(V(\varphi (t))\le V(\psi (t))\), and also \(|\omega |^{\zeta }> 0\), \(cos(\frac{q\pi }{2})>0\) which denoting that the zero solution of (13) is asymptotically stable. This completes the proof.

Suppose if the coupling term \(\Lambda = 0\), then the error system can be rewritten as

$$\begin{aligned} D^{\zeta }\varphi _{p}(t)= & {} A\varphi _{p}(t)+B (f(\phi _{p}(t))-f(\varsigma _{p}(t-\rho )))+ C(f(\phi _{p}(t-\chi _{1}))\nonumber \\&-f(\varsigma _{p}(t-\chi _{1}-\rho ))) \nonumber \\ \quad&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varphi _{h}(t)+\vartheta _{p}(t) -(Y+\Delta Y)\varphi _{p}(t)\nonumber \\&-\sum _{p=1}^{K}d_{p}\varphi _{p}^{T}(t)\varphi _{p}(t). \end{aligned}$$
(16)

We will obtain the result below in this case. \(\square \)

Corollary 4.2

Under the assumptions \([\mathcal {A}_{1}]\), \([\mathcal {A}_{2}]\) and \([\mathcal {A}_{3}]\) holds, and for a given \(Y > 0\) the drive system is synchronized with the response system, if the following condition is satisfied

$$\begin{aligned} \Phi > C\frac{K_{1}}{\epsilon } \end{aligned}$$
(17)

where \(-\Phi = \lambda _{max}(P)\) , where \(\eta = \lambda _{min}(\frac{W_{\Gamma }+W_{\Gamma }^{T}}{2})\), \(W_{\Gamma } = \sum _{h=1}^{Z}\Gamma _{h}\), \(\eta _{o}= \sum _{h=1}^{Z}\Vert \Gamma _{h}\Vert \),

\(\tilde{P} =\sum _{h=1}^{Z}\sum _{p=1}^{K} diag\{\varpi _{11}^{h}, \varpi _{22}^{h},...,\varpi _{NN}^{h}\}\), \(P_{i} = \sum _{h=1}^{Z}\sum _{q=1, q\ne p}^{K}\varpi _{pq}^{h}\), \(P=2 A+2B(W_{p}\Gamma _{p}-\rho _{p}I_{n_{p}})+2((\eta -\eta _{o}) \tilde{P} +\eta _{o}\frac{P_{i}+P_{i}^{T}}{2})-4Y-4Z_{1}-4Z_{2}\) p = 1,2,...,K.

5 Numerical Simulations

Throughout this section, numerical example is given to illustrate Robust non-fragile lag synchronization of FMCDN.

Example 5.1

Consider a general FMCDN with identical nodes, then the dynamics of node is given by

$$\begin{aligned} D^{\zeta }_{t} \varsigma _{p}(t)= & {} A\varsigma _{p}(t)+B f(\varsigma _{p}(t))+ Cf(\varsigma _{p}(t-\chi _{1}))+\sum _{h=4}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varsigma _{q}(t)\nonumber \\&+\sum _{h=1}^{4}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\varsigma _{q}(t-\chi _{2}). \end{aligned}$$

and the response system is given by,

$$\begin{aligned} D^{\zeta }_{t} \phi _{p}(t)= & {} A\phi _{p}(t)+B f(\phi _{p}(t))+ Cf(\phi _{p}(t-\chi _{1}))\nonumber \\&+\sum _{h=1}^{4}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \phi _{q}(t)\nonumber \\&+\sum _{h=1}^{Z}\sum _{q=1}^{K}\pi _{pq}^{h}\Lambda _{h}\phi _{q}(t-\chi _{2})\nonumber \\&+\vartheta _{p}(t) +u_{p}(t) \end{aligned}$$

where \(\zeta = 0.98\), \(f(\varsigma _{p}(t))= cos(\varsigma _{p}(t))\);\(f(\varsigma _{p}(t-\chi _{1})) = sin(\varsigma _{p}(t)-\chi _{1})\); \(\chi _{1} = 035\);\(\chi _{2}=1.45\); \(\rho = 0.50\); \(\vartheta _{p}(t)=(0.02^{*}sin(\varsigma ),0.01^{*}sin(\varsigma ),0.03^{*}sin(\varsigma ))^{T}\);\((Y+\Delta Y) = (150.75+0.2^{*}tanh(\varsigma ),180.85+0.2^{*}tanh(\varsigma ),200.74+0.2^{*}tanh(\varsigma ))^{T}\)

$$\begin{aligned} A&= \left( \begin{array}{ccc} -40.58 &{} 0 &{} 0 \\ 0 &{} -45.27 &{} 0 \\ 0 &{} 0 &{} -49.05 \\ \end{array} \right) \quad B= \left( \begin{array}{ccc} -2 &{} 0 &{} 0 \\ 0 &{} -2.01 &{} 0 \\ 0 &{} 0 &{} -2.08 \\ \end{array} \right) \quad \\ C&= \left( \begin{array}{ccc} -0.02 &{} 0 &{} 0 \\ 0 &{} -0.4 &{} 0 \\ 0 &{} 0 &{} -0.8 \\ \end{array} \right) \\ \Gamma ^{1}&= \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 2 \\ \end{array} \right) \quad \Gamma ^{2}= \left( \begin{array}{ccc} 0.5 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0 &{} 0 &{} -0.1 \\ \end{array} \right) \quad \Gamma ^{3} = \left( \begin{array}{ccc} 2 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0 &{} 0 &{} 0.5 \\ \end{array} \right) \quad \\ \Gamma ^{4}&= \left( \begin{array}{ccc} -1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -0.5 \\ \end{array} \right) \Lambda ^{1}= \left( \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 2 &{} 0 \\ 0 &{} 0 &{} 0.1 \\ \end{array} \right) \quad \Lambda ^{2}= \left( \begin{array}{ccc} 2 &{} 0 &{} 0 \\ 0 &{} -0.2 &{} 0 \\ 0 &{} 0 &{} -0.3 \\ \end{array} \right) \quad \\ \Lambda ^{3}&= \left( \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 0.5 &{} 0 \\ 0 &{} 0 &{} 0.6 \\ \end{array} \right) \quad \Lambda ^{4} = \left( \begin{array}{ccc} 0.01 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0 &{} 0 &{} -0.3 \\ \end{array} \right) \\ \varpi ^{1}&= \left( \begin{array}{ccccc} 1 &{} 0 &{} -1 &{} 2 &{} 3 \\ 0 &{} -2 &{} 0 &{} -2 &{} 1 \\ -1 &{} -2.4 &{} 2 &{} 1 &{} 0 \\ 0 &{} -3.5 &{} -1 &{} -2.1 &{} 1 \\ -2.4 &{} -0.1 &{} -1 &{} 0 &{} -3 \\ \end{array} \right) \quad \varpi ^{2}= \left( \begin{array}{ccccc} -0.2 &{} 0 &{} 0.2 &{} 0.1 &{} 0.25 \\ 0 &{} -0.1 &{} 0.5 &{} 0 &{} 0.4\\ 0.1 &{} 0.4 &{} 0.2 &{} 0.5 &{} -0.1 \\ 0.2 &{} 0.5 &{} 0.4 &{} 0.2 &{} 0.2 \\ 0.25 &{} 0.4 &{} 0.2 &{} 0.2 &{} -0.3 \\ \end{array} \right) \quad \\ \varpi ^{3}&= \left( \begin{array}{ccccc} -0.5 &{} 0 &{} 0.1 &{} 0 &{} 0.4 \\ 0 &{} -0.2 &{} 0.4 &{} 0 &{} 0.3\\ 0.1 &{} 0.4 &{} -0.4 &{} 0.3 &{} 0.2 \\ 0 &{} 0 &{} 0.3 &{} -0.3 &{} 0.5 \\ 0.4 &{} 0.3 &{} 0.2 &{} 0.5 &{} -0.1 \\ \end{array} \right) \quad \varpi ^{4}= \left( \begin{array}{ccccc} -0.4 &{} -0.1 &{} 0.2 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} -0.2 &{} 0 &{} 0.3\\ 0 &{} 0.1 &{} -0.3 &{} -0.1 &{} 0 \\ 1 &{} 0.5 &{} -0.2 &{} 0.1 &{} -0.1 \\ 0 &{} 1 &{} 0.1 &{} 0 &{} 0.1 \\ \end{array} \right) \quad \\ \pi ^{1}&= \left( \begin{array}{ccccc} 0.6 &{} 0.2 &{} 0.1 &{} 0.1 &{} 1 \\ 0.3 &{} -0.7 &{} 0.5 &{} 0.2 &{} 0 \\ 0.1 &{} 0.5 &{} -0.25 &{} 0.2 &{} 0.1 \\ 0.3 &{} 0.4 &{} 0.5 &{} -0.3 &{} 0.2 \\ 0 &{} 1 &{} 0.1 &{} -0.25 &{} -0.2 \\ \end{array} \right) \quad \pi ^{2}= \left( \begin{array}{ccccc} 0.5 &{} 0.2&{} 0.1 &{} 0.1 &{} 0 \\ 0.2 &{} -0.8 &{} 0.1 &{} 0 &{} 0.2\\ 0.1 &{} 0.3 &{} -1.1 &{} 0.1 &{} 0.4 \\ 0.1 &{} 0 &{} 0.4 &{} -0.3 &{} 0.2 \\ 0 &{} 0.2 &{} 0 &{} 0.1 &{} -0.6 \\ \end{array} \right) \quad \\ \pi ^{3}&= \left( \begin{array}{ccccc} 0.7 &{} 0.3 &{} 0.1 &{} 0.1 &{} 1 \\ 0 &{} -0.8 &{} 0.3 &{} 0.2 &{} 0\\ 0.2 &{} 0.1 &{} -0.3 &{} 1 &{} 0.1 \\ 0.1 &{} 0 &{} 0.2 &{} -1.1 &{} 0.2 \\ 0.1 &{} 0 &{} 0 &{} 0.2 &{} -0.6 \\ \end{array} \right) \quad \pi ^{4}= \left( \begin{array}{ccccc} 0.5 &{} 0.5 &{} 0.1 &{} 0 &{} 0.2 \\ 0.2 &{} -0.4 &{} 0 &{} 0.1 &{} 0.1\\ 0.1&{} 0 &{} -0.25 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 &{} -0.4 &{} 0.3 \\ 0.2 &{} 0.1 &{} 0 &{} 0.3 &{} -0.6 \\ \end{array} \right) \end{aligned}$$

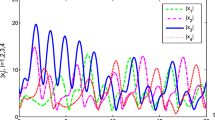
By the simple computation, we get \(\lambda _{max}(EE^{T})\lambda _{max}(\tilde{E}\tilde{E}^{T}) = 1.314\); \(\eta = -1.80\); \(\eta _{o} = 2.50\); \(\Phi = 635.6975\); \(C\frac{K_{1}}{\epsilon }+\frac{1}{2\epsilon } = 300.0120\). Hence form the computational values, theorem (4.1) is satisfied. The Fig. 1 shows the evolution of synchronization error of \(\varphi _{p1} (p = 1,2,3,4,5)\) identical nodes without controller. After inserting the non-fragile controller to the system, the error is completely reduced which the trajectories goes to zero which is shown in Fig. 2. Figures 3 and 4 are the evolution of errors for \(\varphi _{p2}\) and \(\varphi _{p3}\) \((p = 1, 2, 3)\) nodes without controller and with controller respectively (Figs. 5, 6).

Fig. 1
figure 1

Evolution of synchronization error \(\varphi _{p1}(t)\) (without controller), P = 1,2,3,4,5

Full size image
Fig. 2
figure 2

Evolution of synchronization error \(\varphi _{p1}(t)\) (with controller), P =1,2,3,4,5

Full size image
Fig. 3
figure 3

Evolution of synchronization error \(\varphi _{p2}(t)\) (without controller), P = 1,2,3,4,5

Full size image
Fig. 4
figure 4

Evolution of synchronization error \(\varphi _{p2}(t)\) (with controller), P = 1,2,3,4,5

Full size image
Fig. 5
figure 5

Evolution of synchronization error \(\varphi _{p3}(t)\) (without controller), P = 1,2,3,4,5

Full size image
Fig. 6
figure 6

Evolution of synchronization error \(\varphi _{p3}(t)\) (with controller), p = 1,2,3,4,5

Full size image
Fig. 7
figure 7

Evolution of synchronization error \(\varphi _{p1}(t)\) (without controller), P = 1,2,3,4,5

Full size image
Fig. 8
figure 8

Evolution of synchronization error \(\varphi _{p1}(t)\) (with controller), P =1,2,3,4,5

Full size image

Example 5.2

Consider a general FMCDN without considering any coupling delays, then the dynamics of node can be given by

$$\begin{aligned} D^{\zeta }_{t} \varsigma _{p}(t)= & {} A\varsigma _{p}(t)+B f(\varsigma _{p}(t))+ Cf(\varsigma _{p}(t-\chi _{1}))+\sum _{h=4}^{Z}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \varsigma _{q}(t) \end{aligned}$$

and the response system is given by,

$$\begin{aligned} D^{\zeta }_{t} \phi _{p}(t)= & {} A\phi _{p}(t)+B f(\phi _{p}(t))+ Cf(\phi _{p}(t-\chi _{1}))\\&+\sum _{h=1}^{4}\sum _{q=1}^{K}\varpi _{pq}^{h}\Gamma _{h} \phi _{q}(t)+\vartheta _{p}(t) +u_{p}(t) \end{aligned}$$

where \(\zeta = 0.93\), \(f(\varsigma _{p}(t))= cos(\varsigma _{p}(t))\);\(f(\varsigma _{p}(t-\chi _{1})) = sin(\varsigma _{p}(t)-\chi _{1})\); \(\chi _{1} = 0.15\); \(\rho = 0.63\); \(\vartheta _{p}(t)=(0.02^{*}sin(\varsigma ),0.01^{*}sin(\varsigma ),0.03^{*}sin(\varsigma ))^{T}\);\((Y+\Delta Y) = (100.02+0.2^{*}tanh(\varsigma ),140.74+0.2^{*}tanh(\varsigma ),180.49+0.2^{*}tanh(\varsigma ))^{T}\)

$$\begin{aligned} A= & {} \left( \begin{array}{ccc} -40.58 &{} 0 &{} 0 \\ 0 &{} -45.27 &{} 0 \\ 0 &{} 0 &{} -49.05 \\ \end{array} \right) \quad B= \left( \begin{array}{ccc} -2 &{} 0 &{} 0 \\ 0 &{} -2.01 &{} 0 \\ 0 &{} 0 &{} -2.08 \\ \end{array} \right) \quad \\ C= & {} \left( \begin{array}{ccc} -0.02 &{} 0 &{} 0 \\ 0 &{} -0.4 &{} 0 \\ 0 &{} 0 &{} -0.8 \\ \end{array} \right) \quad \\ \Gamma ^{1}= & {} \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 2 \\ \end{array} \right) \quad \Gamma ^{2}= \left( \begin{array}{ccc} 0.5 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0 &{} 0 &{} -0.1 \\ \end{array} \right) \quad \Gamma ^{3} = \left( \begin{array}{ccc} 2 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 \\ 0 &{} 0 &{} 0.5 \\ \end{array} \right) \quad \\ \Gamma ^{4}= & {} \left( \begin{array}{ccc} -1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} -0.5 \\ \end{array} \right) \quad \Lambda ^{1}= \left( \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 2 &{} 0 \\ 0 &{} 0 &{} 0.1 \\ \end{array} \right) \quad \Lambda ^{2}= \left( \begin{array}{ccc} 2 &{} 0 &{} 0 \\ 0 &{} -0.2 &{} 0 \\ 0 &{} 0 &{} -0.3 \\ \end{array} \right) \quad \\ \Lambda ^{3}= & {} \left( \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 0.5 &{} 0 \\ 0 &{} 0 &{} 0.6 \\ \end{array} \right) \quad \Lambda ^{4} = \left( \begin{array}{ccc} 0.01 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0 &{} 0 &{} -0.3 \\ \end{array} \right) \quad \\ \varpi ^{1}= & {} \left( \begin{array}{ccccc} 1 &{} 0 &{} -1 &{} 2 &{} 3 \\ 0 &{} -2 &{} 0 &{} -2 &{} 1 \\ -1 &{} -2.4 &{} 2 &{} 1 &{} 0 \\ 0 &{} -3.5 &{} -1 &{} -2.1 &{} 1 \\ -2.4 &{} -0.1 &{} -1 &{} 0 &{} -3 \\ \end{array} \right) \quad \varpi ^{2}= \left( \begin{array}{ccccc} -0.2 &{} 0 &{} 0.2 &{} 0.1 &{} 0.25 \\ 0 &{} -0.1 &{} 0.5 &{} 0 &{} 0.4\\ 0.1 &{} 0.4 &{} 0.2 &{} 0.5 &{} -0.1 \\ 0.2 &{} 0.5 &{} 0.4 &{} 0.2 &{} 0.2 \\ 0.25 &{} 0.4 &{} 0.2 &{} 0.2 &{} -0.3 \\ \end{array} \right) \quad \\ \varpi ^{3}= & {} \left( \begin{array}{ccccc} -0.5 &{} 0 &{} 0.1 &{} 0 &{} 0.4 \\ 0 &{} -0.2 &{} 0.4 &{} 0 &{} 0.3\\ 0.1 &{} 0.4 &{} -0.4 &{} 0.3 &{} 0.2 \\ 0 &{} 0 &{} 0.3 &{} -0.3 &{} 0.5 \\ 0.4 &{} 0.3 &{} 0.2 &{} 0.5 &{} -0.1 \\ \end{array} \right) \quad \varpi ^{4}= \left( \begin{array}{ccccc} -0.4 &{} -0.1 &{} 0.2 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} -0.2 &{} 0 &{} 0.3\\ 0 &{} 0.1 &{} -0.3 &{} -0.1 &{} 0 \\ 1 &{} 0.5 &{} -0.2 &{} 0.1 &{} -0.1 \\ 0 &{} 1 &{} 0.1 &{} 0 &{} 0.1 \\ \end{array} \right) \quad \\ \pi ^{1}= & {} \left( \begin{array}{ccccc} 0.6 &{} 0.2 &{} 0.1 &{} 0.1 &{} 1 \\ 0.3 &{} -0.7 &{} 0.5 &{} 0.2 &{} 0 \\ 0.1 &{} 0.5 &{} -0.25 &{} 0.2 &{} 0.1 \\ 0.3 &{} 0.4 &{} 0.5 &{} -0.3 &{} 0.2 \\ 0 &{} 1 &{} 0.1 &{} -0.25 &{} -0.2 \\ \end{array} \right) \quad \pi ^{2}= \left( \begin{array}{ccccc} 0.5 &{} 0.2&{} 0.1 &{} 0.1 &{} 0 \\ 0.2 &{} -0.8 &{} 0.1 &{} 0 &{} 0.2\\ 0.1 &{} 0.3 &{} -1.1 &{} 0.1 &{} 0.4 \\ 0.1 &{} 0 &{} 0.4 &{} -0.3 &{} 0.2 \\ 0 &{} 0.2 &{} 0 &{} 0.1 &{} -0.6 \\ \end{array} \right) \quad \\ \pi ^{3}= & {} \left( \begin{array}{ccccc} 0.7 &{} 0.3 &{} 0.1 &{} 0.1 &{} 1 \\ 0 &{} -0.8 &{} 0.3 &{} 0.2 &{} 0\\ 0.2 &{} 0.1 &{} -0.3 &{} 1 &{} 0.1 \\ 0.1 &{} 0 &{} 0.2 &{} -1.1 &{} 0.2 \\ 0.1 &{} 0 &{} 0 &{} 0.2 &{} -0.6 \\ \end{array} \right) \quad \pi ^{4}= \left( \begin{array}{ccccc} 0.5 &{} 0.5 &{} 0.1 &{} 0 &{} 0.2 \\ 0.2 &{} -0.4 &{} 0 &{} 0.1 &{} 0.1\\ 0.1&{} 0 &{} -0.25 &{} 0 &{} 0 \\ 0 &{} 0.1 &{} 0 &{} -0.4 &{} 0.3 \\ 0.2 &{} 0.1 &{} 0 &{} 0.3 &{} -0.6 \\ \end{array} \right) \quad \end{aligned}$$
Fig. 9
figure 9

Evolution of synchronization error \(\varphi _{p2}(t)\) (without controller), P = 1,2,3,4,5

Full size image
Fig. 10
figure 10

Evolution of synchronization error \(\varphi _{p2}(t)\) (with controller), P = 1,2,3,4,5

Full size image
Fig. 11
figure 11

Evolution of synchronization error \(\varphi _{p3}(t)\) (without controller), P = 1,2,3,4,5

Full size image
Fig. 12
figure 12

Evolution of synchronization error \(\varphi _{p3}(t)\) (with controller), p = 1,2,3,4,5

Full size image

By the simple computation, we get \(\eta = 0.80\); \(\eta _{o} = 0.50\); \(\Phi = 350.010\); \(C\frac{K_{1}}{\epsilon } = 10.338\). Hence form the computational values, corollary (4.2) is satisfied. The Fig. 7 shows the evolution of synchronization error of \(\varphi _{p1} (p = 1, 2, 3, 4, 5)\) identical nodes without controller. After inserting the non-fragile controller to the system, the error is completely reduced which the trajectories goes to zero which is shown in Fig. 8. Figures 9, 10 are the evolution of errors for \(\varphi _{p2}\) and \(\varphi _{p3}\) \((p = 1,2,3,4,5)\) nodes without controller and with controller respectively (Figs. 11, 12).

6 Conclusions

In this problem, we investigated the fractional order lag synchronization for multi-weighted complex dynamical networks with coupling delays via non-fragile control. As we introduced a general multi-weighted complex network model including the coupling delays with external disturbances and analyzed the lag synchronization criteria using the state feedback non-fragile control. Based on the Lyapunov stability theory and comparison principle, we ensured our model guarantees the lag synchronization under the controller. To check the feasibility of the results obtained, a numerical example is drawn up. In future, we will consider the impulses and uncertainty and analyzing its synching criteria.