1 Introduction

In recent years, recurrent neural networks (RNNs) have received increasing research interests from many fields of science and technology due to their widespread applications in associative memories, signal processing, pattern recognition, and optimization problems [1, 2]. It is known that these applications are closely dependent on the dynamic properties of neural networks. For this reason, qualitative analysis is essential and important in the design and implementation of neural networks.

Compared with traditional neural network models, discontinuous neural networks, especially, with discontinuous activations possess obvious preponderance since it has the ability to non-linear mapping. In ideal circumstances, it can approximate many linear and non-linear relationship. At the same time, it has the self-learning autogenous shrinkage characteristics, and has the strong robustness and fault tolerance. Considering this fact, much efforts have been devoted to studying the dynamical properties of neural networks with discontinuous activations, see [3,4,5,6,7,8,9,10,11] and the references therein.

Nowadays, complex-valued recurrent neural networks (CVRNNs) have stirred enormous research interest because of their prominent values in such as physical systems dealing with electromagnetic, light, ultrasonic, and quantum waves [12]. Since CVRNNs posses complex-valued state, activation function output, and connection weight, they have a number of advantages that real-valued recurrent neural networks (RVRNNs) do not have, for example, the single real-valued neuron cannot deal with the XOR problem and the detection of symmetry problem, but a single complex-valued neuron with the orthogonal decision boundaries can successfully accomplish these problems [13], which shows that the complex-valued neurons have strong computing capabilities and thus CVRNNs have widespread engineering applications in than RVRNNs. Currently, there are some prominent results on dynamical analysis of various CVRNNs, see [14,15,16,17,18,19,20] and the references therein.

It should be noted that the existing references mainly focused on the stability or dissipativity problems, and the activation functions employed in their results are continuous cases. Synchronization, as a class of nonlinear characteristics, has attracted much attention in many scientific disciplines [21, 22] since it can be applied to combinatorial optimization, image processing, and secure communication [23]. However, results on synchronization of discontinuous CVRNNs are still quite rare (see [24,25,26,27]), a common limitation in these studies is that the discontinuity of activations as well as the complex range of system parameter variations, which leads to the theoretical and technical difficulties in studying the synchronization dynamics of CVRNNs. On the other hand, to the best of the authors’ knowledge, the exponential synchronization issue for delayed CVRNNs with discontinuous activations has not been reported yet in the existing literature.

Motivated by the aforementioned discussions, this paper studies the global exponential synchronization problem for a class of delayed CVRNNs with discontinuous activations. By utilizing the drive-response scheme, and exploiting the theory of differential equations with discontinuous right-hand sides, novel discontinuous state feedback controllers are designed and new algebra criteria are established to achieve the exponential stability of error CVRNNs. Then, exponential synchronization of drive-response CVRNNs can be realized. Finally, The effectiveness and advantages of the proposed results are verified via a numerical example.

The outline of this paper is organized as follows. The model description and some preliminaries are presented in Sect. 2. The main results are established in Sect. 3. In Sect. 4, an illustrative numerical example is provided. Finally, conclusions are drawn in Sect. 5.

Notations Let \(\mathbb {R}\) and \(\mathbb {R}^{n}\) be the space of real numbers, and the n dimensional real Euclidean space respectively, while \(\mathbb {C}\) and \(\mathbb {C}^{n}\) respectively denote the set of all complex numbers, and the set of all n-dimensional complex-valued vectors. Given the column vector \(x=(x_{1},x_{2},\ldots ,x_{n})^\mathrm{T}\in \mathbb {R}^{n}\), where the superscript ‘\(\mathrm{T}\)’ represents the transpose of a vector, \(\Vert x\Vert \) is the Euclidean vector norm, i.e., \(\Vert x\Vert =(\sum \nolimits _{i=1}^{n}x_{i}^2)^{\frac{1}{2}}\).

2 Model Description and Preliminaries

In this paper, we consider the following delayed CVRNNs with discontinuous activations:

$$\begin{aligned} \dot{z}_{j}(t)=-\,d_{j}z_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}f_{k}(z_{k}(t))+\sum \limits _{k=1}^{n}b_{jk}f_{k}(z_{k}(t-\tau (t)))+I_{j},\ j=1,2,\ldots ,n,\nonumber \\ \end{aligned}$$
(2.1)

where \(z= (z_1, z_2, \ldots , z_n)^\mathrm{T}\in \mathbb {C}^{n}\) is the state vector, \(f(z(\cdot ))=(f_{1}(z_{1}(\cdot )),f_{2}(z_{2}(\cdot )),\ldots ,f_{n}(z_{n}(\cdot )))^\mathrm{T}\in \mathbb {C}^{n} \) denotes the vector-valued activation function, \(D=\mathrm{diag}\{d_{1}, d_{2},\ldots ,d_{n}\}\in \mathbb {R}^{n\times n}\) with \(d_{j}>0 (j=1,2,\ldots ,n)\) represents the self-feedback connection weight matrix, \(A = (a_{jk})_{n\times n} \in \mathbb {C}^{n\times n}\) and \(B = (b_{jk})_{n\times n} \in \mathbb {C}^{n\times n}\) are the connection weight matrix and the delayed connection weight matrix, respectively, \(\tau (t) \) denotes the time-varying transmission delay and satisfies \(0\le \tau (t)\le \tau \), \(I=(I_1, I_2, \ldots , I_n)^\mathrm{T}\in \mathbb {C}^{n}\) is the external input vector. Herein, the initial condition associated with the CVRNNs (2.1) is given by

$$\begin{aligned} z_{j}(s)=\varphi _{j}(s)+\mathrm{i}\phi _{j}(s),\quad s\in [-\,\tau , 0], \ j=1,2,\ldots ,n, \end{aligned}$$

where \(\varphi _{j}(s), \phi _{j}(s)\in C([-\,\tau , 0], \mathbb {R})\), and \(C([-\,\tau , 0], \mathbb {R})\) denotes the space of continuous functions mapping \([-\,\tau , 0]\) into \(\mathbb {R}\) equipped with the supremum norm \(\Vert \cdot \Vert \).

Let \(z_{j}(t)=x_{j}(t)+\mathrm{i}y_{j}(t), I_{j}=I_{j}^{R}+\mathrm{i}I_{j}^{I}, a_{jk}=a_{jk}^{R}+\mathrm{i}a_{jk}^{I}, b_{jk}=b_{jk}^{R}+\mathrm{i}b_{jk}^{I}, f_{k}(z_{k}(t))=f_{k}^{R}(x_{k}(t),y_{k}(t))+\mathrm{i}f_{k}^{I}(x_{k}(t),y_{k}(t)),\) in which \(\mathrm{i}\) denotes the imaginary unit, i.e., \(\mathrm{i}^{2}=-1\). For simplicity, set \(x_{k}=x_{k}(t), y_{k}=y_{k}(t), x_{k}^{\tau }=x_{k}(t-\tau (t)), y_{k}^{\tau }=y_{k}(t-\tau (t))\). Then CVRNNs (2.1) can be rewritten into the equivalent real and imaginary parts as

$$\begin{aligned} \dot{x}_{j}(t)=\,&-d_{j}x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}f_{k}^{R}(x_{k},y_{k})-\sum \limits _{k=1}^{n}a_{jk}^{I}f_{k}^{I}(x_{k},y_{k})+\sum \limits _{k=1}^{n}b_{jk}^{R}f_{k}^{R}\left( x_{k}^{\tau },y_{k}^{\tau }\right) \nonumber \\&-\sum \limits _{k=1}^{n}b_{jk}^{I}f_{k}^{I}\left( x_{k}^{\tau },y_{k}^{\tau }\right) +I_{j}^{R},\nonumber \\ \dot{y}_{j}(t)=\,&-d_{j}y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}f_{k}^{R}(x_{k},y_{k})+\sum \limits _{k=1}^{n}a_{jk}^{R}f_{k}^{I}(x_{k},y_{k})+\sum \limits _{k=1}^{n}b_{jk}^{I}f_{k}^{R}\left( x_{k}^{\tau },y_{k}^{\tau }\right) \nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}f_{k}^{I}\left( x_{k}^{\tau },y_{k}^{\tau }\right) +I_{j}^{I}. \end{aligned}$$
(2.2)

Note that the activation function depends on the real and imaginary parts of the state variable of the neuron, which is a bivariate function, so we assume that the activation function belongs to the following function class.

Definition 2.1

(Function class\(\mathscr {F}\)). We say \(f\in \mathscr {F}\) if f satisfies the following assumption:

  1. (i)

    \(f(\cdot ,\cdot )\) is continuous at countable open domains \(G_{s}\) and discontinuous at the boundary of \(G_{s}\), which is composed by finite smooth curves. Herein, \(G_{s_{1}}\bigcap G_{s_{2}}=\emptyset , \) for \( s_{1}\ne s_{2}\), and \(\bigcup \nolimits _{s=1}^{\infty }( G_{s} \bigcup \partial G_{s})=\mathbb {R}^{2}\).

  2. (ii)

    The limitation \(\lim \nolimits _{\mathbf{z}\rightarrow \mathbf{z_{0}}, \mathbf{z_{0}}\in \partial G_{s}}f(\mathbf{z})\) exists.

Remark 2.1

Since the discontinuous activation functions depend on both the real and imaginary parts, in order to make better use of the theory of differential inclusion, we give a reasonable definition to define the discontinuities of activation functions, which is essentially different from the real-valued case in [3,4,5]. On the other hand, in the literature [20, 26], the real and imaginary parts are dependent on the real and imaginary parts of the activations, respectively. From the viewpoint of information storage, such networks under the design of complex-valued activation functions are more suitable for the tasks of high-capacity associative memories than the corresponding ones in [20, 26].

Since \(f_{k}^{R}, f_{k}^{I}\in \mathscr {F}\) for each \(k=1,2,\ldots ,n\), by using the theory of Filippov [28] in studying the properties of solutions for differential equations with discontinuous right-hand sides, we can obtain the following differential inclusion:

$$\begin{aligned} \dot{x}_{j}(t)\in&-d_{j}x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}\mathbb {F}\left[ f_{k}^{R}\right] (x_{k},y_{k})-\sum \limits _{k=1}^{n}a_{jk}^{I}\mathbb {F}\left[ f_{k}^{I}\right] (x_{k},y_{k})+\sum \limits _{k=1}^{n}b_{jk}^{R}\mathbb {F}\left[ f_{k}^{R}\right] \left( x_{k}^{\tau },y_{k}^{\tau }\right) \nonumber \\&-\sum \limits _{k=1}^{n}b_{jk}^{I}\mathbb {F}\left[ f_{k}^{I}\right] \left( x_{k}^{\tau },y_{k}^{\tau }\right) +I_{j}^{R},\nonumber \\ \dot{y}_{j}(t)\in&-d_{j}y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}\mathbb {F}\left[ f_{k}^{R}\right] (x_{k},y_{k})+\sum \limits _{k=1}^{n}a_{jk}^{R}\mathbb {F}\left[ f_{k}^{I}\right] (x_{k},y_{k})+\sum \limits _{k=1}^{n}b_{jk}^{I}\mathbb {F}\left[ f_{k}^{R}\right] \left( x_{k}^{\tau },y_{k}^{\tau }\right) \nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}\mathbb {F}\left[ f_{k}^{I}\right] \left( x_{k}^{\tau },y_{k}^{\tau }\right) +I_{j}^{I}, \end{aligned}$$
(2.3)

where \(\mathbb {F}[f_{k}^{(R\ or\ I)}](\mathbf{z})=\bigcap \nolimits _{\delta >0}\bigcap \nolimits _{\mu (\mathscr {N})=0}\overline{\mathrm{co}}[f_{k}^{(R\ or\ I)}(B(\mathbf{z},\delta )\setminus \mathscr {N})]\), where \(\overline{\mathrm{co}}(\Omega )\) denotes the closure of the convex hull of set \(\Omega \), \(B(\mathbf{z},\delta )=\{\mathbf{y}:\Vert \mathbf{y}-\mathbf{z}\Vert \le \delta , z\in \mathbb {R}^{2}\}\) is the ball with center at z and radius \(\delta \), and \(\mu (\mathcal {N})\) is Lebesgue measure of set \(\mathcal {N}\).

By using the measurable selection theorem [29], if \(x_{j}(t)\) and \(y_{j}(t)\) are solutions of (2.2), there exist measurable selections \(\gamma _{k}^{(R\ or \ I)}(t)\in \mathbb {F}[f_{k}^{(R\ or\ I)}(x_{k}(t),y_{k}(t))] \) such that for almost all (a.a.) \(t\in [-\,\tau , T), T\in [0, \infty ),\) the following equation holds:

$$\begin{aligned} \dot{x}_{j}(t)=\,&-d_{j}x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}\gamma _{k}^{R}(t)-\sum \limits _{k=1}^{n}a_{jk}^{I}\gamma _{k}^{I}(t)+\sum \limits _{k=1}^{n}b_{jk}^{R}\gamma _{k}^{R}(t-\tau (t))\nonumber \\&-\,\sum \limits _{k=1}^{n}b_{jk}^{I}\gamma _{k}^{I}(t-\tau (t))+I_{j}^{R},\nonumber \\ \dot{y}_{j}(t)=\,&-\,d_{j}y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}\gamma _{k}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}\gamma _{k}^{I}(t)+\sum \limits _{k=1}^{n}b_{jk}^{I}\gamma _{k}^{R}(t-\tau (t))\nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}\gamma _{k}^{I}(t-\tau (t))+I_{j}^{I}, j=1,2,\ldots ,n. \end{aligned}$$
(2.4)

In this paper, we shall make drive-response delayed CVRNNs with discontinuous activations achieve exponential synchronization by designing some effective controllers. For simplicity, we refer to system (2.4) as the drive system, the response system is given as follows:

$$\begin{aligned} \dot{\tilde{x}}_{j}(t)=\,&-\,d_{j}\tilde{x}_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}\tilde{\gamma }_{k}^{R}(t)-\sum \limits _{k=1}^{n}a_{jk}^{I}\tilde{\gamma }_{k}^{I}(t)+\sum \limits _{k=1}^{n}b_{jk}^{R}\tilde{\gamma }_{k}^{R}(t-\tau (t))\nonumber \\&-\,\sum \limits _{k=1}^{n}b_{jk}^{I}\tilde{\gamma }_{k}^{I}(t-\tau (t))+I_{j}^{R}+u_{j}^{R},\nonumber \\ \dot{\tilde{y}}_{j}(t)=\,&-\,d_{j}\tilde{y}_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}\tilde{\gamma }_{k}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}\tilde{\gamma }_{k}^{I}(t)+\sum \limits _{k=1}^{n}b_{jk}^{I}\tilde{\gamma }_{k}^{R}(t-\tau (t))\nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}\tilde{\gamma }_{k}^{I}(t-\tau (t))+I_{j}^{I}+u_{j}^{I}, j=1,2,\ldots ,n, \end{aligned}$$
(2.5)

where \(\tilde{x}_{j}(t), \tilde{y}_{j}(t)\) denote the states of the response system, \(u_{j}^{R}, u_{j}^{I}\) are the external control inputs to realize exponential synchronization, the other system parameters are the same as those in (2.1).

Define the error signal between the drive system (2.4) and the response system (2.5) as \(e_{j}(t)=\tilde{z}_{j}(t)-z_{j}(t)=e_{j}^{R}(t)+\mathrm{i} e_{j}^{I}(t)=\tilde{x}_{j}(t)-x_{j}(t)+\mathrm{i}(\tilde{y}_{j}(t)-y_{j}(t))\), and subtract (2.5) from (2.1) yields the following error system:

$$\begin{aligned} \dot{e}_{j}^{R}(t)=\,&-\,d_{j}e_{j}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}\left( \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right) -\sum \limits _{k=1}^{n}a_{jk}^{I}\left( \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right) \nonumber \\&+\,\sum \limits _{k=1}^{n}b_{jk}^{R}\left( \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right) \nonumber \\&-\,\sum \limits _{k=1}^{n}b_{jk}^{I}\left( \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right) +u_{j}^{R},\nonumber \\ \dot{e}_{j}^{I}(t)=\,&-\,d_{j}e_{j}^{I}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}\left( \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right) +\sum \limits _{k=1}^{n}a_{jk}^{R}\left( \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right) \nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{I}\left( \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right) \nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}\left( \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right) +u_{j}^{I}, \quad j=1,2,\ldots ,n. \end{aligned}$$
(2.6)

In order to establish our main results, we make the following assumption on the discontinuous activations.

Assumption 1

For any \(x_{k}, y_{k}, \tilde{x}_{k}, \tilde{y}_{k}\in \mathbb {R}\), there exist nonnegative constants \(\lambda _{k}^{RR}, \lambda _{k}^{RI}, \lambda _{k}^{IR}, \lambda _{k}^{II}, \mu _{k}^{R},\) and \(\mu _{k}^{I}\) such that

$$\begin{aligned} \left| \tilde{\gamma }_{k}^{R}-\gamma _{k}^{R}\right| \le \,&\lambda _{k}^{RR}\left| \tilde{x}_{k}-x_{k}\right| +\lambda _{k}^{RI}\left| \tilde{y}_{k}-y_{k}\right| +\mu _{k}^{R}, \nonumber \\ \left| \tilde{\gamma }_{k}^{I}-\gamma _{k}^{I}\right| \le \,&\lambda _{k}^{IR}\left| \tilde{x}_{k}-x_{k}\right| +\lambda _{k}^{II}\left| \tilde{y}_{k}-y_{k}\right| +\mu _{k}^{I}, \end{aligned}$$
(2.7)

where \(\gamma _{k}^{(R\ or \ I)}\in \mathbb {F}[f_{k}^{(R\ or\ I)}(x_{k},y_{k})] \) and \(\tilde{\gamma }_{k}^{(R\ or \ I)}\in \mathbb {F}[f_{k}^{(R\ or\ I)}(\tilde{x}_{k},\tilde{y}_{k})] , k=1,2,\ldots ,n\).

Assumption 2

The delay \(\tau (t)\) satisfies \(\dot{\tau }(t)\le \rho <1\), where \(\rho \) is a positive constant.

Remark 2.2

When the activation \(f_{k}^{(R\ or\ I)}(x_{k},y_{k})\) is a continuous function, \(\mathbb {F}[f_{k}^{(R\ or\ I)}(x_{k},y_{k})]\) is indeed single-valued, and \(\mu _{k}^{R}\) and \(\mu _{k}^{I}\) are equal to 0, then (2.7) reduces to the well-known Lipschitz condition which has widely used in such as [14, 17], which implies that (2.7) not only is an extension of the real-valued case but also generalizes the complex-valued activation function.

Before proceeding, some definitions and lemmas are needed which play important roles in the proof of our main results.

Definition 2.2

Drive-response systems (2.4) and (2.5) are said to be globally exponentially synchronized, if there are control inputs \(u_{j}^{R}(t),u_{j}^{I}(t)\), and further there exist constants \(M>1\) and \(\varepsilon >0\) such that

$$\begin{aligned} \Vert e^{R}(t)\Vert +\Vert e^{I}(t)\Vert \le M\sup \limits _{-\tau \le s\le 0}\left[ \Vert \tilde{\varphi }-\varphi \Vert +\Vert \tilde{\phi }-\phi \Vert \right] e^{-\varepsilon t},\quad \text {for\ all}\quad t>0. \end{aligned}$$

The constant \(\varepsilon \) is said to be the degree of exponential synchronization.

Lemma 2.3

(Halanay inequality [30]). Assume that constant numbers \(\zeta _{1}\) and \(\zeta _{2}\) satisfy \(\zeta _{1}>\zeta _{2}>0\), V(t) is a nonnegative continuous function on \([t_{0}-\tau , t_{0}]\) and satisfies the following inequality:

$$\begin{aligned} D^{+}V(t)\le -\,\zeta _{1}V(t)+\zeta _{2}\sup \limits _{t-\tau \le s\le t}V(s),\quad t\ge t_{0}, \end{aligned}$$

where \(\tau \ge 0\) is a constant. Then, for \(t\ge t_{0}\), we have

$$\begin{aligned} V(t)\le \sup \limits _{t_{0}-\tau \le s\le t_{0}}V(s)e^{-\zeta t_{0}}, \end{aligned}$$

in which \(\zeta \) is the unique positive solution of the equation \(\zeta =\zeta _{1}-\zeta _{2}e^{\zeta \tau }\).

3 Main Results

In this section, we first establish some sufficient criteria for global exponential synchronization of discontinuous drive-response CVRNNs (2.4) and (2.5) under the following state feedback controllers:

$$\begin{aligned} u_{j}^{R}(t)=-p^{R}_{j}e^{R}_{j}(t)-q^{R}_{j}\mathrm{sign}(e^{R}_{j}(t)),\quad u_{j}^{I}(t)=-p^{I}_{j}e^{I}_{j}(t)-q^{I}_{j}\mathrm{sign}(e^{I}_{j}(t)). \end{aligned}$$
(3.1)

Theorem 3.1

Let \(f_{k}^{R}, f_{k}^{I}\in \mathscr {F}, k=1,2,\ldots ,n\), and Assumptions 1 and 2 hold. Then discontinuous response system (2.5) with the feedback controllers (3.1) can be globally exponentially synchronized with drive system (2.4), if there exist positive constants \(p_{j}^{R}, p_{j}^{I},q_{j}^{R},q_{j}^{I}(j=1,\ldots ,n)\) such that

$$\begin{aligned} 2p_{j}^{R}>&-2d_{j}+8n+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\\&+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}+\frac{1}{1-\rho }\mathscr {F}_{j},\\ 2p_{j}^{I}>&-2d_{j}+8n+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\\&+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}+\frac{1}{1-\rho }\mathscr {T}_{j}, \end{aligned}$$

and

$$\begin{aligned} q_{j}^{R}\ge & {} \sum \limits _{k=1}^{n}\mu _{k}^{R}\left| a_{jk}^{R}\right| +\sum \limits _{k=1}^{n}\mu _{k}^{I}\left| a_{jk}^{I}\right| +\sum \limits _{k=1}^{n}\mu _{k}^{R}\left| b_{jk}^{R}\right| +\sum \limits _{k=1}^{n}\mu _{k}^{I}\left| b_{jk}^{I}\right| ,\nonumber \\ q_{j}^{I}\ge & {} \sum \limits _{k=1}^{n}\mu _{k}^{R}\left| a_{jk}^{I}\right| +\sum \limits _{k=1}^{n}\mu _{k}^{I}\left| a_{jk}^{R}\right| +\sum \limits _{k=1}^{n}\mu _{k}^{I}\left| b_{jk}^{R}\right| +\sum \limits _{k=1}^{n}\mu _{k}^{I}\left| b_{jk}^{I}\right| , \end{aligned}$$
(3.2)

where

$$\begin{aligned} \mathscr {F}_{j}&=\,&\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\quad +\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \left( \lambda _{j}^{IR}\right) ^{2},\\ \mathscr {T}_{j}&=\,&\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \left( \lambda _{j}^{II}\right) ^{2}, \end{aligned}$$

and \(\varepsilon >0\).

Remark 3.1

In view of (3.2) and the continuity arguments, we can obtain that

$$\begin{aligned} 2p_{j}^{R}\ge&\varepsilon -2d_{j}+8n+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\nonumber \\&+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}+\frac{1}{1-\rho }\mathscr {F}_{j}e^{\varepsilon t},\nonumber \\ 2p_{j}^{I}\ge&\varepsilon -2d_{j}+8n+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\nonumber \\&+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}+\frac{1}{1-\rho }\mathscr {T}_{j}e^{\varepsilon t}. \end{aligned}$$
(3.3)

Proof

Consider the following Lyapunov functional defined by

$$\begin{aligned} V_{1}(t)=\,&e^{\varepsilon t}\sum \limits _{j=1}^{n}\left( e_{j}^{R}(t)\right) ^{2}+\frac{1}{1-\rho }\sum \limits _{j=1}^{n}\int _{t-\tau (t)}^{t}\mathscr {F}_{j}(e_{j}^{R}(s))^{2}e^{\varepsilon (s+\tau )}ds\nonumber \\&+e^{\varepsilon t}\sum \limits _{j=1}^{n}\left( e_{j}^{I}(t)\right) ^{2}+\frac{1}{1-\rho }\sum \limits _{j=1}^{n}\int _{t-\tau (t)}^{t}\mathscr {T}_{j}(e_{j}^{I}(s))^{2}e^{\varepsilon (s+\tau )}ds. \end{aligned}$$
(3.4)

Calculate the upper right Dini-derivative of \(V_{1}(t)\) along the solutions of (2.6), we obtain

$$\begin{aligned} D^{+}V_{1}(t)=\,&\varepsilon e^{\varepsilon t}\sum \limits _{j=1}^{n}\left( e_{j}^{R}(t)\right) ^{2}+2e^{\varepsilon t}\sum \limits _{j=1}^{n}e_{j}^{R}(t)\dot{e}_{j}^{R}(t)\nonumber \\&+\frac{1}{1-\rho }\sum \limits _{j=1}^{n}\mathscr {F}_{j}\left( e_{j}^{R}(t)\right) ^{2}e^{\varepsilon (t+\tau )}-\frac{1-\dot{\tau }(t)}{1-\rho }\sum \limits _{j=1}^{n}\mathscr {F}_{j}\left( e_{j}^{R}(t-\tau (t))\right) ^{2}e^{\varepsilon (t-\tau (t)+\tau )}\nonumber \\&+\varepsilon e^{\varepsilon t}\sum \limits _{j=1}^{n}\left( e_{j}^{I}(t)\right) ^{2}+2e^{\varepsilon t}\sum \limits _{j=1}^{n}e_{j}^{I}(t)\dot{e}_{j}^{I}(t)\nonumber \\&+\frac{1}{1-\rho }\sum \limits _{j=1}^{n}\mathscr {T}_{j}\left( e_{j}^{I}(t)\right) ^{2}e^{\varepsilon (t+\tau )}-\frac{1-\dot{\tau }(t)}{1-\rho }\sum \limits _{j=1}^{n}\mathscr {T}_{j}\left( e_{j}^{I}(t-\tau (t))\right) ^{2}e^{\varepsilon (t-\tau (t)+\tau )}\nonumber \\ \le \,&\varepsilon e^{\varepsilon t}\sum \limits _{j=1}^{n}\left( e_{j}^{R}(t)\right) ^{2}-2e^{\varepsilon t}\sum \limits _{j=1}^{n}d_{j}\left( e_{j}^{R}(t)\right) ^{2}+e^{\varepsilon t}\left[ \underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right| }_{\mathbb {I}_{1}}\right. \nonumber \\&+\underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right| }_{\mathbb {I}_{2}}\nonumber \\&+\underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right| }_{\mathbb {I}_{3}}\nonumber \\&\left. +\underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right| }_{\mathbb {I}_{4}}\right] \nonumber \\&-2e^{\varepsilon t}\sum \limits _{j=1}^{n}p_{j}^{R}\left( e_{j}^{R}(t)\right) ^{2}-2e^{\varepsilon t}\sum \limits _{j=1}^{n}q_{j}^{R}\left| e_{j}^{R}(t)\right| \nonumber \\&+\frac{1}{1-\rho }\sum \limits _{j=1}^{n}\mathscr {F}_{j}\left( e_{j}^{R}(t)\right) ^{2}e^{\varepsilon (t+\tau )}-\sum \limits _{j=1}^{n}\mathscr {F}_{j}\left( e_{j}^{R}(t-\tau (t))\right) ^{2}e^{\varepsilon t}\nonumber \\&+\varepsilon e^{\varepsilon t}\sum \limits _{j=1}^{n}\left( e_{j}^{I}(t)\right) ^{2}-2e^{\varepsilon t}\sum \limits _{j=1}^{n}d_{j}\left( e_{j}^{I}(t)\right) ^{2}\nonumber \\&+e^{\varepsilon t}\left[ \underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right| }_{\mathbb {I}_{5}}\right. \nonumber \\&+\underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right| }_{\mathbb {I}_{6}}\nonumber \\&+\underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right| }_{\mathbb {I}_{7}}\nonumber \\&\left. +\underbrace{\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right| }_{\mathbb {I}_{8}}\right] \nonumber \\&-2e^{\varepsilon t}\sum \limits _{j=1}^{n}p_{j}^{I}\left( e_{j}^{I}(t)\right) ^{2}-2e^{\varepsilon t}\sum \limits _{j=1}^{n}q_{j}^{I}\left| e_{j}^{I}(t)\right| \nonumber \\&+\frac{1}{1-\rho }\sum \limits _{j=1}^{n}\mathscr {T}_{j}\left( e_{j}^{R}(t)\right) ^{2}e^{\varepsilon (t+\tau )}-\sum \limits _{j=1}^{n}\mathscr {T}_{j}\left( e_{j}^{R}(t-\tau (t))\right) ^{2}e^{\varepsilon t},\nonumber \\ \quad {\mathrm{for}}\,{\mathrm{a.a.}}\ t\ge 0. \end{aligned}$$
(3.5)

Now we estimate \( \mathbb {I}_{i}(i=1,\ldots ,8)\) term by term. Firstly, according to (2.7), we have

$$\begin{aligned} \mathbb {I}_{1}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| \left( \lambda _{k}^{RR}\left| e_{k}^{R}(t)\right| +\lambda _{k}^{RI}\left| e_{k}^{I}(t)\right| +\mu _{k}^{R}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\left| e_{j}^{R}(t)\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| a_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| . \end{aligned}$$
(3.6)

For \(\mathbb {I}_{2}\), one has

$$\begin{aligned} \mathbb {I}_{2}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| \left( \lambda _{k}^{IR}\left| e_{k}^{R}(t)\right| +\lambda _{k}^{II}\left| e_{k}^{I}(t)\right| +\mu _{k}^{I}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}\left| e_{j}^{R}(t)\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| a_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| . \end{aligned}$$
(3.7)

For \(\mathbb {I}_{3}\), we can also get from (2.7) that

$$\begin{aligned} \mathbb {I}_{3}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| \left( \lambda _{k}^{RR}\left| e_{k}^{R}(t-\tau (t))\right| +\lambda _{k}^{RI}\left| e_{k}^{I}(t-\tau (t))\right| +\mu _{k}^{R}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\left| e_{j}^{R}(t-\tau (t))\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\left| e_{j}^{I}(t-\tau (t))\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| b_{jk}^{R}\right| \left| e_{j}^{R}(t)\right| . \end{aligned}$$
(3.8)

For the fourth term \( \mathbb {I}_{4}\), we have

$$\begin{aligned} \mathbb {I}_{4}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| \left( \lambda _{k}^{IR}\left| e_{k}^{R}(t-\tau (t))\right| +\lambda _{k}^{II}\left| e_{k}^{I}(t-\tau (t))\right| +\mu _{k}^{I}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}\left| e_{j}^{R}(t-\tau (t))\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{R}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}\left| e_{j}^{I}(t-\tau (t))\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| b_{jk}^{I}\right| \left| e_{j}^{R}(t)\right| . \end{aligned}$$
(3.9)

Similar to the estimations of \(\mathbb {I}_{i}\), \(\mathbb {I}_{4+i}(i=1,\ldots ,4)\) can be estimated as follows:

$$\begin{aligned} \mathbb {I}_{5}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| \left( \lambda _{k}^{RR}\left| e_{k}^{R}(t)\right| +\lambda _{k}^{RI}\left| e_{k}^{I}(t)\right| +\mu _{k}^{R}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\left| e_{j}^{R}(t)\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| a_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| , \end{aligned}$$
(3.10)

and

$$\begin{aligned} \mathbb {I}_{6}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| a_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| \left( \lambda _{k}^{IR}\left| e_{k}^{R}(t)\right| +\lambda _{k}^{II}\left| e_{k}^{I}(t)\right| +\mu _{k}^{I}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}\left| e_{j}^{R}(t)\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| a_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| . \end{aligned}$$
(3.11)

Moreover,

$$\begin{aligned} \mathbb {I}_{7}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| \left( \lambda _{k}^{RR}\left| e_{k}^{R}(t-\tau (t))\right| +\lambda _{k}^{RI}\left| e_{k}^{I}(t-\tau (t))\right| +\mu _{k}^{R}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\left| e_{j}^{R}(t-\tau (t))\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\left| e_{j}^{I}(t-\tau (t))\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| b_{jk}^{I}\right| \left| e_{j}^{I}(t)\right| , \end{aligned}$$
(3.12)

and

$$\begin{aligned} \mathbb {I}_{8}=\,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| \left| \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right| \nonumber \\ \le \,&\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\left| b_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| \left( \lambda _{k}^{IR}\left| e_{k}^{R}(t-\tau (t))\right| +\lambda _{k}^{II}\left| e_{k}^{I}(t-\tau (t))\right| +\mu _{k}^{I}\right) \nonumber \\ \le \,&n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \left( \lambda _{j}^{IR}\right) ^{2}\left| e_{j}^{R}(t-\tau (t))\right| ^{2}\nonumber \\&+n\sum \limits _{j=1}^{n}\left| e_{j}^{I}(t)\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \left( \lambda _{j}^{II}\right) ^{2}\left| e_{j}^{I}(t-\tau (t))\right| ^{2}+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| b_{jk}^{R}\right| \left| e_{j}^{I}(t)\right| . \end{aligned}$$
(3.13)

Inserting the above estimates (3.6)-(3.13) into (3.5), we deduce that

$$\begin{aligned} D^{+}V_{1}(t)\le \,&e^{\varepsilon t}\sum \limits _{j=1}^{n}\left[ \varepsilon -2d_{j}+8n+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}\right. \nonumber \\&+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RR}\right) ^{2}\nonumber \\&\left. +\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{IR}\right) ^{2}+\frac{1}{1-\rho }\mathscr {F}_{j}e^{\varepsilon \tau }-2p_{j}^{R}\right] \left| e_{j}^{R}(t)\right| ^{2}\nonumber \\&+e^{\varepsilon t}\sum \limits _{j=1}^{n}\left[ \varepsilon -2d_{j}+8n+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}\right. \nonumber \\&+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| ^{2}\left( \lambda _{j}^{RI}\right) ^{2}\nonumber \\&\left. +\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| ^{2}\left( \lambda _{j}^{II}\right) ^{2}+\frac{1}{1-\rho }\mathscr {T}_{j}e^{\varepsilon \tau }-2p_{j}^{I}\right] \left| e_{j}^{I}(t)\right| ^{2}\nonumber \\&+e^{\varepsilon t}\sum \limits _{j=1}^{n}\left[ -2q_{j}^{R}+\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| a_{jk}^{R}\right| +\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| a_{jk}^{I}\right| +\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| b_{jk}^{R}\right| \right. \nonumber \\&\left. +\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| b_{jk}^{I}\right| \right] \left| e_{j}^{R}(t)\right| \nonumber \\&+e^{\varepsilon t}\sum \limits _{j=1}^{n}\left[ -2q_{j}^{I}+\sum \limits _{k=1}^{n}2\mu _{k}^{R}\left| a_{jk}^{I}\right| +\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| a_{jk}^{R}\right| +\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| a_{jk}^{R}\right| \right. \nonumber \\&\left. +\sum \limits _{k=1}^{n}2\mu _{k}^{I}\left| b_{jk}^{R}\right| \right] \left| e_{j}^{I}(t)\right| . \end{aligned}$$
(3.14)

It follows from (3.3) and (3.14) that

$$\begin{aligned} D^{+}V_{1}(t)\le 0, \quad \mathrm{for\ a.a.} \ t\ge 0, \end{aligned}$$

that is, \(V_{1}(t)\) is a monotonically decreasing function. Then we have \(V_{1}(t)\le V(0)\).

On the other hand, it follows from (3.4) that

$$\begin{aligned} V_{1}(0)\le \,&\big [\Vert e^{R}(0)\Vert ^{2}+\Vert e^{I}(0)\Vert ^{2}\big ]\nonumber \\&+\frac{\tau e^{\varepsilon \tau }}{1-\rho }\max \left\{ \sum \limits _{j=1}^{n}\mathscr {F}_{j},\sum \limits _{j=1}^{n}\mathscr {T}_{j}\right\} \sup \limits _{-\tau \le s\le 0}[\Vert e^{R}(s)\Vert ^{2}+\Vert e^{I}(s)\Vert ^{2}]\nonumber \\ \le \,&\left[ 1+\frac{\tau e^{\varepsilon \tau }}{1-\rho }\max \left\{ \sum \limits _{j=1}^{n}\mathscr {F}_{j},\sum \limits _{j=1}^{n}\mathscr {T}_{j}\right\} \right] \sup \limits _{-\tau \le s\le 0}[\Vert e^{R}(s)\Vert ^{2}+\Vert e^{I}(s)\Vert ^{2}]\nonumber \\ \triangleq&\xi \sup \limits _{-\tau \le s\le 0}[\Vert e^{R}(s)\Vert ^{2}+\Vert e^{I}(s)\Vert ^{2}]. \end{aligned}$$
(3.15)

Furthermore,

$$\begin{aligned} V_{1}(t)\ge&e^{\varepsilon t}\left[ \sum \limits _{j=1}^{n}(e_{j}^{R}(t))^{2}+\sum \limits _{j=1}^{n}(e_{j}^{I}(t))^{2}\right] \nonumber \\ =\,&e^{\varepsilon t}\left[ \Vert e^{R}(t)\Vert ^{2}+\Vert e^{I}(t)\Vert ^{2}\right] . \end{aligned}$$
(3.16)

Then, we have from (3.15) and (3.16) that

$$\begin{aligned} \Vert e^{R}(t)\Vert ^{2}+\Vert e^{I}(t)\Vert ^{2}\le \xi \sup \limits _{-\tau \le s\le 0}[\Vert e^{R}(s)\Vert ^{2}+\Vert e^{I}(s)\Vert ^{2}]e^{-\varepsilon t}, \end{aligned}$$

which gives

$$\begin{aligned} \Vert e^{R}(t)\Vert +\Vert e^{I}(t)\Vert \le \sqrt{2\xi }\sup \limits _{-\tau \le s\le 0}[\Vert e^{R}(s)\Vert +\Vert e^{I}(s)\Vert ]e^{-\frac{\varepsilon }{2} t}. \end{aligned}$$

Then, according to Definition 2.2, the response system (2.5) with state feedback controllers (3.1) can be globally exponentially synchronized with discontinuous drive system (2.4). \(\square \)

If there is no differentiability imposed on the time delay, that is, if Assumption 2 does not hold, we can establish the following delay-independent synchronization criteria by constructing proper Lyapunov functional.

Theorem 3.2

Let \(f_{k}^{R}, f_{k}^{I}\in \mathscr {F}, k=1,2,\ldots ,n\), and Assumption 1 hold. Then the response system (2.5) is globally exponentially synchronized with the drive system (2.4) under the feedback controllers (3.1),

$$\begin{aligned} p_{j}^{R}\ge&-d_{j}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{RR}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{IR}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{RR}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{IR},\\ p_{j}^{I}\ge&-d_{j}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{RI}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{II}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{RI}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{II},\\ q_{j}^{R}\ge&\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \mu _{j}^{I}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \mu _{j}^{I},\\ q_{j}^{I}\ge&\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \mu _{j}^{I}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \mu _{j}^{I},\\ \end{aligned}$$

and \( \zeta _{1}>\zeta _{2}, \) where

$$\begin{aligned} \zeta _{1}=\,&\min \limits _{1\le j\le n}\left\{ d_{j}+p_{j}^{R}-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{RR}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{IR}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{RR}-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{IR},\right. \\&\left. d_{j}+p_{j}^{I}-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{RI}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{II}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{RI}-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{II}\right\} ,\\ \zeta _{2}=\,&\max \limits _{1\le j\le n}\left\{ \sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{RR}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{IR}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{RR}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{IR},\right. \\&\left. \sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{RI}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{II}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{RI}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{II}\right\} , \end{aligned}$$

and \(\zeta \) is the unique positive solution of the equation \(\zeta =\zeta _{1}-\zeta _{2}e^{\zeta \tau }\).

Proof

Consider the following Lyapunov functional defined by

$$\begin{aligned} V_{2}(t)=\Vert e^{R}(t)\Vert _{1}+\Vert e^{I}(t)\Vert _{1}=\sum \limits _{j=1}^{n}\Big [|e_{j}^{R}(t)|+|e_{j}^{I}(t)|\Big ]. \end{aligned}$$

Calculate the upper right Dini-derivative of \(V_{2}(t)\) along the solutions of (2.6), we can get by recalling the estimates in the proof of Theorem 3.1 that

$$\begin{aligned} D^{+}V_{2}(t)\le \,&-\sum \limits _{j=1}^{n}d_{j}\left| e_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{jk}^{R}\right| \left| \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right| \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{jk}^{I}\right| \left| \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right| +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{jk}^{R}\right| \left| \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right| \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{jk}^{I}\right| \left| \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right| - \sum \limits _{j=1}^{n}p_{j}^{R}\left| e_{j}^{R}(t)\right| -\sum \limits _{j=1}^{n}q_{j}^{R}\\&-\sum \limits _{j=1}^{n}d_{j}\left| e_{j}^{I}(t)\right| +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{jk}^{I}\right| \left| \tilde{\gamma }_{k}^{R}(t)-\gamma _{k}^{R}(t)\right| \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{jk}^{R}\right| \left| \tilde{\gamma }_{k}^{I}(t)-\gamma _{k}^{I}(t)\right| +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{jk}^{I}\right| \left| \tilde{\gamma }_{k}^{R}(t-\tau (t))-\gamma _{k}^{R}(t-\tau (t))\right| \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{jk}^{R}\right| \left| \tilde{\gamma }_{k}^{I}(t-\tau (t))-\gamma _{k}^{I}(t-\tau (t))\right| -\sum \limits _{j=1}^{n}p_{j}^{I}\left| e_{j}^{I}(t)\right| -\sum \limits _{j=1}^{n}q_{j}^{I}\\ \le \,&-\sum \limits _{j=1}^{n}d_{j}\left| e_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \left( \lambda _{j}^{RR}\left| e_{j}^{R}(t)\right| +\lambda _{j}^{RI}\left| e_{j}^{I}(t)\right| +\mu _{j}^{R}\right) \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \left( \lambda _{j}^{IR}\left| e_{j}^{R}(t)\right| +\lambda _{j}^{II}\left| e_{j}^{I}(t)\right| +\mu _{j}^{I}\right) \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \left( \lambda _{j}^{RR}\left| e_{j}^{R}(t-\tau (t))\right| +\lambda _{j}^{RI}\left| e_{j}^{I}(t-\tau (t))\right| +\mu _{j}^{R}\right) \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \left( \lambda _{j}^{IR}\left| e_{j}^{R}(t-\tau (t))\right| +\lambda _{j}^{II}\left| e_{j}^{I}(t-\tau (t))\right| +\mu _{j}^{I}\right) \\&-\sum \limits _{j=1}^{n}p_{j}^{R}\left| e_{j}^{R}(t)\right| -\sum \limits _{j=1}^{n}q_{j}^{R}\\&-\sum \limits _{j=1}^{n}d_{j}\left| e_{j}^{I}(t)\right| +\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \left( \lambda _{j}^{RR}\left| e_{j}^{R}(t)\right| +\lambda _{j}^{RI}\left| e_{j}^{I}(t)\right| +\mu _{j}^{R}\right) \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \left( \lambda _{j}^{IR}\left| e_{j}^{R}(t)\right| +\lambda _{j}^{II}\left| e_{j}^{I}(t)\right| +\mu _{j}^{I}\right) \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \left( \lambda _{j}^{RR}\left| e_{j}^{R}(t-\tau (t))\right| +\lambda _{j}^{RI}\left| e_{k}^{I}(t-\tau (t))\right| +\mu _{j}^{R}\right) \\&+\sum \limits _{j=1}^{n}\sum \limits _{k=1}^{n}\left| b_{jk}^{R}\right| \left( \lambda _{j}^{IR}\left| e_{j}^{R}(t-\tau (t))\right| +\lambda _{j}^{II}\left| e_{j}^{I}(t-\tau (t))\right| +\mu _{j}^{I}\right) \\&- \sum \limits _{j=1}^{n}p_{j}^{I}\left| e_{j}^{I}(t)\right| -\sum \limits _{j=1}^{n}q_{j}^{I}\\ =\,&-\sum \limits _{j=1}^{n}\left[ d_{j}+p_{j}^{R}-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{RR}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{IR}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{RR}\right. \\&\left. -\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{IR}\right] \left| e_{j}^{R}(t)\right| \\&-\sum \limits _{j=1}^{n}\left[ d_{j}+p_{j}^{I}-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{RI}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{II}-\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \lambda _{j}^{RI}\right. \\&-\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \lambda _{j}^{II}\bigg ]\left| e_{j}^{I}(t)\right| \\&\left. +\sum \limits _{j=1}^{n}\bigg [\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{RR}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{IR}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{RR}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{IR}\right] \\&\quad \left| e_{j}^{R}(t-\tau (t))\right| \\&+\sum \limits _{j=1}^{n}\left[ \sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{RI}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{II}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \lambda _{j}^{RI}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \lambda _{j}^{II}\right] \left| e_{j}^{I}(t-\tau (t))\right| \\&+\sum \limits _{j=1}^{n}\left[ -q_{j}^{R}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \mu _{j}^{I}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \mu _{j}^{I}\right] \\&+\sum \limits _{j=1}^{n}\left[ -q_{j}^{I}+\sum \limits _{k=1}^{n}\left| a_{kj}^{I}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| a_{kj}^{R}\right| \mu _{j}^{I}+\sum \limits _{k=1}^{n}\left| b_{kj}^{I}\right| \mu _{j}^{R}+\sum \limits _{k=1}^{n}\left| b_{kj}^{R}\right| \mu _{j}^{I}\right] \\ \le \,&-\zeta _{1}\sum \limits _{j=1}^{n}\left[ \left| e_{j}^{R}(t)\right| +\left| e_{j}^{I}(t)\right| \Big ]+\zeta _{2}\sum \limits _{j=1}^{n}\Big [\left| e_{j}^{R}(t-\tau (t))\right| +\left| e_{j}^{I}(t-\tau (t))\right| \right] \\ \le \,&-\zeta _{1}V_{2}(t)+\zeta _{2}\sup \limits _{t-\tau \le s\le 0}V_{2}(s). \end{aligned}$$

It follows from Lemma 2.3 that

$$\begin{aligned} V_{2}(t)=\Vert e^{R}(t)\Vert _{1}+\Vert e^{I}(t)\Vert _{1}\le \sup \limits _{-\tau \le s\le 0}V_{2}(s)e^{-\zeta t},\quad t\ge 0, \end{aligned}$$

where \(\zeta \) is the unique positive solution of the equation \(\zeta =\zeta _{1}-\zeta _{2}e^{-\zeta t}\). Then, according to Definition 2.2, the response system (2.5) with state feedback controllers (3.1) can be globally exponentially synchronized with discontinuous drive system (2.4). \(\square \)

Remark 3.2

In recent years, various dynamical behaviors of CVNNs with continuous activations have been extensively investigated by many authors, see [14, 16,17,18,19,20] and the reference therein. However, exponential synchronization issue of delayed CVNNs with discontinuous activations has not yet been discussed in the existing literature. Thus, in this paper, to shorten up such a gap, we have analyzed a class of delayed CVRNNs with discontinuous activations. Some new sufficient criteria are established by the aid of theories of differential equations with discontinuous right-hand sides, and inequality techniques to ensure the exponential synchronization of the considered system. Moreover, it is admitted that the theoretical results established in Theorems 3.1 and 3.2 can be directly extended to the delayed CVRNNs in the continuous case by the same arguments which are utilized in above theorems.

4 A Numerical Example

To authenticate the effectiveness of the theoretical results in Sect. 3, let us consider the following example.

Example 4.1

For \(n=2\), the drive system (2.4) and the response system (2.6) of CVRNNs with the following parameters:

$$\begin{aligned} D= & {} \left( \begin{array}{ccc} 3 &{} 0 \\ 0 &{} 3 \end{array} \right) , A=\left( \begin{array}{ccc} 0.25-0.6\mathrm{i} &{} -\,1.4+1.5\mathrm{i} \\ -\,2-0.8\mathrm{i} &{} -\,2.2+0.2\mathrm{i} \end{array} \right) , B=\left( \begin{array}{ccc} 1.2+1.1\mathrm{i} &{} -\,1.2-\mathrm{i} \\ 0.8-0.8\mathrm{i} &{} 0.2-0.5\mathrm{i} \end{array} \right) ,\\ I= & {} \left( \begin{array}{ccc} 0.5+\mathrm{i} \\ 0.4+0.6\mathrm{i} \end{array} \right) , \tau =0.5, \end{aligned}$$

the discontinuous complex-valued activation function is:

$$\begin{aligned} f_{k}(s)=\left\{ \begin{array}{ll} -(\mathrm{Re}(s)+1)-(\mathrm{Im}(s)+1)\mathrm{i},\quad \mathrm{Re}(s)<0\ \mathrm{and}\ {\mathrm{Im}(s)<0},\\ -(\mathrm{Re}(s)+1)+(\mathrm{Im}(s)+1)\mathrm{i},\quad \mathrm{Re}(s)<0\ \mathrm{and}\ {\mathrm{Im}(s)>0},\\ (\mathrm{Re}(s)+1)-(\mathrm{Im}(s)+1)\mathrm{i},\quad \mathrm{Re}(s)>0\ \mathrm{and}\ {\mathrm{Im}(s)<0},\\ (\mathrm{Re}(s)+1)+(\mathrm{Im}(s)+1)\mathrm{i},\quad \mathrm{Re}(s)>0\ \mathrm{and}\ {\mathrm{Im}(s)>0}. \end{array} \quad k=1,2. \right. \end{aligned}$$
(4.1)

The state feedback controllers are designed as:

$$\begin{aligned} \left\{ \begin{array}{ll} u_{1}^{R}(t)=-9.6e_{1}^{R}(t)-17\text {sign}(e_{1}^{R}(t)),\\ u_{2}^{R}(t)=-10.95e_{1}^{R}(t)-15.5\text {sign}(e_{2}^{R}(t)), \end{array} \right. \end{aligned}$$
(4.2)

and

$$\begin{aligned} \left\{ \begin{array}{ll} u_{1}^{I}(t)=-9.3e_{1}^{I}(t)-17\text {sign}(e_{1}^{I}(t)),\\ u_{2}^{I}(t)=-9.53e_{1}^{I}(t)-15.5\text {sign}(e_{2}^{I}(t)), \end{array} \right. \end{aligned}$$
(4.3)

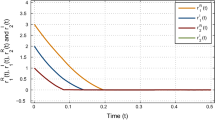
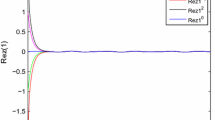
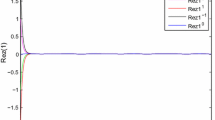
where \(e_{j}^{R}(t)=\tilde{x}_{j}(t)-x_{j}(t), e_{j}^{I}(t)=\tilde{y}_{j}(t)-y_{j}(t), j=1,2.\) It is readily seen that the activation function (4.1) satisfies (2.7) with \(\lambda _{k}^{RR}=1, \lambda _{k}^{RI}=0, \mu _{k}^{R}=2, \lambda _{k}^{IR}=0, \lambda _{k}^{II}=1, \mu _{k}^{I}=2, k=1,2.\) In addition, we take the initial conditions of (2.4) and (2.5) as \(z_{1}(s)=-\,4+\mathrm{i}, z_{2}(s)=2-4\mathrm{i}, \tilde{z}_{1}(s)=2-\mathrm{i}, \tilde{z}_{2}(s)=3+\mathrm{i}, s\in [-\,0.5, 0]\), respectively. One can easily verify that all the conditions in Theorem 3.1 hold. Therefore, we can conclude from Theorem 3.1 that drive system (2.4) and response system (2.5) are globally exponentially synchronized under the designed state feedback controllers (4.2)–(4.3). Figure 1 shows the state trajectories of synchronization errors \(e_{i}^{R}(t)\) and \(e_{i}^{I}(t), i=1,2\), respectively.

Fig. 1
figure 1

The real and imaginary parts of synchronization errors

Full size image

It is easy to see from Fig. 1 that the systems (2.4) and (2.5) with the network parameters and the controller above are globally exponentially synchronized. This is in accordance with the conclusion of Theorem 3.1.

5 Conclusion

In this paper, based on the theories of differential inclusions, and inequality techniques, we have discussed the global exponential synchronization problem for delayed CVRNNs with discontinuous activations. Under the framework of drive-response scheme, by designing some novel state feedback controllers to the response system, new criteria have been established such that the drive CVRNNs globally exponentially synchronize with the response CVRNNs. Finally, a numerical example is presented to substantiate the effectiveness of the proposed theoretical results.

We would also like to point out that it is interesting and challenging to consider more different delays, such as infinitely distributed delay, leakage delays or proportional delays, and their effects on synchronization dynamics of CVNNs with discontinuities. Another interesting yet challenging problem is to study synchronization dynamics of reaction-diffusion CVNNs with discontinuities. These problems are our future research directions.