1 Introduction

Recurrently, connected neural network has been extensively investigated in various science and engineering fields such as pattern classification, parallel computation, signal processing, associative memories, and solving some complicated optimization problems [1,2,3,4]. In these applications, which are depended on the dynamical behaviors of neural networks. Hence, it is extremely important to study the dynamical behaviors of neural networks in the practical design. For instance, when solving a periodic oscillation problem by neural networks, there must translate into considering dynamical behaviors for networks. As is well known that the research on neural networks not only involve discussion of stability property, but also involve other dynamical behaviors as bifurcation, periodic oscillatory, and chaos. In some applications, the properties of almost periodic solutions are very interest and important. Thus, it is great significant to study the almost periodic solution of the neural networks.

The complex-valued neural networks is an extension of real-valued neural networks, which have been presented and investigated, see [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Compared with real-valued neural networks, complex-valued neural networks have specific different from those in real-valued connected neural networks. In general, complex-valued neural networks have more complicated than the real-valued ones in some aspects. For the practical applications in physical systems, complex-valued neural networks become strongly desired. For example, light, quantum waves, ultrasonic, and electromagnetic [23, 24]. Therefore, it is necessary and vital to discuss the dynamical behaviors of complex-valued neural networks such as the stability of almost periodic solution. However, to the best of the authors’ knowledge, almost periodic solution for delayed complex-valued neural networks was seldom investigated.

It is well known that activation functions play a vital part in the dynamical behaviors of neural networks. As often, activation functions of neural networks are assumed to be continuous, bounded, globally Lipschitz, even smooth. Dynamical behaviors of neural networks depend on the structures of activation functions. In the past few years, there have two kinds of activation functions considered for neural network, i.e. continuous activation function and discontinuous activation functions. As pointed by Forti and Nistri [25], connected neural networks with discontinuous activation functions are important and do frequently arise in practical application when handling with dynamical systems with discontinuous right-hand sides. For this reason, much efforts has been committed to analyzing the dynamical behavior of the neural networks with discontinuous activation functions [26,27,28,29]. However, almost periodic dynamical behaviors for delayed complex-valued neural networks with discontinuous activation functions was seldom investigated.

Unfortunately, time delays are often arise in many practical applications of neural networks because of the finite switching speed of amplifiers and propagation time, such as control, signal processing, associative memory, and pattern recognition. In the past few years, there have a lot of articles on considering the dynamical behaviors for delayed complex-valued neural networks, see [30,31,32]. Time delays is a origin of instability and oscillation in neural networks. Moreover, the stability analysis is a prime research topic in neural networks theory. Therefore, it is important and necessary to study the dynamical behaviors of complex-valued neural networks with time delays, as the existence, uniqueness, and stability of almost periodic solutions.

From many applications, we know that almost periodic oscillatory is an universal phenomenon in the real world, it is more actual than others. In the dynamical behavior point of view, periodic parameters of dynamical networks often turn out to experience uncertain perturbations. That is, parameter can be taken as a periodic small error. The almost periodic neural networks are regard as a natural extension of the periodic ones, and which is more accordant with reality. Considering the importance of almost periodic property, much more efforts have been devoted to researching almost periodic the dynamical behaviors of connected neural networks, see [30, 31, 33,34,35,36,37,38]. Based on a fixed theorem and stability definition, Huang and Hu considered the multistability problem of delayed complex-valued neural networks with discontinuous real-imaginary-type activation functions [39]. In [40], Liang et al. study the multistability of complex-valued neural networks with discontinuous activation functions. Wang et al. researched the dynamical behavior of Complex-Valued Hopfield neural networks with discontinuous activation functions [41]. In [42], Yan researched the almost periodic dynamics of the delayed complex-valued recurrent neural networks with discontinuous activation functions. Compared with the almost periodic dynamics of real-valued neural networks, complex-valued are more complicated and suitable. However, to the best of our knowledge, almost periodic dynamics for complex-valued recurrent neural networks was seldom considered.

This paper investigates the almost periodic dynamical behaviors for complex-valued neural networks with discontinuous activation functions. The highlights of this paper are listed as follows: Firstly, The almost periodic solution is proposed in the complex domain, which is more feasible in practice compared to the periodical scheme. Furthermore, we considered decomposing complex-valued neural networks into real-valued, which the activation function has continuous real part and discontinuous imaginary. Secondly, the decomposed activation function is not assumed monotonous. Under these circumstances, we reconsider almost periodic dynamical behaviors by generalized Lyapunov function method. Lastly, the almost periodic dynamics for complex-valued neural networks with discontinuous functions is investigated, and some judgment conditions are obtained. the issue of time-varying delay is also considered, which make our research have more general significance.

The structure of the remaining paper is organized as follows. In Sect. 2, Complex-valued neural networks is formulated, and some preliminaries are presented. In Sect. 3, the existence of almost periodic solution for the dynamic system is obtained via some assumptions of activation functions. In Sect. 4, the uniqueness and global exponential stability of almost periodic solution are achieved. In Sect. 5, an example is presented to explicate the validity of our theoretical results. Lastly, some conclusions are shown in Sect. 6.

Notations The notations are quite standard in this paper. \(\Vert z\Vert \) denote the 1-norm of vector \(z(t)=\left( z_{1}(t),z_{2}(t),\ldots ,z_{n}(t)\right) ^{T}\in \mathbb {C}^{n}, \Vert z(t)\Vert =\left\{ \sum \nolimits _{j=1}^{n}\xi _{j}|z_{j}^{R}(t)|+\sum \nolimits _{j=1}^{n}\phi _{j}|z_{j}^{I}(t)|\right\} \) where \(\xi _{j}, \phi _{j}>0, j=1,2,\ldots ,n\). \(\overline{co}(E)\) is the closure of the convex hull of some set E. \(B(x,\delta )\) denotes the open \(\delta \)-neighborhood of a set \(x\subset R^{n}: B(x,\delta )=\{y\in R^{n}:\inf \limits _{z\in x}\Vert y-z\Vert <\delta \}\) for some \(\Vert \cdot \Vert ,~C([0,T],R^{n}),\ L^{1}([0,T],R^{n})\), and \(L^{\infty }([0,T],R^{n})\) are the spaces of continuous vector function, square integrable vector function, and essentially bounded function on [0, T], respectively. Z denotes the integer.

2 Model Formulation and Preliminaries

Consider the complex-valued dynamical networks with almost periodic coefficients described by the following delayed integro-differential equations:

$$\begin{aligned} \frac{dz_{j}(t)}{dt}= & {} -\,d_{j}(t)z_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}(t)f_{k}(z_{k}(t))\nonumber \\&+\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}(z_{k}(t-s)) d_{s}K_{jk}(t,s)+u_{j}(t), \quad j=1,2,\ldots ,n, \end{aligned}$$
(1)

where \(j=1, 2, \ldots , n\) \(z_{j}(t)\in \mathbb {C}\) is the state of the j-th neuron at time t; \(d_{j}(t)>0\) represents the positive rate with which the j-th unit will reset its potential to the resting state in isolation when disconnected from the network; \(f_{j}(\cdot ):\mathbb {C}\rightarrow \mathbb {C}\) are complex-valued activation functions; \(a_{jk}(t)\in \mathbb {C}\) are the connection strength of the k-th neuron on the j-th neuron; \(d_{s}K_{jk}(t,s)\) are Lebesgue-Stieltjes measures with respect to s.

Assumption 1

Let \(z=z^{R}+iz^{I}\), \(f_{j}(z)\) can be decomposed to its real and imaginary parts as \(f_{j}(z)=f_{j}^{R}(z^{R})+if_{j}^{I}(z^{I})\), where \(f_{j}^{R}(\cdot )\) is continuous on any compact interval of R, and \(f_{j}^{I}(\cdot )\) is continuous except on a finite number set of isolation points \(\{\rho _{k}^{j}: \rho _{k}^{j}<\rho _{k+1}^{j}, k\in \mathbb {Z}\}\), where \(f_{j}^{I}(\cdot )=g_{j}(\cdot )+h_{j}(\cdot )\), \(g_{j}\) is a monotonic continuous on R and \(h_{j}\) is continuous except on a countable set of isolation points \(\{\rho _{k}^{j}\}\), \(f_{j}^{R}(\cdot ), g_{j}(\cdot )\) are local Lipschizan, i.e., for any \(\zeta ,\varsigma \in (\rho _{k}^{j},\rho _{k+1}^{j})\) there exists positive constants \(L_{j}^{f}\) and \(L_{j}^{g}\), \(j=1,2,\ldots ,n\), such that \(|f_{j}^{R}(\zeta )-f_{j}^{R}(\varsigma )|\le L_{j}^{f}|\zeta -\varsigma |, \ |g_{j}(\zeta )-g_{j}(\varsigma )|\le L_{j}^{g}|\zeta -\varsigma |\).

Denote \(z_{j}(t)=x_{j}(t)+iy_{j}(t)\) with \(x_{j}(t)\) and \(y_{j}(t)\in R\), then the network (1) can be rewritten in the equivalent forms as follows:

$$\begin{aligned} \frac{dx_{j}(t)}{dt}=&-d_{j}(t)x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{R}(x_{k}(t))- \sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{I}(y_{k}(t))\nonumber \\&+\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j}^{R}(t), \end{aligned}$$
(2a)
$$\begin{aligned} \frac{dy_{j}(t)}{dt}=&-d_{j}(t)y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{I}(y_{k}(t))+ \sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{R}(x_{k}(t))\nonumber \\&+\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{I}(y_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j}^{I}(t). \end{aligned}$$
(2b)

The following assumptions are also needed for the systems (2a)–(2b).

Assumption 2

\(d_{j}(t), a_{jk}^{R}(t), a_{jk}^{I}(t), u_{j}^{R}(t), u_{j}^{I}(t), d_{s}K_{jk}(t,s)\) are all continuous almost functions on R. i.e., for any \(\varepsilon >0\), there exists \(l=l(\varepsilon )>0\), for any interval \([\alpha ,\alpha +l]\) containing \(\omega \), such that

$$\begin{aligned}&|d_{j}(t+\omega )-d_{j}(t)|<\varepsilon , \quad \left| a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right|<\varepsilon , \quad \left| a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right|<\varepsilon ,\\&\left| u_{j}^{R}(t+\omega )-u_{j}^{R}(t)\right|<\varepsilon , \quad \left| u_{j}^{R}(t+\omega )-u_{j}^{R}(t)\right|<\varepsilon , \quad \int _{0}^{\infty }\left| d_{s}K_{jk}(t+\omega )-d_{s}K_{jk}(t,s)\right| <\varepsilon , \end{aligned}$$

hold for all \(j,k=1,2,\ldots ,n\) and \(t\in R\). Moreover, \(d_{s}K_{jk}(t,s)\) is dominated by some Lebesgue-Stieltjes \(d\overline{K}_{jk}(s)\) independent of t, i.e., \(\int _{0}^{+\infty }f(s)|d_{s}K_{jk}(t,s)|<\int _{0}^{+\infty }f(s)|d\overline{K}_{jk}(s)|\), where f(s) is any nonnegative measurable function.

Assumption 3

There exist positive constant \(\xi _{j}, \phi _{j}>0\) and \(d_{j}(t)>\delta >0\) such that \(\Gamma _{j}^{1}(t)<0, \Gamma _{j}^{2}(t)<0\) and \(\Upsilon _{j}^{1}(t)<0\),

where \(j=1,2,\ldots ,n\)

$$\begin{aligned} \Gamma _{j}^{1}(t)= & {} (- \,d_{j}(t)+\delta )\xi _{j}+\xi _{j}a_{jj}^{R}(t)L_{j}^{f}+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}L_{j}^{f}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}L_{j}^{f}\left| a_{kj}^{I}(t)\right| \\&+\,\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{f}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \\ \Gamma _{j}^{2}(t)= & {} (- \, d_{j}(t)+\delta )\phi _{j} +\phi _{j}a_{jj}^{R}(t)L_{j}^{g}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| L_{j}^{g}+\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{g}\left| a_{kj}^{I}(t)\right| \\&+\,\sum \limits _{k=1}^{n}\phi _{k}L_{j}^{g}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \\ \Upsilon _{j}^{1}(t)= & {} \xi _{j}a_{jj}^{I}(t)+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| +\phi _{j}a_{jj}^{R}(t)+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| \\&+\,\sum \limits _{k=1}^{n}\phi _{k}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \end{aligned}$$

Definition 1

For given continuous functions \(\theta _{k}(s)\) and \(\varphi _{k}(s)\) defined on \((-\infty , 0]\) as well as the measurable functions \(\upsilon _{k}(s)\in \overline{co}[f_{k}^{I}(\varphi _{k}(s))]\) for almost all \(s\in (-\infty , 0]\), the absolute continuous function \(z(t)=x(t)+iy(t)\) with \(x_{k}(s)=\theta _{k}(s)\), \(y_{k}(s)=\varphi _{k}(s)\) for all \(s\in (-\infty , 0]\) is said to be a solution of the systems (2a)–(2b) on [0, T] if there exist measurable function \(\gamma _{k}^{I}(t)\in \overline{co}[f_{k}^{I}(y_{k}(t)]\) for almost all \(t\in [0,T]\) such that

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dx_{j}(t)}{dt}=-\,d_{j}(t)x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{R}(x_{k}(t))-\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\gamma _{k}(t)\\ \qquad \qquad \quad +\,\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j}^{R}(t)\quad a.e.~t\in [0,T)\\ \frac{dy_{j}(t)}{dt}=-\,d_{j}(t)y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\gamma _{k}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{R}(x_{k}(t))\\ \qquad \qquad \quad +\,\sum \limits _{k=1}^{n}\int _{0}^{\infty }\gamma _{k}((t-s))d_{s}K_{jk}(t,s)+u_{j}^{I}(t)\quad a.e.~t\in [0,T)\\ \end{array} \right. \end{aligned}$$
(3)

and \(\gamma _{k}(s)=\upsilon _{k}(s)\) for almost all \(s\in (-\,\infty , 0]\), where \(k=1,2,\ldots ,n\).

Definition 2

Let \(z^{*}(t)=\left( z_{1}^{*}(t),z_{2}^{*}(t),\ldots ,z_{n}^{*}(t)\right) ^{T}\) is a solution of the given initial value problem of system (1), \(z^{*}(t)\) is called to be globally exponentially stable, if for any solution \(z(t)=\left( z_{1}(t),z_{2}(t),\ldots ,z_{n}(t)\right) ^{T}\) of the dynamical system (1), i.e. there exist constants \(M>0\), and \(\delta >0\) such that

$$\begin{aligned} \Vert z(t)-z^{*}(t)\Vert \le Me^{-\delta t}, \quad t\ge t_{0}\ge 0. \end{aligned}$$

As introduced by Fink [43] and He [44], the following concept of almost periodic solution is presented.

Definition 3

[37] A continuous function \(z(t):R \rightarrow \mathbb {C}^{n}\) is said to be almost periodic function on R, if for any \(\varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0\), for any interval with length \(l(\varepsilon )\), there exist a number \(\omega =\omega (\varepsilon )\) in this interval \([\alpha ,\alpha +l]\), such that \(\Vert z(t+\omega )-z(t)\Vert <\varepsilon \), for all \(t\in R\).

A chain rule for computing the time derivative of the composed function \(V(q(t)):[0, +\,\infty )\rightarrow R\), where \(q(t):[0, +\,\infty )\rightarrow R^{n}\) is absolutely continuous on any compact interval \([0, +\,\infty )\).

Lemma 1

(Chain Rule) [37] Assume that \(V(t):R^{n}\rightarrow R\) is \(C-regular\), and that q(t) is absolutely continuous on any compact interval of \([0, +\,\infty )\), then q(t) and \(V(t):[0, +\,\infty )\rightarrow R^{n}\) are differential for \(a.e.\ t\in [0, +\,\infty )\) and we have

$$\begin{aligned} \frac{dV(q(t))}{dt}=\left\langle \varsigma (t),\frac{dq(t)}{dt}\right\rangle \quad \quad \varsigma (t)\in \partial V(q(t)). \end{aligned}$$

3 The Existence of Almost Periodic Solution for the Dynamic System

In this section, the existence of almost periodic solution of system (1) is considered primarily. We applied with a suitable Lyapunov function that some sufficient criteria are obtained to guarantee the existence of the almost periodic solution.

Lemma 2

Suppose that the Assumptions 1–3 are satisfied, then for any initial value of the dynamical system (1), there exists a solution \(z(t)=x(t)+\,iy(t)\) associated with a measurable function \(\gamma (t)\) a.e. \(t\in R\). Moreover, for any solution there exists constant \(M>0\), such that \(\Vert z(t)\Vert <M\), for \(t\in R\) and \(\Vert \gamma (t)\Vert <M\) for \(a.e.\ t\in R\).

Proof

Define set-valued map as follows:

$$\begin{aligned} \frac{dx_{j}(t)}{dt}\rightarrow & {} -\,d_{j}(t)x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{R}(x_{k}(t))- \sum \limits _{k=1}^{n}a_{jk}^{I}(t)\overline{co}\left[ f_{k}^{I}(y_{k}(t))\right] \\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j}^{R}(t)\\ \frac{dy_{j}(t)}{dt}\rightarrow & {} -\,d_{j}(t)y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\overline{co}\left[ f_{k}^{I}(y_{k}(t))\right] + \sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{R}(x_{k}(t))\\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }\overline{co}\left[ f_{k}^{I}(y_{k}(t-s))\right] d_{s}K_{jk}(t,s)+u_{j}^{I}(t), \end{aligned}$$

it is easy to see that this set-valued map are upper semi-continuous with nonempty compact convex values, which implies that the local solution x(t), y(t) of the (2a)–(2b) are obviously exist. That is to say that the initial valued problem of the systems (2a)–(2b) have at least a solution \(\left( x(t),y(t)\right) \) on [0, T) for some \(T\in (0, +\,\infty ]\). \(\square \)

Next, we will show that \(\lim \nolimits _{t\rightarrow T^{-}}\Vert z(t)\Vert <+\infty \) if \(T<+\infty \), which means that the maximal existing interval of z(t) can be extend to \(+\infty \). Note that \(f^{I}_{k}(y_{k}(t))=g_{k}(y_{k}(t))+h_{k}(y_{k}(t))\). There exists a vector function \(\eta (t)=\left( \eta _{1}(t),\eta _{2}(t),\ldots ,\eta _{n}(t)\right) ^{T}:(-\infty ,T)\rightarrow R^{n}\), such that \(\eta _{k}(t)+g_{k}(y_{k}(t))=\gamma _{k}(t)(k=1,2,\ldots ,n)\) where \(\eta _{k}(t)\in \overline{co}[h_{k}(y_{k}(t))]\), for \(a.e.\ t\in (-\,\infty , T)\).

Construct a function as follows:

$$\begin{aligned} V(t)=V_{1}(t)+V_{2}(t), \end{aligned}$$

where

$$\begin{aligned} V_{1}(t)= & {} \sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}|x_{j}(t)|+\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}|y_{j}(t)| \\ V_{2}(t)= & {} \sum \limits _{j,k=1}^{n}\xi _{j}\int _{0}^{\infty }\int _{t-s}^{t}\left| f_{k}^{R}(x_{k}(\rho ))\right| e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \\&\quad +\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }\int _{t-s}^{t}[|g_{k}(y_{k}(\rho ))|+|\eta _{k}(\rho )|] e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \end{aligned}$$

From (3), we obtained

$$\begin{aligned} \dot{x}_{j}(t)= & {} -\,d_{j}(t)x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{R}(x_{k}(t))-\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\gamma _{k}(t)\\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j}^{R}(t)\\= & {} -\,d_{j}(t)x_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{R}(x_{k}(t)) -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)[g_{k}(y_{k}(t))+\eta _{k}(t)]\\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j}^{R}(t)\\ \dot{y}_{j}(t)= & {} -\,d_{j}(t)y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\gamma _{k}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{R}(x_{k}(t))\\&+\,\sum \limits _{k=1}^{n}\int _{0}^{\infty }\gamma _{k}(t-s)d_{s}K_{jk}(t,s)+u_{j}^{I}(t)\\= & {} -\,d_{j}(t)y_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)[g_{k}(y_{k}(t))+\eta _{k}(t)]+ \sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{R}(x_{k}(t))\\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }[g_{k}(y_{k}(t-s))+\eta _{k}(t-s)]d_{s}K_{jk}(t,s)+u_{j}^{I}(t). \end{aligned}$$

Then, we have

$$\begin{aligned} |\dot{x}_{j}(t)|=v_{j}(t)\dot{x}_{j}(t), \quad |\dot{y}_{j}(t)|=w_{j}(t)\dot{y}_{j}(t), \end{aligned}$$

where \(v_{j}(t)=sign(x_{j}(t))\), if \(x_{j}(t)\ne 0\); \(x_{j}(t)\) can be arbitrarily select in \([-1,1]\), if \(x_{j}(t)=0\). In particular, we can select \(v_{j}(t)\) as follows

$$\begin{aligned} v_{j}(t)=\left\{ \begin{array}{ll} 0, &{}\qquad \qquad \qquad x_{j}(t)=\gamma _{j}(t)=0,\\ -sign\{\eta _{j}(t)\}, &{}\qquad \qquad \qquad x_{j}(t)=0, \gamma _{j}(t)\ne 0,\\ sign\{x_{j}(t)\}, &{}\qquad \qquad \qquad x_{j}(t)\ne 0.\\ \end{array} \right. \end{aligned}$$
(4)

Thus, we have

$$\begin{aligned} v_{j}(t)x_{j}(t)=|x_{j}(t)|,\quad v_{j}(t)\eta _{j}(t)=-|\eta _{j}(t)|,\quad j=1,2,\ldots ,n. \end{aligned}$$

Similarly, we can choose \(w_{j}(t)\) as follows

$$\begin{aligned} w_{j}(t)=\left\{ \begin{array}{ll} 0, &{}\qquad \qquad \qquad y_{j}(t)=\gamma _{j}(t)=0;\\ sign\{\eta _{j}(t)\}, &{}\qquad \qquad \qquad y_{j}(t)=0, \gamma _{j}(t)\ne 0;\\ sign\{y_{j}(t)\}, &{}\qquad \qquad \qquad y_{j}(t)\ne 0.\\ \end{array} \right. \end{aligned}$$
(5)

We have

$$\begin{aligned} w_{j}(t)y_{j}(t)=|y_{j}(t)|,\quad w_{j}(t)\eta _{j}(t)=|\eta _{j}(t)|,\quad j=1,2,\ldots ,n. \end{aligned}$$

Calculate the derivation of V(t) with respect to t along the solution trajectories of the systems (2a)–(2b) in the sense of (3) by using Lemma 1, one gets that

$$\begin{aligned} \dot{V}_{1}(t)= & {} \sum \limits _{j=1}^{n}\delta \xi _{j}e^{\delta t}|x_{j}(t)|+\sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}\frac{d|x_{j}(t)|}{dt}+\sum \limits _{j=1}^{n}\delta \phi _{j}e^{\delta t}|y_{j}(t)|+\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}\frac{d|y_{j}(t)|}{dt}\\= & {} \sum \limits _{j=1}^{n}\delta \xi _{j}e^{\delta t}|x_{j}(t)|+\sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}v_{j}(t)\dot{x}_{j}(t) {+}\sum \limits _{j=1}^{n}\delta \phi _{j}e^{\delta t}|y_{j}(t)|{+}\,\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}w_{j}(t)\dot{y}_{j}(t)\\\le & {} \sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}\left\{ (-d_{j}(t){+}\delta )|x_{j}(t)|+a_{jj}^{R}(t)\left| f_{j}^{R}(x_{j}(t))\right| {+}\sum \limits _{k=1,k\ne j}^{n}\left| a_{jk}^{R}(t)\right| \left| f_{k}^{R}(x_{k}(t))\right| \right. \\&\quad +\,a_{jj}^{I}(t)|\eta _{j}(t)|+\sum \limits _{k=1,k\ne j}^{n}\left| a_{jk}^{I}(t)\right| |\eta _{k}(t)|+\sum \limits _{k=1}^{n}\left| a_{jk}^{I}(t)\right| |g_{k}(y_{k}(t))|\\&\quad +\left. \sum \limits _{k=1}^{n}\int _{0}^{\infty }\left| f_{k}^{R}(x_{k}(t-s))\right| d_{s}K_{jk}(t,s)+\left| u_{j}^{R}(t)\right| \right\} \\&\quad +\,\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}\left\{ (-d_{j}(t)+\delta )|y_{j}(t)|\right. \\&\quad +\,\sum \limits _{k=1}^{n}\left| a_{jk}^{R}(t)\right| |g_{k}(y_{k}(t))|+a_{jj}^{R}(t)|\eta _{j}(t)|+\sum \limits _{k=1,k\ne j}^{n}\left| a_{jk}^{R}(t)\right| |\eta _{k}(t)|\\&\quad +\,a_{jj}^{R}(t)|g_{j}(y_{j}(t))|+\sum \limits _{k=1}^{n}\left| a_{jk}^{I}(t)\right| |f_{k}(x_{k}(t))|\\&\quad +\,\left. \sum \limits _{k=1}^{n}\int _{0}^{\infty }|\gamma _{k}(t-s)|d_{s}K_{jk}(t,s)+\left| u_{j}^{I}(t)\right| \right\} \\\le & {} \sum \limits _{j=1}^{n}e^{\delta t}\left\{ (-d_{j}(t)+\delta )\xi _{j}+\xi _{j}a_{jj}^{R}(t)L_{j}^{f}\right. \\&\quad +\,\left. \sum \limits _{k=1,k\ne j}^{n}\xi _{k}L_{j}^{f}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}L_{j}^{f}\left| a_{kj}^{I}(t)\right| \right\} |x_{j}(t)|\\&\quad +\,\sum \limits _{j=1}^{n}e^{\delta t}\left\{ \xi _{j}a_{jj}^{I}(t)\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| +\phi _{j}a_{jj}^{R}(t)\right. \end{aligned}$$
$$\begin{aligned}&\quad +\,\left. \sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| \right\} |\eta _{j}(t)|\\&\quad +\,\sum \limits _{j=1}^{n}e^{\delta t}\left\{ (-d_{j}(t)+\delta )\phi _{j}+\phi _{j}a_{jj}^{R}(t)L_{j}^{g}\right. \\&\quad +\,\left. \sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| L_{j}^{g}+\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{g}\left| a_{kj}^{I}(t)\right| \right\} |y_{j}(t)|\\&\quad +\,\sum \limits _{j=1}^{n}e^{\delta t}\left\{ \sum \limits _{k=1}^{n}\xi _{j}\int _{0}^{\infty }\left| f_{k}^{R}(x_{k}(t-s))\right| d_{s}K_{jk}(t,s)\right. \\&\quad +\,\left. \sum \limits _{k=1}^{n}\phi _{j}\int _{0}^{\infty } |\gamma _{k}(t-s)|d_{s}K_{jk}(t,s)\right\} \\&\quad +\,\sum \limits _{j=1}^{n}e^{\delta t}\left\{ \xi _{j}\left| u_{j}^{R}(t)\right| +\phi _{j}\left| u_{j}^{I}(t)\right| \right\} \end{aligned}$$

Let us continue to calculate the derivative of \(V_{2}(t)\).

$$\begin{aligned} \dot{V}_{2}(t)= & {} \sum \limits _{j,k=1}^{n}\xi _{j}\int _{0}^{\infty }\left| f_{k}^{R}(x_{k}(t))\right| e^{\delta (t+s)}d_{s}\left| \overline{K}_{jk}(s)\right| \\&\quad -\sum \limits _{j,k=1}^{n}\xi _{j}\int _{0}^{\infty }\left| f_{k}^{R}(x_{k}(t-s))\right| e^{\delta t}d_{s}\left| \overline{K}_{jk}(s)\right| \\&\quad +\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }[|g_{k}(y_{k}(t))|+|\eta _{k}(t)|]e^{\delta (t+s)}d_{s}\left| \overline{K}_{jk}(s)\right| \\&\quad -\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }[|g_{k}(y_{k}(t-s))|+|\eta _{k}(t-s)|]e^{\delta t}d_{s}\left| \overline{K}_{jk}(s)\right| \\ \end{aligned}$$

Therefore,

$$\begin{aligned} \dot{V}(t)= & {} \dot{V}_{1}(t)+\dot{V}_{2}(t) \nonumber \\\le & {} \sum \limits _{j=1}^{n}e^{\delta t}\left\{ (-d_{j}(t)+\delta )\xi _{j}+\xi _{j}a_{jj}^{R}(t)L_{j}^{f}+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}L_{j}^{f}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}L_{j}^{f}\left| a_{kj}^{I}(t)\right| \right. \nonumber \\&\quad +\left. \sum \limits _{k=1}^{n}\xi _{k}L_{j}^{f}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \right\} |x_{j}(t)|+\sum \limits _{j=1}^{n}e^{\delta t}\left\{ \xi _{j}a_{jj}^{I}(t)+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| \right. \nonumber \\&\quad +\left. \phi _{j}a_{jj}^{R}(t)+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \right\} |\eta _{j}(t)| \nonumber \\&\quad {+}\sum \limits _{j=1}^{n}e^{\delta t}\left\{ (-d_{j}(t){+}\delta )\phi _{j}{+}\phi _{j}a_{jj}^{R}(t)L_{j}^{g}{+}\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| L_{j}^{g}\right. {+}\sum \limits _{k{=}1}^{n}\xi _{k}L_{j}^{g}\left| a_{kj}^{I}(t)\right| \nonumber \\&\quad +\left. \sum \limits _{k=1}^{n}\phi _{k}L_{j}^{g}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \right\} |y_{j}(t)|+\sum \limits _{j=1}^{n}e^{\delta t}\left\{ \xi _{j}\left| u_{j}^{R}(t)\right| +\phi _{j}\left| u_{j}^{I}(t)\right| \right\} \nonumber \\= & {} \sum \limits _{j=1}^{n}e^{\delta t}\Gamma _{j}^{1}(t)|x_{j}(t)|+\sum \limits _{j=1}^{n}e^{\delta t}\Gamma _{j}^{2}(t)|y_{j}(t)|+\sum \limits _{j=1}^{n}e^{\delta t}\Upsilon _{j}^{1}(t)|\eta _{j}(t)| \nonumber \\&\quad +\sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}\left| u_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}\left| u_{j}^{I}(t)\right| \end{aligned}$$
(6)

It follows form the Assumption 3 and (6) that

$$\begin{aligned} \frac{dV(t)}{dt}\le e^{\delta t}\widehat{u}, \qquad for\quad a.e.\quad t\in [0,+\infty ), \end{aligned}$$

where \(\widehat{u}=\sup \limits _{t\ge 0}\Vert u(t)\Vert <+\infty ,\ u(t)=\left( u_{1}(t),u_{2}(t),\cdots ,u_{n}(t)\right) ^{T}\), which implies that

$$\begin{aligned} V(t)\le V(0)+\frac{1}{\delta }\widehat{u}e^{\delta t}. \end{aligned}$$
(7)

Combining the definition of V(t) and (7), one has

$$\begin{aligned} \Vert z(t)\Vert \le e^{-\delta t}V(t)\le V(0)+\frac{1}{\delta }\widehat{u}. \end{aligned}$$

Thus, there exists constant \(M'=V(0)+\frac{1}{\delta }\widehat{u}\), such that \(\Vert z(t)\Vert <M'\), for \(t\in R\). Furthermore, \(\lim \limits _{t\rightarrow T^{-}}\Vert z(t)\Vert <+\,\infty \), which means \(T=+\,\infty \). That is to say that the dynamical system (1) has a global solution for any initial valued problem.

Moreover, we have

$$\begin{aligned} \Vert z(t)\Vert =\sum \limits _{j=1}^{n}\xi _{j}|x_{j}(t)|+\sum \limits _{j=1}^{n}\phi _{j}|y_{j}(t)|\le M_{0}, \quad t\in R, \end{aligned}$$
(8)

where \(M_{0}=V(0)+\frac{1}{\delta }\widehat{u}+\Vert \theta \Vert \). \(\Vert \theta \Vert =\sup \nolimits _{-\infty \le s\le 0}\left\{ \sum \limits _{k=1}^{n}\xi _{k}|x_{j}(s)|+\sum \limits _{k=1}^{n}\phi _{k}|y_{j}(s)|\right\} \).

Due to \(f_{j}^{I}(\cdot )\) have finite number of discontinuous points on any compact interval of R. In speciality, \(f_{j}^{I}(\cdot )\) have finite number of discontinuous points on compact interval \([-\,M_{0},M_{0}]\). Without loss of generality, we select discontinuous points \(\{\rho _{k}^{j}:k=1,2,\ldots ,l_{j}\}\) of \(f_{j}^{I}(\cdot )\) on the interval \([-\,M_{0},M_{0}]\), and satisfied \(-\,M_{0}<\rho _{1}^{j}<\rho _{2}^{j}<\cdots<\rho _{l_{j}}^{j}<M_{0}\). First, let us consider a series of continuous function of \(f_{j}^{I}(\cdot )\) as follows:

$$\begin{aligned} f_{j}^{1}(y)= & {} \left\{ \begin{array}{ll} f_{j}^{I}(y), &{}\qquad \qquad \quad y\in \left. \left[ -M_{0},\rho _{1}^{j}\right. \right) ,\\ f_{j}^{I}\left( \rho _{1}^{j}-0\right) , &{}\qquad \qquad \quad y=\rho _{1}^{j};\\ \end{array} \right. \\ f_{j}^{k}(y)= & {} \left\{ \begin{array}{ll} f_{j}^{I}\left( \rho _{k-1}^{j}-0\right) , &{}\qquad \qquad y=\rho _{k-1}^{j},\\ f_{j}^{I}(y), &{}\qquad \qquad y\in \left( \rho _{k-1}^{j},\rho _{k}^{j}\right) ,\\ f_{j}^{I}\left( \rho _{k}^{j}+0\right) , &{}\qquad \qquad y=\rho _{k}^{j};\\ \end{array} \right. \ k=2,\ldots ,l_{j}-1.\\ f_{j}^{l_{j}}(y)= & {} \left\{ \begin{array}{ll} f_{j}^{I}\left( \rho _{l_{j}}^{j}+0\right) , &{}\qquad \qquad \quad y=\rho _{l_{j}}^{j},\\ f_{j}^{I}(y),&{}\qquad \qquad \quad y\in \left. \left( \rho _{l_{j}}^{j},M_{0}\right. \right] . \\ \end{array} \right. \end{aligned}$$

Denote

$$\begin{aligned} M_{j}^{1}=\max \left\{ \max \limits _{y\in \left[ -M_{0},\rho _{1}^{j}\right] }\left\{ f_{j}^{1}(y)\right\} ,\max \limits _{2\le k\le l_{j}-1}\left\{ \max \limits _{y\in \left[ \rho _{k-1}^{j},\rho _{k}^{j}\right] }\left\{ f_{j}^{k}(y)\right\} \right\} ,\max \limits _{y\in \left[ \rho _{l_{j}}^{j},M_{0}\right] }\left\{ f_{j}^{l_{j}}(y)\right\} \right\} \end{aligned}$$

and

$$\begin{aligned} m_{j}^{1}=\min \left\{ \min \limits _{y\in \left[ -M_{0},\rho _{1}^{j}\right] }\left\{ f_{j}^{1}(y)\right\} ,\min \limits _{2\le k\le l_{j}-1}\left\{ \min \limits _{y\in \left[ \rho _{k-1}^{j},\rho _{k}^{j}\right] }\left\{ f_{j}^{k}(y)\right\} \right\} ,\min \limits _{y\in \left[ \rho _{l_{j}}^{j},M_{0}\right] }\left\{ f_{j}^{l_{j}}(y)\right\} \right\} . \end{aligned}$$

It easy to see that

$$\begin{aligned} \left| \overline{co}\left[ f_{j}^{I}(y_{j}(t))\right] \right| \le \max \left\{ \left| M_{j}^{1}\right| ,\left| m_{j}^{1}\right| \right\} , \quad j=1,2,\ldots ,n. \end{aligned}$$

Note that \(\gamma _{j}(t)\in \overline{co}[f_{j}^{I}(y_{j}(t))]\), for \(a.e.\ t\in R\) and \(j=1,2,\ldots ,n\). Thus \(|\gamma _{j}(t)|\le \max \{|M_{j}^{1}|,|m_{j}^{1}|\},\ for\ a.e.\ t\in R\), and \(j=1,2,\ldots ,n\),

which implies that

$$\begin{aligned} \Vert \gamma (t)\Vert \le \max \left\{ \sum \limits _{j=1}^{n}\left| M_{j}^{1}\right| ,\sum \limits _{j=1}^{n}\left| m_{j}^{1}\right| \right\} ,\quad j=1,\ldots ,n,\quad a.e.\quad t\in R. \end{aligned}$$
(9)

Let \(M=\max \left\{ M_{0},\sum \limits _{j=1}^{n}\left| M_{j}^{1}\right| ,\sum \limits _{j=1}^{n}\left| m_{j}^{1}\right| \right\} \). Hence, from (8) and (9), we have

$$\begin{aligned} \Vert z(t)\Vert \le M, \quad t\in R, \end{aligned}$$
(10)

and

$$\begin{aligned} \Vert \gamma (t)\Vert \le M, \quad t\in R. \end{aligned}$$
(11)

The proof of the Lemma 2 is complete.

Lemma 3

Suppose that the Assumptions 1–3 are satisfied, then any solution of system (1) in the sense of (3) is asymptotically almost periodic, i.e., for any \(\varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0\), for any interval with length \(l(\varepsilon )\), there exist a number \(\omega =\omega (\varepsilon )\) in this interval \([\alpha ,\alpha +l]\), such that

$$\begin{aligned} \Vert z(t+\omega )-z(t)\Vert \le \varepsilon \end{aligned}$$

hold for all \(t\ge T\).

Proof

Construct the following auxiliary functions

$$\begin{aligned} \epsilon _{j}^{1}(t,\omega )= & {} u_{j}^{R}(t+\omega )-u_{j}^{R}(t)-x_{j}(t+\omega )[d_{j}(t+\omega )-d_{j}(t)]\nonumber \\&\quad +\sum \limits _{k=1}^{n}\left[ a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right] f_{k}^{R}(x_{k}(t+\omega ))\nonumber \\&\quad -\sum \limits _{k=1}^{n}\left[ a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right] \gamma _{k}(t+\omega )\nonumber \\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(t+\omega -s))[d_{s}K_{jk}(t+\omega ,s)-d_{s}K_{jk}(t,s)] \end{aligned}$$
(12)
$$\begin{aligned} \epsilon _{j}^{2}(t,\omega )= & {} u_{j}^{I}(t+\omega )-u_{j}^{I}(t)-y_{j}(t+\omega )[d_{j}(t+\omega )-d_{j}(t)]\nonumber \\&\quad +\sum \limits _{k=1}^{n}\left[ a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right] \gamma _{k}(t+\omega )\nonumber \\&\quad +\sum \limits _{k=1}^{n}\left[ a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right] f_{k}^{R}(x_{k}(t+\omega ))\nonumber \\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }\gamma _{k}(t+\omega -s)[d_{s}K_{jk}(t+\omega ,s)-d_{s}K_{jk}(t,s)]. \end{aligned}$$
(13)

From the Assumption 2 and the boundedness of \(z(t), f^{R}(x)\) and \(\gamma (t)\), it easy to see that for any \(\varepsilon >0\), there exists \(l=l(\varepsilon )>0\) such that for any interval \([\alpha ,\alpha +l]\) containing at least one point \(\omega \) with satisfying the following inequalities:

$$\begin{aligned}&|d_{j}(t+\omega )-d_{j}(t)|<\frac{\delta \epsilon }{20nM\Delta }, \left| u_{j}^{R}(t+\omega )-u_{j}^{R}(t)\right|<\frac{\delta \epsilon }{20n\Delta },\\&\quad \left| u_{j}^{I}(t+\omega )-u_{j}^{I}(t)\right|<\frac{\delta \epsilon }{20n\Delta },\\&\left| a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right|<\frac{\delta \epsilon }{20n^{2}M\Delta }, \left| a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right|<\frac{\delta \epsilon }{20n^{2}M\Delta },\\&\int _{0}^{\infty }|d_{s}K_{jk}(t+\omega ,s)-d_{s}K_{jk}(t,s)|<\frac{\delta \epsilon }{20n^{2}M\Delta }. \end{aligned}$$

where \(\Delta \triangleq \max \limits _{1\le j\le n}\{\xi _{j},\phi _{j}\}\). Hence, we have

$$\begin{aligned} \left| \varepsilon _{j}^{1}(t,\omega )\right|< & {} \frac{\delta \epsilon }{4n\Delta }, \quad for \ a.e.\ t\in R \end{aligned}$$
(14)
$$\begin{aligned} \left| \varepsilon _{j}^{2}(t,\omega )\right|< & {} \frac{\delta \epsilon }{4n\Delta }, \quad for \ a.e.\ t\in R \end{aligned}$$
(15)

Denote \(\widehat{x}(t)=x(t+\omega )-x(t), \widehat{y}(t)=y(t+\omega )-y(t)\). It follows from (2a) and (2b) that

$$\begin{aligned} \frac{d\widehat{x}_{j}(t)}{dt}= & {} -\,d_{j}(t)\widehat{x}_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ f_{k}^{R}(x_{k}(t+\omega ))-f_{k}^{R}(x_{k}(t))\right] \\&\quad -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)[\gamma _{k}(t+\omega )-\gamma _{k}(t)]\\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }\left[ f_{k}^{R}(x_{k}(t+\omega -s))-f_{k}^{R}(x_{k}(t-s))\right] d_{s}K_{jk}(t,s)+\varepsilon _{j}^{1}(t,\omega )\\ \frac{d\widehat{y}_{j}(t)}{dt}= & {} -d_{j}(t)\widehat{y}_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)[\gamma _{k}(t+\omega )-\gamma _{k}(t)]\\&\quad +\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ f_{k}^{R}(x_{k}(t+\omega ))-f_{k}^{R}(x_{k}(t))\right] \\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }[\gamma _{k}(x_{k}(t+\omega -s))-\gamma _{k}(x_{k}(t-s))]d_{s}K_{jk}(t,s)+\varepsilon _{j}^{2}(t,\omega ) \end{aligned}$$

Consider the following candidate function:

$$\begin{aligned} L(t)=L_{1}(t)+L_{2}(t), \end{aligned}$$

where

$$\begin{aligned} L_{1}(t)= & {} \sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}\left| \widehat{x}_{j}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}\left| \widehat{y}_{j}(t)\right| \\ L_{2}(t)= & {} \sum \limits _{j,k=1}^{n}\xi _{j}\int _{0}^{\infty }\int _{t-s}^{t}\left| f_{k}^{R}(x_{k}(\rho +\omega ))-f_{k}^{R}(x_{k}(\rho ))\right| e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \\&\quad +\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }\int _{t-s}^{t}|g_{k}(y_{k}(\rho +\omega ))-g_{k}(y_{k}(\rho ))| e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \\&\quad +\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }\int _{t-s}^{t}|\eta _{k}(\rho +\omega )-\eta _{k}(\rho )|e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \end{aligned}$$

Let

$$\begin{aligned} \frac{d\left| \widehat{x}_{j}(t)\right| }{dt}= & {} v_{j}(t)\dot{\widehat{x}}_{j}(t),\\ \frac{d\left| \widehat{y}_{j}(t)\right| }{dt}= & {} w_{j}(t)\dot{\widehat{y}}_{j}(t) \end{aligned}$$

where \(v_{j}(t)=sign(x_{j}(t+\omega )-x_{j}(t))\), if \(x_{j}(t+\omega )\ne x_{j}(t)\); \(x_{j}(t+\omega )-x_{j}(t)\) can be arbitrarily select in \([-1,1]\), if \(x_{j}(t+\omega )=x_{j}(t)\). In particular, we can select \(v_{j}(t)\) as follows:

$$\begin{aligned} v_{j}(t)=\left\{ \begin{array}{ll} 0, &{}\quad x_{j}(t+\omega )-x_{j}(t)=\gamma _{j}(t+\omega )-\gamma _{j}(t)=0,\\ -sign\{\eta _{j}(t+\omega )-\eta _{j}(t)\}, &{}\quad x_{j}(t+\omega )=x_{j}(t), \gamma _{j}(t+\omega )\ne \gamma _{j}(t),\\ sign\{x_{j}(t+\omega )-x_{j}(t)\}, &{}\quad x_{j}(t+\omega )\ne x_{j}(t)x_{j}(t).\\ \end{array} \right. \end{aligned}$$
(16)

Thus, we have

$$\begin{aligned} v_{j}(t)\{x_{j}(t+\omega )-x_{j}(t)\}= & {} |x_{j}(t+\omega )-x_{j}(t)|,\\ v_{j}(t)\{\eta _{j}(t+\omega )-\eta _{j}(t)\}= & {} -|\eta _{j}(t+\omega )-\eta _{j}(t)|,\quad j=1,2,\ldots ,n. \end{aligned}$$

Similarly, we can choose \(w_{j}(t)\) as follows:

$$\begin{aligned} w_{j}(t)=\left\{ \begin{array}{ll} 0, &{}\quad y_{j}(t+\omega )-y_{j}(t)=\gamma _{j}(t+\omega )-\gamma _{j}(t)=0,\\ sign\{\eta _{j}(t+\omega )-\eta _{j}(t)\}, &{}\quad y_{j}(t+\omega )=y_{j}(t), \gamma _{j}(t+\omega )\ne \gamma _{j}(t),\\ sign\{y_{j}(t+\omega )-y_{j}(t)\}, &{}\quad y_{j}(t+\omega )\ne y_{j}(t).\\ \end{array} \right. \end{aligned}$$
(17)

We have

$$\begin{aligned} w_{j}(t)\{y_{j}(t+\omega )-y_{j}(t)\}= & {} |y_{j}(t+\omega )-y_{j}(t)|,\\ w_{j}(t)\{\eta _{j}(t+\omega )-\eta _{j}(t)\}= & {} |\eta _{j}(t+\omega )-\eta _{j}(t)|, \quad j=1,2,\ldots ,n. \end{aligned}$$

By the similar way utilized in Lemma 2, and combining the inequalities (14), (15), one has

$$\begin{aligned} {\begin{array}{ll} \frac{dL(t)}{dt}\le \frac{\delta }{2}\epsilon e^{\delta t},&{}\qquad \qquad for\quad a.e.\quad t\in \left[ \left. 0,+\infty \right) \right. .\\ \end{array}} \end{aligned}$$

Then

$$\begin{aligned} \Vert z(t+\omega )-z(t)\Vert \le e^{-\delta t}L(t)\le e^{-\delta t}L(0)+e^{-\delta t}\int _{0}^{t}\dot{L}(s)ds. \end{aligned}$$

Note that L(0) is constant, and we can pick a sufficiently large \(T>0\) such that

$$\begin{aligned} e^{-\delta t}L(0)<\frac{\varepsilon }{2}, \quad for \quad t\ge T. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \Vert z(t+\omega )-z(t)\Vert \le e^{-\delta t}L(0)+\frac{\varepsilon }{2}<\varepsilon , \quad for\ \ t\ge T. \end{aligned}$$

The proof of the Lemma 3 is completed. \(\square \)

Theorem 1

Suppose that the Assumptions 1–3 are satisfied, then system (1) has at least one almost periodic solution in the sense of (3).

Proof

Let z(t) be any solution of the neural network system (3). We can select a sequence \(\{t_{k}\}_{k\in N}\) satisfying \(\lim \nolimits _{k\rightarrow +\infty }t_{k}=+\infty \) and such that

$$\begin{aligned} \left| \varepsilon _{j}^{1}(t,t_{k})\right| \le \frac{1}{k}, \quad for \ \ t\in R, \end{aligned}$$
(18)

and

$$\begin{aligned} \left| \varepsilon _{j}^{2}(t,t_{k})\right| \le \frac{1}{k}, \quad for \ \ t\in R \end{aligned}$$
(19)

where \(j=1,2,\ldots ,n, \ \varepsilon _{j}^{1}(t,t_{k}), \varepsilon _{j}^{2}(t,t_{k})\) are the auxiliary functions (12) and (13) defined in the proof of Lemma 3.

It follows from (10) and (11) that there exists \(M^{*}>0\) such that \(|z'_{j}(t)|\le M^{*}\) for \(a.e.\ t\in R\). Thus, the sequence \(\{z(t+t_{k})\}_{k\in N}\) is equi-continuous and uniformly bounded. By the Arzela-Ascoli theorem and diagonal selection principle, we can choose a subsequence of \(\{t_{k}\}\) (still denoted by \(\{t_{k}\}\)), such that \(z(t+t_{k})\) converges uniformly to some absolutely continuous function \(z^{*}(t)\) on any compact interval [0, T].

Next, we will prove that \(z^{*}(t)\) is an almost periodic solution of system (1) in the sense (3). Firstly, we prove that \(z^{*}(t)\) is a solution of system (1) in the sense (3).

According to Lebesgue’s dominated convergence theorem, for any \(t\in R\), we have

$$\begin{aligned} z_{j}^{*}(t+l)-z_{j}^{*}(t)=&\lim \limits _{k\rightarrow +\infty }[z_{j}(t+t_{k}+l)-z_{j}(t+t_{k})] \\ =&\lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\dot{z}_{j}(\theta +t_{k})d\theta \\ =&\lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\dot{x}_{j}(\theta +t_{k})d\theta +\lim \limits _{k\rightarrow +\infty }i\int _{t}^{t+l}\dot{y}_{j}(\theta +t_{k})d\theta \\ =&\lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\left[ -d_{j}(\theta )x_{j}(\theta +t_{k})+\sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )f_{k}^{R}(x_{k}(\theta +t_{k}))\right. \\&\quad -\left. \sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )\gamma _{k}(\theta +t_{k})\right] +\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}(\theta +t_{k}-s))d_{s}K_{jk}(\theta ,s)\\&\quad +u_{j}^{R}(\theta )+\varepsilon _{j}^{1}(\theta ,t_{k})]d\theta \\&\quad +\lim \limits _{k\rightarrow +\infty }i\int _{t}^{t+l}\left[ -d_{j}(\theta )y_{j}(\theta +t_{k})+\sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )\gamma _{k}(\theta +t_{k})\right. \\&\quad +\left. \sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )f_{k}^{R}(x_{k}(\theta +t_{k}))\right] +\sum \limits _{k=1}^{n}\int _{0}^{\infty }\gamma _{k}(\theta +t_{k}-s)d_{s}K_{jk}(\theta ,s)\\&\quad +u_{j}^{I}(\theta )+\varepsilon _{j}^{2}(\theta ,t_{k})]d\theta \\ \end{aligned}$$
$$\begin{aligned} =&\int _{t}^{t+l}\left[ -d_{j}(\theta )x_{j}^{*}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )f_{k}^{R}(x_{k}^{*}(\theta ))-\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )\gamma _{k}^{*}(\theta )\right. \\&\quad +\left. \sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}^{*}(\theta -s))d_{s}K_{jk}(\theta ,s)+u_{j}^{R}(\theta )\right] d\theta \\&\quad +i\int _{t}^{t+l}\left[ -d_{j}(\theta )y_{j}^{*}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )\gamma _{k}^{*}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )f_{k}^{R}(x_{k}^{*}\theta )\right. \\&\quad +\left. \sum \limits _{k=1}^{n}\int _{0}^{\infty }\gamma _{k}^{*}(\theta -s)d_{s}K_{jk}(\theta ,s)+u_{j}^{I}(\theta )\right] d\theta \\&\quad +\lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\left[ \varepsilon _{j}^{1}(\theta ,t_{k})+i\varepsilon _{j}^{2}(\theta ,t_{k})\right] d\theta \end{aligned}$$

From (18) and (19), it is easy to conclude that

$$\begin{aligned} \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\left[ \varepsilon _{j}^{1}(\theta ,t_{k})+i\varepsilon _{j}^{2}(\theta ,t_{k})\right] d\theta =0. \end{aligned}$$
(20)

Therefore, it implied that the following equations hold

$$\begin{aligned} x_{j}^{*}(t+l)-x_{j}^{*}(t)= & {} \int _{t}^{t+l}\left[ -d_{j}(\theta )x_{j}^{*}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )f_{k}^{R}(x_{k}^{*}(\theta ))-\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )\gamma _{k}^{*}(\theta )\right. \\&\quad +\left. \sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}^{R}(x_{k}^{*}(\theta -s))d_{s}K_{jk}(\theta ,s)+u_{j}^{R}(\theta )\right] d\theta \\ y_{j}^{*}(t+l)-y_{j}^{*}(t)= & {} \int _{t}^{t+l}\left[ -d_{j}(\theta )y_{j}^{*}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )\gamma _{k}^{*}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )f_{k}^{R}(x_{k}^{*}(\theta )\right. \\&\quad +\left. \sum \limits _{k=1}^{n}\int _{0}^{\infty }\gamma _{k}^{*}(\theta -s)d_{s}K_{jk}(\theta ,s)+u_{j}^{I}(\theta )\right] d\theta \end{aligned}$$

Thence, \(z^{*}(t)=x^{*}(t)+iy^{*}(t)\) is a solution of system (1).

In the following, we claim that \(\gamma _{j}^{*}(t)\in \overline{co}[f_{j}^{I}(y_{j}^{*}(t))]\) for \(a.e.\ t\in R\), Note that y(t) converges to \(y^{*}(t)\) uniformly with respect to \(t\in R\) and \(\overline{co}[f_{j}^{I}(y_{j}^{*}(t))]\) are upper semi-continuous set-valued map, for any \(\varepsilon >0\), there exists \(N>0\) such that \(f^{I}(y(t+t_{k}))\in B(\overline{co}[f^{I}(y(t))],\varepsilon )\) for \(k>N\) and \(t\in R\). Since that \(\overline{co}[f^{I}(y(t))]\) is convex and compact, then \(\gamma (t)\in B(\overline{co}[f^{I}(y(t))],\varepsilon )\), which implies \(\gamma ^{*}_{j}(t)\in B(\overline{co}[f^{I}_{j}(y_{j}(t))],\varepsilon )\) holds for any \(t\in R\). Because of the arbitrary of \(\varepsilon \), we know that \(\gamma ^{*}_{j}(t)\in \overline{co}[f_{j}^{I}(y_{j}^{*}(t))]\) for \(a.e.\ t\in R\).

Secondly, we prove that \(z^{*}(t)=x^{*}(t)+iy^{*}(t)\) is an almost periodic solution of systems (1). By the Lemma 3, For any \(\varepsilon >0\), there exist \(T>0\) and \(l=l(\varepsilon )\) such that any interval \([\alpha ,\alpha +l]\) contains an \(\omega \) such that

$$\begin{aligned} \Vert z(t+\omega )-z(t)\Vert <\varepsilon \end{aligned}$$

hold for all \(t\ge T\). Therefore, there exists sufficiently large constant \(K>0\) such that

$$\begin{aligned} \Vert z(t+t_{k}+\omega )-z(t+t_{k})\Vert <\varepsilon \end{aligned}$$

holds for all \(k>K\) and \(t\in R\). As \(k\rightarrow +\infty \), we can conclude that\(\Vert z^{*}(t+\omega )-z^{*}(t)\Vert <\varepsilon \) for all \(t\in R\). This implies that \(z^{*}(t)\) is an almost periodic solution of the neural network system (1). The proof is complete. \(\square \)

4 The Uniqueness and Global Exponential Stability Analysis for Dynamical Networks

In this section, we will research the uniqueness and global exponential stability of almost periodic solution obtained in Sect. 3 for the dynamical networks (1). By utilizing a suitable Lyapunov function, some sufficient criteria are obtained to guarantee that networks has a uniqueness and global exponential stability almost periodic solution.

Theorem 2

Suppose that the Assumptions 1–3 are satisfied, then system (1) has a unique almost periodic solution, which is globally exponentially stable in the sense of (3).

Proof

Let \(z(t)=x(t)+iy(t)\) and \(\widetilde{z}(t)=\widetilde{x}(t)+i\widetilde{y}(t)\) be any two solutions of neural network system (1) associated with \(\gamma (t), \widetilde{\gamma }(t)\) and initial value pairs \((\psi ,\mu ), (\widetilde{\psi }, \widetilde{\mu })\) respectively. \(\square \)

Note that \(f^{I}_{j}=g_{j}+h_{j}\). There exists two vector functions \(\eta (t)=\left( \eta _{1}(t),\cdots ,\eta _{n}(t)\right) ^{T}\), and \(\widetilde{\eta }(t)=\left( \widetilde{\eta }_{1}(t),\ldots ,\widetilde{\eta }_{n}(t)\right) \) such that \(\eta _{j}(t)+g_{j}(y_{j}(t))=\gamma _{j}(t), \widetilde{\eta }_{j}(t)+g_{j}(\widetilde{y}_{j}(t))=\widetilde{\gamma }_{j}(t),\ (j=1,2,\ldots ,n)\), where \(\eta _{j}(t)\in \overline{co}[h_{j}(y_{j}(t))], \widetilde{\eta }_{j}(t)\in \overline{co}[h_{j}(\widetilde{y}_{j}(t))]\), for \(a.e.\ t\in (-\infty ,T)\).

Construct the following candidate function:

$$\begin{aligned} W(t)=W_{1}(t)+W_{2}(t), \end{aligned}$$

where

$$\begin{aligned} W_{1}(t)= & {} \sum \limits _{j=1}^{n}\xi _{j}e^{\delta t}\left| x_{j}(t)-\widetilde{x}_{j}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}e^{\delta t}\left| y_{j}(t)-\widetilde{y}_{j}(t)\right| , \\ W_{2}(t)= & {} \sum \limits _{j,k=1}^{n}\xi _{j}\int _{0}^{\infty }\int _{t-s}^{t}\left| f_{k}^{R}(x_{k}(\rho ))-f_{k}^{R}(\widetilde{x}_{k}(\rho ))\right| e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \\&\quad +\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }\int _{t-s}^{t}\left| g_{k}(y_{k}(\rho ))-g_{k}(\widetilde{y}_{k}(\rho ))\right| e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| \\&\quad +\sum \limits _{j,k=1}^{n}\phi _{j}\int _{0}^{\infty }\int _{t-s}^{t}\left| \eta _{k}(\rho )-\widetilde{\eta }_{k}(\rho )\right| e^{\delta (\rho +s)}d\rho \left| d\overline{K}_{jk}(s)\right| . \end{aligned}$$

Now, let us calculate the derivative of W(t) with respect to t along the solution trajectories of the systems (2a)–(2b) in the sense of (3) by using Lemma 1, we get that

$$\begin{aligned} \dot{x}_{j}(t)-\dot{\widetilde{x}}_{j}(t)= & {} -\,d_{j}(t)\left[ x_{j}(t)-\widetilde{x}_{j}(t)\right] +\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ f_{k}^{R}(x_{k}(t)) -f_{k}^{R}\left( \widetilde{x}_{k}(t)\right) \right] \\&\quad -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ g_{k}(y_{k}(t))-g_{k}\left( \widetilde{y}_{k}(t)\right) + \eta _{k}(t)-\widetilde{\eta }_{k}(t)\right] \\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }\left[ f_{k}^{R}(x_{k}(t-s))-f_{k}^{R}\left( \widetilde{x}_{k}(t-s)\right) \right] d_{s}K_{jk}(t,s)\\ \dot{y}_{j}(t)-\dot{\widetilde{y}}_{j}(t)= & {} -\,d_{j}(t)\left[ y_{j}(t)-\widetilde{y}_{j}(t)\right] +\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ f_{k}^{R}(x_{k}(t))-f_{k}\left( \widetilde{x}_{k}(t)\right) \right] \\&\quad +\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ g_{k}(y_{k}(t))-g_{k}\left( \widetilde{y}_{k}(t)\right) + \eta _{k}(t)-\widetilde{\eta }_{k}(t)\right] \\&\quad +\sum \limits _{k=1}^{n}\int _{0}^{\infty }\left[ g_{k}(y_{k}(t-s))-g_{k}\left( \widetilde{y}_{k}(t-s)\right) )\right. \\&\qquad \quad +\left. \eta _{k}^{R}(t-s)-\widetilde{\eta }_{k}(t-s)\right] d_{s}K_{jk}(t,s) \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \frac{d\left| x_{j}(t)-\widetilde{x}_{j}(t)\right| }{dt}=v_{j}(t)\left\{ \dot{x}_{j}(t)-\dot{\widetilde{x}}_{j}(t)\right\} ,\quad \frac{d\left| y_{j}(t)-\widetilde{y}_{j}(t)\right| }{dt}=w_{j}(t)\left\{ \dot{y}_{j}(t)-\dot{\widetilde{y}}_{j}(t)\right\} \end{aligned}$$

where \(v_{j}(t)=sign\{x_{j}(t)-\widetilde{x}_{j}^{R}(t)\}\), if \(x_{j}(t)\ne \widetilde{x}_{j}(t)\); while \(v_{j}(t)\) can be arbitrarily select in \(\{-1,1\}\), if \(x_{j}(t)=\widetilde{x}_{j}(t)\). In particular, we can select \(v_{j}(t)\) as follows:

$$\begin{aligned} v_{j}(t)=\left\{ \begin{array}{ll} 0, &{}\qquad \qquad x_{j}(t)-\widetilde{x}_{j}(t)=\gamma _{j}(t)-\widetilde{\gamma }_{j}(t)=0,\\ -sign\left\{ \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right\} , &{}\qquad \qquad x_{j}(t)=\widetilde{x}_{j}(t), \gamma _{j}(t)\ne \widetilde{\gamma }_{j}(t),\\ sign\left\{ x_{j}(t)-\widetilde{x}_{j}(t)\right\} , &{}\qquad \qquad x_{j}(t)\ne \widetilde{x}_{j}(t).\\ \end{array} \right. \end{aligned}$$

Thus, we have

$$\begin{aligned} v_{j}(t)\left\{ x_{j}(t)-\widetilde{x}_{j}(t)\right\} =\left| x_{j}(t)-\widetilde{x}_{j}(t)\right| , \quad v_{j}(t)\left\{ \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right\}= & {} -\left| \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right| . \end{aligned}$$

Similarly, we can choose \(w_{j}(t)\) as follows

$$\begin{aligned} w_{j}(t)=\left\{ \begin{array}{ll} 0, &{}\qquad \qquad y_{j}(t)-\widetilde{y}_{j}(t)=\gamma _{j}(t)-\widetilde{\gamma }_{j}(t)=0,\\ sign\left\{ \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right\} , &{}\qquad \qquad y_{j}(t)=\widetilde{y}_{j}(t), \gamma _{j}(t)\ne \widetilde{\gamma }_{j}(t),\\ sign\left\{ y_{j}(t)-\widetilde{y}_{j}(t)\right\} , &{}\qquad \qquad y_{j}(t)\ne \widetilde{y}_{j}(t).\\ \end{array} \right. \end{aligned}$$

We have

$$\begin{aligned} w_{j}(t)\left\{ y_{j}(t)-\widetilde{y}_{j}(t)\right\} =\left| y_{j}(t)-\widetilde{y}_{j}(t)\right| ,\quad w_{j}(t)\left\{ \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right\} =\left| \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right| . \end{aligned}$$

Therefore,

$$\begin{aligned} \dot{W}(t)= & {} \dot{W}_{1}(t)+\dot{W}_{2}(t) \nonumber \\\le & {} \sum \limits _{j=1}^{n}e^{\delta t}\left\{ (-d_{j}(t)+\delta )\xi _{j}+\xi _{j}a_{jj}^{R}(t)L_{j}^{f}+ \sum \limits _{k=1,k\ne j}^{n}\xi _{k}L_{j}^{f}\left| a_{kj}^{R}(t)\right| \right. \nonumber \\&\quad +\left. \sum \limits _{k=1}^{n}\phi _{k}L_{j}^{f}\left| a_{kj}^{I}(t)\right| +\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{f}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \right\} \left| x_{j}(t)-\widetilde{x}_{j}(t)\right| \nonumber \\&\quad +\sum \limits _{j=1}^{n}e^{\delta t}\left\{ \xi _{j}a_{jj}^{I}(t)+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| +\phi _{j}a_{jj}^{R}(t)+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| \right. \nonumber \\&\quad +\left. \sum \limits _{k=1}^{n}\phi _{k}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \right\} \left| \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right| +\sum \limits _{j=1}^{n}e^{\delta t}\left\{ (-d_{j}(t)+\delta )\phi _{j}\right. \nonumber \\&\quad +\phi _{j}a_{jj}^{R}(t)L_{j}^{g}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| L_{j}^{g}+\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{g}\left| a_{kj}^{I}(t)\right| \nonumber \\&\quad +\left. \sum \limits _{k=1}^{n}\phi _{k}L_{j}^{g}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| \right\} \left| y_{j}(t)-\widetilde{y}_{j}(t)\right| \nonumber \\\le & {} \sum \limits _{j=1}^{n}e^{\delta t}\Gamma _{j}^{1}(t)\left| x_{j}(t)-\widetilde{x}_{j}(t)\right| +\sum \limits _{j=1}^{n}e^{\delta t}\Gamma _{j}^{2}(t)\left| y_{j}(t)-\widetilde{y}_{j}(t)\right| \nonumber \\&\quad +\sum \limits _{j=1}^{n}e^{\delta t}\Upsilon _{j}^{1}(t)\left| \eta _{j}(t)-\widetilde{\eta }_{j}(t)\right| \end{aligned}$$
(21)

It follows form the Assumption 3 and (21) that one has

$$\begin{aligned} \frac{dW(t)}{dt}\le 0,\qquad for\ a.e.\ t\in [0,+\infty ). \end{aligned}$$
(22)

Note that

$$\begin{aligned} \Vert z(t)-\widetilde{z}(t)\Vert =\sum \limits _{j=1}^{n}\xi _{j}\left| x_{j}(t)-\widetilde{x}_{j}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\left| y_{j}(t)-\widetilde{y}_{j}(t)\right| . \end{aligned}$$
(23)

It follows from (22) and (23) that one has

$$\begin{aligned} \Vert z(t)-\widetilde{z}(t)\Vert \le e^{-\delta t}W(t)\le e^{-\delta t}W(0). \end{aligned}$$
(24)

Let \(M=M(\psi ,\mu ,\widehat{\psi },\widehat{\mu })=W(0)\), then \(\Vert z(t)-\widetilde{z}(t)\Vert \le Me^{-\delta t}\). We know that there exists an almost periodic solution for system (1) in the sense (3). Hence, one has

$$\begin{aligned} \Vert z(t)-z^{*}(t)\Vert \le O(e^{-\delta t}). \end{aligned}$$
(25)

which implies that the almost periodic solution \(z^{*}(t)\) is globally exponentially stable. Finally, we point that the almost periodic solution of system (1) is unique. Actually, suppose that \(z^{*}(t)\) and \(u^{*}(t)\) are two almost periodic solutions of the system (1). Applying (25) again gives

$$\begin{aligned} \Vert z{*}(t)-u^{*}(t)\Vert \le O(e^{-\delta t}). \end{aligned}$$
(26)

From Levitan and Zhikov [45], we conclude that if \(z^{*}(t)\) and \(u^{*}(t)\) are two almost periodic functions satisfying (25), then \(z^{*}(t)=u^{*}(t)\). Therefore, the almost periodic solution of system (1) is unique.

5 Applications of the Main Results

In this section, we consider the complex-valued neural networks with discontinuous activations and dalyed as specific cases in the main theorem.

Due to any periodic function can be regard as an almost periodic function, all the works also applied to periodic case. Now, replacing Assumption 3, we assume the following assumption.

Assumption 4

For each \(j=1,2,\ldots ,n, a_{jk}(t), b_{jk}(t), u_{j}(t)\) are all continuous functions on \(\mathbb {C}\), and \(d_{j}(t)>0\) is continuous function in R. there exists \(\omega >0\) such that

$$\begin{aligned}&d_{j}(t+\omega )=d_{j}(t), \ a_{jk}^{R}(t+\omega )=a_{jk}^{R}(t), \quad a_{jk}^{I}(t+\omega )=a_{jk}^{I}(t)\\&u_{j}^{R}(t+\omega )=u_{j}^{R}(t), \quad u_{j}^{R}(t+\omega )=u_{j}^{R}(t), \quad b_{jk}^{R}(t+\omega )=b_{jk}^{R}(t), \quad b_{jk}^{I}(t+\omega )=b_{jk}^{I}(t) \end{aligned}$$

hold for all \(j,k=1,2,\ldots ,n\) and \(t\in R\).

According to the Theorems 1 and 2, the following corollary can be obtained immediately.

Corollary 1

Suppose that the Assumptions 1 and 4 are satisfied, then system (1) has a unique periodic solution, which is globally exponentially stable.

Furthermore, a constant can be regarded as a periodic function with any periodic. For example, the following delayed complex-valued neural networks

$$\begin{aligned} \frac{dz_{j}(t)}{dt}= & {} -\,d_{j}z_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}f_{k}(z_{k}(t))\nonumber \\&+\sum \limits _{k=1}^{n}\int _{0}^{\infty }f_{k}(z_{k}(t-s))d_{s}K_{jk}(t,s)+u_{j},\quad j=1,\ldots ,n \end{aligned}$$
(27)

Assumption 5

Assume that the delays \(\tau _{jk}(t)\) are continuous functions and satisfy \(\tau '_{jk}(t)<1\) for \(j,k=1,2,\ldots ,n\). Moreover, there exist positive constant \(\xi _{j}, \phi _{j}\) and \(d_{j}>\delta >0\), such that \(\overline{\Gamma }_{j}<0\) and \(\overline{\Upsilon }_{j}(t)<0\), \(j=1,2,\ldots ,n,\).

where

$$\begin{aligned} \overline{\Gamma }_{j}^{1}(t)&=(-d_{j}+\delta )\xi _{j}+\xi _{j}a_{jj}^{R}L_{j}^{f}+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}L_{j}^{f}\left| a_{kj}^{R}\right| +\sum \limits _{k=1}^{n}\phi _{k}L_{j}^{f}\left| a_{kj}^{I}\right| \\&\quad +\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{f}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| ,\\ \overline{\Gamma }_{j}^{2}&=(-d_{j}+\delta )\phi _{j} +\phi _{j}a_{jj}^{R}L_{j}^{g}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}\right| L_{j}^{g}+\sum \limits _{k=1}^{n}\xi _{k}L_{j}^{g}\left| a_{kj}^{I}\right| \\&\quad +\sum \limits _{k=1}^{n}\phi _{k}L_{j}^{g}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| m,\\ \overline{\Upsilon }_{j}^{1}&=\xi _{j}a_{jj}^{I}+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{I}\right| +\phi _{j}a_{jj}^{R}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}\right| +\sum \limits _{k=1}^{n}\phi _{k}\int _{0}^{\infty }e^{\delta s}\left| d\overline{K}_{kj}(s)\right| . \end{aligned}$$

Corollary 2

Suppose that the Assumptions 1, 2, 5 are satisfied, then system (21) has a unique periodic solution which is globally exponentially stable.

6 Numerical Example

In this section, a numerical example is provided to illustrate the validity of the theoretical results obtained in Theorem 2.

If \(d_{s}K_{jk}(t,s)=b_{jk}(t)\sin s e^{-2s}ds\). Hence, the delayed system (1) change to a systems with discrete delays:

$$\begin{aligned} \frac{dz_{j}(t)}{dt}= & {} -\,d_{j}(t)z_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}(t)f_{k}(z_{k}(t))\nonumber \\&\quad +\sum \limits _{k=1}^{n}b_{jk}(t)\int _{0}^{+\infty }\sin s e^{-2s}f_{k}(z_{k}(t-\tau _{jk}(t)))ds\nonumber \\&\quad +\,u_{j}(t), j=1,2,\ldots ,n \end{aligned}$$
(28)

In this case, \(b_{jk}(t)\) are almost periodic function for all \(j,k=1,2,\ldots ,n\).

Example 1

Consider the complex-valued neural networks consisting of two subnetworks as follows:

$$\begin{aligned} \dot{z}_{1}(t)= & {} -\,4z_{1}(t)+\left[ (-0.5+0.01\sin \sqrt{2}t)+(0.01\sin \sqrt{2}t)i\right] f_{1}(z_{1}(t))\nonumber \\&\quad -\,[0.01+0.01i]f_{2}(z_{2}(t))+(0.01\sin \sqrt{2}t)\int _{0}^{+\infty }\sin s e^{-2s}f_{1}(z_{1}(t-s))ds\nonumber \\&\quad +\,(0.01\sin \sqrt{2}t)\int _{0}^{+\infty }\sin s e^{-2s}f_{1}(z_{1}(t-s))ds+(0.2\sin \sqrt{2}t+0.1\cos \sqrt{5}t)\nonumber \\&\quad +\,(0.2\sin \sqrt{2}t+0.1\cos \sqrt{5}t)i \nonumber \\ \dot{z}_{2}(t)= & {} -\,6z_{2}(t)+\left[ 0.01\sin \sqrt{2}t+(0.01\cos \sqrt{2}t)i\right] f_{1}(z_{1}(t))\nonumber \\&\quad -\,[0.4+(0.01\cos \sqrt{2}t)i]f_{2}(z_{2}(t))\nonumber \\&\quad +\,0.01\cos \sqrt{5}t\int _{0}^{+\infty }\sin s e^{-2s}f_{1}(z_{1}(t-s))ds\nonumber \\&\quad -\,0.01\sin t\int _{0}^{+\infty }\sin s e^{-2s}f_{2}(z_{2}(t-s))ds\nonumber \\&\quad +\,(0.3\cos \sqrt{3}t-0.1\sin t)+(0.3\cos \sqrt{3}t-0.1\sin t)i \end{aligned}$$
(29)

where discontinuous activation functions \(f=f^{R}+f^{I}i\),

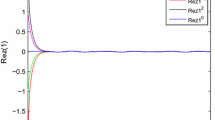
$$\begin{aligned} f^{R}(x)=x-0.1,\quad f^{I}(y)=\left\{ \begin{array}{ll} -1, &{}\quad y\in (-\,\infty ,-\,1)\\ \frac{1}{2}, &{}\quad y\in (-\,1,1)\\ 1 &{}\quad y\in (1,+\,\infty )\\ \end{array} \right. \end{aligned}$$

It easy to see that \(f_{k}^{R}(\cdot ), f_{k}^{I}(\cdot )\) are local Lipschitz with \(L_{k}^{f}=L_{k}^{g}=2\). We observed \(d_{1}(t)=4,\ d_{2}(t)=6,\ a_{11}^{R}=-0.5+0.01\sin \sqrt{2}t, \ a_{11}^{I}(t)=0.01\sin \sqrt{2}t,\ a_{12}^{R}(t)=-0.01,\ a_{12}^{I}(t)=-0.01,\ a_{21}^{R}(t)=0.01\cos \sqrt{2}t,\ a_{21}^{I}(t)=0.01\sin \sqrt{2}t,\ a_{22}^{R}(t)=-0.4,\) \(\ a_{22}^{I}(t)=-0.01\cos \sqrt{3}t,\ b_{11}(t)=0.01\sin \sqrt{2}t,\ b_{12}(t)=-0.01\sin \sqrt{2}t,\)  \(\ b_{21}(t)=0.01\cos \sqrt{5}t,\ b_{22}(t)=0.01\sin t,\ u^{R}_{1}(t)=0.02\sin \sqrt{2}t+0.01\cos \sqrt{5}t,\ u^{I}_{1}(t)=0.02\sin \sqrt{2}t+0.01\cos \sqrt{5}t,\ u^{R}_{2}(t)=0.03\cos \sqrt{3}t-0.01\sin t,\ u^{I}_{2}(t)=0.03\cos \sqrt{3}t-0.01\sin t,\ |d\overline{K}_{jk}(s)|=0.01e^{-2s}ds\), satisfied with Assumption 2. Let \(\delta =0.01,\ \xi _{1}=\xi _{2}=\phi _{1}=\phi _{2}=1\), we have \(\Gamma _{1}^{1}<0,\ \Gamma _{2}^{1}<0, \Gamma _{1}^{2}<0, \Gamma _{2}^{2}<0, \Upsilon _{1}^{1}<0,\ \Upsilon _{2}^{1}<0\). According to the Theorem 1 and 2, the system (29) has a unique global almost periodic solution and exponential stability. The dynamical behavior of system (29) are illustrated in Figs. 1, 2, 3 and 4, where we give five initial valued of system (29).

Fig. 1
figure 1

Time-domain behavior of the state variable \(Rez_{1}\) for system (29) with five random initial conditions

Full size image
Fig. 2
figure 2

Time-domain behavior of the state variable \(Imz_{1}\) for system (29) with five random initial conditions

Full size image
Fig. 3
figure 3

Time-domain behavior of the state variable \(Rez_{2}\) for system (29) with five random initial conditions

Full size image
Fig. 4
figure 4

Time-domain behavior of the state variable \(Imz_{2}\) for system (29) with five random initial conditions

Full size image

Remark 1

When \(a_{jk}^{I}(t)=b_{jk}^{I}(t)=0\) and \(f_{k}(\cdot )\) are real functions, the system (1) becomes a real-valued system as in [33]. In this paper, we firstly investigate the uniqueness and stability of almost periodic solution for delayed complex-valued neural networks with Almost periodic coefficients and discontinuous activations. It is a special kind of discontinuous complex-valued activation functions in which real parts and imaginary parts are discontinuous. Therefore, complex-valued neural networks are more suitable than real-valued neural networks.

Remark 2

In this paper, It is different from Article [42], which assumption 2 are no longer monotonic. Firstly, The almost periodic solution is proposed in the complex domain, which is more feasible in practice compared to the periodical scheme. Furthermore, we considered decomposing complex-valued neural networks into real-valued, which the activation function has continuous real part and discontinuous imaginary. Secondly, the decomposed activation function is not assumed monotonous. Under these circumstances, we reconsider almost periodic dynamical behaviors by generalized Lyapunov function method. Lastly, the almost periodic dynamics for complex-valued neural networks with discontinuous functions is investigated, and some judgment conditions are obtained. the issue of time-varying delay is also considered, which make our research have more general significance.

7 Conclusion

In past decades, the theory framework of the discontinuous neural networks and its application was set up in practice. In this article, we present the almost periodic solution of the complex-valued neural networks with discontinuous activations depending on the concept of Fillipov solution. Under the assumptions of the complex-valued activation functions decomposed into continuous real part and discontinuous imaginary part, we validated that the exponential convergence of the almost periodic solution by using the diagonal dominant principle, and non-smooth analysis theory with generalized Lyapunov approach. Furthermore, we achieved the existence, uniqueness and global stability of almost periodic solution for the complex-valued neural networks. Finally, a numerical example demonstrates the effectiveness of our obtained theoretical results.