1 Introduction

Recently, the connected neural networks have been widely investigated due to the successful applications in many fields, such as signal processing, pattern recognition, associative memories, complicated optimization [1–3]. These applications are mainly based on dynamical behaviors of neural networks. Therefore, it is extremely indispensable to analyze the dynamics of neural networks.

As a generalization of the real-valued neural networks, the states, connection weights and activation functions of the complex-valued neural networks are complex-valued. Generally, complex-valued neural networks have many differences and more complicated characteristics than real-valued ones. This becomes strongly required owing to their practical applications in physical networks dealing with light, ultrasonic and quantum [4, 5]. In fact, complex-valued neural networks (CVNNs) make it successful to solve many problems which cannot be dealt with their real-valued neural networks. For example, both the detection of symmetry problem and XOR problem can be handled with a single complex-valued neuron with the orthogonal decision boundaries [6], but cannot be solved with a single real-valued neuron. Consequently, it is extremely necessary to research the dynamical behaviors of complex-valued neural networks, especially the stability problems of complex-valued neural networks.

In the past few years, there have been many results on the stability of CVNNs, such as [7–16]. As we know, there have many applications of periodic oscillations in the recurrent neural networks, such as pattern recognition [17, 18], robot motion control [19] and machine learning [20, 21]. Therefore, it is very significant to research the existence and stability of periodic solutions for connected neural networks. We observed that the periodic parameters of dynamical system are often regarded as experienced uncertain perturbations. That is, parameters can be looked upon as a periodic small error. Under this circumstance, the almost periodic oscillatory behavior makes closer to reality. The almost periodic neural networks can be seemed as a natural generalization of the periodic neural networks. Compared with the almost periodic dynamics of real-valued neural networks, complex-valued are more complicated and suitable. However, to the best of our knowledge, almost periodic dynamics for complex-valued recurrent neural networks was seldom considered.

As we know, the activation functions play a vital part in the dynamical analysis of recurrent neural networks. Stability of neural networks depends heavily on the structures of activation functions. In recent years, there have been considered two kinds of activation functions for recurrent neural networks, that is, continuous activation functions and discontinuous activation functions, respectively. In real-valued neural networks, their activation functions are often selected to be smooth, bounded and even globally Lipschitz. In the complex domain, we know that every bounded entire function must be constant by Liouville’s theorem. Therefore, when complex-valued activation functions are entire and bounded, it must be a constant. It is obviously unsuitable. Therefore, activation functions are important problem for the complex-valued neural networks. In [8], Hu and Wang considered a class of continuous-time recurrent neural networks with two kinds of activation functions. Some criterions for existence, uniqueness and global stability of a unique equilibrium point are obtained. In [9], when activation functions can be decomposed into their real and imaginary parts, authors researched the asymptotical stability of delayed complex-valued neural networks. In [10], authors considered the asymptotical stability of complex-valued neural networks with constant delay. Moreover, the activation functions satisfy Lipschitz continuous in the complex domain. On the other hand, while handling with the dynamical systems having high-slope nonlinear elements, discontinuous activation functions often emerge in applications. For this, many researchers have been dedicated to investigate the dynamics for neural networks with discontinuous activation functions. However, almost periodic dynamics for delayed complex-valued recurrent neural networks with discontinuous activation functions was considered.

Unfortunately, time delays are usually inescapable in many physical, chemical and neural networks because of the limited switching speed of neuron amplifiers and propagation time, for example, pattern recognition, image processing, signal processing and associative memory. As everyone knows, time delays often have effect on the stability of neural network and may bring about instability. Thus, it is very important to study the dynamical behaviors of neural networks with time delays.

In the past few years, Hopfield neural networks with discontinuous activations have been received much attention, and many works obtained are concerned with equilibrium points [22–27], periodicity [28–30], almost periodicity [31–41] and many others. Considering the practical importance of almost periodic phenomenon, the stability of almost periodic solution for delayed, impulsive and discontinuous neural networks was proved by Allegretto et al. In [42], they considered the existence, uniqueness and global stability of the almost periodic solutions for delayed neural network with discontinuous activation functions. In [36], they studied the almost periodic dynamics for a class of delayed neural networks with discontinuous activation functions and give a condition that guarantee a stable almost periodic solution of the discontinuous network under the diagonal dominance principle. However, all discussions in these articles are main relay on the assumption that discontinuous activation functions are monotone nondecreasing. In [43], the authors discussed almost periodic solution of impulsive Hopfield neural networks. When the mixed delays neural network without global Lipschitz activation functions, paper [44] gives a stability sufficient condition of neural networks. Agarwal et al. researched almost periodic dynamics for impulsive delayed neural networks on almost periodic time scales, see [45].

Based on the above arguments, the almost periodic dynamical behaviors for delayed complex-valued recurrent neural networks with discontinuous activations functions are discussed. An equivalent discontinuous right-hand equation was constructed by decomposing real and imaginary parts of delayed complex-valued neural networks. The main intent of this article is to consider the dynamical behavior of complex-valued recurrent neural networks with discontinuous activation functions. Firstly, we give the existence of the almost periodic solution of the equivalent discontinuous right-hand equation under the framework of Filippov. Secondly, we obtain a condition that can guarantee the existence, the uniqueness and global exponential stability of the almost periodic solution of the discontinuous systems. Finally, when the connection strength is constant coefficients or periodic coefficients, the corresponding works will be obtained.

The rest of the article is structured as follows. In Sect. 2, some preliminaries, formulated and lemmas of complex-valued neural networks are presented. In Sect. 3, the uniqueness and global exponential stability of almost periodic solution of the dynamical system is obtained via some assumptions of the activation functions. Moreover, some corollaries with some specific cases are given. In Sect. 4, an example validates the validity of our results. At last, we come to some conclusions in Sect. 5.

Notations The notations are quite standard in this article. We denoted the solution of system (2a) and (2b) with \(Z(t,\phi ,\lambda )\). \(Z(t)=\left( z^{R}(t),z^{I}(t)\right) ^{T}\), where \(z^{R}(t)=\left( z_{1}^{R}(t),z_{2}^{R}(t),\ldots ,z_{n}^{R}(t)\right) ^{T}\), and \(z^{I}(t)=\left( z_{1}^{I}(t),z_{2}^{I}(t),\ldots ,z_{n}^{I}(t)\right) ^{T}, \gamma (t)=\left( \gamma ^{R}(t),\gamma ^{I}(t)\right) ^{T}\), where \(\gamma ^{R}(t)=\left( \gamma _{1}^{R}(t),\gamma _{2}^{R}(t),\ldots ,\gamma _{n}^{R}(t)\right) ^{T}\), and \(\gamma ^{I}(t)=\left( \gamma _{1}^{I}(t),\gamma _{2}^{I}(t),\ldots ,\gamma _{n}^{I}(t)\right) ^{T}\). \(\Vert Z(t)\Vert\) denote the 1-norm of vector \(Z=\left( z^{R},z^{I}\right) ^{T}\in R^{2n}: \Vert Z(t)\Vert =\sum _{j=1}^{n}\xi _{j}|z_{i}^{R}(t)|+\sum _{j=1}^{n}\phi _{j}|z_{i}^{I}(t)|\) where \(\xi _{j}, \phi _{j}>0, j=1,2,\ldots ,n\). \(B(x,\delta )\) denotes the open \(\delta -\)neighborhood of a set \(x\subset R^{n}: B(x,\delta )=\{y\in R^{n}:\inf_{z\in x}\Vert y-z\Vert <\delta \}\) for some \(\Vert \cdot \Vert ,\,C([0,T],R^{n})\), denote the spaces of continuous vector function, \(L^{1}([0,T],R^{n})\) represent square integrable vector function, and \(L^{\infty }([0,T],R^{n})\) denote essentially bounded function on [0, T]. \({\mathbb {Z}}\) denotes the integer; \(f'\) denotes the derivative of f.

2 Preliminaries

Consider complex-valued neural networks with asynchronous time delays and almost periodic coefficients described by the following nonlinear differential equations:

$$\begin{aligned} \frac{{\text {d}}z_{j}(t)}{{\text {d}}t}=-d_{j}(t)z_{j}(t)+\mathop {\sum }\limits _{k=1}^{n}a_{jk}(t)f_{k}(z_{k}(t)) +\mathop {\sum }\limits _{k=1}^{n}b_{jk}(t)f_{k}(z_{k}(t-\tau _{jk}(t)))+u_{j}(t) \end{aligned}$$
(1)

where \(j=1,2,\ldots , n, \ z_{j}(t)\in {\mathbb {C}}\) is the state of the jth neuron at \(t, d_{j}(t)>0\) represents the self-feedback connection weight, \(a_{jk}(t)\in {\mathbb {C}}\) is the connection strength of the kth neuron on the jth neuron; \(b_{jk}(t)\in {\mathbb {C}}\) is the delayed feedback of the kth neuron on the jth neuron with time-varying delay; \(u_{j}(t)\in {\mathbb {C}}\) denotes the external input to the jth neuron. \(\tau _\mathrm{jk}(t)\) is the time-varying transmission delay satisfying \(0\le \tau _{jk}(t)\le \tau\); \(f_{k}(\cdot ):{\mathbb {C}}\rightarrow {\mathbb {C}}\) denotes the nonlinear activation function which is supposed to satisfy the condition given:

Assumption 1

Let \(z=z^{R}+iz^{I}, f_{j}(z)\) can be expressed by its real and imaginary parts as \(f_{j}(z)=f_{j}^{R}(z^{R})+if_{j}^{I}(z^{I})\), where \(f_{j}^{R}(\cdot ),\ f_{j}^{I}(\cdot ): R\rightarrow R, f_{j}(z_{j})\) are continuous except on a finite number set of isolation points \(\left\{ \alpha _{k}^{j}:\alpha _{k}^{j}<\alpha _{k+1}^{j}, \ k\in {\mathbb {Z}}\right\}\), and \(\left\{ \beta _{k}^{j}:\beta _{k}^{j}<\beta _{k+1}^{j},\ k\in {\mathbb {Z}}\right\}\) on any compact interval of R, respectively, where the left and right limits satisfy \(f_{j}^{R-}\left( \alpha _{k}^{j}\right)<f_{j}^{R+}\left( \alpha _{k}^{j}\right) , f_{j}^{I-}\left( \beta _{k}^{j}\right) <f_{j}^{I+}\left( \beta _{k}^{j}\right)\);

Furthermore, the following assumption is made on the nonlinear activation function.

Assumption 2

\(f_{j}^{R}(\cdot )\) and \(f_{j}^{I}(\cdot )\) are monotonically nondecreasing and local Lipschitz except on a set of isolated points \(\left\{ \alpha _{k}^{j}\right\}\) and \(\left\{ \beta _{k}^{j}\right\}\), respectively. i.e., for any \(u, v\in \left( \alpha _{k}^{j}, \alpha _{k+1}^{j}\right)\) or \(\left( \beta _{k}^{j}, \beta _{k+1}^{j}\right)\), there exists positive constant \(L_{j}^{R}\), and \(L_{j}^{I}\) \(j=1,2,\ldots ,n\), such that \(\left| f_{j}^{R}(u)-f_{j}^{R}(v)\right| \le L_{j}^{R}|u-v|, \left| f_{j}^{I}(u)-f_{j}^{I}(v)\right| \le L_{j}^{I}|u-v|\).

Denote \(z_{j}(t)=z_{j}^{R}(t)+iz_{j}^{I}(t)\) with \(z_{j}^{R}(t)\) and \(z_{j}^{I}(t)\in R\), then network (1) can be replaced in the equivalent forms as shown:

$$\begin{aligned} \frac{{\text {d}}z_{j}^{R}(t)}{{\text {d}}t}=&-d_{j}(t)z_{j}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{R}\left( z_{k}^{R}(t)\right) -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{I}\left( z_{k}^{I}(t)\right) \nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)f_{k}^{R}\left( z_{k}^{R}(t-\tau _{jk}(t))\right) -\sum \limits _{k=1}^{n}b_{jk}^{I}(t)f_{k}^{I}\left( z_{k}^{I}(t-\tau _{jk}(t))\right) +u_{j}^{R}(t), \end{aligned}$$
(2a)
$$\begin{aligned} \frac{{\text {d}}z_{j}^{I}(t)}{{\text {d}}t}=&-d_{j}(t)z_{j}^{I}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)f_{k}^{I}\left( z_{k}^{I}(t)\right) + \sum \limits _{k=1}^{n}a_{jk}^{I}(t)f_{k}^{R}\left( z_{k}^{R}(t)\right) \nonumber \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)f_{k}^{I}\left( z_{k}^{I}(t-\tau _{jk}(t))\right) +\sum \limits _{k=1}^{n}b_{jk}^{I}(t)f_{k}^{R}\left( z_{k}^{R}(t-\tau _{jk}(t))\right) +u_{j}^{I}(t), \end{aligned}$$
(2b)

The following assumptions are also required for systems (2a)–(2b).

Assumption 3

\(d_{j}(t), a_{jk}^{R}(t), a_{jk}^{I}(t), b_{jk}^{R}(t), b_{jk}^{I}(t), u_{j}^{R}(t), u_{j}^{I}(t), \tau _{jk}(t)\) are all continuous almost periodic functions in R. i.e., for any \(\varepsilon >0\), there exists \(l=l(\varepsilon )>0\) such that for any interval \([\alpha ,\alpha +l]\), there exists \(\omega \in [\alpha ,\alpha +l]\) such that

$$\begin{aligned}&\left| d_{j}(t+\omega )-d_{j}(t)\right|<\varepsilon , \ \left| a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right|<\varepsilon , \ \left| a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right|<\varepsilon \\&\left| u_{j}^{R}(t+\omega )-u_{j}^{R}(t)\right|<\varepsilon , \ \left| u_{j}^{I}(t+\omega )-u_{j}^{I}(t)\right|<\varepsilon , \ \left| b_{jk}^{R}(t+\omega )-b_{jk}^{R}(t)\right|<\varepsilon , \\&\left| \tau _{jk}(t+\omega )-\tau _{jk}(t)\right|<\varepsilon , \ \left| b_{jk}^{I}(t+\omega )-b_{jk}^{I}(t)\right| <\varepsilon . \end{aligned}$$

hold for all \(j,k=1,2,\ldots ,n\) and \(t\in R\).

Assumption 4

The delays \(\tau _{jk}(t)\) are continuous functions and satisfied with \(\tau '_{jk}(t)<1\) for \(j,k=1,2,\ldots ,n\). Moreover, there exist positive constants \(\xi _{j}, \phi _{j}\) and \(\delta\) such that \(d_{j}(t)>\delta >0, \Gamma _{j}(t)<0\) and \(\Upsilon _{j}(t)<0\).

where \(j=1,2,\ldots ,n\)

$$\begin{aligned} \Gamma _{j}(t)&=a_{jj}^{R}(t)\xi _{j}+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}\left| a_{kj}^{I}(t)\right| +\sum \limits _{k=1}^{n}\xi _{k}\frac{\left| b_{kj}^{R} \left( \varphi _{kj}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{kj}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\\&+\sum \limits _{k=1}^{n}\phi _{k}\frac{\left| b_{kj}^{I} \left( \varphi _{kj}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{kj}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}},\\ \Upsilon _{j}(t)&=a_{jj}^{R}(t)\phi _{j}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| +\sum \limits _{k=1}^{n}\xi _{k}\frac{\left| b_{kj}^{I}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{jk}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\\&+\sum \limits _{k=1}^{n}\phi _{k}\frac{\left| b_{kj}^{R}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{jk}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}} \end{aligned}$$

in which \(\varphi _{jk}^{-1}\) is the inverse function of \(\varphi _{jk}=t-\tau _{jk}(t), \tau _{jk}^{M}=\max _{1\le j, k\le n}\left\{ \tau _{jk}(t)\right\} \ j,k=1,2,\ldots ,n\).

First of all, the solution of delayed differential equations (2a)–(2b) with discontinuous right-hand side is defined in the sense of Filippov [46].

Definition 1

For given continuous functions \({\widetilde{\varphi }}_{k}(s)\) and \({\widehat{\varphi }}_{k}(s)\) defined on \([-\tau , 0]\) as well as the measurable functions \(\psi _{k}(s)\in {\overline{co}}\left[ f_{k}^{R}({\widetilde{\varphi }}_{k}(s))\right]\) and \({\widehat{\psi }}_{k}(s)\in {\overline{co}}\left[ f_{k}^{I}({\widehat{\varphi }}_{k}(s))\right]\) for almost all \(s\in [-\tau , 0]\), the absolute continuous function \(\left( z^{R}(t), z^{I}(t)\right)\) with \(z^{R}(t)=\left( z_{1}^{R}(t), z_{2}^{R}(t),\ldots , z_{n}^{R}(t)\right) ^{T}, z^{I}(t)=\left( z_{1}^{I}(t), z_{2}^{I}(t),\ldots , z_{n}^{I}(t)\right) ^{T}\) and \(z_{k}^{R}(s)={\widetilde{\varphi }}_{k}(s), z_{k}^{I}(s)={\widehat{\varphi }}_{k}(s)\) for all \(s\in [-\tau , 0]\) is said to be a solution of systems (2a)–(2b) on [0, T] if there exist measurable functions \(\gamma _{k}^{R}(t)\in {\overline{co}}\left[ f_{k}^{R}\left( z_{k}^{R}(t)\right) \right] , \gamma _{k}^{I}(t)\in {\overline{co}}\left[ f_{k}^{I}\left( z_{k}^{I}(t)\right) \right]\) for almost all \(t\in [0,T]\) such that

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\text {d}}z_{j}^{R}(t)}{{\text {d}}t}=-d_{j}(t)z_{j}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\gamma _{k}^{R}(t)-\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\gamma _{k}^{I}(t)+ \sum \limits _{k=1}^{n}b_{jk}^{R}(t)\times \\ \qquad \qquad \gamma _{k}^{R}(t-\tau _{jk}(t))-\sum \limits _{k=1}^{n}b_{jk}^{I}(t)\gamma _{k}^{I}(t-\tau _{jk}(t))+u_{j}^{R}(t)\quad \hbox {a.e.}\,t\in [0,T)\\ \frac{{\text {d}}z_{j}^{I}(t)}{{\text {d}}t}=-d_{j}(t)z_{j}^{I}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\gamma _{k}^{I}(t)+\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\gamma _{k}^{R}(t)+ \sum \limits _{k=1}^{n}b_{jk}^{R}(t)\times \\ \qquad \qquad \gamma _{k}^{I}(t-\tau _{jk}(t))+\sum \limits _{k=1}^{n}b_{jk}^{I}(t)\gamma _{k}^{R}(t-\tau _{jk}(t))+u_{j}^{I}(t)\quad \hbox {a.e.}\,t\in [0,T)\\ \end{array} \right. \end{aligned}$$
(3)

and \(\gamma _{k}^{R}(s)={\widetilde{\varphi }}_{k}(s), \gamma _{k}^{I}(s)={\widehat{\varphi }}_{k}(s)\) for almost all \(s\in [-\tau , 0]\), where \(k=1,2,\ldots ,n\).

Definition 2

Let \({\widetilde{Z}}(t)=\left( {\widehat{z}}_{1}^{R}(t), {\widehat{z}}_{2}^{R}(t),\ldots , {\widehat{z}}_{n}^{R}(t), {\widehat{z}}_{1}^{I}(t), {\widehat{z}}_{2}^{I}(t),\ldots , {\widehat{z}}_{n}^{I}(t)\right) ^{T}\) be a solution for systems (2a)–(2b), \({\widetilde{Z}}(t)\) is said to be globally exponentially stable, if for any solution \(Z(t)=\left( z^{R}(t),z^{I}(t)\right) ^{T}\) of systems (2a)–(2b), there exist constants \(M>0\) and \(\delta >0\) such that

$$\begin{aligned} \Vert Z(t)-{\widehat{Z}}(t)\Vert \le Me^{-\delta t}, \quad t\ge t_{0}\ge 0. \end{aligned}$$

As introduced by Fink [47] and He [48], the following concept of almost periodic solution is presented.

Definition 3

[36] A continuous function \(Z(t): R \rightarrow R^{2n}\) is said to be almost periodic in R, if for any \(\varepsilon >0\), it is possible to find a real number \(l=l(\varepsilon )>0\); for any interval with length \(l(\varepsilon )\), there exists a number \(\omega =\omega (\varepsilon )\) in this interval such that \(\Vert Z(t+\omega )-Z(t)\Vert <\varepsilon\) for all \(t\in R\).

The time derivative of the composed function \(V(q(t)):[0,+\infty )\rightarrow R\) can be calculated by a chain rule, where \(q(t):[0,+\infty )\rightarrow R^{n}\) is absolutely continuous on any compact interval \([0,+\infty )\).

Lemma 1

(Chain rule) [36] Assume that \(V(t):R^{n}\rightarrow R\) is C-regular, and that q(t) is absolutely continuous on any compact interval \([0,+\infty )\), then q(t) and \(V(q(t)):[0,+\infty )\rightarrow R\) are differential for a.e. \(\ t\in [0,+\infty )\), and we have

$$\begin{aligned} \frac{{\text {d}}V(z(t))}{{\text {d}}t}=\left\langle \varsigma (t),\frac{{\text {d}}z(t)}{{\text {d}}t}\right\rangle \quad \forall \varsigma (t)\in \partial V(z(t)). \end{aligned}$$

3 Main results

In this section, the existence of almost periodic solution of systems (2a)–(2b) was considered primarily. We applied with a suitable Lyapunov function so that some sufficient criteria are achieved to guarantee the existence of the almost periodic solution.

Lemma 2

Under Assumptions 1–4, there exists a solution \((Z,\gamma )\) of systems (2a)–(2b) on \([0,+\infty )\) for any given initial value, i.e., the solution Z of systems (2a)–(2b) is defined for \(t\in [0,+\infty )\) and \(\gamma\) is defined for \(t\in [0,+\infty )\) up to a set with measure zero. Moreover, there exists a constant \(M>0\) such that \(\Vert Z\Vert <M\) for \(t\in [-\tau ,+\infty )\) and \(\Vert \gamma \Vert <M\) for a.e. \(t\in [-\tau ,+\infty )\).

Proof

Define set-valued map as follows:

$$\begin{aligned} \frac{{\text {d}}z_{j}^{R}(t)}{{\text {d}}t}\rightarrow & {} -d_{j}(t)z_{j}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t){\overline{co}}\left[ f_{k}^{R}\left( z_{k}^{R}(t)\right) \right] -\sum \limits _{k=1}^{n}a_{jk}^{I}(t){\overline{co}}\left[ f_{k}^{I}\left( z_{k}^{I}(t)\right) \right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)\times {\overline{co}}\left[ f_{k}^{R}\left( z_{k}^{R}(t-\tau _{jk}(t))\right) \right] -\sum \limits _{k=1}^{n}b_{jk}^{I}(t){\overline{co}}\left[ f_{k}^{I}\left( z_{k}^{I}(t-\tau _{jk}(t))\right) \right] +u_{j}^{R}(t),\\ \frac{{\text {d}}z_{j}^{I}(t)}{{\text {d}}t}\rightarrow & {} -d_{j}(t)z_{j}^{I}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t){\overline{co}}\left[ f_{k}^{I}\left( z_{k}^{I}(t)\right) \right] +\sum \limits _{k=1}^{n}a_{jk}^{I}(t){\overline{co}}\left[ f_{k}^{R}\left( z_{k}^{R}(t)\right) \right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t){\overline{co}}\left[ f_{k}^{I}\left( z_{k}^{I}(t-\tau _{jk}(t))\right) \right] +\sum \limits _{k=1}^{n}b_{jk}^{I}(t){\overline{co}}\left[ f_{k}^{R}\left( z_{k}^{R} (t-\tau _{jk}(t))\right) \right] +u_{j}^{I}(t) \end{aligned}$$

it is apparent that this set-valued map is upper semi-continuous with nonempty compact convex values, which implies that the local solution \(Z(t)=(z^{R}(t),\ z^{I}(t))^{T}\) of systems (2a)–(2b) obviously exists. That is to say that the initial valued problem of systems (2a)–(2b) has at least a solution \(Z(t)=\left( z^{R}(t),z^{I}(t)\right) ^{T}\) on [0, T) for some \(T\in (0,+\infty ]\).

Next, we will show that \(\lim \nolimits _{t\rightarrow T^{-}}\Vert Z(t)\Vert <+\infty\) if \(T<+\infty\), which means that the maximal existing interval of Z(t) can be extended to \(+\infty\). Construct a function as follows:

$$\begin{aligned} V(t)=V_{1}(t)+V_{2}(t) \end{aligned}$$

where

$$\begin{aligned} V_{1}(t)=&\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\left| z_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\hbox {e}^{\delta t}\left| z_{j}^{I}(t)\right| , \nonumber \\ V_{2}(t)=&\sum \limits _{j,k=1}^{n}\xi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{R}\left( z_{k}^{R}(\rho )\right) \right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \nonumber \\&+\sum \limits _{j,k=1}^{n}\xi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{I}\left( z_{k}^{I}(\rho )\right) \right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \nonumber \\&+\sum \limits _{j,k=1}^{n}\phi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{I}\left( z_{k}^{I}(\rho )\right) \right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \nonumber \\&+\sum \limits _{j,k=1}^{n}\phi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{R}\left( z_{k}^{R}(\rho )\right) \right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho . \end{aligned}$$
(4)

To calculate the derivative of V(t) along the solution trajectories of systems (2a)–(2b) in the sense of (3) by utilizing Lemma 1, one gets that

$$\begin{aligned} \frac{{\text {d}}V(t)}{{\text {d}}t}= & {} \sum \limits _{j=1}^{n}\delta \xi _{j}\hbox {e}^{\delta t}\left| z_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\left| {\dot{z}}_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\delta \phi _{j}\hbox {e}^{\delta t}\left| z_{j}^{I}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\hbox {e}^{\delta t}\left| {\dot{z}}_{j}^{I}(t)\right| \\= & {} \sum \limits _{j=1}^{n}\delta \xi _{j}\hbox {e}^{\delta t}\left| z_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\hbox {sign}\left( z_{j}^{R}(t)\right) \left( {\dot{z}}_{j}^{R}(t)\right) +\sum \limits _{j=1}^{n}\delta \phi _{j}\hbox {e}^{\delta t}\left| z_{j}^{I}(t)\right| \\&+\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}sign\left( z_{j}^{I}(t)\right) \left( {\dot{z}}_{j}^{I}(t)\right) +\sum \limits _{j,k=1}^{n}\xi _{j}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(t)\right) } \left| \gamma _{k}^{R}(t)\right| \hbox {e}^{\delta \left( t+\tau _{jk}^{M}\right) }-\\&\sum \limits _{j,k=1}^{n}\xi _{j}\left| b_{jk}^{R}(t)\right| \left| \gamma _{k}^{R}\left( t-\tau _{jk}(t))\right) \right| \hbox {e}^{\delta \left( t-\tau _{jk}(t)+\tau _{jk}^{M}\right) }\\&+\sum \limits _{j,k=1}^{n}\xi _{j}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(t)\right) }\left| \gamma _{k}^{I}(t)\right| \hbox {e}^{\delta \left( t+\tau _{jk}^{M}\right) }\\&-\sum \limits _{j,k=1}^{n}\xi _{j}\left| b_{jk}^{I}(t)\right| \left| \gamma _{k}^{I}\left( t-\tau _{jk}(t)\right) \right| \hbox {e}^{\delta \left( t-\tau _{jk}(t)+\tau _{jk}^{M}\right) }\\&+\sum \limits _{j,k=1}^{n}\phi _{j}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(t)\right) }\left| \gamma _{k}^{I}(t)\right| \hbox {e}^{\delta \left( t+\tau _{jk}^{M}\right) } \\&-\sum \limits _{j,k=1}^{n}\phi _{j}\left| b_{jk}^{R}(t)\right| \left| \gamma _{k}^{I}\left( t-\tau _{jk}(t)\right) \right| \hbox {e}^{\delta \left( t-\tau _{jk}(t)+\tau _{jk}^{M}\right) }\\&+\sum \limits _{j,k=1}^{n}\phi _{j}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(t)\right) }\left| \gamma _{k}^{R}(t)\right| \hbox {e}^{\delta \left( t+\tau _{jk}^{M}\right) } \\ \end{aligned}$$
$$\begin{aligned}&-\sum \limits _{j,k=1}^{n}\phi _{j}\left| b_{jk}^{I}(t)\right| \left| \gamma _{k}^{R}\left( t-\tau _{jk}(t)\right) \right| \hbox {e}^{\delta \left( t-\tau _{jk}(t)+\tau _{jk}^{M}\right) }\nonumber \\\le & {} \sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}[-d_{j}(t)+\delta ]\left| z_{j}^{R}(t)\right| \nonumber \\&+\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\left| \gamma _{j}^{R}(t)\right| \left\{ a_{jj}^{R}(t)\xi _{j}+ \sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{R}(t)\right| \right. \nonumber \\&\left. +\sum \limits _{k=1,}^{n}\phi _{k}\left| a_{kj}^{I}(t)\right| +\sum \limits _{k=1,}^{n}\xi _{k}\frac{\left| b_{kj}^{R} \left( \varphi _{kj}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{kj}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\right. \nonumber \\&\left. +\sum \limits _{k=1,}^{n}\phi _{k}\frac{\left| b_{kj}^{I} \left( \varphi _{kj}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{kj}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\right\} \nonumber \\&+\sum \limits _{j=1}^{n}\phi _{j}\hbox {e}^{\delta t}[-d_{j}(t)+\delta ]\left| z_{j}^{I}(t)\right| \nonumber \\&+\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\left| \gamma _{j}^{I}(t)\right| \left\{ a_{jj}^{R}(t)\phi _{j}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| \right. \nonumber \\&\left. +\sum \limits _{k=1}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}\frac{\left| b_{kj}^{R} \left( \varphi _{kj}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{kj}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\right. \nonumber \\&\left. +\sum \limits _{k=1}^{n}\xi _{k}\frac{\left| b_{kj}^{I} \left( \varphi _{kj}^{-1}(t)\right) \right| }{1-\tau '_{kj} \left( \varphi _{kj}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\right\} \nonumber \\&+\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}|u_{j}^{R}(t)\left| +\sum \limits _{j=1}^{n}\phi _{j}\hbox {e}^{\delta t}|u_{j}^{I}(t)\right| \end{aligned}$$
(5)

It follows from (5) and Assumption 4 that

$$\begin{aligned} \frac{{\text {d}}V(t)}{{\text {d}}t}\le \hbox {e}^{\delta t}{\widehat{u}},\quad \hbox {a.e.}\quad t\in [0,+\infty ) \end{aligned}$$

where \({\widehat{u}}=\sup \limits _{t\ge 0}\Vert u(t)\Vert <+\infty\), which implies that

$$\begin{aligned} V(t)\le V(0)+\frac{1}{\delta }{\widehat{u}}\hbox {e}^{\delta t}. \end{aligned}$$
(6)

Combining the definition of V(t) and (6), one has

$$\begin{aligned} \Vert Z(t)\Vert \le \hbox {e}^{-\delta t}V(t)\le {\overline{M}}. \end{aligned}$$

where \({\overline{M}}=V(0)+\frac{1}{\delta }{\widehat{u}}\), which shows that Z(t) is bounded on its existence interval \([-\tau ,T]\). Therefore, \(\lim _{t\rightarrow T^{-}}\Vert Z(t)\Vert <+\infty\), which means \(T=+\infty\). That is, systems (2a)–(2b) have a global solution for any initial values problem.

Moreover, we have

$$\begin{aligned} \Vert Z(t)\Vert =\sum \limits _{j=1}^{n}\xi _{j}\left| z_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\left| z_{j}^{I}(t)\right| \le M_{0}, \quad t\in [-\tau ,+\infty ) \end{aligned}$$

where \(M_{0}=V(0)+\frac{1}{\delta }\left( {\widehat{u}}_{j}^{R}+{\widehat{u}}_{j}^{I}\right) +\Vert \theta \Vert , \Vert \theta \Vert =\sup _{-\tau \le s\le 0}\left\{ \sum _{k=1}^{n}\xi _{k}\left| {\widetilde{\varphi }}(s)\left| +\sum _{k=1}^{n}\phi _{k}\right| {\widehat{\varphi }}(s)\right| \right\}\).

\(f_{j}^{R}\) and \(f_{j}^{I}\) have finite number of discontinuous points on any compact interval of R. In speciality, \(f_{j}^{R}\) and \(f_{j}^{I}\) have finite number of discontinuous points on compact interval \([-M_{0},M_{0}]\). Without loss of generality, we select discontinuous points \(\left\{ \alpha _{k}^{j}:k=1,2,\ldots ,l_{j}\right\}\) and \(\left\{ \beta _{k}^{j}:k=1,2,\ldots ,l_{j}\right\}\) for \(f_{j}^{R}\) and \(f_{j}^{I}\) on the interval \([-M_{0},M_{0}]\), respectively, and assume that \(-M_{0}<\alpha _{1}^{j}<\alpha _{2}^{j}<\cdots<\alpha _{l_{j}}^{j}<M_{0}, -M_{0}<\beta _{1}^{j}<\beta _{2}^{j}<\cdots<\beta _{l_{j}}^{j}<M_{0}\). Discuss a battery of continuous functions of \(f_{j}^{R}\) as follows:

$$\begin{aligned} f_{j}^{1}(z^{R})=&\left\{ \begin{array}{ll} f_{j}^{R}(z^{R}), &{}\quad \hbox {if} \ z^{R}\in \left[ -M_{0},\alpha _{1}^{j}\right) ,\\ f_{j}^{R}\left( \alpha _{1}^{j}-0\right) , &{}\quad \hbox {if} \ z^{R}=\alpha _{1}^{j}; \end{array} \right. \\ f_{j}^{k}(z^{R})=&\left\{ \begin{array}{ll} f_{j}^{R}\left( \alpha _{k-1}^{j}-0\right) , &{}\quad \hbox {if} \ z^{R}=\alpha _{k-1}^{j},\\ f_{j}^{R}(z^{R}), &{}\quad \hbox {if} \ z^{R}\in \left( \alpha _{k-1}^{j},\alpha _{k}^{j}\right) ,\\ f_{j}^{R}\left( \alpha _{k}^{j}+0\right) , &{}\quad \hbox {if} \ z^{R}=\alpha _{k}^{j}; \end{array} \right. \\ f_{j}^{l_{j}}(z^{R})=&\left\{ \begin{array}{ll} f_{j}^{R}\left( \alpha _{l_{j}}^{j}+0\right) , &{}\quad \hbox {if} \ z^{R}=\alpha _{l_{j}}^{j},\\ f_{j}^{R}(z^{R}), &{}\quad \hbox {if} \ z^{R}\in \left( \alpha _{l_{j}}^{j},M_{0}\right] . \end{array} \right. \end{aligned}$$

where \(k=2,\ldots ,l_{j}-1\).

Denote

$$\begin{aligned} M_{j}^{1}= & {} \max \left\{ P_{1}, Q_{1}, W_{1}\right\} ,\ m_{j}^{1}=\min \left\{ P_{1}', Q_{1}', W_{1}'\right\} ,\\ P_{1}= & {} \max \limits _{z^{R}\in \left[ -M_{0},\alpha _{1}^{j}\right] }\left\{ f_{j}^{1}(z^{R})\right\} ,\ Q_{1}=\max \limits _{2\le k\le l_{j}-1}\left\{ \max \limits _{z^{R}\in \left[ \alpha _{k-1}^{j}\alpha _{k}^{j}\right] }\left\{ f_{j}^{k}(z^{R})\right\} \right\} ,\\ W_{1}= & {} \max \limits _{z^{R}\in \left[ \alpha _{l_{j}}^{j},M_{0}\right] }\left\{ f_{j}^{l_{j}}(z^{R})\right\} \ P_{1}'=\min \limits _{z^{R}\in \left[ -M_{0},\alpha _{1}^{j}\right] }\left\{ f_{j}^{1}(z^{R})\right\} ,\\ Q_{1}'= & {} \min \limits _{2\le k\le l_{j}-1}\left\{ \min \limits _{z^{R}\in \left[ \alpha _{k-1}^{j},\alpha _{k}^{j}\right] }\left\{ f_{j}^{k}(z^{R})\right\} \right\} ,\ W_{1}'=\min \limits _{z^{R}\in \left[ \alpha _{l_{j}}^{j},M_{0}\right] }\left\{ f_{j}^{l_{j}}(z^{R})\right\} . \end{aligned}$$

It is easy to see that

$$\begin{aligned} \left| {\overline{co}}\left[ f_{j}^{R}\left( z_{j}^{R}(t)\right) \right] \right| \le \max \left\{ \left| M_{j}^{1}\right| ,\left| m_{j}^{1}\right| \right\} , \quad j=1,2,\ldots ,n. \end{aligned}$$

Similarly, consider a battery of continuous functions of \(f_{j}^{I}\):

$$\begin{aligned} f_{j}^{1}(z^{I})=&\left\{ \begin{array}{ll} f_{j}^{I}(z^{I}), &{}\quad \hbox {if} \ z^{I}\in \left[ -M_{0},\beta _{1}^{j}\right) ,\\ f_{j}^{I}\left( \beta _{1}^{j}-0\right) , &{}\quad \hbox {if} \ z^{I}=\beta _{1}^{j}; \end{array} \right. \\ f_{j}^{k}(z^{I})=&\left\{ \begin{array}{ll} f_{j}^{I}\left( \beta _{k-1}^{j}-0\right) , &{}\quad \hbox {if} \ z^{I}=\beta _{k-1}^{j},\\ f_{j}^{I}(z^{I}), &{}\quad \hbox {if} \ z^{I}\in \left( \beta _{k-1}^{j},\beta _{k}^{j}\right) ,\\ f_{j}^{I}\left( \beta _{k}^{j}+0\right) , &{}\quad \hbox {if} \ z^{R}=\beta _{k}^{j}; \end{array} \right. \\ f_{j}^{l_{j}}(z^{I})=&\left\{ \begin{array}{ll} f_{j}^{I}\left( \beta _{l_{j}}^{j}+0\right) , &{}\quad \hbox {if} \ z^{I}=\beta _{l_{j}}^{j},\\ f_{j}^{I}(z^{I}), &{}\quad \hbox {if} \ z^{I}\in \left( \beta _{l_{j}}^{j},M_{0}\right] . \end{array} \right. \end{aligned}$$

where \(k=2,\ldots ,l_{j}-1\).

Denote

$$\begin{aligned} M_{j}^{2}=\max \left\{ P_{2}, Q_{2}, W_{2}\right\} , \quad m_{j}^{2}=\min \left\{ P_{2}', Q_{2}', W_{2}'\right\} . \end{aligned}$$

where

$$\begin{aligned} P_{2}= & {} \max \limits _{z^{I}\in \left[ -M_{0},\beta _{1}^{j}\right] }\left\{ f_{j}^{1}(z^{I})\right\} ,\ Q_{2}=\max \limits _{2\le k\le l_{j}-1}\left\{ \max \limits _{z^{I}\in \left[ \beta _{k-1}^{j},\beta _{k}^{j}\right] }\left\{ f_{j}^{k}(z^{I})\right\} \right\} ,\\ W_{2}= & {} \max \limits _{z^{I}\in \left[ \beta _{l_{j}}^{j},M_{0}\right] }\left\{ f_{j}^{l_{j}}(z^{I})\right\} ,\ P_{2}'=\min \limits _{z^{I}\in \left[ -M_{0},\beta _{1}^{j}\right] }\left\{ f_{j}^{1}(z^{I})\right\} ,\\ Q_{2}'= & {} \min \limits _{2\le k\le l_{j}-1}\left\{ \min \limits _{z^{I}\in \left[ \beta _{k-1}^{j},\beta _{k}^{j}\right] }\{f_{j}^{k}(z^{I})\}\right\} \ W_{2}'=\min \limits _{z^{I}\in \left[ \beta _{l_{j}}^{j},M_{0}\right] }\left\{ f_{j}^{l_{j}}(z^{I})\}\right\} . \end{aligned}$$

Similarly, one gets that

$$\begin{aligned} \left| {\overline{co}}\left[ f_{j}^{I}\left( z_{j}^{I}(t)\right) \right] \right| \le \max \left\{ \left| M_{j}^{2}\right| ,\left| m_{j}^{2}\right| \right\} , \quad j=1,2,\ldots ,n. \end{aligned}$$

Note that \(\gamma _{j}^{R}(t)\in {\overline{co}}\left[ f_{j}^{R}\left( z_{j}^{R}(t)\right) \right]\) and \(\gamma _{j}^{I}(t)\in {\overline{co}}\left[ f_{j}^{I}\left( z_{j}^{I}(t)\right) \right]\) for \(\hbox {a.e.}\ t\in [-\tau ,+\infty ), \quad j=1,2,\ldots ,n\). Hence, \(\max \left\{ \left| \gamma _{j}^{R}(t)\right| , \left| \gamma _{j}^{I}(t)\right| \right\} \le \max \left\{ \left| M_{j}^{1}\right| , \left| m_{j}^{1}\right| , \left| M_{j}^{2}\right| , \left| m_{j}^{2}\right| \right\}\) for a.e. \(t\in [-\tau ,+\infty ), \quad j=1,2,\ldots ,n\), which implies that

$$\begin{aligned} \Vert \gamma (t)\Vert \le&\max \left\{ \sum \limits _{j=1}^{2n}\xi _{j}\left| M_{j}^{1}\right| ,\sum \limits _{j=1}^{2n}\xi _{j}\left| m_{j}^{1}\right| ,\sum \limits _{j=1}^{2n}\phi _{j}\left| M_{j}^{2}\right| , \sum \limits _{j=1}^{2n}\phi _{j}\left| m_{j}^{2}\right| \right\} ,\\&\hbox {a.e.}\quad t\in [-\tau ,+\infty ). \end{aligned}$$

Let

$$\begin{aligned} M=\max \left\{ M_{0},\sum \limits _{j=1}^{2n}\xi _{j}\left| M_{j}^{1}\right| ,\sum \limits _{j=1}^{2n}\xi _{j}\left| m_{j}^{1}\right| ,\sum \limits _{j=1}^{2n}\phi _{j}\left| M_{j}^{2}\right| , \sum \limits _{j=1}^{2n}\phi _{j}\left| m_{j}^{2}\right| \right\} . \end{aligned}$$

Hence, we have

$$\begin{aligned} \Vert \gamma (t)\Vert \le M, \quad \hbox {a.e.} \ t\in [-\tau ,+\infty ). \end{aligned}$$

The proof of Lemma 2 is complete.

Lemma 3

Suppose that Assumptions 1–4 hold, then any solution of systems (2a)–(2b) is asymptotically almost periodic, i.e., for any \(\varepsilon >0\), there exist \(T>0, l=l(\varepsilon )\) and \(\omega =\omega (\epsilon )\) in any interval \([\alpha ,\alpha +l]\) such that

$$\begin{aligned} \Vert Z(t+\omega )-Z(t)\Vert \le \varepsilon \end{aligned}$$

for all \(t\ge T\).

Proof

Construct the following auxiliary functions:

$$\begin{aligned} \varepsilon _{j}^{1}(t,\omega )=&-z_{j}^{R}(t+\omega )[d_{j}(t+\omega )-d_{j}(t)]\nonumber \\&+\sum \limits _{k=1}^{n}\left[ a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right] \gamma _{k}^{R}(t+\omega )\nonumber \\&-\sum \limits _{k=1}^{n}\left[ a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right] \gamma _{k}^{I}(t+\omega )\nonumber \\&+\sum \limits _{k=1}^{n}\left[ b_{jk}^{R}(t+\omega )-b_{jk}^{R}(t)\right] \gamma _{k}^{R}(t+\omega -\tau _{jk}(t+\omega ))\nonumber \\&-\sum \limits _{k=1}^{n}\left[ b_{jk}^{I}(t+\omega )-b_{jk}^{I}(t)\right] \gamma _{k}^{I}(t+\omega -\tau _{jk}(t+\omega ))\nonumber \\&+u_{j}^{R}(t+\omega )-u_{j}^{R}(t) \end{aligned}$$
(7a)
$$\begin{aligned} \varepsilon _{j}^{2}(t,\omega )=&-z_{j}^{I}(t+\omega )[d_{j}(t+\omega )-d_{j}(t)]\nonumber \\&+\sum \limits _{k=1}^{n}\left[ a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right] \gamma _{k}^{I}(t+\omega )\nonumber \\&+\sum \limits _{k=1}^{n}\left[ a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right] \gamma _{k}^{R}(t+\omega )\nonumber \\&+\sum \limits _{k=1}^{n}\left[ b_{jk}^{R}(t+\omega )-b_{jk}^{R}(t)\right] \gamma _{k}^{I}(t+\omega -\tau _{jk}(t+\omega ))\nonumber \\&+\sum \limits _{k=1}^{n}\left[ b_{jk}^{I}(t+\omega )-b_{jk}^{I}(t)\right] \gamma _{k}^{R}(t+\omega -\tau _{jk}(t+\omega ))\nonumber \\&+u_{j}^{I}(t+\omega )-u_{j}^{I}(t) \end{aligned}$$
(7b)

In the light of Assumption 3 and the boundedness of Z(t) and \(\gamma (t)\), for any \(\varepsilon >0\), there exists \(l=l(\varepsilon )>0\) and at least one point \(\omega\) in any interval \([\alpha ,\alpha +l]\) satisfying the following inequalities:

$$\begin{aligned}&|d_{j}(t+\omega )-d_{j}(t)|<\frac{\delta \epsilon }{24nM\Delta },\\&\left| u_{j}^{R}(t+\omega )-u_{j}^{R}(t)\right|<\frac{\delta \epsilon }{24n\Delta }, \\&\left| u_{j}^{I}(t+\omega )-u_{j}^{I}(t)\right|<\frac{\delta \epsilon }{24n\Delta }, \\&\left| a_{jk}^{R}(t+\omega )-a_{jk}^{R}(t)\right|<\frac{\delta \epsilon }{24n^{2}M\Delta },\\&\left| a_{jk}^{I}(t+\omega )-a_{jk}^{I}(t)\right|<\frac{\delta \epsilon }{24n^{2}M\Delta },\\&\left| b_{jk}^{R}(t+\omega )-b_{jk}^{R}(t)\right|<\frac{\delta \epsilon }{24n^{2}M\Delta },\\&\left| b_{jk}^{I}(t+\omega )-b_{jk}^{I}(t)\right| <\frac{\delta \epsilon }{24n^{2}M\Delta }. \end{aligned}$$

where \(0<\xi \triangleq \min _{1\le j\le n}\le \Delta \triangleq \max _{1\le j\le n}\{\xi _{j}\}\). Hence, one has

$$\begin{aligned} \left| \varepsilon _{j}^{1}(t,\omega )\right| <\frac{\delta \epsilon }{4n\Delta }, \quad \hbox {for} \ \hbox {a.e.}\ t\in [-\tau ,+\infty ) \end{aligned}$$
(8)

and

$$\begin{aligned} \left| \varepsilon _{j}^{2}(t,\omega )\right| <\frac{\delta \epsilon }{4n\Delta }, \quad \hbox {for} \ \hbox {a.e.}\ t\in [-\tau ,+\infty ) \end{aligned}$$
(9)

Denoting \(X_{j}(t)=\left( x^{R}_{j}(t),x^{I}_{j}(t)\right) ^{T}\), with \(x^{R}_{j}(t)=z^{R}_{j}(t+\omega )-z^{R}_{j}(t)\) and \(x^{I}_{j}(t)=z^{I}_{j}(t+\omega )-z^{I}_{j}(t)\), then, one obtains that

$$\begin{aligned} \frac{{\text {d}}x_{j}^{R}(t)}{{\text {d}}t}=&-d_{j}(t)x_{j}^{R}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ \gamma _{k}^{R}(t+\omega )-\gamma _{k}^{R}(t)\right] -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ \gamma _{k}^{I}(t+\omega )-\gamma _{k}^{I}(t)\right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)\left[ \gamma _{k}^{R}(t+\omega -\tau _{jk}(t+\omega )) -\gamma _{k}^{R}(t-\tau _{jk}(t))\right] \\&-\sum \limits _{k=1}^{n}b_{jk}^{I}(t)\left[ \gamma _{k}^{I}(t+\omega -\tau _{jk}(t+\omega )) -\gamma _{k}^{I}(t-\tau _{jk}(t))\right] +\varepsilon _{j}^{1}(t,\omega ) \end{aligned}$$

and

$$\begin{aligned} \frac{{\text {d}}x_{j}^{I}(t)}{{\text {d}}t}=&-d_{j}(t)x_{j}^{I}(t)+\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ \gamma _{k}^{I}(t+\omega )-\gamma _{k}^{I}(t)\right] + \sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ \gamma _{k}^{R}(t+\omega )-\gamma _{k}^{R}(t)\right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)\left[ \gamma _{k}^{I}(t+\omega -\tau _{jk}(t+\omega ))-\gamma _{k}^{I}(t-\tau _{jk}(t))\right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{I}(t)\left[ \gamma _{k}^{R}(t+\omega -\tau _{jk}(t+\omega ))-\gamma _{k}^{R}(t-\tau _{jk}(t))\right] +\varepsilon _{j}^{2}(t,\omega ) \end{aligned}$$

Construct the following candidate function:

$$\begin{aligned} L(t)=L_{1}(t)+L_{2}(t) \end{aligned}$$

where

$$\begin{aligned} L_{1}(t)=&\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\left| x_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\hbox {e}^{\delta t}\left| x_{j}^{I}(t)\right| , \\ L_{2}(t)=&\sum \limits _{j,k=1}^{n}\xi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{R}(\rho +\omega )-\gamma _{k}^{R}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \\&+\sum \limits _{j,k=1}^{n}\xi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{I}(\rho +\omega )-\gamma _{k}^{I}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \\&+\sum \limits _{j,k=1}^{n}\phi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) }\left| \gamma _{k}^{I}(\rho +\omega )- \gamma _{k}^{I}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \\&+\sum \limits _{j,k=1}^{n}\phi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{R}(\rho +\omega )-\gamma _{k}^{R}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \ \ \end{aligned}$$

\(\square\)

By the similar way utilized in Lemma 2, and combining inequalities (8), (9), one has

$$\begin{aligned} \frac{{\text {d}}L(t)}{{\text {d}}t}\le \hbox {e}^{\delta t}\frac{\delta }{2}\epsilon , \quad \hbox {for}\quad \hbox {a.e.}\quad t\in [0,+\infty ). \end{aligned}$$

Note that L(0) is a constant, then one can pick a sufficiently large \(T>0\) such that

$$\begin{aligned} \hbox {e}^{-\delta t}L(0)<\frac{\varepsilon }{2}, \quad t\ge T. \end{aligned}$$

Then,

$$\begin{aligned} \Vert X(t)\Vert \le \hbox {e}^{-\delta t}L(t)\le \hbox {e}^{-\delta t}L(0)+\hbox {e}^{-\delta t}\int _{0}^{t}{\dot{L}}(s){\text {d}}s<\varepsilon . \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \Vert Z(t+\omega )-Z(t)\Vert \le \hbox {e}^{-\delta t}L(0)+\frac{\varepsilon }{2}<\varepsilon , \quad \hbox {for}\ \ t\ge T. \end{aligned}$$

The proof of Lemma 3 is complete.

Theorem 1

Suppose that Assumptions 1–4 hold, then systems (2a)–(2b) have at least a almost periodic solution in the sense of (3).

Proof

Let \(Z(t)=\left( (z^{R}(t))^{T},(z^{I}(t))^{T}\right) ^{T}\) be any solution of system (3). Then one can select a sequence \(\{t_{k}\}_{k\in N}\) satisfying \(\lim _{k\rightarrow +\infty }t_{k}=+\infty\), and such that

$$\begin{aligned} \left| \varepsilon _{j}^{1}(t,t_{k})\right| \le \frac{1}{k}, \quad \hbox {for} \ \ t\in [-\tau ,+\infty ), \end{aligned}$$
(10)

and

$$\begin{aligned} |\varepsilon _{j}^{2}(t,t_{k})|\le \frac{1}{k}, \quad \hbox {for} \ \ t\in [-\tau ,+\infty ) \end{aligned}$$
(11)

where \(j=1,2,\ldots ,n, \varepsilon _{j}^{1}(t,t_{k}), \varepsilon _{j}^{2}(t,t_{k})\) are the auxiliary functions (7a) and (7b) defined. \(\square\)

It follows from Lemma 2 that there exists \(M^{*}>0\) such that \(|Z'_{j}(t)|\le M^{*}\) for \(a.e\ t\in [-\tau ,+\infty )\). Thus, the sequence \(\{Z(t+t_{k})\}_{k\in N}\) is equi-continuous and uniformly bounded. By the Arzela–Ascoli theorem and diagonal selection principle, we can choose a subsequence of \(\{t_{k}\}\) (denoted by \(\{t_{k}\}\)), such that \(Z(t+t_{k})\) converges uniformly to some absolutely continuous function \({\widehat{Z}}(t)\) on any compact interval [0, T].

Next, we claim that \({\widehat{Z}}(t)\) is an almost periodic solution of systems (2a)–(2b) in the sense of (3). Firstly, \({\widehat{Z}}(t)\) is a solution of system (2a)–(2b) in the sense of (3).

By Lebesgue’s dominated convergence theorem, for any \(t\in [-\tau ,+\infty )\), and \(l\in R\), one has

$$\begin{aligned} {\widehat{z}}_{j}^{R}(t+l)-{\widehat{z}}_{j}^{R}(t)= & {} \lim \limits _{k\rightarrow +\infty }\left[ z_{j}^{R}(t+t_{k}+l)-z_{j}^{R}(t+t_{k})\right] \\= & {} \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}{\dot{z}}_{j}^{R}(\theta +t_{k}){\text {d}}\theta \\= & {} \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\left[ -d_{j}(\theta )z_{j}^{R}(\theta +t_{k})+ \sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )\gamma _{k}^{R}(\theta +t_{k})-\right. \\&\left. \sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )\gamma _{k}^{I}(\theta +t_{k})\right] +\sum \limits _{k=1}^{n}b_{jk}^{R}(\theta )\gamma _{k}^{R}(\theta +t_{k}-\tau _{jk}(\theta +t_{k}))\\&-\sum \limits _{k=1}^{n}b_{jk}^{I}(\theta )\gamma _{k}^{I}(\theta +t_{k}-\tau _{jk}(\theta +t_{k}))+u_{j}^{R}(\theta )+\varepsilon _{j}^{1}(\theta ,t_{k}){\text {d}}\theta \\= & {} \int _{t}^{t+l}\left[ -d_{j}(\theta ){\widehat{z}}_{j}^{R}(\theta )+ \sum \limits _{k=1}^{n}a_{jk}^{R}(\theta ){\widehat{\gamma }}_{k}^{R}(\theta )-\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta ){\widehat{\gamma }}_{k}^{I}(\theta )\right. \\&\left. +\sum \limits _{k=1}^{n}b_{jk}^{R}(\theta ){\widehat{\gamma }}_{k}^{R}(\theta -\tau _{jk}(\theta ))- \sum \limits _{k=1}^{n}b_{jk}^{I}(\theta ){\widehat{\gamma }}_{k}^{I}(\theta -\tau _{jk}(\theta ))\right. \\&\left. +u_{j}^{R}(\theta )\right] {\text {d}}\theta +\lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\varepsilon _{j}^{1}(\theta ,t_{k}){\text {d}}\theta \\ \end{aligned}$$

and

$$\begin{aligned} {\widehat{z}}_{j}^{I}(t+l)-{\widehat{z}}_{j}^{I}(t)= & {} \lim \limits _{k\rightarrow +\infty }\left[ z_{j}^{I}(t+t_{k}+l)-z_{j}^{I}(t+t_{k})\right] \\= & {} \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}{\dot{z}}_{j}^{I}(\theta +t_{k}){\text {d}}\theta \\= & {} \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\left[ -d_{j}(\theta )z_{j}^{I}(\theta +t_{k})+ \sum \limits _{k=1}^{n}a_{jk}^{R}(\theta )\gamma _{k}^{I}(\theta +t_{k})\right. \\&\left. +\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta )\gamma _{k}^{R}(\theta +t_{k})\right] +\sum \limits _{k=1}^{n}b_{jk}^{R}(\theta )\gamma _{k}^{I}(\theta +t_{k}-\tau _{jk}(\theta +t_{k}))\\&+\sum \limits _{k=1}^{n}b_{jk}^{I}(\theta )\gamma _{k}^{R}(\theta +t_{k}-\tau _{jk}(\theta +t_{k}))+u_{j}^{I}(\theta )+\varepsilon _{j}^{2}(\theta ,t_{k}){\text {d}}\theta \\= & {} \int _{t}^{t+l}\left[ -d_{j}(\theta ){\widehat{z}}_{j}^{I}(\theta )+ \sum \limits _{k=1}^{n}a_{jk}^{R}(\theta ){\widehat{\gamma }}_{k}^{I}(\theta )+\sum \limits _{k=1}^{n}a_{jk}^{I}(\theta ){\widehat{\gamma }}_{k}^{R}(\theta )\right. \\&\left. +\sum \limits _{k=1}^{n}b_{jk}^{R}(\theta ){\widehat{\gamma }}_{k}^{I}(\theta -\tau _{jk}(\theta ))+ \sum \limits _{k=1}^{n}b_{jk}^{I}(\theta ){\widehat{\gamma }}_{k}^{R}(\theta -\tau _{jk}(\theta ))+u_{j}^{I}(\theta )\right] {\text {d}}\theta \\&+\lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\varepsilon _{j}^{2}(\theta ,t_{k}){\text {d}}\theta \end{aligned}$$

From (10) and (11), it is easy to conclude that

$$\begin{aligned} \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\varepsilon _{j}^{1}(\theta ,t_{k}){\text {d}}\theta =0,\ \lim \limits _{k\rightarrow +\infty }\int _{t}^{t+l}\varepsilon _{j}^{2}(\theta ,t_{k}){\text {d}}\theta =0. \end{aligned}$$
(12)

Therefore, \({\widehat{Z}}(t)\) is a solution of systems (2a)–(2b).

Secondly, we claim that \({\widehat{\gamma }}_{k}^{R}(t)\in {\overline{co}}\left[ f_{k}^{R}\left( {\widehat{z}}_{k}^{R}(t)\right) \right] , {\widehat{\gamma }}_{k}^{I}(t)\in {\overline{co}}\left[ f_{k}^{I}\left( {\widehat{z}}_{k}^{I}(t)\right) \right]\) for \(\hbox {a.e.}\ t\in [-\tau ,+\infty )\). Note that Z(t) uniformly converges to \({\widehat{Z}}(t)\) with respect to \(t\in [-\tau ,+\infty )\) and \({\overline{co}}\left[ f_{k}^{R}\right] , {\overline{co}}\left[ f_{k}^{I}\right]\) are upper semi-continuous set-valued map, for any \(\varepsilon >0\), there exists \(N>0\) such that \(f^{R}\left( z^{R}(t+t_{k})\right) \in B({\overline{co}}[f^{R}(z^{R}(t))],\varepsilon )\) for \(k>N\) and \(t\in [-\tau ,+\infty )\). Noting that \({\overline{co}}[f^{R}(z^{R}(t))]\) is convex and compact, then \(\gamma ^{R}(t)\in B({\overline{co}}[f^{R}(z^{R}(t))],\varepsilon )\), which implies \({\widehat{\gamma }}^{R}_{k}(t)\in B\left( {\overline{co}}\left[ f^{R}_{k}\left( z^{R}_{k}(t)\right) \right] ,\varepsilon \right)\) holds for any \(t\in [-\tau ,+\infty )\). Repeating the above method, we can prove \({\widehat{\gamma }}^{I}_{k}(t)\in B\left( {\overline{co}}\left[ f^{I}_{k}\left( z^{I}_{k}(t)\right) \right] ,\varepsilon \right)\). Because of the arbitrary of \(\varepsilon\), we know that \({\widehat{\gamma }}_{k}^{R}(t)\in {\overline{co}}[f_{k}^{R}({\widehat{z}}_{k}^{R}(t))], {\widehat{\gamma }}_{k}^{I}(t)\in {\overline{co}}[f_{k}^{I}({\widehat{z}}_{k}^{I}(t))]\) for \(\hbox {a.e.}\ t\in [-\tau ,+\infty )\).

Finally, \({\widehat{Z}}(t)=\left( {\widehat{z}}^{R}(t),{\widehat{z}}^{I}(t)\right)\) is an almost periodic solution of the neural network systems (2a)–(2b). By Lemma 3, For any \(\varepsilon >0\), there exist \(T>0\) and \(l=l(\varepsilon )\) such that any interval \([\alpha ,\alpha +l]\) contains an \(\omega\) such that

$$\begin{aligned} \Vert Z(t+\omega )-Z(t)\Vert <\varepsilon \end{aligned}$$

hold for all \(t\ge T\). Therefore, there exists sufficiently large constant \(K>0\) such that

$$\begin{aligned} \Vert Z(t+t_{k}+\omega )-Z(t+t_{k})\Vert <\varepsilon \end{aligned}$$

holds for all \(k>K\) and \(t\in [-\tau ,+\infty )\). As \(k\rightarrow +\infty\), we can conclude that\(\Vert {\widehat{z}}(t+\omega )-{\widehat{z}}(t)\Vert <\varepsilon\) for all \(t\in [-\tau ,+\infty )\). This implies that \({\widehat{z}}(t)\) is an almost periodic solution of the neural network systems (2a)–(2b). The proof is complete.

Next, we will research the uniqueness and global exponential stability of the almost periodic solution obtained in Theorem 1 for the dynamical networks (2a)–(2b). By utilizing a generalization Lyapunov function, some sufficient criteria are gained to assure that networks have a uniqueness and global exponential stability almost periodic solution.

Theorem 2

Under Assumptions 1–4, then systems (2a)–(2b) have a unique almost periodic solution which is globally exponentially stable in the sense of (3).

Proof

Let Z(t) and \({\widehat{Z}}(t)\) be any two solutions of systems (2a)–(2b) associated with \(\gamma (t), {\widehat{\gamma }}(t)\) and initial value pairs \((\psi ,\mu ), ({\widehat{\psi }}, {\widehat{\mu }})\), respectively.

It follows from (3) that

$$\begin{aligned} {\dot{z}}_{j}^{R}(t)-\dot{{\widehat{z}}}_{j}^{R}(t)=&-d_{j}(t)\left[ z_{j}^{R}(t)-{\widehat{z}}_{j}^{R}(t)\right] +\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ \gamma _{k}^{R}(t) -{\widehat{\gamma }}_{k}^{R}(t)\right] -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ \gamma _{k}^{I}(t)-{\widehat{\gamma }}_{k}^{I}(t)\right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)\left[ \gamma _{k}^{R}(t-\tau _{jk}(t))-{\widehat{\gamma }}_{k}^{R}(t-\tau _{jk}(t))\right] - \sum \limits _{k=1}^{n}b_{jk}^{I}(t)\left[ \gamma _{k}^{I}(t-\tau _{jk}(t))-\right. \\&\left. {\widehat{\gamma }}^{I}_{k}(t-\tau _{jk}(t))\right] \\ {\dot{z}}_{j}^{I}(t)-\dot{{\widehat{z}}}_{j}^{I}(t) =&-d_{j}(t)\left[ z_{j}^{I}(t)-{\widehat{z}}_{j}^{I}(t)\right] +\sum \limits _{k=1}^{n}a_{jk}^{R}(t)\left[ \gamma _{k}^{I}(t) -{\widehat{\gamma }}_{k}^{I}(t)\right] -\sum \limits _{k=1}^{n}a_{jk}^{I}(t)\left[ \gamma _{k}^{R}(t)-{\widehat{\gamma }}_{k}^{R}(t)\right] \\&+\sum \limits _{k=1}^{n}b_{jk}^{R}(t)\left[ \gamma _{k}^{I}(t-\tau _{jk}(t))-{\widehat{\gamma }}_{k}^{I}(t-\tau _{jk}(t))\right] - \sum \limits _{k=1}^{n}b_{jk}^{I}(t)\left[ \gamma _{k}^{R}(t-\tau _{jk}(t))\right. \\&\left. -{\widehat{\gamma }}^{R}_{k}(t-\tau _{jk}(t))\right] \end{aligned}$$

Then, one has the following inequalities:

$$\begin{aligned} \left| {\dot{z}}_{j}^{R}(t)-\dot{{\widehat{z}}}_{j}^{R}(t)\right| =&sign\left\{ {\dot{z}}_{j}^{R}(t)-\dot{{\widehat{z}}}_{j}^{R}(t)\right\} \left( {\dot{z}}_{j}^{R}(t)-\dot{{\widehat{z}}}_{j}^{R}(t)\right) \\ \le&-d_{j}(t)\left| z_{j}^{R}(t)-{\widehat{z}}_{j}^{R}(t)\right| \\&+\left| \gamma _{j}^{R}(t) -{\widehat{\gamma }}_{j}^{R}(t)\right| \left[ a_{jj}^{R}(t)+\sum \limits _{k=1,k\ne j}^{n}\left| a_{kj}^{R}(t)\right| \right] \\&+\sum \limits _{k=1}^{n}\left| a_{jk}^{I}(t)\right| \left| \gamma _{k}^{I}(t)-{\widehat{\gamma }}_{k}^{I}(t)\right| \\&+\sum \limits _{k=1}^{n}\left| b_{jk}^{R}(t)\right| \left| \gamma _{k}^{R}(t-\tau _{jk}(t))-{\widehat{\gamma }}_{k}^{R}(t-\tau _{jk}(t))\right| \\&+\sum \limits _{k=1}^{n}\left| b_{jk}^{I}(t)\right| \left| \gamma _{k}^{I}(t-\tau _{jk}(t))- {\widehat{\gamma }}^{I}_{k}(t-\tau _{jk}(t))\right| \end{aligned}$$

and

$$\begin{aligned} \left| {\dot{z}}_{j}^{I}(t)-\dot{{\widehat{z}}}_{j}^{I}(t)\right| =&\hbox {sign}\left\{ {\dot{z}}_{j}^{I}(t)-\dot{{\widehat{z}}}_{j}^{I}(t)\right\} \left( {\dot{z}}_{j}^{I}(t)-\dot{{\widehat{z}}}_{j}^{I}(t)\right) \\ \le&-d_{j}(t)\left| z_{j}^{I}(t)-{\widehat{z}}_{j}^{I}(t)\right| \\&+\left| \gamma _{j}^{I}(t) -{\widehat{\gamma }}_{j}^{I}(t)\right| \left[ a_{jj}^{R}(t)+\sum \limits _{k=1,k\ne j}^{n}\left| a_{kj}^{R}(t)\right| \right] \\&+ \sum \limits _{k=1}^{n}\left| a_{jk}^{I}(t)\right| \left| \gamma _{k}^{R}(t)-{\widehat{\gamma }}_{k}^{R}(t)\right| \\&+\sum \limits _{k=1}^{n}\left| b_{jk}^{R}(t)\right| \left| \gamma _{k}^{I}(t-\tau _{jk}(t))-{\widehat{\gamma }}_{k}^{I}(t-\tau _{jk}(t))\right| \\&+\sum \limits _{k=1}^{n}\left| b_{jk}^{I}(t)\right| \left| \gamma _{k}^{I}(t-\tau _{jk}(t))- {\widehat{\gamma }}^{I}_{k}(t-\tau _{jk}(t))\right| \end{aligned}$$

Construct the following candidate Lyapunov functions:

$$\begin{aligned} W(t)=W_{1}(t)+W_{2}(t) \end{aligned}$$

where

$$\begin{aligned} W_{1}(t)=&\sum \limits _{j=1}^{n}\xi _{j}\hbox {e}^{\delta t}\left| z_{j}^{R}(t)-{\widehat{z}}_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\hbox {e}^{\delta t}\left| z_{j}^{I}(t)-{\widehat{z}}_{j}^{I}(t)\right| , \\ W_{2}(t)=&\sum \limits _{j,k=1}^{n}\xi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{R}(\rho )-{\widehat{\gamma }}_{k}^{R}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \\&+\sum \limits _{j,k=1}^{n}\xi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } |\gamma _{k}^{I}(\rho )-{\widehat{\gamma }}_{k}^{I}(\rho )|\hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \\&+\sum \limits _{j,k=1}^{n}\phi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{R}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) }\left| \gamma _{k}^{I}(\rho )- {\widehat{\gamma }}_{k}^{I}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \\&+\sum \limits _{j,k=1}^{n}\phi _{j}\int _{t-\tau _{jk}(t)}^{t}\frac{\left| b_{jk}^{I}\left( \varphi _{jk}^{-1}(\rho )\right) \right| }{1-\tau '_{jk}\left( \varphi _{jk}^{-1}(\rho )\right) } \left| \gamma _{k}^{R}(\rho )-{\widehat{\gamma }}_{k}^{R}(\rho )\right| \hbox {e}^{\delta \left( \rho +\tau _{jk}^{M}\right) }{\text {d}}\rho \end{aligned}$$

To calculate the derivative of W(t) with respect to t along the solution trajectories of systems (2a)–(2b) in the sense (3) of by applying Lemma 1, one obtains that

$$\begin{aligned} \frac{{\text {d}}W(t)}{{\text {d}}t}\le&\sum \limits _{j=1}^{n}\hbox {e}^{\delta t}\xi _{j}(-d_{j}(t)+\delta )\left| z_{j}^{R}(t)-\widehat{z}_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\hbox {e}^{\delta t}\phi _{j}(-d_{j}(t)+\delta )\left| z_{j}^{I}(t)-\widehat{z}_{j}^{I}(t)\right| +\\&\sum \limits _{j=1}^{n}\hbox {e}^{\delta t}\left| \gamma _{j}^{R}(t)-\widehat{\gamma }_{j}^{R}(t)\right| \left\{ a_{jj}^{R}(t)\xi _{j} +\sum \limits _{k=1,k\ne j}^{n}\xi _{k}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\phi _{k}\left| a_{kj}^{I}(t)\right| \right. \\&\left. +\sum \limits _{j,k=1}^{n}\xi _{k}\frac{\left| b_{kj}^{R}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{jk}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}} +\sum \limits _{j,k=1}^{n}\phi _{k}\frac{\left| b_{kj}^{I}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{jk}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\right\} +\\&+\sum \limits _{j=1}^{n}\hbox {e}^{\delta t}\left| \gamma _{j}^{I}(t)-\widehat{\gamma }_{j}^{I}(t)\right| \left\{ a_{jj}^{R}(t)\phi _{j}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}(t)\right| +\sum \limits _{k=1}^{n}\xi _{k}\left| a_{kj}^{I}(t)\right| +\right. \\&\left. +\sum \limits _{j,k=1}^{n}\xi _{k}\frac{\left| b_{kj}^{I}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{jk}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}} +\sum \limits _{j,k=1}^{n}\phi _{k}\frac{\left| b_{kj}^{R}\left( \varphi _{jk}^{-1}(t)\right) \right| }{1-\tau '_{kj}\left( \varphi _{jk}^{-1}(t)\right) }\hbox {e}^{\delta \tau _{kj}^{M}}\right\} \\ \end{aligned}$$

It follows from Assumption 4 that

$$\begin{aligned} \frac{{\text {d}}W(t)}{{\text {d}}t}\le 0, \quad \hbox {a.e.}\ t\in [0,+\infty ). \end{aligned}$$
(13)

Note that

$$\begin{aligned} \Vert Z(t)-{\widehat{Z}}(t)\Vert =&\sum \limits _{j=1}^{n}\xi _{j}\left| z_{j}^{R}(t)-{\widehat{z}}_{j}^{R}(t)\right| +\sum \limits _{j=1}^{n}\phi _{j}\left| z_{j}^{I}(t)-{\widehat{z}}_{j}^{I}(t)\right| . \end{aligned}$$
(14)

It follows from (13) and (14) that one has

$$\begin{aligned} \Vert Z(t)-{\widehat{Z}}(t)\Vert \le \hbox {e}^{-\delta t}W(t)\le \hbox {e}^{-\delta t}W(0). \end{aligned}$$
(15)

Let \(M=M(\psi ,\mu ,{\widehat{\psi }},{\widehat{\mu }})=W(0)\), then \(\Vert z(t)-{\widehat{z}}(t)\Vert \le M\hbox {e}^{-\delta t}\). Moreover, there exists an almost periodic solution for systems (2a)–(2b) in the sense of (3). Hence, one has

$$\begin{aligned} \Vert Z(t)-Z^{*}(t)\Vert \le O(\hbox {e}^{-\delta t}), \end{aligned}$$
(16)

which implies that almost periodic solution \(Z^{*}(t)\) is globally exponentially stable. Finally, it should be pointed out that almost periodic solutions of system (2a)–(2b) are unique. Actually, assume that \(Z^{*}(t)\) and \(U^{*}(t)\) are two almost periodic solutions.

$$\begin{aligned} \Vert Z^{*}(t)-U^{*}(t)\Vert \le O(\hbox {e}^{-\delta t}). \end{aligned}$$
(17)

According to Levitan and Zhikov(1982), we conclude that if \(Z^{*}(t)\) and \(U^{*}(t)\) are two almost periodic functions satisfying (17), then \(Z^{*}(t)=U^{*}(t)\). Therefore, the almost periodic solution is unique. The proof is complete.

Finally, we study a specific case in the main theorem. Due to that periodic function can be regard as an almost periodic function, all fruits use to periodic case. Now, taking the place of Assumption 3, the following assumption holds. \(\square\)

Assumption 5

\(d_{j}(t), a_{jk}^{R}(t), a_{jk}^{I}(t), b_{jk}^{R}(t), b_{jk}^{I}(t), u_{j}^{R}(t), u_{j}^{I}(t), \tau _{jk}(t)\) are continuous functions in R. i.e., for any \(\varepsilon >0\), there exists \(l=l(\varepsilon )>0\) such that for any interval \([\alpha ,\alpha +l]\), there exists \(\omega \in [\alpha ,\alpha +l]\) such that

$$\begin{aligned} d_{j}(t+\omega )=&d_{j}(t), \ \tau _{jk}(t+\omega )=\tau _{jk}(t), \\ a_{jk}^{R}(t+\omega )=&a_{jk}^{R}(t), \ a_{jk}^{I}(t+\omega )=a_{jk}^{I}(t), \\ u_{j}^{R}(t+\omega )=&u_{j}^{R}(t), \ u_{j}^{I}(t+\omega )=u_{j}^{I}(t),\\ b_{jk}^{R}(t+\omega )=&b_{jk}^{R}(t), \ b_{jk}^{I}(t+\omega )=b_{jk}^{I}(t). \end{aligned}$$

hold for all \(j,k=1,2,\ldots ,n\) and \(t\in R\).

According to Theorem 1 and Theorem 2, the following corollary is true.

Corollary 1

If assumptions 1, 2, 4, 5 are satisfied, then system (2a)–(2b) has a unique periodic solution, where it is globally exponentially stable.

Furthermore, a constant is a periodic function with any periodic. Therefore, the following complex-valued delayed neural networks are

$$\begin{aligned} \frac{{\text {d}}z_{j}(t)}{{\text {d}}t}&=-d_{j}z_{j}(t)+\sum \limits _{k=1}^{n}a_{jk}f_{k}(z_{k}(t)) +\sum \limits _{k=1}^{n}b_{jk}f_{k}(z_{k}(t-\tau _{jk}(t)))+u_{j},\nonumber \\&j=1,\ldots ,n \end{aligned}$$
(18)

Assumption 6

Assume that the delays \(\tau _{jk}(t)\) are continuous function and satisfying \(\tau '_{jk}(t)<1\) for \(j,k=1,2,\ldots ,n\). Moreover, there exist positive constants \(\xi _{j}, \phi _{j}\) and \(d_{j}>\delta >0\), such that \({\overline{\Gamma }}_{j}<0\) and \({\overline{\Upsilon }}_{j}<0, j=1,2,\ldots ,n\).

where

$$\begin{aligned} {\overline{\Gamma }}_{j}=&a_{jj}^{R}\xi _{j}+\sum \limits _{k=1,k\ne j}^{n}\xi _{k}|a_{kj}^{R}| +\sum \limits _{k=1,}^{n}\phi _{k}\left| a_{kj}^{I}\right| +\sum \limits _{k=1,}^{n} \xi _{k}\left| b_{kj}^{R}\right| \hbox {e}^{\delta \tau _{kj}^{M}}+\sum \limits _{k=1,}^{n}\phi _{k}\left| b_{kj}^{I}\right| \hbox {e}^{\delta \tau _{kj}^{M}}\\ {\overline{\Upsilon }}_{j}=&a_{jj}^{R}\phi _{j}+\sum \limits _{k=1,k\ne j}^{n}\phi _{k}\left| a_{kj}^{R}\right| +\sum \limits _{k=1}^{n}\xi _{k}\left| a_{kj}^{I}\right| +\sum \limits _{j,k=1}^{n}\xi _{k}\left| b_{kj}^{I}\right| \hbox {e}^{\delta \tau _{kj}^{M}}+\sum \limits _{j,k=1}^{n}\phi _{k}\left| b_{kj}^{R}\right| \hbox {e}^{\delta \tau _{kj}^{M}} \end{aligned}$$

and \(\tau _{jk}^{M}(t)=\max \{\tau _{jk}(t)\}, \ j,k=1,2,\ldots ,n\).

The following corollary is also true.

Corollary 2

If Assumptions 1, 2, 6 are satisfied, then system (18) has a unique solution with any initial valued; moreover, system (18) has a unique equilibrium, where it is globally exponentially stable.

4 Numerical example

In this section, an example validates the validity of our results which is obtained in Theorem 1 and Theorem 2.

Example 1

Considering complex-valued dynamical networks constituting of two subnetworks as follows:

$$\begin{aligned} {\dot{z}}_{1}(t)=&-2z_{1}(t)+[(-0.5+0.01\sin \sqrt{2}t)\nonumber \\&+(0.01\sin \sqrt{2}t)i]f_{1}(z_{1}(t))-[0.01+0.01i]f_{2}(z_{2}(t))\nonumber \\&+[(-0.05+0.01\sin \sqrt{2}t)\nonumber \\&+(0.01\sin \sqrt{2}t)i]f_{1}(z_{1}(t-0.1))\nonumber \\&-[0.01+0.01i]f_{2}(z_{2}(t-0.1))\nonumber \\&+(0.02\sin \sqrt{2}t+0.01\cos \sqrt{5}t)\nonumber \\&+(0.02\sin \sqrt{2}t+0.01\cos \sqrt{5}t)i \nonumber \\ {\dot{z}}_{2}(t)=&-2z_{2}(t)+(0.01+0.01i)f_{1}(z_{1}(t))\nonumber \\&-[0.4+(0.01\cos \sqrt{2}t)i]f_{2}(z_{2}(t))\nonumber \\&+(0.01+0.1i)f_{1}(z_{1}(t-0.1))\nonumber \\&-[(0.04+0.01\cos \sqrt{2}t)i]f_{2}(z_{2}(t-0.1))\nonumber \\&+(0.03\cos \sqrt{3}t-0.01\sin t)\nonumber \\&+(0.03\cos \sqrt{3}t-0.01\sin t)i \end{aligned}$$
(19)

where the discontinuous activation functions are given as follows:

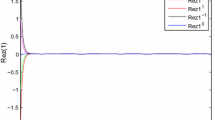
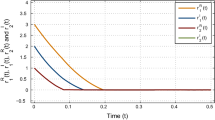
$$\begin{aligned} f^{R}_{k}(x)=f^{I}_{k}(x)=\left\{ \begin{array}{ll} -2, &{}\quad x\in (-\infty ,-1)\\ 0, &{}\quad x\in (-1,1)\\ 3 &{} \quad x\in (1,+\infty ) \end{array} \right. \end{aligned}$$

Obviously, \(f^{R}_{k}(\cdot ), f^{I}_{k}(\cdot )\) is local Lipschitz with Lipschitz constants \(L_{j}^{R}=L_{j}^{I}=0.01\). Observing that \(d_{1}(t)=d_{2}(t)=2, \tau _{jk}=0.1, a_{11}^{R}(t)=-0.5+0.01\sin \sqrt{2}t,\ a_{11}^{I}(t)=0.01\sin \sqrt{2}t,\ a_{12}^{R}(t)=-0.01,\ a_{12}^{I}(t)=-0.01,\ a_{21}^{R}(t)=0.01,\ a_{21}^{I}(t)=0.01,\ a_{22}^{R}(t)=-0.4,\ a_{22}^{I}(t)=-0.01\cos \sqrt{2}t,\ b_{11}^{R}(t)=-0.05+0.01\sin \sqrt{2}t,\ b_{11}^{I}(t)=0.01\sin \sqrt{2}t\), \(b_{12}^{R}(t)=-0.01,\ b_{12}^{I}(t)=-0.01,\ b_{21}^{R}(t)=0.01,\ b_{21}^{I}(t)=0.01,\ b_{22}^{R}(t)=-0.04\), \(b_{22}^{I}(t)=-0.01\cos \sqrt{2}t,\ u^{R}_{1}(t)=0.02\sin \sqrt{2}t+0.01\cos \sqrt{5}t,\ u^{I}_{1}(t)=0.02\sin \sqrt{2}t+0.01\cos \sqrt{5}t,\ u^{R}_{2}(t)=0.03\cos \sqrt{3}t-0.01\sin t,\ u^{I}_{2}(t)=0.03\cos \sqrt{3}t-0.01\sin t\) are satisfied with Assumption 3. Let \(\delta =0.01,\ \xi _{1}=\xi _{2}=\phi _{1}=\phi _{2}=1\), we have \(\Gamma _{1}<0,\ \Gamma _{2}<0, \Upsilon _{1}<0,\ \Upsilon _{2}<0\). According to Theorems 1 and 2, system (19) has a unique almost periodic solution, which is globally exponentially stable. The dynamics of system (19) are illustrated in Figs. 1, 2, 3, and 4, where we give five initial values of system (19).

Fig. 1
figure 1

Time-domain behavior of the state variable \(Rez_{1}\) for system (19) with five random initial conditions, \(\tau _{jk}(t)=0.1\)

Full size image
Fig. 2
figure 2

Time-domain behavior of the state variable \(Imz_{1}\) for system (19) with three random initial conditions, \(\tau _{jk}(t)=0.1\)

Full size image
Fig. 3
figure 3

Time-domain behavior of the state variable \(Rez_{2}\) for system (19) with three random initial conditions, \(\tau _{jk}(t)=0.1\)

Full size image
Fig. 4
figure 4

Time-domain behavior of the state variable \(Imz_{2}\) for system (19) with three random initial conditions, \(\tau _{jk}(t)=0.1\)

Full size image

Remark 1

When \(a_{jk}^{I}(t)=b_{jk}^{I}(t)=0\) and \(f_{k}(\cdot )\) are real functions, system (1) becomes a real-valued system as in [25]. In this paper, we firstly investigate the uniqueness and stability of almost periodic solution for delayed complex-valued recurrent neural networks with discontinuous activation functions. It is a special kind of discontinuous complex-valued activation functions in which real parts and imaginary parts are discontinuous. Therefore, complex-valued neural networks are more suitable than real-valued neural networks.

5 Conclusion

In the past decades, the theory framework of the discontinuous neural networks and its application was set up in practice. In this article, we propose the almost periodic solution of the complex-valued neural networks with discontinuous activations depending on the concept of Filippov solution. Under these assumptions, we proved the exponential convergence of the almost periodic solution using the diagonal dominant principle, 1-norm and nonsmooth analysis theory with generalized Lyapunov approach. We obtain the existence, uniqueness and global stability of almost periodic solution for the complex-valued neural networks. Finally, a numerical example demonstrates the effectiveness of our obtained theoretical results.