1 Introduction

Owing to the rapid development of computer science and big data technology, text processing, particularly digital image processing, has recently attracted widespread attention of researchers and has become a hot research field [1, 18, 21, 29, 30]. Digital images typically show various texts; in addition, encryption is needed in almost all aspects of modern life, and the requirements for security and humanity are increasing. Because the amount of data is large and the pixels in adjacent areas are strongly correlated in general images, traditional image processing algorithms, including RSA [5] and DES [6], are unsuitable, and the development of new image encryption schemes is challenging.

By contrast, a chaotic signal is widely utilized as an external key in image encryption owing to its pseudo-randomness and sensitivity to the initial conditions. Chaotic keys refer to the uncertain signals generated by certain systems, and they have potential applications in physics, biology, chemistry, and medical analysis [4, 7, 12, 14, 15, 23, 25, 27, 28]. For chaotic image encryption, many studies have been conducted, based upon which, it has been proven that the use of chaos is a superior method for image encryption [11, 13, 24, 33].

Traditionally, image encryption has been divided into pixel- and bit-levels [8, 16, 20, 31, 32, 34]. Although pixel-level image encryption is fast, bit-level encryption achieves better results; thus, both methods have been utilized in recent studies. For example, Yao et al. [31] obtained an encrypted image by scrambling the image pixels and diffusing the image information using a chaotic logistic map. However, other researchers have focused on bit-level image encryption. For instance, Teng et al. [20] proposed an image encryption algorithm with bit-level scrambling. Gray image encryption [8, 11, 13, 16, 20, 24, 32, 33] and color image encryption [9, 17, 19, 26, 31] have also been extensively researched. For example, Faragallah et al. [9] proposed a color image cryptosystem with a chaotic baker map, and Parvaz et al. [17] designed a combined chaotic system and applied it to color image encryption.

In general, chaotic signals are directly used in image encryption. However, the generated signals are fixed once the initial values and parameters of the chaotic system are selected. Differing from previous studies, in the present study, coarse-grained methods are applied to chaotic signals before the signals are used as keys, which makes the signals unpredictable while applying different coarse-grained methods. In addition, to obtain various chaotic signals, a discrete logistic map and a coupled fractional lattice chaotic system (CFLCS) are considered during the encryption process. In addition, image information is divided into high and low bits throughout the entire encryption process. During the scrambling, with the generated coarse-grained fractional chaotic signals, the high bits are row- and column-scrambled. By contrast, the low bits are global scrambled using coarse-grained logistic chaotic map signals. During the diffusion process, the bit streams are also handled through a cyclic shift and XOR operation with coarse-grained chaotic signals. Motivated by the aforementioned analysis, a novel bit-level color image encryption algorithm with different coarse-grained chaotic signals is proposed in this paper. The contributions of this paper are as follows: 1. The coarse-grained method is utilized to handle different kinds of chaotic signals and make the signals unpredictable. 2. Different scrambling methods are used in the high and low bits simultaneously. 3. The bit planes are decomposed, and parallel processing is utilized in different planes for both scrambling and diffusion. 4. Chaotic signals for the encryption of different planes in a color image are concurrently generated using CFLCS. The remainder of this paper is organized as follows. In the following section, the main image encryption algorithm is proposed. Section 3 provides the experimental results and corresponding analysis. Finally, some concluding remarks are given in section 4.

2 The coarse-grained chaotic system and encryption algorithm

In this section, the coarse-grained chaos-based image encryption algorithm is described. For greater efficiency and security, a discrete chaotic map and continuous fractional chaotic system are considered. First, take the following logistic map (1) as an example of a discrete chaotic map. The equation can be defined as

$$ x\left(k+1\right)=\mu x(k)\left(1-x(k)\right),\kern1.00em k=0,1,2\dots $$
(1)

where discrete state x(k) ∈ (0, 1)  and control parameter μ ∈ [0, 4]. When 3.5699456 < u ≤ 4, the Logistic map is chaotic.

In the previous study, once the initial value and system parameter of system (1) are fixed, the chaotic signals generated are fixed because of the fine-grained iteration step. If the initial value and system parameter are known, the keys will no longer be safe. To make the chaos signal more secure, coarse-grained methods will be applied in the signals before encryption. For example, a coarse-grained parameter C can be brought in, and a key signal with C chaotic signals can be generated. For the sake of simplicity, the mean value of the chaotic signals is calculated as the final key in this paper. With the same initial value, x0 = 0.3874926, and system parameter, μ = 3.999999, but different coarse-grained parameters 4 and 8, the derived key signals are as shown in Fig. 1. The corresponding NIST test results are shown as following Table 1.

Fig. 1
figure 1

Discrete key signals with different coarse-grained parameters

Full size image
Table 1 The test results of NIST SP800–22 for different coarse-grained parameters
Full size table

From Table 1, it is exhibited that all p-values for different coarse-grained parameters are greater than 0.01, and NIST tests are all passed. This means that the proposed coarse-grained signals are sufficiently good and it can be utilized in the code applications which require randomness.

However, for a continuous chaotic system signal, the coarse-grained method will be more suitable for dealing with an analog signal because the discretization will be completed during the coarse-grained process. As a result, the derived key signal can be directly utilized to encrypt the digital images. In the following section, a coarse-grained simulation based on fractional chaotic signals is described. Before the simulation, the following fractional definition should first be introduced.

  • Definition 1 (Caputo differential definition) [3]:

The Caputo fractional differential definition is most commonly expressed in the following form:

Dqu(t) = Js − qu(s)(t)(q > 0),where s is an integer which is not less than q, u(s) is the s-order derivative, and Jq is the q-order Reimann–Liouville integral operator in the following form:

$$ {J}^qv(t)=\frac{\int_0^t{\left(t-\tau \right)}^{q-1}v\left(\tau \right) d\tau}{\varGamma (q)}, $$

where Γ is the Gamma function, and Dq represents a θ-order Caputo differential operator.

Based on Definition 1, the CFLCS [22] can be expressed as follows:

$$ {D}^q{\boldsymbol{w}}_i(t)=\left(1-\varepsilon \right)f\left({\boldsymbol{w}}_i(t)\right)+\frac{1}{2}\varepsilon f\left({\boldsymbol{w}}_{i+1}(t)\right)+\frac{1}{2}\varepsilon f\left({\boldsymbol{w}}_{i-1}(t)\right) $$
(2)

where ε is the coupled intensity, w is the state vector, i(i = 1, 2, ⋯, n) is the lattice index, and n is the lattice length. As a whole, system (2) is periodically connected. In detail, local system f is set as the following Lorenz system form

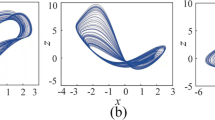
$$ \left\{\begin{array}{l}\dot{x}=a\left(y-x\right)\\ {}\dot{y}= bx-y- xz\\ {}\dot{z}= xy- cz\end{array}\right. $$
(3)

where x, y, and z are state variables of the Lorenz system, and the system parameters are a = 10, b = 28, and \( c=\frac{8}{3} \). With randomly generated initials, by applying the coarse-grained method to the chaotic signals from system (2), the derived key signals for different coarse-grained parameters C1 = 2 and C2 = 3 are shown in Fig. 2.

Fig. 2
figure 2

The key signals generated with coarse-grained parameters C1 and C2 from different chaotic state signals in system (3): a The first system states generated keys, b The second system states generated keys, c The third system states generated keys

Full size image

With the coarse-grained keys generated using the above logistic map and the CFLCS signals, the digital images can be encrypted with proper scrambling and diffusion algorithms. It should be noted that, because fractional system (2) can generate three different coarse-grained keys simultaneously, as shown in Fig. 3, the keys can be applied in the encryption of R, G, and B channels in parallel for color images. The entire encryption can be applied as indicated in Fig. 3. For the proposed method, images can be recovered using a symmetrical decryption method and a detailed encryption analysis, as described in the following subsections.

Fig. 3
figure 3

The global flow diagram for color image encryption with coarse-grained keys

Full size image

2.1 Scrambling analysis

In this section, the pixels of a color image in different channels are translated into different bit streams, and these bits are scrambled using different methods. The detailed steps are provided as follows:

  1. Step 1.

    For a given color image F of height × width, generate R, G, and B vectors Fr, Fg, and Fb, respectively. For each Fr, Fg, or Fb vector, the following steps are applied.

  2. Step 2.

    Extract the high bit planes in the corresponding channel and reconstruct the bit matrix. For the fifth through the eighth bits, the sizes of the extracted bit planes BPi(i = 5, 6, 7, 8) are all height × width. Combine these bit planes as vector H = [BP5 BP6 BP7 BP8 ]height × 4width.

  3. Step 3.

    With the above coarse-grained methods and CFLCS (2), generate encryption keys k1 and k2. The lengths of k1 and k2 are height and 4width, respectively. Using the MATLAB function sort(•), obtain index vectors Index1 and Index2 from k1 and k2, respectively.

  4. Step 4.

    From i = 1 to i = height, apply the loop operation Q(:, i) = P(:, index2(i)). From i = 1 to i = 4 × width, apply the loop operation Q(:, i) = P(:, index2(i)). Then, the high bit planes are obtained as a row vector H = reshape(Q, 1, 4 × height × width).

  5. Step 5.

    Extract the low bit planes in the corresponding channel and reconstruct the bit matrix. For the first through the fourth bits, BPi(i = 1, 2, 3, 4)can be obtained and reshaped as BPi = reshape(BPi, 1, height × width). Then, the low bit planes can be expressed as L = [BP1 BP2 BP3 BP4 ]1 × (4 × height × width).

  6. Step 6.

    With the above coarse-grained methods and logistic map (1), generate a 4 × height × width encryption key k, and sort k to obtain the corresponding vector Index. From i = 1 to i = 4 × height × width, conduct the loop operation O(1, i) = L(1, index(i)). Then, reset L = O, and complete the scrambling process.

It can be observed that both the CFLCS and the logistic map chaotic signals are utilized in the scrambling. In addition, high bits and low bits are scrambled using different methods according to the importance of different bits to make the scrambling robust. For the CFLCS, three different keys based on coarse-grained chaotic signals in different states can be applied in the scrambling of the R, G, and B channels simultaneously, thereby making the encryption more efficient.

2.2 Diffusion analysis

In any R, G, or B channel, for bit vectors H and L after scrambling, the following diffusion operations should be applied:

  1. Step 1.

    With a logistic map (1), generate chaotic signals, and apply a coarse-grained process with parameter C to obtain diffusion key T. Reset Ts = mod(floor(T × 1014), 256), and extract the bit vectors BCi(i = 1, 2, ⋯, 8) from Ts. Then, reconstruct vectorsB1and B2 as B1 = [BC1 BC3 BC5 BC7 ]1 × (4 × height × width) and B2 = [BC2 BC4 BC6 BC8 ]1 × (4 × height × width), respectively.

  2. Step 2.

    Based on the calculation, obtain the summation of all bits in BPi(i = 5, 6, 7, 8) as sum1. Next, obtain the summation of all bits in BPi(i = 1, 2, 3, 4) as sum2. Apply a cyclic shift operation asL = circshift(LΤ, C × sum1 + sum2)Τ.

  3. Step 3.

    Move on to the diffusion with the XOR operation as follows:

$$ \left\{\begin{array}{l}L(1)=L(1)\oplus H(1)\oplus L\left(4\times height\times width\right)\oplus {B}_1(1)\\ {}L(i)=L(i)\oplus H(i)\oplus L\left(i-1\right)\oplus {B}_1(i),i=2,3,\cdots, 4\times height\times width,\end{array}\right.. $$
(4)
  1. Step 4.

    Analogously, for high bits, apply a cyclic shift operation as H = circshift(HΤ, C × sum2 + sum1)Τ. Then do the XOR operation as:

$$ \left\{\begin{array}{l}H(1)=L(1)\oplus H(1)\oplus H\left(4\times height\times width\right)\oplus {B}_2(1)\\ {}H(i)=L(i)\oplus H(i)\oplus H\left(i-1\right)\oplus {B}_2(i),i=2,3,\cdots, 4\times height\times width,\end{array}\right.. $$
(5)
  1. Step 5.

    Recombine the color image with the derived bit streams in the R, G, and B channels after the diffusion. The encryption is then complete.

Similar to the scrambling, the diffusion of high bit streams and low bit streams are different. In addition, the proposed encryption is a symmetrical encryption method, and the encrypted image can be recovered with a completely reversed decryption process.

3 Performance analysis

In this section, simulations to analyze the encryption algorithm are conducted using MATLAB R2014a on identical Thinkpad L470 laptops running Microsoft Windows 10, with a 2.70 or 2.90 GHz Intel(R) Core(™) i7-7500U CPU and 16.0 GB of RAM. The color images included “Girl.tiff,” “Tree.tiff,” “House.tiff,” and “Baboon.tiff.” and these images are from test collections USC-SIPI. Using the aforementioned methods, the original, encrypted, and decrypted images are shown in Fig. 4.

Fig. 4
figure 4

Encryption and decryption results: a Original image of Girl, b Encrypted image of Girl, c Decrypted image of Girl, d Original image of Baboon, e Encrypted image of Baboon, f Decrypted image of Baboon, g Original image of Tree, h Encrypted image of Tree, i Decrypted image of Tree, j Original image of House, k Encrypted image of House, l Decrypted image of House

Full size image

Figures 4a-c present a Girl image, an encrypted Girl image, and a decrypted Girl image, respectively. Figures 4d-f depict a Baboon image, an encrypted Baboon image, and a decrypted Baboon image, respectively. Figures 4g-i show a Tree image, an encrypted Tree image, and a decrypted Tree image, respectively. Figures 4j-l present a House image, an encrypted House image, and a decrypted House image, respectively. It can be observed that, for different color images, any information in the encrypted images is difficult to identify, and the encrypted image can be successfully recovered.

3.1 Histogram analysis

In this section, histograms of the original image and an encrypted image are described. It should first be noted that a histogram is used to display the distribution pixel information of an image, and an ideal algorithm can generate an encrypted image with uniformly distributed histograms. If the histograms are sufficiently flat, a statistical attack will be useless in the pixel analysis. Taking the Lena image as an example, the distributions of all 256 pixels are as shown in Fig. 5.

Fig. 5
figure 5

Histogram of original images and encrypted Lena images: a Original image of Lena, b Encrypted image of Lena, c Red component of (a), d Red component of (b), e Green component of (a), f Green component of (b), g Blue component of (a), h Blue component of (b)

Full size image

Histograms of the encrypted images are presented in Fig. 5d, f, h. Compared with the histograms in Fig. 5c, e, g before encryption, the histograms after encryption are flat and can effectively resist a statistical attack.

3.2 Key space analysis

For a robust algorithm, larger key space means the algorithm is more secure because one cannot find out the correct keys from the large key space. From the global encryption process described in sections 2.1 and 2.2, it can be observed that three discrete logistic chaotic series and a fractional chaotic series will be generated. Let us suppose that the computational accuracy is 10−15, the key space of the discrete initial values for logistic chaos is 1015 × 3, and the key space of the parameter for logistic chaos is (4 − 3.57) × 1015 × 3. Assuming that the coupling number of the lattices is n = 10, the fractional order is 0 < q ≤ 1, and the coupling strength is 0 < ε < 1. Then, the key space of the parameter for CFLCS chaos is 1015 × 2, and the key space of the discrete initial values for logistic chaos is 1015 × 10. The entire key space is at least (4 − 3.57) × 10270, and the key space is sufficiently large to resist the force attack effectively. In addition, for the coarse-grained chaotic methods, different coarse-grained parameters lead to different chaotic signals (from Fig. 1). Thus, the key signals are can vary based on the strength of the security.

3.3 Information entropy analysis

Information entropy is one of the most important properties in the analysis of the encryption performance. By defining the information source as m, the information entropy formula can be depicted as follows:

$$ H(m)=\sum \limits_{i=0}^{L-1}p\left({m}_i\right)\mathit{\log}\frac{1}{p\left({m}_i\right)} $$
(6)

where L is the total number of symbols, and function p(•) is the occurrence probability of the corresponding symbol. In general, the information entropy is close to the ideal value of 8 if the encryption algorithm is good. In this paper, the information entropies of the proposed algorithm for different color images are listed in Table 2, and comparisons of the proposed algorithm with some of the latest effective encryption algorithms are listed in Table 3. Compared with previous studies, our entropy schemes are slightly larger; thus, when our scheme is used, the encrypted images can effectively resist possible statistical analysis attacks.

Table 2 Information entropies of encrypted images
Full size table
Table 3 Information entropy comparisons of “Lena image” with some Ref.
Full size table

3.4 Differential attack analysis

To resist the differential attack, two criteria, namely the number of pixels change rate (NPCR) and the unified average changing intensity (UACI), are utilized to analyze the effectiveness. NPCR and UACI are based on a test of two encrypted images generated from the original images with just one bit being slightly different. The ideal values for NPCR and UACI are 99.6094% and 33.4635%, respectively. The NPCR and UACI of our proposed method for different color images are listed in Table 4, and comparisons of the NPCR and UACI obtained using our method with those obtained using other methods are listed in Table 5. Compared with previous studies, the values of NPCR and UACI obtained using the proposed method are closer to the ideal values.

Table 4 NPCR and UACI for encrypted color images
Full size table
Table 5 NPCR and UACI comparisons of “Lena image” with some Refs
Full size table

3.5 Correlation of adjacent pixels

To test resistance to a statistical attack further, the correlation is selected to test the relationship between two adjacent series. In general, the correlations in the original image are always close to 1, but in the encrypted images, they are close to zero. In the following image analysis, correlations between two adjacent pixels horizontally, vertically, and diagonally for different color images are presented in Table 5, and comparisons of these values with those obtained using other methods are shown in Table 6. The related correlation equations for two pixel series x = {xi} and y = {yi} are defined as follows:

$$ \left\{\begin{array}{l}{r}_{xy}=\frac{\operatorname{cov}\left(x,y\right)}{\sqrt{D(x)}\sqrt{D(y)}}\\ {}\operatorname{cov}\left(x,y\right)=\frac{1}{N}\sum \limits_{i=1}^N\left[{x}_i-E(x)\right]\left[{y}_i-E(y)\right]\\ {}D(x)=\frac{1}{N}\sum \limits_{i=1}^N{\left[{x}_i-E(x)\right]}^2\\ {}E(x)=\frac{1}{N}\sum \limits_{i=1}^N{x}_i\end{array}\right. $$
(7)
Table 6 Correlations of the original image (OI) and corresponding encrypted image (EI)
Full size table

In addition, by taking the airplane image as an example, the horizontal, vertical, and diagonal correlation scatter diagrams of the original and encrypted images are as shown in Figs. 6 and 7, respectively. Figure 6a, e, and i are three components of the airplane image. Figure 6b, c, and d show the horizontal, vertical, and diagonal correlation values in the red channel. Figure 6f, g, and h depict the horizontal, vertical, and diagonal correlation values in the green channel. Analogously, the horizontal, vertical, and diagonal correlation values in the blue channel are presented in Fig. 6j, k, and l. It can be observed that the correlation values in the original image are extremely high. By contrast, these correlation values in the encrypted components in Fig. 7b-d, f-h, and j-l are low, and adjacent pixels cover the corresponding whole plane. In addition, from Table 6 and Figs. 6 and 7, it can be observed that the proposed method is effective at not only encrypting different types of images to resist a statistical attack but also breaking the relationships between adjacent pixels.

Fig. 6
figure 6

Adjacent pixel correlation of the original Airplane image: a R component, b Horizontal of (a), c Vertical of (a), d Diagonal of (a), e G component, f Horizontal of (e), g Vertical of (e), h Diagonal of (e), i B component, j Horizontal of (i), k Vertical of (i), l Diagonal of (i)

Full size image
Fig. 7
figure 7

Adjacent pixel correlation of the encrypted Airplane image: a R component, b Horizontal of (a), c Vertical of (a), d Diagonal of (a), e G component, f Horizontal of (e), g Vertical of (e), h Diagonal of (e), i B component, j Horizontal of (i), k Vertical of (i), l Diagonal of (i)

Full size image

3.6 Key sensitivity analysis

A key sensitivity analysis is provided in this section. According to the image encryption technology, a good encryption algorithm will lead to an unfeasible decryption from even a minuscule key change. In the following analysis, the sensitivity of the keys for logistic map parameter u and coarse-grained parameter C will be provided. Set a minuscule change of δ = 10−15for key u, and add a change of 1 for key C. Taking the Lake image as an example, the derived encryption and decryption images are as shown in Fig. 8.

Fig. 8
figure 8

Key sensitive analysis of the color Lake image: a The original image of the Lake, b Encrypted image of (a), c Encrypted image of (a) with modified u, d Difference of (b) and (c), e Encrypted image of (a) with modified C f Difference of (b) and (e), g Decrypted image of (a) with u and C, h Decrypted image of (c), i Decrypted image of (e), j Decrypted image of (a) with modified u k Decrypted image of (a) with modified C

Full size image

Figure 8a shows the original Lake image, and Fig. 8b is an encrypted image with correct keys u and C. With the change in parameter u, the image in Fig. 8a is encrypted as shown in Fig. 8c, and the differences between Fig. 8b and c can be seen in Fig. 8d. It can be concluded that the tiny change in u will result in completely different encrypted images. Analogously, the same conclusion for key C can be derived in Fig. 8e and f. With correct keys, the image in Fig. 8b can be recovered as in Fig. 8g. However, when the correct keys and algorithm are used, the images in Fig. 8c and e will not be decrypted, as shown in Fig. 8h and i. In addition, the changed keys will not decrypt the image in Fig. 8b, as shown in Fig. 8j and k. From Fig. 8, it can be observed that the images will be recovered using only the exactly correct parameters, thereby demonstrating that our proposed algorithm is a robust algorithm with good key sensitivity.

In order to further test the key sensitivity and do contrast test with other algorithms, the MSE(Mean Square Error) and PSNR(Peak Signal to Noise Ratio) analysis are done in the Lena image as following Table. 7.

Table 7 MSE and PSNR of Lena image
Full size table

From Table 7, it can be found that MSE values are all very large and PSNR values are all smaller than 10 in different components. Compared with listed references, the proposed algorithm has larger MSE values and smaller PSNR values. It means the algorithm is very sensitive to keys and it is robust to resist to possible key attacks.

3.7 Plain-text sensitivity analysis

Similar to a key sensitivity analysis, the plain-text sensitivity analysis is another important index for testing the encryption algorithm. This means that a good algorithm should also be sensitive to tiny changes in the plain-text information. Taking the Peppers image as an example, by changing the pixel at position (10,10) by only 1 bit, the derived results are as shown in Fig. 9.

Fig. 9
figure 9

Plain-text sensitive analysis of the color Peppers image: a The original image of the Peppers, b Encrypted image of (a), c Encrypted image of (a) with one-bit change, d Difference of (b) and (c)

Full size image

Figure 9a is the original image of the Peppers and Fig. 9b is the encrypted image with no change in the plain-text. With the tiny changed plain-text, the image Fig. 9a is encrypted as Fig. 9c and the difference between Fig. 9b and c can been seen in Fig. 9d. It can be concluded that our proposed algorithm is a robust algorithm with good plain-text sensitivity.

3.8 Resistance to salt-and-pepper noise

There are different types of noise in practice, among which salt-and-pepper noise is a typical example and has a strong influence on the encrypted image. To test the resistance, three salt-and-pepper noises with different intensities were considered in color Baboon, Car, and Map images. The encrypted images with salt-and-pepper noise and the recovered images are shown in Fig. 10.

Fig. 10
figure 10

Encryption and decryption with salt-and-pepper noise: a Encrypted image with noise intensity 0.02, b Encrypted image with noise intensity 0.05, c Encrypted image with noise intensity 0.1, d Decrypted image of (a), e Decrypted image of (b), f Decrypted image of (c)

Full size image

Figure 10a shows an encrypted Baboon image with a noise intensity of 0.02. Figure 10b presents an encrypted Car image with a noise intensity of 0.05. Figure 10c shows an encrypted Map image with a noise intensity of 0.1. Figure 10d–f present the corresponding decrypted images. It can be observed that the recovered images are all recognizable under different noise intensities, thereby indicating that the proposed method is robust to noise attacks.

3.9 Resistance to cropping attacks

The information in an image may not only be influenced by noise but also become lost during the storage procedure. To test resistance to information loss, we added cropping attacks to the encrypted images of Female, House, Tree, and Map2. In addition, different information loss percentages are considered. The experiments are shown in Fig. 11.

Fig. 11
figure 11

Encryption and decryption with cropping attack: images with following cropping proportions a 6.25%, b 25%, c 50%, d 56.25%, e Decrypted image of (a), f Decrypted image of (b), g Blue component of (c), h Decrypted image of (d)

Full size image

Figure 11a shows an encrypted Female image with 6.25% information loss. Figure 11b shows an encrypted House image with 25% information loss. Figure 11c shows an encrypted Tree image with 50% information loss. Figure 11d shows an encrypted Map2 image with 56.25% information loss. Finally, Fig. 11e–h present the corresponding decrypted images. It can be observed that the recovered images are all recognizable under the different information loss percentages, thereby indicating that the proposed method is robust to cropping attacks.

4 Conclusion

In this paper, a color image encryption algorithm based on coarse-grained chaotic keys is proposed. The coarse-grained method enables the derived chaotic series to be unfixed even with same initial value and chaotic parameter. In addition, both a discrete logistic map and a fractional chaotic system are utilized to generate chaotic signals for the coarse-grained process. During the encryption process, parallel bit-level scrambling, including a high bit row, column scrambling, and low bit global scrambling, are operated. In addition, a further cyclic shift and XOR diffusion are applied to the diffused bit streams. During the simulation, the key space, information entropy, correlation analysis, key sensitivity, plain-text sensitivity, and resistance to differential, noise, and cropping attacks are presented, thereby demonstrating the advantages of the proposed approach. Both theoretical analysis and simulation results indicate that the coarse-grained fractional chaotic encryption algorithm is effective and robust to various types of attacks.