1 Introduction

Digital information has evolved through decades with extensive growth in its capabilities. In particular, the past 10 years have seen a massive increase in usage of digital data accompanied with day-to-day advancing electronic devices such as smartphones, robotic devices, electronic readers, etc. Such devices ascertain fast processing, immense data storage and computational capabilities. The security concern related to data dissemination, especially images and videos, is still an active area of research. As compared to advancements in technology, most of the security measures such as encryption schemes are based on methodologies that were followed 10 years ago. The classical methods that include data encryption standards (DES), advanced encryption standards (AES), blowfish, etc. are not suitable for bulk data [1, 2] such as image and video. This prompted researchers to come up with some alternative methods for bulk data encryption rather than relying on pure number theory.

For image encryption, there are numerous methods proposed in the literature that include dynamical chaos-based ciphers [3,4,5] and their hybridization with finite state machine [6], with optimized S-Box generation [7], cascade coupling [8, 9], higher dimensional chaos with DNA [10], parallel with compressive sensing [11]. On the other hand, optical transforms-based image encryption is an active area of research due to the inherent property of high speed and massive parallelism. The transform orders that provide an extra degree of freedom to the encryption scheme serve as secret keys. The transform-based image encryption is inspired from the classical double random phase encoding scheme (DRPE) [12,13,14] which is implemented with an optical setup comprising of lenses, spatial light modulators (SLM) and charged coupled devices (CCD). Most commonly used optical image encryption schemes include Fractional Fourier transform (FrFT) [15,16,17,18], Fresnel transform [19, 20], Gyrator transform [21, 22], Mellin transform [23, 24], Hartley transform [25,26,27], etc.

According to a recent survey reported by Ghadirili et al. [28], 32.03% of total published works on image encryption are based on chaos and only 8.65% are based on transform domain-based encryption schemes. Although the optical transform-based algorithms offer high speed, parallel data processing and thus for image encryption, provide greater flexibility for manipulating parameters such as wavelength, polarization, amplitude or phase but still their usage in practical implementation is less preferred owing to drawback related to complex domain outcome and smaller keyspace. Various researches on cryptanalysis have shown that these algorithms are vulnerable to chosen-plaintext attack (CPA), known-plaintext attack (KPA) and some heuristic attacks [29,30,31]. Chen et al. [29] suggested that a larger keyspace is required to avoid blind decryption. The reuse of keys should also be avoided [31] following a one-time pad approach.

As mentioned by Ghadirili et al. [28], chaos-based image encryption is preferred owing to its inherent characteristics of high sensitivity to seed values, randomness and ergodicity. The chaotic maps are broadly classified as 1D or higher dimensional maps, whereas 1D maps are simple in hardware implementation but due to certain flaws such as the existence of blank windows in bifurcations, smaller keyspace, etc., lead to their vulnerability to potential attacks [5, 32]. On the other hand, higher dimensional chaotic maps are complex and have larger keyspace but are not cost-effective in hardware implementation [33, 34]. Hybridization of chaotic maps is looked upon as one of the solutions to overcome these limitations [28, 35]. Working toward hybridization, there are number of schemes recently proposed [27, 36,37,38,39] that combine chaos with transform domain encryption. Such schemes are based on combination of chaos-dependent permutation along with a particular transform for making the image unintelligible where the order of their application may vary. Either permutation is followed by transform or permutation is performed in the spatial domain prior to transform. However, such schemes are unable to provide enough security although their immunity to noise and data occlusion attacks is fairly good [39, 40]. Moreover, many such schemes fail to provide testimony against most of the classical attacks and differential attacks [29, 30, 41, 42]. Some of the most recently proposed schemes [18, 22, 26, 40, 43,44,45,46] lack such analysis.

Keeping into consideration all above-stated limitations in the transform and chaos-based encryption schemes, we propose a novel opto-digital method of color image encryption in which the image to be encrypted is initially processed nonlinearly in the spatial domain with the help of a compound chaotic mapping followed by a reality preserving 2D fractional Hartley transform operation to convert the processed image in the optical domain. The transform coefficients obtained are further scrambled with the help of a piecewise linear chaotic map to enhance the security. The input parameters of chaotic maps thus used and the fractional-order of the fractional Hartley transform serve as the secret symmetric keys for encryption/decryption. The performance and security analyses prove that the proposed scheme is robust and efficient for the secure transmission of images. The proposed scheme is highly sensitive to the keys and has a larger keyspace and thus can withstand various cryptanalytic attacks. Its distinct feature of the complete elimination of the complex coefficient terms makes it suitable for real-time image transmission.

This paper is organized as follows: Introduction in Sect. 1 is followed by Sect. 2 that describes the preliminaries such as fractional transform, reality preserving methodology, chaotic maps, compound mapping, etc., used in the proposed image encryption method. Section 3 elaborates the step-by-step procedure used for the proposed image encryption/decryption, and Section 4 gives the results of performance and security analyses of the proposed scheme. A comparative analysis is included in Sect. 5. Finally, the work is concluded in Sect. 6.

2 Preliminaries

2.1 Fractional integral transform

Fractional transforms have found many applications in the field of engineering and science ever since the advent [16, 47, 48] and later for applications in optics [15, 49, 50]. With the evolution of the digital era, the fractional transforms were studied for their digital representations [17, 51, 52]. The ordinary Fourier transform is the generalized form of fractional-order transforms where the transform order is unity. The integer orders when replaced with fractional orders expand the application area of these transforms. Particularly in optical processing, these transforms are useful in digital holography, as means of modeling speckle fields propagating through apertured optical systems, in quantum optics, in optical encryption by means of random phase encoding (DRPE), in wave field theory to describe the reflection of coherent light from a non-uniform surface which is beneficial in meteorology. The basic form of the integral transform is the Fourier transform. Fourier is obtained following integral representations for \(f\left(x\right)\) and its nth integral as:

$${D}^{n}f\left(x\right)=\frac{1}{2\pi } {\int }_{-\infty }^{\infty }f\left(\xi \right)\mathrm{d}\xi {\int }_{-\infty }^{\infty }{t}^{n} \mathrm{cos}\left\{t\left(x-\xi \right)+\frac{n\pi }{2}\right\}\mathrm{d}t$$
(1)

where \(\xi \) depicts the frequency. Replacing ‘\(n\)’ by an arbitrary fractional number ‘\(\alpha \)’ gives the fractional-order equivalent transform of the function \(f\left(x\right).\) The arbitrary angle \(\alpha \) corresponds to the angle of rotation in the time–frequency domain. It is also understood as the Wigner rotation as explained in position–momentum paradigm [15]. The fractional transform integral is said to be in purely time domain for \(\alpha \) = 0 and in purely frequency domain if \(\alpha \) = 1. Thus, a fractional order corresponds to the collective time–frequency domain which gives an extra degree of freedom for its application to image encryption. The Fourier transform and Hartley transform are closely related [25, 52] as the eigenvalues of the DFT are also the eigenvalues of the Hartley transform. Thus, a fractional Hartley transform can also be represented by a fractional Fourier transform [5, 7]. Hartley transform of a function \(f\left(x\right)\) is given by

$$H\left(\zeta \right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f\left(x\right)\mathrm{cas} \left(\zeta x\right)\mathrm{d}x$$
(2)

where radian frequency variable \(\zeta =2\pi f\) and \(\mathrm{cas}\) function is defined as \(\mathrm{cas}\left(\zeta {x}\right)=\mathrm{cos}\left({\zeta x}\right)+\mathrm{sin}\left({\zeta x}\right)\). The fractional Hartley transform of a time-domain signal is defined as:

$${H}^{\alpha }\left\{f\left(t\right)\right\}\left(\zeta \right)={\int }_{-\infty }^{\infty }f\left(t\right){S}_{\alpha }\left(t,\zeta \right)\mathrm{d}t$$
(3)

where the fractional Hartley kernel is defined as:

$${S}_{\alpha }\left(t,\zeta \right)={\left(\frac{1-j\mathrm{cot}\alpha }{2\pi }\right)}^{1/2} {e}^{\frac{j{\zeta }^{2}}{2}\mathrm{cot}\alpha } {e}^{\frac{j{t}^{2}}{2}\mathrm{cot}\alpha }*\frac{1}{2}\left[\left(1-j{e}^{j\alpha }\right)\mathrm{cas}\left(\mathrm{csc}\alpha \cdot \zeta t\right)+ \left(1+j{e}^{j\alpha }\right)\mathrm{cas}\left(-\mathrm{csc}\alpha \cdot \zeta t\right)\right].$$
(4)

In the discrete domain, the eigenvectors of discrete fractional Fourier transform (DFrFT) are also the eigenvectors of discrete fractional Hartley transform (DFrHT). Thus, in terms of the Fourier transform, FrHT for a 2D signal can be represented as:

$${H}^{\alpha ,\beta }\left(u,v\right)=\left(1-\frac{\mathrm{exp}\left[j\left({\phi }_{1}+{\phi }_{2}\right)\right]}{2}\right){F}^{\alpha ,\beta }\left(u,v\right)+\left(1+\frac{\mathrm{exp}\left[j\left({\phi }_{1}+{\phi }_{2}\right)\right]}{2} \right){F}^{\alpha ,\beta }\left(-u,-v\right)$$
(5)

where \({F}^{\alpha ,\beta }\) corresponds to the fractional Fourier transform coefficient, \({\phi }_{1 }=\frac{\alpha \pi }{2}\), \({\phi }_{2}=\frac{\beta \pi }{2}\), \(\left|{\phi }_{1}\right|,\left|{\phi }_{2}\right|< \pi \), \(\left(u,v\right)\) represent the transform domain.

Therefore, fractional Hartley transform is the real part of fractional Fourier transform plus the negative of the imaginary part of the fractional Fourier transform [27]. The DFrHT possesses all the basic properties that are required in a fractional integral transform. The optical realization of fractional Hartley is described in [53]. However, the transform coefficients of a fractional Hartley transform are complex. These complex values need a holographic technique to record two images, one for spectrum and another for phase. This makes the storage and transmission less efficient due to double memory space requirements. Moreover, the computation complexity also increases during inverse operation.

2.2 Reality preserving method

The reality preserving concept was first introduced by Venturini and Duhamel [54] to overcome the complexity issue in the transform domain, where a reality preserving alternative to the complex fractional cosine and sine transforms was proposed. The reality preserving algorithm maintains most of the desired properties of the transform. As the resulting transform can have continuously increasing decorrelation power as the fractional order varies from ‘0’ to ‘1’ with an order of ‘0’ corresponding to no decorrelation and order of ‘1’ corresponding to a base transform with maximum decorrelation. This decorrelation power is used in various signal processing applications. Reality preserving can be employed where an orthogonal reality preserving transform is required and the de-correlating power is to be controlled by some parameter. The steps for deriving a reality preserving equivalent of FrHT are as follows:

Step 1 For a 1D FrHT of length, \({\rm M}\): Let \({\mathcal{H}}_{\mathcal{a},\frac{M}{2}}\) be a complex-valued fractional Hartley transform matrix with size \(M/2\)(\(M\) is even). The real input signal is represented by \(y= {\left\{{y}_{0},{y}_{1},{y}_{2},\dots {y}_{M-2},{y}_{M-1}\right\}}^{t}\) from which a permutation matrix (P) is obtained as, \({y}^{{\prime}}= {\left\{ {y}_{0}^{{\prime}},{y}_{1}^{{\prime}},{ y }_{2}^{{\prime}}, {\dots y}_{M-2}^{\prime} {{y}_{M-1}^{{\prime}}}\right\}}^{t}\) denoted as \({y}^{{\prime}}=Py\),

Step 2 \( \widehat{y}=\left\{{y}_{0}^{{\prime}}+\left.j{y}_\frac{M^{\prime}}{2}\right| \left.{y}_{1}^{\prime}+{y}_{{\frac{M}{2}+1}}^{\prime}\right|\ldots \left.{y}_{\frac{M}{2}-1}^{\prime}+jy_{2}^{\prime}\right|\left.y^{\prime}+jy_{M-1}^{\prime}\right|\right\}^{t}\) is the complex vector built from \(y\). Further, a transform output is obtained from this complex vector such that,

$$\widehat{z}={FrH}^{\mathcal{a} }\left(\widehat{y }\right).$$

Step 3 The Reality preserving equivalent of transform is obtained as \({z}^{{\prime}}=\left\{\left(Re\, \widehat{z}\right), \left(Im \,\widehat{z}\right)\right\} ; z= {P}^{-1}({{z}^{{\prime}})}^{t}\), t represents transpose. Thus, \(z= {P}^{-1}{\mathrm{RPFrHT}}_{\mathcal{a}}Py\)

$${\rm RPFrHT}_{\mathcal{a}}=\left[\begin{array}{cc}Re({\mathcal{H}}_{\mathcal{a}})& -Im({\mathcal{H}}_{\mathcal{a}})\\ Im({\mathcal{H}}_{\mathcal{a}})& Re({\mathcal{H}}_{\mathcal{a}})\end{array}\right]{\mathrm{is}\,\mathrm{obtained}\,\mathrm{from}}\,{\mathcal{H}}_{\mathcal{a},M/2}+j{\mathcal{H}}_{\mathcal{a},M/2}.$$
(6)

2.3 Chaotic maps

Dynamical chaos, observed in many nonlinear dynamical systems, is a deterministic, bounded, aperiodic behavior possessing sensitivity on initial conditions/system parameters. Along with the crucial feature of sensitivity on the initial condition, chaotic systems possess many other interesting and universal features like ergodicity, mixing, invariant density measure, positive metric entropy (KS-entropy), etc. These features make them suitable for use in secure communication. During the last two–three decades, the use of chaotic systems has been explored extensively and a well-defined close relationship between chaotic systems and ideal cryptographic systems has emerged [33]. According to Shannon [55], in order to attain a perfect secrecy, a combination of diffusion and confusion is essential in a cryptographic system. For images, which are characterized by the bulk of data, high correlation and redundancies, the chaotic systems have been found most suitable for achieving the desired level of permutation and substitution [4, 34]. In the proposed image encryption, we use chaotic systems as the source for introducing confusion and diffusion in conjunction with the optical process governed by the reality preserving fractional Hartley transform. The purpose of using transform is to bring the data from the spatial domain to the combined time–frequency domain so that the chaos-based analysis may not be feasible for the intruder. In the following paragraph, we briefly describe the chaotic systems being used in the proposed image encryption scheme.

2.3.1 For permutation/scrambling stage: Piecewise linear chaotic map (PWLCM)/Zhao map

The mathematical form of PWLCM [56] used for diffusion in the proposed image encryption scheme is as follows:

$$ f\left( {y,\varepsilon } \right) = \left\{ {\begin{array}{*{20}l} {\frac{y}{\varepsilon }, } \hfill & { y \in \left[ {0,\varepsilon } \right) } \hfill \\ {\frac{y - \varepsilon }{{\frac{1}{2} - \varepsilon }}, } \hfill & { y \in \left[ {\varepsilon ,\frac{1}{2}} \right]} \hfill \\ {F\left( {1 - y,\varepsilon } \right),} \hfill & { y \in \left( { \frac{1}{2}, 1} \right]} \hfill \\ \end{array} } \right. $$
(7)

where \(\varepsilon \) (\(0<\varepsilon <1/2)\) is the control/system parameter. If \(Y \in \left[\mathrm{0,1}\right]\), it is known as normalized PWLCM. In this paper, we are using a normalized PWLCM [57] that can be expressed using a simple affine transformation:

$${F}_{\left[\mathrm{0,1}\right]}\left(y\right)=\frac{F\left(\frac{y-{\gamma }_{1}}{{\gamma }_{2}-{\gamma }_{1}}\right)-{\gamma }_{1}}{{(\gamma }_{2}-{\gamma }_{1})}{:}\,\left[\mathrm{0,1}\right]\to \left[\mathrm{0,1}\right].$$
(8)

2.3.2 For substitution: Compound chaotic maps

Due to some inherent weaknesses in one-dimensional maps for cryptographic applications [41] and to enhance the robustness in the complete parameter range, researchers have used a combination of chaotic systems, i.e., compound chaotic map [3, 8, 58]. In the proposed work, we use a similar nonlinear combination of three seed maps, \(F\left({x}_{n}\right),G\left({x}_{n}\right)\) and \(H({x}_{n})\). A compound chaos is defined by, \({x}_{n+1}=\left(F\left(G\left({x}_{n}\right)\right)+ H\left({x}_{n}\right)\right)\mathrm{mod}\,1\). The mod operation is to ensure that the output sequence is restricted in the range [0, 1]. The combination of the two maps improves the chaotic behavior [8]. Further, the addition of the third map (modulo 1) enhances the mixing and results in enhanced complexity.

In the proposed image encryption scheme, logistic map (L), tent map (T), and sine map (S) are used for compound mapping.

  1. (a)

    Logistic map: It is originally introduced as a demographic model [59] and is mathematically defined as:

    $${x}_{n+1}=L\left({x}_{n}\right)=\mu {x}_{n}\left(1-{x}_{n}\right)=4r{x}_{n}\left(1-{x}_{n}\right) , 0<{x}_{n}<1$$
    (8)

    where \(\mu \in \left[\mathrm{0,4}\right]\) or \(r\in [\mathrm{0,1}]\) is the control parameter, also known as the bifurcation parameter. The 1D logistic map is chaotic for its control parameter range as \(0.9\le r <1\).

  2. (b)

    Tent map: It is the simplest piecewise linear chaotic map and is a topological conjugate of logistic map [60] defined in the interval [0, 1] and mathematically described as:

    $$ x_{n + 1} = T\left( {x_{n} } \right) = \left\{ {\begin{array}{*{20}l} {2rx_{n} ,} \hfill & {{\text{if}}\,0 \le x_{n} \le 0.5} \hfill \\ {2r\left( {1 - x_{n} } \right) , } \hfill & {{\text{if}}\,0.5 < x_{n} \le 1 } \hfill \\ \end{array} } \right. $$
    (10)

    where \(0<r\le 1\). The chaotic behavior is observed for \(0.61<r<1\)

  3. (c)

    Sine map: Sine map is another simplest 1D nonlinear map [32], mathematically described as:

    $${x}_{n+1}=S\left({x}_{n}\right)=r{{\rm sin}}\left(\pi {x}_{n}\right).$$
    (11)

The chaotic behavior in this map is observed for \(r\in \left[0.87, 1\right]\). It is qualitatively identical to the logistic map as the topological entropy of the sine map is equal to that of the logistic map at \(r=1.\) Figure 1 illustrates the complete schematics of developing these three compound chaotic maps (CCM), CCM1, CCM2, and CCM3. The mathematical representation of each CCM is given in Table 1.

Fig. 1
figure 1

Generation of compound chaotic maps form basic maps

Full size image
Table 1 Mathematical representation of compound chaotic maps
Full size table

3 Encryption and decryption procedure


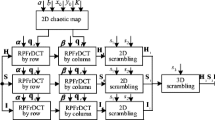
In this section, we describe the processes of encryption and decryption in detail. The proposed encryption process is based on three different stages. A chaos-based substitution/confusion in the spatial domain is the first stage followed by optical processing using reality preserving fractional Hartley transform and finally the third stage of chaos-based diffusion /scrambling in the transform domain. There are a total of 24 keys used in the encryption process that includes nine keys for confusion (first stage), six keys for optical transform and then nine keys for scrambling in the transform domain.

Encryption

3.1 Stage 1: Substitution based on compound chaos (CCM)

The input image ‘P’ of size \(M\times N\times 3\) is decomposed into its red (R), green (G) and blue (B) component images each of size \(M\times N\). The first level of encryption is based on compound chaotic maps described in Sect. 2.3.2. For example, the CCM used for the red component \({(R)}_{M\times N}\) is \(\left({T}\left({L}\right)+{L}\right) {\rm mod}\,1\) compound chaotic map (CCM1) with parameters \(\{{c1}_{0},u1,i1\}\) where \({\mathrm{c}1}_{0}\) denotes the initial value, \(u1\) is the bifurcation parameter and \(\mathrm{i}1\) is the number of iterations to be discarded as transient. For CCM1, a chaotic sequence is iterated for \(i1+MN\) different values, i.e., {\({c1}_{i1+M\times N}\}\). The initial \(i1\) iterations are discarded in order to avoid any computational error and also to increase the security. A similar process is followed for other CCMs. The values of sequence thus obtained are in floating point. These are converted to integer form as:

$$\widehat{c}=\left({c}_{\left(1\times M\times N\right)}\times {10}^{14}\right) \mathrm{mod}\,256.$$
(12)

The integer sequence is then reshaped to a 2D image of size \(M\times N\) and is used for the substitution of each color component of the input image, \({P}^{{\prime}}\in [R,G,B]\) as:

$$S=bitxor\left({\widehat{c}}_{\left(M\times N\right)},{{P}^{{\prime}}}_{\left(M\times N\right)}\right).$$
(13)

3.2 Stage 2: Reality preserving 2D fractional Hartley transform

The outcome from Stage 1 in the spatial domain is then transformed via a fractional Hartley transform with a reality preserving algorithm. The transformation results in the complex coefficients which in optical processing require special holographic techniques for recording. In the digital domain, it becomes difficult to store and transmit the complex coefficients as it leads to increased complexity and memory requirements. To overcome such issues, a reality preserving algorithm [54] is used to obtain transform in the real domain as explained in Sect. 2.2. The substituted outcome of Stage 1 is transformed using the steps explained in Sect. 2.2. It is likely to mention that 1D transformation has to be extended to 2D for image data. The 1D RPFrHT can be easily extended to 2D by cascading two transforms, one along rows of the image and another along with the columns. This requires two different transform orders \((\alpha ,\beta )\) for both directions. For the sake of brevity, the individual steps of transformation are not again illustrated here. However, to correlate with explanation given in Sect. 2.2, final outcome of 1D RPFrHT for input as substituted image of Stage 1 is represented as:

$$\begin{aligned}\widehat{Z}&=\left\{Re\left(Fr{H}^{\alpha }\left(N\right)\right)+j\times Im\left(Fr{H}^{\alpha }\left(N\right)\right)\right\} \left\{Re\left(\widehat{S}\right)+j\times Im\left(\widehat{S}\right)\right\}\\ \Rightarrow Z&=\left[\begin{array}{c}Re(Fr{H}^{\alpha }\left(N\right)Re\left(\widehat{S}\right)-Im(\left(Fr{H}^{\alpha }\left(N\right)\right)Im\left(\widehat{S}\right)\\ Im\left(Fr{H}^{\alpha }\left(N\right)\right) Re\left(\widehat{S}\right)+Re\left(Fr{H}^{\alpha }\left(N\right)\right) Im\left(\widehat{S}\right)\end{array}\right]\\ &= \left[\begin{array}{cc}Re\left(Fr{H}^{\alpha }\left(N\right)\right)& - Im\left(Fr{H}^{\alpha }\left(N\right)\right)\\ Im\left(Fr{H}^{\alpha }\left(N\right)\right)& Re\left(Fr{H}^{\alpha }\left(N\right)\right) \end{array}\right]\left[\begin{array}{c}Re\left(\widehat{S}\right)\\ Im\left(\widehat{S}\right)\end{array}\right]\\ & \quad \therefore Z=RPDFr{H}^{\alpha }T\left(N\right)\times S\end{aligned}$$
(14)

This 1D \(\mathrm{RPDFrHT}\) can be extended to 2D by following the same procedure as shown above but in y-direction. For that, each column is treated as a different array and the values are wrapped to half along each column to obtain a matrix of dimensions \(M/2\times N\). The transform order along y-direction, i.e., along each column, is denoted by \(\beta .\) Hence, a \(2\mathrm{DRPDFrHT}\) can be described as a cascaded operation of two \(1\mathrm{D RPDFrHT}\)’s as:

$$2{{\rm DRPFr HT}}^{\left\{\alpha ,\beta \right\}}T\left\{{S}_{\left(M,N\right)}\right\}=1{\rm DRPFrHT}^{\left(\alpha \right)}\left(N\right){\cdot S}_{\left(M,N\right)}\cdot 1{\rm DRPFrHT}^{\left(\beta \right)}\left(M\right)$$
(15)

where \(\left(M,N\right)\) represents the size of the image, (\(\alpha ,\beta )\) are the transform orders, \({S}_{\left(M,N\right)}\) is the substituted image of Stage 1. The above-stated procedure is repeated for each color component image with a different set of transform orders.

3.3 Single-bit phase modulation

The transformed image, obtained after reality preserving 2D fractional Hartley transform, in its coefficient has both positive and negative values which are not suitable for optical detection by CCD camera if an optical setup is used. In the digital domain, negative values cannot be realized while storing and retrieving. This issue needs to be handled for the complete recovery of data during the reverse process. A phase modulation method is used with a single bit of the data representing it as either a negative or positive value. This can be termed as a single-bit phase modulation method. In this method, we use a variable \({P}_{b}(u,v)\) which is assigned a bit ‘0’ for positive value and bit ‘1’ for negative value corresponding to the transform coefficients \({h}_{\left(k+1\right)}(u,v)\):

$$ P_{b} \left( {u,v} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\,h_{{\left( {k + 1} \right)}} \left( {u,v} \right) < 0} \hfill \\ {0,} \hfill & {\text{otherwise }} \hfill \\ \end{array} } \right. $$
(16)

This single bit value is extracted for each color component and then is concatenated into a single image. This matrix of size \(M\times N\times 3\) can be used as a public key as it does not reveal any intuitive information about the encrypted data. Moreover, as it is a single-bit matrix, storage and transmission will not be an issue of concern. During the decryption process, the original transform coefficients are obtained as:

$${{h}^{{\prime}}}_{\left(k+1\right)}\left(u,v\right)= {h}_{\left(k+1\right)}\left(u,v\right)\times [{\rm exp}\left(i\pi {P}_{b}\left(u,v\right)\right].$$
(17)

3.4 Stage 3: Chaotic scrambling using PWLCM

As explained in Sect. 2.3.1, a PWLCM map is used for generating a chaotic sequence owing to its LE (Lyapunov exponent) being positive over the entire range of its control parameters. Three different PWLCM or W-maps are used each for red, green and blue components of the transform coefficients obtained in Stage 2. For the transform coefficients of size \(\mathrm{M}\times \mathrm{N}\) corresponding to each color component, the PWLCM with parameters \(\left\{{x}_{0},u,t\right\}\) is iterated for (\(t+M\times N\)) number of iterations and a sequence of \(M\times N\) is generated by discarding first \(t\) terms to avoid any computational error of transients.

Step 1 The chaotic sequence generated by each PWLCM can be represented as:

$${P}_{l}={P}_{t+1 ,}{P}_{t+2 },{P}_{t+3},\ldots {P}_{t+MN-1},{P}_{t+MN}.$$
(18)

Step 2 The chaotic sequence is then sorted in ascending/descending order into a vector, and the index of the vector is stored as the address into another vector as: \(\left[\mathrm{ind},{P}_{s}\right]=\mathrm{sort}({P}_{l})\). This changes the positions of the elements. Record the new index of \({P}_{s}\), i.e., mth element of \({P}_{s}\) corresponds to \(\mathrm{ind}\left\{m\mathrm{th}\right\}\) element of \({P}_{l}\).

Step 3 The 2D transform matrix of Stage 2 is reshaped into the 1D sequence of size \(MN\times 1\). Vectorization is performed to convert \(M\times N\) transform coefficients to a matrix of size \(M\times N\times 1\) by extracting the values column by column.

Step 4 Now, the recorded index of the sorted vector \(\mathrm{ind}\) is used to reorder (permute/scramble) the 1D transform vector as \(\mathrm{RPFrHT}\left(\mathrm{ind}\right).\) Finally, this 1D matrix is converted into 2D image format by reconverting it into \(M\times N\) vector.


In this stage, the initial value, control parameter and number of iterations to be discarded \(\left\{{x}_{0},u,t\right\}\) are used as the secret keys. Therefore, there are a total of nine keys for scrambling (three each for R, G and B individually). The scrambled transform coefficients give a final encrypted image which can now be transmitted over a public channel. The complete encryption process is shown in Fig. 2.

Fig. 2
figure 2

Encryption process

Full size image

Decryption

The decryption procedure is illustrated in Fig. 3. Decryption is exactly the reverse of that of encryption. Exactly the same keys (all 24 keys) are required in each stage of decryption to completely recover the original image, thus making it a symmetric key cryptographic process.

Fig. 3
figure 3

Decryption process

Full size image

The output of Stage 3 of the encryption process which is scrambled transform coefficients is descrambled using the same PWLCM’s with parameters \(\left\{{x}_{0},u,t\right\}\) as used during encryption. The descrambled image components are then inverse transformed with (\({\mathrm{RPFrHT})}^{-1}\) which is similar to the forward transform with the same transform orders but with negative values (six keys). The next step is the generation of the CCMs with nine keys of Stage 1. The generated CCMs need to be exactly same as used during the forward procedure, for them to be substituted with the inverse transform coefficients to retrieve the original image components.

4 Simulation results

The proposed scheme is realized in MATLAB 9.0, on a personal computer with Intel(R) Core (TM) i5 8250U CPU (3.45 GHz), 8 GB RAM, and 1 TB hard disk capacity. Two standard images (Lena, Baboon) taken from the SIPI dataset [61] are considered as test images for visual analysis and statistical analysis. The simulation results for numerical analysis are evaluated for a number of other images taken from the same dataset. The secret keys used in this simulation are randomly generated using a random number generator in MATLAB. The simulations are done with the same set of secret keys throughout this work. The distribution of keys and their corresponding values are given in Table 2.

Table 2 Secret keys in each stage of encryption
Full size table

4.1 Experimental analysis

Figure 4 shows encryption at each stage from left to right. Figure 4a, f shows the original standard color test images (Lena and Baboon). The first stage of encryption is the substitution with compound chaotic maps as described in Sect. 3.1, and the results obtained for this stage using the secret keys (Table 2) for red, green and blue channels, respectively, are shown in Fig. 4b, g. In order to enhance the security, a plain image-dependent session key is generated for each color channel (δr, δg, δb). Also, the session keys are added either to the initial condition or to control parameter alternatively to further create more confusion for any intruder. The next stage is to obtain the reality preserving fractional Hartley transform (RPFrHT) of the image by following the procedure described in Sect. 3.2. The secret keys at the transform stage are basically the pairs of fractional transform orders along the rows and columns of red, green and blue channels, respectively, as shown in Table 2. The resultant transformed images are shown in Fig. 4c, h. The transform output also has certain negative-valued coefficients which are stored in a single-bit phase modulation matrix by storing a bit ‘0’ for positive value and bit ‘1’ for negative value of the coefficients, and the resultant matrix in the form of an image is shown in Fig. 4d, i. It can be seen that transform output has some visual patterns which need to be removed. Therefore, the third and final stage is to permute the transformed image obtained after the second stage with the piecewise linear chaotic map as described in Sect. 3.4. The set of secret keys (Table 2) are used to permute each component image to make it a random noise-like image. The resultant images after the permutation are shown in Fig. 4e, j. This is the final encrypted image that is transmitted over the public channel along with the single-bit phase modulation matrix.

Fig. 4
figure 4

Perceptual security analysis at each stage of encryption (left to right)

Full size image

The decryption is exactly the reverse of that of the encryption procedure. If the same sets of keys (as used during encryption) are supplied at all stages of decryption, the original image can be recovered without any loss of data. The complete process of decryption of encrypted images is shown in Fig. 5. Figure 5a, f shows encrypted images of Lena and Baboon, respectively. The encrypted image will be first processed for descrambling/inverse permutation using PWLCM with the same set of secret keys as used for Stage 3 of encryption. The resultant images after the inverse permutation are shown in Fig. 5c, h. This transformed image (which carries the magnitude of transform coefficients) along with the single-bit phase modulation matrix as shown in Fig. 5b, g collectively represents the exact transform coefficients to be processed for the next stage of decryption, i.e., inverse reality preserving Hartley transformation. This combination (images in Fig. 5b, g along with Fig. 5c, h) is processed for inverse RPFrHT with the same pairs of fractional orders as supplied in Stage 2 of the encryption but with negative sign (as explained in Sect. 3). The resultant images after the inverse transform are shown in Fig. 5d, i. Now the third stage of decryption is executed on the image shown in Fig. 5d, i by following the procedure explained in Sect. 3.1 based on the compound chaotic maps (described in Sect. 2.3.2) and subject to the same set of secret keys for the red, green and blue channels as used in Stage 1 of encryption. The resulting images are the final decrypted/recovered images which are shown in Fig. 5e, j.

Fig. 5
figure 5

Illustration of decryption at each stage of recovering the original image (left to right)

Full size image

We have also experimented with a lot of other images having widely different contents using several combinations of secret keys and analyzed the corresponding encrypted and decrypted images with all intermediated images. We observe that the proposed method completely converts the images into visually obfuscated data and gives a lossless recovery in decryption.

4.2 Security analysis

The major concern of any cryptosystem lies in the level of security it provides. In other words, a good encryption technique should be robust against all sorts of cryptanalytics, statistical and brute-force attacks. In this section, we attempt to provide a complete investigation on the security of the proposed encryption technique.

4.2.1 Brute-force attack

In cryptographic applications, the most important part is the selection of keys. The keyspace should be large enough to counter any brute-force attack. This type of attack is based on exhaustive key searching where the adversary gets capability of recovering the original information by searching all possible keys in the keyspace until a correct key is found. The resistance to brute-force attack is the measure of the keyspace. A larger keyspace ensures better resistance. The keyspace should be > 2120 to preclude any eavesdropping [33, 62].

In this scheme, 24 keys are used with different precision levels. There are 12 keys with a precision of 10–15, six keys with the precision of 10–4, six keys with integer values (4 digits). Therefore, the total keyspace can be evaluated as

$${10}^{15\times 12}\times {10}^{4\times 6}\times {10}^{4\times 6}\approx {10}^{228},$$

which is sufficiently larger than 2120 to resist any brute-force attack.

4.2.2 Perceptual security analysis

Perceptual security analysis determines the measure of dissimilarity between plain and encrypted images.

The utmost requirement of encryption is to make the information unintelligible and obfuscate the pixels in such a way that it appears as random white noise. It is evident from Fig. 4 that the final encrypted images are completely random and thus are visually unrecognizable.

Apart from visual quality, the perceptual security analysis results are numerically represented in terms of certain parameters, viz. peak signal-to-noise ratio (PSNR), mean square error (MSE) and spectral similarity index (SSIM). For a pair of original and encrypted images represented as \({o}_{i,j}\) and \({e}_{i,j}\), respectively, these parameters are defined as:

$$\mathrm{PSNR}\left(o,e\right) =10{\mathrm{log}}_{10}\frac{{(L-1)}^{2}}{\frac{1}{MN}\sum_{i=1}^{M}\sum_{j=1}^{N}\left[{o}_{i,j}-{e}_{i,j}\right]}$$
(19)
$$\mathrm{MSE}(o,e)=\frac{1}{MN}\sum_{i=1}^{M}\sum_{j=1}^{N}[{\left|{o}_{i,j}-{e}_{i,j}\right|}^{2}]$$
(20)
$$\mathrm{SSIM}\left(o,e\right)= \frac{\left(2{\mu }_{o}{\mu }_{e}+{C}_{1}\right)(2{\sigma }_{o,e}+ {C}_{2})}{\left({\mu }_{o }^{2}+{\mu }_{e}^{2}+{C}_{1}\right)({\sigma }_{o}^{2}+{\sigma }_{e}^{2}+{C}_{2})}$$
(21)

where \([M,N]\) is the image size, \(L\) is the highest intensity value (256 for an 8-bit image), \({\mu }_{o},{\mu }_{e},{\sigma }_{o},{\sigma }_{e},{\sigma }_{oe}\) are mean, variance and covariance of original and encrypted images. \({{C}}_{1},{{C}}_{2}\) are constants that are used to stabilize division with a weak denominator.

Mean square error (MSE) is an error metric that allows to compare pixel values of original with that of the encrypted image. Thus, a high value of MSE is desirable during encryption and in the decryption process, MSE should be ideally ‘0′ for lossless image recovery. PSNR is used as a metric for spectral information measure and is an error metric that is used as quality measure statistics of an image with respect to a reference image. The higher the value of PSNR, the better is its quality. Thus, two similar images will have infinite PSNR. However, a \(\mathrm{PSNR}\ge \) 28 is considered satisfactory for a reconstructed image. The purpose of evaluating PSNR is to show that the PSNR of the encrypted image with respect to the original image is very low (\(\ll 28)\) which indicates a significant difference between the original and encrypted image. However, there is a limitation of just relying on the MSE and PSNR values as these measures utilize only numeric values of pixels and do not consider other factors of the human visual system (HVS). Wang et al. [63] proposed Structural Similarity Index (SSIM) as another metric that considers three main biological factors, viz. luminance, contrast and structure comparison between an image and a reference image, and is a method of subjective evaluation for quantifying the visual image quality. \({{\rm SSIM}} \in [-\mathrm{1,1}]\) with a value of ‘1’ for ideally similar images.

Different images along with test images are simulated for these parameters’ evaluation. The simulated results are given in Table 3. As is evident from the results, the PSNR of encrypted images is very low (\(\ll 28)\) with MSE values ( \(\cong {10}^{4}\)) very high. SSIM of encrypted images is near to ‘zero’. All these parameters indicate that the encrypted images have high perceptual security.

Table 3 Parameter evaluation for perceptual security analysis
Full size table

During decryption, it is recommended to have decryption error negligibly low [66] for applications such as biometrics and secure military communications. The decryption error of decrypted image, \(\mathrm{De}(i,j)\) corresponding to plain image \(\mathrm{Pl}(i,j)\) of size \(M\times N\) is evaluated [67] as

$$\mathrm{DErr}=\left(\frac{1}{MN}\sum_{i=1}^{M}\sum_{j=1}^{N}Q\left(i,j\right)\right)\times 100\%$$
(22)

where \({ }Q\left( {i,j} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\rm Pl}\left( {i,j} \right) = {\rm De}\left( {i,j} \right) } \hfill \\ {0,} \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.\)

The decryption error of all the images is ‘zero’ in the proposed scheme. We have also checked the objective metrics for the same to validate our claim. The objective metrics are the same for all test images and are listed in Table 4.

Table 4 Parameters for recovered images
Full size table

4.2.3 Statistical analysis

4.2.3.1 Histogram analysis

An image histogram depicts the intensity value distribution of image pixels against each gray level. This statistical data can reveal some crucial information for an intruder to decrypt image by analyzing its histogram. Also, this information can be used to mount more statistical attacks. Thus, it becomes necessary to investigate the histograms of the encrypted image. The histogram of an encrypted image should be different from that of the actual image and also independent of the content of the actual image. As shown in Fig. 6, the first and third rows are the RGB channel histograms of plain image Lena and Baboon respectively. The second and fourth rows depict corresponding histograms of encrypted images. It is evident from Fig. 6 that the histograms of the encrypted image are quite different from that of the original image. One more important point worth mentioning here is that the histograms of the final encrypted image are always independent of the original image and hence, do not reveal any information about the original image.

Fig. 6
figure 6

a–c Are RGB histograms of plain image Lena, d–f are histograms of Lena in the encrypted domain, g–i are RGB histograms of plain image Baboon, j–l are histograms (Baboon) in the encrypted domain

Full size image
4.2.3.2 Correlation analysis

The adjacent pixels in an ordinary image with definite visual content are highly correlated in horizontal, vertical and diagonal directions. A good encryption scheme should be capable to make the correlation sufficiently low in order to resist the statistical attacks. To analyze and compare the correlations of adjacent pixels in the plain and encrypted image, correlation analysis of the proposed scheme is done.

We have randomly selected \(100\times 100\) pixels of the red channel from each image. (For brevity, only red channel for both the test images is shown.) Figure 7a–c shows the horizontal, vertical and diagonally shifted pixels of plain image Lena, and Fig. 7d–f shows corresponding correlation plots in encrypted image. Similarly, Fig. 7g–i shows the horizontal, vertical and diagonally shifted pixels of plain image Baboon, and Fig. 7j–l shows corresponding correlation plots in encrypted Baboon. In order to quantify the adjacent pixel correlation in the encrypted image, correlation coefficients are computed through Eq. (23) where \({x}_{k}\) and \({y}_{k}\) are gray values for \(kth\) pair of selected adjacent pixels.

Fig. 7
figure 7

Correlation analysis: a–c are H, V, D correlation plots for plain image Lena, d–f are H, V, D correlation plots for corresponding encrypted pixels of image Lena, g–i are H, V, D correlation plots for plain image Baboon, j–l are H,V,D of encrypted image Baboon

Full size image
$${r}_{xy}=\frac{\frac{1}{M}\sum_{k=1}^{M} {(x}_{k}-E\left(x\right)\left({y}_{k}- E\left(y\right)\right) }{\sqrt{D\left(x\right)D\left(y\right)}}$$
(23)

where \(D\left(x\right)=\frac{1}{M}\sum_{k=1}^{M}{({x}_{k}-E(x))}^{2}\), \(D\left(y\right)=\frac{1}{M}\sum_{k=1}^{M}{({y}_{k}-E(y))}^{2}\)

$$E\left(x\right)=\frac{1}{M}\sum_{k=1}^{M}{x}_{k} , \quad E\left(y\right)=\frac{1}{M}\sum_{k=1}^{M}{y}_{k}$$

The correlation analysis is done for all the images in the horizontal, vertical and diagonal directions. We observe that the adjacent pixels are highly correlated in the plain images. However, this correlation is completely removed after the encryption of the images using the proposed image encryption technique. The quantitative results of the correlation coefficients between the horizontally, vertically and diagonally adjacent pixels distributions are given in Table 5 for the encrypted images only (for all three color components). A very low value (\(\approx \) 0) of the correlation coefficients for encrypted images proves no correlation and hence resistance to statistical attacks.

Table 5 Correlation analysis for encrypted images (RGB)
Full size table

4.2.4 Key sensitivity analysis

A cryptosystem is evaluated for its effectiveness in terms of key sensitivity. Therefore, the sensitivity of the keys should be as high as possible. There are two aspects of evaluation for key sensitivity: (1) During encryption, a completely different ciphertext should be generated with a very minute change in key, and (2) During decryption, there should be incorrect recovery (almost a random noise-like) with wrong keys. A key sensitivity parameter (KS) is introduced in [72] which should be ideally 100% for two completely dissimilar images.

However, in practical terms, KS should be as close to 100%. For each key, KS is evaluated in the encryption stage corresponding to each wrong key. For example, the value for the key (K1) gives ciphered image (\({C}_{1})\), and for altered key with very minute variation \(\left({K}_{1}^{{\prime}}\right)\) another ciphered image \(\left({C}_{2}\right)\) is obtained. Therefore, KS parameter for two ciphered images, \({C}_{1}\) and \({C}_{2}\) is as:

$${\rm KS}=\frac{1}{M\times N}\sum_{m=1}^{M} \sum_{n=1}^{N}{C}_{1}(m,n)\otimes {C}_{2}(m,n)$$
(24)

where \({C}_{1}\) and \({C}_{2}\) are two different ciphered images with the difference in any one of the keys,

$$ C_{1} \left( {m,n} \right) \otimes C_{2} \left( {m,n} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{1} \left( {m,n} \right) \ne C_{2} \left( {m,n} \right) } \hfill \\ {0,} \hfill & {C_{1} \left( {m,n} \right) = C_{2} \left( {m,n} \right)} \hfill \\ \end{array} } \right. $$
(25)

The KS value for each key in all three stages of encryption is evaluated (for image Lena) as shown in Tables 6 (for Stage 1), 7 (for Stage 2), 8 (for Stage 3). The KS values are very close to 100% which clearly indicates that key sensitivity is extremely high at the encryption side. It has also been observed that the key sensitivity of Stage 2 (transform stage) is evaluated at different precisions. The KS is a little less when a precision of 10–4 is used. This depicts that using only transform for decorrelating the pixels cannot provide optimum security and hence the addition of other security layers is essential.

Table 6 Key sensitivity at Stage 1 of encryption
Full size table
Table 7 Key sensitivity at Stage 2 of encryption
Full size table
Table 8 Key sensitivity at Stage 3 of encryption
Full size table

At decryption, key sensitivity is measured in terms of MSE plots corresponding to deviation in each key over a range in close proximity. For this, each key value is little deviated by infinitesimally small values and the decrypted image is evaluated for its MSE with reference to the original image. It is observed while simulation that the recovery with each wrong key gives a completely random image. For avoiding any redundancy in results, the MSE plots for wrong keys are generated corresponding to each stage for the Red channel only (\({K}_{1}\)–\({K}_{3}\): Stage 1,\( {K}_{10}\)–\({K}_{11}\): Stage 2, \({K}_{16}\)–\({K}_{18}\): Stage 3). The reader may refer to Table 2 for the description of keys.

The MSE plots depict high sensitivity as there is an error of order of 104 with a deviation of as minute as an order of 10–15 in the key values for chaotic maps (keys \({K}_{1}\)–\({K}_{3}\)) as shown in Fig. 8a–c. For MSE plots of keys at stage 2, the values are deviated by 10–4 in transform order along x-direction (\({K}_{10}\)) in Fig. 8d, along y-direction (\({K}_{11}\)) in Fig. 8e and collectively for both (\({K}_{10}\),\( {K}_{11}\)) in Fig. 8f . For MSE plots corresponding to keys at stage 3, deviation in key values (\({K}_{16}\), \({K}_{17}\), \({K}_{18}\)) of an order of 10–15 is plotted and shown in Fig. 8g–i, respectively. It is observed that MSE plots of other channels are similar.

Fig. 8
figure 8

MSE plots for deviation from correct values a for key K1, b for key K2, c for key K3, d for key K10, e for key K11, f for deviation in both (K10, K11) collectively, g for key K16, h for key K17, i for key K18

Full size image

4.2.5 Information entropy analysis

Entropy refers to the measure of amount of information in any signal. For image, the amount of information entropy/Shannon entropy depends on the probability of occurrence of particular pixel intensity in the histogram. For a flat image, entropy is \(zero\) and for an encrypted image, its entropy is defined as the amount of uncertainty associated with the random image. The random variable can be a quantitative measure of any one of the pixel entities such as color, luminance, saturation, etc. Entropy is thus a statistical measure of randomness. For an image R with pixel values \({\mathrm{r}}_{\mathrm{i}}\), its entropy is explicitly defined as:

$$H\left(R\right)= -\sum_{i=1}^{M}p({r}_{i}){\mathrm{log}}_{b} p({r}_{i}),$$
(26)

where \(p\) is the probability of occurrence of \({r}_{i}\mathrm{th}\) pixel; \(b\) is the base of log which can be \(\mathrm{e},10\,\mathrm{ or \,}2\). In an image with maximum \(n\, \mathrm{bit}s, M={2}^{n}\), b = 2.

Recently, another measure for image randomness is introduced [73] which is coined as local entropy measure. It is based on Shannon entropy measure over local image pixels. Local entropy measure is able to overcome certain weaknesses of Shannon entropy measure. Some of proved weaknesses in [73] are unfair randomness comparisons for images of variant sizes, failure to distinguish image randomness before and after shuffling, inaccurate values in the case of synthesized images, etc.

Local entropy is the mean entropy of several nonoverlapping image blocks that are randomly selected from the source image. In order to differentiate from local entropy, Shannon entropy is termed as global entropy. Local entropy is evaluated over a certain number of nonoverlapping blocks (k) of image pixels (TB), therefore termed as (k, TB)-local entropy as:

$$\overline{{H}_{(k,{T}_{B})}\left(S\right)}= \sum_{i=1}^{k}\frac{H\left({S}_{i}\right)}{k}$$
(27)

where Si are randomly selected nonoverlapping image blocks as S1, S2, S3 … Sk and TB are the number of pixels in each block, Sk. For image intensity level, L = 2 (binary image), \({ T}_{B}^{L=2}=2\). Similarly, for L = 256 \({T}_{B}^{L=256}=1936\) and the total number of nonoverlapping blocks should not be less than 30 \((k\ge 30)\).

The entropy analysis results of a few test plain images and their corresponding encrypted images are given in Table 9. The values of information entropy for the encrypted images are almost converging to a value of 7.9999, i.e., the highest possible value of information entropy for an 8-bit random image. The local entropy values are also evaluated, and it is observed that local entropy is close to global entropy. This ensures that the proposed scheme gives randomness in encrypted domain indicating a negligible information leakage and thus is secure against entropy attack.

Table 9 Entropy analysis for global (Shannon) and local entropy
Full size table

4.2.6 Differential attack analysis

A differential attack is successful when an intruder is able to retrieve some clue about secret keys by slightly changing the plain image and comparing it with the encrypted image. In order to ensure robustness to such attack, it is required that a minute change in the plain image should be able to generate a huge difference in encrypted image. In other words, the diffusion of the system should be able to spread the difference over the entire image. There are two indicators that are used to quantify robustness to differential attack, NPCR (number of pixel change rate) and UACI (unified average change in intensity) [76, 77]. For a plain image with width W and height H,, let there be two ciphertexts generated (C1, C2) corresponding to the plain image and another with altered value at pixel location (i, j). These measures are mathematically defined as:

$$\mathrm{NPCR}=\left(\frac{1}{WH}\right)\sum_{i=1}^{W}\sum_{j=1}^{H}D\left(i,j\right)\times 100\%$$
(28)

where \(D\left( {i,j} \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & { C_{1} \left( {i,j} \right) \ne C_{2} \left( {i,j} \right) } \hfill \\ {0,} \hfill & {\text{ otherwise}} \hfill \\ \end{array} } \right.\)

$$\mathrm{UACI}=\frac{1}{WH}\left[\sum_{i=1}^{W}\sum_{j=1}^{H}\left|\frac{{C}_{1}(i,j)-{C}_{2}(i,j)}{L-1}\right|\right]\times 100\%$$
(29)

where L = 256 for an 8-bit image. For a 256 Gy-level image encryption, the expected value of NPCR is 99.6094%, whereas that of UACI is 33.4635%. In the proposed scheme, we have modified a randomly selected pixel location (126, 137) for evaluating these parameters. The corresponding NPCR, UACI values are given in Table 10.

Table 10 Differential attack analysis
Full size table

4.2.7 Classical attack analysis

There are four types of such attacks that include ciphertext only attack where it is assumed that the adversary has access to few ciphertext only [42], plaintext attack where it is assumed to have access to set of plaintext only, known-plaintext attack where knowledge of a set of plaintexts and corresponding ciphertext is available to the adversary and fourth is a chosen-plaintext attack where it is assumed that the adversary has access to set of plaintexts to be encrypted to obtain ciphertexts. As known ciphertext attack provides more information to an adversary, it is believed that if a ciphertext can resist a chosen ciphertext attack, it can also resist other types of attacks [78]. The proposed scheme is designed such that it is highly sensitive to keys. Moreover, the ciphertext is dependent on plaintexts as the initial conditions of the chaotic maps that are used in Stage 1 of encryption strongly depend on the plain input. Therefore, a unique ciphertext is generated corresponding to each plaintext. Hence, the proposed scheme is robust to the chosen ciphertext attack.

4.2.8 Data occlusion attack

There is a possibility of data loss while communicating images over heavy traffic channels or due to insecure channels. An effective encryption scheme should be able to recover the image even after occlusion attack if the data are uniformly diffused over the entire image. Post-processing techniques can be further used to recover the losses. To check the tolerance of the proposed scheme, encrypted data are subjected to varying amounts of data loss and corresponding decrypted images are checked for perceptual security. In Fig. 9, the first and third rows depict cropping in encrypted data (Lena image), whereas in the second and fourth rows corresponding decrypted images are shown. It is observed that image contour is still recoverable with up to 50% of data loss. The average values for data loss up to 12.5%, 25% and 50% are recorded in Table 11. The numerical values clearly indicate that the proposed scheme can resist data loss for recovery of the image which can be further improved by applying data post-processing techniques.

Fig. 9
figure 9

Data occlusion attack analysis. The first and third rows show the encrypted images cropped from different locations, and second and fourth rows show the corresponding decrypted images with different visual clarity

Full size image
Table 11 Averaged parameter values
Full size table

4.3 Noise attack analysis

Robustness against noise is an important index to check for the encryption scheme as distortion, degradation and corrupted data (coding error) are common in communication channels. The proposed scheme is checked for the addition of Gaussian noise with zero mean and varying variances to get data corresponding to different SNR (signal-to-noise ratio) between noisy and noise-free encrypted images. This can be mathematically explained as:

$${{I}_{e}}^{{\prime}}={I}_{e}(1+\sigma G)$$

where \({{I}_{e}}^{{\prime}}\) is noisy image \({I}_{e}\) is the encrypted image, \(G\) represents the Gaussian noise with \(\sigma \) as its standard deviation. Figure 10 shows decrypted images when the encrypted images are distorted with different noise levels. The noise levels are quantified according to the SNR of noisy image with reference to encrypted image. MSE values are plotted for different SNR values. The plot clearly shows that error is proportional to the amount of noise in the encrypted domain. It is evident from Fig. 10 that image contour is detectable with as low as SNR of 1 dB, thereby giving testimony to the fact that the proposed scheme performs fair enough in a noisy environment and thus can resist noise attack.

Fig. 10
figure 10

Noise attack analysis. a–f are decrypted images with SNR of 1 dB, 5 dB, 10 dB, 15 dB, 20 dB and 25 dB, respectively. g is the corresponding plot of SNR vs. mean square error in decrypted image

Full size image

4.3.1 Speed analysis

The run time of an encryption algorithm is an important issue for real-time applications. Optical transforms have an inherent property of fast and parallel processing. This is due to the optical setup that comprises SLM (for processing complex coefficients) and CCD (for storage). However, in the digital domain, the run time of an algorithm depends on the complexity associated with it. Therefore, a compromise between speed and complexity is highly desirable. The proposed scheme has multiple security layers for attaining substitution, transformation and permutation. The average encryption and decryption times are recorded in Table 12. It is likely to mention that run time can be further improved by optimization methods.

Table 12 Time analysis for the encryption algorithm (time in s)
Full size table

5 Comparative analysis

This section gives a brief summary on various comparisons of the proposed scheme with other similar state-of-the-art schemes. Firstly, by using a reality preserving algorithm [54], the complex computation is eliminated completely which is inherited in all DRPE and other optical transform domain-based encryption schemes [19, 21, 31, 36, 80, 81]. Another limitation in such similar schemes is the shorter key space, thereby leading to possibility of brute-force attack [28, 29, 82]. Table 13 lists some of the recent schemes with their key space for comparison with that of the proposed scheme.

Table 13 Comparative for keyspace analysis
Full size table

On the bases of histogram analysis, the histogram in the encrypted domain with the proposed scheme is nearly uniform as compared to other similar schemes with optical transform domain [18, 19, 23, 40, 45, 64, 87]. The uniform histogram gives higher security against entropy attacks. A comparison of entropy values for RGB of image Lena is listed in Table 9.

Any encryption algorithm can be characterized by its decorrelating ability. For a comparison on this, Table 14 lists some of the recent published works in terms of their averaged correlation coefficients (with reference to Lena image).

Table 14 Comparison of averaged correlation coefficients
Full size table

Another important parameter for comparison is the decrypted image quality. To check, we have evaluated decryption error (DErr) as explained at the end of Sect. 4.2.2. DErr is ‘zero’ for all test images which clearly depicts that proposed scheme is lossless unlike some other recent schemes that are either fixed/single transform order-based [23, 40, 46, 65, 67, 86, 88] or others that are based on multiple parameters [43, 64, 74, 79, 89]. The PSNR of the decrypted image with reference to the original image (Lena image) is listed in Table 4. The proposed scheme is also robust to differential attacks as is evident from the analysis for NPCR and UACI values (Table 10).

6 Conclusion

Recently, many researchers have come up with image encryption schemes based on the optical transform domain. To overcome the limitations of shorter keyspace with the only transform-based approach, researchers have intertwined chaos and fractional transform domain in some way or other to get the benefit of both. Most of the schemes are focused on decorrelation based on fractional transform and chaos-based scrambling with different orders of their operation to improve security and also to enlarge the keyspace. However, these schemes fail to provide enough security due to certain limitations of the transform domain. The proposed scheme is based on three security layers with compound chaos-based substitution followed by decorrelation of pixels with a reality preserving fractional Hartley transform and another chaos-based permutation, thereby facilitating a lossless recovery at decryption. The proposed scheme is a novel method that not only enlarges the keyspace but also provides better robustness to most of the possible attacks. Security analysis and comparative analysis collectively give testimony to the efficacy of the scheme.