A novel chaotic system with hidden attractor and its application in color image encryption

Abstract

In this paper, a novel fractional-order no-equilibrium chaotic system with hidden attractor is presented. The dynamical characteristics of the fractional-order system are analyzed by the phase diagram, Lyapunov exponents, bifurcation diagram, complexity, and attractor basin. Based on the above analysis, an image encryption scheme performs discrete cosine transform on the R, G, and B channels of the original color image to get the corresponding sparse coefficient matrices. Then, the measurement matrix generated by the Hadamard matrix and the chaotic pseudo-random sequence is used to compress and perceive the sparse coefficient matrices. In addition, the row and column scrambling and GF (257) domain diffusion algorithm are performed on the compressed pixel matrix to obtain the final cipher image. Experimental results and performance analysis display that the scheme has high compressibility and security. Even if the compression rate is 0.25, the calculated PSNR values are around 30. In addition, the χ²-value of the encrypted Lena image is 248.2824, and the algorithm has passed the UACI and NPCR tests and can resist differential attacks. Therefore, the proposed algorithm is effectively.

1 Introduction

In 2011, Leonov and Kuznetsov put forward the concept of hidden attractor [22, 25]. Generally, chaotic systems with no equilibrium point, stable equilibrium point and infinite number of unstable equilibrium points are classified as chaotic systems with hidden attractors. This kind of chaotic system has some hidden chaotic characteristics, which has potential application value in the field of nonlinear terms and engineering applications [18, 20, 23, 24, 37,38,39,40,41, 44, 45, 49]. In 2013, Jafari et al. [18]. listed a series of elementary 3-D chaotic systems without equilibrium points. Research on chaotic systems without equilibrium points has also become a focus. Wang and Chen gave a chaotic system without equilibrium points, on this basis, a chaotic system with any number of equilibrium points was constructed [49]. In 2015, a chaotic system containing nonlinear exponential terms is studied, with no equilibrium point but has rich dynamical characteristics [38]. In 2016, a 4-D hyperchaotic system with hidden attractors and its dynamical characteristics, control, and synchronization are analyzed by Vaidyanathan [45]. Pham et al. [40] discovered a 3-D chaotic system without equilibrium points, analyzed the basic dynamical characteristics of the system, and implemented the circuit of the system. All of the above are studies of some integer order no-equilibrium chaotic systems. However, the properties of the fractional-order chaotic system without equilibrium have not been researched, the dynamical characteristics of the fractional-order no-equilibrium system is analyzed. At present, the methods for solving fractional differential equations mainly include the frequency domain approximation method [19], predictor-corrector method [10], and Adomian decomposition method (ADM). Compared with the other two methods, ADM decomposition method has high calculation accuracy, fast convergence speed, and less computer resource consumption [53]. Therefore, the ADM decomposition algorithm is chosen to solve the fractional chaotic system in this paper. In addition, a very important application field of chaotic system is image encryption, so we not only analyze the chaotic system with no equilibrium point of fractional order, but also study its application.

Nowadays, digital images have become one of the major interactive objects on the Internet, especially in the medical, military and national defense fields, which means that we have hidden security risks when transmitting images [15]. Generally the amount of image data is large and the storage cost is high. Therefore, the image should be compressed and encrypted during the image transmission process. Due to pseudo-random characteristics of chaotic system and the high sensitivity to initial values, image encryption algorithms based on chaotic systems have become a hot spot in information security research [3, 21, 47, 52, 54]. So far, various chaotic image encryption algorithms have been proposed [1, 4, 5, 8, 9, 12,13,14, 16, 17, 26,27,28, 30, 35, 51, 55,56,57,58]. In 2020, A color image encryption system was proposed by Hu et al. [14], this algorithm uses chaotic pseudo-random sequences and matrix convolution operations to scramble and diffuse the pixel matrix, respectively. In 2019, Hasanzadeh et al. [12] introduced a color image encryption scheme based on the replacement box and Chen hyper-chaotic system, which has a massive secret key space and secret key sensitivity. Based on the coupled hyperchaotic system and Galois field arithmetic operations, Liu et al. proposed a medical image encryption scheme. [28]. Yang et al. [56] introduced a diffusion algorithm using the complex chaotic system and the gravity law model. These algorithms are sufficiently secure, but further research found that there is a considerable storage cost during image transmission. Zhu and Chen used a low-dimensional chaotic system and block compressive sensing to encrypt color image [58]. Mou et al. [35] studied image compression and encryption algorithm that combined 3D hyper-chaotic system and compressive sensing.

Based on the above research background, the dynamic characteristics of fractional order no-equilibrium chaotic system are analyzed, and it is applied in the field of image encryption, and an encryption algorithm with high efficiency and low storage space is designed. This system could complete image encryption and compression simultaneously and has high compressibility and security. Firstly, a fractional-order no-equilibrium chaotic system is given, which is solved by the ADM decomposition algorithm. Using phase diagram, Lyapunov exponents and bifurcation diagram to analyze the dynamical characteristics of the fractional-order no-equilibrium chaotic system, and obtaining the optimal parameter range for applying the system to the image encryption system. Moreover, the generated chaotic pseudo-random sequences are used in the entire cryptographic system. Secondly, the Hadamard matrix and chaotic pseudo-random sequences are used to construct the measurement matrix of the R, G, and B channels of the color image. Finally, the compressed R, G, and B channels are scrambled separately, and the scrambled channels are diffused based on the GF (257) domain and chaotic pseudo-random sequences to obtain the final cipher image.

The rest of this paper is organized as follows. The dynamical characteristics of the fractional-order no-equilibrium chaotic system are analyzed in Section 2, The color image encryption scheme is introduced in detail in Section 3, the simulation results and the performance analysis of the proposed scheme are illustrated in Section 4. Finally, conclude in Section 5.

2 Fractional-order no-equilibrium chaotic system

2.1 Fractional-order no-equilibrium chaotic system model

The no-equilibrium chaotic system can be defined as

$$ \begin{cases} \dot{x}=y\\ \dot{y}=-x-yz\\ \dot{z}=xy+\alpha x^{2}+\beta y^{2}-\gamma \\ \end{cases}. $$

(1)

here α, β, γ are parameters and α, β, γ> 0, the state variables are represented by x, y, z.

According to the definition of Caputo fractional calculus and the system (1), the mathematical expression of the fractional-order no-equilibrium system is

$$ \begin{cases} *D_{{t_{0}}}^{q}x = y \\ *D_{{t_{0}}}^{q}y = - x - yz \\ *D_{{t_{0}}}^{q}z = xy + \alpha {x^{2}} + \beta {y^{2}} - \gamma \\ \end{cases}. $$

(2)

here q means the order of the fractional system equation, and 0<q ≤ 1.

2.2 Solution of the fractional-order no-equilibrium chaotic system

Solving the fractional-order system equation by ADM algorithm, the linear, non-linear and constant terms of the system (2) are

$$ \left[ \begin{array}{l} L{x_{1}} \\ L{x_{2}} \\ L{x_{3}} \end{array} \right] = \left[ \begin{array}{l} {x_{2}} \\ - {x_{1}} \\ 0 \end{array} \right], \left[ \begin{array}{l} N{x_{1}} \\ N{x_{2}} \\ N{x_{3}} \end{array} \right] = \left[ \begin{array}{l} 0 \\ - {x_{2}}{x_{3}} \\ {x_{1}}{x_{2}} + \alpha {({x_{1}})^{2}} + \beta {({x_{2}})^{2}} \end{array} \right], \left[ \begin{array}{l} {g_{1}} \\ {g_{2}} \\ {g_{3}} \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \\ - \gamma \end{array} \right] $$

(3)

The non-linear term needs further decomposition. As the ADM decomposition algorithm has fast convergence [32], only the first five terms of the non-linear term can be decomposed to ensure the calculation accuracy. The non-linear term is decomposed into

$$ \left\{ \begin{array}{l} {A_{2}^{0}} = - {x_{2}^{0}}{x_{3}^{0}} \\ {A_{2}^{1}} = - {x_{2}^{1}}{x_{3}^{0}} - {x_{2}^{0}}{x_{3}^{1}} \\ {A_{2}^{2}} = - {x_{2}^{2}}{x_{3}^{0}} - {x_{2}^{1}}{x_{3}^{1}} - {x_{2}^{0}}{x_{3}^{2}} \\ {A_{2}^{3}} = - {x_{2}^{3}}{x_{3}^{0}} - {x_{2}^{2}}{x_{3}^{1}} - {x_{2}^{1}}{x_{3}^{2}} - {x_{2}^{0}}{x_{3}^{2}} \\ {A_{2}^{4}} = - {x_{2}^{4}}{x_{3}^{0}} - {x_{2}^{3}}{x_{3}^{1}} - {x_{2}^{2}}{x_{3}^{2}} - {x_{2}^{1}}{x_{3}^{3}} - {x_{2}^{0}}{x_{3}^{4}} \end{array} \right. $$

(4)

$$ \left\{ \begin{array}{l} {A_{3}^{0}} = {x_{1}^{0}}{x_{2}^{0}} + \alpha {({x_{1}^{0}})^{2}} + \beta {({x_{2}^{0}})^{2}} \\ {A_{3}^{1}} = {x_{1}^{1}}{x_{2}^{0}} + {x_{1}^{0}}{x_{2}^{1}} + 2\alpha {x_{1}^{1}}{x_{1}^{0}} + 2\beta {x_{2}^{1}}{x_{2}^{0}} \\ {A_{3}^{2}} = {x_{1}^{2}}{x_{2}^{0}} + {x_{1}^{1}}{x_{2}^{1}} + {x_{1}^{0}}{x_{2}^{2}} + 2a{x_{1}^{2}}{x_{1}^{0}} + a{x_{1}^{1}}{x_{1}^{1}} \\ \begin{array}{*{20}{c}} {} & { + 2\beta {x_{2}^{2}}{x_{2}^{0}} + \beta {x_{2}^{1}}{x_{2}^{1}}} \end{array} \\ {A_{3}^{3}} = {x_{1}^{3}}{x_{2}^{0}} + {x_{1}^{2}}{x_{2}^{1}} + {x_{1}^{1}}{x_{2}^{2}} + {x_{1}^{0}}{x_{2}^{2}} + 2\alpha {x_{1}^{3}}{x_{1}^{0}} + 2\alpha {x_{1}^{1}}{x_{1}^{2}} \\ \begin{array}{*{20}{c}} {} & { + 2\beta {x_{2}^{3}}{x_{2}^{0}} + 2\beta {x_{2}^{1}}{x_{2}^{2}}} \end{array} \\ {A_{3}^{4}} = {x_{1}^{4}}{x_{2}^{0}} + {x_{1}^{3}}{x_{2}^{1}} + {x_{1}^{2}}{x_{2}^{2}} + {x_{1}^{1}}{x_{2}^{3}} + {x_{1}^{0}}{x_{2}^{4}} + 2\alpha {x_{1}^{4}}{x_{1}^{0}} + 2\alpha {x_{1}^{3}}{x_{1}^{1}} \\ \begin{array}{*{20}{c}} {} & { + \alpha {x_{1}^{2}}{x_{1}^{2}} + 2\beta {x_{2}^{4}}{x_{2}^{0}} + 2\beta {x_{2}^{3}}{x_{2}^{1}} + \beta {x_{2}^{2}}{x_{2}^{2}}} \end{array} \end{array} \right. $$

(5)

The solution of system (2) is defined as

$$ {\tilde x_{j}}(t) = {c_{j}^{0}} + {c_{j}^{1}}{\textstyle\frac{{{{(t - {t_{0}})}^{q}}}}{{{\varGamma} (q + 1)}}} + {c_{j}^{2}}{\textstyle\frac{{{{(t - {t_{0}})}^{2q}}}}{{{\varGamma} (2q + 1)}}} + {c_{j}^{3}}{\textstyle\frac{{{{(t - {t_{0}})}^{3q}}}}{{{\varGamma} (3q + 1)}}} + {c_{j}^{4}}{\textstyle\frac{{{{(t - {t_{0}})}^{4q}}}}{{{\varGamma} (4q + 1)}}} + {c_{j}^{5}}{\textstyle\frac{{{{(t - {t_{0}})}^{5q}}}}{{{\varGamma} (5q + 1)}}} $$

(6)

where h = t − t₀ is time step, j = 1, 2, 3. And

$$ \left\{ \begin{array}{l} {C_{10}} = {x_{1}^{0}} \\ {C_{20}} = {x_{2}^{0}} \\ {C_{30}} = {x_{3}^{0}} - {\textstyle\frac{{\gamma {h^{q}}}}{{{\varGamma} (q + 1)}}} \end{array} \right. $$

(7)

$$ \left\{ \begin{array}{l} {C_{11}} = {C_{2}^{0}} \\ {C_{21}} = - {C_{1}^{0}} - {C_{2}^{0}}{C_{3}^{0}} \\ {C_{30}} = {C_{1}^{0}}{C_{2}^{0}} + \alpha {({C_{1}^{0}})^{2}} + \beta {({C_{2}^{0}})^{2}} \end{array} \right. $$

(8)

$$ \left\{ \begin{array}{l} {C_{12}} = {C_{2}^{1}} \\ {C_{22}} = - {C_{1}^{1}} - {C_{2}^{1}}{C_{3}^{0}} - {C_{2}^{0}}{C_{3}^{1}} \\ {C_{32}} = {C_{1}^{1}}{C_{2}^{0}} + {C_{1}^{0}}{C_{2}^{1}} + 2\alpha {C_{1}^{1}}{C_{1}^{0}} + 2\beta {C_{2}^{1}}{C_{2}^{0}} \end{array} \right. $$

(9)

$$ \left\{ \begin{array}{l} {C_{13}} = {C_{2}^{2}} \\ {C_{23}} = - {C_{1}^{2}} - {C_{2}^{2}}{C_{3}^{0}} - {C_{2}^{1}}{C_{3}^{1}}{\textstyle\frac{{{\varGamma} (2q + 1)}}{{{{\varGamma}^{2}}(q + 1)}}} - {C_{2}^{0}}{C_{3}^{2}} \\ {C_{33}} = {C_{1}^{2}}{C_{2}^{0}} + {C_{1}^{1}}{C_{2}^{1}}{\textstyle\frac{{{\varGamma} (2q + 1)}}{{{{\varGamma}^{2}}(q + 1)}}} + {C_{1}^{0}}{C_{2}^{2}} + 2\alpha {C_{1}^{2}}{C_{1}^{0}} + \alpha {C_{1}^{1}}{C_{1}^{1}}{\textstyle\frac{{{\varGamma} (2q + 1)}}{{{{\varGamma}^{2}}(q + 1)}}} \\ \begin{array}{*{20}{c}} {} & { + 2\beta {C_{2}^{2}}{C_{2}^{0}} + \beta {C_{2}^{1}}{C_{2}^{1}}{\textstyle\frac{{{\varGamma} (2q + 1)}}{{{{\varGamma}^{2}}(q + 1)}}}} \end{array} \end{array} \right. $$

(10)

$$ \left\{ \begin{array}{l} {C_{14}} = {C_{2}^{3}} \\ {C_{24}} = - {C_{1}^{3}} - {C_{2}^{3}}{C_{3}^{0}} - ({C_{2}^{2}}{C_{3}^{1}} + {C_{2}^{1}}{C_{3}^{2}}){\textstyle\frac{{{\varGamma} (3q + 1)}}{{{\varGamma} (q + 1)(2q + 1)}}} - {C_{2}^{0}}{C_{3}^{0}} \\ {C_{34}} = {C_{1}^{3}}{C_{2}^{0}} + ({C_{1}^{1}}{C_{2}^{2}} + {C_{1}^{2}}{C_{2}^{1}}){\textstyle\frac{{{\varGamma} (3q + 1)}}{{{\varGamma} (q + 1)(2q + 1)}}} + {C_{1}^{0}}{C_{2}^{3}} + 2\alpha {C_{1}^{3}}{C_{1}^{0}} \\ \begin{array}{*{20}{c}} {} & { + 2\alpha {C_{1}^{2}}{C_{1}^{1}}{\textstyle\frac{{{\varGamma} (3q + 1)}}{{{\varGamma} (q + 1)(2q + 1)}}} + 2\beta {C_{2}^{3}}{C_{2}^{0}} + 2\beta {C_{2}^{1}}{C_{2}^{2}}{\textstyle\frac{{{\varGamma} (3q + 1)}}{{{\varGamma} (q + 1)(2q + 1)}}}} \end{array} \end{array} \right. $$

(11)

$$ \left\{ \begin{array}{l} {C_{15}} = {C_{2}^{4}} \\ {C_{25}} = - {C_{1}^{4}} - {C_{2}^{4}}{C_{3}^{0}} - {C_{2}^{2}}{C_{3}^{2}}{\textstyle\frac{{{\varGamma} (4q + 1}}{{{{\varGamma}^{2}}(2q + 1)}}} - ({C_{2}^{3}}{C_{3}^{1}} + {C_{2}^{1}}{C_{3}^{3}}){\textstyle\frac{{{\varGamma} (4q + 1)}}{{{\varGamma} (q + 1)(3q + 1)}}} \\ \begin{array}{*{20}{c}} {} & { - {C_{2}^{0}}{C_{3}^{4}}} \end{array} \\ {C_{35}} = {C_{1}^{4}}{C_{2}^{0}} + ({C_{1}^{3}}{C_{2}^{1}} + {C_{1}^{1}}{C_{2}^{3}}){\textstyle\frac{{{\varGamma} (4q + 1)}}{{{\varGamma} (q + 1)(3q + 1)}}} + {C_{1}^{2}}{C_{2}^{2}}{\textstyle\frac{{{\varGamma} (4q + 1}}{{{{\varGamma}^{2}}(2q + 1)}}} + {C_{1}^{0}}{C_{2}^{4}} \\ \begin{array}{*{20}{c}} {} & { + 2\alpha {C_{1}^{4}}{C_{1}^{0}} + \alpha {C_{1}^{2}}{C_{1}^{2}}{\textstyle\frac{{{\varGamma} (4q + 1}}{{{{\varGamma}^{2}}(2q + 1)}}} + 2\alpha {C_{1}^{1}}{C_{1}^{3}}{\textstyle\frac{{{\varGamma} (4q + 1)}}{{{\varGamma} (q + 1)(3q + 1)}}} + 2\beta {C_{2}^{4}}{C_{2}^{0}}} \end{array} \\ \begin{array}{*{20}{c}} {} & { + \beta {C_{2}^{2}}{C_{2}^{2}}{\textstyle\frac{{{\varGamma} (4q + 1}}{{{{\varGamma}^{2}}(2q + 1)}}} + 2\beta {C_{2}^{1}}{C_{2}^{3}}{\textstyle\frac{{{\varGamma} (4q + 1)}}{{{\varGamma} (q + 1)(3q + 1)}}}} \end{array} \end{array} \right. $$

(12)

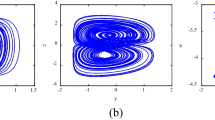
Selecting the system parameters α = 0.5, β = 0.1, γ = 1.3 and q = 0.67, iteration time step h = 0.01, the initial values are [x₀,y₀,z₀] = [0, 0.1, 0]. The phase diagrams of fractional-order no-equilibrium system in different planes are plotted in Fig. 1, the corresponding Lyapunov exponents of the system are LE₁ = 0.2306, LE₂ = 0, LE₃ = − 13.676, and Lyapunov dimension D_L = 2.0167. Since there is only one Lyapunov exponent greater than 0, it means that the system is chaotic [6, 34], and the calculated maximum Lyapunov exponent of the system is positive, indicating that the system is in a chaotic state.

Fig. 1

Chaotic attractor phase diagram (a) x − y plane (b) x − z plane (c) y − z plane

It is obtained from reference [40] that the Lyapunov exponent of an integer-order no-equilibrium chaotic system is LE₁ = 0.0453, LE₂ = 0, LE₃ = − 3.2903. The analysis shows that when the order q is a fraction, the maximum Lyapunov exponent of the system obtained is far much larger than the integer order system, the chaotic performance of the fractional-order no-equilibrium system has been greatly improved compared with the integer-order system, so the fractional-order no-equilibrium chaotic system has more complex dynamic characteristics, the system is more suitable for image encryption.

2.3 Equilibrium point analysis

The equilibrium point of the system can be found by making the equation of fractional-order no-equilibrium chaotic system equal to 0, so

$$ y=0 $$

(13)

$$ -x-yz=0 $$

(14)

$$ xy + \alpha {x^{2}} + \beta {y^{2}} - \gamma = 0 $$

(15)

2.4 Dynamical characteristics of the fractional-order no-equilibrium chaotic system

The parameters are set to α = 0.5, β = 0.1, γ = 1.3, h = 0.01, the initial values x₀ = [0, 0.1, 0], when the order q ∈ [0.45,1], the LEs and bifurcation diagram of the system are presented in Fig. 2. The bifurcation trajectory enters chaotic state after an obvious period-doubling bifurcation. Besides, the smallest order that can produce chaos is q = 0.565×3 = 1.695. A positive Lyapunov exponent indicates that the phase volume of the system continues to expand and fold, causing the originally similar trajectories in the attractors to become increasingly uncorrelated, and the initial value of the system is highly sensitive. It can be seen from Fig. 2 that when q = 1, the system is in the form of integer-order, and it can be clearly seen that when q < 1, the Lyapunov exponent of the fractional-order chaotic system is significantly higher than that of the integer-order chaotic system, and the initial value of the system is more sensitive.

Fig. 2

LEs and bifurcation diagram with order q ∈ [0.45,1]

Fixed q = 0.67, α ∈[0.3, 0.7], and other parameter values remain unchanged, the LEs and bifurcation diagram are plotted in Fig. 3. From the bifurcation diagram, we can see that the no-equilibrium system has obvious periodic bifurcation and is correspondingly consistent with the Lyapunov exponents. Keeping other parameter values, α = 0.5, the LEs and bifurcation diagram of β ∈[0, 0.2] are shown in Fig. 4. Moreover, setting β = 0.1, γ ∈[1.1, 1.5], and other parameter values remain unchanged, the corresponding LEs and bifurcation diagram are presented in Fig. 5. When the order q is a fraction, the maximum LE of the system is much larger than the integer order. Obviously, the dynamical characteristics of the fractional-order no-equilibrium chaotic system are rich. In addition, we refer to a chaotic system with equilibrium points, whose LES and bifurcation diagram are shown in Fig. 6, and compare its LEs and bifurcation diagram with parameters changing with system 2. It can be seen that when parameters change, the LEs value of system 2 is larger than that of reference [42], so the randomness of the system is better.

Fig. 3

LEs and bifurcation diagram with parameter α ∈[0.3, 0.7]

Fig. 4

LEs and bifurcation diagram with parameter β ∈[0, 0.2]

Fig. 5

LEs and bifurcation diagram with parameter γ ∈[1.1, 1.5]

2.5 Complexity analysis

When chaotic sequences are applied to chaotic secure communication or image encryption, it needs to have high randomness and strong complexity. The LEs and bifurcation diagram can qualitatively analyze the dynamical characteristics of the system, but cannot quantitatively reflect the randomness and complexity of the chaotic sequences. Therefore, spectral entropy (SE) and C₀ complexity algorithms are adopted to analyze the complexity and randomness of fractional-order no-equilibrium system. Taking the system parameters β = 0.1, γ = 1.3, h = 0.01, and the initial condition is [0, 0.1, 0]. According to the spectral entropy (SE) and C₀ complexity algorithm, the complexity of the fractional-order no-equilibrium chaotic system when the order q and the parameter α change simultaneously are calculated as shown in Fig. 7a and b. Different colors indicate different complexity, the lighter the color, the smaller the complexity values in the interval, the worse the randomness of the sequences. The greater the complexity of the chaotic sequence and the greater its randomness, the more difficult it is for the sequence to be recovered. It can be seen from Fig. 7 that when q = 1, the system is in the form of integer-order, the color in this range is the lightest and the complexity is the lowest. When 0.45< q < 0.8, the darker the color, the greater the complexity. Compared with the integer-order system, fractional-order no-equilibrium chaotic system is more suitable for image encryption systems.

Fig. 6

LEs and bifurcation diagram of reference [42]

Fig. 7

The complexity of α ∈[0.3, 0.7], q ∈[0.45, 1]: (a) SE complexity (b) C₀ complexity

Setting α = 0.5, q = 0.67, other parameter values remain unchanged, and the SE complexity and C₀ complexity of the system when the parameters β and γ change at the same time are illustrated in Fig. 8a and b. It can be seen from the figure that when 0.63<α< 0.7, 0.45<q< 0.53, 0.09<β< 0.2, 1.2<γ< 1.35, the color is the darkest, the complexity and randomness of the system are the best. Therefore, when the system is applied to image encryption, the chaotic sequences in this area should be selected.

Fig. 8

The complexity of β ∈[0, 0.2], γ ∈[1.1, 1.5]: (a) SE complexity (b) C₀ complexity

2.6 Attractor basin

The dynamic map reflects the state information of the chaotic attractor, which can provide an effective parameter selection basis for the application of the chaotic system in engineering. Setting iteration time step h = 0.01 initial values x₀ = [0, 0.1, 0]. The attractor basin of the q-α plane when β = 0.1, γ = 1.3 is shown in Fig. 9a, and the attractor basin of the β-γ plane when α = 0.65, q = 0.47 is plotted in Fig. 9b. It can be clearly seen from Fig. 9a that there are yellow and red parts, which represent the limit cycle and chaotic state, respectively. In Fig. 9b, there are yellow, orange and blue, which are limit cycles, chaotic states and divergence state, respectively. When applying the chaotic system to secure communication, the red and orange area should be selected. In addition, the attractor state may jump at the boundary point, so the boundary point of each area should be carefully selected.

Fig. 9

Attractor basin (a) α ∈[0.3, 0.7], q ∈[0.45, 1] (b) β ∈[0, 0.2], γ ∈[1, 1.5]

2.7 DSP implementation of fractional-order no-equilibrium chaotic system

DSP digital signal processor has the advantages of good stability, high precision, strong programmability, and easy implementation. Therefore, the DSP platform implements digital hardware implementation of the fractional-order no-equilibrium chaotic system. The hardware realization platform is illustrated in Fig. 10. Here the DSP chip is TMS320F28335, and the time series generated by DSP is converted by 16-bit dual-channel D/A converter DAC8552 [11, 29, 31]. Letting α = 0.5, β = 0.1, γ = 1.3, q = 0.67, and h = 0.01, the initial values x₀ = [0, 0.1, 0], Fig. 11a–c show the phase diagram of the fractional-order no-equilibrium chaotic map captured by the oscilloscope, which are the same as the computer simulation results.

Fig. 10

DSP implementation platform

Fig. 11

Phase diagram realized by DSP platform (a) x − y plane (b) x − z plane (c) y − z plane

3 Application of fractional-order no-equilibrium chaotic system in image encryption

3.1 Encryption algorithm

A color image encryption algorithm based on the fractional-order no-equilibrium chaotic system is introduced in this section. The algorithm divides the color image into R, G, B three channels, which are performed: DCT sparse transformation, scrambling algorithm, and diffusion algorithm based on GF (257) domain. The encryption scheme for an image of size N*N (N = 256) is shown in Fig. 12, and the specific steps are as follows:

• Step 1: Input the original color image I with a size of N × N and decompose it into R (red), G (green), B (blue) three-channel images.

• Step 2: The sparse coefficient matrices R₁, G₁ and B₁ are got by using the discrete cosine transform (DCT) to sparse the R, G, B three-channel pixel matrices.

• Step 3: The fractional-order no-equilibrium chaotic system is iterated L (L = m + s) times to obtain three chaotic sequences, the sequence x is quantized by (16), which is discarded first s items to get a pseudo-random sequence X of length m. Moreover, the elements of X are sorted in descending order to obtain the index sequence S.

  $$ x(i) = mod(floor((x(i) + abs(x(i)))*{10^{16}}),256) + 1\\ $$

  (16)

• Step 4: According to sequence S and the Hadamard matrix of N × N, determine the measurement matrix ϕ of m × N. The Hadamard matrix is generated by

  $$ \left[ {\begin{array}{*{20}{c}} 1 & 1 \\ 1 & { - 1} \end{array}} \right] $$

  (17)

• Step 5: According to (18), the three-channel sparse coefficient matrices of R₁, G₁ and B₁ are compressed and sampled to obtain the compressed image pixel matrices R₂, G₂ and B₂ of m × m.

  $$ \left\{ {\begin{array}{*{20}{c}} {{R_{2}} = {\varPhi} ({\varPhi} {R_{1}})'} \\ {{G_{2}} = {\varPhi} ({\varPhi} {G_{1}})'} \\ {{B_{2}} = {\varPhi} ({\varPhi} {B_{1}})'} \end{array}} \right. $$

  (18)

• Step 6: The element values of matrices R₂, G₂ and B₂ are quantized to an integer in the range of 0-255 by (19).

  $$ \left\{ {\begin{array}{*{20}{c}} {{R_{3}} = round(255*(C11 - Min({R_{2}}))/(Max({R_{2}}) - Min({R_{2}})))} \\ {{G_{3}} = round(255*(C11 - Min({G_{2}}))/(Max({G_{2}}) - Min({G_{2}})))} \\ {{B_{3}} = round(255*(C11 - Min({B_{2}}))/(Max({B_{2}}) - Min({B_{2}})))} \end{array}} \right. $$

  (19)

• Step 7: Scrambling of the pixel matrix. Flip the odd-numbered column elements of the matrices R₃, G₃, B₃ and then generate a non-repetitive random integer sequence M with a length of m and values between 1 and m, which scrambles the rows of the three-channel pixel matrices.

• Step 8: Set the parameters and initial values of the chaotic system (2), and then the system iterates t + 2 × m × m times, where t is generated by the three-channel pixel matrices R, G, B. According to (20) and (21), pseudo-random sequences X, Y are generated from chaotic sequences y and z. The pseudo-random sequences S1 and S2 of forward diffusion and reverse diffusion are obtained by X and Y, respectively.

  $$ \left\{ {\begin{array}{*{20}{c}} {X = mod(floor(abs(y)*{{10}^{16}}),256)} \\ {Y = mod(floor(abs(z)*{{10}^{16}}),256)} \end{array}} \right. $$

  (20)
  $$ \begin{array}{l} S1 = X(1:m \times m) \\ S2 = Y(1:m \times m) \end{array} $$

  (21)

• Step 9: The multiplication table of GF (257) domain can be generated by the computer. Then, with the help of (22) and (23), the scrambled R, G, B three-channel pixel matrices are diffused.

  $$ \left\{ \begin{array}{l} {C_{i,H}} = {C_{i - 1,H}} \times {S_{i,H}} \times {I_{i,H}},{C_{i,L}} = {C_{i - 1,L}} \times {S_{i,L}} \times {I_{i,L}} \\ C = ({C_{i,H}} \times 16 + {C_{i,L}}) \end{array} \right. $$

  (22)
  $$ \left\{ \begin{array}{l} {C_{i,H}} = {C_{i + 1,H}} \times {S_{i,H}} \times {I_{i,H}},{C_{i,L}} = {C_{i + 1,L}} \times {S_{i,L}} \times {I_{i,L}} \\ C = ({C_{i,H}} \times 16 + {C_{i,L}}) \end{array} \right. $$

  (23)

  in which, (22) and (23) are the forward diffusion process and the reverse diffusion process, respectively. I represents one-dimensional vector of the pixel matrix. C and S are cryptographic vectors, initial values C₀ comes from the secret key (i = 1, 2, 3, ..., m × m), H is the upper 4 bits of the data, and L represents the lower 4 bits of the data.

• Step 10: Integrate the three-channels of R, G, and B the encrypted image C is obtained.

Fig. 12

Encryption flow chart

3.2 Decryption algorithm

As shown in Fig. 13, the decryption process of the color image can be realized by the reverse operation encryption process. It is worth mentioning that the OMP algorithm realizes the reconstruction of the image. The specific decryption steps are as follows:

• Step 1: Dividing the encrypted image C into three-channels of R, G, and B. The pseudo-random sequence S1, S2 generated by step 8 of the encryption algorithm performs inverse diffusion processing in the GF (257) domain on pixel matrices of each channel. The diffusion processes are

  $$ \left\{ \begin{array}{l} {I_{i,H}} = {C_{i,H}} \div {C_{i + 1,H}} \div {S_{i,H}},{I_{i,L}} = {C_{i,L}} \div {C_{i + 1,L}} \div {S_{i,L}} \\ {I_{i}} = ({I_{i,H}} \times 16 + {I_{i,L}}) \end{array} \right. $$

  (24)
  $$ \left\{ \begin{array}{l} {I_{i,H}} = {C_{i,H}} \div {C_{i - 1,H}} \div {S_{i,H}},{I_{i,L}} = {C_{i,L}} \div {C_{i - 1,L}} \div {S_{i,L}} \\ {I_{i}} = ({I_{i,H}} \times 16 + {I_{i,L}}) \end{array} \right. $$

  (25)

• Step 2: The M sequence generated by step 7 of the encryption algorithm inversely scrambles the rows of the three-channel pixel matrices, and then flips the odd-numbered column elements of the pixel matrices.

• Step 3: Use the OMP algorithm and the measurement matrix generated in step 4 of the encryption algorithm to reconstruct the three-channel planar sparse pixel matrices with a size of N × N.

• Step 4: The three-channel pixel matrices of the decrypted image are got by inverse discrete cosine transform (IDCT), which are combined to get the decrypted image.

Fig. 13

The architecture of decryption algorithm

4 Encryption simulation results and performances analysis

4.1 Experimental results

To verify the reliability and security of the algorithm, we encrypt the four different 512×512 color images and four different 256×256 color images. The chaotic system parameters are α = 0.65, β = 0.1, γ = 1.3, q = 0.47, h = 0.01, initial values [x₀, y₀, z₀] = [0, 0.1, 0], CR = 0.75, the encryption and decryption algorithms have the same key. The compression ratio CR is calculated by

$$ CR = \frac{{{C_{{\text{heigt}}}} \times {C_{{\text{width}}}}}}{{{I_{{\text{heigt}}}} \times {I_{{\text{width}}}}}}\ $$

(26)

here I is plain image, C is encrypted image. The original 512×512 color images “4.1.03”, “4.1.04”, “House” and “Airplane” are shown in Fig. 14a, the encrypted images are illustrated in Fig. 13b, the corresponding decrypted images are in Fig. 14c. Figure 15a plotted the original 256×256 color images “Lena”, “Pepper”, “Barbara” and “Fruits”, the encrypted images are in Fig. 15b, and the corresponding decrypted images are shown in Fig. 15c. From Figs. 14b and 15b, the compressed and encrypted images are obviously smaller than the corresponding original image, and the cipher images completely change the characteristics of the plaintext images. The encryption scheme can reduce the network transmission pressure and carry out safe transmission. In addition, the decrypted images shown in Figs. 14c and 15c are basically the same as their corresponding original images. The algorithm has good encryption and decryption effects. Selecting the color image Lena with a size of 256×256, and divide it into three channels of R, G, B, the encryption and decryption process flow chart as shown in Fig. 16.

Fig. 14

Simulation results of 512×512 color images“4.1.0”, “4.1.04”, “House” and “Airplane” (a) original color images (b) encrypted images (c) decrypted images

Fig. 15

Simulation results of 256×256 color images“Lenna”, “Pepper”, “Barbara” and “Fruits” (a) original color images (b) encrypted images (c) decrypted images

Fig. 16

Lena image is divided into R, G, B three-channel encryption and decryption process

4.2 The compression ratio analysis

In this subsection, the mean structural similarity (MSSIM) and peak signal to noise ratio (PSNR) are adopted to evaluate image compression performance with different compression rates.

4.2.1 Mean structural similarity (MSSIM)

The mean structural similarity (MSSIM) is an index to evaluate the similarity of two images, which is defined as

$$ L(x,y) = \frac{{2{u_{x}}{u_{y}} + {{({K_{1}} \times L)}^{2}}}}{{{u_{x}^{2}} + {u_{y}^{2}} + {{({K_{1}} \times L)}^{2}}}} $$

(27)

$$ C(x,y) = \frac{{2{\sigma_{x}}{\sigma_{y}} + {{\left( {{K_{\text{2}}} \times L} \right)}^{\text{2}}}}}{{{\sigma_{x}^{2}} + {\sigma_{y}^{2}} + {{\left( {{K_{\text{2}}} \times L} \right)}^{\text{2}}}}} $$

(28)

$$ S(x,y) = \frac{{{\sigma_{xy}} + {{{{\left( {{K_{\text{2}}} \times L} \right)}^{\text{2}}}} / 2}}}{{{\sigma_{x}}{\sigma_{y}} + {{{{\left( {{K_{\text{2}}} \times L} \right)}^{\text{2}}}} 2}}} $$

(29)

$$ {\text{SSIM}}(x,y) = L(x,y) \times C(x,y) \times S(x,y) $$

(30)

$$ {\text{MSSIM}}(x,y) = \frac{1}{M}\sum\limits_{k = 1}^{M} {{\text{SSIM}}({x_{k}},{y_{k}})} $$

(31)

where x is the original color image and y is the decrypted image. u_x, u_y, σ_x, σ_y are the mean, variance values of x and y, respectively. and σ_xy represents the covariance of x and y. The parameters are as follows: K₁ = 0.01, K₂ = 0.03, L = 255 and M = 64.

Table 1 lists the MSSIM values of each channel of 256×256 color images at different compression ratios. From Table 1, the MSSIM values of different images are similar at the same compression ratios, so the proposed algorithm is stable. When the compression ratio changes, the values of MSSIM will change accordingly, so images can be effectively compressed and encrypted according to different actual needs.

Table 1 MSSIM values of different images at different CRs

4.2.2 Peak signal to noise ratio (PSNR)

Peak signal to noise ratio is an important indicator to judge the ability of image reconstruction, which calculation is as follows:

$$ {\text{PSNR}} = 10 \times {\log_{10}}\left( {\frac{{{{255}^{2}}}}{{{{(1} / {H \times W}})\sum\limits_{i = 1}^{H} {\sum\limits_{j = 1}^{W} {{{(L(i,j) - l(i,j))}^{2}}} } }}} \right) $$

(32)

here L(i,j) is the decrypted image and l(i,j) is the original image. H and W represent the length and width of the image. Table 2 shows the PSNR values of each channel of 256×256 color images at different compression ratios. It can be seen that even if there is very little information sampled at CR = 0.25, the values of PSNR are close to 30, so the image reconstruction effect is better and is beneficial to transmission.

Table 2 PSNR values of different images at different CRs

4.3 Key space

The sum of the keys in the image encryption process is the key space, which is a necessary condition for measuring the encryption scheme. In order to resist brute force attack, the key space should be greater than 2¹⁰⁰. In the proposed method, if the calculation accuracy is 10^− 15, the key space is (10¹⁵)⁹ = 10¹³⁵ ≈ 2⁴⁴⁸. Moreover, considering the key t related to the plaintext, the key of the algorithm is> 2⁴⁴⁸, which is large enough to resist brute force attacks. Under the same encryption algorithm and calculation precision, the key space of the integer-order no-equilibrium chaotic system is 2³⁹⁸ [40], which is smaller than that of the fractional-order chaotic system. In contrast, fractional-order no-equilibrium chaotic systems is more suitable for image encryption system.

4.4 Key sensitivity

Key sensitivity analyzes the difference between two cipher images got when the same plain image is encrypted with a slight change in the key. If the two cipher images are significantly different, the key sensitivity of cryptographic system is extreme. If the difference between the two cipher images is small, the key sensitivity of the cryptographic system is weak. An excellent cryptographic system should be sufficiently sensitive to all secret keys. In this test, the“Peppe” image is used as the test image, and the original image and the encrypted image C with the correct key are displayed in Fig. 17a and b, The secret key is changed to α + 10^− 15, β + 10^− 15, γ + 10^− 15, h+ 10^− 15, q+ 10^− 15, m+ 10^− 15, x₀ + 10^− 15, y₀ + 10^− 15, z₀ + 10^− 15, the new encrypted images are C1, C2, C3, C4, C5, C6, C7, C8, C9, which are shown in Fig. 17c–k, The differences between the original cipher image and the new cipher images are represented in Fig. 17l–t. The test results show that when the key is slightly changed, the two cipher images got by encrypting the same plain image are significantly different. So the key of the proposed algorithm is sufficiently sensitive.

Fig. 17

Key sensitivity analysis results (a) Original “Pepper” image (b) Cipher image C (c) Cipher image C1 (d) Cipher image C2 (e) Cipher image C3 (f) Cipher image C4 (g) Cipher image C5 (h) Cipher image C6 (i) Cipher image C7 (j) Cipher image C8 (k) Cipher image C9 (l) |C-C1| (m) |C-C2| (n) |C-C3| (o) |C-41| (p) |C-C5| (q) |C-C6| (r) |C-C7| (s) |C-C8| (t) |C-C9|

4.5 Statistical analysis

4.5.1 Histogram analysis

The histogram is a statistical table reflecting the pixel distribution of an image. The cipher image should disrupt the statistical characteristics of the plain image to prevent an attacker from obtaining effective statistical information. Figure 18 draws the histogram of the plain image and the cipher image of “Lena”. In this test, the pixel value distribution of the histogram of the encrypted image is uniform. Compared with the histogram of the original image, the encrypted image completely changes the statistical characteristics of the original image. On the other hand, χ²-values statistics are usually used to show the uniformity of the image histogram, Table 3 lists the χ²-values of different images. From the χ²-values in Table 3, we can see that the cipher images are uniformly distributed.

Fig. 18

Histogram of original image and encrypted image (a1) R channel of the original image (a2) G channel of the original image (a3) B channel of the original image (b1) R channel of the encrypted image (b2) G channel of the encrypted image (b3) B channel of the encrypted image

Table 3 the χ²-values of different images

4.5.2 Correlation analysis

The adjacent pixel correlation coefficient is a performance index for evaluating the cryptographic system, and it reflects the correlation between adjacent pixels. The closer the correlation coefficient is to 0, the better the cryptographic system. The correlation of adjacent pixels can be reduced by an effective encryption algorithm. The correlation coefficient is calculated by

$$ \left\{ {\begin{array}{*{20}{c}} {{\rho_{uv}} = \frac{{{\text{cov}} (u,v)}}{{\sqrt{D(u)} \sqrt{D(v)} }}} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\text{cov}} (u,v) = \frac{1}{N}\sum\limits_{i = 1}^{N} {({x_{i}} - E(u))({y_{i}} - E(v))} } \\ {D(u) = \frac{1}{N}\sum\limits_{i = 1}^{N} {{{({u_{i}} - E(u))}^{2}}} } \end{array}} \\ {E(u) = \frac{1}{N}\sum\limits_{i = 1}^{N} {{u_{i}}} } \end{array}} \end{array}} \right. $$

(33)

where u, v, are the gray values of two adjacent pixels

Randomly select 2000 pixel pairs and measure the correlation coefficients in the horizontal, vertical, and diagonal directions. Figure 19 depicts the correlation of adjacent pixels of different images in various directions, and Table 4 lists the correlation coefficients of adjacent pixels of different images. For original images, the correlation coefficients of adjacent pixels are close to 1, which has a powerful correlation. After encryption, the correlation coefficients of adjacent pixels in all directions are close to 0, it indicates that adjacent pixels have almost no correlation. In addition, it can be seen from Fig. 19 that the encryption algorithm breaks the correlation between adjacent pixels in all directions. Table 5 compares the correlation coefficients between the proposed scheme and other schemes. From the results, the encrypted image in this paper has less correlation than other schemes in all directions.

Fig. 19

Correlation analysis (first line is original “Lena” image, second line is encrypted “Lena” image) (a1) and (a2) Horizontal direction (b1) and (b2) Vertical (c1) and (c2) Diagonal

Table 4 Correlation coefficients of different images

Table 5 Compare correlation coefficients with other algorithms

4.6 Information entropy

We analyze the randomness of color images through information entropy. For an image with 256 gray values, the closer the entropy value is to 8, the stronger the randomness of the image information, the amount of understood image information is less. We calculated the information entropy of different images and their corresponding encrypted images, and listed calculation results in Table 6. Moreover, Table 6 shows the information entropy of each channel. The information entropy values of the cipher images are closer to 8 than that of the plain images, so the information leakage of the encrypted image may be very small, which means that the proposed algorithm can resist statistical attacks. The information entropy values of the Lena image under different algorithms are listed in Table 7. It can be seen that compared to other algorithms, the information entropy in this paper is closer to the theoretical value.

Table 6 Information entropy values of different images

Table 7 Information entropy of image under different algorithms

4.7 Differential attacks

Generally, NPCR (pixel change rate) and UACI (uniform average change intensity) are used to analyze whether the cryptosystem can resist differential attacks. For two cipher images C1 and C2, whose plain images differ by 1 bit of pixel value, the NPCR and UACI of them are defined by

$$ \begin{array}{l} {\text{NPCR}} = \frac{1}{{M \times N}}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {E(i,j) \times 100\% } } \\ {\text{UACI}} = \frac{1}{{M \times N}}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\frac{{\left| {{C_{1}}(i,j) - {C_{2}}(i,j)} \right|}}{{255}} \times 100\% } } \end{array} $$

(34)

where M and N are the size of cipher images, if C1(i,j) = C2(i,j), then D(i,j) = 0. Otherwise, E(i,j) = 1. The theoretical expectations of NPCR and UACI are 99.6094% and 33.4635%, respectively. A new standards for NPCR and UACI are established by Wu et al. [50]. If the calculated NPCR value is greater than the critical value under the significance level α, the NPCR test passed. The NPCR at significant level α is calculated as

$$ {\text{NPCR}}_{\alpha}^ * = \frac{{H - {{\varPhi}^ - }^{1}(\alpha )\sqrt {{H / {(M \times N}})} }}{{H + 1}} $$

(35)

here H represents the maximum allowable value of image pixel value. For UACI, if the calculated value of UACI is in the interval (UACI$^{*-}_{\alpha }$,UACI$^{*+}_{\alpha }$), This represents passing the UACI test.

$$ \begin{array}{l} {\text{UACI}}_{\alpha}^{* - } = \frac{{H + 2}}{{3H + 3}} - {{\varPhi}^{- 1}}(\frac{\alpha }{2})\sqrt {\frac{{(H + 2)({H^{2}} + 2H + 3)}}{{18{{(H + 1)}^{2}}M \times N \times H}}} \\ {\text{UACI}}_{\alpha}^{* + } = \frac{{H + 2}}{{3H + 3}} + {{\varPhi}^{- 1}}(\frac{\alpha }{2})\sqrt {\frac{{(H + 2)({H^{2}} + 2H + 3)}}{{18{{(H + 1)}^{2}}M \times N \times H}}} \end{array} $$

(36)

In this test, randomly select a pixel value of the plain image and modified it. The average test results of UACI and NPCR are listed in Tables 8 and 9, respectively. As we can see, NPCR test values are greater than the critical values, UACI test values are within the theoretical allowable ranges. This shows that the algorithm has passed NPCR and UACI tests and has the ability to resist differential attacks [13]. Table 10 lists the comparison results with other schemes. From Table 10, our results are closer to the ideal value than other schemes.

Table 8 NPCR test values of different images

Table 9 UACI test values of different images

Table 10 The NPCR and UACI values of the images under different algorithms

4.8 Cropping and noise attack analysis

Generally, color image unavoidably presents with noise interference and data loss in actual encryption and transmission processing. Therefore, the image encryption system is required to have good robustness to resist noise attacks and data loss. In order to evaluate the robust performance of the algorithm, the following tests are performed. The encrypted image is added with salt and pepper noises of 0.001, 0.01, 0.1 and 0.2, and the experimental results are displayed in Fig. 20. Even if there is noise interference, the main information of the original image can be identified by the decryption algorithm, when the noise increases to 0.1 and 0.2, the decrypted images become faintness, but the basic contour of the plain image can still be decrypted. Besides, the encrypted image data is lost 1/16, 1/8, 1/4 and 1/2, and the decrypted images are plotted in Fig. 21. Obviously, the decrypted images can identify most of the main information of the original images. In summary, the proposed algorithm is robust against noise interference and data loss, and is suitable for practical applications.

Fig. 20

Noise Attack: 4.1.04 (256××256) has salt and pepper noise of (a) 0.001, (b) 0.01, (c) 0.1and (d) 0.2; the decrypted image of (e) Figs. 15a, f Fig. 15b, g Fig. 15c and h Fig. 15d

Fig. 21

Cropping Attack: 4.1.04 (256×256) has data loss of (a) 1/16, (b) 1/8, (c) 1/4 and (d) 1/2; the decrypted image of (e) Fig. 16a, f Fig. 16b, g Fig. 16c and h Fig. 16d

5 Conclusion

A fractional-order non-equilibrium chaotic system with hidden attractors is proposed, and its dynamical characteristics are analyzed. The complexity and attractor basin are used to analyze and determine the optimal parameter range of the system in the secure communication system. Moreover, we design an image encryption scheme in which compression and encryption are performed simultaneously. The scheme uses random row and column scrambling and GF (257) domain diffusion algorithm to encrypt images. The key is related to the plaintext, which can improve the resistance to known or selected plaintext attacks. The experimental results indicate that the encrypted image is obviously smaller than the original image, and the information of the original image is successfully destroyed. The algorithm has good compression performance. Even the CR = 0.25, the obtained PSNR values and MSSIM values are large enough to still identify the main information of the original image. In addition, the proposed algorithm can resist various attacks such as differential attacks, shearing attacks, and noise attacks. Statistical analysis, secret key space and secret key sensitivity analysis prove the security and effectiveness of the algorithm and the algorithm has good practical application value.