1 Introduction

Digital images, as a multimedia resource, have played an important role in the modern big data era. There are many application fields for them in our daily life, for example, the fields of medicine institution, aerospace, education, electronic commerce, military affairs and so on. To share image information, we can conveniently transmit it over the open network by computer or other mobile equipment. However, unauthorized cryptanalysis is a big threat to the communication of images [1, 2]. More importantly, some images concern individual privacy or national strategy, for example, ECGs (Electrocardiographs) or satellite reconnaissance. Thus, the question of how to efficiently protect the security of a communicated image has attracted a large amount of attention from experts and scholars all over the world [3,4,5]. It is noted that images have inherent characteristics different to those found in text [6, 7] such as high redundancy, bulk data capacity, and strong correlation. Consequently, traditional ciphers such as AES (Advanced Encryption Standard), DES (Data Encryption Standard), and IDEA (International Data Encryption Algorithm) are not suitable for efficiently encrypting images [8, 9].

Fig. 1
figure 1

Classical permutation–diffusion mechanism

Full size image

Recently, image encryption schemes using chaos have shown their superior performance [10,11,12]. This may be attributable to properties of chaotic systems such as high sensitivity to initial conditions, non-periodicity, nonlinearity, and pseudo-randomness [13,14,15]. As early as 1998, Fridrich [16] proposed a symmetric encryption scheme for images using a two-dimensional chaotic map. Permutation–diffusion architecture was suggested to encrypt image content, where a permutation operation is performed to change the positions of pixels, while a diffusion to alter gray values. Figure 1 shows the classical permutation–diffusion mechanism, which has been widely studied and applied [17,18,19]. For example, a new color image encryption algorithm was proposed in [20] with a new revised one-dimensional chaotic map. Compared to the traditional one-dimensional chaotic map, the revised one-dimensional chaotic map exhibits better chaotic behavior. Firstly, the method [20] reshapes a color image of size \(M\times N\) into an one-dimensional image matrix, P, with length 3MN. It then produces a permutation position matrix, \(X'\), from chaotic sequence X to shuffle pixel positions for P and obtain a permuted image, \(P'\). After that, a diffusion operation for \(P'\), using a diffusion matrix \(D'\) from X, is taken to achieve C. A rotating function is applied to C to get \(C'\). Finally, the cipher-image is formed after reshaping \(C'\) into an R, G, and B color image. In [21], a new hyperchaotic system in four dimensions was designed for image encryption. First, image scrambling is applied to image blocks of size \(256\times 256\), in which index sequences S and T are generated from chaotic sequences to translate the row and column for each block. As for the operation of value substitution, the method changes the values based on the pseudo-random sequence RandImage produced from a pseudo-random sequence generator. A new confusion scheme based on paired interpermuting planes [22] was implemented into an image encryption algorithm. It is noted that the algorithm [22] employs a ‘exchange and random access strategy’ to replace the traditional confusion operation. In the diffusion stage, the confused image is transformed into a one-dimensional array; then, a bitwise XOR operation is applied to get the cipher-image. One-time key was simulated in [23] to enhance the sensitivity, in which MD5 of the mouse-position from entropy was employed. To implement the double effects of diffusion, bit-level permutation [24] was designed in confusion stage. Being activated by deoxyribonucleic acid (DNA) coding, a new method encryption algorithm [25] has been proposed to confuse the pixels by transforming the nucleotide into its base pair for random times. By using a perceptron model within a neural network, a novel image encryption algorithm under perceptron model was suggested in [26].

There are also many other encryption algorithms [27,28,29,30,31,32,33] that have been proposed to protect image content. For example, a quantum realization of the generalized Arnold transform was designed for image encryption in [30]. To decrease the transmission burden, a new compression–encryption scheme was proposed [31] with the help of compressive sensing. Moreover, the fractional Mellin transform was introduced for compression–encryption scheme [32]. However, security problems still threaten the communication of digital image. Some algorithms were found to be insecure, for example, Parvin et al. [34] proposed an image encryption scheme in which a operation of two-stage permutation and one-stage substitution is adopted. After setting the secret keys, three pseudo-random keystreams are generated, i.e., \(K_{1}\) for circular shift by row, \(K_{2}\) for circular shift by column, and \(K_{3}\) for substitution. However, the keystreams are produced with no relationship to the plain-image; thus, by chosen-plaintext attack [35], it was proven that the encryption scheme in [34] can be cracked. In [36], Brownian motion and PWLCM (piecewise linear chaotic map) are applied into image encryption algorithm. It uses Brownian motion to scramble the image; in particular, the sum of image pixels is used in the image permutation to update the initial keys \(u_{0}\) and \(v_{0}\) of the logistic map. PWLCM is then employed to generate the pseudo-random sequence D for the diffusion operation. However, the secret keys can be divulged by chosen-plaintext attacks [37]. As for the class of image encryption schemes based on the Chinese remainder theorem, for example [38], the equivalent secret key of CECRT (Compression–Encryption and Chinese Remainder Theorem) can be recovered easily due to properties of the CRT (Chinese Remainder Theorem) [39], and the keystream is only dependent on the secret keys. It has been proven that the attack complexity is O(L) for a plaintext with length L. Moreover, most image encryption algorithms [40, 41] commonly divide the encryption process into two separate processes, i.e., permutation and diffusion, and do not connect them into one entirety, so, separate attacks can also crack their algorithms [42, 43]. Additionally, there are some image encryption schemes which attempt to avoid the permutation–diffusion structure, for example, one-round diffusion [44] or permutation-only [45] was employed. However, they have been pointed out to be insecure [45,46,47]. Some bit level based on image encryption algorithms have also been proposed, for example [48, 49]. The novelty of these methods is that they can exchange bit positions and then alter simultaneously pixel values. However, they should spend more time on transforming between the decimal numbers and binary numbers.

Based on the analysis above, an efficient pixel-level-based chaotic image encryption algorithm is suggested in this paper to try to satisfy the secure communication requirements for images: (1) to solve the problems of permutation-only or diffusion-only methods, and the low security existing in Fridrich’s scheme [43], a permutation–rewriting–diffusion (PRD) is designed. (2) To frustrate the known-plaintext and chosen-plaintext attacks, the keystreams used in stages of permutation and diffusion are dependent on the image. (3) To avoid the separate attack, a connection of permutation with diffusion is established to make them into a whole. It is noted that [42] in a substitution–diffusion-based chaotic image encryption algorithm, the two stages of confusion and diffusion are solely finished by substitution and the diffusion operations, respectively. Therefore, the two stages can be attacked separately [42] under this design. The rest of this paper is organized as follows. The PRD-based image encryption algorithm is introduced in Sect. 2. Then, experiments and security analysis are given in Sect. 3 in order to show the good efficiency of the proposed algorithm. Finally, some conclusions are drawn in Sect. 4.

2 PRD-based image encryption algorithm

2.1 Chaotic map

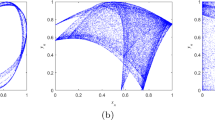
To avoid the small key space existing in one-dimensional chaotic maps, for example logistic map, two- or more-dimensional map is suggested to satisfy the requirement of the minimum key space of \(2^{100}\approx 10^{30}\) [29]. In this paper, a TD-SLMM (two-dimensional sine logistic modulation map) [10] is employed to produce a chaotic sequence as pseudo-random outputs, which can be defined and seen as

$$\begin{aligned} \left\{ \begin{array}{ll} x_{i+1}=\alpha (\text {sin}(\pi y_{i})+\beta )x_{i}(1-x_{i}), \\ y_{i+1}=\alpha (\text {sin}(\pi x_{i+1})+\beta )y_{i}(1-y_{i}), \end{array}\right. \end{aligned}$$
(1)

where \(\alpha \in [0, 1]\) and \(\beta \in [0, 3]\) are seen as open control parameters. The action of \(\beta \) is used to modulate the output and enhance the nonlinearity and randomness [10]. When \(\beta \) is set close to 3 with \(\alpha \) close to 1, the TD-SLMM has hyperchaotic behavior with two positive Lyapunov exponent values. The performance of chaotic behavior for the TD-SLMM can be seen in [10]. Figure 2 shows the chaotic behavior by x-ordinary and y-ordinary. However, the degradation exists in each chaotic system (map); we can turn to the analysis method by [50] and it is out of our scope. As we know that it needs more time to solve differential equation in continual system, for example, Chen chaotic system, and Lorenz chaotic system, by mathematical method. So, we consider the chaotic map TD-SLMM in discrete case with two dimensions. Of course, for an extensive generality, the TD-SLMM can also be changed to other two-dimensional chaotic map.

Fig. 2
figure 2

Chaotic behavior: a x-ordinary, b y-ordinary

Full size image

2.2 The proposed algorithm

In the traditional Fridrich method, two operations are employed: permutation and diffusion. In the first place, permutation is used to exchange the position of pixels reducing the high correlation existing in two adjacent pixels. However, only the removal of pixels is carried out in this stage not changing of pixel values. That is to say, each pixel keeps the same value before and after permutation. As a result, the pixel distribution (or histogram) will also remain invariant. To enhance the security, diffusion is then employed after permutation to alter the pixel values for the permuted image. Therefore, the distribution of pixels will be different after diffusion compared to that of the plain-image. However, there is no connection between permutation and diffusion, so, separate attacks [42] may analyze the structure and reveal the original information. As a remedy, a new PRD-based image encryption algorithm is designed in this paper, the contributions of which are: (1) the connection of permutation and diffusion into a whole to solve the shortcomings of Fridrich’s structure, and then frustrate the separate attack. (2) The use of a PRD-based algorithm to implement double diffusion effects to enhance the security of Fridrich’s structure. (3) The design of a keystream dependent upon the plain-image in both permutation and diffusion operations to avoid known-plaintext and chosen-plaintext attacks.

Suppose that the plain-image of size \(m\times n\) is P, and the corresponding cipher-image is C with the same size. Then, \(x_{0}\) and \(y_{0}\) are the initial conditions for permutation stage, while \(z_{0}\) and \(w_{0}\) are the initial conditions for diffusion. To ensure a high randomness, the control parameters are fixed at \(\alpha =0.9998\), \(\beta =2.9925\).

  1. (1)

    Permutation-based encryption algorithm

The function of permutation is to shuffle the pixel position but not change the gray values. Let s be the statistical characteristics extracted from P, computed as

$$\begin{aligned} s=\sqrt{\sum P_{i,j}^2+a}, \end{aligned}$$
(2)

where \(a\ge 1\) is a control parameter used to avoid black image attacks. We know that if the keystream is generated only from keys, with no relationship to the plain-image, then the designed algorithm will be insecure against known-plaintext and chosen-plaintext attacks. To ensure security, the keys \(x_{0}\) and \(y_{0}\) in the permutation stage are designed to be influenced by s as

$$\begin{aligned} \left\{ \begin{array}{ll} x'_{0}= x_{0}+\frac{s+1}{256(mn+a)}~\text {mod}~1, \\ y'_{0}= y_{0}+\frac{s+2}{256(mn+a+1)}~\text {mod}~1. \end{array}\right. \end{aligned}$$
(3)

In this case, the keys \(x'_{0}\) and \(y'_{0}\) will be different after being updated with respect to different plain-images. Then, with the new values of \(x'_{0}\) and \(y'_{0}\) iterated into the TD-SLMM, sequence \(\{x'_{0}, y'_{0}, x'_{1}, y'_{1}, \ldots \}\) is obtained after numerous rounds of iteration. To avoid the transient effect [6], the previous t iterated values should not be used, for example, t is set as 200 in this paper. That is to say, the random sequence is collected as \(s=\{x'_{t+1}, y'_{t+1}, x'_{t+2}, y'_{t+2}, \ldots \}\). Suppose that the vector for row permutation is \(h=\{x'_{t+1}, x'_{t+2}, \ldots , x'_{t+m}\}\), while \(l=\{y'_{t+1}, y'_{t+2}, \ldots , y'_{t+n}\}\) is the vector for column permutation. Then, a circular permutation [7] for both rows and columns is carried out to obtain the permuted image R. Before permutation, vectors h and l should be processed to meet the size of the pre-encrypted image, where

$$\begin{aligned} \left\{ \begin{array}{ll} h\doteq \lceil h\times 10^{14}\rceil ~\text {mod}~n, \\ l\doteq \lceil l\times 10^{14}\rceil ~\text {mod}~m, \end{array}\right. \end{aligned}$$
(4)

\(\lceil x\rceil \) rounds the element x to the nearest integer toward minus infinity.

  1. (2)

    Rewriting-based encryption algorithm

In the traditional Fridrich encryption scheme, only the exchange of pixel positions is considered before the diffusion operation. Moreover, there are two mutually independent stages: permutation and diffusion. The effects of confusion and diffusion are implemented only by the permutation and diffusion operations, respectively. As a result, it has been found that the above two stages can be attacked separately [42]. To solve this problem, a rewriting operation of pixels in the permuted image is suggested between permutation and diffusion in the proposed algorithm.

Let the parameter \(\lambda \) equal \(\lambda =\lceil (x_{0}+y_{0}+z_{0}+w_{0})\times 10^{14}\rceil ~\text {mod}~255+1\), which is dependent on the secret keys. The rewriting function for the permuted image is defined as

$$\begin{aligned} Q=R+\lambda E_{m\times n}~\text {mod}~256, \end{aligned}$$
(5)

where \(E_{m\times n}\) represents an \(m\times n\) matrix with ones as elements. Therefore, pixel distribution for Q will be different from that of R. The whole algorithm will then be blended together by parameter \(\lambda \).

  1. (3)

    Diffusion-based encryption algorithm

To enhance the security, the diffusion operation is required to make a histogram uniform in the cipher-image, especially a huge difference from that of the plain-image. More important, the primary objective is to achieve a tiny change in one pixel spreading over the entire image by pixel value modification. As a result, the avalanche effect can be carried out in this stage. For the keys \(z_{0}\) and \(w_{0}\), a preprocess for them is defined as

$$\begin{aligned} \left\{ \begin{array}{l} z'_{0}=z_{0}+\frac{x_{0}}{b}~\text {mod}~1, \\ w'_{0}=w_{0}+\frac{y_{0}}{d}~\text {mod}~1, \end{array}\right. \end{aligned}$$
(6)

where b and d are bigger prime numbers. Obviously, former values of \(x_{0}\) and \(y_{0}\) will influence the values of \(z_{0}\) and \(w_{0}\). Therefore, it can combine the permutation and diffusion operations into a whole. Then, by iterating the map TD-SLMM with \(z'_{0}\) and \(w'_{0}\), a random matrix M is obtained after numerous rounds of iteration. To meet the gray scale for a gray image, each element of M is processed by

$$\begin{aligned} M_{i,j}=\lceil M_{i,j}\times 10^{14}\rceil ~\text {mod}~256. \end{aligned}$$
(7)

For the diffusion by rows, the operation can be seen as

$$\begin{aligned} \left\{ \begin{array}{ll} tp=\lceil (x_{0}+y_{0})\times 10^{14}+(\sum _{j=i+1}^{m} Q_{j,t})\times i\rceil ~\text {mod}~256, \\ E_{i}=E_{i-1}+Q_{i}+(tp\times e_{n}+M_{i})~\text {mod}~256, i=1,2,\ldots ,m, \end{array}\right. \end{aligned}$$
(8)

where \(t=\lceil (z_{0}+w_{0})\times 10^{14}\rceil ~\text {mod}~n+1\), \(e_{n}\) is a \(1\times n\) vector with ones as its elements, \(E_{0}\) is a zeros vector, and \(Q_{m+1,t}=0\). Then, we obtain image E. Similarly, for the diffusion in the column direction, the operation can also be applied by exchanging \(x_{0}+y_{0}\), t and \(z_{0}+w_{0}\) in Eq. (8). However, to save the time consumption, only diffusion in the row, column or both directions be chosen randomly. Finally, the cipher-image C is achieved. Moreover, to satisfy a certain security level, more than one round of encryption is found necessary [42, 51] for better performance.

2.3 Flowchart for encryption process

In this section, to clearly express the whole encryption process with a PRD structure, a flowchart is displayed in Fig. 3 with an algorithm to show the implement of our encryption method. The complexity for the whole algorithm is O(n) for a message with length n, which belongs to complexity P.

Fig. 3
figure 3

Flowchart

Full size image
Fig. 4
figure 4

Tests: Plain-images: a Lena, b boat, c man; Cipher-images: d Lena, e boat, f man; decryption results: g Lena, h boat, i man

Full size image
Fig. 5
figure 5

Sensitivity tests: a plain-image, b cipher-image, c decryption with \(x_{0}+10^{-14}\), d decryption with \(y_{0}+10^{-14}\), e decryption with \(z_{0}+10^{-14}\), f decryption with \(w_{0}+10^{-14}\)

Full size image

Algorithm

Input: image P, keys \(x_{0}\), \(y_{0}\), \(z_{0}\), \(w_{0}\),

         control parameters a, b, d.

Output: image C.

  Set \(E=zeros(m,~n)\), \(C=E\).

  Generate s by Eq. (2).

  Do permutation operation according to h and l.

  Do rewriting operation by Eq. (5) using \(\lambda \).

  Produce M using Eq. (7) after updating keys.

  Implement diffusion operation using Eq. (8) for row.

  Implement diffusion operation for column (optional).

  Obtain cipher-image C.

As for the decryption of a received cipher-image by using our PRD method, the encryption process can be done in the inverse direction due to the symmetric structure. The order for inverse is diffusion, rewriting, and permutation. Fortunately, an extra transmission is not needed in the proposed algorithm.

3 Experiments and security analysis

3.1 Experiments

To show the performance and demonstrate the efficiency of new method, simulated experiments are undertaken in this section. The keys and parameters used in the proposed algorithm are \(x_{0}=0.0056\), \(y_{0}=0.3678\), \(z_{0}=0.6229\), \(w_{0}=0.7676\), \(a=11\), \(b=113\), and \(d=217\). To avoid the transient effect [13], previous 200 iterated values of the chaotic sequence are discarded. The test data, chosen at random, consist of a size \(256\times 256\) image Lena, a size \(512\times 512\) image of Boat, and a size \(1024\times 1024\) image Man. Figure 4a–c shows the plain-images of them, while Fig. 4d–f shows the corresponding cipher-images, respectively. So, no useful information can be found in the cipher-images produced by the proposed method. Using correct initial conditions, parameter values, and the keys, original images can be recovered seeing Fig. 4g–i.

3.2 Key space analysis and its sensitivity

A large key space is needed in a good encryption algorithm to resist brute-force attack, and the scheme should have high sensitivity to any key used. Keys are composed of \(x_{0}\), \(y_{0}\), \(z_{0}\), and \(w_{0}\), that is, the key space can reach as large as \(10^{56}\) if the precision is set to \(10^{-14}\). Therefore, it is infeasible to make a brute-force attack. Moreover, to demonstrate high sensitivity, an image of Peppers, of size \(512\times 512\), was randomly chosen for testing. Figure 5a shows the plain-image, while Fig. 5b displays the corresponding cipher-image. But, original plain-image cannot be restored when a tiny change is made to the keys. Figure 5c–f shows incorrect decryption results by adding \(10^{-14}\) to the keys \(x_{0}\), \(y_{0}\), \(z_{0}\), and \(w_{0}\), respectively. From them, the proposed algorithm can perform high key sensitivity.

3.3 Histogram analysis

By using our algorithm, Fig. 6a–d shows the results of histogram test for plain-images by Boat and Peppers. It is found that the cipher-images have fairly uniform distribution for gray values, significantly different from that of their respective plain-images, of which means that applying histogram attacks will be very difficult.

Fig. 6
figure 6

Histogram tests: a plain-image of boat, b cipher-image of a, c plain-image of Peppers, d cipher-image of c

Full size image

3.4 Chi-square analysis

For a message, Chi-square [53] analysis can also determine whether the distribution is uniform or not. The definition for Chi-square is seen as

$$\begin{aligned} \chi _{test}^{2}=\sum _{i=1}^{k}\frac{(o_{i}-e_{i})^2}{e_{i}}, \end{aligned}$$
(9)

where \(k=256\) for a grayscale image, \(o_{i}\) and \(e_{i}\) represent the observed occurrence frequency and the expected occurrence frequency for each gray value, respectively. Table 1 gives the results for different images. All values produced by our method are smaller than the theoretical value 294, which implies that the gray distribution is in uniformity [53]. Therefore, our method passes the Chi-square test.

3.5 Know-plaintext and chosen-plaintext attacks

The encryption structure of PRD algorithm includes permutation, rewriting, and diffusion. The statistical property s, extracted from plain-image, is used to update the keys \(x_{0}\) and \(y_{0}\), that is, the keystream generated will be different with respect to different plain-images. In order to frustrate the separation attack and avoid the shortcoming existing in the Fridrich structure, a simple rewriting operation is designed by connecting all the keys. Furthermore, in the diffusion stage, the function (8) is proposed to make the keystream \(tp\times e_{n}+M_{i}\) dependent on the permuted image. As a result, both permutation and diffusion can enhance the security of our algorithm and resist known-plaintext and chosen-plaintext attacks.

3.6 Comparisons

  1. (1)

    Information entropy

Table 1 Chi-square tests
Full size table

We usually employ information entropy to test the randomness for messages, which is given by

$$\begin{aligned} I(\varphi )=\sum _{i=1}^{2^{Lgh}-1}\phi (\varphi _{i})\text {log}_{2}\frac{1}{\phi (\varphi _{i})} \end{aligned}$$
(10)

where Lgh is the length of the pixel value in form of bits, and \(\varphi \) denotes the test message with the probability of each \(\varphi _{i}\) written as \(\phi (\varphi _{i})\). After using our encryption algorithm, the results are listed in Table 2 for different images. Obviously, all values in encrypted images are approaching the theoretical value of 8. Moreover, some comparisons for different cipher-images are also given in Table 3. Therefore, the proposed encryption method demonstrates better performance.

Table 2 Information entropy for different images
Full size table
Table 3 Comparison of information entropy
Full size table
Table 4 UACI and NPCR tests
Full size table
Table 5 Comparison of UACI and NPCR by two bits change
Full size table
  1. (2)

    Plaintext sensitivity

To test whether a slight change in the same plain-image can produce a completely different cipher-image, the UACI (unified averaged changed intensity) and NPCR (number of pixel changing rate) are used to measure the sensitivity of plain-images. They are defined by

$$\begin{aligned} \text {UACI}=\frac{1}{m\times n}\left[ \sum _{i,j}\frac{|C_{1}(i,j)-C_{2}(i,j)|}{255}\right] \times 100, \end{aligned}$$
(11)
$$\begin{aligned} \text {NPCR}=\frac{\sum _{ij}D(i,j)}{m\times n}\times 100\%, \end{aligned}$$
(12)

where \(C_{1}\) and \(C_{2}\) denote the two cipher-images which have a one-bit change corresponding to same plain-image. \(D(i,j)=0\) if \(C_{1}(i,j)=C_{2}(i,j)\), else, \(D(i,j)=1\). The ideal value for UACI is about 33.4635%, while the ideal value for NPCR is about 99.6094% [51, 52]. Table 4 lists the results for the test images using our method. [The position is randomly chosen as (23, 15).] To demonstrate further the high sensitivity to the plaintext by using our method, two positions are changed at the same time but with the same pixel summation for the plain-image. [The positions are randomly chosen as (11, 131) and (236, 207).] Moreover, by using the proposed algorithm, other comparisons are shown in Tables 5 and 6 to prove the increased performance.

  1. (3)

    Speed analysis

For real-time communication, time cost is an important factor to influence the use of an algorithm. To test the speed of our method, Table 7 shows the comparison with some references. Obviously, the proposed algorithm is an efficient way to communicate over the network.

3.7 Randomness test by TestU01

As for randomness test by TestU01, one usually applies SmallCrush, Crush, and BigCrush test batteries. Then, the test can be passed if the P-value is within the range [0.001, 0.9990]. In our process, we do the TestU01 for the randomness [58] with results (the number passed) listed in Table 8.

3.8 Chosen-plaintext attack

Commonly, attacks of ciphertext only, known plaintext, chosen plaintext and chosen ciphertext are taken to cryptanalyze a cryptosystem. Among these, if a cryptosystem can resist chosen ciphertext attack, then it can resist others [60]. In our method, the new algorithm is sensitive to both plain-image and keys. Any tiny change in them will lead to a different cipher-image. At the permutation stage, the keystream is dependent on the plain-image. Then, in diffusion stage, current row in cipher-image is related to current row in permuted image, former row in cipher-image, and remaining rows in permuted image. As a result, the proposed algorithm can resist the chosen-plaintext and ciphertext attacks [60].

3.9 Discussion

As to the application of nonlinear dynamics in image encryption, some reviews were presented in [61]. According to the checklist steps [61], Table 9 gives a requirement analysis step-by-step. Therefore, one can check these checklist steps before completing an encryption algorithm based on chaos.

Table 6 Other comparisons with [55, 56]
Full size table
Table 7 Speed analysis and comparison (unit: second)
Full size table
Table 8 Statistical test comparison
Full size table
Table 9 Checklist requirement analysis
Full size table

4 Conclusions

A new pixel-level image encryption algorithm using chaotic map has been proposed in this paper. The results of our analysis have shown that the cipher-image produced in our method does not leak any information contained in the plain-image. Information entropy, histogram, and Chi-square are analyzed to show uniform gray distribution. Then, both key sensitivity and plaintext sensitivity are analyzed to show the good performance of high sensitivity by using the proposed algorithm. The PRD structure has been designed as a remedy for the weakness to separation attacks found in traditional methods. Fortunately, in both stages of permutation and diffusion, keystreams are generated related to the image, allowing strong resistance against known-plaintext and chosen-plaintext attacks.