Introduction

Incompressible viscous flow over a porous channel was presented by Berman [1]. The perturbation method has been applied using the normal wall velocity to be equal. Berman [1] worked was an effort by Sellars [2]. Sellars [2] was done work for high suction Reynolds for laminar flow at porous wall. Sellars [2] work was extended by Wah [3] was presented incompressible viscous flow over uniform porous channel. Terrill [4] was done work on the Wah [3] idea. Terrill [4] discussed the incompressible viscous flow over uniform porous channel for large injection. Sastry and Rao [5] have deliberated the micropolar fluid at porous wall channel, numerical scheme based upon differentiation, parametric extrapolation and quasi linearization. Srinivasacharya et al. [6] deliberated the time-dependent flow of micro-polar fluid in the parallel plates. They applied the perturbation method using the suction Reynolds number to fine the results of flow behaviors. Xu et al. [7] analyzed the time-dependent micropolar fluid flow at the flat surface under stagnation point. He fined the results through series methods. Elbashbeshy et al. [8] premeditated the Maxwell time-dependent micropolar fluid at linear stretching surface with MHD. Devakar and Raje [9] have been discussed numerical results of immiscible micropolar fluid unsteady flow in horizontal channel. Waqas et al. [10] studied the micropolar fluid flow in porous medium. Bhattacharjee et al. [11] worked for the micropolar fluid flow in single porous layer. Recently, a few authors have been worked done on the unsteady micropolar fluid flow with various effects which see Refs. [12,13,14,15].

During the previous not many decades, important progress was made in the study of non-viscous liquids owing to their uses in automotive and industrial sectors. These liquids' rheological properties are extremely useful in depicting the remarkable highlights associated with a few liquids in nature these as ketchup, shampoo, water, paints, etc. Classical Navier–Stokes equations cannot exhibit the characteristics that are significant in many fluids, such as colloidal suspension, crystals like liquid, blood of animal, polymeric liquids and small amounts of polymeric fluids, such as body torque, micro-rotation, spin inertia and couple stress. Eringen [16] was pioneered of the micropolar fluid theory. Eringen [17] was analyzed and discussed the jumped conditions, constitutive equations of the microfluent media and basic field equations. Shukla and Isa [18] studied about the generalization Reynolds equations of the micropolar lubricants for one-dimensional slider baring. They highlighted the solid-particle additives in their solution. Lockwood et al. [19] have been discussed the elastohydrodynamic contact and lyotropic fluid crystals in viscometric flow. Khonsari and Brewe [20] studied the micropolar fluid using the finite journal bearings lubricated on the surface. Micropolar fluid flow under the stagnation point region at a stretching surface was initiated by Nazar et al. [21]. Ishak et al. [22] explored the micropolar fluid flow at a vertical permeable surface under the stagnation point. Hayat et al. [23] discussed the axisymmetric micropolar fluid with unsteady stretching sheet analytically. Nadeem et al. [24] pioneered the micropolar fluid flow in rotating horizontal parallel plates to find the solution numerically and analytically. Sheikholeslami et al. [25] highlighted the effects of entropy generations and heat transfer through heat exchangers. Subhani and Nadeem [26] studied the mixture of nanoparticles with based micropolar fluid numerically. Micropolar fluid flow has been observed over a stretching surface, and the effect has been illustrated using different methods see Refs. [27,28,29,30].

Boundary layer flow with uniform free stream at a fixed flat plate has been discussed by Blasius [31]. The numerical method applied on the Blasius [31] work has been discussed via Howarth [32]. Rather than the Blasius [31] work, Sakiadis [33] presented the boundary layer flow induced in a quiescent ambient fluid by a moving plate. Tsou et al. [34] discussed analytically and tentatively progression of boundary layer on the consistent moving surface. The results of Sakiadis [33] are corroborated by Tsou et al. [34]. Crane extended Tsou et al. [34] work on the stretching plate. Crane [35] applied this definition to a stretching plate with stretching velocity in a quiescent fluid that differs with a fixed point distance and proposed an objective analytical solution. In addition, Miklavčič and Wang [36] demonstrated the flow of fluid at shrinking surface where the velocity is heading toward a fixed point. Fang [37] has studied the power law velocity at a shrinking surface using the exact solutions for involving physical parameters. Akbar et al. [38] studied, and discussed numerically, the tangent hyperbolic fluid at a stretching surface. Hussain et al. [39] addressed the movement of micropolar fluid at a stretch sheet at the boundary layer. Halim et al. [40] have been discussed the slipped stretched surface with nanomaterial flow of Maxwell fluid. Alblawi et al. [41] have been worked on the curved surface over an exponential stretching numerically. Khan et al. [42] elaborated the influence of unsteady nanomaterial fluid flow over curved surface. Ahmed and Khan [43] investigated the influence of magneto-nanomaterial fluid flow at a porous curved surface. Sheikholeslami et al. [44] elaborated the mathematical model on the nanomaterial fluid flow while applied the MHD on the inclined surface. Ahmed and Khan [45] worked on the numerical results of MHD Sisko nanomaterial fluid flow at moving curved surface. Most of authors have been studied the flow over stretching surface with various assumptions see Refs. [46,47,48,49,50,51,52,53,54,55,56,57].

In the current examination, time-dependent flow of magnetized micropolar fluid at a curved surface is considered. Thermal and velocity slips at surface are taken into account. The developed mathematical model under the flow assumptions is constructed as partial differential equations. By means of similarity transformations, above system is transformed as dimensionless. The dimensionless system solved through the numerical scheme (\(bvp4c\)). The effects of contributing parameters are highlighted through graphs and table. Our results are compared with decay literature.

Formulations

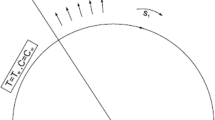
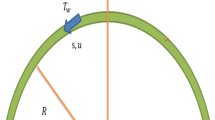
Developed mathematical model using the Navier Stoke equations under the flow assumptions on the curved surface discussed see in Fig. 1. Time-dependent flow of magnetized micropolar fluid at a curved stretching surface has been considered in current study. Where (\(r, s\)) are radial components which \(s\) is the arc length and \(r\) is normal to tangent. The developed model was transformed into the differential equations by means of the boundary layer approximations. The reduced differential equations as following:

$$R\frac{{\partial H_{2} }}{\partial s} + \frac{\partial }{\partial r}\left( {\left( {r + R} \right)H_{1} } \right) = 0,$$
(1)
$$\frac{1}{\rho }\frac{\partial p}{{\partial s}} - \frac{{u^{2} }}{r + R} = 0,$$
(2)
$$\frac{\partial u}{{\partial t}} + \frac{R}{r + R}u\frac{\partial u}{{\partial s}} + v\frac{\partial u}{{\partial r}} + \frac{{k^{*} }}{\rho }\frac{\partial N}{{\partial r}} - \frac{{\mu_{e} }}{4\pi \rho }\left[ {\begin{array}{*{20}c} {\frac{{H_{1} H_{2} }}{r + R} + H_{2} \frac{{\partial H_{1} }}{\partial r}} \\ {\frac{{RH_{1} }}{r + R}\frac{{\partial H_{1} }}{\partial s}} \\ \end{array} } \right] = \left( {\nu + \frac{{k^{*} }}{\rho }} \right)\left[ {\begin{array}{*{20}c} { + \frac{{\partial^{2} u}}{{\partial r^{2} }}} \\ { + \frac{1}{r + R}\left( {\frac{\partial u}{{\partial r}} - \frac{u}{r + R}} \right)} \\ \end{array} } \right] - \frac{1}{\rho }\left( {\frac{R}{r + R}} \right)\frac{\partial p}{{\partial r}},$$
(3)
$$\frac{{\partial H_{1} }}{\partial t} + \frac{R}{r + R}u\frac{{\partial H_{1} }}{\partial s} + v\frac{{\partial H_{1} }}{\partial r} + \frac{{H_{1} H_{2} }}{r + R} - \left[ {\begin{array}{*{20}c} {\frac{vu}{{r + R}} + H_{2} \frac{\partial v}{{\partial r}}} \\ {\frac{{RH_{1} }}{r + R}\frac{\partial u}{{\partial s}}} \\ \end{array} } \right] = \mu_{e} \left[ {\begin{array}{*{20}c} { + \frac{{\partial^{2} H_{1} }}{{\partial r^{2} }} - \frac{{H_{1} }}{{\left( {r + R} \right)^{2} }}} \\ { + \frac{1}{r + R}\frac{{\partial H_{1} }}{\partial r}} \\ \end{array} } \right],$$
(4)
$$\frac{\partial N}{{\partial t}} + \frac{Ru}{{r + R}}\frac{\partial N}{{\partial s}} + v\frac{\partial N}{{\partial r}} = - \frac{{\gamma^{*} }}{j\rho }\left( {\frac{1}{r + R}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial r^{2} }}} \right) - \frac{{k^{*} }}{j\rho }\left( {\begin{array}{*{20}c} {\frac{1}{r + R}\frac{\partial u}{{\partial r}}} \\ { + 2N} \\ { + \frac{u}{r + R}} \\ \end{array} } \right),$$
(5)
$$\frac{\partial T}{{\partial t}} + \frac{Ru}{{r + R}}\frac{\partial T}{{\partial s}} + v\frac{\partial T}{{\partial r}} = \alpha \left( {\frac{1}{r + R}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial r^{2} }}} \right),$$
(6)
Fig. 1
figure 1

Flow analysis of magnetized micropolar fluid

Full size image

Concerned boundary conditions are

$$v = 0, u = u_{{\text{w}}} + L\left[ {\frac{\partial u}{{\partial r}} + k^{*} N + \frac{u}{r + R}} \right], - k\frac{\partial T}{{\partial r}} = h_{{\text{w}}} \left( {T_{{\text{w}}} - T} \right), \frac{{\partial H_{1} }}{\partial r} = H_{2} = 0,\quad N = - n\frac{\partial u}{{\partial r}}\;{\text{at}}\;r \to 0\;,u = 0, H_{2} = \frac{{asH_{0} .}}{1 - \alpha t}, T \to T_{\infty } , N \to 0, \;{\text{at}}\; r \to \infty .$$
(7)

where, velocity vectors are \(u\) and \(v\), in the direction of \(s\)- and \(r\)- correspondingly. The \(R\), \(\rho\), \(\nu\), \(\alpha\), \(\tau\), \(c_{{\text{p}}}\), \(h_{{\text{w}}}\), and p are defined as bellow. Further, \(\gamma\) is assumed in the form, \(\gamma = \left( {\mu + \frac{{k^{*} }}{2}} \right)j = \mu \left( {1 + \frac{{K_{1} }}{2}} \right)j, j = \frac{\nu }{a}\). Here, \(K_{1} = \frac{{k^{*} }}{\mu }\) is the micropolar parameter. The above Eqs. 1–7 are transferred into ordinary differential equations; we used following non-dimensional variable [32].

$$u = \frac{a}{{\left( {1 - \alpha t} \right)}}f^{\prime}\left( \eta \right), v = - \frac{R}{r + R}\sqrt {\frac{\nu a}{{\left( {1 - \alpha t} \right)}}} f\left( \eta \right), \eta = \sqrt {\frac{a}{{\nu \left( {1 - \alpha t} \right)}}} r, T = T_{{\text{w}}} + \frac{{T_{0} \theta \left( \eta \right)}}{{\left( {1 - \alpha_{0} t} \right)^{2} }}$$
(8)

Using Eq. (8), Eqs. 2–7 are reduced as

$$P^{\prime} = \frac{1}{\eta + K}f^{{\prime}{2}} ,$$
(9)
$$\left( {1 + K_{1} } \right)\left( {\begin{array}{*{20}c} {f^{\prime\prime\prime} + \frac{1}{\eta + K}f^{\prime\prime}} \\ { - \frac{1}{{\left( {\eta + K} \right)^{2} }}f^{\prime}} \\ \end{array} } \right) - A\left( {\frac{\eta }{2}f^{\prime\prime} + f^{\prime}} \right) + \frac{K}{\eta + K}\left( {f^{{\prime}{2}} - ff^{\prime\prime}} \right) + \frac{K}{{\left( {\eta + K} \right)^{2} }}ff^{^{\prime}} - \frac{\beta K}{{\eta + K}}\left[ {\begin{array}{*{20}c} {gg^{\prime\prime} - g^{{\prime}{2}} } \\ { + \frac{{gg^{\prime}}}{\eta + K}} \\ \end{array} } \right] - K_{1} h^{\prime} = \frac{2KP}{{\eta + K}},$$
(10)
$$\lambda \left( {\begin{array}{*{20}c} {g^{\prime\prime\prime} + \frac{1}{\eta + K}g^{\prime\prime}} \\ { - \frac{1}{{\left( {\eta + K} \right)^{2} }}g^{\prime}} \\ \end{array} } \right) + \frac{K}{\eta + K}\left( {fg^{\prime\prime} - gf^{\prime\prime}} \right) + \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {\frac{1}{\gamma }ff^{\prime} - \gamma gg^{\prime}} \right) - A\left( {\frac{\eta }{2}g^{\prime\prime} + g^{\prime}} \right) = 0,$$
(11)
$$\left( {1 + \frac{{K_{1} }}{2}} \right)\left( {h^{\prime\prime} + \frac{1}{\eta + K}h^{\prime}} \right) + \frac{K}{\eta + K}\left( {fh^{\prime} - hf^{\prime}} \right) - K_{1} \left( {2h + \frac{1}{\eta + K}f^{\prime} + f^{\prime\prime}} \right) - A\left( {\frac{\eta }{2}h^{\prime} + \frac{3}{2}h} \right) = 0,$$
(12)
$$\frac{1}{Pr}\left( {\theta^{\prime\prime} + \frac{1}{\eta + K}\theta ^{\prime}} \right) + \frac{K}{\eta + K}\left( {f\theta^{\prime} - f^{\prime}\theta } \right) + A\left( {\frac{\eta }{2}\theta ^{\prime} + 2\theta } \right) = 0,$$
(13)

Eliminating the pressure term by comparing Eqs. (9) and (10) we have,

$$\left( {1 + K_{1} } \right)\left( {f^{iv} + \frac{{2f^{\prime\prime\prime}}}{\eta + K} - \frac{{f^{\prime\prime}}}{{\left( {\eta + K} \right)^{2} }} + \frac{{f^{\prime}}}{{\left( {\eta + K} \right)^{3} }}} \right) + \frac{K}{\eta + K}\left( {ff^{\prime\prime\prime} - f^{\prime}f^{\prime\prime}} \right) + \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {ff^{\prime\prime} - f^{{\prime}{2}} } \right) - \frac{K}{{\left( {\eta + K} \right)^{3} }}ff^{\prime}\frac{\beta K}{{\eta + K}}\left[ {\begin{array}{*{20}c} {g^{\prime}g^{\prime\prime} - gg^{\prime\prime\prime} + \frac{{gg^{\prime}}}{{\left( {\eta + K} \right)^{2} }}} \\ { - \frac{1}{\eta + K}\left( {g^{{\prime}{2}} - gg^{\prime}} \right)} \\ \end{array} } \right] - \frac{A}{\eta + K}\left( {f^{\prime} + \frac{\eta }{2}f^{\prime\prime}} \right) - \frac{A}{2}\left( {3f^{\prime\prime} + \eta f^{\prime\prime\prime}} \right) - K_{1} \left( {h^{\prime\prime} + \frac{1}{\eta + K}h^{\prime}} \right) = 0,$$
(14)

The relevant boundary conditions becomes,

$$\begin{aligned} f\left( \eta \right) & = 0, f^{^{\prime}} \left( \eta \right) = 1 + \delta \left[ {\left( {1 - n} \right)f^{\prime\prime}\left( \eta \right) + \frac{{f^{\prime}\left( \eta \right)}}{\eta + K}} \right],\quad g\left( \eta \right) = 0, \\ g^{\prime}\left( \eta \right) & = 1, h\left( \eta \right) = - nf^{\prime\prime}\left( \eta \right), \theta^{\prime}\left( \eta \right) + Bi\left( {1 - \theta \left( \eta \right)} \right) = 0,\quad {\text{at}}\; \eta \to 0, \\ f^{\prime}\left( \eta \right) & = f^{\prime\prime}\left( \eta \right) = \theta \left( \eta \right) = g\left( \eta \right) = h\left( \eta \right) = 0 \quad {\text{at}}\;\eta \to \infty , \\ \end{aligned}$$
(15)

Here, \(K\), \(K_{1}\), \(\beta\) \(A,\) \(\delta ,\) \(n,\) \(\lambda\), \(\gamma\), are signifying the curvature, micropolar, magnetic, unsteadiness, slip, micro gyration, reciprocal magnetic Prandtl number and dimensionless parameter, respectively. Further, \({\text{Bi}}\) and \({\text{Pr }}\) are denoting the Biot number and Prandtl number, respectively. The above-mentioned parameters are given as, \(K = R\sqrt {\frac{a}{{2\nu l\left( {1 - \alpha_{0} t} \right)}}}\),\({\text{Bi}} = \frac{{h_{{\text{w}}} }}{k}\sqrt {\frac{a}{{2l\nu \left( {1 - \alpha_{0} t} \right)}}}\) and \({\text{Pr}} = \frac{\nu }{ \alpha }\). The local skin friction and local Nusselt are quite important form engineering prospect. The physical quantities examined the behavior of flow and transfer rate of heat; these are defined as,

$${\text{Nu}}_{{\text{s}}} = \frac{{\tau_{{{\text{rs}}}} }}{{\rho u_{{\text{w}}}^{2} }} , \quad {\text{Nu}}_{{\text{s}}} = \frac{{sq_{{\text{m}}} }}{{k\left( {T_{{\text{w}}} - T_{\infty } } \right)}} ,$$
(16)

In above expressions, \(\tau_{{{\text{rs}}}}\) and \(q_{{\text{m}}}\) depict the heat flux and shear stress, respectively, and they are represented as,

$$\left. {\tau_{{{\text{rs}}}} = \left( {1 + K_{1} } \right)\left( {\frac{1}{r + R}\frac{\partial u}{{\partial r}} + k^{*} N + \frac{u}{r + R}} \right)} \right|_{r = 0} ,\quad \left. {q_{{\text{m}}} = - k\left( {\frac{\partial T}{{\partial r}}} \right)} \right|_{{{\text{r}} = 0}} ,$$
(17)

In the dimensionless form,

$$\left( {{\text{Re}}_{{\text{s}}} } \right)^{\frac{1}{2}} C_{{\text{f}}} = \left( {K_{1} \left( {1 - n} \right)f^{\prime\prime}\left( 0 \right) + \frac{f^{\prime}\left( 0 \right)}{{\eta + K}}} \right)\theta^{\prime}\left( 0 \right), \quad {\text{Nu}}_{{\text{s}}} \left( {{\text{Re}}_{{\text{x}}} } \right)^{{ - \frac{1}{2}}} = - \theta^{\prime}\left( 0 \right),$$
(18)

Here local Reynolds number is \({\text{Re}}_{{\text{s}}} = u_{{\text{w}}} \sqrt {\frac{{2l\left( {1 - \alpha_{0} t} \right)}}{\nu a}}\).

Nomenclature

\(K\) (1)

Curvature parameter

\(\tau_{{{\text{rs}}}}\)/pa

Wall shear stress

\({u}\;\left( {\text{m}} {\text{s}}^{-1} \right)\)

Velocity vector r-direction

\(v\;\left( {\text{m}} {\text{s}}^{-1} \right)\)

Velocity vector s-direction

\(\beta\)(1)

Magnetic field

\({\text{Re}}_{{\text{s}}}\) (1)

Reynolds number

\(A\) (1)

Unsteadiness parameter

\({\text{Bi}}\) (1)

Biot number

\(\delta\) (1)

Velocity slip

\({\text{Pr}}\) (1)

Prandtl number

\(n\) (1)

Micro-gyration

\(R\) (m)

Radius of curvature

\(\lambda\) (1)

Reciprocal magnetic Prandtl number

\(\rho \,\left( {{\text{kg m}}^{-3} } \right)\)

Fluid density

\(\gamma\) (1)

Dimensionless parameter

\(\nu \;\left( {{\text{m}}^{2} {\text{s}}^{-1}} \right)\)

Viscosity of kinematic

\(\alpha \;\left( {{\text{m}}^{2} {\text{s}}^{-1}} \right)\)

Thermal diffusivity

\(\tau\) (1)

Ratio between heat capacity and base fluid

\(c_{{\text{p}}}\) (\({\text{J kg}}^{-1}\;{\text{K}}^{-1}\))

Specific heat

\(\mu \;\left( {{\text{Ns m}}^{-2} } \right)\)

Dynamic viscosity

\(q_{{\text{m}}}\) (\({\text{W m}}^{-2}\))

Heat flux

\(T_{\infty } \;\left( K \right)\)

Ambient temperature

\(t\;\left( {\text{s}} \right)\)

Time

\(T_{{\text{w}}} \;\left( K \right)\)

Wall temperature

Numerical procedure

In a recent analysis, we considered the time-dependent induced magnetic field with base micropolar fluid flow over a curved surface. The bvp4c numerical technique was applied to solve the nonlinear differential equations. The equations in the differential forms (11–14) subject to the boundary conditions are transformed into the first order differential equations. We reduced the higher order differential system in the initial value problem. The procedure of the numerical technique is defined below:

$$f\left( \eta \right) = y\left( 1 \right),$$
(19)
$$f^{\prime}\left( \eta \right) = y\left( 2 \right),$$
(20)
$$f^{\prime\prime}\left( \eta \right) = y\left( 3 \right),$$
(21)
$$f^{\prime\prime\prime}\left( \eta \right) = y\left( 4 \right),$$
(22)
$$f^{\prime\prime\prime\prime}\left( \eta \right) = yy1,$$
(23)
$$yy1 = - \left( {1 + K_{1} } \right) \left( {\frac{K}{\eta + K}\left( {y\left( 1 \right)y\left( 4 \right) - y\left( 2 \right)y\left( 3 \right)} \right) + \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {y\left( 1 \right)y\left( 3 \right) - y\left( 2 \right)y\left( 2 \right)} \right) - \frac{K}{{\left( {\eta + K} \right)^{3} }}y\left( 2 \right)y\left( 1 \right) + \frac{\beta K}{{\eta + K}}\left[ {\begin{array}{*{20}c} {y\left( 6 \right)y\left( 7 \right) - y\left( 5 \right)yy2 + \frac{y\left( 5 \right)y\left( 6 \right)}{{\left( {\eta + K} \right)^{2} }}} \\ { - \frac{1}{\eta + K}\left( {y\left( 6 \right)y\left( 6 \right) - y\left( 5 \right)y\left( 6 \right)} \right)} \\ \end{array} } \right] - \frac{A}{\eta + K}\left( {y\left( 2 \right) + \frac{\eta }{2}y\left( 3 \right)} \right) - \frac{A}{2}\left( {3y\left( 3 \right) + \eta y\left( 4 \right)} \right) - K_{1} \left( {yy3 + \frac{1}{\eta + K}y\left( 9 \right)} \right)} \right) - \frac{2y\left( 4 \right)}{{\eta + K}} + \frac{y\left( 3 \right)}{{\left( {\eta + K} \right)^{2} }} - \frac{y\left( 2 \right)}{{\left( {\eta + K} \right)^{3} }},$$
(24)
$$g\left( \eta \right) = y\left( 5 \right),$$
(25)
$$g^{\prime}\left( \eta \right) = y\left( 6 \right),$$
(26)
$$g^{\prime\prime}\left( \eta \right) = y\left( 7 \right),$$
(27)
$$g^{\prime\prime\prime}\left( \eta \right) = yy2,$$
(28)
$$yy2 = \lambda^{ - 1} \left( {\frac{K}{\eta + K}\left( {y\left( 1 \right)y\left( 7 \right) - y\left( 5 \right)y\left( 3 \right)} \right) + \frac{K}{{\left( {\eta + K} \right)^{2} }}\left( {\frac{1}{\gamma }y\left( 2 \right)y\left( 1 \right) - \gamma y\left( 6 \right)y\left( 5 \right)} \right) - A\left( {\frac{\eta }{2}y\left( 7 \right) + y\left( 6 \right)} \right)} \right) - \frac{1}{\eta + K}y\left( 7 \right) + \frac{1}{{\left( {\eta + K} \right)^{2} }}y\left( 6 \right),$$
(29)
$$h\left( \eta \right) = y\left( 8 \right),$$
(30)
$$h^{\prime}\left( \eta \right) = y\left( 9 \right),$$
(31)
$$h^{\prime\prime}\left( \eta \right) = yy3,$$
(32)
$$yy3 = - \left( {1 + \frac{K}{2}} \right)^{ - 1} \left( { \frac{{K^{*} }}{{\eta + K^{*} }}y\left( 1 \right)y\left( 9 \right) - \frac{{K^{*} }}{{\eta + K^{*} }}y\left( 2 \right)y\left( 8 \right) - K\left( {2y\left( 8 \right) + y\left( 3 \right) + \frac{y\left( 2 \right)}{{\eta + K^{*} }}} \right) - A\left( {\frac{\eta }{2}y\left( 9 \right) + \frac{3}{2}y\left( 8 \right)} \right)} \right) - \frac{y\left( 9 \right)}{{\eta + K^{*} }},$$
(33)
$$\theta \left( \eta \right) = y\left( {10} \right),$$
(34)
$$\theta ^{\prime}\left( \eta \right) = y\left( {11} \right),$$
(35)
$$\theta ^{\prime\prime}\left( \eta \right) = yy4,$$
(36)
$$yy4 = - \Pr \left( {\frac{K}{\eta + K}\left( {y\left( 1 \right)y\left( {11} \right) - y\left( {10} \right)y\left( 2 \right)} \right) + A\left( {\frac{\eta }{2}y\left( {11} \right) + 2y\left( {10} \right)} \right)} \right) - \frac{1}{\eta + K}y\left( {11} \right),$$
(37)

With related boundary conditions are

$$y0\left( 1 \right); \quad y0\left( 2 \right) = 1 + \delta \left[ {\left( {1 - n} \right)y0\left( 3 \right) + \frac{y0\left( 2 \right)}{{\eta + K}}} \right],\quad y0\left( 5 \right); \quad y0\left( 6 \right) - 1;\quad y0\left( 8 \right) + ny0\left( 3 \right);\quad y0\left( {11} \right) + {\text{Bi}}\left( {1 - y\left( {10} \right)} \right);\quad y\inf \left( 2 \right);\quad y\inf \left( 3 \right);\quad y\inf \left( 6 \right);\quad y\inf \left( 8 \right);\quad y\inf \left( {10} \right);$$
(38)

Results and discussion

We developed the mathematical model to analyze the unsteady flow of micropolar fluid at a Riga curved surface under slip effects. Effects of involving parameters, namely \(A\)(\({\text{unsteady}}\;{\text{parameter}}\)), \(K\left( {{\text{curvature }}\;{\text{parameter}}} \right)\), \(\delta\), \(K_{1}\) (micropolar parameter), \(\beta\), \(\lambda\), \(\gamma\) (dimensionless parameter), \({\text{Bi}}\) (Biot number) and \({\text{Pr}}\) (Prandtl number) are highlighted through graphs. Figures 2–6 reveals the influence of unsteady parameter \(A\), \(\delta\), \(\beta\), \(K\), \(K_{1}\) on the \(f^{\prime}\left( \eta \right)\) for week concentration. Figure 2 reveals the impacts of \(A\) on the \(f^{\prime}\left( \eta \right)\). The boundary layer of the \(f^{\prime}\left( \eta \right)\) reduced when the values of \(A\) increases. Unsteady parameters \(A\) reduced the velocity of flow when the values increase unsteady parameters increases. Figure 3 indications the effects of \(\beta\) on the \(f^{\prime}\left( \eta \right)\). It is noted that \(f^{\prime}\left( \eta \right)\) slow done toward surface as well as \(\beta\) increases. Figure 4 indications the effects of \(\delta\) on the \(f^{\prime}\left( \eta \right)\). The \(f^{\prime}\left( \eta \right)\) shows the behavior higher as well as \(\delta\) increases, because velocity slip accelerates the flow which increases the fluid velocity in our case. Figure 5 illustrates the influence of \(K\) on the \(f^{\prime}\left( \eta \right)\). \(f^{\prime}\left( \eta \right)\) shows the behavior higher as well as \(K\) increases because the dynamic viscosity of the fluid reduced and dynamic viscosity of the micropolar increases which increases the velocity profile. The curvature parameter accelerates the flows which increase the fluid velocity in our case. Figure 6 shows the impact of \(K_{1}\) on the \(f^{\prime}\left( \eta \right)\). It is noted that \(f^{\prime}\left( \eta \right)\) slow done toward surface as well as \(K_{1}\) increases. Figures 7–9 indication the effects of \(K\), \(\gamma\) and \(\lambda\) on the magnetic profile. It is detected that \(g^{\prime}\left( \eta \right)\) slows down toward the surface for higher values of \(A\) which reveals in Fig. 7. The curve of the magnetic profile is toward the surface, when is increased. Figure 8 indications the effects of on the. The curved of the declined toward surface for increasing values of. Figure 9 indications the effects on the. The curved of the declined toward surface for increasing values of. Figures 10–12 depict the impacts of, and micropolar profile. Figure 10 shows the influence of on the micropolar profile. It is seen that the micropolar profile slows down when rises. Figure 11 highlights the impacts of on the micropolar profile. Micropolar profile found to be rises when the values of enhance. Micropolar parameter shows the influence on the micropolar profile which is seen in Fig. 12. Micropolar profile decelerates for higher values of. Because increase which reduces the micropolar profile thickness. Effect of,, and on the displays in Figs. 13–16. Figure 13 reveals the influence of on the. The curve reduced for higher of. Figure 14 highlights the on the temperature. increase which increase the temperature away on the surface. Figure 15 reveals the influence of on temperature profile. The curvature parameter increases which enhance the temperature near the surface. Figure 16 reveals the influence of on temperature profile. The increases which declines the temperature profile. Table 1 shows the effects of,,,, and of the and. The effects of on the and which reveals in Table 1. It is seen that the enhances which enhances the while reduces the. The inspiration of unsteady parameter on the and. Higher values of unsteady parameter which reduced the skin fraction and enhance the near the surface. The magnetic parameter increases with reduced the and no effects found on the. The micropolar parameter increases with condensed the heat transfer rate and no effects found on the heat transfer. Large of parameter declined the skin fraction and heat transfer at surface. The rises when the Biot number growths. Table 2 exhibits the best comparison with decay literature Rosca and Pop [51] and Saleh et al. [52] and the rest of the physical parameters is for various value of stretching parameter of. All the results are found to be best comparison with decay results. Table 3 reveals the comparison bvp4c with shooting method. The best agreement found in both numerical methods.

Fig. 2
figure 2

Impacts of \(A\) on the \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 3
figure 3

Impacts of \(\beta\) on the \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 4
figure 4

Impacts of \(\delta\) on the \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 5
figure 5

Impacts of \(K\) on the \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 6
figure 6

Impacts of on the \(f^{\prime}\left( \eta \right)\)

Full size image
Fig. 7
figure 7

Impacts of K on the g(η)

Full size image
Fig. 8
figure 8

Impacts of \(\gamma\) on the \(g\left( \eta \right)\)

Full size image
Fig. 9
figure 9

Impacts of \(\lambda\) on the \(g\left( \eta \right)\)

Full size image
Fig. 10
figure 10

Impacts of \(A\) on the \(h\left( \eta \right)\)

Full size image
Fig. 11
figure 11

Impacts of \(K\) on the \(h\left( \eta \right)\)

Full size image
Fig. 12
figure 12

Impacts of \(K_{1}\) on the \(h\left( \eta \right)\)

Full size image
Fig. 13
figure 13

Impacts of \(A\) on the \(\theta \left( \eta \right)\)

Full size image
Fig. 14
figure 14

Impacts of \(Bi\) on the \(\theta \left( \eta \right)\)

Full size image
Fig. 15
figure 15

Impacts of \(K\) on the \(\theta \left( \eta \right)\)

Full size image
Fig. 16
figure 16

Impacts of \(Pr\) on the \(\theta \left( \eta \right)\)

Full size image
Table 1 Numerical effects of involving parameters on the and
Full size table
Table 2 Comparison results of current analysis with Rosca and Pop [51] and Saleh et al. [52], the rest of the physical parameters is
Full size table
Table 3 Comparison bvp4c with shooting method
Full size table

Final remarks

The developed mathematical model under the unsteady magnetized of micropolar fluid flow over a curved surface is examined with slip effects in current analysis. Numerical technique was applied to solve dimensionless system to inspect the flow behavior on the curved surface. Some significant results are highlighted below:

  • Heat transfer reduced due to rising curvature, while surface friction increases.

  • Fraction between surface and fluid increases and declined for augmenting the magnetic field.

  • Heat transfer improved for rising the values of Biot number.

  • Fraction between surface and fluid reduced for enhancing of micropolar parameter.

  • Our results found to be best agreement with Rosca and Pop [51] and Saleh et al. [52].