Introduction

Because of simplicity, cost-effectiveness and low noise of free convection, this mode can affect thermal behaviour of a wide range of engineering equipment. The natural convection mechanism transpires under the impact of the magnetic field in multiple processes including metal casting, the liquid cooling blanket of the fusion reactors and crystal growth. However, the existence of Lorentz force imposes an adverse effect on the phenomenon and deteriorates the convective flow. In an investigation of free convection within a cavity under magnetic field influence, Rudraiah [1] observed that the stronger Hartmann destroys the convective heat transportation rate and this suppression is more characteristic in the regions of the low Grashof number. Kakarantzas et al. [2] investigated liquid metal MHD flow inside a container and reported that the implication of Hartmann flow deteriorates nanomaterial velocity. In a similar way, Selimefendigil and Oztop [3] and Sheikholeslami [4] demonstrated an inverse association between the Lorentz force and Nusselt number.

In the above-mentioned scenarios, the undesirable impact of Hartmann number on free convection can be compensated to some extent by replacing the conventional coolants with the metallic nanofluids [5,6,7,8,9]. The term nanofluid is expressed for the colloidal solution of the traditional fluids and the nano-sized metallic or non-metallic particles exhibiting superior thermal behaviour than that of the hosting fluid and the suspended particles [10]. The magnetohydrodynamic (MHD) natural convection of the nanofluids for multiple operating conditions and nanofluid combinations has been presented by several studies. Sheremet et al. [11] analysed the MHD water–Cu nanofluid in a wavy enclosure under the influence of an isothermal corner heater. Kefayati [12, 13] implemented the FDLBM to scrutinize nanomaterial-free convection through a square cavity. Using the numerical approach, Sheikholeslami et al. [14,15,16,17,18] studied MHD and EHD convective transportation of water-based nanomaterials in a square enclosure, concentric annulus, semi-annulus and cubic cavity.

Fewer reports presented the MHD convective transportation within porous media. The permeable media possesses the advantages of the low density and large area for the optimal heat transfer. Selimefendigil and Oztop [19] scrutinized vented enclosure influenced by Lorentz forces to analyze mixed convection. Rashad et al. [20] explored the mutual impact of the internal heat generation and Lorentz forces on free convective flow of the copper–water within a rectangular tank. Finding new carrier fluid with greater thermal properties has been scrutinized by several researchers [21,22,23,24,25,26,27,28,29,30,31,32,33].

The objective of this investigation is to scrutinize study the impact of the nanoparticle shape variation on the MHD-free convection and the radiation of the Al2O3–water nanomaterial within a porous medium by implementing the CVFEM approach. The considered radiation parameter, shape factor, Hartmann number and particle volume fraction ranges are \(0 \le {\text{Rd}} \le 0.8\), \(3 \le m \le 5.7\), \(0 \le {\text{Ha}} \le 20\) and \(0\% \le \varphi \le 5\%\) respectively.

Formulation of problem and simulation

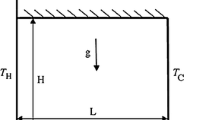
In the present problem, the impact of Hartmann flow on the behaviour of nanomaterial in a permeable geometry has been emphasized. CVFEM has been employed concerning triangular element. The imposed boundary conditions have been also depicted in Fig. 1. In order to model the porous terms, the Darcy law has been implemented. Shape factor influences on nanomaterial properties have been modelled. The problem under consideration has below equations:

Fig. 1
figure 1

a Current porous domain, b CVFEM element

Full size image
$$\frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} = 0$$
(1)
$$\frac{{\mu_{\text{nf}} }}{K}u = - \frac{\partial P}{\partial x} + \sigma_{\text{nf}} B_{0}^{2} \left[ {\left( {\sin \gamma } \right)v\left( {\cos \gamma } \right) - u\left( {\sin \gamma } \right)^{2} } \right]$$
(2)
$$\begin{aligned} \frac{{\mu_{\text{nf}} }}{K}v & = - \frac{\partial P}{\partial y} + \left( {T - T_{\text{c}} } \right)g\rho_{\text{nf}} \beta_{\text{nf}} \\ & \quad + \,\sigma_{\text{nf}} B_{0}^{2} \left( {\cos \gamma } \right)\left[ {\left( {\sin \gamma } \right)u - \left( {\cos \gamma } \right)v} \right] \\ \end{aligned}$$
(3)
$$\begin{aligned} \frac{1}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}\frac{{\partial q_{\text{r}} }}{\partial y} + \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) & = k_{\text{nf}} \left( {\rho C_{\text{p}} } \right)_{\text{nf}}^{ - 1} \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right), \\ & \quad \left[ {T^{4} \cong 4T_{\text{c}}^{3} T - 3T_{\text{c}}^{4} ,q_{\text{r}} = - \frac{{4\sigma_{\text{e}} }}{{3\beta_{\text{R}} }}\frac{{\partial T^{4} }}{\partial y}} \right] \\ \end{aligned}$$
(4)

The thermophysical properties of nanomaterial were estimated by the below equations

$${{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} } \mathord{\left/ {\vphantom {{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} } {\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}} \right. \kern-0pt} {\left( {\rho C_{\text{p}} } \right)_{\text{f}} }} = PP,\,\,\,PP = (1 - \phi ) + {{\phi \left( {\rho C_{\text{p}} } \right)_{\text{s}} } \mathord{\left/ {\vphantom {{\phi \left( {\rho C_{\text{p}} } \right)_{\text{s}} } {\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}} \right. \kern-0pt} {\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}$$
(5)
$$\left( {\rho \beta } \right)_{\text{nf}} = \left( {\rho \beta } \right)_{\text{f}} (1 - \phi ) + \phi \left( {\rho \beta } \right)_{\text{s}}$$
(6)
$$\rho_{\text{nf}} - \phi \rho_{\text{s}} = (1 - \phi )\rho_{\text{f}}$$
(7)
$$\begin{aligned} 1 + A & = \sigma_{\text{s}} /\sigma_{\text{f}} ,\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} = B, \\ B - 1 & = 3\phi \frac{A}{A + 3 - \phi A} \\ \end{aligned}$$
(8)

The effective viscosity \(\mu_{\text{nf}}\) as involving Brownian motion:

$$\begin{aligned} & \mu_{\text{eff}} = \left( {\left[ {1 - \phi } \right]^{ - 2.5} + \frac{{k_{\text{Brownian}} }}{{\Pr_{\text{f}} k_{\text{f}} }}} \right)\mu_{\text{f}} \\ & g^{\prime}(d_{\text{p}} ,\phi ,T) = gg \\ & k_{\text{Brownian}} = 5 \times 10^{4} c_{\text{p,f}} gg\rho_{\text{f}} \phi \sqrt {\frac{{\kappa_{\text{b}} T}}{{\rho_{\text{p}} d_{\text{p}} }}} \\ & gg = {\text{Ln}}\left( T \right)\left( {a_{1} + a_{3} {\text{Ln}}\left( \phi \right) + a_{4} {\text{Ln}}\left( {d_{\text{p}} } \right){\text{Ln}}\left( \phi \right) + a_{2} {\text{Ln}}\left( {d_{\text{p}} } \right) + a_{5} {\text{Ln}}\left( {d_{\text{p}} } \right)^{2} } \right) \\ & \quad \quad + \left( {a_{6} + {\text{Ln}}\left( {d_{\text{p}} } \right)a_{10} {\text{Ln}}\left( {d_{\text{p}} } \right) + a_{8} {\text{Ln}}\left( \phi \right) + a_{9} {\text{Ln}}\left( {d_{\text{p}} } \right){\text{Ln}}\left( \phi \right) + a_{7} {\text{Ln}}\left( {d_{\text{p}} } \right)} \right) \\ \end{aligned}$$
(9)

The impact of the nanoparticle shape factor has been involved in the estimation of the effective thermal conductivity \(k_{\text{nf}}\) as:

$$\begin{aligned} k_{\text{p}} - k_{\text{f}} & = {\text{kr}} \\ \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} & = \frac{{{\text{kr}}\,m\phi + k_{f} + {\text{kr}}\,\phi + mk_{\text{f}} + k_{\text{p}} }}{{k_{\text{p}} + m\,k_{\text{f}} + kr\,\phi + k_{\text{f}} }} \\ \end{aligned}$$
(10)

The various shape factors, related coefficient and properties are enlisted in Tables 1–3 [34].

Table 1 The coefficient values of Al2O3–water nanofluid
Full size table
Table 2 Thermophysical properties of water and nanoparticles
Full size table
Table 3 Different values of m
Full size table

Equation (11) has been considered to attain the dimensionless form.

$$\,\left( {y,x} \right) = \left( {Y,X} \right)L,\varPsi = \psi /\alpha_{\text{nf}} ,\,\theta = \frac{{T - T_{\text{c}} }}{\Delta T},\Delta Tk_{\text{f}} L^{ - 1} = q^{''}$$
(11)

The final expression can be written as:

$$\begin{aligned} \frac{{\partial^{2} \varPsi }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPsi }}{{\partial Y^{2} }} & = - \,{\text{Ha}}\frac{{A_{6} }}{{A_{5} }}\left[ {\left( {\cos \gamma } \right)\frac{{\partial^{2} \varPsi }}{{\partial X^{2} }}\left( {\cos \gamma } \right) + 2\frac{{\partial^{2} \varPsi }}{\partial X\,\partial Y}\left( {\sin \gamma } \right)\left( {\cos \gamma } \right)\, + \frac{{\partial^{2} \varPsi }}{{\partial Y^{2} }}\left( {\sin^{2} \gamma } \right)} \right] \\ & \quad - \frac{{A_{3} \,A_{2} }}{{A_{4} \,A_{5} }}\frac{\partial \theta }{\partial X}{\text{Ra}} \\ \end{aligned}$$
(12)
$$\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }}} \right) + \left( {1 + \frac{4}{3}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)^{ - 1} {\text{Rd}}} \right)\frac{{\partial^{2} \theta }}{{\partial Y^{2} }} = - \frac{\partial \varPsi }{\partial X}\frac{\partial \theta }{\partial Y} + \frac{\partial \theta }{\partial X}\frac{\partial \varPsi }{\partial Y}$$
(13)

In two recent equations, the definition of new parameters is:

$$\begin{aligned} & {\text{Ha}} = \frac{{\sigma_{\text {f}} K\,B_{0}^{2} }}{{\mu_{\text{f}} }},\,{\text{Ra}} = \frac{{g\,K\,\left( {\rho \beta } \right)_{\text{f}} L\,\Delta T}}{{\mu_{\text {f}} \,\alpha_{\text{f}} }},\,\,{\text{Rd}} = {{4\sigma_{\text{e}} T_{\text{c}}^{3} } \mathord{\left/ {\vphantom {{4\sigma_{\text{e}} T_{\text{c}}^{3} } {\left( {\beta_{\text{R}} k_{\text{f}} } \right)}}} \right. \kern-0pt} {\left( {\beta_{\text{R}} k_{\text{f}} } \right)}} \\ & A_{1} = \frac{{\rho_{\text{nf}} }}{{\rho_{\text {f}} }},\,\,\,\,\,\,A_{2} = \frac{{\left( {\rho C_{\text{P}} } \right)_{\text{nf}} }}{{\left( {\rho C_{\text{P}} } \right)_{\text{f}} }},\,\,\,A_{5} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},\, \\ & A_{3} = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }},\,\,\,\,A_{6} = \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }},\,\,\,A_{4} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} \\ \end{aligned}$$
(14)

In addition, the boundaries are summarized as:

$$\begin{array}{*{20}l} {\theta = 0.0} \hfill & {{\text{on}}\,{\text{ outer}}\,{\text{ surfaces}}} \hfill \\ {\varPsi = 0.0} \hfill & {{\text{all }}\,{\text{boundaries}}} \hfill \\ {\frac{\partial \theta }{\partial n} = 1.0} \hfill & {{\text{on }}\,{\text{inner }}\,{\text{surface}}} \hfill \\ \end{array}$$
(15)

To calculate \({\text{Nu}}_{\text{loc}}\) and \({\text{Nu}}_{\text{ave}}\), the below equations were employed:

$${\text{Nu}}_{\text{loc}} = \frac{1}{\theta }\left( {1 + \frac{4}{3}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)^{ - 1} {\text{Rd}}} \right)\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)$$
(16)
$${\text{Nu}}_{\text{ave}} = \frac{1}{S}\int\limits_{0}^{s} {{\text{Nu}}_{\text{loc}} } \,{\text{d}}s$$
(17)

Sheikholeslami [34] is the pioneer of CVFEM. This technique combines FEM and FVM and uses the benefits of both approaches. In the final step, the Gauss–Seidel technique has been applied to find the values of scalars in each corner of triangular element. Various improvements in numerical approaches have been reported in recent decade [35,36,37,38,39,40,41,42,43,44,45,46,47].

In order to attain mesh insensitive results, a mesh analysis has been conducted for all the states. Table 4 is an example which demonstrates the results of various mesh sizes for a certain case. Furthermore, to ensure the correctness of the written code, the outputs have been compared with the previously published studies [1] which employed the same code. Table 5 validates that the present results are in reasonable accordance with the past literature. In addition, other validation exists in Refs. [48, 49].

Table 4 Variation of \({\text{Nu}}_{\text{ave}}\) with change of mesh size at \({\text{Ra}} = 600\),\({\text{Rd}} = 0.8,{\text{Ha}} = 20\) and \(\phi = 0.04.\)
Full size table
Table 5 Variation of \({\text{Nu}}_{\text{ave}}\) at Pr = 0.733
Full size table

Results and discussion

In the present investigation, the role of nanoparticle shape on the transportation of nanomaterial within porous tank with employing buoyancy and radiation parameters was depicted. To control the velocity, magnetic force was involved. The results have been analysed to predict the impact of the radiation parameter (\(0 \le {\text{Rd}} \le 0.8\)), shape factor (\(3 \le m \le 5.7\)), Hartmann number (\(0 \le {\text{Ha}} \le 20\)) and concentration (\(0\% \le \varphi \le 5\%\)) of the alumina nanoparticles.

Figure 2 illustrates the impact of platelet-shaped (\(m = 5.7\)) nanoparticles addition (\(\varphi = 4\%\)) on the streamlines and the isotherm profiles of the porous medium at \({\text{Ra }}\) = 600 and \({\text{Rd }}\) = 0.8 without magnetic field effect. It is evident that the convective coefficient reduces while the Ψmax augments with the introduction of the nanomaterial within hosting fluid because knf is greater than kf. The impact of the Hartmann number on the nanofluid migration at \({\text{Rd}}\) = 0.8, \(m\) = 5.7, \(\varphi\) = 4% for the \(Ra = 100\) and \({\text{Ra}} = 600\) is illustrated in Figs. 3 and 4. The impact of the Lorentz forces results in the augmentation of temperature surface. The fluid convection incites a clockwise recirculating eddy which is subdivided into the bottom and top sections of the cavity, and this division is more perceptible at lower \({\text{Ra}}\) and higher \({\text{Ha}}\). Lorentz forces results in the augment of Ψmax. The mode of heat transfer is conductive at lower \({\text{Ra}}\), while it is relatively convective at the higher \({\text{Ra}}\).

Fig. 2
figure 2

Impacts of \(\phi\) on nanofluid behaviour (\(\phi = 0.04\) (—) and \(\phi = 0\) (- - -)) when \({\text{Ra}} = 600,{\text{Ha}} = 0,m = 5.7,{\text{Rd}} = 0.8\)

Full size image
Fig. 3
figure 3

Impacts of Ha on nanofluid flow when \({\text{Ra}} = 100,{\text{Rd}} = 0.8,m = 5.7,\phi = 0.04\)

Full size image
Fig. 4
figure 4

Impacts of Ha on nanofluid flow when \({\text{Ra}} = 600,{\text{Rd}} = 0.8,m = 5.7,\phi = 0.04\)

Full size image

The dependence of Nuavg on the shape factor (\(m\)), (\({\text{Rd)}}\), (\({\text{Ha}}\)) have been shown in Fig. 5. Results show that Nuavg observes the direct dependence on the \(m\). The platelet shapes (\(m = 5.7\)) demonstrated the best performance of all the selected nanoparticle shapes followed by cylindrical (\(m = 4.8\))-, brick (\(m = 3.7\))- and spherical (\(m = 3\))-shaped particles. Like \(m\), the \({\text{Rd}}\) also demonstrates a direct relationship with the Nuavg. However, compared to the \(m\), \({\text{Ra}}\) and the \({\text{Ha}}\), the results of Nuavg are more sensitive towards the variation of the \({\text{Rd}}\). The trend of the Nuavg is also ascending as a function of the \({\text{Ha}}\) and \({\text{Ra}}\); however, for the conditions of constant a \({\text{Rd }}\), \(m\) and \(\varphi ,\) the Nuavg demonstrates declining trend with the increasing values of \({\text{Ha}}\) and \({\text{Ra}}\). Based on the results, a correlation for the estimation of the Nuavg as a function of the considered parameter can be predicted as;

Fig. 5
figure 5figure 5

Impacts of \({\text{Ra}},\,{\text{Ha}},{\text{Rd}},m,\phi\) on \({\text{Nu}}_{\text{ave}}\)

Full size image
$$\begin{aligned} {\text{Nu}}_{\text{ave}} & = 1.86 + 0.042\,m + 0.64\,{\text{Rd}} + 0.3\,{\text{Ra}} - 0.25\,{\text{Ha}} \\ & \quad + 7 \times 10^{ - 3} m\,{\text{Ha}} - 0.16\,{\text{Rd}}\,{\text{Ha}} - 0.3\,{\text{Ra}}\,{\text{Ha}} + 1.4 \times 10^{ - 4} \,{\text{m}}^{2} \\ \end{aligned}$$
(18)

The validly of the proposed correlation is applicable for the studied radiation parameter (\(0 \le {\text{Rd}} \le 0.8\)), shape factor (\(3 \le m \le 5.7\)), nanomaterial concentration (\(0\% \le \varphi \le 5\%\)), Hartmann number (\(0 \le {\text{Ha}} \le 20\)) and (\(100 \le {\text{Re}} \le 600\)).

Conclusions

The manuscript investigates the influence of the nanomaterial shape variation on the MHD-free convection and the radiative heat transfers of the Al2O3–water nanomaterial within a porous medium by employing the CVFEM approach. The considered radiation parameter, shape factor, Hartmann number and particle volume fraction ranges are \(0 \le {\text{Rd}} \le 0.8\), \(3 \le m \le 5.7\), \(0 \le {\text{Ha}} \le 20\) and \(0\% \le \varphi \le 5\%\), respectively. The findings of the study can be concluded as:

  • The higher shape factor augments the Nuave. The platelet shapes (\(m = 5.7\)) demonstrated the highest Nuavg followed by cylindrical (\(m = 4.8\))-, brick (\(m = 3.7\))- and spherical (\(m = 3\))-shaped particles.

  • Compared to the \(m\), \({\text{Ra}}\) and the \({\text{Ha}}\), the results of Nuave are more sensitive towards the variation of the \({\text{Rd}}\). The convective mode is predominating when Ha = 0.