Introduction

Investigating nanomaterials (which are fabricated by dispersion of nanoparticles into fluid) attracted more attention during the last decade because they are practical to control fluid stream and heat transfer rate in various-shaped channels or cavities. Open cavities are typically categorized into four regular coordinates: curvilinear, spherical, Cartesian and circular coordinates [1,2,3,4,5,6,7,8,9,10]. Based on the results of Kouloulias et al. [11], the metal oxide and the semimetal oxide raised the absorption specifications of carbon dioxide, and these procedures involving stream impediment might jeopardize the relevant process of dispersing the carbon dioxide. Numerically, the free convection of tilted wavy permeable tank accumulated with a nanomaterial at appearance of Lorentz effect has been surveyed by Bondareva et al. [12], and based on outputs, a rise in Ha results in reduction in Nu. Augmentation of efficiency is the main goal of several researchers [13,14,15,16,17,18,19,20,21,22], and they tried to suggest various methods. The free convection of a nanomaterial-accumulated annulus under the fixed heat flux was analyzed by Hu et al. [23] who concluded that suspending the nanoparticles in typical fluid changed the stream pattern. Based on their results, Nu had a positive correlation with the volume fraction of nanoparticles, radial ratio and Re. Additionally, they found that Nu is smaller for positive values of eccentricity compared to the other cases. The transient free convection in a wavy surface tank under tilted magnetic effect was scrutinized by Sheremet et al. [24] who utilized mathematical model. According to their outcomes, growth in Ha results in an increase in Nu. Also, reducing the tilted angle results in generation of weaker cell. Moreover, growing the wavy contraction ratio results in a growth in the amplitude of the wave. External free convection of nanomaterial flowing on a semiinfinite sheet numerically was simulated by Narahari et al. [25]. The authors discovered that the temperature, the velocity and the concentration of the nanoparticle evolve with time and they become stable when time progressed. The local Nu increased slightly when the Brownian motion terms increased; however, it was reduced when the thermophoresis terms grew. Based on their results, the impact of buoyancy ratio terms on the local Nu was negligible. Not only simulation tools but also the optimization techniques are significant to reach the best design [26,27,28,29,30,31,32,33,34,35]. Sheikholeslami and Vajravelu [36] executed the magneto-nanofluid behavior in cavity. They showed that the heat transportation is reduced by the presence of buoyancy forces. Kolsi et al. [37] analyzed the MHD flow of CNT/H2O flowing in a cavity. They employed FEM for their analysis. They observed a linear growth in Nu in their unit. The interaction between nanoparticles at the existence of magnetic area and internal heat production along a vertical rough plate has been scrutinized by Mustafa et al. [38]. They discovered that Cf and Nu were subtractive functions of the amplitude of wavy sheet. Several external forces have been involved in domains to control the flow rate [39,40,41,42,43,44,45,46,47,48,49,50,51]. The impact of isoflux obstacle inside a container accumulated with air on the free convection was investigated by Hussain [52]. Based on their results, both heat functions and heat lines methods are applied effectively for introducing the buoyancy effect in wavy tanks accumulated with nanofluid. Several publications were published about hydrothermal efficiency [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73]. Uddin and Rahman [74] analyzed the transient free convective stream of nanomaterial in a container. The author concluded that the nanoparticles were uniformly suspended inside a basis fluid as the particles diameter ranged from 1 to 10 nm. The mean Nu soared when the nanoparticles’ volume fraction increased; however, it plummeted when the nanoparticles’ diameter grew.

Considering the above brief review, the topic of simulating nanomaterial transportation in existence of magnetic field is significant. The current research was devoted to CVFEM modeling of hybrid nanomaterial within a permeable chamber with imposing of external Lorentz. Outputs in view of thermal and flow-style behaviors were analyzed, and various cases were involved to demonstrate the role of effective variables.

Formulation of problem

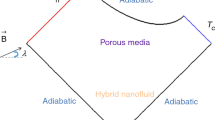
The representation of 2D chamber is illustrated in Fig. 1. The hot wall was located in right side and left surface is cold and rest walls are adiabatic. The testing fluid is hybrid nanomaterial, which includes hybrid nanopowders (iron oxide and MWCNT) and water [75]. The zone is porous and impact of permeability was added as source term of momentum. Additionally, negative effect of magnetic field on transportation of nanomaterial was involved in the model. Steady two-dimensional PDEs which must be solved are:

Fig. 1
figure 1

Porous chamber with nanomaterial

Full size image
$$\frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} = 0$$
(1)
$$\begin{aligned} & - \left( {T_{\text{c}} - T} \right)\sin \gamma g\beta_{\text{nf}} - \frac{{\mu_{\text{nf}} }}{K}\frac{1}{{\rho_{\text{nf}} }}u \\ & \quad - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial x} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} }}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) \\ & \quad + \sigma_{\text{nf}} B_{0}^{2} \left[ { - u\left( {\sin \lambda } \right)^{2} + 0.5v\left( {\sin 2\lambda } \right)} \right] = v\frac{\partial u}{\partial y} + u\frac{\partial u}{\partial x} \\ \end{aligned}$$
(2)
$$\begin{aligned} & - \frac{{\mu_{\text{nf}} }}{K}\frac{1}{{\rho_{\text{nf}} }}v + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} }}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \cos \gamma \left( {T_{\text{c}} - T} \right)g\beta_{\text{nf}} \\ & \quad - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial y} + B_{0}^{2} \sigma_{\text{nf}} u\left( {\sin \lambda } \right)\left( {\cos \lambda } \right) \\ & \quad + \sigma_{\text{nf}} B_{0}^{2} \left[ { - v\left( {\cos \lambda } \right)^{2} } \right] = u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} \\ \end{aligned}$$
(3)
$$\begin{aligned} \frac{1}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}\frac{{\partial q_{\text{r}} }}{\partial y} + \left( {v\frac{\partial T}{\partial y} + u\frac{\partial T}{\partial x}} \right) & = k_{\text{nf}} \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right)\left( {\rho C_{\text{p}} } \right)_{\text{nf}}^{ - 1} , \\ & \quad \left[ {T^{4} \cong 4T_{\text{c}}^{3} T - 3T_{\text{c}}^{4} ,q_{\text{r}} = - \frac{{4\sigma_{\text{e}} }}{{3\beta_{\text{R}} }}\frac{{\partial T^{4} }}{\partial y}} \right] \\ \end{aligned}$$
(4)

Greater thermal features can be obtained if two nanopowders are mixed together. So, we utilized hybrid nanopowders in the current research. According to [75], to estimate the properties of hybrid nanomaterial, we can employ the previous experimental data which are more realistic. In this approach, homogenous model is involved and computational cost is reduced in this modeling.

To decrease the number of unknown scalars, we introduced new parameter (vorticity) as below:

$$\begin{aligned} \omega + \frac{\partial u}{\partial y} - \frac{\partial v}{\partial x} & = 0, \\ \frac{\partial \psi }{\partial x} & = - v, \\ \frac{\partial \psi }{\partial y} & = u \\ \end{aligned}$$
(5)

Definition of variables can be written as:

$$\begin{aligned} \Delta T & = \frac{{q^{\prime\prime}L}}{{k_{\text{f}} }},U = \frac{uL}{{\alpha_{\text{nf}} }},\varOmega = \frac{{\omega L^{2} }}{{\alpha_{\text{nf}} }}, \\ \theta & = \frac{{T - T_{\text{c}} }}{\Delta T},\varPsi = \frac{\psi }{{\alpha_{\text{nf}} }},V = \frac{vL}{{\alpha_{\text{nf}} }} \\ \end{aligned}$$
(6)

So, the last format of formulation can be presented as:

$$\frac{{\partial^{2} \varPsi }}{{\partial Y^{2} }} + \frac{{\partial^{2} \varPsi }}{{\partial X^{2} }} = - \varOmega ,$$
(7)
$$\begin{aligned} & U\frac{\partial \varOmega }{\partial X} + \frac{\partial \varOmega }{\partial Y}V = \Pr \frac{{A_{5} }}{{A_{1} }}\frac{{A_{2} }}{{A_{4} }}\left( {\frac{{\partial^{2} \varOmega }}{{\partial Y^{2} }} + \frac{{\partial^{2} \varOmega }}{{\partial X^{2} }}} \right) - \frac{{A_{2} }}{{A_{4} }}\frac{{A_{5} }}{{A_{1} }}\varOmega \frac{\Pr }{\text{Da}} \\ & \quad + \Pr \,{\text{Ha}}^{2} \frac{{A_{6} }}{{A_{1} }}\frac{{A_{2} }}{{A_{4} }}\left( {\frac{\partial U}{\partial X}\cos \lambda \sin \lambda - \frac{\partial V}{\partial X}\left( {\cos \lambda } \right)^{2} + \frac{\partial U}{\partial Y}\left( {\sin \lambda } \right)^{2} - \frac{\partial V}{\partial Y}\cos \lambda \sin \lambda } \right) \\ & \quad + \Pr \,{\text{Ra}}\frac{{A_{3} A_{2}^{2} }}{{A_{1} A_{4}^{2} }}\left( {\frac{\partial \theta }{\partial X}\cos \gamma - \frac{\partial \theta }{\partial Y}\sin \gamma } \right), \\ \end{aligned}$$
(8)
$$\left( {1 + \frac{4}{3}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)^{ - 1} {\text{Rd}}} \right)\frac{{\partial^{2} \theta }}{{\partial Y^{2} }} + \left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }}} \right) = \frac{\partial \theta }{\partial X}\frac{\partial \varPsi }{\partial Y} - \frac{\partial \varPsi }{\partial X}\frac{\partial \theta }{\partial Y}$$
(9)

To complete the definition of formulation, we need to introduce the below parameters:

$$\begin{aligned} A_{5} & = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},{\text{Ra}} = g\left( {\rho \beta } \right)_{\text{f}} \Delta {\text{TL}}^{3} /\left( {\mu_{\text{f}} \alpha_{\text{f}} } \right),\,A_{3} = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}, \\ A_{1} & = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }},A_{2} = \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }},{\text{Ha}} = LB_{0} \sqrt {\sigma_{\text{f}} /\mu_{\text{f}} } , \\ A_{4} & = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }},\Pr = \upsilon_{\text{f}} /\alpha_{\text{f}} ,A_{6} = \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} \\ \end{aligned}$$
(10)

The best function to evaluate the strength of convection is Nu:

$${\text{Nu}}_{\text{loc}} = \frac{\partial \theta }{\partial n}\left( {1 + \frac{4}{3}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)^{ - 1} {\text{Rd}}} \right)\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)$$
(11)
$${\text{Nu}}_{\text{ave}} = \frac{1}{S}\int\limits_{0}^{s} {{\text{Nu}}_{\text{loc}} } \,{\text{d}}s$$
(12)

After reducing pressure terms, the final dimensionless equations should be solved and CVFEM in-house code was developed for this goal. This code was written by Sheikholeslami [76]. He employed this approach for various fields of fluids and published it in various journals. He published his experience as a reference book. Grid independency procedure is vital in numerical simulation, and one example is provided in Table 1. The best grid is that size in which Nu has no changes after using smaller size.

Table 1 Values of Nu with use of various grids at \({\text{Ra}} = 10^{5}\), \({\text{Rd}} = 0.8,{\text{Da}} = 100,{\text{Ha}} = 60\) and \(\phi = 0.003\)
Full size table

Results and discussion

In the present simulation, variations in isotherm style and nanomaterial flow structure were analyzed within a preamble media. Imposing of Lorentz force as well as radiation terms was involved in governing equations. We employed in-house Fortran code to simulate the problem based on CVFEM, and this code was verified with comparing with [77]. Figure 2 depicts the low values of deviation and guarantees the correctness of outputs.

Fig. 2
figure 2

Verification of CFEM with [77] when Gr = 1e5

Full size image

The dependence of flow structure on permeability and strength of magnetic force is exhibited in Fig. 3. As it is obvious from this graph, permeability is more effective when Ha = 0. Nanomaterial can move though the chamber easier if Da augments while Lorentz forces prevent the fluid to migrate. Therefore, augmenting Ha results in lower Ψ which means lower convective intensification.

Fig. 3
figure 3

Streamline changes with rise in permeability [\({\text{Da}} = 100\) (dashed lines) and \({\text{Da}} = 0.01\) (straight lines)] at \({\text{Ra}} = 10^{3} ,{\text{Rd}} = 0.8\)

Full size image

Change in intensity of convection is examined in Figs. 4 and 5 for various values of Da and Ha. Maximum values of Ψ within the domain are in dependence on Da, Ra, Ha and Rd. The left wall is cold, while the right straight surface is hot, so one counterclockwise cell generates which makes separation of thermal boundary from the surface. More intensive circulation can be obtained with rise in Da, which means positive effect of permeability on flow of hybrid nanomaterial. Augmenting Ha reflects an increment in thermal boundary layer thickness. Single cell exists in streamline, and with imposing of Ha, the center of cell shifts downward. And its power reduces. However, augmenting permeability of the zone will be helpful in view of thermal penetration. More smooth separation from the hot wall can be obtained for greater Da, which reveals greater convective mode. Larger density of isotherm near hot wall appears with rise in Da, which reflects more interaction of nanomaterial with hot surface. More uniform scattering of isotherm will appear in existence of Ha, which proves the unfavorable impact of Ha on ∇T. It is possible to conclude that such force has controlling role of thermal performance. To clarify the impact of various variables on Nu, new formulation is extracted as:

Fig. 4
figure 4

Hydrothermal changes with increase in Ha at \({\text{Ra}} = 10^{5} ,{\text{Da}} = 0.01,{\text{Rd}} = 0.8\)

Full size image
Fig. 5
figure 5

Hydrothermal changes with increase in Ha at \({\text{Ra}} = 10^{5} ,{\text{Da}} = 100,{\text{Rd}} = 0.8\)

Full size image
$$\begin{aligned} {\text{Nu}}_{\text{ave}} & = 0.83 + 0.81{\text{Rd}} + 0.098{\text{Da}}^{*} + 1.51\log ({\text{Ra}}) \\ & \quad - 0.67{\text{Ha}}^{*} - 1.37{\text{Ha}}^{*} \,\log ({\text{Ra}})\, - 0.19{\text{Da}}^{*} \,{\text{Ha}}^{*} \\ & \quad + 0.19\log ({\text{Ra}})\,\,{\text{Da}}^{*} + 0.01{\text{Da}}^{*} {\text{Rd}}\, - 0.71{\text{Rd}}\,{\text{Ha}}^{*} \\ \end{aligned}$$
(13)

Additionally, for graphical demonstration of distribution of Nu with respect to parameters, Fig. 6 is drawn. With growth of Ha, ∇T decreases and lower Nu can be achieved. This negative effect augments with increase in Da, which indicates that more intense convection can be affected more by Lorentz forces. When no resistance force exists against the nanomaterial flow, the positive effect of permeability can be more observable. Dependency of Nu on Rd reduces with imposing of Ha. In greater values of Ha, Rd has no effect on Nu. Growth of buoyancy force leads to more convective intensity, and Nu augments with rise in Rd, which means that permeability and Da have similar impact on thermal performance and augmenting such parameters results in greater convection. In spite of positive effect of Rd on Nu, this factor has no effective role on isotherms.

Fig. 6
figure 6

Using various \({\text{Ra}},\,{\text{Ha}},{\text{Rd}},{\text{Da}}\) and obtained \({\text{Nu}}_{\text{ave}}\)

Full size image

Conclusions

Laminar nanomaterial convection modeling by means of CVFEM was scrutinized in current article. The geometry has one curved adiabatic wall and one left straight hot wall. To extend the governing equations, radiation and Lorentz forces were included and permeable medium was imposed. Distributions of Nu, isotherm and Ψ were reported in outputs. Separation from right surface becomes smoother if convection intensifies which occurs for greater Da and Ra. Selecting media with grater permeability can intensify the Nu, and it is more effective in the absence of Ha term in equations. Growth of Rd leads to increase in Nu. Higher values of Ra reflect smoother separation of boundary layer.