Introduction

Nanotechnology is one of the most brilliant areas in fluid mechanics that attract the researchers due to its greater capability. Nanomaterial is the new invent which is achieved by applying nano powders [1,2,3,4,5,6,7,8,9,10,11]. The special features of nanofluid can be used in thermal and heat enhancement applications due to the flow field changes under the influence of magnetic fields [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Variety of researches were done in this field [27,28,29,30,31,32,33,34,35,36,37,38]. In one of the new investigations, Taslimifar et al. [39] reported in their study the using of nanomaterial in steady with using Kelvin forces. Gandomkar et al. [40] investigated pulsating ferrofluid heat pipe, to discover the best design between three different studied cases of magnetic field. Khoshmehr et al. [41] scrutinized the influences of combined ferrofluid and magnetic field in the boiling phenomena. Their experiment revealed that applying magnetic force led to enhancement in the boiling heat flux. Ahmad and Iqbal [42] presented a study on ferrofluid with temperature dependence viscosity affected by no-slip condition. Their results showed the concentration enhanced by enhancing viscous dissipation and Schmidt number. Strek and Jopek [43] investigated ferrofluid heat transfer under the impact of Kelvin forces. Shima and Philip [44] illustrated from their study on magnetic field effect on thermophysical properties that these properties could be changed significantly by changing magnetic field parameters. Simulation-based demonstrations help the researchers to find best configuration [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. Gavili et al. [65] investigation on thermal conductivity of ferrofluid revealed that applying a magnetic source significantly increased thermal conductivity. Mehrali et al.’s [66] study on entropy generation of hybrid graphene–magnetite nanomaterial illustrated the irreversibility reduced significantly compared to raw H2O. Abdel-wahed [67] investigation on ferrofluid predicted that nano size particles improved the Nu and decreased the surface shear stress, whereas curvature of the tube caused negative impact on Nu. Various numerical methods exist to evaluate performance of system [68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88]. Krishna Shah and Khandekar [89] also conducted a study on potential of ferrofluids for heat transfer augmentation, via numerical simulations. They found that higher volume fraction loading and magnetic fields applying resulted in better efficiency and local Nusselt number observed to reach a significant increase higher than no magnetic field case. Heat transfer efficiency of heat pipe with three different working fluids was studied by Hao et al. [90]. They found that startup efficiency of acetone-filled heat pipe is the best and friction of acetone-filled heat pipes showed the lowest efficiency. Sheikholeslami et al. [91] scrutinized the impact of external force on ferrofluid heat transfer argumentation in ribbed channel. They studied different parameters such as magnetic sources arrangement and their magnitude on improving heat transfer from the channel.

In this study, changes in thermophysical parameters of a ferrofluid with a multivariable dependence viscosity in a wavy microchannel are presented. The impacts of parameters such as Re, wave amplitude, magnetic number and concentration on heat transfer coefficient, Nu, f on the domain have been investigated, and their influences are compared together.

Governing equation

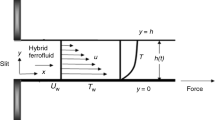
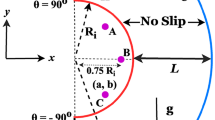
The schematic of the considered geometry for the problem, a wavy microchannel with current-carrying wire as external source of magnetic field, and some of the boundary conditions in two horizontal and vertical cross sections are shown in Fig. 1. Equations of steady-state conditions are as follows [91]:

$$\nabla \cdot \rho_{\text{nf}} \vec{U} = 0$$
(1)
$$\frac{{D\vec{U}}}{Dt} = - \frac{1}{{\uprho_{\text{nf}} }}{\nabla }P + v_{\text{nf}} {\nabla }^{2} \vec{U} + \frac{{\upmu_{0} }}{{\uprho_{\text{nf}} }}M{\nabla }\vec{H} + \vec{F}_{\text{L}}$$
(2)
Fig. 1
figure 1

Geometry and mesh

Full size image

The term \(\frac{{\mu_{0} }}{\rho }M\nabla \vec{H}\) is representative of magnetic force, and FL is Lorentz force consequent of the MHD.

Equations with considering FHD can be presented as follows [91,92,93]:

$$\uprho_{\text{nf}} \left[ {\frac{\partial v}{\partial t} + w\frac{\partial v}{\partial z} + v\frac{\partial v}{\partial y} + u\frac{\partial v}{\partial x}} \right] = - \nabla P + \mu_{\text{nf}} \left( {\nabla^{2} v} \right) +\upmu_{0} M\frac{{\partial \vec{H}}}{\partial y} - \sigma_{\text{nf}} B_{\text{x}}^{2} u + \sigma_{\text{nf}} B_{\text{x}} B_{\text{y}} u$$
(3)
$$\rho_{\text{nf}} \left[ {\frac{\partial u}{\partial t} + w\frac{\partial u}{\partial z} + v\frac{\partial u}{\partial y} + u\frac{\partial u}{\partial x}} \right] = - \nabla P + \mu_{\text{nf}} \left( {\nabla^{2} u} \right) + \mu_{0} M\frac{{\partial \vec{H}}}{\partial x} - \sigma_{\text{nf}} B_{\text{y}}^{2} u + \sigma_{\text{nf}} B_{\text{x}} B_{\text{y}} \upsilon$$
(4)
$$\frac{\partial w}{\partial y} + \frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} = 0$$
(5)
$$\begin{aligned} & (\rho C_{p} )_{{{\text{nf}}}} \left( {w\frac{{\partial T}}{{\partial z}} + v\frac{{\partial T}}{{\partial y}} + u\frac{{\partial T}}{{\partial x}}} \right) = K_{{{\text{nf}}}} \left( {\frac{{\partial ^{2} T}}{{\partial y^{2} }} + \frac{{\partial ^{2} T}}{{\partial z^{2} }} + \frac{{\partial ^{2} T}}{{\partial x^{2} }}} \right) \\ & \quad + \sigma _{{{\text{nf}}}} {\text{(uB}}_{{\text{y}}} {\text{ - }}\upsilon {\text{B}}_{{\text{x}}} {\text{)}}^{2} + \mu _{{{\text{nf}}}} \left( {2\left( {\frac{{\partial u}}{{\partial x}}} \right)^{2} + 2\left( {\frac{{\partial u}}{{\partial y}}} \right)^{2} + 2\left( {\frac{{\partial u}}{{\partial z}}} \right)^{2} + CurlV} \right) \\ & \quad - \mu _{0} T\frac{{\partial M}}{{\partial x}}\left( {u\frac{{\partial \bar{H}}}{{\partial x}} + \upsilon \frac{{\partial \bar{H}}}{{\partial y}} + w\frac{{\partial \bar{H}}}{{\partial z}}} \right) \\ \end{aligned}$$
(6)

The terms \(\mu_{0} M\frac{{\partial \vec{H}}}{\partial x}\) and \(\mu_{0} M\frac{{\partial \vec{H}}}{\partial y}\) show the magnetic force effect. The terms \(\sigma_{\text{nf}} B_{\text{y}}^{2} u + \sigma_{\text{nf}} B_{\text{x}} B_{\text{y}} \upsilon\) and \(\sigma_{\text{nf}} B_{\text{x}}^{2} u + \sigma_{\text{nf}} B_{\text{x}} B_{\text{y}} u\) in (4) and (5) are representatives of Lorentz force. For the different magnetization M, the following equation is derived [91]:

$$M = (T_{\text{c}}^{'} - T)\bar{H}K^{'}$$
(7)

Hx and Hy are defined as [91]:

$$H_{\text{x}} = \left( {x - a} \right)\frac{1}{2\pi }\frac{\gamma }{{(a - x)^{2} - (b - y)^{2} }},\quad H_{\text{y}} = \left( {b - y} \right)\frac{1}{2\pi }\frac{\gamma }{{(a - x)^{2} - (b - y)^{2} }}$$
(8)

Here (a, b) is the coordinate of wire. H as the magnetic field intensity was defined as follows [91]:

$$H = \sqrt {Hx^{2} + Hy^{2} } = \frac{\gamma }{{2\pi (x - a)^{2} - (y - b)^{2} }}$$
(9)

Magnetic numbers (Mnf) and Hartmann as two important parameters appearing in magnetic problems are defined as follows:

$${\text{Mn}}_{\text{f}} = \frac{{h^{2} \mu_{0} kH^{2} }}{{v_{\text{nf}}^{2} \rho_{\text{nf}} }} = \frac{{h^{2} B_{{}} M}}{{v_{\text{nf}}^{2} \rho_{\text{nf}} }}$$
(10)
$${\text{Ha}} = B_{\text{y}} D\sqrt {\frac{{\sigma_{\text{nf}} }}{{\mu_{\text{nf}} }}}$$
(11)

where h is the microchannel height.

$${\text{Mn}}_{\text{f}} = \frac{{h^{2} \mu_{0} \chi H_{0}^{2} }}{{v_{\text{nf}}^{2} \rho_{\text{nf}} }}$$
(12)

where B0 is the highest value of magnetic field and \(\upchi\) is magnetic susceptibility.

$$R_{\text e} = \frac{VD}{{\nu_{\text{nf}} }}{\text{Nu}}_{\text{loc}} = \frac{hl}{{K_{\text{nf}} }}\quad C_{\text{f}} = \frac{{\tau_{\text{w}} }}{{\frac{1}{2}\rho_{\text{nf}} U_{\text{in}}^{2} }}$$
(13)
$$\begin{aligned} (\rho C_{\text{p}} )_{\text{nf}} & = (\rho C_{\text{p}} )_{\text{f}} (1 - \varphi ) + (\rho C_{\text{p}} )_{\text{f}} \varphi \\ \rho_{\text{nf}} & = \rho_{\text{f}} (1 - \varphi ) + \rho_{\text{s}} \varphi \\ \end{aligned}$$
(14)
$$\alpha_{\text{nf}} = \frac{{K_{\text{nf}} }}{{(\rho C_{\text{p}} )_{\text{nf}} }}$$
(15)
$$\frac{{K_{\text{nf}} }}{{K_{\text{f}} }} = \frac{{K_{\text{s}} + 2K_{\text{f}} - 2\varphi (K_{\text{f}} - K_{\text{s}} )}}{{K_{\text{s}} + 2K_{\text{f}} - \varphi (K_{\text{f}} - K_{\text{s}} )}}$$
(16)

Also \(\sigma_{\text{nf}}\) is defined (see for details [91]) as:

$$\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} = 1 + \left[ {3\varphi \left( {\frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }} - 1} \right)} \right]\frac{1}{{\left( {\frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }} + 2} \right) - \varphi \left( { - 1 + \frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }}} \right)}}$$
(17)

The viscosity of nanofluid considered from correlations is extracted from experimental data proposed by nonlinear fitting by Wang et al. [92]. The ranges of volume fraction and temperature were considered 0.5–5% and 293–333 K, respectively, and the final equation for viscosity that is considered in this study is given as follows:

$$\mu_{\text{nf}} = (316.0629 - 27886.4807\phi^{2} + 0.035H^{2} + 4263.02\phi + 3.1H)e^{ - 0.02T}$$
(18)

Geometry definition and boundary conditions

In the current article, a wavy duct as shown in Fig. 1 is studied. The direction of the fluid flow is in wave form with a sine curve expressed by the trigonometric function, as below.

$$y = A\sin \left( {2\pi \cdot \frac{z}{\lambda }} \right)$$
(19)

where A and k are defined as amplitude and wavelength, respectively. The SIMPLE velocity–pressure coupling method is used for simulation. To discretize the convection terms, second-order upwind scheme is employed. The results of mesh independency examination are shown in Fig. 1c. Two maximum grids are in good agreement with each other in value of average Nusselt, and their tolerance is lower than 1%; therefore, a grid with 1,700,000 elements is selected and used for this simulation (Fig. 2).

Fig. 2
figure 2

Validation of Nusselt number and magnetic fields effect in a channel

Full size image

Simulation, geometry and boundary conditions data are presented in Table 1.

Table 1 Quantities of parameters in simulation
Full size table

For validation a comparison between the theoretical investigation and present simulation is shown in Fig. 3. It can be observed that the current outputs are in excellent agreement with theoretical one. For the magnetic field validation, the velocity profile of fluid flow imposed by an external magnetic field in a channel which is done by Aminifar et al. [94] is considered. The results predicted a good agreement between results in this study and Aminifar et al. study.

Fig. 3
figure 3

Comparison of streamlines in a cavity due to FHD with [95]

Full size image

Furthermore, the streamlines due to the external magnetic field under a channel in our simulation are compared with Tzirtzilakis and Xenosstudy [95] at Re = 400 and Mn = 256 (Fig. 4). There is a proper and very good treaty between results of current code and [95].

Fig. 4
figure 4

Effect of magnetic number on thermophysical parameters

Full size image

Results

In this section the effect of different influential parameters is studied. To better consideration and assessment of parameters effect, in every section one parameter is considered as variable and the rest of them are considered fixed. Figure 4 illustrates the impact of B on thermophysical parameters (see Table 2).

Table 2 Simulation condition for magnetic field effect
Full size table

As it is obvious by augmenting Mn due to the increasing recirculation and fluid–solid interaction, the thermal boundary layer has been affected and consequently the Nusselt number and heat transfer are increased. Furthermore, it is clear that due to the increase in fluid–solid interaction, the pressure loss and friction coefficient are enhanced.

Figure 5 shows a comparison of the wall temperature in various magnetic numbers. As it can be seen, by increasing the magnetic number because of increasing the wall–fluid interaction and collision, and as a result increasing the heat transfer rate, the temperature of the bottom wall is significantly decreased and it shows the significant impact of Mn on cooling application in microchannels.

Fig. 5
figure 5

Effect of magnetic number on bottom wall temperature

Full size image

Figure 6 presents a comparison between nanofluid temperatures in different cross sections in the microchannel under influence of different magnitudes of magnetic field. It is clear that, from the inlet toward the outlet, the temperature of the ferrofluid due to the heat transfer between hot wall and nanofluid is increased; however, it is demonstrated that by increasing the magnetic number, because of increasing recirculation in fluid and increasing collision, the diffusivity of heat transfer in the fluid is increased and the maximum temperature in the outlet flow for the higher magnetic number is lower and also the temperature distribution is more uniform in the fluid field.

Fig. 6
figure 6

Effect of magnetic number on temperature distribution in nanofluid

Full size image

The impact of volume fraction of magnetic nanoparticles is investigated in Fig. 5 and Table 3.

Table 3 Simulation condition for volume fraction effect
Full size table

It is shown that by increasing the volume fraction, the heat transfer coefficient and Nusselt number that are representative of heat transfer augmentation are enhanced. The results indicate that by augmenting the \(\varphi\) from 0.5 to 4.5%, the Nusselt number is increased by 33.3%. It is due to the increase in the wall–fluid interaction because of increasing the magnetic field effect on flow field by increasing the volume fraction. Friction coefficient and pressure loss are also increased by augmenting \(\varphi\), about 0.63% and 0.66%, respectively (Fig. 7).

Fig. 7
figure 7

The effect of volume fraction on thermophysical properties

Full size image

Effect of volume fraction on temperature distribution on the nanofluid field and microchannel wall is presented in Fig. 8. It is conducted that by augmenting \(\varphi\), as it is mentioned, due to the increasing magnetic field effect and consequently fluid–solid interaction, the temperature on the wall along the channel is decreased. The diffusivity of heat transfer on the fluid by increasing volume fraction is also increased, and the temperature distribution is changed in the flow field (Fig. 9).

Fig. 8
figure 8

Temperature distribution for various volume fraction

Full size image
Fig. 9
figure 9

Effect of Reynolds number on thermophysical parameters

Full size image

Reynolds number is another physical parameter that has been investigated in this study (see Table 4).

Table 4 Simulation condition for Reynolds number effect
Full size table

The results illustrated that in a constant magnetic field, increasing the Reynolds number has an opposite effect on Nusselt and also heat transfer coefficient. By increasing the Reynolds from 50 to 250, the Nusselt and heat transfer decreased by about 8.6%. Increasing Reynolds number reduces the hydrodynamics and thermal boundary layer and consequently the heat transfer coefficient. However, in this investigation, the results demonstrated that magnetic number has a more dominant effect and compares the Reynolds number effect. Consequently, when the Reynolds number increases, the impact of Mn will reduce and also the total effect leads to a decrease in heat transfer. Additionally, it is revealed that augmenting the Reynolds number will rise the friction coefficient and pressure drop significantly by about 6 and 8 times, respectively.

Figure 10 shows a comparison of temperature contour and streamlines for various Reynolds numbers. As it is clear from the figure, in the lowest Reynolds number due to the higher amount of magnetic field effect on nanofluid compared to the inertia force, the flow field experienced higher intensity of recirculation and consequently interaction with walls. Therefore, heat transfer between hot wall and cold nanofluid is increased, and as it is obvious, the fluid temperature is much higher than other cases in the domain. However, by increasing Reynolds number, because of increasing the momentum of the fluid and consequently inertia force, the influence of magnetic field is faded. By decreasing the effect of magnetic field, the intensity of recirculation and interaction between fluid and wall are decreased, and as a result, the diffusivity of heat on the fluid is reduced and the fluid temperature is decreased.

Fig. 10
figure 10

Temperature distribution and streamlines for various Reynolds number

Full size image

Figure 11 illustrates the impact of inlet temperature on thermophysical properties.

Fig. 11
figure 11

Effect of inlet temperature on thermophysical properties

Full size image

It is cleared that by increasing inlet temperature, due to reducing the viscosity the pressure drop and friction coefficient are reduced (see Table 5). However, inlet temperature compared to other considered parameters did not have a significant effect on thermal performance and there is a just slight increase in both Nusselt and heat transfer coefficient. Another parameter that is investigated in wavy microchannel in presence of external magnetic field is wave’s amplitude (see Table 6).

Table 5 Simulation condition for inlet temperature effect
Full size table
Table 6 Simulation condition for wave’s amplitude effect
Full size table

It is revealed that by increasing wave amplitude, due to the increase in the recirculation size and intensity, the interaction of fluid and structure is increased and consequently a noteworthy augmentation in the Nu by about 40%, respectively, has been observed. On the other hand, increasing fluid–solid collision increased the friction coefficient and pressure drop significantly that is a negative effect in channels (Fig. 12).

Fig. 12
figure 12

Effect of wave amplitude on thermophysical properties

Full size image

Temperature distribution in various amplitudes of wavy wall is shown in Fig. 13. It is illustrated that by increasing the amplitude, due to the increase in the interaction momentum and recirculation, the heat diffusivity on the ferrofluid is increased, and consequently, the temperature on the surface decreased along the channel and the fluid experienced more uniform temperature and more average temperature in higher amplitudes.

Fig. 13
figure 13

Temperature distribution in various amplitudes of wavy wall

Full size image

As it is mentioned in the paper, for this study the viscosity of fluid is considered as a multivariable dependence variables consisted of temperature, volume fraction and magnetic field magnitude; therefore, in this section the changes on viscosity distribution in the ferrofluid are investigated. For this purpose, the temperature contour of four cross sections along the microchannel is considered. The results show that by increasing magnetic number the viscosity of fluid is increased and also a more uniform distribution of viscosity can be observed in the case with the highest magnetic number. The changes of the viscosity by Reynolds number show that in the higher Reynolds number due to the lower temperature, the viscosity is reduced in the ferrofluid. Comparison of the effect of inlet temperature on viscosity indicates that in the minimum studied inlet temperature, due to the minimum temperature of ferrofluid in the domain, the viscosity is lower than higher inlet temperature and maximum one. Additionally, it is illustrated by augmenting the \(\varphi\) of ferrofluid, and the viscosity in the domain is increased. In all the figures, it can be observed that the overall viscosity range in the domain alongside the microchannel from inlet to outlet is increased and it is because of enhancing temperature of the fluid field from inlet to outlet (Fig. 14).

Fig. 14
figure 14figure 14

Influence of various parameters on viscosity distribution

Full size image

Comparison for different investigated parameters on friction coefficient and Nu is illustrated in Fig. 15. As it is clear from the figure, excepted of Reynolds number in constant magnetic field, the rest of considered variables showed a positive effect on Nusselt number; meanwhile, the magnetic field and wave amplitude have the most influence, respectively. Also it is conducted although the amount of the friction coefficient for the wave amplitude and magnetic number is more than other variables and points because of the Reynolds number in which their effect studied on in (maximum Re = 250), however, depends on the trend of the graphs, and increase in Reynolds number is shown the worst effect on friction coefficient and consequently pressure loss.

Fig. 15
figure 15

Comparison of influence of parameters on friction coefficient and Nusselt number as non-dimensional variables

Full size image

Conclusions

Treatment of a ferrofluid with a multivariable dependence viscosity in a microchannel under impact of an external non-uniform magnetic field due to a current-carrying wire is studied. The effect of various variables such as inlet temperature, Re, magnetic field magnitude and volume fraction on Nu, heat transfer coefficient, friction coefficient and pressure loss. The simulation conditions of all investigated cases are explained in results section. The results predicted that the magnetic field intensity growing has a important role on heat transfer augmentation and improving heat transfer and cooling in the microchannel; however, due to the increasing collision and interaction between ferrofluid and structure, the friction coefficient and pressure loss are also increased. Reynolds number showed a significant influence on increasing friction effect and pressure loss; however, in the lower Reynolds number, magnetic effect showed a more dominant effect compared to Reynolds and augmenting Nu. In the higher volume fraction the influence of Kelvin force is higher than lower magnetic number, and therefore due to the increasing recirculation and fluid–solid interaction, the Nu increased. Investigation of viscosity distribution in the fluid domain showed a significant change due to the magnetic field and volume fraction. A comparison among variables effect as non-dimensional parameters showed that Reynolds number and volume fraction had a worst effect on friction coefficient, whereas magnetic number and wave’s amplitude increasing had a best impact on heat transfer augmentation.