Introduction

Heat transfer near stretching sheets boundary layer is relevant to a extensive range of usages such as extrusion, rotating and cooling fibers and polymers [1,2,3,4,5,6,7]. In these applications, the cooling process should be carefully controlled since the products’ properties strongly depend on the amount of heat transfer which required significant amount of energy [8,9,10,11,12,13,14,15]. Due to the high demand for energy, economic and environmental aspects of the energy sources have become important in the present century; fossil fuels do not keep their significance any more due to the increase in human population [15,16,17,18,19,20,21,22,23,24,25]. Concerns on the harmful impact of fossil fuels on our health and environment have created urgent needs for alternative resources. There has been significant growth in the use of renewable sources, directly and indirectly, such as sun (solar energy, wind and hydropower), gravity (ebb and flow) and the core of earth (geothermal) [25,26,27,28,29,30,31,32,33,34,35]. Among these resources, solar energy contributes the smallest to the environmental impacts compared to other renewable energy sources, and it can be utilized on a larger scale worldwide [35,36,37,38,39,40,41,42,43,44,45]. Nanomaterial has a wide range of application in different devices such as electronic cooling devices, transformer cooling, cooling and heating procedure of energy conversion and cancer therapy [45,46,47,48,49,50]. Choi [51] studied nanofluids in terms of their applications, and he claims that such fluids are the best option for increasing the performance in conventional fluids. The specifications of TiO2–H2O applied was evaluated by Khedkar et al. [52] who found that dispersing powders increased the efficiency by 14%. Nanomaterials are introduced as effective carrier fluids [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. Mixed convection of a nanomaterial within a lid-driven geometry has been demonstrated by Zhou et al. [73] who applied different heat sources. Raising the volume fraction of nanoparticles by 6 percent led the efficiency to grow continuously.

For cooling a heat generation element in a cavity, Miroshnichenko et al. [74] utilized a nanofluid. They managed to minimize the average temperature of the heater, as they utilized the nanofluid in natural convection. An investigation on performance of alumina-oil flowing within an annulus was conducted by Chun et al. [75] who observed an important growth of performance. To find the best optimized values of parameters, various methods were utilized [76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93]. Empirically, the thermal conductivity of aluminum oxide-silver/H2O hybrid nanofluid has been studied by Aparna et al. [94]. Based on their results, nanofluids’ thermal conductivity grew as the temperature or the volume fraction rose. They found that the effect of temperature on knf was more considerable at greater volume concentration of particle. Numerically, the stream of MHD nanofluid for three-dimensional stream moved by a stretching plate has been scrutinized by Ahmad et al. [95]. The effect of different operant fluids’ features on mixed convection was researched by Prasad et al. [96]. Based on their results, Biot number raises the temperature for greater amounts illustrating that the mixed convection is the main heat transfer medium in the proposed geometry. A 2D mixed convection problem was studied by Jmai et al. [97] who concentrated on the impacts of the driven speed of wall on performance. They managed to find a correlation between nanoparticles volume fraction and Ri (Richardson number) in various speeds of the wall. MHD pseudo nanomaterial transient stream and its performance in a limited thin membrane on a stretching plate including inner heat production were studied by Lin et al. [98]. Various authors tried to present effective techniques for augmenting heat transfer [99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115]. Al2O3–Cu/water hybrid nanofluid by a thermochemical technique was synthesized by Suresh et al. [116] who surveyed its thermophysical features in various volume fractions ranging from 0.1 percent to 2 percent and compared these values with the amounts achieved from theoretical correlations. They found that knf of hybrid material is greater than that of mono nanomaterial. A nanofluid 3D mixed convection stream in the existence of Lorentz force has been scrutinized by Zhou et al. [117] who demonstrated that Richardson number has a considerable impact on the mixed convection stream dynamics, no more so than for Ri lower than. However, applying nanofluid raises the heat transfer rate in low Ra values. This decent effect is weakened as Ra increases. An empirical investigation on knf of SiO2/water, Al2O3/water nanofluid and their hybrid combinations was performed by Moldoveanu et al. [118] who presented some correlations for hybrid and mono nanofluids as to the temperature and the particle volume fraction. The impacts of CuO–water nanofluid and water on heat transfer rate, coefficient, pressure fall, exergy destruction and frictional drop was surveyed by Khairul et al. [119] who reported that the Nu of nanofluid grew about 18.50–27.20% compared to pure water.

The main objective of current work is to study the influence of Lorentz on CuO–water nanomaterial on a stretching sheet. Current article aims to understand the impacts of thermal radiation on CuO–water nanofluid using KKL pattern and how the model parameters influence the heat transfer.

Mathematic description

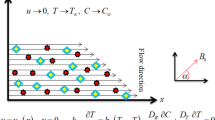
Figure 1 schematically shows the test case considered in the present work. \(U_{\text{w}} \left( x \right)\) is the stretching flow velocity which is equivalent to \(ax\), and \(U_{\infty } \left( x \right)\) is the free flow velocity, which is equivalent to \(bx\). \(T_{\text{w}} \left( x \right) = T_{\infty } + cx^{\text{n}}\) is the sheet temperature and \(\left( {B_{\text{0}} } \right)\) is the magnetic field utilized. The simulations are based on the single-phase pattern that considers the impact of thermal radiation. The main features of CuO and water are presented in Table 1. The boundary conditions and the partial differential equations are expressed as:

$$\frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} = \text{0,}$$
(1)
$$\rho_{{\text{nf}}} \left( { - U_{\infty } \frac{{\text{d}U_{\infty } }}{{\text{d}x}} + \frac{\partial u}{\partial y}v + \frac{\partial u}{\partial x}u} \right) = \mu_{{\text{nf}}} \frac{{\partial^{2} u}}{{\partial y^{2} }} + \sigma_{{\text{nf}}} B_{\text{0}}^{2} \left( { - u + U_{\infty } } \right),$$
(2)
$$\left( {\rho C_{\text{p}} } \right)_{{\text{nf}}} \left( {\frac{\partial T}{\partial x}u + \frac{\partial T}{\partial y}v} \right) = - \frac{{\partial q_{\text{r}} }}{\partial y} + k_{{\text{nf}}} \frac{{\partial^{2} T}}{{\partial y^{2} }},$$
(3)
$$\begin{array}{*{20}l} {v = \text{0},\quad T = T_{\text{w}} \left( x \right),\quad u = U_{\text{w}} \left( x \right)} \hfill & {\quad @y = \text{0}} \hfill \\ {T = T_{\infty } ,\quad u = U_{\infty } \left( x \right)} \hfill & {\quad @y \to \infty } \hfill \\ \end{array}$$
(4)

\(q_{\text{r}}\) is the radiation heat flux obtained using the Rosseland estimation \(q_{\text{r}} = - \frac{{4\sigma_{\text{e}} }}{{3\beta_{\text{R}} }}\frac{{\partial T^{4} }}{\partial y}\) where \(\beta_{\text{R}} ,\,\sigma_{\text{e}}\) are the mean absorbency factors and the Stefan–Boltzmann constant, respectively. Temperature variations are small, and hence, Taylor series \(T^{4}\) can be considered as \(T^{4} \cong 4T_{\text{c}}^{3} T - 3T_{\text{c}}^{4}\) where Tc is cooling temperature.

Fig. 1
figure 1

Geometry and related boundaries

Full size image
Table 1 Comparison of \(- \theta^{\prime}\left( \text{0} \right)\) for various \(\lambda\) when \(M = \text{0},\;S = \text{0},\;\varepsilon = \text{0},\;\text{Pr} = \text{0}.\text{05},\;\phi = \text{0},\;K_{\text{1}} = \text{0}\)
Full size table

As provided in Ref. [115], the efficient electrical conductivity, heat capacity and density of CuO–water can be obtained using:

$$\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} = 1 + \frac{{3\left( { - 1 + \sigma \sigma } \right)\phi }}{{ - \left( { - 1 + \sigma \sigma } \right)\phi + \left( { + 2 + \sigma \sigma } \right)}},\quad \sigma \sigma = \sigma_{\text{s}} /\sigma_{\text{f}}$$
(5)
$$\varsigma_{\text{nf}} = (1 - \phi )\varsigma_{\text{f}} + \varsigma_{\text{s}} \phi ,\quad \varsigma = \rho C_{\text{p}}$$
(6)
$$\rho_{\text{nf}} = \rho_{\text{s}} \phi + \rho_{\text{f}} (1 - \phi ),$$
(7)

By utilizing KKL pattern, μnf and Knf of CuO–water are modeled as

$$k_{\text{nf}} = k_{\text{static}} + k_{\text{Brownian}} ,$$
(8)
$$\frac{{k_{\text{static}} }}{{k_{\text{f}} }} = 1 + \frac{{3\left( {\frac{{k_{\text{p}} }}{{k_{\text{f}} }} - 1} \right)\phi }}{{\left( {\frac{{k_{\text{p}} }}{{k_{\text{f}} }} + 2} \right) - \left( {\frac{{k_{\text{p}} }}{{k_{\text{f}} }} - 1} \right)\phi }},$$
(9)
$$R_{\text{f}} + \frac{{d_{\text{p}} }}{{k_{\text{p}} }} = \frac{{d_{\text{p}} }}{{k_{{{\text{p}},{\text{eff}}}} }},\quad R_{\text{f}} = 4 \times 10^{ - 8} \,{\text{km}}^{2} /{\text{W}}$$
(10)
$$k_{\text{Brownian}} = c_{{{\text{p}},{\text{f}}}} \rho_{\text{f}} \sqrt {\frac{{T\kappa_{\text{b}} }}{{d_{\text{p}} \rho_{\text{p}} }}} \phi g^{\prime}(T,\phi ,d_{\text{p}} )\left( {10^{4} \times 5} \right)$$
(11)
$$\mu_{{\text{eff}}} = \frac{{\mu_{\text{f}} }}{{\left( {1 - \phi } \right)^{2.5} }} + \frac{{k_{{\text{Brownian}}} }}{{k_{\text{f}} }}\frac{{\mu_{\text{f}} }}{{{ \Pr }_{\text{f}} }}$$
(12)

Values for the function g and coefficients a1 to a10 for CuO–water and its properties were mentioned in [115].

The dimensionless parameters can be expressed as:

$$v = - \frac{\partial \psi }{\partial x}\quad \text{and}\quad u = \frac{\partial \psi }{\partial y}$$
(13)
$$\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\quad \eta = y\left( {\frac{{\upsilon_{{\text{nf}}} }}{a}} \right)^{ - 1/2} ,\quad f\left( \eta \right) = x^{{ - \text{1}}} \left( {\upsilon_{{\text{nf}}} a} \right)^{{ - \text{1/2}}} \psi$$
(14)

The ODEs companied with the BCs are expressed as below:

$$f^{{{\prime }2}} = \lambda^{2} + f^{{{\prime \prime \prime }}} + ff^{{\prime \prime }} + A_{5} \left( {\lambda - f^{{\prime }} } \right)\frac{M}{{A_{1} }}\text{,}$$
(15)
$$\left( {\text{1} + \frac{{4}}{{3}}\frac{{\text{Rd}}}{{A_{{3}} }}} \right)\theta^{\prime\prime} + \text{Pr}\left( {\frac{{A_{{4}} A_{{2}} }}{{A_{{3}} A_{\text{1}} }}} \right)\left( {f\theta^{\prime} - nf^{\prime}\theta } \right) = 0,$$
(16)
$$\begin{aligned} & f^{\prime}\left( \infty \right) = \lambda ,\quad f\text{(0)} = \text{0,}\quad f^{\prime}\text{(0)} = \text{1,} \\ & \theta \left( \infty \right)\text{ = 0},\quad \theta \text{(0)} = \text{1}, \\ \end{aligned}$$
(17)

The magnetic parameters, velocity ratio, Prandtl number, radiation coefficients and \(A_{\text{i}} ,\;\left( {i = \text{1} \ldots \text{5}} \right)\) are represented as follow:

$$\begin{aligned} A_{2} & = \frac{{(\rho C_{{{\text{p}}\,}} )_{\text{nf}} }}{{(\rho C_{{{\text{p}}\,}} )_{\text{f}} }},\quad \lambda = b/a,\quad M = \sigma_{\text{f}}\, B_{0}^{2} /\left( {\rho_{\text{f}} a} \right),\quad {\text{Rd}} = 4\sigma_{\text{e}} T_{\text{c}}^{3} /\left( {\beta_{\text{R}} k_{\text{f}} } \right), \\ \Pr & = \left( {k_{\text{f}} \rho_{\text{f}} } \right)^{ - 1} \left( {\left( {\rho C_{\text{p}} } \right)_{\text{f}} \mu_{\text{f}} } \right),\quad A_{1} = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }},\quad A_{3} = k_{\text{nf}} /k_{\text{f}} , \\ A_{4} & = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},\quad A_{5} = \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}. \\ \end{aligned}$$
(18)

The Nu and Cf are expressed as:

$${\text{Nu}} = - \theta^{\prime}(0)A_{3} ,\quad C_{\text{f}} = f^{\prime\prime}(0)A_{4}$$
(19)

A RK4 method is applied to solve ODEs.

Results and discussion

To validate the model, the normalized temperature (θ) for various values of \(\lambda\) is first compared to those acquired by Sharma and Singh [120], and the results are presented in Table 1, confirming satisfactory agreement. A comprehensive analysis is achieved to study the impact of key parameters including as velocity ratio, radiation, magnetic parameters, nanoparticles mass fraction and temperature index.

The influence of Lorentz powers and \(\lambda\) on Cf is demonstrated in Fig. 2. Magnetic field leads to produce a Lorentz power, resulting in retardation in the flow. The intensity of the power which is presented by M is increased as the speeds reduce while the temperature augments. For the stretching velocity larger than external flow velocity (i.e., \(b < a\)), flow has an inverse boundary layer. The velocity grows with the augment of velocity ratio factor, but the temperature drops with growing λ. The impacts of velocity ratio and magnetic parameters on Nu as well as on Cf are illustrated in Fig. 2. Nu decreased with rising Lorentz power. Cf increased with rising magnetic factors, while it falls with increasing λ. Figures 3–5 demonstrate influences of n, Rd, M and \(\lambda\) on Nu. It can be found that the influences of the temperature index parameters, which increasing this leads to a decline in the profile of temperature, on the distribution of temperature and on Nusselt number. As a result, Nu in a growing function of temperature index.

Fig. 2
figure 2

Effects of \(\lambda\) and M on Cf

Full size image
Fig. 3
figure 3

Effects of \(n\) and Rd on Nu when \(\lambda = 0.35,\;M = 6\)

Full size image
Fig. 4
figure 4

Effects of \(\lambda\) and n on Nu when \(\text{Rd} = 2.5,\;M = 6\)

Full size image
Fig. 5
figure 5

Effects of Rd and M on Nu when \(\lambda = 0.35,\;n = 2\)

Full size image

According to data, the following correlation is derived:

$$C_{\text{f}} = 1.29 - 0.82\lambda + 0.27M - 0.223\lambda M - 0.485\lambda^{2} - 5.15 \times 10^{ - 3} M^{2}$$
(20)
$$\begin{aligned} \text{Nu} & = 2.27 + 0.59n - 0.96\text{Rd} + 0.14\lambda - 0.14M \\ & \quad - 0.045nM + 0.047\text{Rd}\,M + 0.046\lambda M - 0.094n^{2} - 0.02\lambda^{2} + 0.046M^{2} \\ \end{aligned}$$
(21)

Conclusions

Numerically, magnetic nanofluid stream over a stretching sheet was surveyed considering thermal radiation. The impacts of velocity ratio, nanoparticle mass fraction, temperature index magnetic and radiation coefficients on the velocity and temperature distributions were analyzed. Results illustrate that the width of the hydraulic boundary layer decreased with augmenting magnetic parameters, while it grew with rising velocity ratio factor. The distribution of temperature grew when the magnetic factors and radiation ones increased; however, it declined as the velocity ratio and temperature index parameters rose.