Introduction

In porous media, investigating heat transfer and fluid stream attracted researchers’ attentions within the past ten years. Increasing emphasis on fibrous and efficient granular insulation systems stimulated different investigations in fluid flowing in porous media leading many results to achieve for convective stream in basic geometries in internal and external streams [1,2,3,4,5,6,7,8,9]. These days, thermal transmission can be improved by applying nanofluids which are typical fluids including nanoparticles [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. In various technologies, natural convection plays the main role in different applications of engineering including—building applications, solar applications and electronic applications. Some problems for industrial ovens or boilers are porous media and nonlinear boundaries of closed or open geometries. In addition, operant fluid might be nanofluids or viscous fluids. Recently, many researchers conducted various studies in nanofluids’ convective heat transfer. Typical heat transfer fluids including—oil, ethylene glycol and water—have small rate of k which is a basic restriction in improving the compactness and the efficiency of various electronic applications. Thus, it is required to enhance advanced heat transfer fluids with greater rate of thermal conductivity. By defining nanofluids, such need was tackled [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Keblinski et al. [41] surveyed possible systems for nanoparticle clustering.

Javed and Siddiqui [42] numerically surveyed the effect of magnetic area on free convection stimulated with ferrofluid which has an inner obstacle. They illustrated that such area leads the strength of flow to weaken. The thermal performance of centered sheet on micropolar liquid flow within a tank was surveyed by Muthtamilselvan et al. [43] who illustrated that the presence of micropolar fluid leads the rate of heat transfer to decrease while increasing non-uniformity terms of sheet outputs in an augment in heat transfer rate.

Societies provided various new ways to reach more capable thermal system [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. Saravanan and Sivaraj [73] numerically studied surface radiation and free convection through an enclosure including adiabatic horizontal walls and vertical cold borders. They applied an in-house code improved on the base of FVM. Based on their results, variable heating raises the ∇T. The mixed convection of viscous fluid flowing inside a tank in appearance of cold vertical borders and inner isothermal triangular heater has been investigated by Gangawane et al. [74] via Fluent software. They found that thermal transition in such system can be improved by applying great Pr number fluids and greater blockage. The impacts of Lorentz on alumina nanomaterial combined behavior within a lid-driven tank including a entrally isothermal body were investigated by Mehmood et al. [75] who found that an increase in Hartmann number reduces the mean Nu, the mean entropy generation and Bejan amount because of heat transfer.

As Eastmenet al. [76] reported that nanomaterials have a considerably greater thermal conductivity rate compared with that of typical ones. The represented stream inside a permeable media has been investigated by Zhang and Liu [77] who applied a numerical technique according to the Brinkman–Forchheimer model. In addition to these, some investigations including LTNE model in a porous media have been conducted. Kalidasan et al. [78] scrutinized the free convection of H2O-copper nanomaterial in a tank including 2 blocks. They numerically resolved the equations. Based on their results, the mixture effect of unsteady temperature of wall and nanoparticles destroys the hydrodynamic blockage. Free convection of silver powder including centrally hot sheet in the case of cold vertical surfaces was investigated by Mahalakshmi et al. [79] who applied homogeneous model. According to their results, the thermal transmission increases when the concentration of nanoparticle and Re grows. Numerical approaches were developed for complex physics [80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124]. Numerically, free convection within a permeable tilted tank including a centrally solid obstacle under the impact of magnetic area has been studied by Sivaraj and Sheremet [125] who found that an increase in Hartmann amount suppresses the boundary-induced fluid movement and the strength of thermal transition within the enclosure. The empirical results illustrate a much greater thermal conductivity rate compared with that projected by these models. Yu and Choi [126] represented an alternation statement for estimating the thermal conductivity rate of liquid–solid combination. They reported that a structural model of nanofluids may include a bulk liquid and solid nanoparticle.

In current article, a 2D CVFEM simulation was proposed to investigate the impact of Hartmann number on transportation of hybrid nano-powders. To involve the porous media, non-Darcy terms were included in momentum equations and impact of the presence of radiation term was analyzed.

Definition

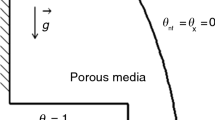
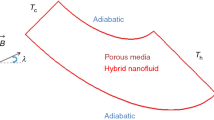
A curved cavity with three walls was scrutinized (Fig. 1). The left surface is hot, and curved wall is adiabatic. To change the flow pattern, magnetic field has been applied, but we neglected the joule heating because the strength of B is not enough to produce such effect. In current simulation, nanomaterial with hybrid particles as introduced in [127] was selected and properties were calculated based of empirical formulas [127]. To reach the accurate data, in current article, the CVFEM which belongs to Sheikholeslami [128] was utilized. Regard to its advantages, accurate solution can be obtained. All walls are impermeable. By adding buoyancy effect, the below formulation can be considered:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ \begin{aligned} & \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} }}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + v\sigma_{\text{nf}} \left( {\cos \lambda } \right)B_{0}^{2} \left( {\sin \lambda } \right) - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial x} - \frac{{\mu_{\text{nf}} }}{K}u\frac{1}{{\rho_{\text{nf}} }} - \left( {T_{\text{c}} - T} \right)\beta_{\text{nf}} g\sin \gamma \\ & \quad + \sigma_{\text{nf}} B_{0}^{2} \left[ { - u\left( {\sin \lambda } \right)^{2} } \right] = v\frac{\partial u}{\partial y} + u\frac{\partial u}{\partial x} \\ \end{aligned} $$
(2)
$$ \begin{aligned} & B_{0}^{2} u\left( {\sin \lambda } \right)\sigma_{\text{nf}} \left( {\cos \lambda } \right) + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} }}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - g\cos \gamma \left( {T_{\text{c}} - T} \right)\beta_{\text{nf}} - \frac{\partial P}{\partial y}\frac{1}{{\rho_{\text{nf}} }} - \frac{1}{{\rho_{\text{nf}} }}\frac{{\mu_{\text{nf}} }}{K}v \\ & \quad + \sigma_{\text{nf}} \left[ { - v\left( {\cos \lambda } \right)^{2} } \right]B_{0}^{2} = v\frac{\partial v}{\partial y} + u\frac{\partial v}{\partial x} \\ \end{aligned} $$
(3)
$$ \frac{1}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}\frac{{\partial q_{r} }}{\partial y} + \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) = k_{\text{nf}} \left( {\rho C_{\text{p}} } \right)_{\text{nf}}^{ - 1} \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right),\left[ {T^{4} \cong 4T_{\text{c}}^{3} T - 3T_{\text{c}}^{4} ,q_{\text{r}} = - \frac{{4\sigma_{\text{e}} }}{{3\beta_{\text{R}} }}\frac{{\partial T^{4} }}{\partial y}} \right] $$
(4)
Fig. 1
figure 1

Curved domain with B

Full size image

Regard to previous article [127], we selected hybrid ferrofluid (MWCNT-Fe3O4) with base fluid of water. To gain the properties, empirical formulas were applied which are valid for φ = 0.003. Equation (6) was considered to simplify formulas.

$$ \begin{aligned} \psi_{y} = u,\,\omega + \frac{\partial u}{\partial y} - \frac{\partial v}{\partial x} = 0,\,\,\psi_{x} = - v,\,\, \hfill \\ \,\, \hfill \\ \end{aligned} $$
(5)

Then, the following equation was developed for the dimensionless variables:

$$ \begin{aligned} & U = \frac{uL}{{\alpha_{\text{nf}} }},\left( {X,Y} \right) = \frac{{\left( {x,y} \right)}}{L},\,\Delta T = \frac{{q^{\prime\prime}L}}{{k_{\text{f}} }}, \\ & \varPsi = \frac{\psi }{{\alpha_{\text{nf}} }},\varOmega = \frac{{\omega L^{2} }}{{\alpha_{\text{nf}} }},V = \frac{vL}{{\alpha_{\text{nf}} }} \\ & \theta = \frac{{T - T_{\text{c}} }}{\Delta T}, \\ \end{aligned} $$
(6)

Considering the above equations, Eqs. (8–10) were obtained:

$$ \frac{{\partial^{2} \varPsi }}{{\partial X^{2} }} + \frac{{\partial^{2} \varPsi }}{{\partial Y^{2} }} = - \varOmega , $$
(7)
$$ \begin{aligned} & U\frac{\partial \varOmega }{\partial X} + \frac{\partial \varOmega }{\partial Y}V = \frac{{A_{2} }}{{A_{4} }}\left( {\frac{{\partial^{2} \varOmega }}{{\partial Y^{2} }} + \frac{{\partial^{2} \varOmega }}{{\partial X^{2} }}} \right)\Pr \frac{{A_{5} }}{{A_{1} }} \\ & \quad + \Pr \frac{{A_{6} }}{{A_{1} }}\left( {\frac{\partial U}{\partial X}\cos \lambda \sin \lambda - \frac{\partial V}{\partial X}\left( {\cos \lambda } \right)^{2} + \frac{\partial U}{\partial Y}\left( {\sin \lambda } \right)^{2} - \frac{\partial V}{\partial Y}\cos \lambda \sin \lambda } \right)\frac{{A_{2} }}{{A_{4} }}\text{Ha}^{2} \\ & \quad + \text{Ra}\Pr \,\left( { - \frac{\partial \theta }{\partial Y}\sin \gamma + \frac{\partial \theta }{\partial X}\cos \gamma } \right)\frac{{A_{3} A_{2}^{2} }}{{A_{1} A_{4}^{2} }} - \frac{\Pr }{\,Da}\frac{{A_{5} }}{{A_{1} }}\frac{{A_{2} }}{{A_{4} }}\varOmega , \\ \end{aligned} $$
(8)
$$ \left( {1 + \frac{4}{3}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)^{ - 1} \text{Rd}} \right)\frac{{\partial^{2} \theta }}{{\partial Y^{2} }} + \left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }}} \right) = - \frac{\partial \theta }{\partial Y}\frac{\partial \varPsi }{\partial X} + \frac{\partial \varPsi }{\partial Y}\frac{\partial \theta }{\partial X} $$
(9)

with following new parameters:

$$ \begin{aligned} & \text{Pr} = \upsilon_{\text{f}} /\alpha_{\text{f}} ,\text{Ra} = g\left( {\rho \beta } \right)_{\text{f}} \Delta \text{TL}^{3} /\left( {\mu_{\text{f}} \alpha_{\text{f}} } \right),\text{Ha} = \text{LB}_{0} \sqrt {\sigma_{\text{f}} /\mu_{\text{f}} } \\ & A_{1} = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }},A_{2} = \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }},A_{3} = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}, \\ & A_{4} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }},A_{5} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},A_{6} = \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} \\ \end{aligned} $$
(10)

Finally, the rate of heat transfer was estimated using Eq. (11) expressed below:

$$ \text{Nu}_{\text{ave}} = \frac{1}{S}\int\limits_{0}^{s} {\text{Nu}_{\text{loc}} } \text{ds},\quad \text{Nu}_{\text{loc}} = \left( {\frac{4}{3}\left( {A_{4} } \right)^{ - 1} \text{Rd} + 1} \right)\frac{\partial \theta }{\partial n}\left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right) $$
(11)

Results and discussion

Inclusion of hybrid powders into H2O creates new carrier fluid, and we utilized such material in porous region and insert the magnetic field. CVFEM in-house code was utilized to simulate this article, and influences of active factors were scrutinized. Profile of θ was compared with previous work and is presented in Fig. 2 which indicates that code has nice accuracy. In Table 1, one example of grid analysis was illustrated [129]. This step is the most important step of numerical modeling to gain independent outputs.

Fig. 2
figure 2

Verification of CVFEM code (compared with [129])

Full size image
Table 1 Variation of \( {\text{Nu}}_{\text{ave}} \) with change of mesh size at \( {\text{Ra}} = 10^{5} \), \( {\text{Rd}} = 0.8,{\text{Da}} = 100,{\text{Ha}} = 60 \) and \( \phi = 0.003 \)
Full size table

Patten of Ψ with rise of Da is shown in Fig. 3. Configurations of θ and Ψ with rise of Ha are depicted in Figs. 4 and 5. Existing two walls with different temperatures lead to form one vortex. Adding external force shifts the vortex center to left side. Permeability and Lorentz effects are opposed to each other. As expected, lower ∇T with rise of Ha changes the main mechanism and provides weaker vortex. With insertion of magnetic force, opposed flow changes the modes from convection to conduction and such behavior can be seen from isotherms changes. Distortion of isotherms increases for greater buoyancy effect, but it changes in appearance of magnetic field. Although increasing Da and Ra generates the thermal plume, adding magnetic field makes it to disappear which is attributed with lower convective strength. Undesirable impact of Ha on Nuave is relevant to this fact that Lorentz forces make nanomaterial flow to reduce. Influence of Da at high Hartmann number is insignificant. To exhibit the various values of Nuave, Fig. 6 was demonstrated which is based on below equation:

$$ \begin{aligned} & \text{Nu}_{{\text{ave}}} = 1.48 + 0.038\text{Da}^{*} \log (\text{Ra}) - 0.17\,\text{Ha}^{*} \text{Rd} + 0.85\log (\text{Ra}) \\ & \quad + 0.023\text{Da}^{*} - 0.16\text{Ha}^{*} - 0.015\text{Da}^{*} \text{Ha}^{*} \\ \quad + 0.021\text{Rd}\,\text{Da}^{*} + 0.81{\text{Rd}} - 0.32{\text{Ha}}^{*} \log ({\text{Ra}}) \\ \end{aligned} $$
(12)
Fig. 3
figure 3

Patten of Ψ with rise of Da (\( {\text{Da}} = 100 \) (—) and \( {\text{Da}} = 0.01 \) (− − −)) when \( {\text{Ra}} = 10^{3} ,{\text{Rd}} = 0.8 \)

Full size image
Fig. 4
figure 4

Configuration of θ and Ψ with rise of Ha at \( {\text{Ra}} = 10^{5} ,{\text{Da}} = 0.01,{\text{Rd}} = 0.8 \)

Full size image
Fig. 5
figure 5

Configuration of θ and Ψ with rise of Ha at \( {\text{Ra}} = 10^{5} ,{\text{Da}} = 100,{\text{Rd}} = 0.8 \)

Full size image
Fig. 6
figure 6

Nuave versus active parameters

Full size image

Augmentation of Da which is related to augmentation in permeability makes Nuave to increase, while Ha has reverse relationship. Both Ra and Rd can enhance the Nuave, so ∇T augments with rise of them. Transverse flow can be achieved with rise of Ha which suppresses the nanomaterial flow and reduces the ∇T. Negative effect on Nuave is reported with rise of Ha. Greater values of Rd provide more negative effect of Ha. Besides, as Rd augments Nuave can enhance according to definition of this factor.

Conclusions

An application of new in-house code for simulating nanomaterial flow has been presented. To manage the treatment of hybrid powders, Lorentz force was applied. Outcomes are classified to exhibit the effect of scrutinized factors. With respect to lower temperature gradient, Nuave decreases with augment of Ha, but reverse trend is reported for Da. With rise of permeability, better mixing of nanomaterial is occurred which provides stronger convective flow. Appearance of magnetic force has unfavorable impact of ∇T, and such impact will maximize with increase in Rd.