1 Introduction

Multiobjective optimization, also known as multicriteria optimization, refers to the process of optimizing several objective functions simultaneously over a feasible region. Usually, for nontrivial problems, it is nearly impossible to find a single point that individually optimizes all given objective functions at the same time. Therefore, the concept of optimality is replaced by the concept of Pareto optimality or efficiency.

Multiobjective optimization problems have been widely applied in many areas, such as engineering [12], management science [31, 35], environmental analysis [13] and design [16] to name just a few. For more details on the applications of multiobjective optimization in economy, industry, agriculture and many more, one can see [24, 26].

Due to its various applications, the research on multiobjective optimization problems has captured a great amount of attention and great development has been made in many aspects including the existence of solutions, the relationships between solutions under different definitions, Farkas-type results, optimality conditions and numerical optimization algorithms, see, for instance, [8, 11, 14, 15, 18, 20, 21, 23, 33, 34] and the references therein.

In the present paper, we focus on optimization algorithms for solving multiobjective optimization problems with not necessarily differentiable or convex objectives over a convex feasible region. Up to now, many classical (i.e., scalar-valued) optimization methods have been successfully extended to the multiobjective optimization setting, such as the projected gradient method [6, 18], steepest descent method [4], Newton method [34], proximal point method [8, 27, 28], trust-region method [33] and several more.

Among these strategies, this paper is concerned with the projected gradient method. As a classical and important basic scheme, the projected gradient method and its modified versions have been used frequently to solve nonsmooth optimization problems [1, 25, 37,38,39,40]. For the multiobjective optimization case, Graña Drummond and Iusem [18] considered two versions of projected gradient methods for constrained vector optimization problems with continuously differentiable objective function. For one version of the algorithm (with exogenously given square summable step lengths), by using an Armijo-like rule, the authors established the convergence of the generated sequence to a weakly efficient optimum when the objective function is convex. For another version of the algorithm (without exogenous step lengths and convexity assumption), they just showed the stationarity of the cluster points (if any), whose convergence to a weakly efficient optimum was established in [17] with the convexity assumption on the objective function. For nondifferentiable convex vector optimization problems, by exploring the structure of the vector problem, Bello Cruz [2] proposed a projected subgradient method and showed that all cluster points of the generated sequence are weakly efficient optimum points of the problem. Recently, Brito et al. [6] and Bento et al. [5] have proposed projected subgradient methods for solving constrained convex multiobjective optimization problems, where the multiobjective function is componentwise convex. By employing a scalarization process, the authors obtained the convergence of the generated sequence toward a Pareto optimal point. Their method serves as the starting point for the algorithm presented in this work. It is, however, extended by means of a more general gradient concept on the one hand and additional algorithmic degrees of freedom on the other hand.

It is worth pointing out that the above-cited work centers on convex optimization models. In many real-life problems, one often encounters the situation that the involved objective function is not necessarily convex. Thus, the study of nonconvex multiobjective optimization problems is of high importance from both the theoretical and the application point of view.

In this paper, we consider constrained quasiconvex multiobjective optimization problems, meaning that each objective function is a quasiconvex function. Our motivation stems from the extensive applications of this type of models in fields like microeconomy or location theory, see [19, 27] and Example 5.4.

For the projected gradient method for quasiconvex multiobjective optimization, let us mention the work in [3], where the objective function is assumed to be continuously differentiable. In [3], the authors showed the convergence of the sequence generated by the method introduced therein to a stationary point and furthermore to a weak Pareto efficient solution when the components of the multiobjective function are pseudoconvex. As to unconstrained nondifferentiable quasiconvex multiobjective optimization problems, by using the lower subdifferentials of the quasiconvex function [30, 36], Cruz Neto et al. [9] proposed a subgradient-type method to obtain the Pareto optimal points. There are, however, no numerical examples to illustrate the implementation of the method therein.

Inspired by the above-mentioned work, we aim to propose a projected subgradient method for solving quasiconvex multiobjective optimization problems on nonempty closed convex subsets of the Euclidean space. In this case, each objective function is not necessarily differentiable. First order descent information regarding the objective function is hereby based on the concept of the Plastria subdifferential, see [30] and Definition 2.3. This subdifferentiability concept was chosen because (a) its actual values can be obtained easily from the classical gradient and the Lipschitz constant of the objective in the smooth case, (b) its definition relies on the lower level sets of the function (making it particularly interesting for (nonsmooth) minimization problems) and (c) albeit from being infinite (therefore well defined in a very general setting), the norm of some elements of the Plastria subdifferential can be bounded from above, which is important from the numerical viewpoint.

Under suitable hypotheses, we obtain total convergence for a Pareto optimal solution of the problem. Furthermore, the performance of our method is illustrated by numerical experiments.

The outline of this article is as follows. In Sect. 2, we recall some basic definitions and preliminary materials that are used in the sequel. We also provide some examples for the proposed subdifferential calculus to prepare the numerical problems and make the paper self-contained. In Sect. 3, we present the algorithm and prove its well-definedness. Sect. 4 contains the convergence analysis of this algorithm. Specifically, the convergence of the sequence produced by the algorithm to a Pareto optimal point of the problem is established under some reasonable assumptions. Numerical examples are presented in Sect. 5 to demonstrate the performance of this method. Finally, we provide some concluding remarks in Sect. 6.

2 Preliminaries and Auxiliary Results

In this section, we recall some notations and results that are used throughout our presentation. We denote by \(\langle \cdot , \cdot \rangle \) the usual inner product of \(\mathbb {R}^n\) and by \(\Vert \cdot \Vert \) its corresponding norm. If A is countable, we denote by \(\# A\) the number of its elements. Let \(\mathbb {R}^m_+\) and \(\mathbb {R}^m_{++}\) denote the nonnegative orthant and positive orthant of \(\mathbb {R}^m\), respectively. We consider the partial orders \(\preceq \) (\(\prec \)) in \(\mathbb {R}^m\), defined by

$$\begin{aligned} x\preceq y ~(\text {resp. }x\prec y) \quad \Leftrightarrow \quad y-x\in \mathbb {R}^m_+ ~(\text {resp. }y-x\in \mathbb {R}^m_{++}). \end{aligned}$$

Consider the function \(F:\mathbb {R}^n{\rightarrow }\mathbb {R}^m\), given by \(F(x)=(f_1(x),f_2(x),\cdots ,f_m(x))\). We are interested in the following multiobjective optimization problem

$$\begin{aligned} \min _{x\in C}F(x), \end{aligned}$$
(1)

where \(C\subseteq \mathbb {R}^n\) is a nonempty closed convex set.

Definition 2.1

A point \(x^*\in C\) is called a weak Pareto optimal point or weak Pareto efficient solution for the problem (1), if there does not exist \(x\in C\) such that \(F(x)\prec F(x^*)\). If there does not exist \(x\in C\) satisfying \(F(x)\preceq F(x^*)\) and \(F(x)\ne F(x^*)\), then \(x^*\) is said to be a Pareto optimal point or Pareto efficient solution for (1).

We will denote the set of Pareto (resp. weak Pareto) efficient solutions of the problem by E (resp. \(E_{\mathrm {w}}\)). For a given \(x\in \mathbb {R}^n\) and a closed convex set \(D\subseteq \mathbb {R}^n\), recall that the orthogonal projection of x onto D, denoted by \(P_D(x)\), is the unique point in D such that \(\Vert x-P_D(x)\Vert =\inf _{y\in D}\Vert x-y\Vert \); moreover, one has

$$\begin{aligned} \langle x-P_D(x), y-P_D(x)\rangle \le 0,\quad y\in D. \end{aligned}$$
(2)

A function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is said to be quasiconvex if for every \(x,y\in \mathbb {R}^n\) and \(\alpha \in [0,1]\),

$$\begin{aligned} f(\alpha x+(1-\alpha )y) \le \max \{f(x), f(y)\}. \end{aligned}$$

It is clear that a convex function is also a quasiconvex function. Following [24, Corollary 6.6], the above definition can be adapted to multiobjective functions as follows.

Definition 2.2

Let the multiobjective function \(F:\mathbb {R}^n\rightarrow \mathbb {R}^m\) be given by \(F=(f_1, f_2,\cdots ,f_m)\). Then F is quasiconvex if each component function \(f_i\) is quasiconvex.

For a given \(z\in \mathbb {R}\) and a function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\), denote by

$$\begin{aligned} S^{\le }_f(z) = \{x\in \mathbb {R}^n: f(x)\le f(z)\}\quad \text {and}\quad S^{< }_f(z) = \{x\in \mathbb {R}^n: f(x) < f(z)\} \end{aligned}$$

the level set and the strict level set of f at z. The following notion of lower subdifferentiability and strict lower subdifferentiability were introduced by Plastria [30], which extend the notion of the Fenchel–Moreau subdifferentials

$$\begin{aligned} \partial ^{\mathrm {F-M}} f(z) = \lbrace s \in \mathbb {R}^n : \langle s,x-z \rangle \le f(x) - f(z) \quad \forall x \in \mathbb {R}^n \rbrace , \end{aligned}$$

of the convex function (see [32]).

Definition 2.3

Given a function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) and a point \(z\in \mathbb {R}^n\), the lower subdifferential, respectively, the strict lower subdifferential (in the sense of Plastria [30]) of f at z are defined by

$$\begin{aligned} \partial ^< f(z) = \{s\in \mathbb {R}^n:\langle s,x-z\rangle \le f(x)-f(z)\quad \forall x\in S^{<}_f(z)\} \end{aligned}$$

and

$$\begin{aligned} \partial ^{\le } f(z) = \{s\in \mathbb {R}^n:\langle s,x-z\rangle \le f(x)-f(z)\quad \forall x\in S^{\le }_f(z)\}. \end{aligned}$$

The function f is said to be lower subdifferentiable (resp. strictly lower subdifferentiable) at z if \(\partial ^<f(z) \ne \emptyset \) (resp. \(\partial ^{\le }f(z) \ne \emptyset \)).

It is clear that \(\partial ^{\le } f(z) \subset \partial ^{<}f(z)\). Moreover, note that (also one can see [30, Theorem 3.1] or [9]) for any \(s\in \partial ^{\le }f(z)\) and any \(\lambda \ge 1\), one has \(\lambda s\in \partial ^{\le }f(z)\), which shows that the set \(\partial ^{\le }f(z)\) is unbounded. Thus, the lower subdifferential (or the strict lower subdifferential) is generally different from the Fenchel–Moreau subdifferential, even for convex functions. However, from the definition it is already clear that the inclusion \(\partial ^{\mathrm {F-M}}f(z) \subseteq \partial ^{\le } f(z)\) holds for any convex function.

The following property of the strict lower subdifferential can be obtained easily from the definition, and one can also refer to [36, Proposition 2.2(a)].

Proposition 2.1

For a function \(f :\mathbb {R}^n\rightarrow \mathbb {R}\) and \(z\in \mathbb {R}^n\), \(0\in \partial ^{\le }f(z)\) if and only if z is a global minimizer of f.

Some other useful properties of the (strict) lower subdifferential for quasiconvex and Lipschitz continuous functions are listed in the following proposition, for (i), one can see [30, Theorem 2.3], while for (ii), one can see [36, Propositions 2.4 and 2.6]. But before stating it, let us first recall that a quasiconvex function f is said to be essentially quasiconvex if each local minimizer of f is global.

Proposition 2.2

Let \(f :\mathbb {R}^n\rightarrow \mathbb {R}\) be a quasiconvex and Lipschitz continuous function with Lipschitz constant L. Then the following assertions hold:

  1. (i)

    For each \(z\in \mathbb {R}^n\), there exists \(s\in \partial ^{<}f(z)\) such that \(\Vert s\Vert \le L\).

  2. (ii)

    Suppose further that f is essentially quasiconvex. Then \(\partial ^{\le }f(z) \ne \emptyset \) for every \(z\in \mathbb {R}^n\), and \(\partial ^{<}f(z) = \partial ^{\le }f(z)\) for every nonminimizer z of f.

Example 2.1

Consider the function (see [9, Example 1] for a similar example and Fig. 1) \(f :\mathbb {R}\rightarrow \mathbb {R}\) given by

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} -\frac{1}{3} - (x-(-1)) &{}\text {for }x \le -1 \\ \frac{x^3}{3} &{}\text {for }x \in (-1,1) \\ \frac{1}{3} + c \cdot (x-1) &{}\text {for }x \ge 1. \end{array}\right. },\qquad (c \ge 0) \end{aligned}$$

The function f is (for \(c \ne 1\)) not differentiable at \(x= \pm 1\) and quasiconvex. As the function is monotone increasing on \([-1,\infty )\), the level sets \(S_f^{\bullet }(z)\) for \(z\in [-1, +\infty )\) are given by

$$\begin{aligned} S_f^{\le } (z) = \lbrace x \in \mathbb {R}| x_0^z \le x \le z \rbrace \,\quad \text { and } \quad S_f^{<} (z) = \lbrace x \in \mathbb {R}| x_0^z \le x < z \rbrace \,, \end{aligned}$$

where \(x_0^z\) denotes the x-coordinate of the left intersection point of \(f \equiv f(z)\), which is always in \({(-\infty , -1]}\).

We calculate the Plastria subdifferential of f for two points:

  1. 1.

    At \(z_0 = \tfrac{1}{2}\), the Plastria subdifferential is given by

    $$\begin{aligned} \partial ^{\le } f (z_0) = {\Big [ \frac{1}{4} ,\infty \Big )}. \end{aligned}$$
  2. 2.

    At \(z_1 = 0\) we can calculate the Plastria subdifferential as

    $$\begin{aligned} \partial ^{\le } f(z_1) = {\Big [ \frac{1}{3}, \infty \Big )}. \end{aligned}$$
Fig. 1
figure 1

Sketch of the function f in Example 2.1, values of \(c>0\) range between 0.05 and 2.0; the thick solid line indicating \(c = \tfrac{1}{2}\)

Full size image

One disadvantage of working with subdifferentials instead of the classical gradient or approximations thereof is the numerical tractability of calculating \(\partial f\).

One can, however, show, cf. [9, Cor. 2.22], that for differentiable function with known Lipschitz constant, an element of the Plastria subdifferential can always be found by appropriately upscaling the gradient \(\nabla f\), immediately widening the potential applications of this subgradient concept.

Example 2.2

A classical example of a quasiconvex function is the negative Gaussian bell curve. In the one-dimensional case, this function is (scaled) given by

$$\begin{aligned} f(x) = -\exp (-x^2/2)\,. \end{aligned}$$

Instead of giving exact formulas for \(\partial ^{\le }f(x)\) or just strongly over-approximating it, we will use a ‘mix’ of the classical gradient and a heuristic to approximate \(\partial ^{\le }f(x)\) for the nonconvex areas.

Between the two inclination points \(x \in [-1,1]\), the function is strictly convex, and for the calculation of \(\partial ^{\le } f(x)\), one can simply rely on the classical gradient of f. If x is exactly at one of these points \(x_0 = \pm 1\), the intersection point of the linear approximation \(f(x_0) + \nabla f(x_0) \cdot (\bullet -x_0)\) with the y-axis is at \(Q^* {:=} (0, -2 \cdot \exp (-1/2)) \approx (0,-1.2131)\). To obtain elements of the Plastria subdifferential for \(|x |> 1\), we can use the slope of the linear interpolant between \(Q^*\) and (x, f(x)). This leads to the formula

$$\begin{aligned} {\tilde{s}} (x) \subset \partial ^{\le } f(x)\,,\quad \text {with}\quad {\tilde{s}}(x) {:=} {\left\{ \begin{array}{ll} x \cdot \exp (-x^2/2) &{}\text {for }|x |\le 1\\ \left( \frac{2}{\sqrt{\exp (1)}}-\exp \left( -x^2/2\right) \right) /x &{}\text {else.} \end{array}\right. } \end{aligned}$$
(3)

In Fig. 2, the result of this approximation is illustrated.

Fig. 2
figure 2

Sketch of the function f in Example 2.2

Full size image

Finally, we conclude this section by presenting the well-known quasi-Fejér convergence theorem, which has been widely used to analyze gradient and subgradient methods, see, among others, [3, 6, 9, 17, 18].

Definition 2.4

A sequence \(\{u_k\}\subseteq \mathbb {R}^n\) is said to be quasi-Fejér convergent to a nonempty set \(U\subseteq \mathbb {R}^n\) if and only if for each \(u\in U\), there exists a summable sequence \(\{\epsilon _k\}\subseteq \mathbb {R}_+\) such that

$$\begin{aligned} \Vert u_{k+1}-u\Vert ^2 \le \Vert u_{k}-u\Vert ^2 + \epsilon _k. \end{aligned}$$

Proposition 2.3

[7, Theorem 1] If \(\{u_k\}\subseteq \mathbb {R}^n\) is quasi-Fejér convergent to a nonempty set \(U\subseteq \mathbb {R}^n\), then \(\{u_k\}\) is bounded. Furthermore, if a cluster point \({\bar{u}}\) of \(\{u_k\}\) belongs to U, then the whole sequence \(\{u_k\}\) converges to \({\bar{u}}\).

3 The Algorithm

In this section, we describe our proposed algorithm to solve (1). In order to guarantee its well-definedness, we assume throughout the whole paper that the following condition holds.

Assumption 3.1

Every component function \(f_i :\mathbb {R}^n\rightarrow \mathbb {R}\), \(i=1,2,\cdots ,m\), of the objective function \(F:\mathbb {R}^n\rightarrow \mathbb {R}^m\) is essentially quasiconvex and Lipschitz continuous with Lipschitz constant L.

Consider the sequences \(\{\gamma _k\}\subseteq (0,1]\) and \(\{\alpha _k\}\subseteq \mathbb {R}_+\) with

$$\begin{aligned} \sum _{k=0}^{+\infty }\gamma _k\alpha _k=+\infty ,\quad \sum _{k=0}^{+\infty }\alpha _k^2<+\infty . \end{aligned}$$
(4)

The projected subgradient algorithm is defined as follows.

Algorithm 3.1

Input: (i) objective mapping \(F =(f_1,f_2,\ldots ,f_m):\mathbb {R}^n \rightarrow \mathbb {R}^m\) with Lipschitz constant \(L > 0\), (ii) nonempty, closed, convex set \(C \subseteq \mathbb {R}^n\), (iii) parameter sequences \(\lbrace \alpha _k \rbrace \subseteq \mathbb {R}_+, \lbrace \gamma _k \rbrace \subseteq (0,1]\) fulfilling (4), (iv) for arbitrary \(k=0,1,\ldots \): nonempty index sets \(\lbrace I_k \rbrace \subseteq \lbrace 1,2,\ldots ,m\rbrace \), (v) weighting parameters \(\lbrace (\lambda _1^k, ..., \lambda _{\# I_k}^k)\rbrace \) such that for all \(k=0,1,\ldots \) it holds \((\lambda _1^k, ..., \lambda _{\# I_k}^k) \subset [0,1]^{\# I_k}\) and \(\sum _{i\in I_k} \lambda _i^k = 1\), (vi) required optimization goal (‘weak’ or ‘strong’ Pareto points).

Step 0: Find an initial iteration point \(x_0\in C\). Set \(k=0\).

Step 1: Take \(s_i^k\in \partial ^{\le } f_i(x_k)\) such that \(\Vert s_i^k\Vert \le L\) for each \(i=1,2,\cdots ,m\). If \(\min _{i=1,2,\cdots ,m}\Vert s_i^k\Vert =0\) (for optimization goal ‘weak’) or

\(\max _{i=1,2,\cdots ,m}\Vert s_i^k\Vert =0\) (for optimization goal ‘strong’), then STOP.

      Otherwise, let \(\eta _k=\max _{i\in I_k}\{\Vert s_i^k\Vert , 1\}\)

      and compute

$$\begin{aligned} v_k {:=} \mathop {{\text {argmin}}}_{v\in C-x_k}h_{x_k}(v), \end{aligned}$$
(5)

      where \(h_{x_k}(v) {:=} \frac{\alpha _k}{\eta _k}\langle \sum _{i\in I_k}\lambda _i^ks_i^k, v\rangle +\frac{\Vert v\Vert ^2}{2}.\)

Step 2: Define

$$\begin{aligned} x_{k+1} = x_k + \gamma _k v_k. \end{aligned}$$
(6)

      Set \(k:=k+1\) and go back to Step 1.

Output: (Weak-) Pareto optimal point \(x^*= x_k\).

Remark 3.1

(Practical Considerations) 

  1. 1.

    The main computational costs of the algorithm lie in the solution of the internal minimization problems \(\min _v h_{x_k}(v)\) (and potentially finding elements of the Plastria subdifferential). These constitute quadratic optimization problems over a convex domain. Techniques from quadratic programming (interior point methods, active set methods, augmented Lagrangian methods, extended simplex schemes and others) or projection-based specially tailored solvers (cf. Proposition 4.2) are the method of choice here.

  2. 2.

    Finding a point \(x_0\) in C is simply stated as the initial step here. If the constraint set can be represented or sufficiently well approximated by linear inequalities, routines from linear programming can be used in Step 0. Otherwise, projection-based algorithms can be used to solve the according feasibility problem.

  3. 3.

    The strict stopping criteria of the algorithm can hardly be reached in a practical implementation of the algorithm. So, instead of the ‘hard’ zeros, it is useful to introduce tolerances for these tests. Even in this case, it rarely happens as one can show that if the algorithm stops at iteration k with optimization goal ‘weak,’ then \(x_k\) is optimal for at least one component of F and in the quasi-interior of C, (in particular a weak Pareto optimal point). If it pre-terminates with optimization goal ‘strong,’ the iterate is optimal for all components of F. (So, there are no conflicting goals in F, yet \(x_k\) is Pareto optimal.)

    In the examples below, the stopping criterion is based on norm of the steps in the iteration.

  4. 4.

    The main purpose of relating the subgradient values \(s_i^k\) to the Lipschitz constant of \(f_i\) is to bound the subdifferential vectors. Practically, the exact Lipschitz constants are often either unknown or of no practical value as the slope of \(f_i\) varies heavily over C. In such cases, it might be useful to change the condition to one involving ‘local’ Lipschitz constants instead.

  5. 5.

    Note that evaluations of the objective function F are not explicitly part of the algorithm. It is much more solely based on subgradient evaluations. So, in a computer implementation, there is potential for strong improvements if the actual objective values are taken into account in, e.g., a local line search that would adapt the value of \(\gamma _k\) in each step instead of fixing it a priori. The general conditions on \(\gamma _k\), \(\alpha _k\), the index sets \(I_k\) and the weight vectors \(\lambda _i^k\) practically include many step size selection algorithms already in the convergence analysis below.

    Note also that the method might arrive in a Pareto optimal point but not immediately ‘recognize’ this as the used subdifferentials are sets not just single points and the underlying optimality conditions are based on \(0 \in \partial ^{\le }\) (so a specific element of \(\partial ^{\le }\)). The conditions on step size parameters, however, ensure that the iterates cannot deviate far away from an already reached optimal point in the iteration.

Remark 3.2

Under the Assumption 3.1, it follows from Propositions 2.1 and 2.2 that for each \(i=1,2,\cdots ,m\), there exists \(s_i^k\in \partial ^{\le }f_i(x_k)\) such that \(\Vert s_i^k\Vert \le L\). Indeed, for any fixed k and \(i\in \{1,2,\cdots ,m\}\), if \(x_k\) is a global minimizer of \(f_i\), then by Proposition 2.1, one can take \(s_i^k=0\); otherwise, Proposition 2.2 ensures the existence of such an \(s_i^k\). As a result, in view of the strong convexity (ensured by the Tikhonov-type quadratic term) of \(h_{x_k}\), the direction \(v_k\) can be obtained.

Remark 3.2 guarantees the well-definedness of our algorithm.

From this point on, we assume without loss of generality that the sequence \(\{x_k\}\) generated by the algorithm is infinite.

Remark 3.3

 

  1. (i)

    The algorithm proposed here uses exogenous weights \(\lambda _i^k\) for the subgradients \(s_i^k\) in a manner of a weighting method. Following [5, 29], the weighting method allows the resulting scalar objective function (a positive linear combination of the objectives) to be solved for a single Pareto optimal solution that represents the preference of the human decision maker, which is well acceptable in applications and favorable for mathematical analysis.

    Note, however, that the algorithm in its general form does not (implicitly or explicitly) fix a weighting and can therefore not be easily recast to a single-objective algorithm applied to the weighted form.

  2. (ii)

    The algorithm proposed in the present paper covers several existing algorithms as special cases. For example, in the case when each \(I_k=\{1,2,\cdots ,m\}\) and the Fenchel–Moreau subdifferential is used, the algorithm presented here reduces to the weighting subgradient algorithm that was introduced in [5], which has been applied to solve the multiobjective optimization problem (1) but under the assumption that each component function \(f_i\) is convex.

    Assuming for a moment that each \(f_i\) is a continuously differentiable quasiconvex function, the sequences \(\{\alpha _k\}\) and \(\{\eta _k\}\) are constant, and each \(I_k =\{i_k\}\) is a singleton with \(i_k := \mathop {{\text {argmax}}}_{i\in \{1,2,\cdots ,m\}}\langle \nabla f_i(x_k), v\rangle \), then the algorithm introduced here reduces to the one in [3], which uses an Armijo-like rule to obtain the step lengths.

4 Convergence Analysis

In this section, we show that the sequence \(\{x_k\}\) generated by our algorithm converges to a Pareto optimal point for (1). We begin the analysis by showing the feasibility of \(\{x_k\}\).

Proposition 4.1

The sequence \(\{x_k\}\) belongs to C.

Proof

The proof is constructed by induction over k. Note that by the initialization of the algorithm, the initial iterate \(x_0\) belongs to C. Assume that \(x_k\in C\). Since \(\gamma _k\in (0,1]\) and \(v_k\in C-x_k\) (which means that \(v_k+x_k\in C\)), rewritten \(x_{k+1} = x_k+\gamma _k v_k\) as

$$\begin{aligned} x_{k+1} = (1-\gamma _k)x_k+\gamma _k(x_k+v_k), \end{aligned}$$

we conclude by the convexity of C that \(x_{k+1}\) belongs to C. \(\square \)

We continue the convergence analysis with the following auxiliary results.

Lemma 4.1

For all \(k\in \mathbb {N}\), \(\Vert v_k\Vert \le 2 \alpha _k\) and \(\Vert x_{k+1}-x_{k}\Vert \le 2\alpha _k\).

Proof

Fix \(k\in \mathbb {N}\). In the case when \(v_k=0\), both assertions are trivial. So we assume that \(v_k\ne 0\). By Proposition 4.1, we obtain that \(0\in C-x_k\). Thus, one has \(h_{x_k}(v_k)\le h_{x_k}(0)\le 0,\) that is

$$\begin{aligned} \frac{\alpha _k}{\eta _k}\left\langle \sum _{i\in I_k}\lambda _i^ks_i^k, v_k\right\rangle +\frac{\Vert v_k\Vert ^2}{2}\le 0. \end{aligned}$$

Then, by applying the Cauchy–Schwarz inequality and recalling that \(\sum _{i\in I_k}\lambda _i^k=1\) and \(\Vert s_i^k\Vert \le \eta _k\), one can get

$$\begin{aligned} \Vert v_k\Vert ^2\le -2\frac{\alpha _k}{\eta _k} \left\langle \sum _{i\in I_k}\lambda _i^ks_i^k, v_k\right\rangle \le 2\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\Vert s_i^k\Vert \Vert v_k\Vert \le 2\alpha _k\Vert v_k\Vert . \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert v_k\Vert \le 2\alpha _k. \end{aligned}$$
(7)

Finally, it follows from (6) and (7) that \(\Vert x_{k+1}-x_{k}\Vert = \gamma _k\Vert v_k\Vert \le 2\alpha _k\). \(\square \)

The next proposition establishes a fundamental inequality satisfied by the iterates of the method.

Proposition 4.2

For all \(z\in C\), it holds that

$$\begin{aligned} \Vert x_{k+1}-z\Vert ^2\le 8\alpha _k^2+\Vert x_{k}-z\Vert ^2+2\frac{\gamma _k\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\langle s_i^k, z-x_k\rangle ,\quad \forall \, k\in \mathbb {N}. \end{aligned}$$

Proof

Let \(z\in C\) and \(k\in \mathbb {N}\). By using (6) and Lemma 4.1, one has

$$\begin{aligned} \begin{aligned} \Vert x_{k+1}-z\Vert ^2&= \Vert x_{k+1}-x_k\Vert ^2+\Vert x_{k}-z\Vert ^2+2\langle x_{k+1}-x_k, x_{k}-z\rangle \\&\le 4\alpha _k^2+\Vert x_{k}-z\Vert ^2+2\gamma _k\langle v_k, x_{k}-z\rangle . \end{aligned} \end{aligned}$$
(8)

Note that from (5) and taking into account the definition of \(h_{x_k}\), we get

$$\begin{aligned} \begin{aligned} v_k&= \mathop {{\text {argmin}}}\limits _{v\in C-x_k}\left\{ \frac{\alpha _k}{\eta _k}\left\langle \sum _{i\in I_k}\lambda _i^ks_i^k, v\right\rangle +\frac{\Vert v\Vert ^2}{2}\right\} \\&= \mathop {{\text {argmin}}}\limits _{v\in C-x_k}\left\{ \left\langle \frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^ks_i^k, v\right\rangle + \frac{1}{2} \left( \Vert v\Vert ^2+\left\| \frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^ks_i^k\right\| ^2\right) \right\} \\&= \mathop {{\text {argmin}}}\limits _{v\in C-x_k}\left\{ \frac{1}{2} \left\| v-\left( -\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^ks_i^k\right) \right\| ^2\right\} \\&= P_{C-x_k}\left( -\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^ks_i^k\right) . \end{aligned} \end{aligned}$$
(9)

Then, by applying (2) with \(D=C-x_k\), \(x = -\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^ks_i^k\) and \(y=z-x_k\), it follows that

$$\begin{aligned} \left\langle -\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^ks_i^k-v_k, z-x_k-v_k\right\rangle \le 0, \end{aligned}$$

which yields that

$$\begin{aligned} \begin{aligned} \langle v_k, x_{k}-z\rangle&\le -\Vert v_k\Vert ^2+\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\langle s_i^k, z-x_k\rangle -\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\langle s_i^k, v_k\rangle \\&\le \frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\langle s_i^k, z-x_k\rangle +\frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\Vert s_i^k\Vert \Vert v_k\Vert \\&\le \frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\langle s_i^k, z-x_k\rangle +\alpha _k\Vert v_k\Vert \\&\le \frac{\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k\langle s_i^k, z-x_k\rangle +2\alpha _k^2, \end{aligned} \end{aligned}$$
(10)

where the third inequality holds by the fact that \(\sum _{i\in I_k}\lambda _i^k\Vert s_i^k\Vert \le \eta _k\) and the last inequality holds by Lemma 4.1. Consequently, by combining (8) and (10), also note that \(\gamma _k\in (0,1]\), we obtain the desired result. \(\square \)

In order to prove the convergence of the sequence \(\{x_k\}\) produced by our algorithm, we will assume the following condition.

A1. The set \(T := \{z\in C: F(z)\preceq F(x_k), \forall \,k\in \mathbb {N}\}\) is nonempty.

This assumption is related to the completeness of the image of F, namely, all nonincreasing sequences with respect to \(\preceq \) in the image of F have a lower bound. It is important to point out that completeness is a standard assumption for ensuring the existence of Pareto optimal points for vector optimization problems [24]. Furthermore, this condition is standard in the analysis of extensions of classical methods to vector optimization, such as the projected gradient method [2, 3, 5, 6, 9, 17, 18], steepest descent method [4] and proximal point method [8, 27, 28].

Proposition 4.3

Assume that A1 holds. Then the sequence \(\{x_k\}\) is quasi-Fejér convergent to T and bounded.

Proof

Let \(z\in T\). Then, we have that for each \(k\in \mathbb {N}\),

$$\begin{aligned} f_i(z)-f_i(x_k) \le 0, \quad \forall \,i\in I_k. \end{aligned}$$
(11)

Since \(s_i^k\in \partial ^{\le }f_i(x_k)\), it holds by definition that

$$\begin{aligned} \langle s_i^k, z-x_k\rangle \le f_i(z)-f_i(x_k), \quad \forall \,i\in I_k. \end{aligned}$$
(12)

From (12) and Proposition 4.2, we obtain

$$\begin{aligned} \Vert x_{k+1}-z\Vert ^2 \le \Vert x_{k}-z\Vert ^2+8\alpha _k^2+2\frac{\gamma _k\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k(f_i(z)-f_i(x_k)). \end{aligned}$$
(13)

Combining this with (11) yields that

$$\begin{aligned} \Vert x_{k+1}-z\Vert ^2\le \Vert x_{k}-z\Vert ^2+8\alpha _k^2. \end{aligned}$$

Then, by (4) and Definition 2.4 with \(\epsilon _k = 8\alpha _k^2\), we conclude that the sequence \(\{x_k\}\) is quasi-Fejér convergent to T. The boundedness of \(\{x_k\}\) follows from Proposition 2.3. \(\square \)

To conclude that the sequence converges to a Pareto optimal point for (1), we need the following requirement.

A2. Assume, there exists a number \({\underline{\lambda }} > 0\) such that for each \(z \in T\), it holds

$$\begin{aligned} i_k {:=} \mathop {{\text {argmax}}}_{i=1,2,\cdots ,m}\{f_i(x_k)-f_i(z)\}\in I_k\quad \text {and}\quad \lambda _{i_k}^k\ge {\underline{\lambda }}\, ,\quad \forall \, k\in \mathbb {N}. \end{aligned}$$
(14)

From the algorithm’s construction, it is clear that such a constant \({\underline{\lambda }}\) always lies in (0, 1). Now, we present the main convergence result.

Theorem 4.1

Assume that A1 and A2 hold. Then the sequence \(\{x_k\}\) converges to a Pareto efficient solution of the problem (1).

Proof

First, we show that \(\{x_k\}\) converges to some \(x^*\in T\). Take \(z\in T\). Note that \(\eta _k\le L\) for all \(k\in \mathbb {N}\). Then, by using the inequality (13), one has

$$\begin{aligned} \begin{aligned} \frac{2\gamma _k\alpha _k}{L}\sum _{i\in I_k}\lambda _i^k(f_i(x_k)-f_i(z))&\le \frac{2\gamma _k\alpha _k}{\eta _k}\sum _{i\in I_k}\lambda _i^k(f_i(x_k)-f_i(z))\\&\le \Vert x_{k}-z\Vert ^2-\Vert x_{k+1}-z\Vert ^2+8\alpha _k^2. \end{aligned} \end{aligned}$$
(15)

Summing (15) with k between 0 and N, we get

$$\begin{aligned} \begin{aligned} \frac{2}{L} \sum _{k=0}^N\gamma _k\alpha _k\left[ \sum _{i\in I_k}\lambda _i^k(f_i(x_k)-f_i(z))\right]&\le \Vert x_{0}-z\Vert ^2-\Vert x_{N+1}-z\Vert ^2+8\sum _{k=0}^N\alpha _k^2\\&\le \Vert x_{0}-z\Vert ^2+8\sum _{k=0}^\infty \alpha _k^2. \end{aligned} \end{aligned}$$

Letting N go to \(+\infty \) and noting (4), it follows that

$$\begin{aligned} \liminf _{k\rightarrow +\infty }\sum _{i\in I_k}\lambda _i^k(f_i(x_k)-f_i(z))\le 0. \end{aligned}$$

Furthermore, owing to the fact that \(z\in T\) and the definition of \(i_k\) in (14), we have

$$\begin{aligned} \begin{aligned} 0&\le \liminf _{k\rightarrow +\infty }\lambda _{i_k}^k\max _{i=1,2,\cdots ,m}\{f_i(x_k)-f_i(z)\}=\liminf _{k\rightarrow +\infty }\lambda _{i_k}^k(f_{i_k}(x_k)-f_{i_k}(z))\\&\le \liminf _{k\rightarrow +\infty }\sum _{i\in I_k}\lambda _i^k(f_i(x_k)-f_i(z)) \le 0, \end{aligned} \end{aligned}$$

and thus

$$\begin{aligned} \liminf _{k\rightarrow +\infty }\lambda _{i_k}^k\max _{i=1,2,\cdots ,m}\{f_i(x_k)-f_i(z)\} = 0. \end{aligned}$$
(16)

As \(\lambda _{i_k}^k \ge {\underline{\lambda }}\) for each \(k\in \mathbb {N}\), (16) implies that

$$\begin{aligned} \liminf _{k\rightarrow +\infty }\max _{i=1,2,\cdots ,m}\{f_i(x_k)-f_i(z)\} = 0. \end{aligned}$$

Then, one can take a subsequence \(\{x_{k_j}\}\) of \(\{x_k\}\) such that

$$\begin{aligned} \liminf _{k\rightarrow +\infty }\max _{i=1,2,\cdots ,m}\{f_i(x_{k_j})-f_i(z)\} = 0. \end{aligned}$$
(17)

Since \(\{x_k\}\) belongs to C and is bounded by Proposition 4.1 and Proposition 4.3, we may assume that there exists \(x^*\in C\) such that \(\lim _{j\rightarrow +\infty }x_{k_j}=x^*\). Then, by the continuity of the maximal function, we have from (17) that

$$\begin{aligned} \max _{i=1,2,\cdots ,m}\{f_i(x^*)-f_i(z)\} = 0. \end{aligned}$$

Consequently, \(F(x^*)=F(z)\) because \(z\in T\), and so \(x^*\in T\). By applying Proposition 4.3 and Proposition 2.3, one gets that \(\{x_k\}\) converges to \(x^*\in T\). Moreover, from z being arbitrary, we get

$$\begin{aligned} F(x^*) = F(y),\quad \text {for all }y\in T. \end{aligned}$$
(18)

Now, we show that \(x^*\) is a Pareto efficient solution of (1). In fact, if there exists \(y\in C\) such that

$$\begin{aligned} f_i(y)\le f_i(x^*),\quad i=1,2,\cdots ,m, \quad i\ne j, \quad f_j(y)< f_j(x^*), \end{aligned}$$

then \(y\in T\), thus yielding a contradiction to (18). The desired result is proved. \(\square \)

Note that in the special case when \(I_k=\{1,2,\cdots ,m\}\) for all \(k\in \mathbb {N}\), then for each \(z\in T\), the condition \(i_k\in I_k\) in A2 holds automatically. With that in mind, we can think of another condition that is weaker than A2.

A2\(^-\). Let \(I_k=\{1,2,\cdots ,m\}\) for any \(k\in \mathbb {N}\) and assume, there exists a number \({\underline{\lambda }} > 0\) such that for each \(z\in T\), it holds

$$\begin{aligned} \lambda _{i_k}^k\ge {\underline{\lambda }}\quad \text {with}\quad i_k := \mathop {{\text {argmax}}}_{i=1,2,\cdots ,m}\{f_i(x_k)-f_i(z)\} \, ,\quad \forall \, k\in \mathbb {N}. \end{aligned}$$

As illustrated before, such a constant \(\underline{\lambda }\) is in the interval (0, 1). Then, one can obtain directly from Theorem 4.1 the following result, which improves the ones in [5, Theorem 2] and [6, Theorem 3.2] in twofold: (i) Corollary 4.1 extends the results in [5, 6] from the convex case to the qusiconvex case; (ii) the condition \(\lambda _{i}^k\ge {\underline{\lambda }}\), for all \(i=1,2,\cdots ,m\), that is required in [5, 6] is weakened to \(\lambda _{i_k}^k\ge {\underline{\lambda }}\) as stated in A2\(^-\).

Corollary 4.1

Assume that A1 and A2\(^-\) hold. Then the sequence \(\{x_k\}\) converges to a Pareto efficient solution of the problem (1).

5 Numerical Results

In this section, we illustrate the functionality of the proposed method by means of several small-scale examples. Note that Condition A2 is a rather weak one introduced in the theoretical proof to ensure that the sequence generated by the algorithm converges to an efficient solution. It may, however, not be easy to ensure the validity of A2 beforehand. So, in the actual implementation of the algorithm, one can still adopt the relatively strong but easy to operate parameter setting that the weights are always bounded from below by a positive constant, specifically, \(I_k=\{1,2,\cdots ,m\}\) for any \(k\in \mathbb {N}\) and \(\lambda _{i}^k\ge {\underline{\lambda }}>0\) for each \(i\in I_k\). It is seen that, if additionally the weight values \(\lambda _i^k\) are kept constant, the multiobjective optimization problem is then transformed into a scalar one.

We use the first exampleFootnote 1 to illustrate Algorithm 3.1’s parameters and the assumptions in the main convergence result Theorem 4.1.

Example 5.1

Consider the objective function \(F :\mathbb {R}\rightarrow \mathbb {R}^2\) given by

$$\begin{aligned} F = (f_1, f_2) = \begin{pmatrix} \exp (-x)\\ x^2 \end{pmatrix} \qquad \text {and}\qquad C = \mathbb {R}. \end{aligned}$$

This problem is strictly convex and continuously differentiable. The set of Pareto optimal points is given by \(\lbrace x \in \mathbb {R}: 0 \le x \rbrace \), and the Plastria subdifferentials of \(f_1\) and \(f_2\) can be derived from the classical derivatives

$$\begin{aligned} \partial ^{\le } f_1 (x)&= \lbrace s \in \mathbb {R}: s \le \tfrac{\mathrm {d}f_1(z)}{\mathrm {d}z}\vert _{z=x}\rbrace = {(}-\infty , -\exp (-x){]}, \\ \partial ^{\le } f_2 (x)&= \lbrace s \in \mathbb {R}: |s |\ge \tfrac{\mathrm {d}f_2(z)}{\mathrm {d}z}\vert _{z=x}, {\text {sgn}}s = {\text {sgn}} x\rbrace = \lbrace M \cdot x, M \ge 2 \rbrace . \end{aligned}$$

Both components of F are not Lipschitz continuous. However, on any subinterval of the real line that is bounded from below, a Lipschitz constant \(L_1\) for \(f_1\) can be determined and \(f_2\) is Lipschitz continuous on any bounded domain. For the sake of simplicity, we will use \(L_1 = 1\) in the following, meaning that we use \(-1 \in \partial ^{\le }f_1(x_k)\) when the subdifferential (at \(x_k \ge 0\)) is needed.

Theorem 4.1 states that the iterates of Algorithm 3.1 converge toward a Pareto efficient solution provided that Assumptions A1 and A2 are fulfilled. To make this implication more clear, we will consider algorithmic parameters that violate them.

We consider the choice

$$\begin{aligned} \forall k:~ I_k {:=} \lbrace 1 \rbrace \,, \end{aligned}$$

which is obviously not in accordance with A2 as it completely disregards the second component of F. The problem is not constrained, so the minimization of \(h_{x_k}(v)\) can be performed analytically. One obtains

$$\begin{aligned} \min _v h_{x_k}(v) = \min _v \frac{\alpha _k}{\eta _k}\left\langle \lambda _1^k \cdot s_1^k, v\right\rangle + \frac{\Vert v\Vert ^2}{2} \quad \Longrightarrow ~v_k = \alpha _k \,, \end{aligned}$$

where we used \(s_1^k =-1\), \(\lambda _1^k = 1\) and \(\eta _k = 1\) which follow from the above consideration of \(\partial ^{\le }f_1\) and the choice for \(I_k\) (tacitly assuming that \(x_k\) is sufficiently large. For this example, this is without loss of generality.) The iterates of Algorithm 3.1 therefore are explicitly given by

$$\begin{aligned} x_k = x_0 + \sum _{i=0}^{k-1} \gamma _k \cdot \alpha _k\,. \end{aligned}$$

Taking (4) into account, one sees the divergence of \(\{x_k\}\) as \(k \rightarrow \infty \).

To avoid that, next we choose the index set \(I_k = \lbrace 1,2\rbrace \) and modify A2 to

$$\begin{aligned} \exists \underline{\lambda }> 0: ~\forall k:\lambda _1^k,\lambda _2^k \ge \underline{\lambda }\,, \end{aligned}$$

which is yet slightly stronger than A2\(^-\). For a nonnegative starting value \(x_0\), the termination of the search direction \(v_k\) can be performed analytically. One obtains

$$\begin{aligned} v_k = \frac{\alpha _k}{\eta _k} \cdot \bigg (\underbrace{({\lambda _2^k}-1)}_{< 0}\cdot s_1^k -\underbrace{{\lambda _2^k}}_{\ge \underline{\lambda }} \cdot s_2^k \bigg ) \end{aligned}$$

with \(s_1^k \ge -L_1\), \(s_2^k \ge 2 \cdot x_k\), \(\tfrac{\alpha _k}{\eta _k} > 0\). One can see that, however, small \(\underline{\lambda }\) is, \(v_k\) becomes negative when \(x_k\) is sufficiently large. In this case, the sequence \(\{x_k\}\) no longer diverges but converges to a Pareto efficient point.

In an actual implementation, these shortcomings might not be relevant after all: As discussed above, a more practical stopping criterion is to exit the main loop whenever the performed steps of the algorithm are sufficiently small. In Fig. 3, we depict results for a numerical study of this example. The (constant) weight \(\lambda _1\) (x-axis) is varied from zero (corresponding to \(I_k = \lbrace 2 \rbrace \)) to one (as in the divergent example above), and \(\alpha _k = \tfrac{1}{k+1}\), \(\gamma _k = 1\), have been chosen. The initial value has been fixed to \(x_0=1\) and we depict the final iterates \(x^*\) of Algorithm 3.1 (point markers) and the total number of steps (bars). The iteration was stopped as soon as the step size reduced to below \(10^{-4}\). Even though the iterates diverge in exact arithmetic, this is not observed for the numerical approximation (which was computed in double precision) even though the number of steps (bar plot in Fig. 3) increases significantly. Note that the overall high iteration numbers for this experiment result from the poor parameter choice and rough representation \(\partial ^{\le }f_1 (x) \ni -1\) of the Plastria subdifferential.

Fig. 3
figure 3

Numerical results for Example 5.1: \(x^*\) (left y-axis, bullets in the plot) indicate the final iterates of Algorithm 3.1, the bars (right y-axis) show the number of iterations before the main loop terminates due to sufficiently small step lengths

Full size image

The next example was given by Bello Cruz et al. [3] as an counterexample to show that their method may fail when the pseudoconvexity for the quasiconvex objective functions required therein was dropped.

Example 5.2

Consider the quasiconvex multiobjective problem defined by

$$\begin{aligned} F=(f_1, f_2) :\mathbb {R}\rightarrow \mathbb {R}^2\quad \text { with }\quad f_1(x)=\frac{x^5}{5},\quad f_2(x)=\frac{x^3}{3}\quad \text {for all }\, x\in \mathbb {R}, \end{aligned}$$

and the constraint set \(C = [-1,1]\).

It can be verified that the set of stationary points of the problem is \(\{-1, 0\}\), and the set of Pareto efficient solutions (as well as the weak Pareto efficient solutions) is the singleton \(\{-1\}\). (In this academic example there are no conflicting goals involved.) Recall that a point \(x\in C\) is said to be a stationary point if

$$\begin{aligned} -\mathbb {R}^m_{++}\cap J_F(x)(C-x) = \emptyset , \end{aligned}$$

where \(J_F(x)\) is the Jacobian matrix of F at x. Note that in the general setting of the algorithm, the notion of a Jacobian matrix does not have to make sense since it requires some amount of smoothness of the objectives. Since the functions \(f_1\) and \(f_2\) in this example are not pseudoconvex, the authors showed in [3] that there are some cases in which the sequence \(\{x_k\}\) generated by the method proposed therein converges to 0 when starting at \(x_0\in [0, 1]\). Next, we will underline that our method (given some special algorithmic parameters) is feasible with any initial point in C.

1. In this example, we take \(\alpha _k = \frac{1}{k+1}\), \(I_k=\{1, 2\}\), \(\lambda _1^k=\lambda _2^k=\frac{1}{2}\), \(s_1^k=s_2^k=1\) (It can be computed by definition that \(1\in \partial ^{\le }f_i(x)\) for each \(i=1, 2\) and \(x\in C\), so we take these values in the procedure.) and \(\gamma _k=\frac{1}{2}\) for all \(k\in \mathbb {N}\).

First, we consider the case when the initial point \(x_0\in [-1, 0]\). Then, one can obtain by calculation that

$$\begin{aligned} x_k = \frac{1}{2^k}x_0-\frac{2^k-1}{2^k}, \quad \text {for all }\, k\in \mathbb {N}, \end{aligned}$$

and it is seen that \(x_k\) converges to \(-1\). If we consider the stopping criterion \(\Vert x_{k+1}-x_k\Vert <0.0001\), an easy calculation shows that at most \(k=14\) iterations are necessary for the algorithm to solve the problem. (In an actual implementation, the convergence is much faster.)

Now, consider the case when the initial point \(x_0\in (0, 1]\). Then, it can be computed that after \(k=3\) or \(k=4\) iterations, \(x_k\in [-1, 0)\). Consequently, \(x_k\) converges to \(-1\) as shown in the above situation.

2. To further illustrate, we used a MATLAB implementation of the algorithm with \(\gamma _k=0.95\), \(I_k = \{ 1,2\}\), \(\lambda _1^k = \lambda _2^k= \frac{1}{2}\), \(\alpha _k = \frac{1}{k+1}\) and solved the quadratic programming problems numerically using the routine ‘quadprog.m’ from the Optimization toolbox (interior point method). In Fig. 4, we compare Algorithm 3.1 with the projected gradient algorithm of [3] with comparable solver settings. The iteration limit was set to 200, the step tolerance to \(10^{-8}\) in both cases and the initial guesses were varied along the interval \([-1,1]\). The crosses marked as ‘no convergence’ indicate the cases when the projected gradient algorithm failed to converge to the actual solution within the iteration limit (92 out of 200 cases). As can be easily seen, Algorithm 3.1 clearly outperforms similar methods based on the classical gradient with no more than \(k = 8\) iterations to reach a reasonably good approximation and an average iteration count of 7.79 as opposed to the average of 16.92 iterations for the successful runs of the gradient-based method.

Fig. 4
figure 4

Numerical results for Example 5.2

Full size image

This behavior can even be amplified if instead of using a function with one stationary point, we change to one with multiple such ‘traps.’

Example 5.3

Consider the (for simplicity one-dimensional) objective function

$$\begin{aligned} f(x) = \frac{1}{\sqrt{2}} \cdot (x + \sin (x))\,,\quad C = {[0,\infty )}. \end{aligned}$$

If we use a similar setting as before with \(\gamma _k=0.99\) and \(\alpha _k = 5/(k+1)^{9/10}\), step size tolerance \(10^{-7}\) and iteration limit 500, we obtain the results displayed in Fig. 5. To solve the involved quadratic programs, we used IBM ILOG Cplex’s quadratic programming capabilities (i.e., the MATLAB routine cplexqp.m; note, however, that for this simple one-dimensional example, the projection can easily be performed without additional libraries) [22]. The initial guesses were randomly sampled as \(x_0 \in [25, 27]\). Of the 150 experiments, all were solved correctly by Algorithm 3.1 while none(!) of the runs of the gradient-based solvers reached the neighborhood of the Pareto optimal point \(E = \lbrace 0\rbrace \). The average number of iterations for Algorithm 3.1 was 9.447.

Fig. 5
figure 5

Numerical results for the function f in Example 5.3, left: objective; right: final solutions

Full size image

The examples provided so far are for illustrative purposes only and were chosen to underline the generality of Algorithm 3.1 and its convergence as stated in Theorem 4.1 (in particular when comparing to alternatives from the literature). They are not intended to illustrate Algorithm 3.1’s performance or to give a practical application case. In all three examples, a full characterization of the (weak) Pareto optimal points is analytically possible. This characterization can be achieved using methods as outlined, for example, in [14, 15] and details are provided in “Appendix” of this article. Actual numerical test cases will follow in the next two examples.

Now, we present Algorithm 3.1 when applied to a problem from facility location theory.

Example 5.4

Consider the problem of finding an optimal location of a building in the two-dimensional Euclidean plane. Optimality means that the weighted sum of (appropriately measured) distances to already existing facilities should be as small as possible. We use the simple mathematical model, [19]

$$\begin{aligned} f_1(x) = \sum _{i =1}^N \mu _i \cdot \left\Vert x - x_i^{\mathrm {E}}\right\Vert _{p_i} \end{aligned}$$

to implement this requirement, where N is the number of existing facilities, located at \((x_i^{\mathrm {E}})_{i=1}^N {\mathrel {\subseteq }\mathbb {R}^2}\), the weights \((\mu _i)_{i=1}^N {, \mu _i \ge 0\,\forall i}\), measure the importance of that facility and \(p_i \in [1,\infty ]\) gives a certain degree of freedom in modeling the distances. In the numerical example, we used \(N=7\) existing locations with coordinate values in \([-5,4]\) and varying weights between 1 and 2. The norms were partially Euclidean (\(p_i = 2\)), partially the Manhattan norm (\(p_i = 1\)) was inserted, which is very common in facility location problems.

When the weights are all positive (as in our case), the objective function \(f_1\) is convex. Therefore, we introduce a second objective that can measure, for example, the ‘merit distance’ to a hospital. Once a certain distance from that hospital is reached, it does not make a large difference anymore, whether the facility is placed yet further away or not. A quasiconvex function, that can model this is the Gaussian

$$\begin{aligned} f_2(x) = -\exp \left( -\left( \sum _{i=1}^2 \left( x_i - x_i^{\mathrm {H}}\right) ^2/a_i\right) \right) \,, \end{aligned}$$

where \(x=(x_1,x_2)\), \(x^{\mathrm {H}} = \left( x_1^{\mathrm {H}}, x_2^{\mathrm {H}}\right) \) is the position of the hospital and the additional parameters \(a_1, a_2\) give the modeler yet more freedom to fine-tune the model.

To derive the Plastria subdifferential to this function (that is \(f_2\)), the same heuristic as for the one-dimensional case (see Example 2.2) was used. For the first objective \(f_1\), the Plastria subdifferential is identical with the Moreau–Fenchel subdifferential and there are established ways to find elements thereof. In Fig. 6, the objective values of the facility location problem along a grid (\(x,y \in [-5,5]\)) are displayed as small markers. The larger markers indicate the final iterations of Algorithm 3.1 with \(\gamma _k = 0.9\), \(\alpha _k =\frac{1}{k+1}\) and 300 initial values drawn randomly from a normal distribution. We chose \(I_k = \lbrace 1,2 \rbrace \) and \(\lambda _1^k = \lambda _2^k = \tfrac{1}{2}\) for this experiment. The internal optimization problems were not solved by a specialized solver here as constraints were explicitly disregarded for this example. It is apparent how almost all solutions lie along the nonconvex Pareto front of the problem.

Fig. 6
figure 6

Objective space view for the facility location problem

Full size image

To further judge the performance, the optimization process (using the same initial points and comparable numerical settings) was repeated using the algorithm of Cruz Neto et al. [9] (which is similar to Algorithm 3.1 but disregards constraints and the regularization term in \(h_{x_k}(v)\)). The results are also displayed in Fig. 6. As can be seen, Algorithm 3.1 performs more robust for the given tolerances at this problem. However, the average number of iterations was approximately twelve percent higher (219 instead of 195) and for finer tolerances, both algorithms succeed to approximate the Pareto front reliably. Given the simple nature of the problem, it is obvious that both algorithms can easily be tuned to better performance by the use of, for example, improved line search strategies in a next step.

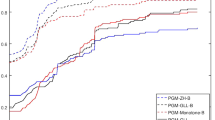
Finally, to illustrate the scalability of Algorithm 3.1, we give an example with varying parameters for the dimension n of the decisions variables, the dimension m of the objective space and the constraints imposed for the definition of the constraint set C.

Example 5.5

We consider again the negative Gaussian as in Examples 2.2 and 5.4. For this experiment (cf. Fig. 7), we used the full index set \(I_k = \lbrace 1, \ldots , m \rbrace \), \(k = 0,1,\ldots \), a value of \(\gamma _k = 0.99\), \(k = 0,1,\ldots \), and \(\alpha _k {:=} \tfrac{5 \cdot n}{k+1}\). The minimization of \(h_{x_k}\) was again carried out using Cplex (standard parameters) and the tolerances (in the projected subgradient method) were set to \(10^{-4}\). The maximum number of iterations was set to 9999 (but in all the optimization runs, this bound was only reached once). The weights \(\lambda _i^k\) were set such that \(\forall k:\, \lambda _1^k = \tfrac{1}{2}\) and the weights on all other objectives were equally distributed.

For the construction of F at given parameters \(n \in \lbrace 2,3,\ldots , 10 \rbrace \), \(m \in \lbrace 2,3,4\rbrace \) and an integer parameter \(p \in \lbrace 0, 2 \rbrace \), we proceeded 100 times as follows:

  1. 1.

    Choose a \(p \times n\) matrix \(A_=\) and a p-dimensional vector \(b_=\) at random and let

    $$\begin{aligned} C {:=} \left\{ x \in \mathbb {R}^n : \left( \forall i: -5 \le x_i \le 5 \right) \wedge \left( A_= \cdot x = b_=\right) \right\} . \end{aligned}$$
  2. 2.

    Choose an initial point \(x_0 \in C\) at random. (in Step 0 of Algorithm 3.1)

  3. 3.

    Define random offset values \(o^{(l)} \in [-5,5]^n\) and (nonlinear) weights \(a^{(l)} \in [5,15]^n\), \(l = 1, \ldots , m\), and set

    $$\begin{aligned} F(x) {:=} \begin{pmatrix} - \exp \left( -\sum _{i=1}^n \frac{x_i - o_i^1}{a_i^1} \right) \\ \vdots \\ - \exp \left( -\sum _{i=1}^n \frac{x_i - o_i^m}{a_i^m} \right) \end{pmatrix}\,. \end{aligned}$$

In Fig. 7, we display the mean number of iterations (dashed lines) and their medians (solid lines) over the varied dimension n of the decision variables x. The experiments were only carried out if \(p < n\) and \(m \le n-p\) was satisfied to ensure that non-Pareto elements of C exist.

A Pareto optimal element could always be found with a single exception for \(m=3\), \(p=0\) and the average number of steps is typically kept below 50, thereby underlining the competitive capacity of Algorithm 3.1.

Fig. 7
figure 7

Numerical results for Example 5.5, dashed lines indicate the average value of iterations, solid lines indicate their median, the disconnected dots (magenta in the online version) display the iteration numbers of every single experiment, the numbers ‘max. it.’ and ‘min. it.’ denote the maximal/minimal number of iterations over all displayed optimization runs in each subplot

Full size image

6 Conclusion and Outlook

In this work, we introduce a projected subgradient method to solve constrained multiobjective optimization problems, where the objective function is assumed to be componentwise essentially quasiconvex and Lipschitz continuous but not necessarily differentiable. Under reasonable assumptions, we show that for any initial point in the constraint set, the sequence produced by our method converges to a Pareto efficient solution of the problem. Analytical tools included the subdifferential calculus in the sense of Plastria and quasi-Fejér convergence. Numerical examples are presented to indicate the practical validity of our method.

As already indicated earlier, there are several possible extensions on the numerical side like the implementation of a penalty-based version to improve the algorithm’s behavior at the boundary of C or improving the stopping criteria of the method. So far, the Plastria subdifferential used was implemented as a deterministic function (always the same subdifferential for the same argument). As, by nature, the subdifferential is a set-valued mapping, extensions in this direction might also open new research directions as do possible extensions of the algorithm that include reusing previous values of the subdifferential (conjugated subdifferential methods or BFGS-type subgradient methods).

The extension of this type of algorithm to more general space is also of great significance, which needs to consider the subdifferential of quasiconvex function in such generalized space, for example the family of quasiconvex subdifferentials presented in [10]. Meanwhile, note that the boundedness property of the subdifferential plays a key role in ensuring the convergence of the algorithm. Therefore, in order to get the expected results in generalized spaces, one needs to explore the related properties of the involving subdifferential.

From the analytical viewpoint, we intend to analyze the rate of convergence of this type and other extended methods for multiobjective optimization problems as a next step.