A Nonmonotone Projected Gradient Method for Multiobjective Problems on Convex Sets

Abstract

In this work we consider an extension of the classical scalar-valued projected gradient method for multiobjective problems on convex sets. As in Fazzio et al. (Optim Lett 13:1365–1379, 2019) a parameter which controls the step length is considered and an updating rule based on the spectral gradient method from the scalar case is proposed. In the present paper, we consider an extension of the traditional nonmonotone approach of Grippo et al. (SIAM J Numer Anal 23:707–716, 1986) based on the maximum of some previous function values as suggested in Mita et al. (J Glob Optim 75:539–559, 2019) for unconstrained multiobjective optimization problems. We prove the accumulation points of sequences generated by the proposed algorithm, if they exist, are stationary points of the original problem. Numerical experiments are reported.

1 Introduction

We consider the multiobjective optimization problem (MOP) on convex sets of the form:

$$\begin{aligned} \text{ Minimize } F(x) \text{ s.t. } x \in C, \end{aligned}$$

(1)

where $F: \mathbb {R}^n \rightarrow \mathbb {R}^r, F(x)=(F_1(x), \cdots , F_r(x))$ is a continuously differentiable multiobjective function in $\mathbb {R}^n$ and $C \subset \mathbb {R}^n$ is a closed and convex set.

As a concept of optimality, we consider the notion proposed by Pareto in [1]. A feasible point is called Pareto optimum or efficient solution [1] if there is no $x \in C$ such that $F(x) \leqslant F(x^*)$ and $F(x) \ne F(x^*)$. A point $x^* \in C$ is said to be a weak Pareto optimum point or a weakly efficient solution if there is no $x \in C$ such that $F(x) < F(x^*)$.

The general procedure we study in this work is the well-known projected gradient method (PGM) for vector optimization studied previously in [2,3,4,5]. These iterative algorithms compute the search direction by solving a convex subproblem that depends on a fixed parameter $\beta >0$ and then they choose the stepsize on the search direction by using the Armijo line search. Thus, those methods share two essential features:

• they are all descent methods: the objective values decrease with each iteration (in the component-wise sense);

• the projected gradient search direction is computed by using a fixed parameter $\beta >0$ instead of an exogenous sequence $\{\beta _k\}$, $\beta _k >0$, as suggested in [6].

Monotone line search methods generate a sequence of feasible iterative points $\{x^k\}$ such that $F(x^{k+1}) < F(x^{k})$. Nonmonotone line search methods permit some growth in the values of the objective function, with the purpose of improving the speed of convergence.

In the present paper, we consider an extension of the earliest nonmonotone line search framework developed by Grippo, Lampariello and Lucidi (GLL) for Newton’s method, [7], in the scalar case. The nonmonotone line search developed in [7] is based on the maximum functional values of the scalar objective function f(x) on some previous iterates: for $r=1$, given $\sigma \in (0,1), M \geqslant 1$ and $d^k \in \mathbb {R}^n$ the step length $\alpha _k$ must satisfy

$$\begin{aligned} f(x^k + \alpha _k d^k) \leqslant M_k + \sigma \alpha _k \nabla f(x^k)^\top d^k, \end{aligned}$$

(2)

where $\displaystyle M_k= \max _{0 \leqslant j \leqslant m(k)} f(x^{k-j})$ and $m(k)=\min \{m(k-1)+1, M\}$.

Nonmonotone line searches were previously used in the context of multiobjective descent methods in [6, 8, 9]. In [8] the authors use nonmonotone line searches for unconstrained MOP. In [6] the authors present the global analysis of a nonmonotone PGM based on the nonmonotone scheme given in [10]. In [9] the authors propose two nonmonotone gradient algorithms for MOP with a convex objective function based on the nonmonotone line search given by [7].

In the present work, we consider the PGM with the max-type nonmonotone line search and we prove that, without convexity assumptions on the multiobjective function, the accumulation points of the sequences generated by the method are stationary for problem (1). Our convergence result expands the global convergence theorems proved in [2,3,4,5]. The major difference between the proposed algorithm and the algorithms in [2,3,4,5] is that the PGM defined in those works is implemented with an Armijo-like rule which means that the sequence of functional values decreases monotonously. Even though in [6] a nonmonotone PGM is considered, the main difference with this paper is that the nonmonotone strategy in [6] is given by the average value of a previous function, whereas in this work the nonmonotone search is based on the maximum of some previous functional values. We emphasize that we are not attempting to find, or somewhat characterize, the set of all Pareto optimal solutions, weak or otherwise.

It is well established in the literature of scalar problems that nonmonotone strategies combined with spectral gradient choices of the step length $\beta _k$ may accelerate the convergence process [11, 12]. Taking this into account, we propose to use a variable step length sequence $\{\beta _k\}$ to analyze the efficiency of the technique with some numerical experiments.

This paper is organized as follows. In Sect. 2 we define the implementable nonmonotone projected gradient method. In Sect. 3 we present the convergence analysis of the method. In Sect. 4 we propose a sequence $\{\beta _k\}$ for MOP based on the spectral gradient method. In Sect. 5 we present some numerical experiments. Conclusions and final remarks are given in Sect. 6.

Notation We denote: $\mathbb {N} = \{0, 1, 2, \cdots \}$, $\mathbb {R}_+ = \{ t \in \mathbb {R} \;|\; t \geqslant 0 \},$ $\mathbb {R}_{++} = \{t \in \mathbb {R} \;|\; t > 0 \},$ $\mathbb {R}^r_{++} = \mathbb {R}_{++} \times \cdots \times \mathbb {R}_{++}$, $\Vert \cdot \Vert \text{ an } \text{ arbitrary } \text{ vector } \text{ norm }.$ If x and y are two vectors of $\mathbb {R}^n$, we write $x \leqslant y$ if $x_i \leqslant y_i, i =1, \cdots , n,$ and $x < y$ if $x_i < y_i, i =1, \cdots , n,$ $v_i$ is the $i-$th component of the vector v. If $F: \mathbb {R}^n \rightarrow \mathbb {R}^m$, $F = (f_1, \cdots , f_m)$, JF(x) stands for the Jacobian matrix of F at x: JF(x) is a matrix in $\mathbb {R}^{m\times n}$ with entries $(JF(x))_{ij}= \frac{\partial f_i(x)}{\partial x_j}$. If $B \in \mathbb {R}^{n \times n}$ is a positive definite matrix, $\Vert B\Vert$ denotes the 2-norm of B. If $K = \{k_0, k_1, k_2, \cdots \}$ is an infinite subset of $\mathbb {N}$ ($k_{j+1}>k_j, \forall j$), we denote $\displaystyle \lim _{k \in K} x^k = \lim _{j \rightarrow \infty } x^{k_j}.$

2 The Nonmonotone Projected Gradient Method for MOP

For the multiobjective problem on the convex set C (1) we say that a point $x^* \in C$ is stationary if and only if

$$\begin{aligned} JF(x^*)(C-\left\{ x^*\right\} )\cap [-\mathbb {R}^r_{++}]=\varnothing , \end{aligned}$$

where $JF (x^*) (C-\left\{ x^*\right\} ): = \left\{ JF (x^*) (x - x^*): x \in C \right\}$ and $C-\left\{ x^*\right\} = \{u-x^* : u \in C \}$.

So $x^* \in C$ is stationary for F if, and only if, $\forall x \in C,$ $\displaystyle \max _{i=1,\cdots ,r}\{\nabla F_i (x^*)^\top (x-x^*)\} \geqslant 0.$

Stationarity is a necessary, but generally not a sufficient condition, for weak Pareto optimality. See [13].

In order to explain how the search direction is computed we define, for a given point $x \in \mathbb {R}^n$, the function $\varphi _x : \mathbb {R}^n \rightarrow \mathbb {R}$ by

$$\begin{aligned} \varphi _x(v) = \displaystyle \max _{i =1,\cdots ,r } \{\nabla F_i (x)^\top v\}. \end{aligned}$$

(3)

Then, we consider the following convex scalar-valued minimization problem

$$\begin{aligned} \displaystyle \min _{v \in C-\{x\}} \beta \varphi _x(v)+ \frac{\left\| v\right\| ^2}{2}, \end{aligned}$$

(4)

where $\beta >0$ is a parameter. This problem is well-defined and it has a unique optimal solution $v_{\beta }(x)$, which is called the projected gradient direction, see [4]. Therefore, $v_{\beta }(x)$ is given by

$$\begin{aligned} v_{\beta }(x)= \displaystyle \underset{v\in C-\left\{ x\right\} }{\arg \min } \beta \varphi _x(v)+ \frac{\left\| v\right\| ^2}{2}. \end{aligned}$$

(5)

Let us call $\theta _{\beta }(x)$ the optimal value of (4), that is to say,

$$\begin{aligned} \theta _{\beta }(x)= \beta \varphi _{x} (v_{\beta }(x)) +\frac{\left\| v_{\beta }(x)\right\| ^2}{2}. \end{aligned}$$

(6)

The following proposition characterizes stationary points of the multiobjective problem (1) in terms of $\theta _{\beta }(\cdot )$ and $v_{\beta }(\cdot )$. The proof follows from Proposition 3 in [5].

Proposition 1

Let $\beta >0, v_{\beta }: C \rightarrow \mathbb {R}^n$ and $\theta _{\beta }: C \rightarrow \mathbb {R}$ be given by (5) and (6). Then, the following statements hold.

• 1. $\theta _{\beta } (x) \leqslant 0$ for all $x \in C.$

• 2. The function $\theta _{\beta }(\cdot )$ is continuous.

• 3. The following conditions are equivalent:

  • (a) The point $x\in C$ is nonstationary.

  • (b) $\theta _{\beta } (x) <0$.

  • (c) $v_{\beta } (x)\ne 0$.

  In particular, x is stationary if and only if $\theta _{\beta } (x) = 0.$

The global convergence result given in Sect. 3 is based on the following properties of $v_{\beta }$ and $\theta _{\beta }$.

Proposition 2

Let $\beta >0, v_{\beta }: C \rightarrow \mathbb {R}^n$ and $\theta _{\beta }: C \rightarrow \mathbb {R}$ be given by (5) and (6). Then,

• 1. $\Vert v_{\beta }(x)\Vert ^2 \leqslant 2 |\theta _{\beta }(x)|$.

• 2. $\beta \varphi _x(v_{\beta }(x))\leqslant - |\theta _{\beta }(x)|$.

Proof

From the theory of convex analysis and optimization we know that, from (5), there exists $w(x) \in \mathbb {R}^r$ such that

$$\begin{aligned}&\displaystyle \sum _{i=1}^r w_i(x) =1, w_i(x) \geqslant 0 \text{ for } \text{ all } i=1, \cdots , r, \end{aligned}$$

(7)

$$\begin{aligned}&\displaystyle w_i(x)(\nabla F_i(x)^\top v_{\beta }(x) - \varphi _{x} (v_{\beta }(x))) =0 \text{ for } \text{ all } i=1, \cdots , r, \end{aligned}$$

(8)

$$\begin{aligned}&\bigg (\beta \sum _{i=1}^r w_i(x) \nabla F_i(x) +v_{\beta }(x)\bigg )^\top (v-v_{\beta }(x)) \geqslant 0 \text{ for } \text{ all } v \in C-\{x\}. \end{aligned}$$

(9)

Then, since (9) holds for all $v \in C-\{x\}$, by considering $v=0$ we conclude that

$$\begin{aligned} \bigg (\beta \sum _{i=1}^r w_i(x) \nabla F_i(x) +v_{\beta }(x)\bigg )^\top (-v_{\beta }(x)) \geqslant 0. \end{aligned}$$

Thus,

$$\begin{aligned} \Vert v_{\beta }(x)\Vert ^2 \leqslant -\beta \sum _{i=1}^r w_i(x) \nabla F_i(x)^\top v_{\beta }(x). \end{aligned}$$

(10)

Therefore, it follows from (7) and (8) that $\displaystyle \varphi _x(v_{\beta }(x)) =\sum \nolimits _{i=1}^r w_i(x) \nabla F_i(x)^\top v_{\beta }(x)$ and, by (10), we have that

$$\begin{aligned} \theta _{\beta }(x)= & {} \beta \sum _{i=1}^r w_i(x) \nabla F_i(x)^\top v_{\beta }(x) + \frac{\Vert v_{\beta }(x)\Vert ^2}{2} \leqslant -\Vert v_{\beta }(x)\Vert ^2 + \frac{\Vert v_{\beta }(x)\Vert ^2}{2}\\= & {} - \frac{\Vert v_{\beta }(x)\Vert ^2}{2}. \end{aligned}$$

Thus,

$$\begin{aligned} \Vert v_{\beta }(x)\Vert ^2 \leqslant 2 |\theta _{\beta }(x)|, \end{aligned}$$

which proves 1.

Since $\theta _{\beta }(x) \leqslant 0$ we have that $|\theta _{\beta }(x)| = - \theta _{\beta }(x)$ and

$$\begin{aligned} \beta \varphi _x(v_{\beta }(x)) + |\theta _{\beta }(x)| = \beta \varphi _x(v_{\beta }(x))- \theta _{\beta }(x) = - \frac{\Vert v_{\beta }(x)\Vert ^2}{2}. \end{aligned}$$

Therefore,

$$\begin{aligned} \beta \varphi _x(v_{\beta }(x))\leqslant - |\theta _{\beta }(x)| \end{aligned}$$

and the conclusion 2 holds

Observe that, for a nonstationary point $x \in C$ we get $\beta \varphi _{x} (v_{\beta }(x)) \leqslant -\frac{\left\| v_{\beta }(x)\right\| ^2}{2} < 0$, which implies that $J F (x) v_{\beta }(x) < 0$ and $v_{\beta }(x)$ is a descent direction for F at x. In a monotone line search method, the stepsize $\alpha _k >0$ is chosen so that $F(x^{k+1}) < F(x^k)$, as suggested in [2,3,4,5]. In a nonmonotone scheme an increase in the objective values can be allowed as done for PGM in [6] by using the nonmonotone line search based on the average of previous function values as proposed in [10].

In the present work we consider the nonmonotone line search framework developed by Grippo et al. [7] that is based on the maximum functional value on some previous iterates. Given $\sigma \in (0,1), M \geqslant 1$ and the search direction $v_{\beta _k}(x^k)$, for each $i =1, \cdots ,r$ we set

$$\begin{aligned} A_i^k = \max \{F_i(x^{k-j}): 0 \leqslant j \leqslant m(k)\}, \end{aligned}$$

(11)

where $m(k)= \min \{k, M\}$. Then, the step $\alpha _k$ must satisfy the inequality (in the component-wise sense)

$$\begin{aligned} \displaystyle F(x^k+\alpha _k v_{\beta _k}(x^k))\leqslant A^k+\sigma \alpha _k JF(x^k) v_{\beta _k}(x^k), \end{aligned}$$

(12)

where $A^k = (A_1^k, \cdots , A_r^k)^\top \in \mathbb {R}^r$.

We can now define an extension of the classical PGM using the nonmonotone line search technique (12) for the constrained MOP (1).

Algorithm 1

(PGM-GLL) Choose $\sigma \in (0,1)$, $M > 0$, $0<\beta _{\min }< \beta _{\max }< \infty$ and $\beta _0 \in \left[ \beta _{\min }, \beta _{\max }\right]$. Let $x^0\in C$ be an arbitrary starting point. Set $k=0.$

Step 1:

Compute the search direction.

$$\begin{aligned} v_{\beta _k}(x^k):=\displaystyle \underset{v \in C-\{x^k\}}{\arg \min } \beta _k\varphi _{x^k}(v)+ \frac{\left\| v\right\| ^2}{2 }. \end{aligned}$$

(13)

Step 2:

Stopping criterion. Compute $\theta _{\beta _k}(x^k) = \beta _k \varphi _{x^k} (v_{\beta _k}(x^k)) +\frac{1}{2}\left\| v_{\beta _k}(x^k)\right\| ^2.$ If $\theta _{\beta _k}(x^k)=0,$ then stop.

Step 3:

Compute the step length. Let $m(k)= \min \{k, M\}$ and choose $\alpha _k$ as the largest $\alpha \in \left\{ \frac{1}{2^j}: j = 0, 1, 2, \cdots , \right\}$ such that (12) holds where $A^k = (A_1^k, \cdots , A_r^k)^\top \in \mathbb {R}^r$ and $A^k_i$ is given by (11).

Step 4:

Set $x^{k+1}=x^k+\alpha _k v_{\beta _k}(x^k).$ Define $\beta _{k+1}$ such that $\beta _{k+1} \in \left[ \beta _{\min }, \beta _{\max }\right]$. Set $k=k+1$, and return to Step 1.

Observe that Algorithm 1 stops at a feasible stationary point of (1) or it generates an infinite sequence $\{x^k\}$ of nonstationary points.

3 Convergence Analysis

In this section we suppose that Algorithm 1 does not have a finite termination and therefore it generates infinite sequences $\{x^k\}, \{v_{\beta _k}(x^k)\}$ and $\{\alpha _k\}$.

Lemma 1

For each k, $F(x^k)\leqslant A^k.$

Proof

It follows easily from the definition of $A^k$, see Lemma 5 in [8].

Lemma 2

Algorithm 1 is well defined: If $x^k$ is not a stationary point, then there exists a stepsize $\alpha _k >0$ satisfying condition (12).

Proof

Since $x^k$ is nonstationary we have that $\theta _{\beta _k}(x^k) <0$ and $JF(x^k) v_{\beta _k}(x^k) <0$. Then, by Proposition 1 in [5] there exists a stepsize $\alpha _k >0$ satisfying the Armijo condition:

$$\begin{aligned} \displaystyle F(x^k+\alpha _k v_{\beta _k}(x^k))\leqslant F(x^k) +\sigma \alpha _k JF(x^k) v_{\beta _k}(x^k). \end{aligned}$$

Then, by Lemma 1 the inequality (12) holds and the proof is complete.

Lemma 3

The scalar sequence $\{\Vert v_{\beta _k}(x^k)\Vert \}$ is bounded.

Proof

See Lemma 3 in [6].

Proposition 3

Let $\{x^k\} \subset \mathbb {R}^n$ be a sequence generated by Algorithm 1 and K an infinite subset of $\mathbb {N}, \beta ^*> 0, x^* \in C$ such that $\displaystyle \lim _{k \in K} x^k = x^*, \lim _{k \in K} \beta _k = \beta ^*$. Then, there exists $K^*$ an infinite subset of K such that

$$\begin{aligned} \lim _{k \in K^*} \theta _{\beta _k}(x^k) =\theta _{\beta ^*}(x^*). \end{aligned}$$

(14)

Proof

See Proposition 1 in [6].

Proposition 4

Let $\{x^k\} \subset \mathbb {R}^n$ be a sequence generated by Algorithm 1. Then

$$\begin{aligned} \displaystyle \lim _{k \rightarrow \infty } \alpha _k |\theta _{\beta _k}(x^k)| =0. \end{aligned}$$

Proof

Follows from the proof of Lemma 8 in [8] and the fact that inequalities 1. and 2. of Proposition 2 hold for the search direction sequence $\{v_{\beta _k}(x^k)\}$.

The following theorem is the main result of this section: the global convergence of Algorithm 1.

Theorem 1

Let $\{x^k\} \subset \mathbb {R}^n$ be a sequence generated by Algorithm 1. Then, every accumulation point of $\{x^k\}$ is a feasible stationary point of (1).

Proof

Let $x^* \in \mathbb {R}^n$ be an accumulation point of $\{x^k\}$. Then, there exists an infinite subset K of $\mathbb {N}$ such that $\displaystyle \lim _{k \in K} x^k = x^*$. The feasibility of $x^*$ follows combining the fact that C is closed with $x^k \in C$ for all k. The sequence $\{\beta _k\}$ is bounded, then there exists $K_0 \subset K$ and $\beta ^* > 0$ such that $\displaystyle \lim _{k \in K_0} \beta _k = \beta ^*$.

By Proposition 4 we have the following two cases: $\mathrm{(a)} \displaystyle \lim _{k \in K_0} |\theta _{\beta _k}(x^k)| =0$, or $\mathrm{(b)} \displaystyle \lim _{k \in K_0} \alpha _k =0.$

In the first case, by Proposition 3 we obtain that $\theta _{\beta ^*}(x^*) =0$ which proves that $x^*$ is a stationary point.

Now we assume that (b) holds. Due to Lemma 3, there exist an infinite subset $K_1, K_1 \subset K_0$ and $v^* \in \mathbb {R}^n$ such that $\displaystyle \lim _{k \in K_1} v_{\beta _k} (x^k) = v^*$ and $\displaystyle \lim _{k \in K_1} \alpha _k =0$. Note that we have

$$\begin{aligned} \displaystyle \max _{i=1,\cdots , r}\{\beta _k \nabla F_i(x^k)^\top v_{\beta _k} (x^k)\} \leqslant \theta _{\beta _k}(x^k)< 0. \end{aligned}$$

So, letting $k \in K_1$ go to infinity we get

$$\begin{aligned} \displaystyle \max _{i=1,\cdots , r}\{\beta ^*\nabla F_i(x^*)^\top v^*\} \leqslant 0. \end{aligned}$$

(15)

Take now a fixed but arbitrary positive integer q. Since $\displaystyle \lim _{k\in K_1} \alpha _k = 0$, for $k \in K_1$ is large enough, we have $\alpha _k < \frac{1}{2^q}$, which means that the nonmonotone condition in Step 3 of Algorithm 1 is not satisfied for $\alpha = \frac{1}{2^q}$ at $x^k$:

$$\begin{aligned} \displaystyle F(x^k+ \frac{1}{2^q} v_{\beta _k}(x^k))\nleqslant A^k+\sigma \frac{1}{2^q}JF(x^k)^\top v_{\beta _k}(x^k), \end{aligned}$$

so for each $k \in K_1$ large enough there exists $i = i(k) \in \{1,\cdots , r\}$ such that

$$\begin{aligned} \displaystyle F_i(x^k+ \frac{1}{2^q} v_{\beta _k}(x^k)) > A_i^k+\sigma \frac{1}{2^q} \nabla F_i(x^k)^\top v_{\beta _k}(x^k). \end{aligned}$$

Since $\{i(k)\}_{k \in K_1} \subset \{1,\cdots , r\}$, there exist an infinite subset $K_2, K_2 \subset K_1$ and an index $i_0$ such that $i_0 = i(k)$ for all $k \in K_2$,

$$\begin{aligned} \displaystyle F_{i_0}(x^k+ \frac{1}{2^q} v_{\beta _k}(x^k)) > A_{i_0}^k+\sigma \frac{1}{2^q} \nabla F_{i_0}(x^k)^\top v_{\beta _k}(x^k) \end{aligned}$$

and, by Lemma 1 we obtain that

$$\begin{aligned} \displaystyle F_{i_0}(x^k+ \frac{1}{2^q} v_{\beta _k}(x^k))\geqslant F_{i_0}(x^k)+\sigma \frac{1}{2^q} \nabla F_{i_0}(x^k)^\top v_{\beta _k}(x^k). \end{aligned}$$

Taking the limit when $k \in K_2$ goes to infinity in the above inequality, we obtain $F_{i_0} (x^* + 1/2^q v^*) \geqslant F_{i_0} (x^*) + \sigma 1/2^q \nabla F_{i_0} (x^*)^\top v^*$. Since this inequality holds for any positive integer q and for $i_0$ (depending on q), by Proposition 1 in [5] it follows that $JF (x^*)v^* \nless 0$, then $\displaystyle \max _{i=1,\cdots , r} \{\nabla F_i (x^*)^\top v^*\} \geqslant 0$, which, together with (15) implies $\theta _{\beta ^*} (x^*) = 0$. Therefore, we conclude that $x^*$ is a stationary point of (1).

Observe that, if we assume that the mapping $F:\mathbb {R}^n \rightarrow \mathbb {R}^r$ is $\mathbb {R}^r$-convex:

$$\begin{aligned} F(\lambda x + (1 - \lambda )z)\leqslant \lambda F(x) + (1 - \lambda )F(z) \end{aligned}$$

for all $x, z \in \mathbb {R}^n$ and all $\lambda \in [0, 1]$, by using Theorem 3.1 in [14] we can guarantee that every accumulation point is a weak Pareto point:

Corollary 1

Assume that $F : \mathbb {R}^n \rightarrow \mathbb {R}^r$ is $\mathbb {R}^r$-convex and let $\{x^k\} \subset \mathbb {R}^n$ be a sequence generated by Algorithm 1. Then, every accumulation point of $\{x^k\}$ is a weak Pareto optimal solution of (1).

4 The Sequence $\beta _k$

The global convergence analysis of the previous section is independent of the choice of $\beta _k$, always between $\beta _{\min }$ and $\beta _{\max }$. In this section we propose a way to choose $\beta _k$ inspired in the spectral PGM for the scalar case.

We observe that problem (4) is similar to the quadratic subproblem used in [12] to compute the search direction. In [12], in order to solve the constrained scalar problem Minimize f(x) subject to $x\in C$ where $f:\mathbb {R}^n\rightarrow \mathbb {R}$ is a continuously differentiable scalar function in $\mathbb {R}^n$ and $C\subseteq \mathbb {R}^n$ is a closed and convex set, the authors suggest computing the search direction by solving the quadratic problem

$$\begin{aligned} \hbox {Minimize }Q_k(d)\hbox { s.t. } x^k+d\in C , \end{aligned}$$

(16)

where $Q_k(d)=\frac{1}{2}d^\top B_kd+\nabla f\left( x^k\right) ^\top d$ and $B_k\in \mathbb {R}^{n\times n}$ is a positive definite matrix such that $\left\| B_k \right\| \leqslant L$ and $\left\| B_k^{-1} \right\| \leqslant L$ for a fixed scalar $L>0$. In fact, they consider the particular case: $B_k=\frac{1}{\lambda _k^{spg}}I$, where $\lambda _k^{spg}$ is the spectral gradient choice defined by

$$\begin{aligned} \lambda _k^{spg}={\left\{ \begin{array}{ll} \min \left\{ \lambda _{\max } , \max \left\{ \lambda _{\min } ,\frac{s_k^\top s_k}{y_k^\top s_k} \right\} \right\} , &{} \text{ if } y_k^\top s_k>0,\\ \lambda _{\max }, &{} \hbox {otherwise,} \end{array}\right. } \end{aligned}$$

where $s_k=x^k-x^{k-1}$ and $y_k=\nabla f\left( x^k\right) -\nabla f\left( x^{k-1}\right)$.

Firstly, we observe that, by comparing problems (4) and (16) we have that the stationarity condition $\theta _{\beta }(x)=0$ for (1) still holds if we consider

$$\begin{aligned} v_{\beta }(x):= \underset{v\in C-\left\{ x\right\} }{\arg \min } \varphi _x (v) + \frac{\left\| v \right\| ^2}{2 \beta } \end{aligned}$$

and $\theta _{\beta }(x):=\varphi _x \left( v_{\beta }(x)\right) ) + \frac{\left\| v_{\beta }(x) \right\| ^2}{2 \beta }$, for any $\beta >0$.

Secondly, we observe that, if $r=1$ then $s_k^\top y_k=s_k^\top \left( \nabla f\left( x^k\right) -\nabla f\left( x^{k-1}\right) \right) =\varphi _{x^k} \left( s_k\right) -\varphi _{x^{k-1}} \left( s_k\right)$. Finally, the previous analysis allows us to consider, in the multiobjective case, a sequence of parameters $\left\{ \beta _k\right\}$ defined as follows

$$\begin{aligned} \beta _k={\left\{ \begin{array}{ll} \min \left\{ \beta _{\max } , \max \left\{ \beta _{\min } ,\frac{s_k^\top s_k}{\varphi _{x^k} \left( s_k\right) -\varphi _{x^{k-1}} \left( s_k\right) } \right\} \right\} , &{} \text{ if } \varphi _{x^k} \left( s_k\right) -\varphi _{x^{k-1}} \left( s_k\right) >0;\\ \beta _{\max }, &{} \hbox {otherwise.} \end{array}\right. } \end{aligned}$$

Therefore, we have an interesting sequence of parameters $\left\{ \beta _k \right\}$ that deserves to be analysed from the practical point of view.

5 Numerical Experiments

In order to exhibit the behavior of the algorithm, we have examined a set of problems taken from the literature [14,15,16,17,18,19,20,21]. All of these problems are box-constrained and the details are presented in Table 1. For each problem we have considered 10 starting points. These points were obtained using random points which belong to the feasible region of each problem. The algorithm has been coded in Python 3.0 and the subproblem (4) was solved with the SLSQP solver [22] included as part of SciPy [23]. The code has been executed on a personal computer with an INTEL core i5-7400 3.00 GHz Processor, 8 GB of RAM and Linux Mint 18.3 operating system.

To carry out an in-depth analysis of our method, we have considered two related algorithms: the one proposed in [6] (PGM-ZH) and the monotone line search version of Algorithm 1 (called PGM-monotone), i.e. Algorithm 1 with the Armijo line search in Step 3.

For each of these algorithms, we have presented a version A with $\beta _k=1$ for all k and a version B where $\beta _k$ has been updated according to the analysis made in Sect. 4.

Table 1 List of test problems

We have established the maximum number of iterations as $maxiter =$ 1 000 and the stopping criterion was $\left| \theta _{\beta _k}(x^k) \right| \leqslant \epsilon = 10^{-6}$. A numerical experiment has previously been carried out in order to choose algorithm-specific parameters such as $\eta$ and M and the line search parameter $\sigma$. In this numerical test, all problems have been tested taking into account 10 initial points to combine all the values of $\sigma =10^{-1},10^{-2},10^{-3},10^{-4}$, $M=5,10,15,20$ and $\eta =0.8,0.85,0.9$. Furthermore, this test has shown that the monotone line search method was the worst-performing method in the sense that for many points it did not converge to several initial points. Then, we have fixed the parameter $\sigma$ in order to obtain the greatest number of starting points convergent to $\sigma =10^{-2}$. Using the same numerical test, we have considered the number of iterations needed to establish convergence of each of the values of $\eta$ and we have observed that $\eta =0.8$ worked better for the method when $\beta _k$ is fixed and updated according to Sect. 4. Finally, for the M parameter of the GLL line search, we have obtained that $M = 15$ was a better option for $\beta _k$ when fixed and $M = 10$ for $\beta _k$ when updated following Sect. 4. For these reasons, these values have been used for each case and the bounds of the sequence $\left\{ \beta _k\right\}$ have been set in $\beta _{\min }=\beta _{\max }^{-1}=10^{-6}$.

For the purpose of evaluating the performance of these algorithms, in Fig. 1 we have compared the algorithms by using a performance profile for the number of iterations for achieving convergence, according to the method proposed in [24]. We have denoted the set of solvers as $\mathcal {S}$ and the set of problems as $\mathcal {P}$. Furthermore, $it_{p,s}$ denotes the number of iterations used by the solver s to solve problem p, the best $it_{p,s}$ for each p as $it^\star _p=\min \left\{ it_{p,s} : \ s\in \mathcal {S} \right\}$. The distribution function $F_{\mathcal {S}} (it)$ for a method s is defined by

$$\begin{aligned} F_{\mathcal {S}}(it)=\frac{\left| \left\{ p\in \mathcal {P} : \ it_{p,s}\leqslant it^\star _p\right\} \right| }{\left| \mathcal {P} \right| }. \end{aligned}$$

To present the results more precisely, we have used a semilogarithmic scale in Fig. 1.

Fig. 1

Performance profiles for projected gradient algorithms with different line search by using the number of iterations as a comparison measurement

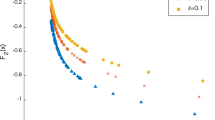
Due that line searches increase the number of function evaluations, which could be a drawback for these algorithms, we also consider a performance profiles for function evaluations in Fig. 2. This second figure presents performance profiles for function evaluations using a semi logarithmic scale too and shows that the performances measured in number of function evaluations and iterations are similar.

We can observe that nonmonotone line searches are faster than monotone ones and use less function evaluations and iterations. The algorithm considering the average line search outperforms the other line searches, at least in our test problems. Also, it is clear the relevance of the use of the sequence $\left\{ \beta _k \right\}$ defined in Sect. 4 as follows: The performance of all algorithms has been improved using the sequence or parameters $\left\{ \beta _k \right\}$. In particular, the PGM-ZH Algorithm was the worst-performing algorithm when $\beta _k$ is fixed, whereas it becomes the best-performing one when $\beta _k$ is updated according to Sect. 4.

Fig. 2

Performance profiles for projected gradient algorithms with different line search by using the number of function evaluations as a comparison measurement

As we have already mentioned in the introduction, we are not attempting to find the set of all Pareto or weak Pareto points. Nevertheless, for the sake of completeness, we have also taken into account some metrics used for evaluating the accuracy in approximation of Pareto fronts. If x is an efficient solution (weakly efficient), then F(x) is a nondominated (weakly non-dominated) point. Let $F_{p,s}$ denote the approximated nondominated front determined by the solver $s\in \mathcal {S}$ for problem $p\in \mathcal {P}$. Let also $F_p$ denote an approximation to the exact nondominated front of problem p, calculated by first forming $\displaystyle \cup _{s\in \mathcal {S}} F_{p,s}$ and then removing from this set any dominated points. Thus, we have considered the following metrics:

• Purity metric [25, 26] is used to compare the nondominated fronts obtained by different solvers. It consists then of computing, for solver $s\in \mathcal {S}$ and problem $p\in \mathcal {P}$, the ratio $c_{p,s}^{F_p}/c_{p,s}$, where $c_{p,s}^{F_p}=\left| F_{p,s}\cap F_p\right|$ and $c_{p,s} = \left| F_{p,s}\right|$. This metric is then represented by a number between zero and one. Higher values for this ratio indicate a better nondominated front in terms of the percentage of nondominated points.

• Spread metric [25, 26] attempts to measure the maximum size of the holes of an approximated nondominated front. Let us assume that solver $s\in \mathcal {S}$ has computed, for problem $p\in \mathcal {P}$, an approximated nondominated front with N points, indexed by $1,\cdots ,N$. We have also considered the extreme points indexed by 0 and $N+1$, these points are computed considering the minimum and maximum value of each objective function among all the points in $F_p$. The metric $\varGamma _{p,s}> 0$ consists of setting:

  $$\begin{aligned} \varGamma _{p,s} = \max _{j\in \left\{ 1,\cdots ,m\right\} } \max _{i\in \left\{ 0,\cdots ,N+1\right\} } \delta _{i,j}, \end{aligned}$$

  where $\delta _{i,j} = f_{i+1,j}- f_{i,j}$ (and we assume that the objective function values have been sorted out by increasing order for each objective j).

• Additive epsilon indicator [25, 26]: The additive epsilon indicator $I_{\epsilon +}$ is based on additive $\epsilon$-dominance:

  $$\begin{aligned} z_1 \preceq _{\epsilon +} z_2 \Leftrightarrow z_i^1 \leqslant \epsilon + z_i^2, \forall i\in \left\{ 1,\cdots ,m\right\} , \end{aligned}$$

  and defined, for each solver $s\in \mathcal {S}$ and problem $p\in \mathcal {P}$, with respect to a nondominated reference set $F_p$ as:

  $$\begin{aligned} I_{\epsilon +}\left( F_{p,s} \right) = I_{\epsilon +}\left( F_{p,s},F_p \right) =\inf \left\{ \epsilon | \ \forall y\in F_p \ \exists \,\, z\in F_{p,s} : z \preceq _{\epsilon +} y \right\} . \end{aligned}$$

These metrics are presented in Tables 2, 3 and 4 where the values indicated with—correspond to the combinations of solvers and problems such that none of the starting points produce convergent sequences.

Table 2 The value of purity metric in solving test problems

Table 3 The value of spread metric in solving test problems

Table 4 The value of epsilon indicator in solving test problems

Table 5 presents a summary of the average number of iterations while Table 6 shows the average number of function evaluations. Finally, Table 7 illustrates the number of instances the problem was solved by each solver. In these tables the best average number of function evaluations and of iterations were written in boldface. Taking these numbers into account, we can observe that for the three line search strategies presented the sequence $\left\{ \beta _k \right\}$ defined in Sect. 4 reduces, most of the time, the number of function evaluations used, at least in our test problems.

Table 5 Number of iterations for each algorithm

Table 6 Number of function evaluations for each algorithm

Table 7 Number of times each problem was solved for each algorithm

6 Conclusions

We have presented a modification of the well-known projected gradient method for multiobjective optimization on convex sets. At each iteration the search direction was computed by considering a variable step length instead of a fixed parameter. The novelty element has been the use of the specific max-type nonmonotone line search instead of the classical Armijo strategy or the average-type update rule.

Stationarity of the accumulation points of the sequences generated by the proposed algorithm has been established in the general case under standard assumptions.

The method was implemented and tested. For a better analysis we also consider the monotone version of the presented algorithm and another algorithm with the nonmonotone line search defined in [6], these three algorithms were considered with the standard step length and the spectral step length. In our experimentation we observe a better performance for the nonmonotone line searches and even better using the spectral step length. As in the scalar case, the nonmonotone line search shows a good performance in combination with spectral step length.