A weighting subgradient algorithm for multiobjective optimization

Abstract

We propose a weighting subgradient algorithm for solving multiobjective minimization problems on a nonempty closed convex subset of an Euclidean space. This method combines weighting technique and the classical projected subgradient method, using a divergent series steplength rule. Under the assumption of convexity, we show that the sequence generated by this method converges to a Pareto optimal point of the problem. Some numerical results are presented.

1 Introduction

The multiobjective optimization, also known as multicriteria optimization, refers to the process of simultaneously optimizing two or more real-valued objective functions. The multiobjective optimization problem has applications in the economy, industry, agriculture, and others fields. For more details see, for example, Luc [11], Miettinen [13], and Pappalardo [14]. Among the strategies that can be used to find one solution of a smooth multiobjective optimization problem, we mention the weighting methods, steepest descent methods and Newton methods. On weighting methods, which are very simple and easy to implement, we refer the reader to Graña Drummond et al. [9], Burachik et al. [5] and references therein. See Fliege and Svaiter [7] and Fukuda and Graña Drummond [8] for more details on the steepest descent method, and to Fliege et al. [6] and references therein for more details on the Newton method. An interesting alternative for the nondifferentiable case is the use of subgradients. See, for example, Alber et al. [1] for the scalar case, Bello Cruz [2], Bento and Cruz Neto [3], and references therein. In the present work, we propose a combination of the weighting technique and the projected subgradient method for finding one solution of a nonsmooth constrained multicriteria optimization problem, where the multiobjective function is component-wise convex. Our aim is to provides an easily implementable scheme with a low-cost iteration. We emphasize that an essential difference between our approach and the projected subgradient method proposed in [2] is that, in [2] the author does not use scalarizations.

Our approach considers a scalarization process to obtain total convergence to a Pareto optimal point, even if the solution set is not a singleton. Furthermore, we present some numerical experiments in order to demonstrate the performance of our method. The rest of this paper is organized as follows. In Sect. 2, we recall some useful basic notions. In Sect. 3, we define the algorithm, and study its convergence properties. In Sect. 4, we present some computational experiments. In Sect. 5, we provide some concluding remarks.

2 Preliminaries

The following notation is used throughout our presentation. We denote by $\langle \, \cdot \, , \cdot \, \rangle$ the usual inner product of ${\mathbb {R}}^n$, and by $\Vert \cdot \Vert$ its corresponding norm. Furthermore, we use the Pareto order, that is, let $I=\{1,\ldots , m\}$, ${{\mathbb {R}}}^{m}_{+} = \{x\in {{\mathbb {R}}}^m{:} x_{i}\ge 0, i \in I\}$ and ${{\mathbb {R}}}^{m}_{++}=\{x\in {{\mathbb {R}}}^m{:}x_{i}> 0, i \in I \}$. For $x, \, y \in {{\mathbb {R}}}^{m}_{+}$, $y\succeq x$ (or $x \preceq y$) means that $y-x \in {{\mathbb {R}}}^{m}_{+}$ and $y\succ x$ (or $x \prec y$) means that $y-x \in {{\mathbb {R}}}^{m}_{++}$.

Consider the function $F{:}{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$, given by $F(x)=(F_1(x),\ldots ,F_m(x))$. We are interested in the multiobjective optimization problem

$$\begin{aligned} \left\{ \min _{x \in C }~F(x), \right. \end{aligned}$$

(1)

where $C\subset {\mathbb {R}}^{n}$ is assumed to be a nonempty closed convex set.

Throughout this paper we assume that each component $F_{i}$ of F is a convex function on an open subset $\Omega$ containing C.

We recall some basic properties of convex functions, where $\partial F_{i}$ denotes the Fenchel–Moreau subdifferential of $F_{i}$.

Proposition 1

(See [17]) For each $i \in \{1, \ldots ,m\}$, we have the following:

• (i) $\partial F_{i}(x)$ is nonempty and compact, for all $x \in C$;

• (ii) $\partial F_{i}$ carries bounded on bounded sets.

Definition 1

A point ${\bar{x}} \in C \subset {\mathbb {R}}^{n}$ is called a weak Pareto optimal point for problem (1) if there exists no other $x \in C$ such that $F(x)\prec F({\bar{x}})$. In this case, we will employ the notation ${\bar{x}} \in WS(F,C)$. If there exists no other $x \in C$ with $F(x)\preceq F({\bar{x}})$ and $F(x) \not = F({\bar{x}})$, then ${\bar{x}}$ is said to be a Pareto optimal point for problem (1), and we will denote this by ${\bar{x}} \in S(F,C)$.

Lemma 1

Assume that ${\bar{x}} \in C$ satisfies $\max _{i} \left( F_{i}(x) - F_{i}({\bar{x}}) \right) \ge 0$ for all $x \in C$. Then, ${\bar{x}} \in WS(F,C)$.

Proof

This is straightforward consequence of Definition 1. $\square$

Let $x\in {\mathbb {R}}^{n}$, and let $D\subset {\mathbb {R}}^{n}$ be a closed convex set. We recall that the orthogonal projection onto D, denoted by $P_{D}(x)$, is the unique point in D such that $\Vert P_{D}(x)-y\Vert \le \Vert x-y\Vert$ for all $y \in D$. Moreover, $P_{D}(x)$ satisfies

$$\begin{aligned} \langle x-P_{D}(x), y-P_{D}(x)\rangle \le 0,\;\; \forall \;\; y \in D. \end{aligned}$$

(2)

Finally, we conclude this section by presenting a well-known result that will be useful in our convergence analysis.

Lemma 2

(See [16]) Let $\{\nu _{k}\}$ and $\{\delta _{k}\}$ be nonnegative sequences of real numbers satisfying $\nu _{k+1} \le \nu _{k} + \delta _{k}$ with $\sum _{k=1}^{+\infty } \delta _{k} < +\infty$. Then, the sequence $\{\nu _{k}\}$ is convergent.

3 The algorithm

In this section we define our proposed algorithm, and demonstrate that it is well defined.

Weighting Subgradient Algorithm (WSA)

Let $\{\lambda _{i}^{k} \} \subset [0,1]$, $\sum _{i=1}^{m}\lambda _{i}^{k}=1 \;\; \forall \; k \in {\mathbb {N}}$, $\{\gamma _{k}\} \subset (0,1)$, and $\{\alpha _{k}\} \subset {\mathbb {R}}_{+}$, with

$$\begin{aligned} \sum _{k=0}^{+\infty } \gamma _{k} \alpha _{k} = +\infty , \; \; \sum _{k=0}^{+\infty } \alpha _{k}^{2} < +\infty . \end{aligned}$$

(3)

Step 0: Choose $x^{0} \in C$. Set $k=0$.

Step 1: Take $s_{i}^{k} \in \partial F_{i}(x^{k})$. If $\min _{i=1,\ldots ,m} \Vert s_{i}^{k}\Vert = 0$, STOP.

Otherwise, obtain $\eta _{k}=\displaystyle \max _{i=1,\ldots ,m} \{1,\Vert s_{i}^{k}\Vert \}$, define $h_{x^{k}}(v) = \frac{\alpha _{k}}{\eta _{k}}\left\langle \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, v\right\rangle +\frac{\Vert v\Vert ^{2}}{2}$ and compute $v^{k}$:

$$\begin{aligned} v^{k}:={\text{ arg }} \displaystyle \min _{v\in C-x^{k}} h_{x^{k}}(v). \end{aligned}$$

(4)

If $v^{k} = 0$, STOP. Otherwise,

Step 2: Compute $x^{k+1}$:

$$\begin{aligned} x^{k+1} := x^{k} + \gamma _{k} v^{k}. \end{aligned}$$

(5)

Remark 1

• (i) Let us note that WSA uses exogenous weights $\lambda _{i}^{k}$ for the subgradients $s_{i}^{k}$ in a manner reminiscent of a weighted-gradient method. See, for example, Graña Drummond et al. [9], Marler and Arora [12].

• (ii) Following [15], the use of weighted method is well acceptable in applications, and is favorable for mathematical analysis. Actually, the a priori selection of weights allows the resulting scalar objective function to be solved for a single Pareto optimal solution that represents the preference of the human decision maker.

In view of the strong convexity of $h_{x^{k}}$, the direction $v^{k}$ is well defined, and problem (4) has a quadratic (scalar-valued) objective function.

Now, we show that the stop criteria is well-defined.

Proposition 2

If the algorithm stops at iteration k, then $x^{k} \in WS(F,C)$.

Proof

Take $k\in {\mathbb {N}}$, and let us suppose that there exists $i_{0}\in \{1,\ldots , m\}$ such that $s_{i_{0}}^{k} = 0$. Hence, taking into account that $F_{i_{0}}$ is a convex function on C, from subgradient’s inequality we get that

$$\begin{aligned} F_{i_{0}}(y) \ge F_{i_{0}}(x^{k}),\qquad y\in C. \end{aligned}$$

Then, it follows that $x^{k} \in WS(F,C)$. Now, assume that $v^{k} = 0$. From (4), combined with the definition of $h_{x^{k}}$, we have

$$\begin{aligned} v^{k}= & {} \text{ argmin }_{v \in C - x^{k}}\left\{ \frac{\alpha _{k}}{\eta _{k}} \left\langle \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, v\right\rangle +\frac{\Vert v\Vert ^{2}}{2}\right\} \nonumber \\= & {} \text{ argmin }_{v \in C - x^{k}}\left\{ \left\langle \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, v\right\rangle +\frac{1}{2} \left\{ \Vert v\Vert ^{2} + \Vert \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}\Vert ^{2} \right\} \right\} \nonumber \\= & {} \text{ argmin }_{v \in C - x^{k}} \frac{1}{2} \left\| v - \left( - \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}\right) \right\| ^{2} \nonumber \\= & {} P_{C - x^{k}} \left( - \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k} \right) . \end{aligned}$$

(6)

Using (2) together with $D = C - x^{k}=\{x - x^{k} {:} x \in C\}$ and $x=- \frac{\alpha _{k}}{\eta _{k}} \displaystyle \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}$, and taking into account that $v^{k}=0$, last equality implies that

$$\begin{aligned} \left\langle \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, v \right\rangle \ge 0, \;\; \forall \; v \in C-x^{k}. \end{aligned}$$

That is,

$$\begin{aligned} \frac{\alpha _{k}}{\eta _{k}} \left\langle \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, y - x^{k} \right\rangle \ge 0,\quad \forall \; y \in C. \end{aligned}$$

Now, from the above inequality, there exists $j \in \{1,\ldots ,m\}$ such that

$$\begin{aligned} \langle s_{j}^{k}, y - x^{k} \rangle \ge 0,\quad \forall \; y \in C. \end{aligned}$$

Using that $F_{i}$ is convex on C for each i, we get that

$$\begin{aligned} \max _{i} \left( F_{i}(y) - F_{i}(x^{k}) \right) \ge F_{j}(y) - F_{j}(x^{k}) \ge \langle s_{j}^{k}, y - x^{k} \rangle \ge 0,\quad \forall \; y \in C. \end{aligned}$$

By combining this with Lemma 1, it follows that $x^{k} \in WS(F,C)$. $\square$

From now on, we assume that $\{x^{k}\}$ is infinite.

4 Convergence analysis

We begin this section by showing that our method is feasible.

Lemma 3

$x^{k}\in C$, for all $k\in {\mathbb {N}}$.

Proof

The proof is constructed by induction on k. Note that $x^{0}\in C$, by the initialization of the algorithm (WSA). Take a fixed $k\in {\mathbb {N}}$, and let us suppose that $x^{k}\in C$. Then, $x^{k+1}=x^{k}+\gamma _{k}v^{k}$, which can be rewritten as

$$\begin{aligned} x^{k+1}=(1-\gamma _{k})x^{k}+\gamma _{k}\left( x^{k}+v^{k}\right) . \end{aligned}$$

Since $v^{k}\in C-x^{k}$, we have in particular that $x^{k}+v^{k} \in C$. Hence, from the last equality combined with the convexity of C, we conclude the induction process, and the desired result is proved. $\square$

Now, we present three preliminary results that will be useful for our convergence analysis.

Lemma 4

For all $k\in {\mathbb {N}}$, the following statements hold:

• (i) $\Vert v^{k} \Vert \le 2\alpha _{k}$;

• (ii) $\Vert x^{k+1}-x^{k}\Vert \le 2\alpha _{k}$.

Proof

• (i) From Lemma 3, we have $0 \in C-x^{k}$. Using (4), for a fixed $k \in {\mathbb {N}}$ we obtain that

  $$\begin{aligned} h_{x^{k}}\left( v^{k}\right) \le h_{x^{k}}(0)=0. \end{aligned}$$

  That is,

  $$\begin{aligned} \frac{\alpha _{k}}{\eta _{k}}\left\langle \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, v^{k}\right\rangle +\frac{\Vert v^{k}\Vert ^{2}}{2} \le 0. \end{aligned}$$

  Therefore, by using the Cauchy–Schwarz inequality in the second inequality, and by recalling that $\Vert s^{k}_{i}\Vert \le \eta _{k}$ in the third, we have

  $$\begin{aligned} \begin{array}{lll} \Vert v^{k}\Vert ^{2} &{} \le &{} -2\frac{\alpha _{k}}{\eta _{k}}\left\langle \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}, v^{k}\right\rangle \le 2\frac{\alpha _{k}}{\eta _{k}} \displaystyle \sum _{i=1}^{m}\lambda _{i}^{k}\Vert s_{i}^{k}\Vert \Vert v^{k}\Vert \\ &{} \le &{} 2\frac{\alpha _{k}}{\eta _{k}} \displaystyle \sum _{i=1}^{m}\lambda _{i}^{k}\eta _{k}\Vert v^{k}\Vert = 2\alpha _{k}\Vert v^{k}\Vert \end{array} \end{aligned}$$

  since $\sum _{i=1}^{m}\lambda _{i}^{k} = 1$ for each $k \in {\mathbb {N}}$.

• (ii) The result follows from (5) and (i):

  $$\begin{aligned} \Vert x^{k+1}-x^{k}\Vert =\gamma _{k}\Vert v^{k}\Vert \le \Vert v^{k}\Vert \le 2\alpha _{k}. \;\;\;\;\; \square \end{aligned}$$

$\square$

Lemma 5

Let $y \in C$. It holds that

$$\begin{aligned} \langle v^{k}, x^{k}-y \rangle \le \frac{\alpha _{k}}{\eta _{k}}\displaystyle \sum _{i=1}^{m}\lambda _{i}^{k}\left\langle s_{i}^{k}, y-x^{k} \right\rangle + 2\alpha _{k}^{2},\;\; k=0,1,\ldots . \end{aligned}$$

Proof

From (6), we have

$$\begin{aligned} v^{k}=P_{C - x^{k}} \left( - \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k} \right) ,\quad k=0,1\ldots . \end{aligned}$$

Therefore, by using (2) with $x=-\frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}s_{i}^{k}$ and $D=C-x^{k}$, it is easy to see that

$$\begin{aligned} \left\langle \frac{-\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k} s_{i}^{k} -v^{k}, w-v^{k} \right\rangle \le 0,\;\; w \in C-x^{k},\quad k=0,1,\ldots . \end{aligned}$$

Note that for each $k\in {\mathbb {N}}$, we have $w=y-x^{k}\in C-x^{k}$. Thus, for this particular choice of w and for $k=0,1,\ldots$, the last inequality implies that

$$\begin{aligned} \begin{array}{lll} \left\langle v^{k}, x^{k}-y\right\rangle &{}\le &{} -\Vert v^{k}\Vert ^{2}+ \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}\left\langle s_{i}^{k}, y-x^{k}\right\rangle - \frac{\alpha _{k}}{\eta _{k}}\langle \sum _{i=1}^{m}\lambda _{i}^{k} s_{i}^{k}, v^{k} \rangle \\ {} &{}\le &{} \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}\left\langle s_{i}^{k}, y-x^{k}\right\rangle + \frac{\alpha _{k}}{\eta _{k}} \Vert \sum _{i=1}^{m}\lambda _{i}^{k} s_{i}^{k} \Vert \Vert v^{k} \Vert \\ {} &{} \le &{} \frac{\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}\langle s_{i}^{k}, y-x^{k}\rangle + \frac{\alpha _{k}}{\eta _{k}} \left( \eta _{k} \Vert v^{k}\Vert \right) , \\ \end{array} \end{aligned}$$

(7)

where the last inequality follows from that fact that $\sum _{i=1}^{m}\lambda _{i}^{k} \Vert s_{i}^{k} \Vert \le \eta _{k}$. Therefore, by combining (7) with item (i) of Lemma 4, we obtain the desired result. $\square$

Lemma 6

For all $y \in C$, the following inequality holds:

$$\begin{aligned} \Vert x^{k+1}-y\Vert ^{2} \le 8\alpha _{k}^{2} + \Vert x^{k}-y\Vert ^{2} + 2\frac{\gamma _{k}\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k} \left( F_{i}(y) - F_{i}\left( x^{k}\right) \right) , \;\; \forall \;\; k \in {\mathbb {N}}. \end{aligned}$$

(8)

Proof

Let $k \in {\mathbb {N}}$, by using Lemmas 4 and 5, and (5), it follows that

$$\begin{aligned} \begin{array}{lll} \Vert x^{k+1}-y\Vert ^{2} &{} = &{} \Vert x^{k+1}-x^{k}\Vert ^{2}+\Vert x^{k}-y\Vert ^{2} + 2 \left\langle x^{k+1}-x^{k}, x^{k}-y \right\rangle \\ &{} \le &{} 4\alpha _{k}^{2}+ \Vert x^{k}-y\Vert ^{2} + 2\gamma _{k} \langle v^{k}, x^{k}-y \rangle \\ &{} \le &{} 4\alpha _{k}^{2}+ \Vert x^{k}-y\Vert ^{2} + 2\frac{\gamma _{k}\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}\langle s_{i}^{k}, y-x^{k}\rangle + 4\gamma _{k}\alpha _{k}^{2} \\ &{} \le &{} 4(1+\gamma _{k})\alpha _{k}^{2}+ \Vert x^{k}-y\Vert ^{2} + 2\frac{\gamma _{k}\alpha _{k}}{\eta _{k}}\displaystyle \sum _{i=1}^{m}\lambda _{i}^{k}\left\langle s_{i}^{k}, y-x^{k}\right\rangle . \\ \end{array} \end{aligned}$$

From $\gamma _{k} \in (0,1)$, last inequality becomes

$$\begin{aligned} \Vert x^{k+1}-y\Vert ^{2} \le 8\alpha _{k}^{2} + \Vert x^{k}-y\Vert ^{2} + 2\frac{\gamma _{k}\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}\left\langle s_{i}^{k}, y-x^{k}\right\rangle . \end{aligned}$$

(9)

Now, taking into account that F is convex, we have

$$\begin{aligned} \left\langle s_{i}^{k}, y-x^{k}\right\rangle \le F_{i}(y) - F_{i}\left( x^{k}\right) , \qquad i=1,\ldots ,m. \end{aligned}$$

Thus, by applying last inequality, (9) yields

$$\begin{aligned} \Vert x^{k+1}-y\Vert ^{2} \le 8\alpha _{k}^{2} + \Vert x^{k}-y\Vert ^{2} + 2\frac{\gamma _{k}\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k} \left( F_{i}(y) - F_{i}\left( x^{k}\right) \right) , \end{aligned}$$

and the desired result is proved. $\square$

We attain stronger convergence results, by assuming the following property.

R1. The set $T:=\{z \in C :F(z) \preceq F(x^{k}), \quad k \in \quad {\mathbb {N}}\}$ is nonempty.

Remark 2

This assumption it appeared in scalar case in Alber et al. [1] and which has been assumed in Bello Cruz [2] on vector optimization setting. Condition R1 extends ${\mathbb {R}}_+^m$-completeness for the constrained case. When $C = {\mathbb {R}}^{n}$, it is a standard assumption of ensuring the existence of Pareto optimal points for vector optimization problems. See, for example, [11]. Furthermore, we know that if $\{ F(x^{k}) \}$ is a decreasing sequence, then $\{x^{k}\}\subset C{\setminus }S(F,C)$, which is a standard result from the extension of classical methods to vector optimization. For more details see, for example, [6]. Finally, R1 holds if S(F, C) is nonempty, for scalar case.

Theorem 1

Assume R1, and let $z \in T$. Then, $\{\Vert x^{k} - z\Vert \}$ is a convergent sequence. Moreover, $\{x^{k}\}$ is bounded.

Proof

Since $z \in T$, it holds that

$$\begin{aligned} F_{i}(z) - F_{i}\left( x^{k}\right) \le 0,\qquad i=1,\ldots ,m. \end{aligned}$$

Using this inequality and (8), we obtain that

$$\begin{aligned} \Vert x^{k+1}-z\Vert ^{2} \le \Vert x^{k}-z\Vert ^{2} + 8\alpha _{k}^{2}. \end{aligned}$$

From (3) and Lemma 2, we conclude the proof. $\square$

A natural choice for the parameters $\{\lambda _{i}^{k}\}$ is given by $\lambda _{i}^{k} = 1/m$, for $i \in \{1,\ldots ,m\}$. More generally, we obtain the convergence of the whole sequence by assuming the following requirement.

R2. There exists a vector ${\underline{\lambda }} \in {\mathbb {R}}^{m}$ such that $0 \prec {\underline{\lambda }} \preceq \lambda ^{k}$ for all $k \in {\mathbb {N}}$.

Theorem 2

Assume that R1 and R2 hold. Then, the whole sequence $\{x^{k}\}$ converges to $x^{*} \in S(F,C)$.

Proof

Firstly, we show that $\{x^{k}\}$ converges to $x^{*} \in T$.

Let us consider $z \in T$, from Theorem 1, it follows that $\{x^{k}\}$ is a bounded sequence. Therefore, by using (8), we can write

$$\begin{aligned} 2\frac{\gamma _{k}\alpha _{k}}{\eta _{k}} \sum _{i=1}^{m}\lambda _{i}^{k}\left[ F_{i}(x^{k})-F_{i}(z)\right] \le \Vert x^{k}-z\Vert ^{2} -\Vert x^{k+1}-z\Vert ^{2} +8\alpha _{k}^{2}. \end{aligned}$$

(10)

Applying the sum from $k=0$ to $k=l$ in (10), we obtain

$$\begin{aligned} 2 \sum _{k=0}^{l} \frac{\gamma _{k} \alpha _{k}}{\eta _k} \left( \sum _{i=1}^{m}\lambda _{i}^{k}[F_{i}(x^{k})-F_{i}(z)]\right) \le \Vert x^{0}-z\Vert ^{2} -\Vert x^{l+1}-z\Vert ^{2} +8\sum _{k=0}^{l}\alpha _{k}^{2}. \end{aligned}$$

Moreover, there exists an $L > 0$ such that $\eta _{k} \le L$, then

$$\begin{aligned} \frac{1}{L}\sum _{k=0}^{+\infty } \gamma _{k} \alpha _{k} \le \sum _{k=0}^{+\infty }\frac{\gamma _{k} \alpha _{k}}{\eta _k}. \end{aligned}$$

By letting l go to $+\infty$, it holds that

$$\begin{aligned} \sum _{k=0}^{+\infty }\frac{\gamma _{k}\alpha _{k}}{\eta _{k}} \left( \sum _{i=1}^{m}\lambda _{i}^{k}[F_{i}(x^{k})-F_{i}(z)]\right) < +\infty . \end{aligned}$$

(11)

From (3), (11) and last inequality, we obtain

$$\begin{aligned} \liminf _{k \rightarrow +\infty } \sum _{i=1}^{m}\lambda _{i}^{k} \left( F_{i}(x^{k}) - F_{i}(z) \right) \le 0. \end{aligned}$$

Therefore, owing to the fact that $z \in T$, we get

$$\begin{aligned} \liminf _{k \rightarrow +\infty } \sum _{i=1}^{m}\lambda _{i}^{k} \left( F_{i}(x^{k}) - F_{i}(z) \right) = 0. \end{aligned}$$

By taking a subsequence $\{x^{k_{j}}\} \subset \{x^{k}\}$ that satisfies the limit above, we obtain

$$\begin{aligned} - F_{p}(z) + \lim _{j\rightarrow +\infty } F_{p}(x^{k_j}) = 0\ \Leftrightarrow \lim _{j\rightarrow +\infty } F_{p}(x^{k_j}) = F_{p}(z),\quad 1 \le p \le m. \end{aligned}$$

(12)

Hence, we have

$$\begin{aligned} 0 \le - F_{p}(z) + F_{p}(x^{k_{j}}) \le \sum _{i=1}^{m} \left[ -F_{i}(z) + F_{i}(x^{k_{j}})\right] ,\qquad 1 \le p \le m. \end{aligned}$$

Without loss of generality, there exists an $x^{*} \in C$ such that $x^{k_{j}}\rightarrow x^{*}$. Because $F_{p}$ is continuous, we have that $F_{p}(x^{k_{j}}) \rightarrow F_{p}(x^{*})$. Then, it follows that $x^{*} \in T$. By using Theorem 1, with $z = x^{*}$, we conclude that $\lim _{j \rightarrow +\infty }\Vert x^{k_j} - x^{*}\Vert = 0$. From Theorem 1, we achieve our desired result.

Finally, we show that $x^{*} \in S(F,C)$.

In fact, take $y \in C$ such that $F(y) \preceq F(x^{*})$. So, $y \in T$. Hence, by using (12), we have $F(y)=F(x^{*})$. The proof is completed. $\square$

5 Numerical results

In this section, two numerical tests are used for the purpose of illustrating the algorithm performance. The algorithm was coded in SCILAB 5.5.2 on a 8 GB RAM 1.60 GHz i5 notebook. For these tests, we adopt the stop condition $\Vert v^{k}\Vert < 10^{(-8)}$ or number of iterations equals to 200. We show a comparison among WSA and two other subgradient-type algorithms. The subgradient method for Vector optimization (SMVO), given by [2], does not use scalarizations and at each iteration, solves a non quadratic problem on C. The relaxed projection method for multiobjective optimization (RPM), given in [4] at each iteration, performs a finite number of projections on suitable halfspaces that contain C.

To apply WSA, the scalarized problem is defined by

$$\begin{aligned} f :{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}, \;\; f(x) = \lambda _{1} F_{1}(x) + \lambda _{2} F_{2}(x) + \ldots + \lambda _{m} F_{m}(x), \end{aligned}$$

where $\lambda _{j} \in (0,1)$, $j=1, \ldots , m$.

Example 1

In this example, we present the results obtained by WSA, RPM and SMVO for three known problems given at [10]. We solved the problem using 100 starting points from a uniform random distribution over the interval (L, U) and $\lambda _{1} = \lambda _{2} = 1/2$. Average number of iterations and CPU time are reported in Table 1.

Table 1 Iterations and CPU time results for three simple problems

In this example, the stepsize sequence was defined using $\alpha _{k} = 9/(k+1),13/(k+1), 12/(k+1)$, respectively, with $\gamma _{k} = 0.95,$ for all $k \in {\mathbb {N}}$. By using the same notation of each bibliographical reference, SMVO, given by [2], uses the stepsize $\beta _{k} = 19/(k+1)$, for all three problems, and RPM considers the stepsize $\beta _{k} = 14/(k+1),14/(k+1), 0.1/(k+1)$, respectively.

In this test, note that WSA has shown the better behavior in terms of computational time.

Example 2

Consider a nondifferentiable multiobjective problem defined by $C = \{ x \in {\mathbb {R}}^{n} :-10 \le x_j \le 10, \; j=1,\ldots ,n \}$ and

$$\begin{aligned} F(x) = \left( \sum _{j=1}^{n-1} \left[ |x_{j} - x_{j+1}| + x_{j+1}^{2} - 2x_{j} \right] , \sum _{j=1}^{n-1} \left[ |x_{j} - x_{j+1}| - 2x_{j+1} \right] \right) . \end{aligned}$$

We solved the problem using 100 starting points from a uniform random distribution in $(-10,10)$. Weight value $\lambda$, average number of iterations, CPU time, average of $\Vert v^{k}\Vert$ and $F(x^{k})$, which is the last iteration, are reported in Table 2.

Table 2 Average of results for different weight values

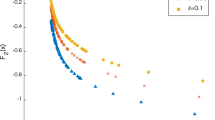
In this example, the stepsize sequence was defined using $\alpha _{k} = 20/(k+1)$ with $\gamma _{k} = 0.9$ for all $k \in {\mathbb {N}}$. By using the same notation of each bibliographical reference, SMVO, given by [2], uses the stepsize $\beta _{k} = 20/(k+1)$ and RPM consider the stepsize $\beta _{k} = 35 / (k+1)$. In Fig. 1, we plot the objective function space and the Pareto optimal front set to confirm our results.

Fig. 1

A comparison among subgradient-type algorithms, with $n=2$

Observe that, as intended, WSA finds a subset of the Pareto frontier.

6 Conclusion

In this work we have presented an implementable algorithm for solving constrained multiobjective optimization problems, which requires only one projection at each iteration. In the convergence analysis, we relaxed the standard hypotheses, and established several results according to the requirements imposed on F and C. First, we found that $\{x^{k}\}$ is bounded. Second, we considered the boundedness of exogenous parameters in order to prove the convergence of the whole sequence $\{x^{k}\}$ to a solution of the problem, without requiring a uniqueness assumption (see [2]). We illustrated the numerical behavior of the algorithm by considering four problems. An interesting future direction would be to consider a more detailed computational experiment.