Monoclonal antibody disposition: a simplified PBPK model and its implications for the derivation and interpretation of classical compartment models

Abstract

The structure, interpretation and parameterization of classical compartment models as well as physiologically-based pharmacokinetic (PBPK) models for monoclonal antibody (mAb) disposition are very diverse, with no apparent consensus. In addition, there is a remarkable discrepancy between the simplicity of experimental plasma and tissue profiles and the complexity of published PBPK models. We present a simplified PBPK model based on an extravasation rate-limited tissue model with elimination potentially occurring from various tissues and plasma. Based on model reduction (lumping), we derive several classical compartment model structures that are consistent with the simplified PBPK model and experimental data. We show that a common interpretation of classical two-compartment models for mAb disposition—identifying the central compartment with the total plasma volume and the peripheral compartment with the interstitial space (or part of it)—is not consistent with current knowledge. Results are illustrated for the monoclonal antibodies 7E3 and T84.66 in mice.

Introduction

Despite the continuing interest in modeling monoclonal antibody (mAb) pharmacokinetics (PK) and the growing mechanistic understanding of molecular processes involved in mAb disposition [1, 2], there is still no clear consensus on the structure & parameterization of physiologically-based pharmacokinetic (PBPK) models [3] nor on the interpretation of classical compartment models [4].

Published PBPK models for mAbs are quite heterogeneous with respect to their representations of physiology and the parameterization of the mechanisms involved in mAb disposition [5–11], e.g., regarding (i) the definition of the relevant tissue spaces (vascular and interstitial tissue space or additionally an endosomal compartment); (ii) how to model extravasation (by diffusive & convective transport or only by convective transport); (iii) the relevance of the neonatal Fc receptor (FcRn) (whether to explicitly account for the interaction with FcRn and whether to use an equilibrium model or a detailed binding kinetics, whether to account for pH-dependent binding); (iv) the importance to explicitly account for endogenous immunoglobulin (IgG); (v) the relevance to include a lymph node compartment; or (vi) how to describe the clearance of mAbs.

In [1], pharmacokinetic studies of 27 commercialized mAbs are reviewed. In most of the cases, the PK of mAbs is described by a classical two-compartment disposition model. Due to the absence of unspecific binding, the central and peripheral compartments are typically associated with plasma and interstitial spaces, respectively. Modeling of mAb elimination processes is quite diverse: It includes linear [12] and/or non-linear [13, 14] clearance(s) from the central compartment, or parallel linear and non-linear clearances from the central and/or peripheral compartment(s) [15, 16]. The non-linearity in the PK is mainly attributed to the saturable binding to the target. Target mediated drug disposition [17–20], and receptor-mediated endocytosis [21, 22] models have been successfully used to mechanistically justify non-linear clearance terms. Much less is known about the physiological mechanisms supporting the linear elimination. IgG-1 like mAbs present common structural properties and molecular mechanisms, independent of the binding to the target. Elimination in the endosomal space and protection from elimination by binding to FcRn is known to be a major process influencing the PK of mAbs in the absence of the target. However, it is not obvious, how to link the non-linear FcRn-mediated salvage mechanism in the endosomes to commonly used linear clearance terms in classical compartment models.

The objectives of this article are (i) to develop a simplified PBPK model to describe the disposition of mAbs that integrates known pharmacologically relevant processes but is parameterized by a minimum number of parameters; and (ii) to derive low-dimensional compartment models consistent with the simplified PBPK model and allow for a mechanistic interpretation. A clearer understanding of the physiological processes to be explicitly considered and the necessary assumptions to make within PBPK models for mAbs are required to increase their use, e.g., for dose projections [3]. In addition, covariate modeling in a population context as well as the integration of more detailed models at the cell-level will greatly benefit from a mechanistic interpretation of low-dimensional compartment models.

Theoretical

Simplified PBPK model for mAb disposition

We propose a novel simplified PBPK model for mAb disposition that has been derived from much more detailed PBPK models [7–10] by model reduction (see Step-wise reduction of a detailed PBPK model of mAb disposition in Appendix) and is in line with recent findings in [23] that report a linear relationship between plasma and tissue concentration of mAbs. The tissue topology and model structure is shown in Fig. 1.

Fig. 1

Structure of the simplified PBPK model for antibody pharmacokinetics. Organs/tissues are interconnected by plasma (red and blue arrows) and lymph (green dashed arrows) flows. The plasma compartment comprises total arterial and venous plasma, including the vascular plasma space associated with the tissues. The tissue compartments account for interstitial, endosomal and intracellular spaces. Each organ/tissue has the potential to play a role in the elimination of IgGs, represented with black arrows

The model accounted for the anatomical compartments plasma (pla), lung (lun), adipose (adi), bone (bon), gut (gut), heart (hea), kidney (kid), liver (liv), muscle (mus), skin (ski) and spleen (spl). The plasma compartment with volume V _pla comprised total arterial and venous plasma, including the vascular space associated with the tissues. The tissue compartments with volume V _tis accounted for interstitial, endosomal and intracellular spaces. Exchange between plasma and tissue was described in terms of the tissue lymph flow L _tis, a tissue partition coefficient K _tis and a reflection coefficient σ_tis. Each tissue was potentially involved in elimination with intrinsic tissue clearance CLint_tis in addition to a plasma clearance CLpla. The rate of change of the concentrations C _pla and C _tis in plasma and the different tissues was described by the system of ordinary differential equations (ODEs):

$$\begin{aligned} V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} \,=\, &L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - \frac{C_{\rm tis}}{K_{\rm tis}} \right)\\ &- {\rm CLint}_{\rm tis} \cdot C_{\rm tis} \end{aligned}$$

(1)

$$\begin{aligned} V_{\rm pla} {\rm \frac{d}{dt}}{C_{\rm pla}} \,=\, &L_{\rm pla} \cdot \Big( C_{\rm in} - (1-\sigma_{\rm pla}) C_{\rm pla} \Big) \\ & - {\rm CLpla} \cdot C_{\rm pla}, \end{aligned}$$

(2)

where the first equation applied to all tissues. The inflowing concentration C _in into plasma was defined by

$$L_{\rm pla} \cdot C_{\rm in} = \sum_{\rm tis} L_{\rm tis} \cdot \frac{C_{\rm tis}}{K_{\rm tis}},$$

where the sum was taken over all tissues considered in the model. ¹ For an i.v. bolus administration, the initial conditions at time t = 0 were set to C _pla(0) = dose/V _pla and C _tis(0) = 0 otherwise. A full set of parameter values for mice is given in Tables 3, 4, 5 and 6.

The above system of ODEs included several physiological processes known to be relevant for mAb disposition: (i) tissue uptake by convection through large pores and transcytosis; the parameter σ _tis is an effective parameter, accounting for the fact that only a fraction (1 − σ _tis) of the plasma concentration is accessible for these processes; (ii) back-flow into the plasma space via the lymph flow or via transcytosis. In the simplified PBPK model, the tissue partition coefficient K _tis accounted for processes influencing tissue distribution; it can be interpreted as the tissue-to-accessible plasma concentration partition coefficient; (iii) elimination of therapeutic antibodies via several processes, like e.g., degradation into the endosomes, Fcγ receptor-mediated clearance, nonspecific endocytosis. These different elimination processes were described as a whole by CLint_tis and CLpla. In summary, the ODEs described the disposition of the mAb assuming an extravasation rate-limited tissue distribution and linear elimination occurring from several sites.

Details of the theoretical derivation of the simplified PBPK model are given in Appendices "The role of FcRn and endogenous IgG in PBPK models of mAb disposition", "Step-wise reduction of a detailed PBPK model of mAb disposition". Here, we summarize the most important assumptions underlying the derivation: It was assumed that (i) the dissociation constants of therapeutic IgG (mAb) and endogenous IgG to FcRn were similar; and (ii) the mAb concentration in plasma was lower than the plasma concentration of endogenous IgG. This can generally be expected to be the case (see "Discussion" section) with the notable exception of intra-venous immunoglobulin (IVIG) therapy; (iii) there is no target present (see below on how to include a target). We showed in Appendix "The role of FcRn and endogenous IgG in PBPK models of mAb disposition" that under conditions (i) and (ii), there is no need to explicitly account for endogenous IgG and the competitive binding of endogenous and therapeutic IgG to FcRn in the endosomal space of endothelial cells, since the clearance term resulting from catabolism in the endosomes was shown to be linear, regardless of the saturation level of FcRn.

While we illustrated our PBPK model in mice, recent findings in [23] reporting about a linear relationship between tissue and plasma concentrations in several preclinical species and human strongly support the extendibility of the simplified PBPK model to these species.

Tissue extraction and elimination-corrected partition coefficients

The following derivation gives key insight on the impact of distribution and elimination on tissue concentration and is important for the parameter estimation step. Introducing the tissue-specific ratio

$$R_{\rm tis} = \frac{{\rm CLint}_{\rm tis} \cdot K_{\rm tis}}{L_{\rm tis}},$$

(3)

we defined the tissue extraction ratio E _tis via the relation

$$(1+R_{\rm tis}) = \frac{1}{1-E_{\rm tis}}.$$

(4)

Using Eq. (3), this resulted in

$$E_{\rm tis} = \frac{{\rm CLint}_{\rm tis} \cdot K_{\rm tis}}{{\rm CLint}_{\rm tis} \cdot K_{\rm tis} + L_{\rm tis}},$$

which is the common form of an extraction ratio—as it is, e.g, analogously defined for the hepatic extraction for small molecules. Based on R _tis, we rewrote the right hand side of Eq. (1) as

$$L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - (1+R_{\rm tis}) \frac{C_{\rm tis}}{K_{\rm tis}} \right),$$

and using Eq. (4) this yielded

$$V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} = L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} \right),$$

(5)

which is parametrized in terms of the elimination-corrected partition coefficient

$$\widehat{K}_{\rm tis} = (1-E_{\rm tis}) \cdot K_{\rm tis}.$$

(6)

Equation (6) was used in the 1st step of the parameter estimation process. We give another representation here that is equivalent to Eqs. (1) and (5) and that was used in the 2nd step of the parameter estimation process. Noting that R _tis = E _tis/(1 − E _tis) and with Eq. (3), we obtained

$${\rm CLint}_{\rm tis} = \frac{L_{\rm tis} R_{\rm tis}}{K_{\rm tis}} = \frac{L_{\rm tis} E_{\rm tis}}{(1-E_{\rm tis}) K_{\rm tis}} = \frac{L_{\rm tis} E_{\rm tis}}{\widehat{K}_{\rm tis}}.$$

(7)

From Eqs. (5) and (7), we obtained the ODE

$$\begin{aligned} V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} \,=\;& L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - (1-E_{\rm tis})\frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} \right) \\ & - L_{\rm tis} E_{\rm tis}\frac{C_{\rm tis}}{\widehat{K}_{\rm tis}}, \end{aligned}$$

(8)

which is parameterized in terms of $\widehat{K}_{\rm tis}$ and E _tis. Note that the second term $L_{\rm tis} E_{\rm tis} C_{\rm tis} / \widehat{K}_{\rm tis}$ equals ${\rm CLint_{tis}} \cdot{C_{\rm tis}}$ according to Eq. (7).

Comparing the three equivalent Eqs. (1), (5) and (8), we concluded that it is not possible to infer from typically available experimental tissue data whether some tissue is eliminating or not. All three equations predict identical tissue concentration-time profiles (for identical input C _pla), with Eq. (1) being interpreted as an eliminating tissue and Eq. (5) allowing the interpretation of a non-eliminating tissue with partition coefficient $\widehat{K}_{\rm tis}$. This was of relevance to the present study, since the extent of elimination of mAbs in the different tissue is still under discussion.

Mechanistic derivation of simple compartment models

The aim was to determine, which simple compartment model structures are consistent with the simplified PBPK model. To this end, we extended the lumping approach presented in [24] to account for peripheral elimination.

We determined the steady state tissue-to-plasma partition coefficient: At steady-state, it is dC _tis,ss/dt = 0 so that we obtained from Eq. (5): $L_{\rm tis} \cdot ( (1-\sigma_{\rm tis}) C_{{\rm pla},{\rm ss}} - C_{{\rm tis},{\rm ss}}/\widehat{K}_{\rm tis})=0.$ This resulted in the steady-state antibody biodistribution coefficient ²

$${\rm ABC}_{\rm tis} = \frac{C_{{\rm tis},{\rm ss}}}{C_{{\rm pla},{\rm ss}}} = (1-\sigma_{\rm tis})\cdot \widehat{K}_{\rm tis}.$$

(9)

In accordance with the above equation, for plasma we formally set $\widehat{K}_{\rm pla} = 1/(1-\sigma_{\rm pla})$ so that ABC_pla = 1. Rearranging Eq. (9) to

$$\widehat{K}_{\rm tis} = \frac{C_{{\rm tis},{\rm ss}}}{(1-\sigma_{\rm tis})C_{{\rm pla},{\rm ss}}}$$

(10)

we can therefore interpret $\widehat{K}_{\rm tis}$ as the elimination corrected tissue-to-accessible plasma partition coefficient and, based on Eq. (6), K _tis as the tissue-to-accessible plasma partition coefficient (comparable to tissue-to-unbound plasma partition coefficients for small molecule drugs).

According to the lumping criterion [24, Eq. (20)], we grouped together tissues ${\rm tis}_1,\ldots,{\rm tis}_k$ to form a lumped compartment ${\rm L}=\{{\rm tis}_1,\ldots,{\rm tis}_k\},$ if the normalized tissue concentration-time profiles coincide, i.e, if

$$\frac{C_{{\rm tis}_1}(t)}{(1-\sigma_{{\rm tis}_1})\cdot \widehat{K}_{{\rm tis}_1}} = \ldots = \frac{C_{{\rm tis}_k}(t)}{(1-\sigma_{{\rm tis}_k})\cdot \widehat{K}_{{\rm tis}_k}}$$

(11)

for t ≥ 0. For later reference, we defined the central compartment as the lumped compartment containing plasma. We next determined the lumped model parameters as in [24]. The lumped tissue volume V _L was defined as

$$V_{\rm L} = \sum_{{\rm tis}\in{\rm L}} V_{\rm tis},$$

where here and below, ${\rm tis}\in{\rm L}$ means that the sum is taken over all tissues that are lumped together into L. For all non-central compartments, the lumped lymph flow L _L and the lumped reflection coefficient σ _L were defined by

$$L_{\rm L} = \sum_{{\rm tis}\in{\rm L}} L_{\rm tis}; \quad L_{\rm L} \cdot (1-\sigma_{\rm L}) = \sum_{{\rm tis}\in{\rm L}} L_{\rm tis}\cdot (1-\sigma_{\rm tis}),$$

while for the central compartment, the central lymph flow and reflection coefficient were defined by

$$L_{\rm cen} = \sum_{\rm L} L_{\rm L}; \quad L_{\rm cen} \cdot (1-\sigma_{\rm cen}) = \sum_{\rm L} L_{\rm L}\cdot (1-\sigma_{\rm L}),$$

(12)

where in the above equations, the sum is taken over all non-central lumped compartments (in case there are any; otherwise L _cen and σ _cen are neither defined nor needed). The concentration C _L of the lumped compartment was defined by

$$V_{\rm L} \cdot C_{\rm L} = \sum_{{\rm tis}\in{\rm L}} V_{\rm tis} \cdot C_{\rm tis},$$

(13)

resulting in the definition of the lumped tissue partition coefficient $\widehat{K}_{\rm L}$ according to

$$V_{\rm L} (1-\sigma_{\rm L})\cdot \widehat{K}_{\rm L} = \sum_{{\rm tis}\in{\rm L}} V_{\rm tis} (1-\sigma_{\rm tis}) \cdot \widehat{K}_{\rm tis}.$$

(14)

We remark that the above equation can also be formulated in terms of ABC values, with $V_{\rm L}\cdot {\rm ABC}_{\rm L} = \sum_{{\rm tis}\in{\rm L}} V_{\rm tis} \cdot {\rm ABC}_{\rm tis}.$ To extend the lumping approach to eliminating tissues, we defined the lumped extraction ratio E _L by

$$E_{\rm L} \cdot L_{\rm L} (1-\sigma_{\rm L}) = \sum E_{\rm tis} \cdot L_{\rm tis} (1-\sigma_{\rm tis}),$$

(15)

where the sum is taken over all ${\rm tis}\in{\rm L}$ for non-central compartments L, while it is taken over all ${\rm tis}\in{\rm cen},{\rm tis}\neq{\rm pla}$ for the central compartment. Using E _L, we defined the lumped partition coefficient K _L from the elimination corrected partition coefficient $\widehat{K}_{\rm L}$ analogously to Eq. (6) by

$$(1-E_{\rm L}) K_{\rm L} = \widehat{K}_{\rm L}.$$

For all non-central compartments, we defined the lumped intrinsic clearance CLint_L analogously to Eq. (7) as

$${\rm CLint}_{\rm L} = \frac{L_{\rm L} \cdot E_{\rm L}}{(1-E_{\rm L})\cdot K_{\rm L}} = \frac{E_{\rm L} \cdot L_{\rm L}(1-\sigma_{\rm L}) }{(1-\sigma_{\rm L})\widehat{K}_{\rm L}}.$$

Finally, for the central compartment, we defined the lumped central clearance CL_cen by

$${\rm CL}_{\rm cen} = E_{\rm cen}\cdot L_{\rm cen}(1-\sigma_{\rm cen}) + {\rm CLpla}.$$

(16)

Based on Eq. (13), we derived the ODE describing the rate of change of the lumped concentrations C _L. For the detailed derivation, see Appendix "Derivation of the ODEs of the lumped compartments". Starting from Eq. (13) and exploiting the lumping criterion, we obtained for all non-central compartments,

$$V_{\rm L} {\rm \frac{d}{dt}}{C_{\rm L}} = L_{\rm L} \left((1-\sigma_{\rm L}) C_{\rm pla} - \frac{C_{\rm L}}{K_{\rm L}} \right) - {\rm CLint}_{\rm L} C_{\rm L}.$$

For the central compartment, we obtained

$$V_{\rm cen} {\rm \frac{d}{dt}}{C_{\rm cen}} = L_{\rm cen} \Big( C_{{\rm in}} - (1-\sigma_{\rm cen})C_{\rm pla} \Big)- {\rm CL}_{\rm cen} C_{\rm pla},$$

based on Eqs. (12) and (16). The inflowing concentration into the central compartment was defined as

$$L_{\rm cen} \cdot C_{\rm in} = \sum_{\rm L} L_{\rm L} \cdot \frac{C_{\rm L}}{K_{\rm L}}.$$

Along the same lines, we established the relationship between the lumped and the original tissue concentration as

$$C_{\rm tis} = (1-\sigma_{\rm tis}) \widehat{K}_{\rm tis} \cdot \frac{C_{\rm L}}{(1-\sigma_{\rm L}) \widehat{K}_{\rm L}}.$$

For the plasma compartment, this specifically reads

$$C_{\rm pla} \;=\; \frac{C_{\rm cen}}{(1-\sigma_{\rm cen}) \widehat{K}_{\rm cen}}.$$

(17)

These equations and relationships are the foundation for the derivation of lumped compartment models in the next section.

Minimal lumped compartment models and their link to classical compartment models

Here we focus on the most commonly used two-compartment model. The one- or three-compartment model equations can be derived analogously.

With the lumped peripheral compartment denoted by 'per', the rate of change of the central and peripheral lumped compartment concentrations C _cen and C _per is given by

$$\begin{aligned} V_{\rm cen} {\rm \frac{d}{dt}}{C_{\rm cen}} =& L \cdot\left( \frac{C_{\rm per}}{K_{\rm per}} - (1-\sigma_{\rm per})\cdot C_{\rm pla} \right)\\ & - {\rm CL}_{\rm cen} \cdot C_{\rm pla} \end{aligned}$$

(18)

$$\begin{aligned} V_{\rm per} {\rm \frac{d}{dt}}{C_{\rm per}} = L \cdot\left( (1-\sigma_{\rm per})\cdot C_{\rm pla} - \frac{C_{\rm per}}{K_{\rm per}} \right) &- {\rm CLint}_{\rm per} \cdot C_{\rm per} \\ \end{aligned}$$

(19)

with initial conditions C _cen(0) = dose/V _cen and C _per(0) = 0. The plasma concentration C _pla is linked to the central concentration as defined in Eq. (17). This lumped model is parameterized in terms of physiological parameters: volume of central and peripheral compartments V _cen and V _per; lumped peripheral lymph flow L = L _per; peripheral reflection coefficient σ _per; central plasma clearance CLpla_cen and peripheral intrinsic clearance CLint_per.

To establish a link to classical two-compartment models, we alternatively parametrized the above lumped model in terms of apparent parameters: central and peripheral volumes of distribution V ₁ and V ₂; central plasma clearance CL₁ and peripheral intrinsic clearance CL₂; and inter-compartment clearance Q. For this parameterization, the rate of change of the plasma and peripheral concentrations C ₁ and C ₂ is defined by the ODEs

$$\begin{aligned} V_1 {\rm \frac{d}{dt}}{C_1} \;=\;& Q\cdot (C_2-C_1) - {\rm CL}_1\cdot C_1 \\ V_2 {\rm \frac{d}{dt}}{C_2} \;=\; & Q\cdot (C_1-C_2) - {\rm CL}_2\cdot C_2 \end{aligned}$$

with C ₁(0) = dose/V ₁ and C ₂(0) = 0 for an i.v. bolus administration. This resulted in the following relationships between the apparent and physiological parameters:

$$\begin{aligned} V_1 \;=\;& V_{\rm cen} \cdot {\rm ABC}_{\rm cen} \\ V_2 \;=\; & V_{\rm per}\cdot {\rm ABC}_{\rm per} /(1-E_{\rm per}) \\ Q \;=\; & L \cdot(1-\sigma_{\rm per}) \cr {\rm CL}_1 \;=\;& {\rm CL}_{\rm cen} \cr {\rm CL}_2 \;=\; & {\rm CLint}_{\rm per}\cdot {\rm ABC}_{\rm per} /(1-E_{\rm per}) \\ C_1 \;=\;& \frac{C_{\rm cen}}{{\rm ABC}_{\rm cen}} \\ C_2 \;=\;& \frac{C_{\rm per}}{{\rm ABC}_{\rm per}/(1-E_{\rm per})} \end{aligned}$$

(20)

with ${\rm ABC}_{\rm cen} = (1-\sigma_{\rm cen})\widehat{K}_{\rm cen}$ and ${\rm ABC}_{\rm per} = (1-\sigma_{\rm per})\widehat{K}_{\rm per}$. The additional factor (1 − E _per) in the relationships for the peripheral parameters accounts for peripheral elimination.

If elimination is assumed to occur only from the central compartment, then CLint_per = 0 and the relationships between physiological and apparent parameters of the central and peripheral compartments become comparable: $V_1= V_{\rm cen} \cdot {\rm ABC}_{\rm cen};$ $V_2 = V_{\rm per} \cdot {\rm ABC}_{\rm per};$ C ₁ = C _cen/ABC_cen and C ₁ = C _per/ABC_per.

Correction for residual blood and antibody biodistribution coefficients

As it would be expected for any low volume of distribution drug, residual blood can have a major impact on experimentally measured tissue concentration [25, Table III, p. 105]. We parameterized our PBPK model in such a way that predictions were independent of residual blood. Instead, correction for residual blood was a post-simulation step.

We denoted the residual blood volume related to a given tissue by V _res,blo and the tissue volume including residual blood by

$$V_{\rm exp} = V_{\rm tis} + V_{\rm res,blo}.$$

We omitted the subscript tis in V _exp and other parameters to keep notation simple. Data on residual blood are typically reported in terms of some ratio relating residual blood to tissue volume or weight. Here, we used the ratio res_blo of residual blood volume to blood-contaminated tissue volume, i.e.,

$${\rm res}_{\rm blo} = \frac{V_{\rm res,blo}}{V_{\rm exp}};$$

see Table 3 for experimentally determined ratios in mice. Based on V _exp, we determined the residual blood volume according to $V_{\rm res,blo} = {\rm res}_{\rm blo} \cdot V_{\rm exp}$.

Denoting by A _res the amount of drug in the residual blood, we obtained

$$V_{\rm res,blo} \cdot C_{\rm blo} = A_{\rm res} = V_{\rm res,pla} \cdot C_{\rm pla},$$

where the residual plasma volume was obtained using the hematocrit (hct) via V _res,pla = (1 − hct)V _res,blo. The residual blood-contaminated tissue concentration C _exp was defined as

$$C_{\rm exp} = \frac{V_{\rm tis} C_{\rm tis} + V_{\rm res,pla} C_{\rm pla}}{V_{\rm exp}}.$$

(21)

Hence, based on the prediction of C _pla and C _tis by the simplified PBPK model, we can directly predict C _exp based on the above equation. If experimental data have already been corrected for residual blood, the PBPK model does not need to be altered.

In [23], antibody biodistribution coefficients relating tissue to plasma concentrations were analyzed for a variety of non-binding mAbs and species (i.e., the species do not express a target for the mAb). The authors found a linear relationship between ‘tissue’ and plasma concentrations. Their analysis was based on a variety of different studies so that estimated ABC values can be expected to be perturbed by residual blood (in line with their comment [23, p.302]). Thus, we denoted by ABC_exp the residual blood-contaminated antibody biodistribution coefficients, i.e.,

$${\rm ABC}_{\rm exp} = \frac{C_{\rm exp}}{C_{\rm pla}}.$$

We corrected ABC_exp for residual blood to determine the ‘pure’ tissue-to-plasma partition coefficients ABC_tis. Dividing Eq. (21) by C _pla yielded

$${\rm ABC}_{\rm exp} = \frac{V_{\rm tis}}{V_{\rm exp}} \frac{C_{\rm tis}}{C_{\rm pla}} + \frac{V_{\rm res,pla}}{V_{\rm exp}}.$$

(22)

Solving for C _tis/C _pla and using the definition of res_blo, we obtained the relation between estimated ABC_exp values in [23] the ABC_tis values defined in Eq. (9) as

$${\rm ABC}_{\rm tis} = \frac{{\rm ABC}_{\rm exp} - (1-{\rm hct}){\rm res}_{\rm blo}}{1-{\rm res}_{\rm blo}}.$$

(23)

Exploiting Eq. (9), we may thus directly use experimentally determined ABC_exp values to determine the elimination-corrected tissue-to-plasma partition coefficients:

$$\widehat{K}_{\rm tis} = \frac{{\rm ABC}_{\rm exp} - (1-{\rm hct}){\rm res}_{\rm blo}}{(1-\sigma_{\rm tis})(1-{\rm res}_{\rm blo})}.$$

(24)

Since in [23], ABC_exp values are shown to be approximately constant for different pre-clinical species and human, we may use relation (24) to also determine $\widehat{K}_{\rm tis}$ values for these species, i.e., rat, monkey and human.

Extension of the simplified PBPK model to account for membrane-bound target receptors

The simplified PBPK model can easily be extended to account for a target. We exemplified the extension for a membrane-bound target (like, e.g., the epidermal-growth-factor receptor EGFR). We modeled the mAb-target interaction by the extended Michaelis–Menten model. See [21, 22] for details, in particular for a mechanistic derivation of such a model and its link to more detailed cell-level systems biology models of the targeted receptor system. The extended Michaelis–Menten model is parameterized in terms of a receptor system capacity B _max (describing the maximal amount of drug that can distribute into the receptor system), the Michaelis–Menten constant K _M and the degradation rate constant k _deg (describing the elimination of the drug by receptor-mediated endocytosis).

We denoted the extra-cellular tissue concentration by C _ex (amount in interstitial and endosomal space divided by V _tis). Then the tissue concentration associated with the receptor system C _RS (amount in the receptor system divided by V _tis) is given by [21, 22]

$$C_{\rm RS}=\frac{B_{\rm max} C_{\rm ex}}{K_{\rm M} + C_{\rm ex}}.$$

Due to the assumptions underlying the extravasation rate-limited tissue model, the interstitial concentration C _int was assumed to be just a multiple of the extra-cellular tissue concentration, i.e, C _int = C _ex/K _int for some K _int. Thus we may either state the extended Michaelis–Menten model in terms of C _int, B _max and K _m , or, as we did, in terms of C _ex, B _max and K _M  = K _m /K _int. Finally, as before, the (total) tissue concentration was defined by

$$C_{\rm tis}=C_{\rm ex,tis}+C_{\rm RS,tis}.$$

For sake of illustration, we assumed that K _M and k _deg were tissue-independent, while B _max = B _max,tis might be different for different tissues, depending on the expression levels. For tissues not expressing the target, we set B _max,tis = 0.

Then, the rate of change of the tissue concentrations and the plasma concentration is given by the following system of ODEs and algebraic equations:

$$\begin{aligned} V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} = L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - \frac{C_{\rm ex,tis}}{K_{\rm tis}} \right) - {\rm CLint}_{\rm tis} \cdot C_{\rm ex,tis} - k_{\rm deg} \frac{B_{\rm max,tis} C_{\rm ex,tis}}{K_{\rm M}+C_{\rm ex,tis}} \end{aligned}$$

(25)

with extra-celluar concentration defined by

$$C_{\rm ex,tis} = \frac{1}{2}\left( C_{\rm eff,tis} + \sqrt{(C_{\rm eff,tis})^2+4K_{\rm M} C_{\rm tis}} \right)$$

(26)

with $C_{\rm eff,tis}= \left(C_{\rm tis} -B_{\rm max,tis} - K_{\rm M}\right);$ while for plasma, it is

$$\begin{aligned} V_{\rm pla} {\rm \frac{d}{dt}}{C_{\rm pla}} = L_{\rm pla} \cdot \Big( C_{\rm in} - (1-\sigma_{\rm pla}) C_{\rm pla} \Big) - {\rm CLpla} \cdot C_{\rm pla}, \end{aligned}$$

(27)

with inflowing concentration into the plasma defined as

$$L_{\rm pla} \cdot C_{\rm in} = \sum_{\rm tis} L_{\rm tis} \cdot \frac{C_{\rm ex,tis}}{K_{\rm tis}}.$$

Note that if B _max,tis = 0 for some tissue then the corresponding square-root term in Eq. (26) gives C _ex,tis = C _tis. In this case, C _RS,tis = 0 as expected and Eq. (25) is identical to Eq. (1). The above stated equations can also be used in the case of a tumor tissue (potentially with a time-dependent tumor tissue volume).

Material and methods

Experimental data

For model development, experimental data of a murine monoclonal IgG1 antibody, 7E3, were extracted from [7] using the software DigitizeIt, version 1.5.8a, Bormann (2001–2006). 7E3 is an anti-platelet mAb with a high affinity for the human glycoprotein IIb/IIIa which does not bind to the murine glycoprotein IIb/IIIa [7]. The experimental data included measurements of ¹²⁵I-labeled 7E3 after a single IV bolus dose of 8 mg/kg in wild-type mice (C57BL/6J strain, 25 g) in the venous plasma and in lung, heart, kidney, muscle, skin, gut, spleen and liver. The residual blood volumes were measured in [25, Table III, p. 105].

For model evaluation, experimental venous plasma data of a murine monoclonal anti-CEA IgG1 antibody, T84.66, were extracted from [9]. T84.66 was administered intravenously to nude (20 g) mice at three dose levels: 1, 10 and 25 mg/kg (n = 4 per dose group).

Semi-mechanistic two-compartment model for the disposition of endogenous IgG and the mAb 7E3 in mice

For use in the parameter estimation process, we present a corrected version of the models published by [26], see also [4]. The disposition of endogenous IgG and mAb was described by a two-compartment model with volumes V _cen and V _endo, respectively. The flow Q _in from the central compartment into the peripheral compartment accounted for the fluid phase endocytosis. The reverse flow Q _out described the FcRn-mediated salvage mechanism of the bound species from catabolism with clearance CL. The competitive binding of IgG_endo and mAb to FcRn was assumed to occur in the peripheral compartment and defined the fraction unbound fu. Then, the rate of change of the central and peripheral concentrations of endogenous and therapeutic IgG was given by the system of ODEs:

$$\begin{aligned} V_{\rm cen}{\rm \frac{d}{dt}}{{\rm IgG}_{{\rm endo},1}} \;=\;& Q_{\rm out} (1-{\rm fu}) {\rm IgG}_{{\rm endo},2}+ k_{\rm synth} \\ &- Q_{\rm in} \cdot{\rm IgG}_{{\rm endo},1} \\ V_{\rm endo}{\rm \frac{d}{dt}}{{\rm IgG}_{{\rm endo},2}} \;=\;& Q_{\rm in} \cdot{\rm IgG}_{{\rm endo},1} - {\rm CL}\cdot{\rm fu}\cdot{\rm IgG}_{{\rm endo},2} \\ & - Q_{\rm out} (1-{\rm fu}) \cdot{\rm IgG}_{{\rm endo},2} \\ V_{\rm cen}{\rm \frac{d}{dt}}{{\rm mAb}_1} \;=\;& Q_{\rm out} (1-{\rm fu}) {\rm mAb}_2 \\ & - Q_{\rm in} \cdot{\rm mAb}_1 \\ V_{\rm endo}{\rm \frac{d}{dt}}{{\rm mAb}_2} \;=\;& Q_{\rm in} \cdot{\rm mAb}_1 - {\rm CL}\cdot{\rm fu}\cdot{\rm mAb}_2 \\ & -Q_{\rm out} (1-{\rm fu}) \cdot{\rm mAb}_2 \\ \end{aligned}$$

(28)

with fu defined in Eq. (32) and FcRn_u defined in Eq. (31) with FcRn_eff = FcRn − [IgG_endo,2 + mAb₂] − K _D. This corrected version of the two-compartment model proposed in [26] was fitted to plasma data of 7E3 in wild-type and FcRn-knockout mice after an i.v. bolus administration of dose = 0.2 mg (i.e., 8 mg/kg for a 25 g mouse) and to the plasma steady-state concentration of endogenous IgG in wild-type mice. The parameter values of the model are summarized in Table 1. The initial conditions (in mg/ml) were ${\rm IgG}_{{\rm endo},1}=2.29,$ ${\rm IgG}_{{\rm endo},2}=39.7, {\rm mAb}_1={\rm dose}/V_{\rm cen}=0.125$ and ${\rm mAb}_2=0.$

Table 1 Parameters values corresponding to the semi-mechanistic two-compartment model, describing the plasma concentrations of 7E3 and the steady state plasma concentrations of IgGendo

Model parameterization

A description of the parameters of the simplified PBPK model is given in Table 2. Physiological and anatomical data were taken from [5, 7, 25, 27–29]. The original parameters are summarized in Table 3 and the derived parameters in Table 4. Note that in [5, 7], the plasma space of each organ/tissue was simplistically denoted as ‘vascular space’. Hence, the plasma volume of each organ/tissue in the simplified PBPK model was equivalent to the values of the ‘vascular volume’ in [5, 7]. There are reports about differences in vasculature pore size between tissues [30] and were implemented in PBPK models in [10] and in [25, Chapter III, p. 74 and Table V, p. 107]. Based on a simulation study (results not shown), we identified three groups of tissues with different reflection coefficients: σ _tis = 0.98 for adipose, bone, muscle and skin; σ _tis = 0.95 for gut, liver and spleen; σ _tis = 0.90 for heart, kidney and lung.

Table 2 Summary of the parameters of the simplified PBPK model

Table 3 Reference tissue-dependent parameters in mice

Table 4 Tissue-dependent parameters for the simplified PBPK model for mice

Parameter estimation

We used MATLAB R2010a for modeling and simulation (ode15s solver with default options). Parameter estimation was performed using the MATLAB optimization toolbox, version 4.2, and the predefined functions ‘lsqcuvefit’ using the Levenberg–Marquardt algorithm and ‘fminsearch’ which uses the simplex search method of Lagarias et al. [33]. Based on the venous plasma and tissue experimental data, the simplified PBPK model was used to estimate the tissue partition coefficients $\widehat{K}_{\rm tis},$ the extraction ratios E_tis (used to determine CLint_tis) and CLpla in a two-steps procedure:

In the first step, only the elimination-correct tissue partition coefficients $\widehat{K}_{\rm tis}$ were estimated. This was done based on tissue data and Eqs. (5) and (21), where the plasma concentration in Eq. (5) was identical to the plasma concentration mAb₁ predicted by the semi-mechanistic two-compartment model in Eq. (28). This way, we enforced reliable plasma-concentration time profiles for the estimation of tissue disposition. Note that the plasma concentration profile can be seen as a marker for tissue elimination. Since we already implicitly accounted for tissue elimination by using the plasma data, it is generally not possible to estimate tissue elimination just from simple tissue data (see also "Tissue extraction and elimination-corrected partition coefficients" section).

In the second step, we used the ‘full’ simplified PBPK model defined by Eqs. (8) and (2) with $\widehat{K}_{\rm tis}$ fixed to the values estimated in the first step. Due to lack of tissue data for adipose and bone, corresponding values were assumed to be the same as for muscle, i.e., $\widehat{K}_{\rm adi}=\widehat{K}_{\rm bon}=\widehat{K}_{\rm mus}$. We estimated the corresponding tissue extraction ratios E_tis and CLpla value using plasma data and assumptions on the sites of elimination. The above procedure can be seen as an extension of the approach described in [29].

Results

Estimating tissue partition coefficients and total plasma clearance in mice

As described in "Parameter estimation" section unknown parameters of the simplified PBPK model were estimated in a two step procedure based on plasma and tissue data of the mAb 7E3. The estimated parameters for $\widehat{K}_{\rm tis}$ together with the resulting antibody biodistribution coefficients ABC_tis derived from Eqs. (23) and (24) are reported in Table 5. Our resulting ABC_tis values are consistent with the values reported in [23]—with differences being due to residual blood contamination and the fact that the values in [23] have been estimated across various species.

Table 5 Elimination-corrected tissue partition coefficients $\widehat{K}_{\rm tis}$ and resulting antibody biodistribution coefficients ABC_tis values according to Eq. (9) (excluding residual blood) and ABC_exp values according to Eq. (22) (including residual blood contribution)

There are no consistent reports about which tissues are involved in mAbs elimination and to which extent. Several authors report that adipose, kidney, liver, muscle, skin and spleen are involved in IgG catabolism [34–36]. As a consequence, we considered different scenarios regarding tissue elimination.

In a first scenario, we assumed that all tissues were eliminating. The estimated E _tis were sensitive to the initial values (therefore, we did not report the values). Interestingly, even though the E _tis values were differing from one fit to another, the total clearance CL_tot remained practically constant. Here, the total clearance was defined as

$${\rm CL}_{\rm tot} = \sum_{{\rm tis}\neq{\rm pla}} E_{\rm tis} \cdot L_{\rm tis} (1-\sigma_{\rm tis}) + {\rm CLpla}.$$

(29)

The second scenario assumed that tissue elimination is linked to FcRn expression levels, which were studied in different tissues of C57BL/6 control mice in [34, Fig. 4, p. 1295]. Notable FcRn expression levels were only identified in adipose, muscle, liver, kidney, skin, and spleen. It appeared that FcRn expression levels were similar and high in kidney and skin, while being similar and low in adipose, liver, muscle and spleen. Two groups of tissues were therefore defined: {kidney, skin} and {adipose, liver, muscle, spleen}. An identical extraction ratio was assigned to each group and estimated, while the extraction of the remaining tissues and the plasma clearance was set to 0. The estimated E_tis for kidney and skin was close to 0 suggesting that no extraction in these two tissues occurred (consistent with the high expression of protecting FcRn). This result was surprising and was not in accordance with [34–36].

In the scenarios 3–6, we only considered one eliminating tissue, exemplified for skin, muscle, liver and spleen. In scenario 7, we assigned all elimination processes to the plasma compartment. The estimated extracting ratios and the plasma clearance for all scenarios as well as the corresponding total clearance CL_tot are reported in Table 6. Surprisingly, for all scenarios, CL_tot was nearly unchanged. These results suggest that, given the mice plasma and tissue data, the individual E _tis cannot be estimated and that it is not possible to determine which tissues are involved in the elimination of mAbs.

These finding apply analogously to the more complex models (see Appendies "Eliminating the need of endogenous IgG" and "An intermediate complexity of PBPK models for mAb disposition"), from which our simplified PBPK model has been derived.

Table 6 Estimated tissue extraction ratios and plasma clearance for scenarios (sc.) 2–7 (see text for details)

Simplified PBPK model predicts plasma and tissue data in mice

Based on the estimated parameters, the simulated concentration-time profiles agreed very well with the experimental data of the mAb 7E3 after an i.v. bolus administration of 8 mg/kg to wild type mice, see Fig. 2 for tissue data and Fig. 6 for plasma data. We concluded that the simplified PBPK model is capable of reproducing the characteristic features of experimental plasma and tissue data profiles.

Fig. 2

Tissues concentration-time profiles of scenario 2 (Table 6) predicted by the simplified PBPK model (with ‘—’ and without ‘- -’ residual blood contamination) compared to experimentally measured concentrations in wild-type mice (blue dots) after i.v. bolus administration of 8 mg/kg 7E3 to wild-type mice. Experimental data were extracted from [7] and represent mean data. For plasma see Fig. 6. The predictions are indistinguishable for scenarios 3–7

To evaluate the impact of residual blood on experimental tissue measurements, tissue concentrations including and excluding residual blood contribution were simulated and are shown in Fig. 2. For most tissue, we observed only little perturbations. For lung, the contribution of residual blood is more pronounced. For spleen, the perturbation is substantial; almost all of the drug in spleen results from the drug in the residual blood.

For model evaluation, we used the simplified PBPK model to predict the plasma concentration of T84.66 [9], a murine IgG1 mAb targeting the carcinoembryonic antigen (CEA). T84.66 was administered to 20 g control mice at 3 dose levels: 5, 10 and 25 mg/kg. To this end, tissue weights were scaled linearly with body weight to account for the difference in body weight (25 vs. 20 g). As shown in Fig. 3, the model predicts accurately the distribution and elimination phase at all 3 dose levels—except for the last time point at 35 days. This last time point, however, is most likely not reliable: a simple linear regression based on the last three time points (12, 21 and 35 days) was performed to determine the resulting half-life. We obtained half-lifes of 40 days (for the low dose of 5 mg/kg) and 24 days (for the high dose of 25 mg/kg), which are in contrast to reported half-lifes of 4–8 days in mice [37].

Fig. 3

Plasma concentration-time profiles in mice predicted by the simplified PBPK model (solid line) compared to experimental plasma concentrations in 20 g nude mice for different doses of the mAb T84.66, an anti-CEA mAb: 25 mg/kg (diamond), 10 mg/kg (square) and 1mg/kg (circle). Experimental data were extracted from [9]

Minimal lumped models and the interpretation of classical compartment models

Based on the extension of the lumping approach in "Mechanistic derivation of simple compartment models" section, we reduced the dimensionality of the simplified PBPK model. The normalized concentration-time profiles of all plasma and tissue compartments, defined in Eq. (11) are shown in Fig. 4. Four groups of kinetically similar tissues were identified: cen={plasma, lung}, L ₁={heart, kidney, liver, spleen}, L ₂={gut} and L ₃={adipose, bone, muscle, skin}. These would be the basis for mechanistically lumped models that aim at predicting the concentration-time profiles of all tissues. Here, however, we are only interested in the minimal lumped model that aims at predicting only the plasma concentration-time profile. This is achieved by further reducing the number of tissue groups. Motivated by the biphasic characteristics of the plasma-concentration time profile, we studied different options of grouping all tissues into a central (cen) and peripheral (per) compartment.

Fig. 4

Identification of groups of compartments with similar normalized concentration-time profiles, as predicted by the simplified PBPK model after an i.v. bolus administration of 8 mg/kg 7E3 to wild-type mice. Similar concentration-time profiles are indicated by identical color

In the first minimal lumped model, we choose cen = {plasma, lung} and the peripheral compartment containing all remaining tissues. In the second minimal lumped model, we choose per = {adipose, bone, gut, muscle, skin} and the central compartment containing all remaining tissues. Depending on which tissues are assumed to be eliminating, there are three different scenarios regarding where to assign clearance processes (see Fig. 5): (i) from the central and peripheral compartments, (ii) from the central compartment only; or (iii) from the peripheral compartment only. Each of these three clearance scenarios could be combined with the different choices of which tissues comprise the central and peripheral compartment.

Fig. 5

Compartment structure of different minimal lumped models that all describe the experimental data (7E3 in wt-mice) equally well

For the choice of per ={adipose, bone, gut, muscle, skin} and the central compartment containing all the remaining tissues, the parameter values of the resulting minimal lumped compartment models are given in Table 7. Figure 6 shows the experimental plasma data in comparison to the predictions of the simplified PBPK model, the minimal lumped two-compartment model, and the semi-mechanistic two-compartment model. Predictions for the simplified PBPK and minimal lumped models were based on the clearance scenario 2. Parameterizations based on other clearance scenarios resulted in indistinguishable predictions (results not shown). All models were in very good agreement with the experimental data (and differ only slightly, e.g., in the terminal phase).

Table 7 Comparison of parameter values corresponding to three minimal lumped two-compartment models (MLMs)

Fig. 6

In silico predictions in comparison to the in vivo plasma data for an i.v. bolus administration of 8 mg/kg 7E3 in wild-type mice (experimental data extracted from [7, Fig. 3, p.699]). Plasma concentration-time profiles of scenario 2 (Table 6) are based on the simplified PBPK model (‘11-cmt PBPK model’), the minimal lumped two-compartment model (‘two-cmt minimal lumped model’) and the semi-mechanistic two-compartment model (‘two-cmt empirical model’). The predictions of the simplified PBPK model based on clearance scenario 2 are indistinguishable from scenarios 3–7

Discussion

A novel simplified PBPK model for the disposition of mAbs is presented and exemplified for the mAb 7E3 in mice. The simplified PBPK model (i) includes explicitly or implicitly relevant physiological processes related to mAb disposition; (ii) is parameterized by a minimum number of parameters to allow stable parameter estimation; and (iii) allows to reproduce the typically observed characteristics of concentration-time profiles in plasma and tissue. A key step in substantially reducing the complexity in comparison to published PBPK models [7–10] was to only implicitly consider the endosomal space and the FcRn-mediated salvage mechanism. Analogous model reduction approaches have been successfully used for small molecule drugs, e.g., when considering the interaction of moderate to strong bases with intra-cellular acidic phospholipids without modeling explicitly diffusion across the cell membrane and binding kinetics to the acidic phospholipids [38].

In summary, the simplified PBPK model for mAb disposition is a whole-body model with extravasation rate-limited tissue distribution and elimination potentially occurring from various tissues and plasma. The tissue model has some analogies to the permeability rate-limited tissue model for small molecule drugs.

Our analysis further highlighted that from common experimental data (only plasma, or plasma and tissue data) it is not possible to infer, which tissues are eliminating. This also holds true for small molecule drugs, where, however, assumptions on which tissues are eliminating (typically liver and/or kidney) are commonly supported by in vitro assay (hepatocytes, microsomes) or additional experimental data (urine). Without such additional information, the location and extent of mAb elimination remains to be elucidated. For monoclonal antibodies, this ambiguity is also reflected in the different assumptions made in published PBPK models about where and how to account for elimination [5–8] and is here further illustrated by the different elimination scenarios (sc. 1–7) in "Estimating tissue partition coefficients and total plasma clearance in mice" section. The ambiguity is also reflected at the level of the ODEs describing the rate of change of tissue concentrations: compare Eqs. (1) and (5). The argument we made is not restricted to the simplified PBPK model but holds also true for the more complex PBPK models (like in Appendix "Step-wise reduction of a detailed PBPK model of mAb disposition"). As expected identifiability problems related to clearance carry over to the classical compartment models (see Fig. 5): A compartment model with linear clearance from the central and/or the peripheral compartment is consistent with the experimental data considered.

Since tissue-to-plasma partition coefficients are small, contamination of tissue samples by residual blood/plasma content can have a large impact on reported tissue concentrations. In [25], residual blood volumes of the harvested organs in mice are reported. As can be inferred from Fig. 2, residual plasma contamination has a large impact for spleen and lung. For most tissues, however, the impact is only minor.

In [3], PBPK models for mAb disposition are reviewed. A surprising 200-fold range of lymph flow values used in published PBPK models for the same tissue was observed. In terms of our simplified PBPK model, this observation can be understood. Given some positive parameter α, the rate of change of the tissue concentration in Eq. (1) can be equivalently expressed as

$$V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} = \widetilde{L}_{\rm tis} \cdot \left( (1-\widetilde\sigma_{\rm tis}) C_{\rm pla} - \frac{C_{\rm tis}}{\widetilde K_{\rm tis}} \right) - {\rm CLint}_{\rm tis} \cdot C_{\rm tis}$$

with $\widetilde{L}_{\rm tis} = \alpha L_{\rm tis};$ $(1-\widetilde\sigma_{\rm tis})=(1-\sigma_{\rm tis})/\alpha$ and $\widetilde K_{\rm tis} = \alpha K_{\rm tis}$. Now, varying α between 1 and 200 would explain the observed range of values for lymph flows in [3]. It also highlights the fact that reported values of σ _tis and K _tis are relative to the lymph flow values, which are commonly assumed to be 2 or 4 % of plasma flow (see Table 4). As expected, steady-state partitioning is not influenced, since α cancels out in Eq. (9).

An important assumption underlying the derivation of the simplified PBPK model was that the concentration of therapeutic IgG are 1–2 orders of magnitude lower than endogenous IgG levels. The assumption holds for many relevant situations: For example, in healthy men, the mean concentration of total endogenous IgGs is 65 μM [39]. We reviewed the maximum concentrations C _max following single or multiple administration of the therapeutic dose for an exemplary set of 6 mAbs registered at the European Medicines Agency (EMEA) in human (cetuximab [40], infliximab [41], rituximab [42], trastuzumab [43], golimumab [44] and tocilizumab [45]). For these mAbs, the mean C _max-values vary from 20.6 nM to 3.2 μM, thus being 1–3 orders of magnitude lower than the concentration of endogenous IgG.

To inform the development and interpretation of classical compartment models, we determined which simple compartment model structures are consistent with the simplified PBPK model. Such an approach has several advantages: (i) the lumping approach links the mechanistic interpretation of a PBPK model to the classical compartment models and thereby suggests possible interpretations; (ii) the model reduction process links the two levels of description and shows that the two approaches are not so different; (iii) if one is interested in parameter estimation for a PBPK model, lumping might provide a means to stabilize the estimation process; (iv) a mismatch between a minimal lumped model arising from a PBPK model and simple compartment model suggests that there is something missing, either in the PBPK model or in the classical compartment model, or in both; (v) the reduction process offers a systematic means to derive covariate relationships for classical compartment models based on the integration of the covariate in the PBPK model. This is usually much simpler due to the mechanistic interpretation of parameters in a PBPK model; see [46] for full details.

Based on the experimental data in mice, we showed that several definitions of the central compartment are consistent with the data (see "Minimal lumped models and the interpretation of classical compartment models" section). The central compartment could comprise only plasma and lung or, e.g., it could comprise all tissues except for adipose, muscle, gut, bone, and skin. Other scenarios are possible.

While it is common knowledge for small molecule drugs that parameters of classical compartment models generally allow only for an apparent interpretation, this seems to be much less acknowledged for monoclonal antibodies. Although mAbs generally do not exhibit non specific binding—in contrast to small molecule drugs—, this does not imply that apparent volumes are identical to anatomical volumes. In general, the following relation holds

$$V_{\rm apparent} = K_{\rm tissue} \cdot V_{\rm anatomical},$$

where K _tissue denotes the tissue-to-plasma partition coefficient. For the mice data, the estimated tissue-to-plasma partition coefficients are identical to the antibody biodistribution coefficients (see Eq. (9) and [23]). The values range from 0.03 to 0.17 (see Table 5) and therefore are quite different from 1—a value that would result in V _apparent = V _anatomical. For the mAb 7E3 in mice, we obtained for the physiological volumes V _cen = 3.4 mL and V _per = 20.0 mL, while the apparent volumes are much smaller with V ₁ = 1.9 mL and V ₂ = 1.1 mL, see Table 7 and Eq. (20). In particular the central volume V ₁ has often been associated with the plasma volume (for mice, it is V _pla = 1.7 mL according to Table 4). Such an interpretation, however, is not supported by classical compartment modeling. It is also not in line with our expectations arising from the simplified PBPK model, neither with the experimental data shown in Fig. 2, which clearly show two groups of tissues, (i) lung, heart, kidney, liver, spleen, gut that behave kinetically similarly to plasma; and (ii) muscle and skin, which both are kinetically similar, but not to plasma.

We finally remark that the simplest way to code the simplified PBPK model in the case of an i.v. administration is based on Eqs. (1–2) with species-dependent parameters given in Table 4, plasma clearance CLpla given in Table 6 (sc. 7) and E _tis = CLint_tis = 0 for all tissues. Due to Eq. (6), the partition coefficients fulfill $K_{\rm tis}=\widehat{K}_{\rm tis}$ and can therefore be taken from Table 5. For extrapolation of the simplified PBPK model to other species/strains, one can make use of the ABC_tis values (see Table 5, assumed to be species-independent in [23]) by exploiting the relationship in Eq. (9). Then, only the physiological data (often readily available from literature) and the plasma clearance CLpla are missing. In addition, the simplified PBPK model can be used to ”extrapolate” to FcRn knockout mice by simply increasing the plasma clearance (by a factor of 23), thereby accounting for the loss in protection from degradation. The partition coefficients, as was already remarked in [23], are comparable for wild type and knock-out mice.

Recently, a minimal PBPK model for mAb disposition was published by Cao et al. [47]. Our model differs in scope since we explicitly (i) allow to take into account and compare to (experimental) tissue data (important in pre-clinical development); (ii) allow to leverage on the antibody biodistribution coefficients (quantifying the extent of tissue distribution of mAbs) that have been very recently introduced in [23] and shown to be species independent; furthermore, we (iii) provide a general strategy for model reduction and a direct link of the resulting minimal lumped models to classical compartment models, thereby supporting this crucial modeling approach (the standard model type in population analysis of clinical data) with structure and interpretation. Our minimal lumped model comprises only 2 compartments (as is the most frequently used number in classical compartment models for mAbs), in contrast to the minimal PBPK model in [47] that comprises 4 compartments; and finally (iv) we provide critical insight into the identifiability issue of detailed PBPK models (as discussed above).

While the focus in this article is on the disposition of mAbs not related to the target, we have outlined in "Extension of the simplified PBPK model to account for membrane bound target receptors" section how to integrate a target into the simplified PBPK model. First results (not shown) support the statement in [9] that in the presence of a significant target mediated elimination pathway, the linear component of the total clearance plays a minor role in determining the disposition of monoclonal antibodies.

In summary, we believe that the results presented herein contribute to a better understanding of mAb disposition and its representation in terms of PBPK and classical compartment models.

The Matlab code is available from the corresponding author’s website (under menu item publications) at URL http://compphysiol.math.uni-potsdam.de.

Appendices

Appendix: The role of FcRn and endogenous IgG in PBPK models of mAb disposition

From saturable IgG–FcRn interaction to linear mAb clearance

We illustrate that under commonly encountered (dosing) conditions, the clearance of mAbs in the endosomal space can be expected to be linear, regardless of the level of saturation of FcRn that protect mAb from degradation.

Denoting by IgG_mAb and IgG_endo the therapeutic and endogenous IgG concentrations in the endosomal space of endothelial cells, the resulting total IgG concentration was given by

$${\rm IgG} = {\rm IgG}_{\rm endo} + {\rm IgG}_{\rm mAb}.$$

In the endosomal space, free IgG binds to free FcRn with a dissociation constant K _D forming an ${\rm IgG}\!:\!{\rm FcRn}$ complex. The relevance of FcRn stems from the fact that it protects IgG from catabolism [48]: While the complex is recycled to the interstitial and/or plasma space, free IgG is eventually catabolized in the lysosomes:

$$\begin{aligned} &{\rm IgG}_{\rm u} + {\rm FcRn}_{\rm u} \;\overset{\overset{K_{\rm D}}{\longrightarrow}}{\longleftarrow}\; {\rm IgG}_{\rm b} \longrightarrow \rm{recycling}\\ &{\rm IgG}_{\rm u} \;\overset{k_{\rm deg}}{\longrightarrow}\; {\rm catabolism} \end{aligned}$$

To study the IgG–mAb interaction in more detail, we denoted by FcRn_u free FcRn, and by IgG_u and IgG_b the free and FcRn-bound IgG. Consequently, IgG_u is the sum of the free endogenous and free therapeutic IgG. Two conservation relations IgG = IgG_u + IgG_b and FcRn = FcRn_u + IgG_b hold.

In the sequel, we made the assumption that the K _D values of IgG_endo and IgG_mAb are comparable. This is a reasonable assumption for most mAbs—however, it does not hold for mAbs specifically engineered for high binding affinity to FcRn.

Binding processes are typically fast compared to the time-scale of other pharmacokinetic processes. Assuming a quasi-steady state for FcRn binding yielded ${\rm IgG}_{\rm u} \cdot {\rm FcRn}_{\rm u} = K_{\rm D} \cdot {\rm IgG}_{\rm b}$. Solving for the bound concentration and exploiting the conservation relations yielded

$${\rm IgG}_{\rm b} = \frac{{\rm FcRn}_{\rm u}}{K_{\rm D} +{\rm FcRn}_{\rm u}} \cdot {\rm IgG}.$$

(30)

Exploiting again the second conservation relation, we obtained

$${\rm FcRn} = {\rm FcRn}_{\rm u} + \frac{{\rm FcRn}_{\rm u}}{K_{\rm D} + {\rm FcRn}_{\rm u}} \cdot {\rm IgG}$$

and finally

$${\rm FcRn}_{\rm u} = \frac{1}{2} \Big({\rm FcRn}_{\rm eff} + \sqrt{({\rm FcRn}_{\rm eff})^2 + 4K_{\rm D}\cdot {\rm FcRn}} \Big)$$

(31)

with FcRn_eff = (FcRn − IgG − K _D). This allowed us to determine the fraction unbound fu_IgG based on Eq. (30) as

$${\rm fu}_{\rm IgG} = \frac{{\rm IgG}_{\rm u}}{{\rm IgG}} = 1-\frac{{\rm IgG}_{\rm b}}{{\rm IgG}} = \frac{K_{\rm D}}{K_{\rm D} + {\rm FcRn}_{\rm u}}$$

(32)

with FcRn_u defined in Eq. (31). We defined the level of saturation of FcRn as

$${\rm FcRn \,saturation \,level} = \frac{{\rm FcRn}-{\rm FcRn}_{\rm u}}{{\rm FcRn}}.$$

Figure 7 (left) shows the FcRn-saturation level as a function of the total IgG concentration, expressed in terms of units of total FcRn. We clearly identified two regimes: (i) for IgG lower than FcRn, the saturation level of FcRn appears to be linearly increasing with increasing IgG concentration; (ii) for IgG larger than total FcRn, the FcRn-saturation level appears to be 1. As shown below in "Theoretical derivation of FcRn saturation level and fraction unbound of mAb" section, this behavior can be theoretically justified based on the reasonable assumption that K _D ≪ FcRn, i.e., that IgG has a very high affinity to FcRn. This assumption is in line with the physiological function of FcRn. For the mAb 7E3 in mice, we estimated the total FcRn concentration to be $2.2 \cdot 10^5$ nM, while K _D was reported to be 4.8 nM (see Table 1), thereby supporting the assumption K _D ≪ FcRn.

Fig. 7

FcRn saturation level (left) and fraction unbound of IgG (right) as a function of the total IgG concentration (stated in units of total FcRn). Due to the high affinity binding of IgG to FcRn, the FcRn saturation level growth practically linearly with IgG concentration, until FcRn is fully saturated. As a consequence, the fraction unbound fu_IgG of IgG is practically zero until IgG concentration exceeds total FcRn concentration, when it follows the form fu_IgG = 1 − FcRn/IgG. We choose FcRn = 10⁵ nM and K _D = 4.8 nM, in line with values reported in Table 1

As shown in Fig. 7 (right), the fraction unbound fu_IgG also exhibited two regimes: (i) a phase of IgG concentration below FcRn, where fu_IgG is almost zero, and (ii) a phase of hyperbolic increase for IgG above FcRn. This behavior can again be justified theoretically, as shown in the Appendix "Theoretical derivation of FcRn saturation level and fraction unbound of mAb" and summarized as

$${\rm fu}_{\rm IgG} = \left\{ \begin{array}{ll} 0; & {\rm IgG} \leq {\rm FcRn} \\ 1-\frac{{\rm FcRn}}{{\rm IgG}}; & {\rm IgG} > {\rm FcRn}\\ \end{array}\right.$$

Without the underlying theoretical justification, such a model was proposed in [4], termed the cutoff model, based on some cutoff value ‘MAX’ (that is identical to total FcRn).

The above derivations have direct impact on modeling endosomal clearance and the FcRn-mediated salvage mechanism for a large number of mAbs. If the total IgG concentration is dominated by endogenous IgG and hardly perturbed by the administration of therapeutic IgG, i.e, IgG_mAb ≪ IgG_endo, which implies IgG ≈ IgG_endo, then the fraction unbound of mAb is constant, i.e.,

$${\rm fu}_{\rm mAb} = {\rm fu}_{\rm IgG} \approx {\rm fu}_{{\rm IgG}_{\rm endo}} = {\rm const}.$$

(33)

Such a situation is quite common for many mAbs. In mice, the baseline concentration of endogenous plasma IgG1 is reported to be 14.7 μM in [26, 49]. In [4], the author showed that the administration of an i.v. bolus of 8 mg/kg therapeutic IgG (7E3) does not affect the overall endogenous plasma level of IgG. The same can be shown to hold true for many mAbs in human (see "Discussion" section). Under such conditions, the extent of saturation of FcRn and consequently the fraction unbound fu_mAb only depends on the endogenous IgG concentration; in other words, it is set by the endogenous IgG levels.

Theoretical derivation of FcRn saturation level and fraction unbound of mAb

The special form of the dependance of the

$${\rm FcRn\,saturation\,level} = 1-\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}$$

(34)

on the total IgG concentration can be theoretically justified from Eq. (31). To this end, we introduced the parameters

$$\epsilon = \sqrt{\frac{K_{\rm D}}{{\rm FcRn}}} \quad{\rm and }\quad {\it x} = 1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}}.$$

(35)

Due to very tight binding of endogenous IgG and mAb to FcRn, we made the reasonable assumption that $\epsilon$ is very small, i.e., $\epsilon\ll1$. For 7E3 in mice, we estimated $\epsilon<5\cdot10^{-3}$ from Table 1. Dividing in Eq. (31) both sides by FcRn yielded the fraction unbound of FcRn:

$$\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}} = \frac{1}{2} \left( 1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}} + \sqrt{\left(1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}}\right)^2 + 4\epsilon^2}\right),$$

(36)

or ${\rm FcRn}_{\rm u}/{\rm FcRn}=1/2\cdot(x+\sqrt{x^2+4\epsilon^2}).$ When ${\rm IgG}/{\rm FcRn}=(1-\epsilon)$, i.e., when (total) IgG concentration is approximately equal to the (total) FcRn concentration, it is x = 0 and therefore ${\rm FcRn}_{\rm u}/{\rm FcRn}=\epsilon$. Now, the larger the IgG concentration, the larger the bound fraction of FcRn and the smaller the unbound fraction of FcRn. Thus, ${\rm IgG}/{\rm FcRn}\geq(1-\epsilon)$ implies

$$\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}\leq \epsilon.$$

(37)

This finally resulted in the lower bound on the FcRn saturation level:

$$\rm{FcRn\,saturation \,level} = 1-\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}} \geq 1-\epsilon$$

(38)

for ${\rm IgG}/{\rm FcRn}\geq(1-\epsilon)$. For the upper bound for small IgG concentrations with $\epsilon< x$, we used a simple estimate on the square-root term $\sqrt{x^2+4\epsilon^2} < \sqrt{x^2+4x\epsilon}$ and applied the Taylor expansion to first order

$$\sqrt{x^2+ 4\epsilon x} \;\dot{ = }\; x + 2\epsilon$$

(39)

for $x\gg \epsilon$. This resulted in

$$\frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}} \leq 1-\epsilon^2-\frac{{\rm IgG}}{{\rm FcRn}} +\epsilon.$$

(40)

On the other hand, by simply neglecting the $4\epsilon^2$ term in the square root in Eq. (36), we obtained

$$1-\epsilon^2 - \frac{{\rm IgG}}{{\rm FcRn}} \leq \frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}.$$

(41)

From these two inequalities and Eq. (34) we finally obtained

$$\frac{{\rm IgG}}{{\rm FcRn}} -\epsilon\cdot(1-\epsilon) \leq \rm{FcRn \,saturation\, level} < \frac{{\rm IgG}}{{\rm FcRn}} + \epsilon^2$$

(42)

for $x\gg \epsilon,$ i.e., ${\rm IgG}/{\rm FcRn}\ll 1-\epsilon-\epsilon^2$. Taken together, Eqs. (38) and (42) theoretically justify the peculiar form of the FcRn-saturation level depicted in Fig. 7 (left).

The above derivation also allowed us to theoretically justify the dependence of the fraction unbound fu_IgG on IgG, as shown in Fig. 7 (right). For ${\rm IgG}/{\rm FcRn}=(1-\epsilon)$ it is ${\rm FcRn}_{\rm u}/{\rm FcRn}=\epsilon$ as before, and

$$\begin{aligned} {\rm fu}_{\rm IgG} =& \frac{K_{\rm D}}{K_{\rm D}+{\rm FcRn}_{\rm u}} = \frac{\epsilon^2}{\epsilon^2+{\rm FcRn}_{\rm u}/{\rm FcRn}} \\ =& \frac{\epsilon^2}{\epsilon^2+\epsilon} = \frac{\epsilon}{1+\epsilon} < \epsilon. \end{aligned}$$

(43)

Since fu_IgG decreases monotonically with decreasing IgG concentration, the bound ${\rm fu}_{\rm IgG}<\epsilon$ continues to hold for all ${\rm IgG}<(1-\epsilon){\rm FcRn}$. For larger IgG concentrations, we started from the relation

$$\begin{aligned} {\rm fu}_{\rm IgG} =& \frac{{\rm IgG}_{\rm u}}{{\rm IgG}} = \frac{{\rm IgG}-({\rm FcRn}-{\rm FcRn}_{\rm u})}{{\rm IgG}} \\ =& 1-\frac{{\rm FcRn}}{{\rm IgG}} + \frac{{\rm FcRn}_{\rm u}}{{\rm FcRn}}\cdot \frac{{\rm FcRn}}{{\rm IgG}}, \end{aligned}$$

(44)

where we exploited IgG_b = FcRn_b = FcRn − FcRn_u. For ${\rm IgG}/{\rm FcRn}\geq (1-\epsilon),$ we obtained with (37) the inequality

$$1-\frac{{\rm FcRn}}{{\rm IgG}} \leq {\rm fu}_{\rm IgG} < 1-\frac{{\rm FcRn}}{{\rm IgG}} +\epsilon \cdot (1-\epsilon),$$

(45)

where the first inequality trivially follows from Eq. (44). Taken together, Eqs. (43) and (45) theoretically justify the peculiar form of the fraction unbound of IgG depicted in Fig. 7 (right).

Step-wise reduction of a detailed PBPK model of mAb disposition

Eliminating the need of endogenous IgG

The starting point of our simplified model was the tissue model of mAb disposition presented in [7, Fig. 2]. The tissue model comprised the vascular, endosomal and interstitial sub-compartments with the corresponding volumes V _p, V _e and V _i. The following processes were considered: (i) transport into the interstitial space via convective transport through the paracellular pores in the endothelium (simplified two-pore model); (ii) convective transport via the lymph fluid from the interstitial space; (iii) uptake from the plasma and interstitial spaces into the endosomal compartments via fluid phase endocytosis; (iv) binding to FcRn in the endosomal compartments, (v) salvage of FcRn-bound complexes to the plasma and interstitial spaces; (vi) lysosomal degradation of the unbound species in the endosomal spaces. The corresponding system of differential equations for the rates of change of the (total) concentration in the vascular space C _p, in the endosomal space C _e and in the interstitial space C _i are given by

$$V_{\rm p} {\rm \frac{d}{dt}}{C_{\rm p}} = Q \cdot C_{\rm in} - (Q-L) \cdot C_{\rm p} - L (1-{\rm \sigma_{\rm vas}}) C_{\rm p}- V_{\rm p} k_{\rm in} \cdot C_{\rm p} + {\rm FR} \cdot V_{\rm e} k_{\rm out} (1-{\rm fu}) C_{\rm e}$$

(46)

$$V_{\rm e} {\rm \frac{d}{dt}}{C_{\rm e}} = V_{\rm p} k_{\rm in} \cdot C_{\rm p} + V_{\rm i} k_{\rm in} \cdot C_{\rm i} - V_{\rm e} k_{\rm out} (1-{\rm fu})\cdot C_{\rm e}-{\rm CL}_{\rm e} \cdot {\rm fu} \cdot C_{\rm e}$$

(47)

$$V_{\rm i} {\rm \frac{d}{dt}}{C_{\rm i}} = L(1-{\rm \sigma_{\rm vas}})C_{\rm p} - L(1-{\rm \sigma_{\rm lymph}}) C_{\rm i} - V_{\rm i} k_{\rm in}\cdot C_{\rm i}+ (1-{\rm FR}) \cdot V_{\rm e} k_{\rm out} (1-{\rm fu})\cdot C_{\rm e},$$

(48)

with the parameters having the following meaning: Q and L denoted the plasma and lymph flows, ${\rm \sigma_{\rm vas}}$ and ${\rm \sigma_{\rm lymph}}$ denoted the vascular and lymphatic reflection coefficients, k _in denoted the endosomal uptake rate constant, k _out denoted the recirculation rate constant, and FR denoted the recirculation fraction of bound antibody from the endosomal into the vascular space. The unbound antibody in the endosomal space was subject to elimination following a linear clearance denoted by CL_e. The fraction unbound fu in the endosome was defined as in Eq. (32).

The authors in [7] explicitly considered endogenous IgG in their model—in addition to therapeutic IgG to account for the competition for binding of mAb and endogenous IgG to FcRn. Based on the observation preceding Eq. (33) and thereon based derivations, we could greatly simplify the above tissue model by only implicitly considering endogenous IgG. We indeed assumed that the fraction unbound of mAb in the endosome is constant. Therefore, we defined the total FcRn-mediated export flow and the endosomal intrinsic clearance as

$$Q_{\rm out} = V_{\rm e} k_{\rm out} \cdot (1-{\rm fu})$$

(49)

$${\rm CLint}_{\rm e} = {\rm CL}_{\rm e} \cdot {\rm fu}.$$

(50)

This was the basis for an intermediate complexcity of a PBPK model for mAbs disposition.

An intermediate complexity of PBPK models for mAb disposition

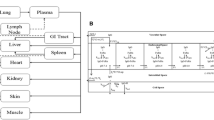
The intermediate PBPK model comprised 32 compartments representing the most relevant anatomical spaces involved in mAb disposition (see Fig. 8): venous (ven) and arterial (art) plasma as well as the vascular plasma (p), endosomal (e) and interstitial (i) spaces of ten tissues. In addition to the process at the tissue level, the model incorporated the distribution of mAb via the plasma flow and the convective transport with the lymph flow from the interstitial spaces back into the plasma circulation. The rates of change of all concentrations are given by

$$\begin{aligned} V_{\rm ven} {\rm \frac{d}{dt}} C_{\rm ven} =& Q_{\rm ven}\cdot (C_{{\rm in},{\rm ven}}-C_{\rm ven}) \\ +& \sum_{\rm tis} L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} \end{aligned}$$

$$\begin{aligned} V_{\rm art} {\rm \frac{d}{dt}} C_{\rm art} = & (Q_{\rm lun} - L_{\rm lun})\cdot C_{{\rm p},{\rm lun}} - Q_{\rm art}\cdot C_{\rm art} \end{aligned}$$

(51)

$$\begin{aligned} V_{{\rm p},{\rm tis}}{\rm \frac{d}{dt}} C_{{\rm p},{\rm tis}} &= Q_{\rm tis}\cdot C_{{\rm in},{\rm tis}} - (Q_{\rm tis}-L_{\rm tis})\cdot C_{{\rm p},{\rm tis}} \\ &\quad- L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) C_{{\rm p},{\rm tis}} - V_{{\rm p},{\rm tis}} k_{\rm in}\cdot C_{{\rm p},{\rm tis}} \\ &\quad + {\rm FR} Q_{{\rm out},{\rm tis}}\cdot C_{{\rm e},{\rm tis}} \end{aligned}$$

(52)

$$\begin{aligned} V_{{\rm e},{\rm tis}}{\rm \frac{d}{dt}} C_{{\rm e},{\rm tis}} = V_{{\rm p},{\rm tis}} k_{\rm in}\cdot C_{{\rm p},{\rm tis}} + V_{{\rm tis},{\rm i}} k_{\rm in}\cdot C_{{\rm tis},{\rm i}} - Q_{{\rm out},{\rm tis}} \cdot C_{{\rm e},{\rm tis}} -{\rm CLint}_{\rm e} \cdot C_{{\rm e},{\rm tis}} \end{aligned}$$

(53)

$$\begin{aligned} V_{{\rm i},{\rm tis}}{\rm \frac{d}{dt}} C_{{\rm i},{\rm tis}} = & L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) C_{{\rm p},{\rm tis}}- V_{{\rm i},{\rm tis}} k_{\rm in}\cdot C_{{\rm i},{\rm tis}}\\ & - L_{\rm tis} (1-{\rm \sigma_{\rm lymph}}) C_{{\rm i},{\rm tis}}\\ & + (1-{\rm FR}) Q_{{\rm out},{\rm tis}}\cdot C_{{\rm e},{\rm tis}}. \end{aligned}$$

(54)

For all tissues except vein, artery, liver and lung, the inflowing concentration C _in was given by C _in, tis = C _art; for lung, it was $C_{{\rm in},{\rm lun}}=C_{\rm ven}$. For vein, it was

$$Q_{\rm ven} C_{{\rm in},{\rm ven}} = \sum_{{\rm tis}}\left(Q_{\rm tis}-L_{\rm tis}\right)\cdot C_{{\rm p},{\rm tis}}$$

(55)

with tis = adi, bon, hea, kid, liv, mus, ski. For liver, it was

$$\begin{aligned} Q_{\rm liv} C_{{\rm in},{\rm liv}} =& \sum_{{\rm tis}}(Q_{\rm tis}-L_{\rm tis})\cdot C_{{\rm p},{\rm tis}}+ \\ &\Big(Q_{\rm liv} - \sum_{\rm tis}Q_{\rm tis}\Big) \cdot C_{\rm art} \end{aligned}$$

(56)

with tis = gut, spl. The mAb was administered via an i.v. bolus infusion. For the vein, the initial condition of the above system of differential equations was set to

$$C_{\rm ven}(0) = \frac{{\rm dose}}{V_{\rm ven}},$$

(57)

while we set C _cmt(0) = 0 for all other compartments ’cmt’.

Fig. 8

Detailed PBPK model structure. Top structure of the PBPK model for mAbs. Organs, tissues and plasma spaces are interconnected by the plasma flow (red and blue solid arrows) and the lymphatic system (green dashed arrows). Bottom detailed organ model comprising a plasma compartment, the endosomal and the interstitial spaces. Q and L represent the plasma and lymph flow, ${\rm \sigma_{\rm vas}}$ and ${\rm \sigma_{\rm lymph}}$ denote the vascular and lymphatic reflection coefficients, k _in is the rate of uptake of mAb from the plasma or interstitial space into the endosomal space. The parameter k _out is the recycling rate constant of mAb from the endosomal space (with a fraction FR recycled into the vascular space), while fuCL_e denotes its linear clearance in the endosomal space

Lumping all (vascular) plasma spaces and tissue sub-compartments

The following reduction was justified based on time-scale arguments. To this end, we considered the generic ODE for the rate of change of the concentration C _cmt of some compartment ‘cmt’ with inflow Q _inflow and outflow Q _outflow:

$$V_{\rm cmt} {\rm \frac{d}{dt}}{C_{\rm cmt}} = Q_{\rm inflow} \cdot C_{\rm in} - Q_{\rm outflow} \cdot C_{\rm cmt}.$$

(58)

The response time τ_cmt—i.e., the time scale, on which the compartment concentration responses to changes in the inflowing concentration C _in—is given by

$$\tau_{\rm cmt} = \frac{\ln(2)}{Q_{\rm outflow}/V_{\rm cmt}}.$$

(59)

Hence, small compartments or compartments with large outflow response quickly to changes in the inflow. Of note, the inflow Q _inflow does only influence the concentration levels C _cmt and its steady state concentration, but has no impact on the response time.

In view of the systems of ODEs Eqs. (51–54), we identified three groups of compartments with different response times (supported by parameters values published in [7–10] and physiological insight):

• Fast: Arterial and venous plasma and peripheral plasma of all tissues with response times

  $$\tau_{\rm art} = \frac{\ln(2)}{Q_{\rm art}/V_{\rm art}}; \quad \tau_{\rm ven} = \frac{\ln(2)}{Q_{\rm ven}/V_{\rm ven}},$$

  and

  $$\tau_{{\rm p},{\rm tis}} = \frac{\ln(2)}{(Q_{\rm tis}-L_{\rm tis})/V_{{\rm p},{\rm tis}}}.$$

  We define τ_pla as the average of the above response times.

• Intermediate: The interstitial space of all tissues, with response times

  $$\tau_{\rm i} < \frac{\ln(2)}{(1-{\rm \sigma_{\rm lymph}})L_{\rm tis}/V_{\rm i}}.$$

  We define τ_int as the average of the above response times. Comparison to plasma response time: V _pla and V _i are roughly of the same order of magnitude (e.g. [5]), while L _tis is roughly two-orders of magnitude smaller than Q _tis, and $(1-{\rm \sigma_{\rm lymph}})=0.8$ [7]. Consequently, plasma & vascular compartments response is approximately two-orders of magnitude faster than the interstitial compartments, i.e., τ_pla ≪ τ_int. Of note, the much slower inflow corresponding to $(1-{\rm \sigma_{\rm vas}})L_{\rm tis}$ does not influence the response time, it only influences the interstitial concentration levels.

• Slow: The endosomal space of all tissues, with response times

  $$\tau_{\rm e} < \frac{\ln(2)}{(Q_{{\rm out},{\rm tis}}+{\rm CLint}_{\rm e})/V_{\rm e}} \leq \frac{\ln(2)}{Q_{{\rm out},{\rm tis}}/V_{\rm e}}.$$

  We define τ_end as the average of the above response times. According to [7], V _e is approximately two-orders of magnitude smaller than V _i, while at the same time Q _out, tis is five orders of magnitude smaller than Q _tis and therefore three orders of magnitude smaller than L _tis. Consequently, interstitial compartments response is approximately one order of magnitude faster than the endosomal compartments, i.e., τ_int < τ_end.

The above time-scale considerations suggest to lump together arterial and venous plasma and all peripheral plasma spaces, resulting in a lumped plasma compartment with total plasma volume V _pla and plasma concentration defined by

$$V_{\rm pla} \cdot C_{\rm pla} = V_{\rm art} C_{\rm art} + V_{\rm ven} C_{\rm ven} + \sum_{\rm tis} V_{{\rm p},{\rm tis}} C_{{\rm p},{\rm tis}}.$$

(60)

Moreover, due to the larger uncertainty of parameters related to the endosomal space, we decided to lump together the interstitial and endosomal space of each tissue. For easier comparison to experimental data, we also included the intracellular space with volume V _c, and defined the tissue volume by V _tis = V _i + V _e + V _c and the tissue concentration by

$$V_{\rm tis} \cdot C_{\rm tis} = V_{\rm i} \cdot C_{\rm i} + V_{\rm e} \cdot C_{\rm e} + V_{\rm c} \cdot C_{\rm c}.$$

(61)

Since the mAb—in the absence of a target—does not distribute in the intracellular space, it is C _c = 0.

We finally derived the ODEs describing the rate of change of C _pla and C _tis in the different tissues. For plasma, we obtained

$$\begin{aligned} V_{\rm pla} {\rm \frac{d}{dt}}{C_{\rm pla}} =& V_{\rm art} {\rm \frac{d}{dt}}{C_{\rm art}} + V_{\rm ven} {\rm \frac{d}{dt}}{C_{\rm ven}} + \sum_{\rm tis} V_{{\rm p},{\rm tis}} {\rm \frac{d}{dt}}{C_{{\rm p},{\rm tis}}} \\ =& \sum_{\rm tis} L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} + {\rm FR} Q_{{\rm out},{\rm tis}} C_{{\rm e},{\rm tis}} \\ & - \left( L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) + V_{{\rm p},{\rm tis}} k_{\rm in} \right) C_{{\rm p},{\rm tis}}. \end{aligned}$$

We subsequently exploited $C_{\rm pla}=C_{\rm ven}=C_{\rm art}=C_{{\rm p},{\rm tis}}$ and made the following assumptions, to derive the final equation for plasma: (i) Since it is difficult to distinguish between the two-pore-related and the fluid-phase endocytotic part of the vascular extravasation, i.e., $L_{\rm tis} (1-{\rm \sigma_{\rm vas}})$ versus $V_{{\rm p},{\rm tis}} k_{\rm in}$, we only used a single term ($L_{\rm tis} (1-\sigma_{\rm tis})$) and introduced an effective lumped reflection coefficient σ_tis such that

$$L_{\rm tis} (1-\sigma_{\rm tis}) = L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) + V_{{\rm p},{\rm tis}} k_{\rm in}$$

(62)

Further, (ii) since we lump all tissue sub-compartments, we assumed that $C_{\rm e}$and $C_{\rm i}$ are multiples of the lumped concentration C _tis, i.e. C _e = α C _tis and $C_{\rm i}=\beta C_{\rm tis}$. Writing moreover $Q_{{\rm out},{\rm tis}}$ as a fraction δ of the lymph flow L _tis yielded

$$\begin{aligned} {L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} + {\rm FR}\, Q_{{\rm out},{\rm tis}} C_{{\rm e},{\rm tis}} } \;=\; L_{\rm tis} \big( (1-{\rm \sigma_{\rm lymph}})\beta + {\rm FR}\, \delta \alpha \big) \cdot C_{\rm tis} \end{aligned}$$

(63)

and allowed us to define the tissue partition coefficient K _tis as

$$\frac{1}{K_{\rm tis}} = (1-{\rm \sigma_{\rm lymph}})\beta + {\rm FR} \,\delta \alpha.$$

As a consequence, we obtained the final ODE for the rate of change of the plasma concentration

$$V_{\rm pla} {\rm \frac{d}{dt}}{C_{\rm pla}} = \sum_{\rm tis} L_{\rm tis} \frac{C_{\rm tis}}{K_{\rm tis}} - L_{\rm tis} (1-\sigma_{\rm tis}) C_{\rm pla},$$

which is identical to Eq. (2). For the tissue concentration C _tis we obtained

$$\begin{aligned} V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} \;=\;& V_{\rm i} {\rm \frac{d}{dt}}{C_{\rm i}} + V_{\rm e} {\rm \frac{d}{dt}}{C_{\rm e}} + V_{\rm c} {\rm \frac{d}{dt}}{C_{\rm c}} \\ \;=\;& \left( L_{\rm tis} (1-{\rm \sigma_{\rm vas}}) + V_{{\rm p},{\rm tis}} k_{\rm in} \right) C_{{\rm p},{\rm tis}} \\ & - L_{\rm tis} (1-{\rm \sigma_{\rm lymph}})C_{{\rm i},{\rm tis}} - {\rm FR}\, Q_{{\rm out},{\rm tis}} C_{{\rm e},{\rm tis}} \\ & - {\rm CLint}_{\rm e} \cdot C_{{\rm e},{\rm tis}}. \end{aligned}$$

Defining the intrinsic tissue clearance ${\rm CLint}_{\rm tis} = {\rm CLint}_{\rm e}\cdot\alpha$ and using the same assumptions and arguments as above, we obtained

$$V_{\rm tis} {\rm \frac{d}{dt}}{C_{\rm tis}} = L_{\rm tis} (1-\sigma_{\rm tis}) C_{\rm pla} - L_{\rm tis} \frac{C_{\rm tis}}{K_{\rm tis}} - {\rm CLint}_{\rm tis} \cdot C_{\rm tis},$$

which is identical to Eq. (1). In summary, we derived our simplified PBPK model given in Eqs. (1–2) from a much more detailed PBPK model by considering time-scale separation and additional well-grounded assumptions. The resulting number of equations was reduced by a factor of approximately 6 and 3 in comparison to [7] and [10], respectively.

Derivation of the ODEs of the lumped compartments

Based on Eq. (13), we derived the ODE describing the rate of change of the lumped concentrations C _L with L = {${\rm tis}_1, \ldots, {\rm tis}_k$}. To this end, we first established the relation between the lumped concentration C _L and some tissue concentrations C _tis with ${\rm tis}\in{\rm L}$. Starting from Eq. (13), we obtained

$$\begin{aligned} V_{\rm L} \cdot C_{\rm L} =& \sum_{i=1}^k V_{{\rm tis}_i} \cdot C_{{\rm tis}_i} \\ =& \sum_{i=1}^k \left( V_{{\rm tis}_i} (1-\sigma_{{\rm tis}_i}) \widehat{K}_{{\rm tis}_i} \cdot \frac{C_{{\rm tis}_i}}{(1-\sigma_{{\rm tis}_i})\cdot \widehat{K}_{{\rm tis}_i}} \right) \cr =& \left( \sum_{i=1}^k V_{{\rm tis}_i} (1-\sigma_{{\rm tis}_i}) \widehat{K}_{{\rm tis}_i} \right) \cdot \frac{C_{\rm tis}}{(1-\sigma_{\rm tis}) \cdot\widehat{K}_{\rm tis}} \\ =& V_{\rm L} (1-\sigma_{\rm L})\cdot \widehat{K}_{\rm L} \cdot \frac{C_{\rm tis}}{(1-\sigma_{\rm tis}) \cdot\widehat{K}_{\rm tis}}, \end{aligned}$$

where we used in the third line the lumping criterion $C_{\rm tis}/((1-\sigma_{\rm tis}) \cdot\widehat{K}_{\rm tis}) = C_{{\rm tis}_i}/((1-\sigma_{{\rm tis}_i})\cdot \widehat{K}_{{\rm tis}_i})$ for ${\rm tis}\in{\rm L}$ and i = 1,…, k; and in the last line we used Eq. (14). Rearranging the above equation yielded

$$C_{\rm tis} = (1-\sigma_{\rm tis}) \widehat{K}_{\rm tis} \cdot \frac{C_{\rm L}}{(1-\sigma_{\rm L}) \widehat{K}_{\rm L}}.$$

(64)

For the plasma compartment, this specifically read

$$C_{\rm pla} = \frac{C_{\rm cen}}{(1-\sigma_{\rm cen}) \widehat{K}_{\rm cen}}.$$

For all compartments except for the central compartment, we obtained

$$\begin{aligned} V_{\rm L} {\rm \frac{d}{dt}}{C_{\rm L}} \;=\;& \sum_{{\rm tis}\in{\rm L}} L_{\rm tis} \cdot \left( (1-\sigma_{\rm tis}) C_{\rm pla} - \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} \right) \\ \;=\;& \sum_{{\rm tis}\in{\rm L}} L_{\rm tis} (1-\sigma_{\rm tis}) \left(C_{\rm pla} - \frac{C_{\rm tis}}{(1-\sigma_{\rm tis})\widehat{K}_{\rm tis}} \right) \\ \;=\;& \sum_{{\rm tis}\in{\rm L}} L_{\rm tis} (1-\sigma_{\rm tis}) \left(C_{\rm pla} - \frac{C_{\rm L}}{(1-\sigma_{\rm L})\widehat{K}_{\rm L}} \right) \\ \;=\;& L_{\rm L}(1-\sigma_{\rm L}) \left( C_{\rm pla} - \frac{C_{\rm L}}{(1-\sigma_{\rm L})\widehat{K}_{\rm L}} \right). \end{aligned}$$

where we exploited Eq. (64) in the third line. Thus

$$\begin{aligned} V_{\rm L} {\rm \frac{d}{dt}}{C_{\rm L}} \;=\;& L_{\rm L} \left((1-\sigma_{\rm L}) C_{\rm pla} - \frac{C_{\rm L}}{\widehat{K}_{\rm L}} \right) \\ \;=\;& L_{\rm L} \left((1-\sigma_{\rm L}) C_{\rm pla} - \frac{C_{\rm L}}{K_{\rm L}} \right) - {\rm CLint}_{\rm L} C_{\rm L}. \end{aligned}$$

For the central compartment, we obtained

$$\begin{aligned} V_{\rm cen} {\rm \frac{d}{dt}}{C_{\rm cen}}&= \sum_{{\rm tis}} L_{\rm tis} \left( \frac{C_{\rm tis}}{K_{\rm tis}} - (1-\sigma_{\rm tis}) C_{\rm pla} \right) +{\ldots} \\ &\quad + \sum_{{\rm tis}\in{\rm cen}} L_{\rm tis} \left((1-\sigma_{\rm tis})C_{\rm pla} - \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} \right)\\ &= \sum_{{\rm tis}\notin{\rm cen}} L_{\rm tis} (1-\sigma_{\rm tis})\left( \frac{C_{\rm tis}}{(1-\sigma_{\rm tis})K_{\rm tis}} - C_{\rm pla} \right) +{\ldots} \\ &\quad+ \sum_{{\rm tis}\in{\rm cen}} L_{\rm tis} \left( \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} - (1-\sigma_{\rm tis})C_{\rm pla} \right) \\ &\quad - E_{\rm tis} L_{\rm tis} \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} - \sum_{{\rm tis}\in{\rm cen}} L_{\rm tis} \cdot \left( \frac{C_{\rm tis}}{\widehat{K}_{\rm tis}} - (1-\sigma_{\rm tis}) C_{\rm pla} \right) \\ &= \sum_{{\rm L}} L_{\rm L} (1-\sigma_{\rm L})\left( \frac{C_{\rm L}}{(1-\sigma_{\rm L})\widehat{K}_{\rm L}} - C_{\rm pla} \right) \\ &\quad - E_{\rm cen} L_{\rm cen} (1-\sigma_{\rm cen}) \cdot C_{\rm pla} \\ &= \sum_{{\rm L}} L_{\rm L} \left( \frac{C_{\rm L}}{\widehat{K}_{\rm L}} - (1-\sigma_{\rm L})C_{\rm pla} \right) -{\rm CLpla}_{\rm cen} \cdot C_{\rm pla}\\ &= L_{\rm cen} \Big( C_{{\rm in},{\rm L}} - (1-\sigma_{\rm cen})C_{\rm pla} \Big) - {\rm CLpla}_{\rm cen} \cdot C_{\rm pla}, \end{aligned}$$

where we exploited in particular Eqs. (12) and (16). These equations are the foundation for the derivation of lumped compartment models in the next section.