INTRODUCTION

Target-mediated disposition (TMD) of a drug refers to the phenomenon that interaction of the drug with its in vivo target (ligand or receptor) significantly influences the drug disposition. A common case of TMD occurs in protein compounds that, upon binding to their cell-surface receptors, undergo endocytosis and subsequent lysosomal degradation. This has been suggested as a mechanism that contributes to systemic clearance for a list of recombinant human protein products including erythropoietin, granulocyte colony stimulating factor, thrombopoietin, interferon-β1a, and vascular endothelial growth factor (2–6). TMD also occurs with many therapeutic monoclonal antibodies (mAbs) that, by design, bind to their pharmacological targets with high affinity and specificity. When the amount or capacity of the accessible target, relative to the drug, is limited, TMD typically manifests nonlinear pharmacokinetics. Dirks and Meibohm recently reviewed population pharmacokinetics of 22 therapeutic mAbs of IgG isotypes, and among them 10 exhibited nonlinear pharmacokinetics because of TMD (7). The actual number is probably higher, since the type of nonlinear pharmacokinetic disposition, as a signature behavior of TMD, is not always observable in experimental data. The reason is that clinical doses, at which drugs are studied, often saturate the target-mediated elimination pathway and thereby mask the nonlinear pharmacokinetics.

When the non-compartmental analysis (NCA) method is used to analyze concentration data alone for drugs with TMD, the type of nonlinear pharmacokinetics is observed commonly as dose-dependence. The total and distributional clearances and the steady-state volume of distribution may appear to decrease with increasing doses or with chronic administration of doses (1,2). Because of the assumption of linear disposition, the NCA method is sometimes inappropriate for pharmacokinetic analysis of drugs with TMD, except perhaps for initial exploration to uncover or confirm TMD. In general, studying pharmacokinetics without considering its target may lead to confusing results. Studying pharmacokinetics with consideration of both drug and target gives better insight into the mechanism of the drug, thus more meaningful for the investigation of pharmacokinetic-pharmacodynamic relationship.

The basic concept of TMD and its related pharmacokinetic characteristics were first introduced by Levy (8). Various models were developed for drugs exhibiting TMD behavior (9,10), and the most popular one has an elimination component taking the form of a Michaelis-Menten function of the drug concentration (see references in (7,11)). This simple nonlinear function represents the complex saturable process of drug associating with and dissociating from the target and, in parallel, the degradation of the drug-target complex, e.g., following receptor-mediated endocytosis. The general framework of the TMD model was, however, first established by Mager and Jusko (1), who explicitly considered the drug-target binding as part of the model and showed examples of fitting simplified versions of the model to clinical data for compounds such as bosentan and interferon-β1a.

The concentrations of the target or the drug-target complex are routinely unavailable and, if available, may not be sufficient to describe the initial binding process. In such cases, the parameters of the TMD model in its most general form are not always identifiable. Some simplifications are needed. The rapid binding (or quasi-equilibrium) (12) and quasi-steady-state (Qss) (13) models with fewer parameters have since been proposed as approximations, under the assumption that initial process of drug binding to the target occurs relatively faster than the usual non-specific drug elimination and transit processes among the compartments. In addition to the tendency towards model over-parameterization caused by limitation of available data for model fitting, there are other difficulties in applying TMD models. The high degree of nonlinearity naturally makes the theory of TMD model less tractable and modeling practice numerically more complex. Model convergence and parameter estimation are sensitive to initial values needed in running nonlinear model-fitting algorithms. The complexity is multiplied when taking a population approach with mixed effects to identify sources of variability in pharmacokinetics, which could be large because of large variability in target.

Over the years, great progress has been made in learning and applying TMD models (2,11–14). A detailed summary of published work on applying TMD models to study biologics can be found in the review paper (11) by Gibiansky and Gibiansky. There the authors offered their expert opinions on TMD models and reasons for over-parameterization, and gave much useful insight and guidance in fitting such models. Despite the signficant advance in understanding TMD models, important open questions remain. The relationships between the general TMD model (1) and its simplifications (e.g., rapid binding and Qss) is not entirely clear. For example, a basic question of whether a general TMD model taking certain sets of parameter values ever becomes a simplified model has not been answered. The converse question is not easy to answer but perhaps more interesting: under what conditions does a simplified model approximate the general TMD model with reasonable accuracy? In that context, the consideration of reasonable accuracy is itself a difficult issue. Some of the basic properties of TMD models, although intuitively obvious, have not been explicitly described or proven. In deriving relationships among TMD models early work either was done heuristically with comparisons based more or less on simulations, thus validity dependent on simulation conditions, or lacked adequate mathematical rigor when deduced. There were models proposed and applied that resembled known simplifications to the general TMD model but appeared still different (e.g., (9,10,15)), which added to the difficulties.

This work is an attempt to organize various types of TMD models including the Michaelis-Menten, Qss, and rapid binding models and clarify the relationships among them. We show that the Michaelis-Menten and Qss models are examples of direct simplifications of the general TMD model and, moreover, suitable approximations if certain requirements on the parameters are met, and we specify these requirements. The argument of suitable approximation is based on the classic singular perturbation theory (16–18) by selecting appropriate scales of time. Other simplifications of the general TMD model can be obtained in ways similar to the Michaelis-Menten and Qss models. Simulations based on known application examples are done for visual comparison of these models. We hope that our work will provide a more rigorous basis for the theoretical and practical research of TMD models, which have become important tools for investigating the pharmacokinetic-pharmacodynamic relationships of many biological compounds, and to stimulate more discovery and development in this area. Although differential equations are presented throughout this work, the only mathematics used is algebra and a minimum of calculus (e.g., transformation of variables). Studying basic properties of the TMD models requires a more analytical, rather than algebraic, approach and will not be presented here.

METHODS

Our model scheme and notations are based on (1,11,13,19) and shown in Fig. 1. The disposition of many protein drugs can be described with a two-compartment model including a central compartment with volume V, representing intra-vascular space, of concentration C and an extra-vascular peripheral compartment, representing tissue space, of amount A T for the free drug. The drug binding to the free target of concentration R is assumed to occur only in the central compartment to form a complex of concentration M. In general, a depot compartment of amount A d is also included to represent usually subcutaneous or intramuscular administration sites for protein drugs.

Fig. 1
figure 1

General target-mediated disposition model. Adapted from Mager and Jusko (1). Symbols are defined in “Methods.”

Full size image

The model assumes that free drug into the central compartment could either be absorbed from the depot with an available dose amount D1 and a rate constant k a, or directly entered as an intravenous (i.v.) bolus injection of a dose amount D2, or an i.v. infusion, represented by an input function In(t) ≥ 0 on an interval [0, τ 0] of time t with 0 < τ 0 < ∞ and In(t) = 0 if t > τ 0. From the central compartment, the free drug can reversibly distribute to the peripheral compartment with rate constants k pt and k tp or irreversibly eliminated with a rate constant k e. The above rate constants are all from first-order processes. When there is no external drug input, the endogenous free target is synthesized in a zero-order process with a rate constant ksyn and degraded in a first-order process with a rate constant k deg; its steady-state concentration is thus k syn/k deg. After administration, the free drug binds to the free target in a second-order process with a rate constant k on, and the complex may dissociate with a rate constant k off and degrade (e.g., after internalization) with a rate constant k met as first-order processes. The drug elimination pathway via binding to the target and subsequent degradation of the complex could be saturated, when the target amount or capacity is limited. Below are the corresponding system of ordinary differential equations (ODEs) with their initial conditions. For notational convenience, we shall replace the drug amounts and input rate by their quotients with a divisor equal to the volume V of the central compartment: \( {B_d} = {A_d}/V,\;{B_T} = {A_T}/V,\;I(t) = {\text{In}}\left( {\text{t}} \right)/V,\;{B_0} = {{\text{D}}_{{1}}}/V,\;{\text{and}}\;{C_0} = {{\text{D}}_{{2}}}/V \). Henceforward variables on the left-hand side of all differential equations will be some concentration terms, expressed in molar units (except the scaled equations in “Approximations”, which are dimensionless).

$$ \begin{array}{*{20}{c}} {\frac{{d{B_d}}}{{dt}} = - {k_{\text{a}}}{B_d},} & {{B_d}(0) = {B_0}} \\ \end{array} $$
(1)
$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = I(t) + {k_{\text{a}}}{B_d} - {k_{\text{on}}}R \cdot C + {k_{\text{off}}}M - ({k_{\text{e}}} + {k_{\text{pt}}})C + {k_{\text{tp}}}{B_T},} & {C(0) = {C_0}} \\ \end{array} $$
(2)
$$ \begin{array}{*{20}{c}} {\frac{{d{B_T}}}{{dt}} = {k_{\text{pt}}}C - {k_{\text{tp}}}{B_T},} & {{B_T}(0) = 0} \\ \end{array} $$
(3)
$$ \begin{array}{*{20}{c}} {\frac{{dR}}{{dt}} = {k_{\text{syn}}} - {k_{{\deg }}}R - {k_{\text{on}}}R \cdot C + {k_{\text{off}}}M,} & {R(0) = {k_{\text{syn}}}/{k_{{\deg }}}} \\ \end{array} $$
(4)
$$ \begin{array}{*{20}{c}} {\frac{{dM}}{{dt}} = {k_{\text{on}}}R \cdot C - ({k_{\text{off}}} + {k_{\text{met}}})M.} & {M(0) = 0} \\ \end{array} $$
(5)

The solution to the above ODE system defines the general TMD model. It follows from the theory of ordinary differential equation that a unique solution to Eqs. 1 to 5 exists in [0, t 0) for some t 0 > 0, and is analytic with obviously suitable assumptions on the input function I(t). Thus, the general TMD model is well-behaved near time 0. It can also be shown that the TMD model, as a solution to the above ODE system, is actually defined and continuous on [0, ∞) and analytic in (τ 0, ∞), where τ 0 is defined so that for t > τ 0 the input function In(t) = 0. For simplicity, we shall restrict our discussion to the case of direct drug input into the central compartment from either an i.v. bolus injection or an i.v. infusion and, if a depot compartment is included, substitute \( I{\left( t \right)}\;{\text{by}}\;I{\left( t \right)} + k_{a} B_{d} = I{\left( t \right)} + k_{a} B_{{0e}} ^{{ - k_{a} t}} \). Thus, the equation on B d is eliminated, and the term k a B d in (2) is removed. Furthermore, to avoid trivial cases of the model we assume that

  • k on, k met + k off, k met + k e > 0;

  • k pt > 0 if and only if k tp > 0; and

  • if k syn and k deg are present in the model then k syn, k deg > 0.

Variations to the above model exist. It has been suggested that a general TMD model with drug-target binding in the peripheral compartment could be more relevant to the mechanism, since the disease-related target sites (e.g., epidermal growth factor receptors overexpressed on tumor cells) often reside in tissues (20,21). Nevertheless, many conclusions drawn in this work could be easily extended.

In “Simplifications” we summarize various simplifications of the general TMD model including those that have not been commonly used. We shall omit the peripheral compartment and consider only a simplified ODE system, since all conclusions on model simplification hold after necessary changes. Thus, the equation on B T is also eliminated without loss of generality. The simplified ODE system consists of Eqs. 4 and 5 and the equation below, which replaces Eq. 2.

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = I(t) - {k_{\text{on}}}R \cdot C + {k_{\text{off}}}M - {k_{\text{e}}}C,} & {C(0) = {C_0}} \\ \end{array} $$
(6)

In “Approximations” the scaling method based on singular perturbation theory is applied to show that in some simplified cases the Michaelis-Menten and Qss models are appropriate approximations of the general TMD model if, as requirements, certain expressions of model parameters (called ε) are close to 0.

As an example of the general TMD model defined in Eqs. 1 to 5, concentration-time profiles of interferon-β1a, a recombinant protein product for treating multiple sclerosis, are plotted at a single i.v. bolus dose of 6 mIU (Fig. 2). The model used is the pharmacokinetic part of an integrated model relating interferon-β1a to neopterin concentrations, developed by Mager and Jusko (5) (see also (1)). In the model, the total target (R tot = R + M) was assumed to be constant, and the elimination rate constant k e of free interferon-β1a was fixed to 0. Table I in (5) contains all parameters used in simulation: k off = 0.111, k pt = 2.18, k tp = 0.0928, k met = 0.707 h−1; k on = 8.71 h−1nM−1; R tot = 1.371 nM; and V = 3.61 L. For reference, profiles from the Michaelis-Menten, Qss, and rapid binding models are also displayed. The ε described above is 4.07 for the Michaelis-Menten model, compared with 0.15 for the Qss model. Overall, the approximation with the Michaelis-Menten model seems poor. For the free target and complex, both rapid binding and Qss models are reasonable approximations with expected under-prediction of the free drug at initial time (not visible from the figure).

Fig. 2
figure 2

Predicted interferon-β1a time-concentration profiles. Black solid line: general TMD model; blue long-dashed line: Qss model; green short-dashed line: rapid binding model; and purple dot and short-dashed line: Michaelis-Menten model. Parameter values from Mager and Jusko (5) and provided in “Methods.”

Full size image

All plots in this work were generated using R software (22), and concentration-time profiles of nonlinear models were simulated using the ordinary differential equation solver package (23).

RESULTS

Simplifications

The system of Eqs. 4 to 6 that defines the general TMD model can be expressed in other equivalent forms using the identities

$$ {C_{\text{tot}}} = C + M\;{\text{and}}\;{R_{\text{tot}}} = R + M, $$
(7)

where C tot and R tot are, respectively, the total drug and target concentrations. The sum of (5) with (6) and (4) gives

$$ \begin{array}{*{20}{c}} {\frac{{d{C_{\text{tot}}}}}{{dt}} = I(t) - {k_{\text{met}}}{C_{\text{tot}}} - ({k_{\text{e}}} - {k_{\text{met}}})C,} & {{C_{\text{tot}}}(0) = {C_0}} \\ \end{array} $$
(8)
$$ \begin{array}{*{20}{c}} {\frac{{d{R_{\text{tot}}}}}{{dt}} = {k_{\text{syn}}} - {k_{{\deg }}}{R_{\text{tot}}} - ({k_{\text{met}}} - {k_{{\deg }}})({C_{\text{tot}}} - C).} & {{R_{\text{tot}}}(0) = {k_{\text{syn}}}/{k_{{\deg }}}} \\ \end{array} $$
(9)

When the identities in (7) are considered, (8) replacing (6) and/or (9) replacing (4) yield four equivalent ODE systems with identical solutions.

Concentration data could be free or total, and could come from any or a combination of the substances of drug, target, and complex. So far only a few studies have collected rich data from adequate number of substances that enable the application of a general TMD model without any simplifications (see (24) for such an example). In practice, data may not be all available perhaps because of assay constraints; if available they may be too sparsely sampled or from too narrow dosage groups to be fully informative (11). The general TMD model used to fit such data could be over-parameterized and unusable. In these cases, any of the equivalent ODE systems defining the general TMD model may be simplified and then used for model fitting. The simplification can be made by modifying or deriving some differential or algebraic equations with assumptions such as rapid binding and quasi-steady state. However, a more direct simplification is to assume constant R tot (1), which has been successfully applied (5,6,25). The assumption holds when the degradation rates of the complex (k met) and free target (k deg) are the same and in reality believed to be similar. The assumption is also convenient if data on the total target are sparse or unavailable, but the amount is considered to be unaltered with the presence of the drug. Under the assumption, Eqs. 5 and 6 with R replaced by R tot − M, where R tot is treated as a parameter, define a simplified version to the general TMD model:

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = I(t) - {k_{\text{on}}}({R_{\text{tot}}} - M)C + {k_{\text{off}}}M - {k_{\text{e}}}C,} & {C(0) = {C_0}} \\ \end{array} $$
(10)
$$ \begin{array}{*{20}{c}} {\frac{{dM}}{{dt}} = {k_{\text{on}}}({R_{\text{tot}}} - M)C - ({k_{\text{off}}} + {k_{\text{met}}})M.} & {M(0) = 0} \\ \end{array} $$
(11)

At times this simplified model is still not parsimonious, which leads to restricting parameters of V, k off, k deg, or k e to literature values or zeros in model fitting (see (1,4) for example). Other simplifications of the general TMD model such as the Michaelis-Menten, Qss, and rapid binding models are needed, if the assumption of constant R tot is invalid. Setting R tot to constant is, however, an independent way of simplification and can be attempted for all models.

In “Michaelis-Menten Model” and “Quasi-Steady-State Model”, we show that the general TMD model defined by (6) (and, respectively, (8)), (9), and (5) leads to the Michaelis-Menten (and, respectively, Qss) model as a simplification under the quasi-steady-state assumption. In “Rapid Binding Model”, we discuss the rapid binding model. In “Others”, we show some other simplifications including the one derived from the equivalent system (6) (or (8)), (4), and (5).

Michaelis-Menten Model

One way of simplifying the general TMD model defined by Eqs. 5, 6 and 9 is to replace (5) with an algebraic equation called the quasi-steady-state assumption, obtained by setting the right-hand side of (5) to zero (13):

$$ {k_{\text{on}}}R \cdot C - ({k_{\text{off}}} + {k_{\text{met}}})M = 0\;{\text{or}}\;R \cdot C - {K_{\text{m}}}M = 0, $$
(12)

where \( {K_{\text{m}}} = { }\left( {{k_{\text{off}}} + {k_{\text{met}}}} \right)/{k_{\text{on}}} \) is the Michaelis-Menten constant (called the steady-state constant K ss in (13)). This idea came from the classical theory of quasi-steady-state approximation to the biochemical enzymatic equations, a subject that has been extensively studied for close to a century. At steady state the Qss assumption should be naturally satisfied for some endogenous substances and is thus an identity. With externally administered protein drugs, it may hold approximately for drug-target complexes after initial binding period.

Equation 12 is equivalent to either expression below of the complex M or free target R:

$$ M = \frac{{{R_{\text{tot}}}C}}{{{K_{\text{m}}} + C}}\quad {\text{and}}\quad R = \frac{{{K_{\text{m}}}{R_{\text{tot}}}}}{{{K_{\text{m}}} + C}}. $$
(13)

Simplifying (6) and (9) with the equation for the complex in (13) gives:

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = I(t) - \frac{{{k_{\text{met}}}{R_{\text{tot}}}}}{{{K_{\text{m}}} + C}}C - {k_{\text{e}}}C,} & {C(0) = {C_0}} \\ \end{array} $$
(14)
$$ \begin{array}{*{20}{c}} {\frac{{d{R_{\text{tot}}}}}{{dt}} = {k_{\text{syn}}} - {k_{{\deg }}}{R_{\text{tot}}} - \frac{{({k_{\text{met}}} - {k_{{\deg }}})C}}{{{K_{\text{m}}} + C}}{R_{\text{tot}}}.} & {{R_{\text{tot}}}(0) = {k_{\text{syn}}}/{k_{{\deg }}}} \\ \end{array} $$
(15)

The model defined by (14) and (15) is called the Michaelis-Menten model and was originally presented in (13). With no peripheral compartments it has five unknown parameters k met, K m, k e, k syn, and k deg, one fewer than the general TMD model since k on and k off are replaced with the Michaelis-Menten constant K m. If k met = 0, the model for C simplifies further to a trivial linear model as an approximation. The complex, total drug, and free target concentrations, if needed, can be obtained using (7) and (13). Note that M (0) > 0, as a result of making the Qss assumption; thus, over-prediction of the complex is expected at initial time. It follows from (15) that the total target R tot(t) as a function of time t exceeds baseline R tot(0) = k syn/k deg for t > 0 if and only if k met < k deg. When k met alone is varied, the maximum total target concentration is the greatest when k met = 0.

If R tot is constant (k met = k deg), Eqs. 14 and 15 reduce to the more familiar Michaelis-Menten model involving only the free drug C:

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = I(t) - \frac{{{V_{{\max }}}}}{{{K_{\text{m}}} + C}}C - {k_{\text{e}}}C,} & {C(0) = {C_0}} \\ \end{array} $$
(16)

where V max = k met R tot. However, we shall still call the solution to Eqs. 14 and 15 with the total target the Michaelis-Menten model, which in the current setup is a direct simplification of the general TMD model. The model in Eq. 16 can result alternatively from assuming constant R tot first and then directly simplifying (10) and (11) under the Qss assumption. This further simplified model has three parameters including V max that replaces k met, k deg(= k met), and k syn. In the case that a bolus injection is the only free drug input into the central compartment (C 0 > 0 and I(t) = 0), the free drug C defined by the Michaelis-Menten model is naturally a so-called total solution in the theory of singular perturbation (i.e., as an approximation over the entire interval t ≥ 0 under the Qss assumption). Moreover, the differential equation for the Michaelis-Menten model can be transformed to an equivalent transcendental equation without derivatives. The free drug C as a solution is closely related to a special function in mathematics. A total solution of the complex M can be constructed also to correct the initial over-estimation resulted from the Qss assumption and, thus, provide a better approximation (see Appendix for more details of the above).

One of the first examples of the Michaelis-Menten model was an application in a psoriatic patient study (10), where Bauer et al. conducted a population pharmacokinetic-pharmacodynamic analysis of efalizumab, a humanized anti-CD11a IgG1 mAb, with a model (Model B in (10)) that was a two-compartment version of the above Michaelis-Menten model. The only difference is that (15) was written as the percent of baseline target (CD11a).

Quasi-Steady-State Model

The quasi-steady-state assumption in Eq. 12 was first adopted in (13) to derive the quasi-steady-state model. Consider the general TMD model defined by (8) (instead of (6) in “Michaelis-Menten Model”), (9), and (5), and replace (5) with the Qss assumption (12). The free drug C can now be solved in terms of C tot and R tot using (7):

$$ C = 0.5\;\left( {{C_{\text{tot}}} - {R_{\text{tot}}} - {K_{\text{m}}} + \sqrt {{{{\left( {{C_{\text{tot}}} - {R_{\text{tot}}} - {K_{\text{m}}}} \right)}^2} + 4{K_{\text{m}}}{C_{\text{tot}}}}} } \right). $$
(17)

The combined differential and algebraic Eqs. 8, 9, and 17 for the variables C tot, R tot, and C define a solution that is the quasi-steady-state model. After the solution is obtained, concentrations of the free target and complex can be derived using equations in (13). The derivative dC/dt of the free drug can be related to C tot, R tot, and their derivatives using (17) or, to have a less cumbersome form, using (7) and (13) (11,12):

$$ \frac{{d{C_{\text{tot}}}}}{{dt}} = \frac{{dC}}{{dt}} + \frac{{{K_{\text{m}}}{R_{\text{tot}}}}}{{{{({K_{\text{m}}} + C)}^2}}}\frac{{dC}}{{dt}} + \frac{C}{{{K_{\text{m}}} + C}}\frac{{d{R_{\text{tot}}}}}{{dt}}. $$
(18)

As in the case of the Michaelis-Menten model, the Qss assumption leads to poor prediction at initial binding time. Since C(0) < C 0 and M(0) > 0, both free drug and complex are affected, unlike the case of the Michaelis-Menten model.

The Qss model has the same set of parameters as the Michaelis-Menten model, one fewer than the general TMD model. If R tot is constant, a further simplification of the Qss model can be made as before. The equation for R tot is removed, and the solution to Eqs. 8 and 17 with R tot taken as a parameter replacing k syn and k deg(= k met) is again called the Qss model. Applications of this model include studies of pharmacokinetics for an anti-IL4-receptor mAb in healthy volunteers and asthmatic subjects (26), and for denosumab, an anti-RANK ligand mAb in advanced cancer patients with solid tumors for skeletal-related events (27).

If R tot is constant, then the last term of the right-hand side of (18) is zero, and the derivative of the free drug concentration C becomes

$$ \frac{{dC}}{{dt}} = \frac{{I(t) - \frac{{{k_{\text{met}}}{R_{\text{tot}}}}}{{{K_{\text{m}}} + C}}C - {k_{\text{e}}}C}}{{1 + \frac{{{K_{\text{m}}}{R_{\text{tot}}}}}{{{{({K_{\text{m}}} + C)}^2}}}}}. $$
(19)

This equation gives a relationship of the free drug between the Michaelis-Menten and Qss models under the assumptions of Qss and constant R tot (see “Michaelis-Menten Model”) and has been attributed to Wagner (11,12).

Rapid Binding Model

Mager and Krzyzanski were the first to see the need for simplifying the general TMD model and proposed the rapid binding (or quasi-equilibrium) model under the rapid binding assumption (12):

$$ {k_{\text{on}}}R \cdot C - {k_{\text{off}}}M = 0\;{\text{or}}\;R \cdot C - {K_{\text{D}}}M = 0, $$

where K D = k off/k on is often compared with the dissociation constant measured in vitro for the affinity between the drug and target. Using (7), one can express C in terms of C tot and R tot, the same as in Eq. 17 except that K D now replaces K m. With the new algebraic expression of C, Eqs. 8 and 9 define the rapid binding model. All subsequent reasoning and derivation in “Quasi-Steady-State Model” including the further simplification by assuming constant R tot hold. In particular, the Wagner Eq. 19 that relates the derivatives of the free and total drug concentrations is obtained with K D replacing the Michaelis-Menten constant K m. Thus, a Michaelis-Menten model as (16) with K D replacing K m again follows and approximates the rapid binding model (12,19) well, if \( {K_{\text{D}}}{R_{\text{tot}}}/{\left( {{K_{\text{D}}} + C} \right)^2} \ll 1 \). Yan et al. showed further by simulation that R tot does not have to be constant for this Michaelis-Menten model to be a good approximation for the free drug C (19).

The rapid binding model has been applied to a list of drug products (2,3,12,25) including denosumab in multiple myeloma patients for bone disorders, and the Qss model was also used to study denosumab in a different disease population (27). Simulation has shown that neither is always a better approximation. Because the only difference between the rapid binding and Qss models is the parameter difference of K D and K m, they are indistinguishable for purposes of model fitting. The parameter K D was fixed to the in vitro dissociation constant in some applications (e.g., (25)) or, if estimated, compared with it as a model-fitting diagnostic or indicator for the model resemblance to the underlying mechanism. Note that

$$ {K_{\text{m}}} = \frac{{{k_{\text{off}}} + {k_{\text{met}}}}}{{{k_{\text{on}}}}} = {K_{\text{D}}} + \frac{{{k_{\text{met}}}}}{{{k_{\text{on}}}}} \geqslant {K_{\text{D}}}, $$
(20)

and that k met is independently estimated in both rapid binding and Qss models. If k met is much smaller than k off (k met ≪ k off), then K m ≃ K D, and the two models are indeed similar; otherwise a question of interpretation needs to be asked after fitting either model: is the fitted parameter K D in some applications of the rapid binding model actually K m (and the converse)? If Qss approximation is more appropriate, the parameter K m estimated in vivo is probably greater than the dissociation constant measured in vitro. Equation 20 gives a reason, even if other factors in the body system are not considered. It has been indeed our experience of compounds that most of them have markedly greater K m from fitting TMD models than the in vitro dissociation constant, consistent with the review comments in (11). Consequently, the closeness of in vivo model-derived K D or K m with in vitro dissociation constant should not always be a requirement for model adequacy. The same caution has to be taken for the Michaelis-Menten models of either one- or two-compartments such as defined in Eq. 16 of “Michaelis-Menten Model” and derived from the Wagner Eq. 19 with K D replacing K m as the Michaelis-Menten constant (19).

The equations for the total, instead of free, drug and target (C tot and R tot) have to be used for the rapid binding simplification, unlike the cases for the Qss assumption. No other equivalent ODE systems defining the general TMD model seem to lead to nontrivial simplifications under the rapid binding assumption. Indeed, when applied to simplifying the ODE system for the free drug with Eq. 6, the assumption gives a solution that is the usual linear model for the free drug C, independent of the target, similar to the case of setting k met = 0 in “Michaelis-Menten Model.” On the other hand, the assumption applied to Eq. 4 implies that the free target R as the solution is constant, which itself invalidates the rapid binding assumption.

The pharmacokinetic-pharmacodynamic relationship of an anti-CD4 mAb TRX1 was studied by Ng, et al. (24). A single 2-hour i.v. infusion of TRX1 at 1, 5, and 10 mg/kg was given to nine healthy subjects. Rich concentration data of TRX1, total and free CD4 were collected for the analysis. Although the general TMD model fit the data quite well, simulation shows that the typical concentration-time profiles of all three simplified models were close to those of the general TMD model (Fig. 3), even for the lowest dose at which differences should be the most discernible. In particular, concentration profiles of the general TMD and Qss models are inseparable most of the time. This indicates that all models should provide good fit to the data. In this case, since k met/k off (=0.27) is small relative to 1, and TRX1 concentration is large relative to the target, the rapid binding and Qss models are expected to be similar. Simulation studies in (19) showed that the Michaelis-Menten model with K D as the Michaelis-Menten constant should also fit the data reasonably well.

Fig. 3
figure 3

Predicted TRX1 time-concentration profiles after 1-mg 2-hour i.v. infusion. Black solid line: general TMD model; blue long-dashed line: Qss model; green short-dashed line: rapid binding model; and purple dot and short-dashed line: Michaelis-Menten model. Parameter values from Ng et al. (24).

Full size image

Interferon-β1a described in “Methods” is an example that the rapid binding and Qss models approximate the general TMD model fairly well for the free dug and the complex, but the approximation from the Michaelis-Menten model is poor (Fig. 2).

Others

The Qss assumption can be exploited in the other two equivalent ODE systems (Eqs. 4 to 6 and Eqs. 4, 5 and 8) that define the general TMD model with similar approaches to “Michaelis-Menten Model” and “Quasi-Steady-State Model.” Thus, a third simplification consists of the two equations below for the free drug and target, replacing Eqs. 4 and 6:

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = I(t) - \frac{{{k_{\text{met}}}}}{{{K_{\text{m}}}}}R \cdot C - {k_{\text{e}}}C,} & {C(0) = {C_0}} \\ \end{array} $$
(21)
$$ \begin{array}{*{20}{c}} {\frac{{dR}}{{dt}} = {k_{\text{syn}}} - {k_{{\deg }}}R - \frac{{{k_{\text{met}}}}}{{{k_{\text{m}}}}}R \cdot C,} & {R(0) = {k_{\text{syn}}}/{k_{{\deg }}}} \\ \end{array} $$
(22)

and the total drug and target concentration, if needed, can be computed using the formulas:

$$ {C_{\text{tot}}} = \left( {1 + \frac{R}{{{K_{\text{m}}}}}} \right)C\,{\text{and }}{R_{\text{tot}}} = \left( {1 + \frac{C}{{{K_{\text{m}}}}}} \right)R. $$

Obviously both C tot and R tot are over-predicted at initial time. The model combines the drug-target association term k on R · C with the dissociation term k off M, which results in a single second-order drug-target association term k met R · C/K m to form the complex. Namely, irreversible binding is the consequence of the simplification. Thus, k met/K m ≤ k on, as expected, and equality holds if and only if k off = 0 (i.e., a true irreversible binding). Different from the Michaelis-Menten and Qss models, the above simplification has two parameters fewer than the general TMD model since k met and K m are not independently identifiable.

Jonsson et al. conducted a population study of a recombinant glycoprotein, antagonistic of the target CD11b, in healthy volunteers and stroke patients (15). Pharmacokinetic samples, neutrophil counts, and numbers of total and free CD11b receptors per neutrophils were collected and used in the study. The free drug in their model was assumed to be eliminated by linear and nonlinear pathways. The nonlinear elimination pathway had two terms: a Michaelis-Menten term, presumably mediated by CD11b receptors that were not on neutrophils, and another term that was of the above form k met R · C/K m with the free drug concentration C and the time-dependent free CD11b receptors R on neutrophils.

Finally, the last of the four ODE systems of the total drug and free target that simplifies the general TMD model based on the Qss assumption is presented below.

$$ \begin{array}{*{20}{c}} {\frac{{d{C_{\text{tot}}}}}{{dt}} = I(t) - {k_{\text{met}}}{C_{\text{tot}}} - \frac{{({k_{\text{e}}} - {k_{\text{met}}}){K_{\text{m}}}}}{{{K_{\text{m}}} + R}}{C_{\text{tot}}},} & {{C_{\text{tot}}}(0) = {C_0}} \\ \end{array} $$
(23)
$$ \begin{array}{*{20}{c}} {\frac{{dR}}{{dt}} = {k_{\text{syn}}} - {k_{{\deg }}}R - \frac{{{k_{\text{met}}}{C_{\text{tot}}}}}{{{K_{\text{m}}} + R}}R.} & {R(0) = {k_{\text{syn}}}/{k_{{\deg }}}} \\ \end{array} $$
(24)

The model has the same set of parameters as the Michaelis-Menten and Qss models. From the Qss assumption, the free drug C and total target R tot can be computed from the expressions below:

$$ C = \frac{{{K_{\text{m}}}{C_{\text{tot}}}}}{{{K_{\text{m}}} + R}}\quad {\text{and}}\quad {R_{\text{tot}}} = \left( {1 + \frac{{{C_{\text{tot}}}}}{{{K_{\text{m}}} + R}}} \right)R, $$

but are under- and over-predicted, respectively, for small t.

Unlike the cases of the Michaelis-Menten and Qss models, assuming constant R tot will not produce any further simplifications for the two models above, since the differential equations for R become invalid, although eliminating R in the equations for the free and total drug concentration generates the corresponding cases of the Michaelis-Menten and Qss models, respectively.

Woo et al. (2) developed a general TMD model of recombinant human erythropoietin to study the pharmacokinetic-pharmacodynamic relationships in rats, monkeys, and human at various doses. For the general TMD model in rats, simulation at a low dose of 10 IU/kg shows that the two models above both perform well as approximations (Fig. 4). There are cases that the two models appear to perform not so well as the Qss model (e.g., the model in (24), plot not shown).

Fig. 4
figure 4

Predicted time-concentration profiles of recombinant human erythropoietin in rats after a bolus i.v. injection of 10 IU/kg. Black solid line: general TMD model; turquoise long-dashed line (Qss 2): two-compartment version of the model defined in Eqs. 21 and 22; and red short-dashed line (Qss 3): 2-compartment version of the model defined in Eqs. 23 and 24. Parameter values from Woo et al. (2).

Full size image

In certain situations, an assumption broader than the quasi-steady state can be made as the basis for simplification of the general TMD model. Consider the equation for the free drug and target, and the complex:

$$ R \cdot C = \kappa M - \alpha R - \beta C + \gamma . $$
(25)

If κ is K D (or K m), and α, β, γ = 0 this equation becomes the rapid binding (or Qss) assumption. If κ, β = 0, α = k deg/k on, and γ = k syn/k on, Gibiansky and Gibiansky (28) derived a simplification for the irreversible binding model (k off = 0) after replacing Eq. 6 by the difference of the Eqs. 4 and 6. If κ, β = 0, α = K m, and γ = V max/k on for some positive constant V max (not necessarily equal to k met R tot), then the Eqs. 6 and 5 can be written as an ODE system of C and M. This ODE system was briefly discussed by Mager and Jusko in (1). The solution, as a simplification of the general TMD model, is not equivalent to those from the rapid binding and Qss assumptions but, interestingly, identical to a model of the central, peripheral, and receptor compartments with nonlinear (or Michaelis-Menten) “distribution” from the central to receptor compartment and linear elimination from both compartments. The condition (25) implies that γ cannot be too small (i.e., γ < 0 and |γ| too large), and other necessary conditions may also be identified. With (25), simplifications to the general TMD model, defined by the four systems of ODEs, can be attempted in a way similar to the rapid binding or Qss approximation.

There are other ways of simplifying the general TMD model. For example, Hayashi et al. proposed a binding model for the population pharmacokinetics and pharmacodynamics of omalizumab, a humanized IgG1 that binds to human IgE as the target and is used to treat moderate to severe persistent allergic asthma (9). The model allowed for different distributional space of the complex from those of omalizumab and IgE. The differential equations for the free drug and IgE, although not given, can be expressed with the usual terms in (6) and (4) after proper scaling by the volumes of distribution for the drug (or target) and the complex. Besides this difference in volume parameters, other aspects of their model are the same as in the rapid binding or Qss model.

Approximations

Although a simplification of the general TMD model can be derived with a broad steady-state assumption such as (25), requirements need to be identified to ensure its appropriateness as an approximation. Seeking the requirements is an entirely different, and often difficult, task from the easy derivation of a simplified model. We propose that the appropriateness of a simplification with the requirements met should be judged under the following criteria, analogous to comparison of two models representing the same biological system:

  • The simplified model has all parameters corresponding to the general TMD model (e.g., V max in the Michaelis-Menten model vs. k met R tot from “Michaelis-Menten Model”).

  • The simplified model is asymptotically well-behaved. Namely, as the requirements become more stringent, the distance between the two models becomes smaller in pre-specified regions. Here the distance between the two model functions (or vectors) f (t) and g(t) is defined by, for example, \( \max _{t} \geqslant \tau _{0} {\left| {f{\left( t \right)} - g{\left( t \right)}} \right|} \) with τ 0 > 0 an arbitrarily fixed constant. This implies that the concentration-time profiles of the two models are close if their corresponding parameters are close (e.g., between V max and k met R tot).

  • Finally, fitting the simplified model to data produced from the general TMD model within the specified parameter range captures parameter information. Namely, as data become more informative the parameters of the simplified model approach those of the general TMD model. This implies that if the concentration-time profiles of the two models are close then the corresponding parameters are close.

Thus, under the criteria a simplified model is not appropriate if its concentration-time profiles are similar to those of the general TMD model, but corresponding parameters are not. Suitable requirements for an appropriate simplification should prevent this from occurring.

In the case of constant total target R tot we derive requirements that, when satisfied, support the Michaelis-Menten and Qss models as suitable approximations of the general TMD model, and we show this using a scaling approach from singular perturbation theory (17,18). For ease of derivation, we consider first in “Michaelis-Menten Model”and “Quasi-Steady-State Model” a simple one-compartment model (k pt = k tp = 0) and assume the case that the drug is only exogenously administered as a bolus injection. Thus, C(0) = C 0 > 0 and I(t) = 0. We describe necessary changes to the requirements in “Others” for the cases of a two-compartment model with more general drug input. The scaling approach requires the selection of two time scales that correspond to the fast phase of mainly bind-ing actions (T f ) and the slow quasi-steady state (T s ). A change of variables of the ODE system defining the (simplified) general TMD model leads to a scaled dimensionless system containing a small parameter ε = T f /T s . Setting ε to zero yields a reduced or degenerate system that is equivalent to a simplification. A theorem by Tikhonov (see (16), for example) states that under certain regularity conditions the solution to the original scaled ODE system corresponding to the general TMD model converges to the solution to the degenerate scaled system as ε goes to 0. The regularity conditions stipulate in our cases that the partial derivative with respect to M of the right-hand side of the equation for the complex is negative when the Qss assumption is satisfied. For both Michaelis-Menten and Qss models, the regularity conditions can be easily verified; thus, the scaled simplification is the limit, as ε approaches zero, of the scaled system of the general TMD model. This implies that in the original scale the simplified model is asymptotically equal to the general TMD model for a small ε.

The time scales T f and T s , and thus ε, depend on the system and pharmacokinetic parameters in the model. For the approximation to be widely applicable, the above convergence of limit should be in a uniform sense with respect to all parameters in the equation in an interval [τ 0, ∞), where τ 0 is any positive constant fixed a priori. This can be done by choosing time scales in such a way that the coefficients of the scaled equations have upper bounds independent of the parameters, so long as ε is required to be small, and that the regularity condition is satisfied at all parameter values in a compact (i.e., closed and bounded) set, defined by parameter upper bounds. Without the uniform convergence, it is possible that ε from a particular scaling approach may tend to 0 but the concentration-time profiles of the general TMD model do not become close to those of a simplification because of changes in parameters not defined in ε.

The small parameter ε with its uniform sense can serve as a measure of the overall closeness of the simplified model to the general TMD model, i.e., for concentrations of both free drug C and complex M. With the requirement on ε (<1), it is possible to estimate the error of the approximation using a Tayler-series-like expansion with respect to ε, and the magnitude of the error should also be in the order of ε.

Michaelis-Menten Model

Under the assumptions specified above, the general TMD model defined by (10) and (11) simplifies to

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = - {k_{\text{on}}}({R_{\text{tot}}} - M)C + {k_{\text{off}}}M - {k_{\text{e}}}C,} & {C(0){ } = {C_0}} \\ \end{array} $$
(26)
$$ { }\begin{array}{*{20}{c}} {\frac{{dM}}{{dt}} = {k_{\text{on}}}({R_{\text{tot}}} - M)C - ({k_{\text{off}}} + {k_{\text{met}}})M.} & {M(0) = 0} \\ \end{array} $$
(27)

At initial time t when binding is the dominant activity, C ≈ C 0. Hence, an approximate solution to (27) can be obtained by solving

$$ \begin{array}{*{20}{c}} {\frac{{dM}}{{dt}} = {k_{\text{on}}}({R_{\text{tot}}} - M){C_0} - ({k_{\text{off}}} + {k_{\text{met}}})M,} & {M(0) = 0} \\ \end{array} $$
(28)

which gives

$$ M \approx {M_0}[1 - \exp ( - {k_{\text{on}}}({K_{\text{m}}} + {C_0})t)],\quad {\text{where}}\quad {M_0} = \frac{{{R_{\text{tot}}}{C_0}}}{{{K_{\text{m}}} + {C_0}}} $$
(29)

The exponential form of the solution in Eq. 29 suggests that we define the fast time scale T f to be \( {[{k_{\text{on}}}({K_{\text{m}}} + {C_0})]^{{ - {1}}}} \). When t is large at the slow quasi-steady state, replacing Eq. 27 with the Qss assumption (the first formula in (13)) and thus eliminating M in Eq. 26 give

$$ \begin{array}{*{20}{c}} {\frac{{dC}}{{dt}} = - \frac{{{k_{\text{met}}}{R_{\text{tot}}}C}}{{{K_{\text{m}}} + C}} - {k_{\text{e}}}C,} & {C(0) = {C_0}} \\ \end{array} $$
(30)
$$ 0 = {k_{\text{on}}}\left( {{R_{\text{tot}}} - M} \right)C - \left( {{k_{\text{off}}} + {k_{\text{met}}}} \right)M{ }. $$
(31)

Equation 30 defines the one-compartment Michaelis-Menten model, the same as (16) with I(t) there equal to 0. The model expression here gives also the rationale for choosing slow time scales to be reciprocals of the maximum elimination rate of the free drug. One such choice is therefore \( {T_s} = { }{\left( {{k_{\text{e}}} + {k_{\text{on}}}{R_{\text{tot}}}} \right)^{{ - {1}}}} \). With this reasoning, we now define other scaling constants for this simple case of the general TMD model. Let

$$ \varepsilon = \frac{{{T_f}}}{{{T_s}}} = \frac{{{k_{\text{e}}}/{k_{\text{on}}} + {R_{\text{tot}}}}}{{{K_{\text{m}}} + {C_0}}} $$
(32)

and make the following change of variables x = C/C 0, y = M/M 0 where M 0 is given in (29), and \( \tau = {T_s}^{{ - 1}}t \). Then, Eqs. 26 and 27 can be written as

$$ \begin{gathered} \hfill \\ \begin{array}{*{20}{c}} {\frac{{dx}}{{d\tau }} = - x + \mu (1 - \lambda )\delta y + \lambda \delta xy,} & {x(0) = 1} \\ \end{array} \hfill \\ \end{gathered} $$
(33)
$$ \begin{array}{*{20}{c}} {\varepsilon \frac{{dy}}{{d\tau }} = x - (1 - \lambda )y - \lambda xy,} & {y(0) = 0} \\ \end{array} $$
(34)

where

$$ \mu = \frac{{{K_{\text{D}}}}}{{{K_{\text{m}}}}},\quad \lambda = \frac{{{C_0}}}{{{K_{\text{m}}} + {C_{{0}}}}},\quad {\text{and}}\quad \delta = \frac{{{R_{\text{tot}}}}}{{{k_{\text{e}}}/{k_{\text{on}}} + {R_{\text{tot}}}}}. $$
(35)

Note that 0 ≤ μ ≤ 1, 0 < λ < 1, and 0 < δ ≤ 1. From Tihonov’s theorem (see (16)), as ε → 0 the solution to (33) and (34) converges to the solution to the degenerate system that consists of Eq. 33 and the algebraic equation

$$ 0 = x - \left( {1 - \lambda } \right)y - \lambda xy, $$
(36)

if 1 − λ + λ x is positive and uniformly bounded away from 0 or, equivalently, \( ({K_{\text{m}}} + C)/({K_{\text{m}}} + {C_0})\; \geqslant \;{\tau_0} > 0 \), where τ 0 is a constant and independent of all parameters. This condition is easily satisfied if K m is not too small relative to C 0. Since the ODE system of (33) and (34) corresponds to that of (26) and (27), and (33) and (36) to (30) and (31), it follows that the Michaelis-Menten model approximates the general TMD model if ε is small.

Various simulation examples in Gibiansky et al. (13) and Peletier and Gabrielsson (14) gave results consistent with the above conclusion. In particular, the higher the initial free drug concentration C 0, the better the Michaelis-Menten model as an approximation to the general TMD model. Figure 5 is a simulation example for model comparison with the parameters from (14): k e = 0.1, k off = k met = 1, k on = 1, and R tot = 1. The concentration-time profiles of the free drug and complex are displayed for the general TMD model and its approximations: the Michaelis-Menten, Qss, and rapid binding models. The alternative Michaelis-Menten model with K D replacing K m is also included. Among the initial concentrations of 0.1, 1, 10, and 100 used in (14), C 0 = 0.1 and 10 are selected. At C 0 = 10 the free drug concentration is quite large relative to the target, and ε = 0.09 from Eq. 32, indicating a good approximation of the Michaelis-Menten model. At C 0 = 0.1, the Michaelis-Menten model (ε = 0.52) starts to be visibly worse, but the Qss model is still a reasonable approximation.

Fig. 5
figure 5

Simulated time-concentration profiles of one-compartment TMD models. Upper panels: C 0 = 0.1; Lower panels: C 0 = 10. Black solid line: general TMD model; blue long-dashed line: Qss model; green short-dashed line: rapid binding model; purple dot and short-dashed line: Michaelis-Menten model; and orange short- and long-dashed line: Michaelis-Menten model with KD as the Michaelis-Menten constant. Parameter values from Peletier and Gabrielsson (14): k e = 0.1, k off = k met = 1, k on = 1, and R tot = 1. All numbers are in arbitrary units.

Full size image

Peletier and Gabrielsson analyzed the dynamic behavior of the TMD model for various parameter ranges and illustrated their results with simulation examples (14). There, a different yet more intuitive choice of change of variables was made, and with the choice a more customary small parameter that is the ratio of the total target and free drug concentrations R tot/C 0 (called μ in Appendix C.1 of (14)) was selected. The authors reasoned geometrically that the Michaelis-Menten model approximates the general TMD model well for small R tot/C 0 when other parameters are fixed. By contrast, \( \varepsilon = {\left( {k_{{\text{e}}} /k_{{{\text{on}}}} + R_{{{\text{tot}}}} } \right)}/{\left( {K_{{\text{m}}} + C_{{\text{0}}} } \right)} \) from our scaling choice shows that the initial free concentration C 0 does not have to be large relative to the total target R tot for the Michaelis-Menten model to be close to the general TMD model. A simulation example in (13) (Case 9 with parameters k e = 0.01, k on = 0.0001, k off = 0.1, k met = 3, R tot = 1000, and C 0 = 200) supports this (Fig. 6, upper panels). In the figure the profiles of the Michaelis-Menten model are not distinguishable from the general TMD model, but the small parameter value of ε is 5, if defined with R tot/C 0, but only 0.035 from the definition in (32). In this example with a small binding rate, the disposition of the free drug is unsaturated and essentially linear with the elimination rate equal to k e + V max/K m. Again for comparison the QE model and the alternative Michaelis-Menten model with K D replacing the Michaelis-Menten constant K m (19) are displayed.

Fig. 6
figure 6

Simulated time-concentration profiles of one-compartment TMD models. Upper panels: k e = 0.01, k on = 0.0001, k off = 0.1, k met = 3, R tot = 1000, and C 0 = 200. Parameter values from Gibiansky et al. (13) (Case 9). Lower panels: kon and Rtot modified to be k on = 0.01 and R tot = 100; other parameters are the same as in the example of the upper panel; Black solid line: general TMD model; blue long-dashed line: Qss model; green short-dashed line: rapid binding model; purple dot and short-dashed line: Michaelis-Menten model; and orange short- and long-dashed line: Michaelis-Menten model with KD as the Michaelis-Menten constant. All numbers are in arbitrary units.

Full size image

Quasi-Steady-State Model

As in “Michaelis-Menten Model” the general TMD model defined by Eqs. 8 and 11 under the simplifying assumptions becomes

$$ \begin{array}{*{20}{c}} {\frac{{d{C_{\text{tot}}}}}{{dt}} = - {k_{\text{e}}}{C_{\text{tot}}} - ({k_{\text{met}}} - {k_{\text{e}}})M,} & {{C_{\text{tot}}}(0) = {C_0}} \\ \end{array} $$
(37)
$$ \begin{array}{*{20}{c}} {\frac{{dM}}{{dt}} = {k_{\text{on}}}({R_{\text{tot}}} - M)({C_{\text{tot}}} - M) - ({k_{\text{off}}} + {k_{\text{met}}})M,} & {M(0) = 0} \\ \end{array} $$
(38)

and the Qss model becomes the joint solution to (37) and the algebraic equation

$$ 0 = {k_{\text{on}}}\left( {{R_{\text{tot}}} - M} \right)\left( {{C_{\text{tot}}} - M} \right) - \left( {{k_{\text{off}}} + {k_{\text{met}}}} \right)M. $$
(39)

The consideration for the choice of time scales and changes of variables are similar to the case of the Michaelis-Menten model but leads to somewhat different results. At initial fast binding time, the total drug concentration is approximately the initial free drug concentration (C tot ≈ C 0), and the second-order term of M in (38) can be ignored since M 2 ≪ M for small t. The solution to the resulting linear differential equation approximates the solution to (38) with C tot = C 0 and shows that the fast time scale may be defined as \( {T_f} = {\left[ {{k_{\text{on}}}\left( {{K_{\text{m}}} + {C_0} + {R_{\text{tot}}}} \right)} \right]^{{ - 1}}} \) .Let \( {T_s} = {\left( {\max \{ {k_{\text{e}}},\;{k_{\text{met}}} - {k_{\text{e}}}\} } \right)^{{ - 1}}} \) and

$$ \varepsilon = \frac{{{T_f}}}{{{T_s}}} = \frac{{\max \{ {k_{\text{e}}},\;{k_{\text{met}}} - {k_{\text{e}}}\} }}{{{k_{\text{on}}}({K_{\text{m}}} + {C_0} + {R_{\text{tot}}})}}. $$
(40)

Let \( x = {C_{\text{tot}}}/{C_0},\;y = M/{M_0} \) where \( {M_0} = {R_{\text{tot}}}{C_0}/\left( {{K_{\text{m}}} + {C_0} + {R_{\text{tot}}}} \right), \), and \( \tau = T_s^{{ - 1}} t \). Then, Eqs. 37 and 38 can be written as

$$ \begin{array}{*{20}{c}} {\frac{{dx}}{{d\tau }} = - \theta x + (\theta - \nu )\gamma y,} & {x(0) = 1} \\ \end{array} $$
(41)
$$ \begin{array}{*{20}{c}} {\varepsilon \frac{{dy}}{{d\tau }} = x - (1 - \lambda + \gamma \lambda )y - \lambda (1 - \gamma )xy + \lambda \gamma (1 - \gamma ){y^2},} & {y(0) = 0} \\ \end{array} $$
(42)

where

$$ \theta = \frac{{{k_{\text{e}}}}}{{\max \{ {k_{\text{e}}},\;{k_{\text{met}}} - {k_{\text{e}}}\} }},\quad \nu = \frac{{{k_{\text{met}}}}}{{\max \{ {k_{\text{e}}},\;{k_{\text{met}}} - {k_{\text{e}}}\} }},\quad \gamma = \frac{{{R_{\text{tot}}}}}{{{K_{\text{m}}} + {C_0} + {R_{\text{tot}}}}}, $$

and λ is defined in (35). The dimensionless parameters satisfy the conditions: 0 ≤ θ ≤ 1, 0 ≤ ν ≤ 2, and 0 < γ < 1. Again, invoking the theorem of Tihonov (16) we conclude that the solution to Eqs. 41 and 42 converges, as ε → 0, to the solution to the degenerate system below, which corresponds to Eqs. 37 and 39 defining the Qss model:

$$ \begin{array}{*{20}{c}} {\frac{{dx}}{{d\tau }} = - \theta x + (\theta - \nu )\gamma y,} & {x(0) = 1} \\ \end{array} $$
$$ 0 = x - \left( {1 - \lambda + \gamma \lambda } \right)y - \lambda \left( {1 - \gamma } \right)xy + \lambda \gamma \left( {1 - \gamma } \right){y^2}, $$

under some regularity condition imposed on the right-hand side of (42). Consequently, the Qss model approximates the general TMD model if ε in (40) is small. The regularity condition requires that \( 1 - \lambda + \gamma \lambda + \lambda \left( {1 - \gamma } \right)x - 2\lambda \gamma \left( {1 - \gamma } \right)y \) is positive and bounded away from 0 or, equivalently, \( \left( {{K_{\text{m}}} + R + C} \right)/\left( {{K_{\text{m}}} + {C_0} + {R_{\text{tot}}}} \right) \geqslant {\tau_0} \) with a fixed constant τ 0 > 0. Note that this condition is met if K m is not too small with respect to C 0 and R tot.

In the simulation example of Fig. 5, ε = 0.29 at initial concentration C 0 = 0.1 (upper panels) and 0.07 at C 0 = 10 (bottom panels) from Eq. 40, indicating a better approximation of the Qss model at C 0 = 10. Although the small parameters ε between the Michaelis-Menten and Qss models in Eqs. 32 and 40 are not exactly comparable, the difference in the expressions suggests greater utility of the Qss model as an approximation. In general, the Michaelis-Menten model is a good approximation, if the total target R tot is small relative to K m + C 0 from (32). This is not the case for the Qss model, which has been demonstrated in applications and simulations (see (13) for more simulation examples). Figure 5 is one more example—the Qss model is a better approximation for both free drug and complex at initial concentration C 0 = 0.1. Nevertheless, the opposite could also be true. For the simulation case in the upper panels of Fig. 6, assume a more reasonable k on = 0.01 and R tot = 100, comparable to the initial free drug concentration of 200. The lower panels in Fig. 6 shows that the Michaelis-Menten model is a better approximation than the Qss model in this case. In the plot for the free drug the Michaelis-Menten model is not distinguishable from the general TMD model. Here the ε from Eq. 32 is 0.20, which does not appear to be a good indicator for the goodness of approximation.

Others

For the frequently applied cases of TMD models with peripheral and depot compartments (thus I(t) ≠ 0), we describe parameter requirements for simplifications to be appropriate approximations. Again, assume constant total target R tot. The scaling approach can be easily adapted from the case of a one-compartment model in “Michaelis-Menten Model” and “Quasi-Steady-State Model”. The scaling factor C 0 for the free and total drug is replaced by \( {C_0} = {C_0} + {B_0} + \int {_{{t > 0}}} I(t)dt \), where B 0 is the depot dose divided by the volume of distribution of the central compartment (see Eq. 1). With this, the change of variables of the complex, the free and total drug remains the same. For the equation of the peripheral compartment (3), the scaled dimensionless variable can be set as z = B T /C 0. The fast time scale need not be changed, but the slow time scale may be chosen as \( {T_s} = {\left( {\max \{ {k_{\text{on}}}{R_{\text{tot}}} + {k_{\text{e}}} + {k_{\text{pt}}},{k_{\text{tp}}}\} } \right)^{{ - 1}}} \) for the Michaelis-Menten model and \( {T_s} = {\left( {\max \{ {k_{\text{e}}} + {k_{\text{pt}}},{k_{\text{met}}} - {k_{\text{e}}} - {k_{\text{pt}}},{k_{\text{tp}}} + {k_{\text{pt}}}\} } \right)^{{ - 1}}} \) for the Qss model. The small parameter for the derivative of the complex, defined as the ratio of T f and T s , in the case of the Michaelis-Menten model is:

$$ \varepsilon = \frac{{\max \;\{ {k_{\text{on}}}{R_{\text{tot}}} + {k_{\text{e}}} + {k_{\text{pt}}},{k_{\text{tp}}}\} }}{{{k_{\text{on}}}({K_{\text{m}}} + {C_0})}}, $$
(43)

and in the case of the Qss model is

$$ \varepsilon = \frac{{\max \;\{ {k_{\text{e}}} + {k_{\text{pt}}},{k_{\text{met}}} - {k_{\text{e}}} - {k_{\text{pt}}},{k_{\text{tp}}} + {k_{\text{pt}}}\} }}{{{k_{\text{on}}}({K_{\text{m}}} + {C_{{0}}} + {R_{\text{tot}}})}}. $$
(44)

Therefore, under similar regularity conditions the Michaelis-Menten and Qss models are suitable approximations of the general TMD models if their respective ε values are small.

Marathe et al. (29) used the same change of variables as in Peletier and Gabrielsson (14) but different fast and slow time scales that were the characteristic times of maximum free target depletion due to binding \( \left( {k_{\text{on}}^{{ - 1}}C_0^{{ - 1}}} \right) \) and of drug elimination \( \left( {k_{\text{e}}^{{ - 1}}} \right) \). Consequently the small parameter is the ratio \( \varepsilon = {k_{\text{e}}}/\left( {{k_{\text{on}}}{C_0}} \right) \). Simulations were conducted to support the rapid binding model as a suitable approximation to the general TMD model. It is interesting to compare their choice of ε and the choice in (14) (ε = R tot/C 0) with ours. The parameters in both ε definitions point to those that should be included in the ε requirement and corroborate those in Eqs. 43 and 44 (except for K m).

The TMD model of interferon-β1a studied in (1,5) is used in “Methods” as an introductory example. The ε values of 4.07 and 0.15, calculated from Eqs. 43 and 44, indicate that the Michaelis-Menten model should be a poor approximation but the Qss model is perhaps reasonable. Another example used in (1) to illustrate the utility of the general TMD model was bosentan, an endothelin receptor antagonist for pulmonary artery hypertension. Concentration data were collected from healthy male subjects receiving 5-minute infusions of 10, 50, 250, 500, and 750 mg. At 250 mg, the ε value is 0.04 for the Qss model and 0.16 for the Michaelis-Menten model. Simulation shows that the rapid binding and Qss models approximate the general TMD model quite well whereas the Michaelis-Menten model does not (plots not shown). The approximation of the Qss model is still reasonable at doses of 10 and 50 mg with ε = 0.15 and 0.32, respectively. For the rapid binding or Qss model, the concentration-time profiles are close to those of the general TMD model over 24 h after dose, except at the first hour. The Michaelis-Menten model is again not a good approximation; the calculated ε values are 3.28 and 0.77 from (43).

The same scaling approach in “Approximations” can be taken for drug-receptor binding occurring in the peripheral, instead of the central, compartment. Under the Qss assumption the ε parameters can be defined for the Michaelis-Menten and Qss models as indicators for the goodness of the approximation.

DISCUSSION

The current drug research and development effort has an increased focus on biological compounds, for which TMD is common and poses unique challenges. Understanding of the TMD is beneficial for the investigation of dose-exposure-response relationships, important for the selection of optimal drug candidate and dose regimen. Models characterizing TMD are, however, complicated with model parameters often not identifiable because of data limitation. In this study we have organized various simplifications of the general TMD model and shown that, in addition to assuming constant R tot, one common approach to simplifying the general TMD model is to replace quite often the equation for the complex by an algebraic one in the system of ODEs defining the general TMD model. The rapid binding and Qss models are examples of simplifications using this approach. The Qss assumption sets the right-hand side of Eq. 5 for the complex to 0 and leads naturally to a “small derivative” of the left-hand side. With the Qss assumption, the four equivalent ODE systems that define the same general TMD model produce four non-equivalent simplifications including the Michaelis-Menten and Qss models. Under some parameter requirements, the Michaelis-Menten and Qss models are appropriate approximations to the general TMD model based on a scaling approach in singular perturbation theory.

Note that the Michaelis-Menten and Qss models, as simplifications of the general TMD model, are not reductions of it; namely, the solution to either simplified ODE system is not a special case of the general TMD model with certain parameter constraints satisfied, unlike the case of assuming constant R tot, a simplification when k met = k deg in the general TMD model. Graphically, since the quasi-steady-state (or rapid binding) assumption invalidates the ODE system for the general TMD model, no concentration-time profiles from the Michaelis-Menten or Qss model will coincide with those from a general TMD model.

For simplifications of the general TMD model, although we have presented the results in the setting of one-compartment models, all conclusions are valid for two-compartment models with necessary changes. Other extensions of the results are also perceivable. By contrast, it is less straightforward to extend the scaling method to identify appropriate requirements for the simplifications to be close to the general TMD model when, for example, R tot is not necessarily constant. Ideally the requirements under which a simplification is close to the general TMD model needs to be quantified. This, in turn, requires that we quantify the “closeness” of a simplification to the general TMD model. As a first attempt, we have defined ε via scaling approach with its magnitude serving as crude guidance for goodness of the approximation. Although ε within specified parameter ranges is uniform in that, as ε approaches 0, the simplification approaches the general TMD model in a pre-defined region, the quantity ε does not have a strict order relationship with respect to the closeness of the approximation. There are indeed many questions remain unanswered. Overall, the general TMD model proposed in (1) and discussed here is itself a simplification of the complex biological system. Competition with endogenous ligands for a binding receptor (as a target) may be built further into the system. Target storage that may replenish target degraded or bound by the drug would be among the next factors to consider. Appropriate simplifications may follow as a result from models for these extensions of mechanisms.

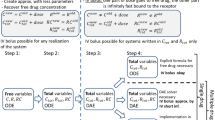
As discussed, the pharmacokinetics of a biological compound with TMD depends on the target and is not always easy to characterize, especially when information of the target is little. Therefore, the investigation of the TMD behavior requires appropriate data that come from studies of adequate designs. Unfortunately, study designs are often not adequate at early learning stages of drug development because of limited experience and knowledge. Consequently, the pharmacometrician who works with such limited information may initially choose a simplified TMD (e.g., Michaelis-Menten) model. As more informative data become available, more elaborate models can be attempted, and decisions have to be made to improve the initial or early TMD models. The improvement could range from keeping a parsimonious model that is minimally mechanistic for only predictive purposes to including many mechanistic components in a model at the risk of over-parameterization in practice. It is for this kind of decisions that we hope the current work is useful; i.e., with a better understanding of various modifications and simplifications of the general TMD model, summarized in Fig. 7, it may be less difficult a task for a pharmacometrician to strike a proper balance by choosing an appropriately mechanistic and, yet, appropriately parsimonious model for studying compounds with TMD behavior.

Fig. 7
figure 7

General target-mediated-disposition model and its simplifications. Assumptions indicated by arrow colors. Blue arrows: Qss assumption; green arrows: rapid binding assumption; red arrows: constant Rtot assumption or k met = k deg; and black arrows: assumptions followed from the Wagner equations (e.g., (19)).

Full size image