Target mediated drug disposition with drug–drug interaction, Part II: competitive and uncompetitive cases

Abstract

We present competitive and uncompetitive drug–drug interaction (DDI) with target mediated drug disposition (TMDD) equations and investigate their pharmacokinetic DDI properties. For application of TMDD models, quasi-equilibrium (QE) or quasi-steady state (QSS) approximations are necessary to reduce the number of parameters. To realize those approximations of DDI TMDD models, we derive an ordinary differential equation (ODE) representation formulated in free concentration and free receptor variables. This ODE formulation can be straightforward implemented in typical PKPD software without solving any non-linear equation system arising from the QE or QSS approximation of the rapid binding assumptions. This manuscript is the second in a series to introduce and investigate DDI TMDD models and to apply the QE or QSS approximation.

Introduction

Drugs interact in many different ways with their targets. Some drug–drug interaction (DDI) mechanisms can be formulated based on first principles such as competitive, uncompetitive or non-competitive behavior [1–3].

The first aim of this manuscript is to introduce competitive and uncompetitive DDI as part of target-mediated drug disposition (TMDD) principles [4, 5]. We investigate pharmacokinetic DDI properties and present the baseline situation for constantly available substances, e.g. necessary to describe interaction of endogenous and exogenous agents.

The second aim is to provide quasi-equilibrium (QE) and quasi-steady state (QSS) approximations for DDI TMDD models with rapid binding [6]. Such approximations result in a collection of differential and algebraic equations [6–8], formulated in total concentration and total receptor variables. In contrast to the single drug case, in the DDI TMDD situation the non-linear equation system providing the free drug concentrations can no longer be solved explicitly, as presented by Yan, Chen and Krzyzanski [9] for competitive DDI TMDD. Therefore, based on the single drug case, we derived an ordinary differential equation (ODE) formulation without solving any equation system [6]. Here we apply the developed method to DDI TMDD models to avoid solving any equation systems and to obtain a formulation in free concentration variables. Our QE or QSS representation for DDI TMDD models can be straightforwardly implemented in standard pharmacokinetic / pharmacodynamic (PKPD) software.

Theoretical

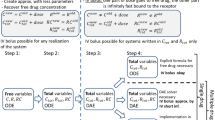
We divided the construction and approximation of a general TMDD model into four steps, see Fig. 1 in [6]. In the following we apply this construction principles to the competitive and uncompetitive DDI TMDD model. To keep the focus on the DDI TMDD models, we provide detailed mathematical derivations in the Appendices.

Competitive TMDD

If two drugs A and B compete for the same receptor R and thereby form two complexes $RC_A$ and $RC_B$, this is called competitive interaction [1–3, 9, 10]. In this mechanism both drugs have equal rights, i.e. if only one drug is on board, the system reduces to the single case. We call this property symmetric DDI behavior.

Original formulation in free variables

The binding kinetics of competitive DDI and its extension to TMDD are presented in Fig. 1a. The original model equations read

$$\begin{aligned} \frac{d}{dt} C_A&= In_A(t) - k_{elA} C_A - k_{onA} C_A \cdot R \nonumber \\&\quad + k_{offA} RC_A \end{aligned}$$

(1)

$$\begin{aligned} \frac{d}{dt} C_B&= In_B(t) - k_{elB} C_B - k_{onB} C_B \cdot R \nonumber \\&\quad + k_{offB} RC_B \end{aligned}$$

(2)

$$\begin{aligned} \frac{d}{dt} R&= k_{syn} - k_{deg} R - k_{onA} C_A \cdot R - k_{onB} C_B \cdot R \nonumber \\&\quad + k_{offA} RC_A + k_{offB} RC_B \end{aligned}$$

(3)

$$\begin{aligned} \frac{d}{dt} RC_A&= k_{onA} C_A \cdot R - (k_{offA} + k_{intA}) RC_A \end{aligned}$$

(4)

$$\begin{aligned} \frac{d}{dt} RC_B&= k_{onB} C_B \cdot R - (k_{offB} + k_{intB}) RC_B \, . \end{aligned}$$

(5)

The initial values of Eqs. (1)–(5) are defined by their steady state baseline values. Under the assumption that the baseline concentrations of the free drugs is $C_A^0 \ge 0$ and $C_B^0 \ge 0$, the receptor and the complexes are in steady state and initial conditions read

$$\begin{aligned} C_X (0)= \,& {} C_X^0 \end{aligned}$$

(6)

$$\begin{aligned} \nonumber R(0) &= R^0 \\ &= \frac{k_{syn}}{k_{deg} + k_{intA} \frac{k_{onA} C_A^0}{k_{offA}+k_{intA}} + k_{intB} \frac{k_{onB} C_B^0}{k_{offB}+k_{intB}} } \end{aligned}$$

(7)

$$\begin{aligned} RC_X (0) &= RC_X^0 = \frac{k_{onX} C_X^0 R^0}{k_{offX} +k_{intX}} \end{aligned}$$

(8)

where X either represents A or B, i.e. $X \in \{A,B\}$. The input functions have the form

$$\begin{aligned} In_X (t)=\, & {} In_{BaseX} + In^{Ad}_X (t) \nonumber \\=\, & {} k_{elX} C_X^0 + k_{intX} RC_X^0 + In^{Ad}_X (t) \end{aligned}$$

(9)

with $In_{BaseX}$ denoting the inflow baseline and $In^{Ad}_X(t)$ standing for the administration of the drugs. Eqs. (7)–(9) are obtained similarly as in the single drug case [6]. Note that for a zero baseline concentration $C_A^0 = C_B^0 =0$ we have $RC_A^0= RC_B^0 =0$, $R^0 = k_{syn}/k_{deg}$ and $In_{BaseA} = In_{BaseB} =0.$

In order to provide valid QE or QSS approximations please note that the competitive TMDD model Eqs. (1)–(5) are symmetric in A and B and have the property that if one drug is absent the model equations reduce to the single TMDD equations for the other drug. This means for the parameter values of the competitive system in particular, the QE or QSS assumptions for each single system have to be satisfied. Thus, as in the single drug case [6] we follow Peletier et al. [11] and assume

$$\begin{aligned} \frac{k_{offX}}{k_{onX}R^0}\ll & {} 1 \end{aligned}$$

(10)

$$\begin{aligned} \max \left( \frac{k_{intX}}{k_{offX}} , \frac{k_{deg}}{k_{offX}} , \frac{k_{elX}}{k_{offX}} \right)< & {} m_X \nonumber \\ \text{ with } \frac{k_{off}}{k_{on}R^0} m_X\ll & {} 1 \, . \; \end{aligned}$$

(11)

In addition, in case of an IV bolus we assume

$$\begin{aligned} \frac{dose_X}{V}> & {} R^0 \, . \; \; \end{aligned}$$

(12)

In case of constant infusion, i.e. $In_X^{Ad} = k_{infX} >0$, $t \ge 0$, we assume

$$\begin{aligned} C_ {ssX}> & {} R^0, \; \; \end{aligned}$$

(13)

with $C_{ssX} = \lim _{t \rightarrow \infty } C_X (t)$ denoting the steady state of the free concentration of drug X.

Final QE and QSS approximation in free variables

We apply the techniques of [6] to Eqs. (1)–(5) (for details see Appendix "Derivation of the final QE and QSS approximation in free concentration variables") and obtain its QE and QSS approximation written as ODE formulation in the original variables:

$$\begin{aligned} \begin{pmatrix} \frac{d}{dt} C_A \\ \frac{d}{dt} C_B \\ \frac{d}{dt} R \end{pmatrix}&= M_{Com} (C_A,C_B,R) \cdot g_{Com}(C_A,C_B,R) \end{aligned}$$

(14)

where matrix $M_{Com} (C_A,C_B,R)$ is listed in Table 1,

$$\begin{aligned}&g_{Com}(C_A,C_B,R) \nonumber \\&= \begin{pmatrix} In_A(t) - k_{elA} C_A - k_{intA} \frac{C_A \cdot R}{K_{YA}} \\ In_B(t) - k_{elB} C_B - k_{intB} \frac{C_B \cdot R}{K_{YB}} \\ k_{syn} - k_{deg} R - k_{intA} \frac{C_A \cdot R}{K_{YA}} - k_{intB} \frac{C_B \cdot R}{K_{YB}} \end{pmatrix} \end{aligned}$$

(15)

with the baseline initial values defined by $g_{Com}(C_A^0,C_B^0,R) = 0$ resulting in

$$\begin{aligned} C_X(0)=\ & {} C_X^0 , \end{aligned}$$

(16)

$$\begin{aligned} R(0)=\, & {} R^0 \; = \; \frac{k_{syn}}{k_{deg} + k_{intA} \frac{C_A^0}{K_{YA}} + k_{intB} \frac{C_B^0}{K_{YB}} } \, , \end{aligned}$$

(17)

and the input functions

$$\begin{aligned} In_X (t)=\, & {} k_{elX} C_X^0 + k_{intX} \frac{C_X^0 R^0}{K_{YX}} + In^{Ad}_X (t), \end{aligned}$$

(18)

with

$$\begin{aligned} K_{DX}=\, & {} \frac{k_{offX}}{k_{onX}} \quad \text{ and } \quad K_{SSX} \; = \; \frac{k_{offX} + k_{intX}}{k_{onX}} \end{aligned}$$

(19)

where Y denotes either D (the dissociation constant) or SS (the steady state constant). According to the rapid binding assumptions, the complexes can be recovered from

$$\begin{aligned} RC_A&= \frac{C_A \cdot R}{K_{YA}} \quad \text{ and } \quad RC_B = \frac{C_B \cdot R}{K_{YB}} \, . \end{aligned}$$

(20)

Eqs. (14)–(20) are the final competitive DDI TMDD model in free concentration variables with QE or QSS approximation.

Similar to the single drug case, one has to investigate the IV bolus situation again, since we are dealing here with two infinitely fast processes running at the same time. We are proceeding as in [6]. We mimic an IV bolus by an IV short infusion, instead of solving the algebraic system of balance equations

$$\begin{aligned} C_A^{new} + \frac{C_A^{new} R^{new}}{K_{YA}}= \,& {} C_A + RC_A + \frac{dose_A}{V} \\ C_B^{new} + \frac{C_B^{new} R^{new}}{K_{YB}}=\, & {} C_B + RC_B + \frac{dose_B}{V} \\ R^{new} + \frac{C_A^{new} R^{new}}{K_{YA}} + \frac{C_B^{new} R^{new}}{K_{YB}}=\, & {} R + RC_A + RC_B \end{aligned}$$

to compute the new states $C_A^{new}, \, C_B^{new}$ and $R^{new}$ after administration, where V is the volume of distribution.

Please note that Eqs. (14)–(20) with a short IV infusion is an easy to use ODE which avoids the computation of the solution of any algebraic system.

The first attempt to derive a QE approximation for a competitive DDI TMDD system was by Yan et al. [9]. They used the total variables $C_{totA} = C_A + RC_A$, $C_{totB} = C_B + RC_B$, $R_{tot} = R+ RC_A + RC_B$ and wrote the algebraic equations (20) of the QE assumptions in the form

$$\begin{aligned}&K_{YA} (C_{totA} - C_A) \nonumber \\ =&(R_{tot} - C_{totA} - C_{totB} + C_A + C_B) C_A \end{aligned}$$

(21)

$$\begin{aligned}&K_{YB} (C_{totB} - C_B) \nonumber \\ =&(R_{tot} - C_{totA} - C_{totB} + C_A + C_B) C_B \, . \end{aligned}$$

(22)

However, in contrast to the single drug case, no explicit solution for $C_A$ and $C_B$ of Eqs. (21)–(22) is known. Thus, the reduction of the differential algebraic model equations to an ordinary differential equation in the total variables $C_{totA}, \, C_{totB}$ and $R_{tot}$ is not possible.

Uncompetitive TMDD

If drug A binds to receptor R forming a complex $RC_A$ and drug B binds now to this complex $RC_A$ only, and additionally forms a complex $RC_{AB}$, this mechanism is called uncompetitive DDI. Hence, drug B acts as an antagonist and its effect depends on prior activation of the recepter R, see [1–3, 10, 13]. We call this unsymmetrical DDI behavior. In case of uncompetitive DDI TMDD, drug A follows TMDD behavior. However, drug B has first-order elimination in absence of $RC_A$ and changes to TMDD behavior in presence of $RC_A$. Interestingly, in unsymmetrical cases, i.e., situations of DDIs where the roles of A and B are not interchangeable, there will be a fundamental difference between the QE and QSS approximation.

Original formulation in free variables

The model equations of the uncompetitive DDI TMDD model in original variables read

$$\begin{aligned} \frac{d}{dt} C_A&= In_A(t) - k_{elA} C_A - k_{onA} C_A \cdot R + k_{offA} RC_A \end{aligned}$$

(23)

$$\begin{aligned} \frac{d}{dt} C_B&= In_B(t) - k_{elB} C_B - k_{onAB} C_B \cdot RC_A \nonumber \\&\quad + k_{offAB} RC_{AB} \end{aligned}$$

(24)

$$\begin{aligned} \frac{d}{dt} R&= k_{syn} - k_{deg} R - k_{onA} C_A \cdot R + k_{offA} RC_A \end{aligned}$$

(25)

$$\begin{aligned} \frac{d}{dt} RC_A&= k_{onA} C_A \cdot R - k_{onAB} C_B \cdot RC_A \nonumber \\&\quad + k_{offAB} RC_{AB} - (k_{offA} + k_{intA}) RC_A \end{aligned}$$

(26)

$$\begin{aligned} \frac{d}{dt} RC_{AB}&= k_{onAB} C_B \cdot RC_A - (k_{offAB} + k_{intAB}) RC_{AB} \, . \end{aligned}$$

(27)

In Fig. 1b the schematic of Eqs. (23)–(27) is presented. The steady state baseline initial values are

$$\begin{aligned} C_X (0)&= C_X^0 \end{aligned}$$

(28)

$$\begin{aligned} R(0)&= R^0 \nonumber \\&= \frac{ k_{syn}}{ k_{deg} + \frac{ k_{intA} C_A^0 K_{SSAB} + k_{intAB} C_A^0 C_B^0 }{ K_{SSAB} K_{SSA} + \frac{C_B^0 k_{intAB}}{k_{onA}} } } \end{aligned}$$

(29)

$$\begin{aligned} RC_A (0)&= RC_A^0 = \frac{C_A^0 R^0 K_{SSAB}}{K_{SSA}K_{SSAB} + C_B^0 \frac{k_{intAB}}{k_{onA}} } \end{aligned}$$

(30)

$$\begin{aligned} RC_{AB} (0)&= RC_{AB}^0 = \frac{C_A^0 C_B^0 R^0 }{K_{SSA}K_{SSAB} +C_B^0 \frac{k_{intAB}}{k_{onA}} } . \end{aligned}$$

(31)

Please note, to shorten the notation in Eqs. (29)–(31) we used $K_{SSX}$ from Eq. (19). The input functions have the form

$$\begin{aligned} In_A (t)=\, & {} k_{elA} C_A^0 + k_{intA} RC_A^0 + k_{intAB} RC_{AB}^0 \nonumber \\&+ In^{Ad}_A (t) \end{aligned}$$

(32)

$$\begin{aligned} In_B (t)=\, & {} k_{elB} C_B^0 + k_{intAB} RC_{AB}^0 + In^{Ad}_B (t) \end{aligned}$$

(33)

where $In^{Ad}_X(t)$ denotes administration of drug A or B.

To locate parameter regions for which the uncompetitive system (23)–(27) admits a valid QE approximation please keep the following properties of the system (23)–(27) in mind. If drug B is absent, the model equations reduce to the single TMDD equations for $C_A, \, R$ and $RC_A$. On the other hand, in absence of drug A due to the unsymmetry in the equations, drug B follows a simple linear one-compartment PK with elimination rate $k_{elB}$. Following Peletier et al. [11] we assume the QE assumptions for the parameter belonging to drug A

$$\begin{aligned} \frac{k_{offA}}{k_{onA}R^0}\ll & {} 1 \end{aligned}$$

(34)

$$\begin{aligned} \max \left( \frac{k_{intA}}{k_{offA}} , \frac{k_{deg}}{k_{offA}} , \frac{k_{elA}}{k_{offA}} \right)< & {} m_A \nonumber \\ \text{ with } \frac{k_{offA}}{k_{onA}R^0} m_A\ll & {} 1. \end{aligned}$$

(35)

In addition, in case of IV bolus we assume

$$\begin{aligned} \frac{dose_A}{V}> & {} R^0 . \end{aligned}$$

(36)

In case of constant infusion of drug A, that is, $In_A^{Ad} = k_{infA} >0$ for $t \ge 0$ we assume

$$\begin{aligned} C_{ssA}> & {} R^0 . \end{aligned}$$

(37)

Moreover, in order to achieve a fast binding of drug B to its complex we in addition assume

$$\begin{aligned}&k_{offAB} \ll k_{onAB} . \end{aligned}$$

(38)

Final QE approximation in free variables

We now apply the principles of [6] to Eqs. (23)–(27) (see Appendix “Derivation of the final QE and QSS approximation in free concentration variables”). The QE approximation provides the algebraic equations

$$\begin{aligned} 0&= C_A R - K_{DA} RC_A \end{aligned}$$

(39)

$$\begin{aligned} 0&= C_B RC_A - K_{DAB} RC_{AB} . \end{aligned}$$

(40)

The QSS approximation of the complexes now reads

$$\begin{aligned} 0&= C_A R - \frac{k_{intAB}}{k_{onA}} RC_{AB} - K_{ssA} RC_A \end{aligned}$$

(41)

$$\begin{aligned} 0&= C_B RC_A - K_{ssAB} RC_{AB} \end{aligned}$$

(42)

see Appendix “QSS approximation” . Interestingly, in Eq. (41) the parameter $k_{onA}$, which should be eliminated by the approximation, is still involved. Hence, traditional singular perturbation theory [6, 15] does not eliminate all production rates. Therefore it seems to be not an adequate reduction tool for this DDI case.

The final equations for uncompetitive DDI TMDD model in free variables with the QE approximation are

$$\begin{aligned} \begin{pmatrix} \frac{d}{dt} C_A \\ \frac{d}{dt} C_B \\ \frac{d}{dt} R \end{pmatrix}&= M_{Un}(C_A,C_B,R) \cdot g_{Un}(C_A,C_B,R) \end{aligned}$$

(43)

where matrix $M_{Un}(C_A,C_B,R)$ is listed in Table 1, and

$$\begin{aligned}&g_{Un}(C_A,C_B,R) \nonumber \\&= \begin{pmatrix} In_A(t) - k_{elA} C_A - k_{intA} \frac{C_A R}{K_{DA}} - k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \\ In_B(t) - k_{elB} C_B - k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \\ k_{syn} - k_{deg} R - k_{intA} \frac{C_A R}{K_{DA}} - k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \end{pmatrix} . \end{aligned}$$

(44)

According to $g_{un}(C_A^0,C_B^0,R) =0$ the baseline initial values read

$$\begin{aligned} C_X(0)&= C_X^0 \end{aligned}$$

(45)

$$\begin{aligned} R(0)&= R^0 \nonumber \\&= \frac{k_{syn}}{k_{deg} + k_{intA} \frac{C_A^0}{K_{DA}} + k_{intAB} \frac{C_A^0 C_B^0}{K_{DA} K_{DAB}} } \end{aligned}$$

(46)

(see Appendix “Baseline initial values for the uncompetitive TMDD model”). The input functions are

$$\begin{aligned} In_A (t)&= k_{elA} C_A^0 + k_{intA} \frac{C_A^0 R^0}{K_{DA}} \nonumber \\&\quad + k_{intAB} \frac{C_A^0 C_B^0 R^0}{K_{DA}K_{DAB}} + In^{Ad}_A (t) \end{aligned}$$

(47)

$$\begin{aligned} In_B (t)&= k_{elB} C_B^0 + k_{intAB} \frac{C_A^0 C_B^0 R^0}{K_{DA}K_{DAB}} + In^{Ad}_B (t). \end{aligned}$$

(48)

From Eqs. (39)–(40) the complexes can be obtained via

$$\begin{aligned} RC_A&= \frac{C_AR}{K_{DA}} \end{aligned}$$

(49)

$$\begin{aligned} RC_{AB}&= \frac{C_A C_B R}{K_{DA} K_{DAB}} \, . \end{aligned}$$

(50)

Drug administration can be performed analogously to the competitive DDI TMDD case. In particular, an IV bolus will be mimicked by a short IV infusion.

Methods

To implement the presented QE or QSS approximation in ODE formulation with free concentration variables, IV bolus administration has to be mimicked by a short IV infusion. Explanation and full details for our ODE formulation with an IV short infusion in ADAPT 5 [16], NONMEM [17], R [18] and MATLAB [19] can be found in [6]. Oral drug administration can be implemented as usual. In Appendix 5, the NONMEM control stream of the competitive DDI TMDD with QE approximation and IV short infusion Eqs. (14)–(18), and ADAPT 5 source code for the uncompetitive DDI TMDD scenario Eqs. (43)–(48) is presented. Full files are available as supplemental material.

We also implemented the original competitive and uncompetitive DDI TMDD model with IV bolus Eqs. (1)–(9) and Eqs. (23)–(33) in ADAPT 5 and produced data with the residual error model

$$\begin{aligned} Var_i = \left( \sigma Y(t_i) \right) ^2 \end{aligned}$$

where $Var_i$ is the variance at the ith time point $t_i$, $\sigma$ is the variance parameter and Y the model prediction.

Results

First, typical concentration profiles and pharmacokinetic interaction properties of the original competitive Eqs. (1)–(9) and uncompetitive Eqs. (23)–(33) DDI TMDD model were produced. Second, the QE approximation quality in ODE formulation in free concentration variables with IV short infusion was visualized for escalating doses. Finally, we fit data produced by the original formulation with our QE approximation in ADAPT 5 and NONMEM.

Typical concentration profiles

Competitive DDI

In competitive DDI both drugs compete for the same receptor, a common behavior in different DDI scenarios. For example, often therapeutic antibodies and hematopoietic growth factors are agents competing for the same receptor with endogenous substances [9]. Also endogenous immunoglobulin G antibodies (IgG) compete with exogenous IgG for the neonatal Fc receptor [9], and erythropoiesis-stimulation agents compete with endogenous erythropoietin for the same receptor.

Two properties of the competitive TMDD model Eqs. (1)–(9) were observed: (i) if model parameters of drug A and B are equal, also the concentration profiles $C_A$ and $C_B$ are equal, (ii) concentration profiles $C_A$ and $C_B$, when administered in combination, appear to be higher up to a certain time point compared to the single profiles, if the number of receptors is equal for the single and multiple case. In Fig. 2a, b, property (ii) is shown in case of no baseline concentration.

Next the pharmacokinetic interaction was assessed. Both drugs interact with each other in a competitive manner and administration of one drug has an effect on the concentration profile of the other drug. Let drug A be present in the system. Administration of drug B causes a decrease in the number of receptors R and simultaneously an increase of the complex $RC_B$. Due to the competing behavior, a release of bounded drug A from the complex $RC_A$ occurs and therefore an increase of the concentration of drug A. Hence, an increase of free drug concentration $C_A$ can occur without actual administration of drug A. As example, this behavior is shown for endogenously available drug A and B at baseline $C_A^0 = C_B^0 > 0$ with different administrations in Fig. 2c, d. In the above examples, a certain set of model parameters ($k_{elA} = 0.1$, $k_{onA} = 2.5$, $k_{offA} = 0.1$, $k_{intA} = 0.1$, $k_{elB} = 0.2$, $k_{onB} = 5$, $k_{offB} = 0.1$, $k_{intB} = 0.1$, $k_{syn} = 5$, and $k_{deg} = 0.25$) was chosen. These settings satisfy the conditions (10)–(13) with $m_A = m_B =2 .5$ and $R^0 \in [10,20]$. The actual value of $R^0$ depends on the baseline values $C_A^0, C_B^0$ with $0 \le C_A^0, C_B^0 \le 1$.

Uncompetitive DDI

In uncompetitive DDI the action of drug B depends on prior activation of receptor R [13], i.e. if drug A does not bind with R producing a complex $RC_A$, drug B is not active in the mechanism. Hence, drug B acts as an antagonist. Uncompetitive interaction is attractive from the perspective of selective drug action [21], but is still a rare mechanism [22]. Some examples without TMDD behavior are: (i) lithium inhibiting inositol monophosphutuse [21] for psychiatric medication, or (ii) memantine an NMDA receptor antagonist for Alzheimer’s disease [13]. Currently we are not aware of uncompetitive DDI TMDD examples. However, investigation of this case is useful to open the route for the more common non-competitive scenario where drug B binds to both, the receptor R and the complex $RC_A$.

In the uncompetitive TMDD setting, drug B binds to the complex $RC_A$ produced by drug A only. Hence, if no drug A is on board, or the complex $RC_A$ is nearly eliminated, drug B follows a first-order elimination process. In contrast, if $RC_A$ is available, drug B follows typical TMDD-like profiles, see Fig. 2e, f.

Again the pharmacokinetic interaction, i.e. the effect of administration of one drug on the profile of the other drug was examined. If drug A is administered, complex $RC_A$ is build up and therefore more targets are available for drug B causing a decrease in its free concentration. For administration of drug B, complex $RC_A$ decreases but only causes a marginal effect on the concentration profile of drug A. For endogenously available drugs at a baseline $C_A^0 = C_B^0 > 0$ the two cases are visualized in Fig. 2g, h. In the above examples, we selected the model parameters as $k_{elA}$ = $k_{elAB}$ = 0.1, $k_{onA}$ = $k_{onAB}$ = 2.5, $k_{offA}$ = $k_{offAB}$ = 0.1, $k_{intA}$ = $k_{intAB}$ = 0.1, $k_{syn}$ = 5 and $k_{deg}$ = 0.25. These parameter values satisfy (34)–(38) with $m_A = 2.5$, $k_{onAB} = 25 k_{offAB}$ and $R^0 \in [10,20]$. As in the competitive case the value of $R^0$ depends on the baseline values $C_A^0, C_B^0$ with $0 \le C_A^0, C_B^0 \le 1$.

Approximation quality of the QE formulation

Competitive

The QE approximation in the ODE formulation with an IV short infusion Eqs. (14)–(18) captures reasonably well the dynamics of the free concentrations from the original Eqs. (1)–(9), see Fig. 3a, b. Next the QE approximation quality if only drug A is administered and concentration of drug B is present was assessed. As an example we consider baseline concentrations $C_A^0, C_B^0 > 0$. For administration of drug A only, the concentration profile of drug B increases. The QE approximation produces an immediate increase of $C_B$ caused by the rapid binding assumption, whereas the original system shows a more slow or fast increase. The sharpness of increase of the original system depends on the magnitude of the values $k_{onB}$ and $k_{offB}$. We increased the values $k_{onB}$ and $k_{offB}$ with an equal ratio $K_{DB}$, and observe that the original system converges to the QE approximation, compare Fig. 3c, d. This shows that the rapid binding in the original system has to be fulfilled in order to obtain a reasonable approximation.

Uncompetitive

Also the QE approximation in ODE formulation with an IV short infusion Eqs. (43)–(48) captures reasonably well the dynamics of free concentrations from the original equations (23)–(33), see Fig. 3e, f. Again drug A administration only in presence of concentration of drug B was examined. Consider as example baseline concentrations $C_A^0, C_B^0 > 0$. For increasing values of $k_{onA}$ and $k_{offA}$ with equal $K_{DA}$ the original system for drug A and drug B converges to the QE approximation. Due to the antagonistic nature of drug B, the $k_{onAB}$ and $k_{offAB}$ do not seem to be related to the process of convergence.

Parameter estimation

The QE approximation of the competitive Eqs. (14)–(18) and uncompetitive Eqs. (43)–(48) DDI TMDD model in ODE formulation with an IV short infusion was applied to fit produced data from the original formulations Eqs. (1)–(9) and (23)–(33). All parameters could be well estimated from the produced data. However, in the uncompetitive case it can be difficult to estimate all three drug B related parameters, since drug B switches from the typical TMDD profile back to first-order elimination, if only few or no complex $RC_A$ is available. Therefore, we fixed $K_{DAB}$ in our example. Applied model parameters for data production, initial estimates and final estimates are listed in Table 2. In Fig. 4 the fits of the competitive case (panels a and b) from NONMEM and the uncompetitive case (panels c and d) in ADAPT 5 are shown.

Discussion

Competitive and uncompetitive DDI was extended with TMDD behavior and the baseline scenario for endogenously available substances was included. DDI TMDD models describe the interaction on the pharmacokinetic level instead on an effect level as presented in [3]. We investigated the properties of the competitive and uncompetitive mechanisms. For example, if both drugs compete for the same receptor, administration of a single drug A only, will have an impact on the present free concentration profile of drug B. However, a systematic investigation with mathematical characterizations of the DDI behaviors is crucial to fully describe and quantify the behaviors of these effects.

We applied the QE or QSS approaches to construct approximations resulting in a collection of differential and algebraic equations. Interestingly, the QSS approximation is not capable of removing all drug related parameters (i.e. $k_{onA}$) in the uncompetitive case.

In the QE or QSS approximation, we now deal with a non-linear equation system for the free drug concentrations, as initially shown in [9] for the competitive DDI case. In total variables, for such systems no explicit solution is known. Therefore, we investigated the single drug case again in a separate manuscript [6], and generalized the presented method to the QE or QSS approximation of DDI TMDD models. An equivalent formulation for the free drug concentrations in ordinary differential equations was obtained without solving any equation system. Our formulation can be implemented in any PKPD software as demonstrated for ADAPT 5 and NONMEM. In the QE or QSS approximation the rapid binding process is approximated by an infinitely fast process. This implies that in the IV bolus situation, which is also an infinitely fast process, one part of the drug goes to the free drug concentration and the other part is infinitely fast bound to the complex. Hence, we mimic the administration of an IV bolus by an IV short infusion. An oral administration can be applied as usual because the drug goes to an additional absorption compartment and not directly to the free drug concentration.

The original DDI TMDD systems can be well described by the QE approximation if the rapid binding assumption in the original system is fulfilled. We demonstrated that e.g. in case of drug A administered to a system where concentration of drug B is present, the $k_{on}$ and $k_{off}$ parameter have to be large, to satisfactorily describe the increase of drug B. This is in accordance with the rapid binding assumption. Moreover, we emphasize that our applied method is valid in general and can be applied to other systems with rapid binding behavior to construct appropriate QE or QSS approximations without running into trouble with solving nonlinear algebraic equations.

Overall we presented DDI mechanisms with TMDD behavior and provided QE approximations which can be straightforward implementation in PKPD software. This opens the route to apply DDI TMDD models (i) for PK DDI characterizations of compounds with TMDD behavior, (ii) as subsystems in physiologically more complex scenarios, such as (minimal) PBPK models, and (iii) as the PK DDI part in PKPD models.

Appendices

Appendix 1: Derivation of the final QE and QSS approximation in free concentration variables

Competitive DDI

Step 1: Total concentration formulation

Similar to the single drug case [6] the key for the QE or QSS approximation is to reformulate Eqs. (1)–(5) in total drug and total receptor concentration variables. With

$$\begin{aligned} C_{totA}&= C_A + RC_A \end{aligned}$$

(51)

$$\begin{aligned} C_{totB}&= C_B + RC_{B} \end{aligned}$$

(52)

$$\begin{aligned} R_{tot}&= R + RC_A + RC_{B} \end{aligned}$$

(53)

we obtain

$$\begin{aligned} \frac{d}{dt} C_{totA}&= In_A(t)- k_{elA} C_A - k_{intA} RC_A \end{aligned}$$

(54)

$$\begin{aligned} \frac{d}{dt} C_{totB}&= In_B(t) - k_{elB} C_B - k_{intB} RC_B \end{aligned}$$

(55)

$$\begin{aligned} \frac{d}{dt} R_{tot}&= k_{syn} - k_{deg} R - k_{intA} RC_A - k_{intB} RC_B \end{aligned}$$

(56)

$$\begin{aligned} \frac{d}{dt} RC_A&= k_{onA} C_A \cdot R - (k_{offA} + k_{intA}) RC_A \end{aligned}$$

(57)

$$\begin{aligned} \frac{d}{dt} RC_B&= k_{onB} C_B \cdot R - (k_{offB} + k_{intB}) RC_B. \end{aligned}$$

(58)

The baseline initial values are

$$\begin{aligned} C_{totX} (0)=\, & {} C_{totX}^0 \;= \; C_X^0 + RC_X^0 \nonumber \\ R_{tot} (0)=\, & {} R_{tot}^0 \; = \; R^0 +RC_A^0 +RC_B^0 \nonumber \\ RC_X (0)=\, & {} RC_X^0 \end{aligned}$$

(59)

for $X \in \{ A,B \}$. The values $C_A^0, \, C_B^0, \, R^0, \, RC_A^0, \, RC_B^0$ in Eq. (59) are chosen according to Eqs. (6)–(8) and the input functions in Eqs. (54)–(55) according to Eq. (9). Substituting free variables in Eqs. (54)–(58) with total variables from Eqs. (51)–(53) we obtain

$$\begin{aligned} \frac{d}{dt} C_{totA}&= In_A(t)- k_{elA} (C_{totA}-RC_A) \nonumber \\&\quad - k_{intA} RC_A \end{aligned}$$

(60)

$$\begin{aligned} \frac{d}{dt} C_{totB}&= In_B(t) - k_{elB} (C_{totB}-RC_B) \nonumber \\&\quad - k_{intB} RC_B \end{aligned}$$

(61)

$$\begin{aligned} \frac{d}{dt} R_{tot}&= k_{syn} - k_{deg} (R_{tot} - RC_A - RC_B) \nonumber \\&\quad - k_{intA} RC_A - k_{intB} RC_B \end{aligned}$$

(62)

$$\begin{aligned} \frac{d}{dt} RC_A&= k_{onA} (C_{totA}-RC_A)(R_{tot}-RC_A-RC_B) \nonumber \\&\quad - (k_{offA} + k_{intA}) RC_A \end{aligned}$$

(63)

$$\begin{aligned} \frac{d}{dt} RC_B&= k_{onB} (C_{totB}-RC_B)(R_{tot}-RC_A-RC_B) \nonumber \\&\quad - (k_{offB} + k_{intB}) RC_B \, . \end{aligned}$$

(64)

In comparison to Eqs. (1)–(5), Eqs. (60)–(64) have the advantage that the parameters $k_{onX}$ and $k_{offX}$ appear in the equations of the complexes only.

Step 2: QE and QSS binding relations

We assume rapid binding between $C_A$ and R, as well as $C_B$ and R. Hence, QE or QSS approximation of the complexes $RC_A$ and $RC_{B}$ in Eqs. (57)–(58) provide the algebraic equations

$$\begin{aligned} 0&= (C_{totA}-RC_A)(R_{tot}-RC_A-RC_B) - K_{YA} RC_A \end{aligned}$$

(65)

$$\begin{aligned} 0&= (C_{totB}-RC_B)(R_{tot}-RC_A-RC_B) - K_{YB} RC_B \end{aligned}$$

(66)

for $Y \in \{ D, SS \}$ with Eq. (19) (see Appendices 2, 3). The differential algebraic equation (DAE) form in total variables is then given by Eqs. (60)–(62), (65)–(66).

Step 3: QE and QSS model equations

To avoid solving the coupled non-linear equation system Eqs. (65)–(66) numerically, we transform Eqs. (54)–(56), (65)–(66) back to the free variables. From Eqs. (65)–(66) we obtain the complexes

$$\begin{aligned} RC_X&= \frac{C_X \cdot R}{K_{XA}} \, . \end{aligned}$$

(67)

The next step is to differentiate Eq. (67) and to express $\frac{d}{dt} C_{totA}, \frac{d}{dt} C_{totB}, \frac{d}{dt} R_{tot}$ appearing at the left hand side of Eqs. (54)–(56) in terms of $C_A, C_B$ and R and their derivatives. Using Eqs. (51)–(53) we can calculate from Eqs. (54)–(56)

$$\begin{aligned} \frac{d}{dt} C_{totA}&= \frac{d}{dt} C_A + \frac{d}{dt} RC_A \nonumber \\&= \frac{d}{dt} C_A + \left( \frac{d}{dt} C_A \right) \frac{R}{K_{YA}} + \left( \frac{d}{dt} R \right) \frac{C_A}{K_{YA}}\nonumber \\&= In_A(t) - k_{elA} C_A - k_{intA} \frac{C_A R}{K_{YA}} \end{aligned}$$

(68)

$$\begin{aligned} \frac{d}{dt} C_{totB}&= \frac{d}{dt} C_B + \frac{d}{dt} RC_B \nonumber \\&= \frac{d}{dt} C_B + \left( \frac{d}{dt} C_B \right) \frac{R}{K_{YB}} + \left( \frac{d}{dt} R \right) \frac{C_B}{K_{YB}} \nonumber \\&= In_B(t) - k_{elB} C_B - k_{intB} \frac{C_B R}{K_{YB}} \end{aligned}$$

(69)

$$\begin{aligned} \frac{d}{dt} R_{tot}&= \frac{d}{dt} R + \frac{d}{dt} RC_A + \frac{d}{dt} RC_B \nonumber \\&= \frac{d}{dt} R + \left( \frac{d}{dt} C_A \right) \frac{R}{K_{YA}} + \left( \frac{d}{dt} R \right) \frac{C_A}{K_{YA}} \nonumber \\&\quad + \left( \frac{d}{dt} C_B \right) \frac{R}{K_{YB}} + \left( \frac{d}{dt} R \right) \frac{C_B}{K_{YB}} \nonumber \\&= k_{syn} - k_{deg} R - k_{intA} \frac{C_A R}{K_{YA}} - k_{intB}\frac{C_B R}{K_{YB}} \, . \end{aligned}$$

(70)

The equivalent matrix form reads

$$\begin{aligned} Q(C_A,C_B,R) \begin{pmatrix} \frac{d}{dt} C_A \\ \frac{d}{dt} C_B \\ \frac{d}{dt} R \end{pmatrix} = g_{Com}(C_A,C_B,R) \end{aligned}$$

(71)

with

$$\begin{aligned}&Q(C_A,C_B,R) \\&= \begin{pmatrix} 1 + \frac{R}{K_{YA}} &{} 0 &{} \frac{C_A}{K_{YA}} \\ 0 &{} 1 + \frac{R}{K_{YB}} &{} \frac{C_B}{K_{YB}} \\ \frac{R}{K_{YA}} &{} \frac{R}{K_{YB}} &{} 1 + \frac{C_A}{K_{YA}} + \frac{C_B}{K_{YB}} \end{pmatrix}\\&g_{Com}(C_A,C_B,R) \\&= \begin{pmatrix} In_A(t) - k_{elA} C_A - k_{intA} \frac{C_A R}{K_{YA}} \\ In_B(t) - k_{elB} C_B - k_{intB} \frac{C_B R}{K_{YB}} \\ k_{syn} - k_{deg} R - k_{intA} \frac{C_A R}{K_{YA}} - k_{intB}\frac{C_B R}{K_{YB}} \end{pmatrix} . \end{aligned}$$

Eq. (71) is equivalent to

$$\begin{aligned} \begin{pmatrix} \frac{d}{dt} C_A \\ \frac{d}{dt} C_B \\ \frac{d}{dt} R \end{pmatrix} = M_{Com}(C_A,C_B,R) g_{Com}(C_A,C_B,R) \end{aligned}$$

(72)

where

$$\begin{aligned} M_{Com}(C_A,C_B,R) = Q^{-1}(C_A,C_B,R) \, . \end{aligned}$$

$Q^{-1}$ denotes the inverse matrix of Q and the explicit representation of $M_{Com}$ is listed in Table 1.

Uncompetitive DDI

Step 1: Total concentration formulation

The total drug and receptor variables are

$$\begin{aligned} C_{totA}&= C_A + RC_A + RC_{AB} \end{aligned}$$

(73)

$$\begin{aligned} C_{totB}&= C_B + RC_{AB} \end{aligned}$$

(74)

$$\begin{aligned} R_{tot}&= R + RC_A + RC_{AB} \end{aligned}$$

(75)

and we obtain

$$\begin{aligned} \frac{d}{dt} C_{totA}&= In_A(t) - k_{elA} C_A - k_{intA} RC_A - k_{intAB} RC_{AB} \end{aligned}$$

(76)

$$\begin{aligned} \frac{d}{dt} C_{totB}&= In_B(t) - k_{elB} C_B - k_{intAB} RC_{AB} \end{aligned}$$

(77)

$$\begin{aligned} \frac{d}{dt} R_{tot}&= k_{syn} - k_{deg} R - k_{intA} RC_A - k_{intAB} RC_{AB} \end{aligned}$$

(78)

$$\begin{aligned} \frac{d}{dt} RC_A&= k_{onA} C_A \cdot R - k_{onAB} C_B \cdot RC_A + k_{offAB} RC_{AB} \nonumber \\&\quad - ( k_{offA} + k_{intA} ) RC_A \end{aligned}$$

(79)

$$\begin{aligned} \frac{d}{dt} RC_{AB}&= k_{onAB} C_B \cdot RC_A - ( k_{offAB} + k_{intAB} ) RC_{AB} . \end{aligned}$$

(80)

The baseline initial values are obtained by applying Eqs. (73)–(75) to the initial values Eqs. (28)–(31). This leads to

$$\begin{aligned} C_{totA} (0)=\, & {} C_{totA}^0 \; = \; C_A^0 + RC_A^0 + RC_{AB}^0 \\ C_{totB} (0)= & {} C_{totB}^0 \; = \; C_B^0 + RC_{AB}^0 \\ R_{tot} (0)= \,& {} R_{tot}^0 \; =\, \; R^0 + RC_A^0 + RC_{AB}^0 \end{aligned}$$

and the input functions Eqs. (32)–(33).

Again substituting the free variables in Eqs. (76)–(80) yields

$$\begin{aligned} \frac{d}{dt} C_{totA}&= In_A(t) - k_{elA} (C_{totA}-RC_A-RC_{AB}) \nonumber \\&\quad - k_{intA} RC_A - k_{intAB} RC_{AB} \end{aligned}$$

(81)

$$\begin{aligned} \frac{d}{dt} C_{totB}&= In_B(t) - k_{elB} (C_{totB}-RC_{AB}) \nonumber \\&\quad - k_{intAB} RC_{AB} \end{aligned}$$

(82)

$$\begin{aligned} \frac{d}{dt} R_{tot}&= k_{syn} - k_{deg} (R_{tot}-RC_A-RC_{AB}) \nonumber \\&\quad - k_{intA} RC_A - k_{intAB} RC_{AB} \end{aligned}$$

(83)

$$\begin{aligned} \frac{d}{dt} RC_A&= k_{onA} (C_{totA}-RC_A-RC_{AB}) \nonumber \\&\quad (R_{tot}-RC_A-RC_{AB}) \nonumber \\&\quad - k_{onAB} (C_{totB}-RC_{AB}) RC_A \nonumber \\&\quad + k_{offAB} RC_{AB} - ( k_{offA} + k_{intA} ) RC_A \end{aligned}$$

(84)

$$\begin{aligned} \frac{d}{dt} RC_{AB}&= k_{onAB} (C_{totB}-RC_{AB}) RC_A \nonumber \\&\quad - ( k_{offAB} + k_{intAB} ) RC_{AB} \, . \end{aligned}$$

(85)

Note that in the formulation Eqs. (81)–(85) the parameter $k_{onX}, \, k_{offX}$, intended for elimination show up in the equations of the complexes only.

Step 2: QE binding relations

In Appendix 2 it is shown that the QE approximation provides the algebraic equations

$$\begin{aligned} 0&= C_A R - K_{DA} RC_A \end{aligned}$$

(86)

$$\begin{aligned} 0&= C_B RC_A - K_{DAB} RC_{AB} \end{aligned}$$

(87)

and the resulting DAE consists of Eqs. (81)–(83), (86), (87).

Step 3: QE model equations

Using Eqs. (73)–(75) and Eqs. (76)–(78) we can compute

$$\begin{aligned} \frac{d}{dt} C_{totA}&= \frac{d}{dt} C_A + \frac{d}{dt} RC_A +\frac{d}{dt} RC_{AB} \nonumber \\&= In_A(t) - k_{elA} C_A - k_{intA} \frac{C_A R}{K_{DA}} \end{aligned}$$

(88)

$$\begin{aligned}&\quad -k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \nonumber \\ \frac{d}{dt} C_{totB}&= \frac{d}{dt} C_B + \frac{d}{dt} RC_{AB} \nonumber \\&= In_B(t) - k_{elB} C_B - k_{intAB} \frac{C_A C_B R}{K_{DAB}K_{DA}} \end{aligned}$$

(89)

$$\begin{aligned} \frac{d}{dt} R_{tot}&=\frac{d}{dt} R +\frac{d}{dt} RC_A +\frac{d}{dt} RC_{AB} \nonumber \\&= k_{syn} - k_{deg} R - k_{intA} \frac{C_A R}{K_{DA}} \nonumber \\&\quad - k_{intAB}\frac{C_A C_B R}{K_{DAB}K_{DA}} \, . \end{aligned}$$

(90)

In addition, from Eqs. (86)–(87) we obtain by differentiation

$$\begin{aligned} \frac{d}{dt} RC_A&= \frac{1}{K_{DA}} \left( \left( \frac{d}{dt}C_A \right) R + C_A \frac{d}{dt} R \right) \end{aligned}$$

(91)

$$\begin{aligned} \frac{d}{dt} RC_{AB}&= \frac{1}{K_{DA} K_{DAB}} \left( \left( \frac{d}{dt} C_A \right) C_B R \right. \nonumber \\&\quad \left. +\, C_A \left( \frac{d}{dt} C_B \right) R + C_A C_B \frac{d}{dt} R \right) . \end{aligned}$$

(92)

With Eqs. (88)–(92) the equivalent matrix form reads

$$\begin{aligned} P(C_A,C_B,R) \begin{pmatrix} \frac{d}{dt} C_A \\ \frac{d}{dt} C_B \\ \frac{d}{dt} R \end{pmatrix} = g_{Un}(C_A,C_B,R) \end{aligned}$$

(93)

with $P(C_A,C_B ,R) = I+\hat{P}(C_A,C_B,R)$,

$$\begin{aligned}&\hat{P}(C_A,C_B,R) \\&= \begin{pmatrix} \frac{R}{K_{DA}} +\frac{C_B R}{K_{DA}K_{DAB}} &{} \frac{C_A R}{K_{DA} K_{DAB}} &{} \frac{C_A}{K_{DA}} + \frac{C_A C_B}{K_{DA}K_{DAB}}\\ \frac{C_B R}{K_{DA}K_{DAB}} &{} \frac{C_A R}{K_{DA}K_{DAB}} &{} \frac{C_A C_B}{K_{DA}K_{DAB}} \\ \frac{R}{K_{DA}} + \frac{C_B R}{K_{DA} K_{DAB}} &{} \frac{C_A R}{K_{DA}K_{DAB}} &{} \frac{C_A}{K_{DA}} + \frac{C_A C_B}{K_{DA}K_{DAB}} \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned}&g_{Un}(C_A,C_B,R) \\&= \begin{pmatrix} In_A(t) - k_{elA} C_A - k_{intA}\frac{C_A R}{K_{DA}}- k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \\ In_B(t) - k_{elB} C_B - k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \\ k_{syn} - k_{deg} R - k_{intA} \frac{C_A R}{K_{DA}} - k_{intAB} \frac{C_A C_B R}{K_{DA} K_{DAB}} \end{pmatrix} . \end{aligned}$$

Finally, Eq. (93) can be written as explicit ODE

$$\begin{aligned} \begin{pmatrix} \frac{d}{dt} C_A \\ \frac{d}{dt} C_B \\ \frac{d}{dt} R \end{pmatrix} = M_{Un}(C_A,C_B,R) g_{Un}(C_A,C_B,R) \end{aligned}$$

where

$$\begin{aligned} M_{Un}(C_A,C_B,R) = P^{-1}(C_A,C_B,R) \end{aligned}$$

is listed in Table 1.

Appendix 2: QE approximation

The QE approximation is based on the theory of Fenichel [14] which allows a specific selection of the rates to be accelerated.

Competitive

To justify the QE approximation we increase the binding rates $k_{onX},k_{offX}$, where $X \in \{A,B\}$, by replacing with $\frac{1}{\varepsilon } k_{onX}$, $\frac{1}{\varepsilon } k_{offX}$ with $\varepsilon > 0$ small in Eqs. (54)–(58). Since the new constants are much larger this can be regarded as rapid binding and we obtain

$$\begin{aligned} \frac{d}{dt} RC_A&= \frac{k_{onA}}{\varepsilon } C_A \cdot R - \left( \frac{k_{offA}}{\varepsilon } + k_{intA} \right) RC_A \end{aligned}$$

(94)

$$\begin{aligned} \frac{d}{dt} RC_B&= \frac{k_{onB}}{\varepsilon } C_B \cdot R - \left( \frac{k_{offB}}{\varepsilon } + k_{intB} \right) RC_B. \end{aligned}$$

(95)

Multiplying Eqs. (94)–(95) by $\varepsilon$ gives

$$\begin{aligned} \varepsilon \frac{d}{dt} RC_A&= k_{onA} C_A \cdot R - \left( k_{offA} + \varepsilon k_{intA} \right) RC_A \end{aligned}$$

(96)

$$\begin{aligned} \varepsilon \frac{d}{dt} RC_B&= k_{onB} C_B \cdot R - \left( k_{offB} + \varepsilon k_{intB} \right) RC_B. \end{aligned}$$

(97)

Taking the limit $\varepsilon \rightarrow 0$ in Eqs. (96)–(97) results in

$$\begin{aligned} 0&= k_{onA} C_A \cdot R - k_{offA} RC_A \end{aligned}$$

(98)

$$\begin{aligned} 0&= k_{onB} C_B \cdot R - k_{offB} RC_B. \end{aligned}$$

(99)

Dividing Eq. (98) by $k_{onA}$ and Eq. (99) by $k_{onB}$ gives the QE approximation of the complexes

$$\begin{aligned} 0&= C_A \cdot R - K_{DA} RC_A \end{aligned}$$

(100)

$$\begin{aligned} 0&= C_B \cdot R - K_{DB} RC_B \, . \end{aligned}$$

(101)

Uncompetitive

Accelerating the binding rates $k_{onX}$ and $k_{offX}$ with $X \in \{A,AB\}$ in Eqs. (76)–(80) gives

$$\begin{aligned} \frac{d}{dt} RC_A&= \frac{k_{onA}}{\varepsilon } C_A R - \frac{k_{onAB}}{\varepsilon } C_B RC_A + \frac{k_{offAB}}{\varepsilon } RC_{AB} \nonumber \\&\quad - \left( \frac{k_{offA}}{\varepsilon } + k_{intA} \right) RC_A \end{aligned}$$

(102)

$$\begin{aligned} \frac{d}{dt} RC_{AB}&= \frac{k_{onAB}}{\varepsilon } C_B RC_A - \left( \frac{k_{offAB}}{\varepsilon } + k_{intAB} \right) RC_{AB} . \end{aligned}$$

(103)

Multiplying Eqs. (102)–(103) by $\varepsilon$ leads to

$$\begin{aligned} \varepsilon \frac{d}{dt} RC_A&= k_{onA}C_A R - k_{onAB} C_B RC_A + k_{offAB} RC_{AB} \nonumber \\&\quad - ( k_{offA} + \varepsilon k_{intA} ) RC_A \end{aligned}$$

(104)

$$\begin{aligned} \varepsilon \frac{d}{dt} RC_{AB}&= k_{onAB} C_B RC_A - ( k_{offAB} + \varepsilon k_{intAB} ) RC_{AB} . \end{aligned}$$

(105)

Taking the limit $\varepsilon \rightarrow 0$ in Eqs. (104)–(105) results in

$$\begin{aligned} 0&= k_{onA}C_A R - k_{onAB} C_B RC_A + k_{offAB} RC_{AB} \nonumber \\&\quad - k_{offA} RC_A \end{aligned}$$

(106)

$$\begin{aligned} 0&= k_{onAB} C_B RC_A - k_{offAB} RC_{AB} \, . \end{aligned}$$

(107)

Substituting Eq. (107) in Eq. (106) leads to

$$\begin{aligned} 0&= k_{onA}C_A R - k_{offA} RC_A \end{aligned}$$

(108)

$$\begin{aligned} 0&= k_{onAB} C_B RC_A - k_{offAB} RC_{AB} \, . \end{aligned}$$

(109)

Dividing Eq. (108) with $k_{onA}$ and Eq. (109) with $k_{onAB}$ gives the QE approximation of the complexes

$$\begin{aligned} 0&= C_A R - K_{DA} RC_A \end{aligned}$$

(110)

$$\begin{aligned} 0&= C_B RC_A - K_{DAB} RC_{AB} \, . \end{aligned}$$

(111)

Appendix 3: QSS approximation

Following the classical singular perturbation theory [15] all complex related processes are assumed to be rapid, including the internalization from the complexes.

Competitive

Accelerating the rates with $\varepsilon$ small in Eqs. (54)–(58) yields

$$\begin{aligned} \frac{d}{dt} RC_A&= \frac{k_{onA}}{\varepsilon } C_A \cdot R - \left( \frac{k_{offA}}{\varepsilon } + \frac{k_{intA}}{\varepsilon } \right) RC_A \end{aligned}$$

(112)

$$\begin{aligned} \frac{d}{dt} RC_B&= \frac{k_{onB}}{\varepsilon } C_B \cdot R - \left( \frac{k_{offB}}{\varepsilon } + \frac{k_{intB}}{\varepsilon } \right) RC_B. \end{aligned}$$

(113)

Multiplying Eqs. (112)–(113) by $\varepsilon$ and taking the limit $\varepsilon \rightarrow 0$

$$\begin{aligned} 0&= k_{onA} C_A \cdot R - \left( k_{offA}+ k_{intA}\right) RC_A \end{aligned}$$

(114)

$$\begin{aligned} 0&= k_{onB} C_B \cdot R - \left( k_{offB} + k_{intB} \right) RC_B. \end{aligned}$$

(115)

Hence, the QSS approximation reads

$$\begin{aligned} 0&= C_A \cdot R - K_{SSA} RC_A \end{aligned}$$

(116)

$$\begin{aligned} 0&= C_B \cdot R - K_{SSB} RC_B. \end{aligned}$$

(117)

Uncompetitive

We obtain from Eqs. (76)–(80) with $\varepsilon$ small

$$\begin{aligned} \frac{d}{dt} RC_A&= \frac{k_{onA}}{\varepsilon } C_A \cdot R -\frac{k_{onAB}}{\varepsilon } C_B \cdot RC_A + \frac{k_{offAB}}{\varepsilon } RC_{AB} \end{aligned}$$

(118)

$$\begin{aligned}&\quad - \left( \frac{k_{offA}}{\varepsilon } + \frac{k_{intA}}{\varepsilon } \right) RC_A \end{aligned}$$

(119)

$$\begin{aligned} \frac{d}{dt} RC_{AB}&= \frac{k_{onAB}}{\varepsilon } C_B \cdot RC_A - \left( \frac{k_{offAB}}{\varepsilon } + \frac{k_{intAB}}{\varepsilon } \right) RC_{AB} \, . \end{aligned}$$

(120)

Multiplying these equations by $\varepsilon$ and then taking the limit $\varepsilon \rightarrow 0$ results in

$$\begin{aligned} 0&= k_{onA}C_A R - k_{onAB} C_B RC_A + k_{offAB} RC_{AB} \\ \nonumber &\quad - ( k_{offA} + k_{intA} ) RC_A \end{aligned}$$

(121)

$$\begin{aligned} 0&= k_{onAB} C_B RC_A - ( k_{offAB} + k_{intAB} ) RC_{AB} \, . \end{aligned}$$

(122)

Inserting Eq. (122) in Eq. (121) gives

$$\begin{aligned} 0&= k_{onA}C_A R - k_{intAB} RC_{AB} - ( k_{offA} + k_{intA} ) RC_A \end{aligned}$$

(123)

$$\begin{aligned} 0&= k_{onAB} C_B RC_A - ( k_{offAB} + k_{intAB} ) RC_{AB} \, . \end{aligned}$$

(124)

Dividing Eq. (123) by $k_{onA}$ and Eq. (124) by $k_{onAB}$ provides

$$\begin{aligned} 0&= C_A R - \frac{k_{intAB}}{k_{onA}} RC_{AB} - K_{SSA} RC_A \end{aligned}$$

(125)

$$\begin{aligned} 0&= C_B RC_A - K_{SSAB} RC_{AB} \, . \end{aligned}$$

(126)

Appendix 4: Baseline initial values for the uncompetitive TMDD model

According to Eqs. (26)–(27) the baseline conditions for the complexes with the concentrations $C_A^0, C_B^0 \ge 0$ are

$$\begin{aligned} \left( \begin{array}{c c} \frac{k_{intA} +k_{offA}}{k_{onA}} &{} \frac{k_{intAB}}{k_{onA}} \\ -C_B^0 &{} \frac{k_{intAB}+k_{offAB}}{k_{onAB}} \end{array} \right) \left( \begin{array}{c} RC_A \\ RC_{AB} \end{array} \right)= & {} \left( \begin{array}{c} C_A^0 R \\ 0 \end{array} \right) . \nonumber \\&\end{aligned}$$

(127)

Applying Cramer’s rule to Eq. (127) and using the definition from Eq. (19) yields the solution

$$\begin{aligned} RC_A^0= & {} \frac{C_A^0 R^0 K_{SSAB}}{K_{SSA}K_{SSAB} + C_B^0 \frac{k_{intAB}}{k_{onA}} } \end{aligned}$$

(128)

$$\begin{aligned} RC_{AB}^0= & {} \frac{C_A^0 C_B^0 R^0 }{K_{SSA}K_{SSAB} + C_B^0 \frac{k_{intAB}}{k_{onA}} } \, . \end{aligned}$$

(129)

Inserting Eqs. (128)–(129) into the baseline condition of the receptor equation (78) leads to

$$\begin{aligned} k_{syn}= & {} \left( k_{deg} + \frac{ k_{intA} C_A^0 K_{SSAB} + k_{intAB} C_A^0 C_B^0 }{ K_{SSAB} K_{SSA} + \frac{C_B^0 k_{intAB}}{k_{onA}} } \right) R, \end{aligned}$$

which is equivalent to

$$\begin{aligned} R^0= & {} \frac{ k_{syn}}{ k_{deg} + \frac{ k_{intA} C_A^0 K_{SSAB} + k_{intAB} C_A^0 C_B^0 }{ K_{SSAB} K_{SSA} + \frac{C_B^0 k_{intAB}}{k_{onA}} } }. \end{aligned}$$

The baseline concentrations of the input functions then follow from Eqs. (76)–(77).

Appendix 5: Source codes

The matrix representation applied in Eqs. (14)–(15) and Eqs. (43)–(44) is of the general form

$$\begin{aligned} \begin{pmatrix} H_1 \\ H_2 \\ H_3 \end{pmatrix} = \begin{pmatrix} M_{11} &{} M_{12} &{} M_{13} \\ M_{21} &{} M_{22} &{} M_{23} \\ M_{31} &{} M_{32} &{} M_{33} \end{pmatrix} \begin{pmatrix} G_1 \\ G_2 \\ G_3 \end{pmatrix} \, . \end{aligned}$$

Hence, performing matrix multiplication the right hand side of the differential equation reads

$$\begin{aligned} H_1&= M_{11} G_1 + M_{12} G_2 + M_{13} G_3 \\ H_2&= M_{21} G_1 + M_{22} G_2 + M_{23} G_3 \\ H_3&= M_{31} G_1 + M_{32} G_2 + M_{33} G_3 \end{aligned}$$

compare the lines 113–128 for the competitive and the lines 221–239 for the uncompetitive case. The variables $H_1$,...,$H_3$ correspond to DADT(1), ..., DADT(3) in NONMEM and XP(1), ..., XP(3) in ADAPT 5.

The lines of the code are numbered for referencing but are not part of the code implementation.

NONMEM control stream for competitive DDI TMDD

The $DES block of the control stream is presented. Additionally, the first lines of the data file is shown to present the IV infusion mechanism. The full control stream is available in the supplemental material.

101: $DES

102: EPSILON = 1e-4

103: ; Dose at T1 = 0

104: INA = 0

105: INB = 0

106: IF (T.GE.0.AND.T.LE.0+EPSILON) THEN

107: INA = 100*EPSILON**(−1)

108: INB = 100*EPSILON**(-1)

109: ENDIF

110: CA = A(1)/V

111: CB = A(2)/V

112: R = A(3)

113: DET = R**2+CA*KDB+CB*KDA+CA*R+CB*R+KDA*KDB+KDA*R+KDB*R

114: G1 = INA - KELA*CA - (KINTA*CA*R)/KDA

115: G2 = INB - KELB*CB - (KINTB*CB*R)/KDB

116: G3 = KSYN-KDEG*R-(KINTA*CA*R)/KDA-(KINTB*CB*R)/KDB

117: M11 = (1/DET)*(DET - R*(R+CB+KDB))

118: M12 = (1/DET)*(CA*R)

119: M13 = (1/DET)*(-CA*(R+KDB))

120: M21 = (1/DET)*(CB*R)

121: M22 = (1/DET)*(DET - R*(R+CA+KDA))

122: M23 = (1/DET)*(-CB*(R+KDA))

123: M31 = (1/DET)*(-R*(R+KDB))

124: M32 = (1/DET)*(-R*(R+KDA))

125: M33 = (1/DET)*(DET-CA*(R+KDB)-CB*(R+KDA))

126: DADT(1) = M11*G1 + M12*G2 + M13*G3

127: DADT(2) = M21*G1 + M22*G2 + M23*G3

128: DADT(3) = M31*G1 + M32*G2 + M33*G3

The first lines of the data file are:

150: #ID TIME TYPE DV MDV

151: 1 0 1 . 1

152: 1 0 2 . 1

153: 1 0.0001 1 . 1

154: 1 0.0001 2 . 1

155: 1 2 1 32.9432 0

156: 1 2 2 28.3621 0

ADAPT 5 source code for uncompetitive DDI TMDD

The subroutine DIFFEQ is presented. For full source code see supplemental material.

201: Subroutine DIFFEQ(T,X,XP)

202: Implicit None

203: Include ’globals.inc’

204: Include ’model.inc’

205: Real*8 T,X(MaxNDE),XP(MaxNDE)

206: Real*8 KELA,KDA,KINTA,KELB,KDAB,KINTAB,KSYN,KDEG

207: Real*8 CA,CB,RR,R0

208: Real*8 DET,M(3,3),G(3)

209: KELA = P(1)

210: KDA = P(2)

211: KINTA = P(3)

212: KELB = P(4)

213: KDAB = P(5)

214: KINTAB = P(6)

215: KSYN = P(7)

216: KDEG = P(8)

217: R0 = KSYN/KDEG

218: CA = X(1)

219: CB = X(2)

220: RR = X(3) + R0

221: DET = RR**2*CA+CA*RR*KDA+CB*RR*KDA+CA**2*RR+CA*CB*KDA

222: & +KDA**2*KDAB+KDA*KDAB*RR+CA*KDA*KDAB

223: G(1) = R(1)-KELA*CA-(KINTA*CA*RR)/KDA

224: & -KINTAB*((CA*CB*RR)/(KDA*KDAB))

225: G(2) = R(2)-KELB*CB-KINTAB*((CA*CB*RR)/(KDA*KDAB))

226: G(3) = KSYN-KDEG*RR-(KINTA*CA*RR)/KDA

227: & -KINTAB*((CA*CB*RR)/(KDA*KDAB))

228: M(1,1) = (1/DET)*(DET-RR*(CA*RR+CB*KDA+KDA*KDAB))

229: M(1,2) = (1/DET)*(-CA*RR*KDA)

230: M(1,3) = (1/DET)*(-CA*(CA*RR+CB*KDA+KDA*KDAB))

231: M(2,1) = (1/DET)*(-CB*RR*KDA)

232: M(2,2) = (1/DET)*(DET-CA*RR*(RR+CA+KDA))

233: M(2,3) = (1/DET)*(-KDA*CA*CB)

234: M(3,1) = (1/DET)*(-RR*(CB*KDA+CA*RR+KDA*KDAB))

235: M(3,2) = (1/DET)*(-CA*RR*KDA)

236: M(3,3) = (1/DET)*(DET-CA*(CA*RR+KDAB*KDA+CB*KDA))

237: XP(1) = M(1,1)*G(1)+M(1,2)*G(2)+M(1,3)*G(3)

238: XP(2) = M(2,1)*G(1)+M(2,2)*G(2)+M(2,3)*G(3)

239: XP(3) = M(3,1)*G(1)+M(3,2)*G(2)+M(3,3)*G(3)

240: Return

241: End

Fig. 1

Schematic of the competitive DDI TMDD model described by Eqs. (1)–(5) (panel a) and the uncompetitive DDI TMDD model described by Eqs. (23)–(27) (panel b)

Fig. 2

Properties of the original DDI TMDD models. Competitive: In panels a and b the single drug profiles of drugs A and B (blue dotted lines) are compared with the competitive model (black solid line) Eqs. (1)–(9) for $dose_A = 100$, $dose_B = 100$ and no baseline $C_A^0 = C_B^0 = 0$. In panels c and d, the effect of the administration of one drug only on a present concentration of the other drug is shown by two examples: (i) drugs A and B are in baseline $C_A^0 = C_B^0 = 1$, and one administration at time $t = 12$ of drug B with $dose_B = 100$ (red dashed lines) causes an increase of drug A concentration, (ii) drug A is administered with $dose_A = 100$ at $t = 0$ and drug B administered with $dose_B = 100$ at $t = 0$ and additionally at $t = 12$ (black solid lines), and causes an increase of drug A concentration. Uncompetitive: In panels e and f the single drug profiles of drugs A and B (blue dotted lines) are compared with the uncompetitive model (black solid lines) Eqs. (23)–(33) for $dose_A = 100$, $dose_B = 100$ and no baseline $C_A^0 = C_B^0 = 0$. In panels g and h drugs A and B are in baseline $C_A^0 = C_B^0 = 1$ with one administration at time $t=5$ of drug A with $dose_A = 100$ and non of drug B (red dashed line) and the other way around (black solid lines) (Color figure online)

Fig. 3

Visualization of the QE approximation. Competitive: In panels a and b concentration profiles from the original formulation (red dashed lines) Eqs. (1)–(9) and the approximation of the QE formulation Eqs. (14)–(18) (black solid lines) are shown for escalating doses of $dose_A = dose_B = 10, 100, 1000$ at $t=0$ and no baseline $C_A^0 = C_B^0 = 0$. In panels c and d the effect of one drug administration on the present concentration of the other drug is shown. The original (red dashed lines) and QE approximation (black solid lines) profiles with a baseline $C_A^0 = C_B^0 = 1$ are shown for a dose of $doseA = 1000$ at $t=0$. The $k_{onB}$ and $k_{offB}$ are multiplied by the factors 0.1, 1 and 10 in such a way that $K_{DB}$ stays the same to show the convergence of the original formulation towards the QE approximation. Uncompetitive: In panels e and f concentration profiles from the original formulation (red dashed lines) Eqs. (23)–(33) and the approximation of the QE formulation Eqs. (43)–(48) (black solid lines) are shown for escalating doses of $dose_A = dose_B = 10, 100, 1000$ at $t=0$ and no baseline $C_A^0 = C_B^0 = 0$. In panels g and h original (red dashed lines) and QE approximation (black solid lines) profiles with a baseline $C_A^0 = C_B^0 = 1$ are shown where for drug A is administered with a dose of $dose_A = 100$ at $t=24$. The $k_{onA}$ and $k_{offA}$ are multiplied by the factors 0.1, 1 and 10 in such a way that $K_{DA}$ stays the same (Color figure online)

Fig. 4

Visualization of plasma concentration versus time data fitting from the original formulation with the QE approximation: Fit (solid lines) of the QE approximation of the competitive Eqs. (14)–(18) in NONMEM (panels a and b) and the uncompetitive DDI TMDD model Eqs. (43)–(48) in ADAPT 5 (panels c and d) in ODE formulation with an IV short infusion. Data (crosses) were produced with the original formulations Eqs. (1)–(9) and Eqs. (23)–(33)

Table 1 Matrices $M_{Com}(C_A,C_B,R)$ and $M_{Un}(C_A,C_B,R)$ for QE approximation of DDI TMDD implementation

Table 2 Estimated model parameters of the QE approximation of the competitive and uncompetitive DDI TMDD models formulated as ODE in free variables