Methods of solving rapid binding target-mediated drug disposition model for two drugs competing for the same receptor

Abstract

The target-mediated drug disposition (TMDD) model has been adopted to describe pharmacokinetics for two drugs competing for the same receptor. A rapid binding assumption introduces total receptor and total drug concentrations while free drug concentrations C _A and C _B are calculated from the equilibrium (Gaddum) equations. The Gaddum equations are polynomials in C _A and C _B of second degree that have explicit solutions involving complex numbers. The aim of this study was to develop numerical methods to solve the rapid binding TMDD model for two drugs competing for the same receptor that can be implemented in pharmacokinetic software. Algebra, calculus, and computer simulations were used to develop algorithms and investigate properties of solutions to the TMDD model with two drugs competitively binding to the same receptor. A general rapid binding approximation of the TMDD model for two drugs competing for the same receptor has been proposed. The explicit solutions to the equilibrium equations employ complex numbers, which cannot be easily solved by pharmacokinetic software. Numerical bisection algorithm and differential representation were developed to solve the system instead of obtaining an explicit solution. The numerical solutions were validated by MATLAB 7.2 solver for polynomial roots. The applicability of these algorithms was demonstrated by simulating concentration–time profiles resulting from exogenous and endogenous IgG competing for the neonatal Fc receptor (FcRn), and darbepoetin competing with endogenous erythropoietin for the erythropoietin receptor. These models were implemented in ADAPT 5 and Phoenix WinNonlin 6.0, respectively.

Introduction

The term “target-mediated drug disposition (TMDD)” has been utilized to describe the phenomenon that the disposition and elimination of a certain drug are significantly affected by binding to its target [1]. Classic examples of drugs exhibiting TMDD pharmacokinetics include therapeutic antibodies and protein hormones [2]. Many of these drugs usually exert their effect through competing for the same receptor (or target) with endogenous substances. Interactions of exogenous drugs with endogenous species are frequently ignored in analyses of pharmacokinetics of the former. Advances in biotechnology made it possible to modify the receptor binding affinity of such drugs to the point that the drug substance and endogenous substance affect pharmacokinetics or efficacy of each other substantially. Important examples include hematopoietic growth factors and therapeutic antibodies.

Hematopoietic growth factors are endogenously produced glycoprotein hormones that stimulate the proliferation and differentiation of hematopoietic progenitor cells [3]. Some well-known lineage-specific growth factors are erythropoietin (EPO), thrombopoietin (TPO) and granulocyte colony-stimulating factor (G-CSF). Examples of their therapeutic counterparts are epoetin (recombinant human EPO), filgrastim (recombinant human G-CSF) and romiplostim (analogue of TPO) [4]. These therapeutic agents compete with endogenous substances for hematopoietic growth factor receptors expressed on the precursor cells and stimulate their proliferation and differentiation [3].

Exogenous therapeutic antibodies compete for the neonatal Fc receptor (FcRn) with endogenous immunoglobulins G (IgG). FcRn is known to play an important role in extending the half-life of IgG compared to other antibody isotypes as well as in maintaining IgG homeostasis in the system circulation [5]. The well accepted mechanism for IgG protection by FcRn involves the IgG uptake into the endosomes by fluid phase endocytosis and binding to FcRn. At acidic endosomal pH condition (pH 6), the IgG/FcRn complex is returned to the plasma membrane where the bound IgG is released back into the circulation at physiological pH whereas the unbound IgG undergoes degradation in lysosomes. Based on this mechanism, a lot of effort has been made to engineer IgG with enhanced binding affinity for FcRn at pH 6 as a strategy to improve IgG systemic persistence which may lead to a potential improvement in IgG-based therapy [6, 7].

A general TMDD pharmacokinetic model has been proposed by Mager and Jusko [8]. In this framework, it is assumed that a single species of drug molecule binds to its target through a second-order rate constant (k _on ) and a first-order dissociation constant (k _off ), forming a drug-target complex. When an exogenous drug competes for the same target with an endogenous substance, a TMDD model with two species of molecules competitively binding to the same target has been used [9, 10]. In this situation, different PK properties and binding processes for two molecular species have been introduced into the model.

Since the binding and dissociation rate constants (k _on and k _off ) are usually not estimable with the available pharmacokinetic data, rapid binding (RB) and quasi-steady-state (QSS) TMDD models have been developed for a single drug situation, in which these rate constants were replaced with the equilibrium dissociation constant K _D (RB) or K _SS (QSS) [11, 12]. Consequently, the concentration of the drug-target complex can be explicitly expressed as a function of free drug concentration [11]. When two molecular species competitively bind to the same target, the concentration of drug-target complexes from two species can be expressed in terms of free drug concentrations by means of the Gaddum equations [13].

The calculation of free drug concentration for the RB or QSS TMDD model for two molecular species competing for the same target is mathematically challenging. When a single drug binds to its target, the free drug concentration can be calculated by solving a quadratic equation and explicitly expressed under RB or QSS assumption [11]. However, when two species of molecules compete for the same target, the free concentrations of these two species are solutions to a system of two quadratic equations with two variables. This provokes a difficulty in implementing such a model, especially in PK software. In the following sections we introduced the rapid binding TMDD model describing two drug species competing for the same target. Our major objective was to propose different methods solving the system equations that can be emulated in PK software. The utilization of these methods was demonstrated through two case studies involving an erythropoiesis-stimulating agent competing with the endogenous EPO for erythropoietin receptor and a monoclonal antibody competing with the endogenous IgG for FcRn.

Theoretical

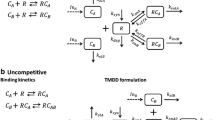
The TMDD model for two drugs competing for the same receptor is shown in Fig. 1. The symbols and notations of this model are similar to the general TMDD model with one drug [8]. As shown in Fig. 1, the key feature of this model is that two molecular species (C _A and C _B ) competitively bind to the same receptor (R). Free drugs in the central compartment (C _A and C _B ) bind to the free receptor (R) at the second-order rate (k _onA and k _onB ) to form drug-receptor complexes (RC _A and RC _B ). The drug-receptor complexes (RC _A and RC _B ) can either be dissociated at the first-order rate (k _offA and k _offB ) or be internalized and degraded at the first-order rate (k _intA and k _intB ). Free drugs (C _A and C _B ) can also be removed from the central compartment by the first-order elimination process (k _elA and k _elB ) or be distributed to the tissue compartment at the first-order rate (k _tpA , k _tpB , k _ptA , k _ptB ). Free receptors (R) are synthesized at the zero-order rate (k _syn ) and degraded at the first-order rate (k _deg ). The input rates (In _A (t) and In _B (t)) can account for any process (zero-order infusion, first-order absorption, etc.) except for intravenous (IV) bolus that may require additional model components. The differential equations are as follows:

$$ \frac{{dC_{A} }}{dt} = In_{A} (t) - k_{onA} R \cdot C_{A} + k_{offA} RC_{A} - (k_{elA} + k_{ptA} )C_{A} + k_{tpA} A_{TA} /V_{c} $$

(1)

$$ \frac{{dA_{TA} }}{dt} = k_{ptA} V_{c} C_{A} - k_{tpA} A_{TA} $$

(2)

$$ \frac{{dRC_{A} }}{dt} = k_{onA} R \cdot C_{A} - k_{offA} RC_{A} - k_{{{int} A}} RC_{A} $$

(3)

$$ \frac{{dC_{B} }}{dt} = In_{B} (t) - k_{onB} R \cdot C_{B} + k_{offB} RC_{B} - (k_{elB} + k_{ptB} )C_{B} + k_{tpB} A_{TB} /V_{c} $$

(4)

$$ \frac{{dA_{TB} }}{dt} = k_{ptB} V_{c} C_{B} - k_{tpB} A_{TB} $$

(5)

$$ \frac{{dRC_{B} }}{dt} = k_{onB} R \cdot C_{B} - k_{offB} RC_{B} - k_{{{int} B}} RC_{B} $$

(6)

$$ \frac{dR}{dt} = k_{syn} - k_{deg} R - k_{onA} R \cdot C_{A} + k_{offA} RC_{A} - k_{onB} R \cdot C_{B} + k_{offB} RC_{B} $$

(7)

Fig. 1

Target-mediated drug disposition for two drugs competing for the same receptor. Symbols are defined in the theoretical

The initial conditions for the above system are defined by the steady-state (baseline) values and additional IV bolus doses of free drugs Dose _A and Dose _B :

$$ C_{A} (0) = \frac{{Dose_{A} }}{{V_{c} }} + C_{A0} $$

(8)

$$ A_{TA} (0) = k_{ptA} V_{c} C_{A0} /k_{tpA} $$

(9)

$$ RC_{A} (0) = k_{onA} R_{0} C_{A0} /(k_{{{int} A}} + k_{offA} ) $$

(10)

$$ C_{B} (0) = \frac{{Dose_{B} }}{{V_{c} }} + C_{B0} $$

(11)

$$ A_{TB} (0) = k_{ptB} V_{c} C_{B0} /k_{tpB} $$

(12)

$$ RC_{B} (0) = k_{onB} R_{0} C_{B0} /(k_{{{int} B}} + k_{offB} ) $$

(13)

$$ R(0) = R_{0} $$

(14)

where the receptor synthesis rate can be calculated from Eq. 7:

$$ k_{syn} = k_{{deg}} R_{0} + k_{onA} R_{0} C_{A0} - \frac{{k_{offA} R_{0} C_{A0} }}{{k_{{{int} A}} + k_{offA} }} + k_{onB} R_{0} C_{B0} - \frac{{k_{offB} R_{0} C_{B0} }}{{k_{{{int} B}} + k_{offB} }} $$

(15)

Similarly, the baseline values for In _A (t) and In _B (t) are defined by the steady states for Eqs. 1 and 4:

$$ In_{A0} = \frac{{k_{{{int} A}} k_{onA} R_{0} C_{A0} }}{{k_{offA} + k_{{{int} A}} }} + k_{elA} C_{A0} $$

(16)

$$ In_{B0} = \frac{{k_{{{int} B}} k_{onB} R_{0} C_{B0} }}{{k_{offB} + k_{{{int} B}} }} + k_{elB} C_{B0} $$

(17)

The rapid binding assumption implies:

$$ \frac{{R \cdot C_{A} }}{{RC_{A} }} = K_{DA} \; {\text{and}}\;\frac{{R \cdot C_{B} }}{{RC_{B} }} = K_{DB} $$

(18)

where K _DA and K _DB are dissociation equilibrium constants for drugs A and B, respectively. Upon introducing the total drug plasma concentrations:

$$ C_{Atot} = C_{A} + RC_{A} \;{\text{and}}\;C_{Btot} = C_{B} + RC_{B} $$

(19)

and total receptor plasma concentration:

$$ R_{tot} = R + RC_{A} + RC_{B} $$

(20)

the drug-receptor complex concentrations RC _A and RC _B can be calculated from Eq. 19 by means of total and free drug concentrations, or equivalently, from Eq. 18 as functions of free drug concentrations and R _tot :

$$ RC_{A} = \frac{{R_{tot} C_{A} /K_{DA} }}{{1 + C_{A} /K_{DA} + C_{B} /K_{DB} }} \;{\text{and}}\;RC_{B} = \frac{{R_{tot} C_{B} /K_{DB} }}{{1 + C_{A} /K_{DA} + C_{B} /K_{DB} }} $$

(21)

Eq. 21 are known in pharmacology as the Gaddum equations [13]. The rapid binding TMDD model for competitive interaction between two drugs is described by the following differential equations:

$$ \frac{{dC_{Atot} }}{dt} = In_{A} (t) - (k_{elA} + k_{ptA} )C_{A} + k_{tpA} A_{TA} /V_{c} - k_{{{int} A}} (C_{Atot} - C_{A} ) $$

(22)

$$ \frac{{dA_{TA} }}{dt} = k_{ptA} V_{c} C_{A} - k_{tpA} A_{TA} $$

(23)

$$ \frac{{dC_{Btot} }}{dt} = In_{B} (t) - (k_{elB} + k_{ptB} )C_{B} + k_{tpB} A_{TB} /V_{c} - k_{{{int} B}} (C_{Btot} - C_{B} ) $$

(24)

$$ \frac{{dA_{TB} }}{dt} = k_{ptB} V_{c} C_{B} - k_{tpB} A_{TB} $$

(25)

$$ \frac{{dR_{tot} }}{dt} = k_{syn} - k_{{deg} } R_{tot} - (k_{{{int} A}} - k_{{deg} } )(C_{Atot} - C_{A} ) - (k_{{{int} B}} - k_{{deg} } )(C_{Btot} - C_{B} ) $$

(26)

where C _A and C _B are the only solutions of the equilibrium equations Eq. 18 rewritten as follows:

$$ (R_{tot} - C_{Atot} - C_{Btot} + C_{A} + C_{B} )C_{A} = K_{DA} (C_{Atot} - C_{A} ) $$

(27)

$$ (R_{tot} - C_{Atot} - C_{Btot} + C_{A} + C_{B} )C_{B} = K_{DB} (C_{Btot} - C_{B} ) $$

(28)

such that:

$$ 0 < C_{A} < C_{Atot} \; {\text{and}}\;0 < C_{B} < C_{Btot} $$

(29)

The initial conditions for Eqs. 22–26 are defined by their steady states and IV bolus doses:

$$ C_{Atot} (0) = \frac{{Dose_{A} }}{{V_{c} }} + C_{Atot0} $$

(30)

$$ A_{TA} (0) = k_{ptA} V_{c} C_{A0} /k_{tpA} $$

(31)

$$ C_{Btot} (0) = \frac{{Dose_{B} }}{{V_{c} }} + C_{Btot0} $$

(32)

$$ A_{TB} (0) = k_{ptB} V_{c} C_{B0} /k_{tpB} $$

(33)

$$ R_{tot} (0) = R_{tot0} $$

(34)

where C _Atot0, C _Btot0, and R _tot0 are the baseline plasma concentrations for total drug A, total drug B, and total receptors, respectively. As for the full model, the receptor synthesis rate can be calculated from Eq. 26:

$$ k_{syn} = k_{{deg} } (R_{tot0} - RC_{A0} - RC_{B0} ) + k_{{{int} A}} RC_{A0} + k_{{{int} B}} RC_{B0} $$

(35)

Similarly, the baseline values for In _A (t) and In _B (t) are defined by the steady states for Eqs. 22 and 24:

$$ In_{A0} = k_{elA} C_{A0} + k_{{{int} A}} RC_{A0} $$

(36)

$$ In_{B0} = k_{elB} C_{B0} + k_{{{int} B}} RC_{B0} $$

(37)

Here RC _A0 and RC _B0 denote the baseline values of the drug-receptor complex concentrations that can be calculated from the Gaddum equations:

$$ RC_{A0} = \frac{{R_{tot0} C_{A0} /K_{DA} }}{{1 + C_{A0} /K_{DA} + C_{B0} /K_{DB} }}\; {\text{and}}\;RC_{B0} = \frac{{R_{tot0} C_{B0} /K_{DB} }}{{1 + C_{A0} /K_{DA} + C_{B0} /K_{DB} }} $$

(38)

The baseline values for total drug concentrations are determined by the baseline values of free drug concentrations:

$$ C_{Atot0} = C_{A0} + RC_{A0} \; {\text{and}}\;C_{Btot0} = C_{B0} + RC_{B0} $$

(39)

In the case where preferred primary parameters are C _Atot0 and C _Btot0 one needs to solve the equilibrium conditions Eqs. 27 and 28 at baseline values for C _A0 and C _B0.

Methods and results

Algebraic solution of equilibrium equations

In “Appendix 1” section we show that the free drug concentrations can be expressed by the following:

$$ C_{A} = \frac{{C_{Atot} K_{DA} }}{{K_{DA} + R_{tot} (1 - z)}}\; {\text{and}}\;C_{B} = \frac{{C_{Btot} K_{DB} }}{{K_{DB} + R_{tot} (1 - z)}} $$

(40)

where z is the only solution of a polynomial equation satisfying:

$$ 0 < z < a_{A} + a_{B} \;{\text{and}}\;z < 1 $$

(41)

Here

$$ a_{A} = \frac{{C_{Atot} }}{{R_{tot} }},a_{B} = \frac{{C_{Btot} }}{{R_{tot} }},k_{A} = \frac{{K_{DA} }}{{R_{tot} }},k_{B} = \frac{{K_{DB} }}{{R_{tot} }} $$

(42)

If K _DA  ≠ K _DB , then the polynomial is cubic:

$$ z^{3} + bz^{2} + cz + d = 0 $$

(43)

where

$$ b = - (2 + k_{A} + k_{B} + a_{A} + a_{B} ) $$

(44)

$$ c = 1 + 2a_{A} + 2a_{B} + k_{A} + k_{B} + k_{B} a_{A} + k_{A} a_{B} + k_{A} k_{B} $$

(45)

$$ d = - (k_{B} a_{A} + k_{A} a_{B} + a_{A} + a_{B} ) $$

(46)

The Existence Theorem in “Appendix 1” section implies that for k _A  ≠ k _B , there are three distinct roots of Eq. 43. Consequently, the determinant Δ of Eq. 43:

$$ \Updelta = Q^{3} + R^{2} $$

(47)

where

$$ Q = \frac{{3c - b^{2} }}{9}\;{\text{and}}\;R = \frac{{9bc - 27d - 2b^{3} }}{54} $$

(48)

must be negative [14]. All roots of the cubic equation Eq. 43 can be represented by means of complex numbers [14]:

$$ z = - \frac{b}{3} + S + T $$

(49)

$$ z = - \frac{b}{3} - \frac{1}{2}\left( {S + T} \right) + \frac{i\sqrt 3 }{2}(S - T) $$

(50)

$$ z = - \frac{b}{3} - \frac{1}{2}\left( {S + T} \right) - \frac{i\sqrt 3 }{2}(S - T) $$

(51)

where

$$ S = \root{3} \of {R + \sqrt \Updelta }\; {\text{and}}\;T = \root{3} \of {R - \sqrt \Updelta } $$

(52)

Note since ∆ < 0, the square root $\sqrt \Updelta$ is an imaginary number. Although each of solutions in Eqs. 49–51 contains complex numbers, their left hand sides are real numbers. Unfortunately, in this form it is difficult to determine which solution satisfies Eq. 41. Since ∆ < 0, one can also utilize a trigonometric representation of the solution of Eq. 41 [15]:

$$ z = - \frac{b}{3} + 2\sqrt { - Q} \cos \left( {\frac{\theta }{3}} \right) $$

(53)

$$ z = - \frac{b}{3} + 2\sqrt { - Q} \cos \left( {\frac{\theta + 2\pi }{3}} \right) $$

(54)

$$ z = - \frac{b}{3} + 2\sqrt { - Q} \cos \left( {\frac{\theta + 4\pi }{3}} \right) $$

(55)

where

$$ \theta = \cos^{ - 1} \left( {\frac{R}{{\sqrt { - Q^{3} } }}} \right) $$

(56)

Note that Eq. 47 implies that Q < 0, and all solutions in Eqs. 53–56 do not contain complex numbers. Similarly to the representation in Eqs. 49–51, it is difficult to determine which of solutions in Eqs. 53–56 satisfies Eq. 41.

In case K _DA  = K _DB solving the equilibrium equations Eqs. 27 and 28 can be reduced to finding a root of a quadratic equation:

$$ z^{2} + bz + c = 0 $$

(57)

where

$$ b = - (1 + a_{A} + a_{B} + k_{A} ) $$

(58)

$$ c = a_{A} + a_{B} $$

(59)

The Existence Theorem implies that for k _A  = k _B , there are two distinct positive roots of Eq. 57. Consequently, the determinant Δ of Eq. 57:

$$ \Updelta = b^{2} - 4c $$

(60)

must be positive. Then the only root of the quadratic equation Eq. 57 satisfying Eq. 41 is:

$$ z = \frac{1}{2}\left( { - b - \sqrt \Updelta } \right) $$

(61)

A MATLAB m-function equilibrium solving the rapid binding TMDD model using the explicit solution is provided in the supplementary material. Computer simulations of TMDD model with two drugs competing for same receptor were performed using the MATLAB m-function equilibrium. To make a comparison of TMDD models between one drug and two drugs situation, free drug concentrations were simulated with K _DA  = K _DB and K _DA  = 10K _DB . From Fig. 2, it can be seen that for K _DA  = K _DB  = 1, the pharmacokinetic profiles for C _A and C _B are identical, resembling the TMDD model with one drug. When K _DA  = 1 and K _DB  = 0.1, compared with the simulation using K _DA  = K _DB  = 1, the C _B (0) (free drug concentration for drug B at t = 0) decreased instantaneously, whereas the C _A (0) (free drug concentration for drug A at t = 0) increased instantaneously. This is due to the stronger receptor binding affinity of C _B , which results in a decrease of free drug concentration C _B (0) after the equilibrium. Since less receptor are available for drug A, C _A (0) increases. The difference between C _A (0) and C _B (0) is more marked with lower IV bolus dose, when bigger portion of drug binds to receptors. Due to the stronger receptor binding affinity, drug B is eliminated faster than drug A (Fig. 2).

Fig. 2

Simulated concentration–time profiles for escalating IV bolus doses (100, 500, 1000 units for both A and B) using TMDD model with two ligands competitively binding to the same target. V _c  = 10, k _elA  = k _elB  = 0.01, k _ptA  = k _ptB  = k _tpA  = k _tpB  = 0, C _A0 = C _B0 = 0, k _intA  = k _intB  = 0.1, R _tot0 = 50, k _deg  = 0.02. For upper two panels, K _DA  = K _DB  = 1. For lower two panels, K _DA  = 1, K _DB  = 0.1. Simulations were performed in MATLAB using the algebraic solution of equilibrium equations

Table 1 Parameter values used for simulating the time courses of model variables from Example 1

Numerical solution of equilibrium equations

If K _DA  ≠ K _DB , then the solutions of the cubic equation Eq. 43 are expressed by means of complex numbers or trigonometric functions. None of these representations is conclusive of which of three roots satisfies Eq. 41. A numerical approach of solving Eq. 43 based on the bisection method [16] can be applied where the solution is guaranteed to satisfy Eq. 41. A flow diagram for the bisection method is shown in Fig. 3. One needs to evaluate the cubic polynomial:

$$ f(z) = z^{3} + bz^{2} + cz + d $$

(62)

at lower z _low and upper z _high bounds of the root z _low  < z < z _high in an iterative manner until the required accuracy (acc) is reached. Each iteration decreases the interval [z _low , z _high ] by half starting from an interval [0, min{1, a _A  + a _B }] which is contained in the interval [0, 1]. Consequently, the accuracy of the solution after n iterations is less than 2⁻ⁿ. For p digit accuracy (acc = 10^−p), the maximal number of iterations N _max  ≥ p log(10)/log(2), which yields for p = 8 N _max  = 27, and for p = 16 N _max  = 54.

Fig. 3

A flow chart illustrating the bisection algorithm for solving equation f(z) = 0. The START and STOP steps denote the beginning and end of the algorithm, respectively. The rectangular boxes represent the assignment steps whereas the diagonal boxes refer to conditional statement with two possible outcomes Yes (if condition is true), and No (if condition is false). The arrows indicate the next steps. The meanings of the symbols a_A, a_B, acc, and N_max are explained in the methods and results

If K _DA  = K _DB , then the root of Eq. 57 satisfying Eq. 41 is identified by Eq. 61, and there is no need for a numerical method for solving the quadratic equation in Eq. 57. Nevertheless, the bisection method will work as well with f(z) defined by the left hand side of Eq. 57. An implementation of the numerical algorithm in a program solving the equilibrium equations Eqs. 27 and 28, requires considering two cases: K _DA  = K _DB , and K _DA  ≠ K _DB . In the former case the root z is given by Eq. 61, and the free drug concentrations C _A and C _B by Eq. 40. In the latter case the root z is produced by the bisection method, and C _A and C _B are expressed by Eq. 40. A MATLAB m-function equilibrium_numer solving the rapid equilibrium TMDD model using the numerical approach is provided in the supplementary material.

Differential solution of equilibrium equations

The equilibrium equations Eqs. 27 and 28 are algebraic equations in unknowns C _A and C _B that are determined by the model variables C _Atot , C _Btot , and R _tot . As demonstrated in previous sections, solving equilibrium equations is mathematically challenging and requires an extra effort. Alternatively, one can differentiate both sides of Eqs. 27 and 28 and obtain a system of differential equations in unknowns dC _A /dt and dC _B /dt. This approach might bypass the need of solving the equilibrium equations using the bisection method (as demonstrated in Example 1). The system of differential solutions is linear with respect to these derivatives and can be solved using the Cramer’s rule [17] (see “Appendix 2” section):

$$ \frac{{dC_{A} }}{dt} = \frac{{K_{DA} CP_{Atot} F - C_{A} F(RP_{tot} - CP_{Atot} - CP_{Btot} ) + K_{DA} C_{B} CP_{Atot} - K_{DB} C_{A} CP_{Btot} }}{{EF + FC_{A} + EC_{B} }} $$

(63)

$$ \frac{{dC_{B} }}{dt} = \frac{{K_{DB} CP_{Btot} E - C_{B} E(RP_{tot} - CP_{Atot} - CP_{Btot} ) + K_{DB} C_{A} CP_{Btot} - K_{DA} C_{B} CP_{Atot} }}{{EF + FC_{A} + EC_{B} }} $$

(64)

where

$$ E = R_{tot} - C_{Atot} - C_{Btot} + C_{A} + C_{B} + K_{DA} $$

(65)

$$ F = R_{tot} - C_{Atot} - C_{Btot} + C_{A} + C_{B} + K_{DB} $$

(66)

$$ CP_{Atot} = In_{A} (t) - (k_{elA} + k_{ptA} )C_{A} + k_{tpA} A_{TA} /V_{c} - k_{{{int} A}} (C_{Atot} - C_{A} ) $$

(67)

$$ CP_{Btot}\;=\;In_{B} (t) - (k_{elB} + k_{ptB} )C_{B} + k_{tpB} A_{TB} /V_{c} - k_{{{int} B}} (C_{Btot} - C_{B} ) $$

(68)

$$ RP_{tot}\;=\;k_{syn} - k_{{deg} } R_{tot} - (k_{{{int} A}} - k_{{deg} } )(C_{Atot} - C_{A} ) - (k_{{{int} B}} - k_{{deg} } )(C_{Btot} - C_{B} ) $$

(69)

The initial conditions for Eqs. 63 and 64 require solving the equilibrium equations Eqs. 27 and 28 evaluated at t = 0 for C _A (0) and C _B (0)

$$ (R_{tot} (0) - C_{Atot} (0) - C_{Btot} (0) + C_{A} (0) + C_{B} (0))C_{A} (0) = K_{DA} (C_{Atot} (0) - C_{A} (0)) $$

(70)

$$ (R_{tot} (0) - C_{Atot} (0) - C_{Btot} (0) + C_{A} (0) + C_{B} (0))C_{B} (0) = K_{DB} (C_{Btot} (0) - C_{B} (0)) $$

(71)

where C _Atot (0), C _Btot (0), and R _tot (0) are defined by Eqs. 30, 32, and 34, respectively. It should be noted that the differential equations Eqs. 63–64 are only valid for the time interval where the time derivatives of C _A and C _B exist. If an additional bolus dose was administered at time t ₀, then in addition to adjusting the values of C _Atot and C _Btot for this input, the equilibrium equations Eqs. 63–64 should be solved at t = t ₀ for C _A (t ₀) and C _B (t ₀), and these values should be used as initial conditions for the ODE system Eqs. 63–69 for times t > t ₀.

The rapid binding model is now fully defined by Eqs. 22–26, 30–39, and 63–71. However, since the differential equations for C _A and C _B are part of the model description, one can use the Gaddum equations Eqs. 38 to eliminate the differential equations for C _Atot and C _Btot :

$$ C_{Atot} = C_{A} + \frac{{R_{tot} C_{A} /K_{DA} }}{{1 + C_{A} /K_{DA} + C_{B} /K_{DB} }} $$

(72)

$$ C_{Btot} = C_{B} + \frac{{R_{tot} C_{B} /K_{DB} }}{{1 + C_{A} /K_{DA} + C_{B} /K_{DB} }} $$

(73)

A MATLAB m-function equilibrium_diff solving the rapid equilibrium TMDD model using the differential solutions is provided in the supplementary material.

Example 1: exogenous and endogenous IgG competing for FcRn receptor

Therapeutic monoclonal antibodies (mAbs) have been under rapid development. The vast majority of the approved mAb therapeutics are of immunoglobulin G (IgG) format. It is known that the neonatal Fc receptor (FcRn) functions as a “salvage receptor” which contributes to the extended pharmacokinetics of IgG. One complexity when studying the IgG/FcRn interaction in vivo is that the high level of endogenous IgGs which compete for FcRn binding with exogenous IgG.

We adopted a previously published model by Hansen et al. [18] to account for the competitive interaction between endogenous IgG (A) and exogenous IgG (B) and FcRn receptor. This model is based on the protection of IgG catabolism by the FcRn receptor. The model structure is shown in Fig. 4. IgGs in the blood central compartment (C _A , C _B ) are taken up into endosomal compartment by fluid phase endocytosis, represented by a first-order process (k _up ). Once inside the endosome, free IgGs (C _EA , C _EB ) can bind to FcRn receptor to form IgG/receptor complexes (RC _EA , RC _EB ). Bound IgGs are recycled and returned to the central compartment by a first-order process k _ret , while unbound IgGs (C _EA , C _EB ) proceed to the lysosomes and undergo degradation by a first-order process k _deg . The differential equations that describe the model are as follows:

$$ \frac{{dC_{A} }}{dt} = In_{A0} - k_{up} C_{A} + k_{ret} \frac{{V_{E} }}{{V_{c} }}(C_{EAtot} - C_{EA} ) $$

(74)

$$ \frac{{dC_{B} }}{dt} = - k_{up} C_{B} + k_{ret} \frac{{V_{E} }}{{V_{c} }}(C_{EBtot} - C_{EB} ) $$

(75)

$$ \frac{{dC_{EAtot} }}{dt} = k_{up} \frac{{V_{C} }}{{V_{E} }}C_{A} - k_{{deg} } C_{EA} - k_{ret} (C_{EAtot} - C_{EA} ) $$

(76)

$$ \frac{{dC_{EBtot} }}{dt} = k_{up} \frac{{V_{C} }}{{V_{E} }}C_{B} - k_{{deg} } C_{EB} - k_{ret} (C_{EBtot} - C_{EB} ) $$

(77)

where C _EAtot and C _EBtot denote the total IgG concentrations in the endosomal compartment. We assume that the total FcRn concentration R _tot is constant. The free endosomal IgG concentrations C _EA and C _EB satisfy the equilibrium equations:

$$ \frac{{C_{EA} (R_{tot} - C_{EAtot} - C_{EBtot} + C_{EA} + C_{EB} )}}{{C_{EAtot} - C_{EA} }} = K_{DA} $$

(78)

$$ \frac{{C_{EB} (R_{tot} - C_{EAtot} - C_{EBtot} + C_{EA} + C_{EB} )}}{{C_{EBtot} - C_{EB} }} = K_{DB} $$

(79)

Fig. 4

Model diagram for IgG pharmacokinetics with exogenous and endogenous IgG competing for FcRn receptor. Symbols are defined in Example 1

Endogenous production rate In _A0 can be represented by:

$$ In_{A0} = k_{up} C_{A0} - k_{ret} \frac{{V_{E} }}{{V_{c} }}(C_{EAtot0} - C_{EA0} ) $$

(80)

$$ C_{EAtot0} = \frac{{k_{up} }}{{k_{ret} }}\frac{{V_{c} }}{{V_{E} }}C_{A0} - \frac{{k_{{deg} } - k_{ret} }}{{k_{ret} }}C_{EA0} $$

(81)

The initial conditions for Eqs. 74–77:

$$ C_{A} (0) = C_{A0} $$

(82)

$$ C_{B} (0) = \frac{Dose}{{V_{c} }} $$

(83)

$$ C_{EAtot} (0) = C_{EAtot0} $$

(84)

$$ C_{EBtot} (0) = 0 $$

(85)

where C _EA0 and C _EAtot0 satisfy the equilibrium equation Eq. 78:

$$ \frac{{C_{EA0} (R_{tot} - C_{EAtot0} + C_{EA0} )}}{{C_{EAtot0} - C_{EA0} }} = K_{DA} $$

(86)

The simulations were performed using the differential method of solving the equilibrium equations implemented in ADAPT 5 program [19]. In this case, using the differential method bypasses the need of solving the equilibrium equations using the bisection method. The initial conditions of the differential equations can be solved explicitly. The ADAPT 5 code is provided in the supplementary material.

For simulations, most model parameters, including endogenous IgG level, were taken from the literature [18] (Table 1). The endogenous IgG production rate In_A0, which is represented by a zero-order process, was calculated based on mass balance at steady-state. To study the effect of FcRn binding affinity of exogenous IgG on concentration level of endogenous IgG and exogenous IgG itself, equilibrium dissociation constant of exogenous IgG K _DB  = K _DA , 0.1 K _DA , and 0.01 K _DA , were used for simulations. Simulated plasma pharmacokinetic profiles of endogenous IgG and exogenous IgG following administration of a single IV bolus dose of 10 mg/kg (66.7 nmol/kg) are shown in Fig. 5. As shown in the upper panel, the exogenous IgG exhibits typical biphasic profile, composed of a rapid distribution phase and a slow elimination phase. Slower decline of the terminal phase of the concentration–time profile of IgG with higher binding affinity is observed. Such an observation is consistent with the FcRn protection theory: IgG with higher FcRn binding affinity has the competitive advantage and is expected to outcompete the high concentration of endogenous IgG for FcRn binding. Therefore, more exogenous IgG is protected by FcRn from lysosomal degradation, which results in longer systemic circulation. Shown in the lower panel are the simulated profiles for endogenous IgG. With the competition from the administered exogenous IgG for FcRn binding, less endogenous IgG is protected by FcRn, the elimination of endogenous IgG is accelerated, and the “steady-state” of endogenous IgG is broken, which leads to the descending in the endogenous IgG concentration–time profile. With the exogenous IgG eliminated from the circulation with time, the competition for FcRn protection from the exogenous IgG is also diminishing and the endogenous IgG is going back to the “steady-state”, showing in the endogenous IgG profile as it is returning back to the baseline. With administration of IgG with higher FcRn binding affinity, which means stronger competition for FcRn protection, the endogenous IgG profile reflects a deeper decline from the baseline and a delayed returning to the baseline. Such simulation results are consistent with the literature observations [20]. Vaccaro et al. found that antibodies with the enhanced FcRn binding affinity at both acidic and neutral pH conditions were more potent in lowering endogenous IgG concentration compared to IVIG treatment (which has similar FcRn binding affinity to endogenous IgG) [20].

Fig. 5

Endogenous IgG plasma concentration profiles (upper panel) and exogeneous plasma concentration profiles (lower panel) after administration of 10 mg/kg (66.7 nmol/kg) exogenous IgG with equilibrium dissociation constant K _DB  = K _DA , 0.1 K _DA , and 0.01 K _DA . Simulations were performed in ADAPT 5 using the differential solution of equilibrium equations

Example 2: recombinant human EPO analogue and endogenous EPO competing for EPOR

In addition to the recombinant human erythropoietin, various erythropoiesis-stimulating agents (ESAs) have been developed such as darbepoetin [21], continuous erythropoietin receptor activator [22], peptidic erythropoiesis receptor agonist [23], etc. These ESAs compete with endogenous erythropoietin for erythropoietin receptor (EPOR) binding and stimulate the proliferation and differentiation of erythroid progenitor cells. Compared with endogenous erythropoietin, they have lower receptor binding affinity and longer half-life. A TMDD model with competitive interaction between endogenous erythropoietin and exogenous ESA provides a more mechanistic description for the pharmacokinetics and may offer further insights in the pharmacodynamics of the latter [10].

We adopted a previously published TMDD model for EPO by Woo et al. [24] and further introduced competitive interaction between endogenous EPO and exogenous ESA. The model structure is presented in Fig. 6. This model is similar to the model proposed in Fig. 1. k _EPO represents the zero-order production rate for the endogenous EPO. Darbepoetin (DA) was employed as exogenous ESA in the model. The endogenous EPO (C _A ) and exogenous DA (C _B ) competitively bind to the EPOR (R), forming drug-receptor complexes (RC _A and RC _B ). The drug-receptor complexes are internalized through the same first-order process [25]. The differential equations that describe the model are as follows:

$$ \frac{{dC_{Atot} }}{dt} = k_{EPO} - (k_{elA} + k_{ptA} )C_{A} + k_{tpA} A_{TA} /V_{c} - k_{int} (C_{Atot} - C_{A} ) $$

(87)

$$ \frac{{dA_{TA} }}{dt} = k_{ptA} V_{c} C_{A} - k_{tpA} A_{TA} $$

(88)

$$ \frac{{dC_{Btot} }}{dt} = - (k_{elB} + k_{ptB} )C_{B} + k_{tpB} A_{TB} /V_{c} - k_{int} (C_{Btot} - C_{B} ) $$

(89)

$$ \frac{{dA_{TB} }}{dt} = k_{ptB} V_{c} C_{B} - k_{tpB} A_{TB} $$

(90)

$$ \frac{{dR_{tot} }}{dt} = k_{syn} - k_{{deg} } R_{tot} - (k_{\text{int}} - k_{{deg} } )(C_{Atot} + C_{Btot} - C_{A} - C_{B} ) $$

(91)

where C _A and C _B are the only solutions of the equilibrium equations Eq. 18 rewritten as follows:

$$ (R_{tot} - C_{Atot} - C_{Btot} + C_{A} + C_{B} )C_{A} = K_{DA} (C_{Atot} - C_{A} ) $$

(92)

$$ (R_{tot} - C_{Atot} - C_{Btot} + C_{A} + C_{B} )C_{B} = K_{DB} (C_{Btot} - C_{B} ) $$

(93)

such that:

$$ 0 < C_{A} < C_{Atot} \;{\text{and}}\;0 < C_{B} < C_{Btot} $$

(94)

Fig. 6

Model diagram for target-mediated drug disposition for darbepoetin competing for EPO receptor with endogenous erythropoietin. Symbols are defined in Example 2

The initial conditions for Eqs. 87–91 are defined by their steady-states and IV bolus doses:

$$ C_{Atot} (0) = \frac{{R_{tot0} C_{A0} /K_{DA} }}{{1 + C_{A0} /K_{DA} }} + C_{A0} $$

(95)

$$ A_{TA} (0) = k_{ptA} V_{c} C_{A0} /k_{tpA} $$

(96)

$$ C_{Btot} (0) = \frac{{Dose_{B} }}{{V_{c} }} $$

(97)

$$ A_{TB} (0) = 0 $$

(98)

$$ R_{tot} (0) = R_{tot0} $$

(99)

Here, RC _A0 represents the EPO-receptor complex concentration that can be calculated from:

$$ RC_{A0} = \frac{{R_{tot} C_{A0} /K_{DA} }}{{1 + C_{A0} /K_{DA} }} $$

(100)

The receptor synthesis rate can be calculated from Eq. 91:

$$ k_{syn} = k_{{deg} } (R_{tot0} - RC_{A0} ) + k_{{{int} A}} RC_{A0} $$

(101)

The zero-order production rate for endogenous EPO can be defined by the steady state for Eq. 87:

$$ k_{EPO} = k_{elA} C_{0} + k_{int} RC_{A0} $$

(102)

The simulated time courses of C _A , C _B and C _A  + C _B are shown in Fig. 7. The parameter values are listed in Table 2. The simulations were performed using the bisection method of solving the equilibrium equations implemented in Phoenix WinNonlin 6.0 (Pharsight Corporation, Cary, NC). The differential solution of the equilibrium equations was not used since the initial condition of the differential equations for free drug after IV bolus dose has to be solved using the bisection method. Therefore, converting the equilibrium equations to a system of differential equations is somewhat redundant in this case. The WinNonlin code is provided in the supplementary material.

Fig. 7

Simulated concentration–time profiles for escalating IV bolus doses (0.1, 0.02, 0.002 nmol/kg) of darbepoetin (DA). Upper panel: concentration–time profiles of endogenous EPO. Dash-dot line represents the baseline EPO level. Middle panel: concentration–time profiles of darbepoetin. Lower panel: concentration–time profile of the sum of DA and EPO. Solid lines represent these profiles when k _EPO  = 0.00043 nM h⁻¹. Dash lines represent these profiles when k _EPO  = 0. Other parameters for simulation are listed in Table 2. Simulations were performed in Phoenix WinNonlin using the bisection method of solving equilibrium equations

Table 2 Parameter values used for simulating the time courses of model variables from Example 2

The systems with and without endogenous EPO were simulated and presented in Fig. 7. It can be seen that the concentration of endogenous EPO goes up immediately after the IV bolus dosing of exogenous darbepoetin, and then returns to baseline. When dose equals 0.1 nmol/kg, the saturation of receptor-mediated clearance of endogenous EPO by exogenous DA leads to a temporary increase in the endogenous EPO concentration, followed by a decreasing phase. The darbepoetin PK profile in the middle panel shows that without presence of endogenous EPO, the DA concentration decreases faster. The lower panel in Fig. 7 shows that after IV bolus dose, the sum of DA and EPO declines more slowly with the presence of endogenous EPO, especially for lower IV bolus dose.

Discussion

The rapid equilibrium TMDD model for two drugs competing for the same receptor requires solving the equilibrium equations for the free drug concentrations. Contrary to the single drug situation, these constitute a system of two second-order polynomials that cannot be reduced to a system of two quadratic equations for each drug concentration separately. The system can be reduced to a single cubic equation that has an explicit solution. Consequently, the free drug concentrations are expressed as explicit functions of the model parameters, total receptor, and total drug concentrations. However, the explicit relationships contain one out of three solutions to a cubic equation that employs complex numbers. An additional hurdle is caused by the lack of information which of three roots is the only admissible. From a programming point of view, if one wants to code the rapid binding TMDD model, PK software needs to support complex numbers and a set of conditional statements needs to be implemented to select a unique solution out of three roots of the cubic equation. Worth mentioning is also a relatively high complexity of the explicit formulas.

Mathematically, the rapid binding TMDD model is a system of differential–algebraic equations [26], where the equilibrium equations stand for the algebraic part of the problem. For numerical solutions, the differential equation solver needs to be augmented by a solution of the algebraic equations that can be obtained by a number of robust algorithms such as the Newton method [16]. In our approach the numerical solution is obtained only for the cubic equation which simplifies the algebraic part of the problem and increases the numerical stability of the method. The selected bisection method is not the fastest, but because of the known lower and upper bounds for the solution, offers a straightforward control of the accuracy of the solution. Additionally, it is relatively easy to implement in a code of PK software.

Instead of solving the equilibrium equations for free drug concentrations, one can consider solving a system of differential equations obtained by differentiation of the equilibrium equation with respect to time and solving it for the time derivatives of free drug concentrations. Such an approach has been proposed to obtain the Michaelis–Menten approximation of the rapid binding TMDD model [27]. However, the equilibrium equations still need to be solved to obtain the initial conditions for the system of differential equations. If the bolus doses were administered at other times, then at each dosing time the equilibrium equations need to be solved, and the differential equations describing the free drug concentrations need to be initiated at these values. This implies that, at least from the computational point of view, converting the equilibrium equations to a system of differential equations is redundant. However, as demonstrated in our Example 1, for some applications of the rapid binding TMDD model the initial conditions can be simplified and solving the equilibrium equations is not necessary.

The rapid binding assumption results in the equilibrium equations. An assumption regarding slow change of the drug-receptor complex results in the quasi-steady-state approximation of the TMDD model [12]. The quasi-steady-state assumption applied to two drugs competing for the same target will lead to a system of equilibrium equations equivalent in structure to ones discussed in this report. Consequently, the presented methods of solving the rapid binding TMDD model apply as well for the quasi-steady-state TMDD model where the equilibrium constant K_D is replaced by the constant K_SS. However, the pharmacological interpretation of the equilibrium equations through the Gaddum equations remains valid only for the former.

A complete demonstration of developed algorithm requires model fitting. However, to fit such a model, the first step is to solve the model equations using PK software. The investigation in this paper demonstrated that obtaining the accurate solution of such model in PK software was not a trivial task. Further studies involving model fitting and parameter estimation are necessary to study the overall performance of this model and they are currently under investigation.

Therapeutic antibodies and hematopoietic growth factors were used as examples to emphasize the importance of the rapid binding TMDD model in describing pharmacokinetics of drugs competing for the same receptor with endogenous substances. However, the presented model is structured to account for any two drugs binding to the same target. The competition for the same receptor between exogenous and endogenous compounds has been reported for a number of protein drugs. An antibody MEDI-575 selectively binds to platelet-derived growth factor receptor (PDGFRα) and blocks Platelet-Derived Growth Factor-AA, a ligand for PDGFRα [9]. A peptibody romiplostim competes with endogenous thrombopoietin for the c-Mpl receptor expressed on platelets and platelets precursors [28]. Similarly, a small molecule eltrombopag is an agonist of the c-Mpl receptor [29]. Another therapeutic application is when two exogenous drugs targeting the same receptor are administered simultaneously or consecutively. In the latter case, the overlap between the washout of one drug and onset of another requires a competitive interaction. Such situation takes place for a two-stage treatment approach for targeting the serum amyloid P component (SAP) by a small molecule Carboxy Pyrrolidine Hexanoyl Pyrrolidine Carboxylate (CPHPC) and anti-SAP monoclonal antibody [30]. First, CPHPC is administered to deplete SAP from plasma, and then anti-SAP antibody is given to remove SAP from amyloid tissues. All of the above examples can potentially require an equilibrium assumption to describe the available PK data, and the techniques presented here can be utilized. As the biotechnology of therapeutic proteins advances, one may expect an increasing number of competitive agonists or antagonists to be developed.

In summary, we proposed a rapid binding TMDD model to describe pharmacokinetics of two drugs competing for the same receptor. Three methods of solving the presented models were introduced involving explicit equations, numerical bisection algorithm, and differential representation. The first method was applied to simulate the signature profiles of the model solutions. The two remaining methods were implemented in PK models of a therapeutic antibody and an erythropoiesis stimulating agent competing with the endogenous substances for the same receptor.

Appendices

Appendix 1

Existence of the unique solution of Eqs. 27 and 28

Let x and y denote the RC _A and RC _B divided by R _tot :

$$ x = \frac{{RC_{A} }}{{R_{tot} }}\; {\text{and}}\;y = \frac{{RC_{B} }}{{R_{tot} }} $$

(103)

Then Eqs. 27 and 28 can be expressed in the following form:

$$ (1 - x - y)(a_{A} - x) = k_{A} x $$

(104)

$$ (1 - x - y)(a_{B} - y) = k_{B} y $$

(105)

Note that because of definitions in Eqs. 103 and 42, x and y satisfy the following relationships:

$$ 0 < x < a_{A} ,0 < y < a_{B} , {\text{ and }} x + y < 1 $$

(106)

Existence Theorem

Let k _A , k _B , a _A , a _B  > 0. If k_A ≠ k_B, then there exist exactly three solutions to Eqs. 104 and 105: (x ₁, y ₁), (x ₂, y ₂), (x ₃, y ₃) such that

• (a) If k _B  > k _A , then:

$$ 0 < x_{1} < a_{A} < x_{2} < x_{3} ,y_{3} < 0 < y_{1} < a_{B} < y_{2} ,\;{\text{and}}\;x_{1} + y_{1} < 1 $$

(107)

• (b) If k _B  < k _A , then:

$$ x_{3} < 0 < x_{1} < a_{A} < x_{2} {\text{ and }} 0 < y_{1} < a_{B} < y_{2} < y_{3} ,\;{\text{and}}\;x_{1} + y_{1} < 1 $$

(108)

If k _A  = k _B , then there exist exactly two solutions to Eqs. 104 and 105: (x ₁, y ₁), (x ₂, y ₂) such that:

$$ 0 < x_{1} < a_{A} < x_{2} {\text{ and }} 0 < y_{1} < a_{B} < y_{2} ,\;{\text{and}}\;x_{1} + y_{1} < 1 $$

(109)

Proof of Existence Theorem is based on the observation that the solutions of Eqs. 104 and 105 can be geometrically interpreted as intersections of the following curves:

$$ y = 1 - x + \frac{{k_{A} x}}{{x - a_{A} }} $$

(110)

$$ x = 1 - y + \frac{{k_{B} y}}{{y - a_{B} }} $$

(111)

The curves of Eqs. 110 and 111 are transformed Eqs. 104 and 105, respectively. The asymptotes of Eq. 110 are:

$$ x = a_{A} \; {\text{and}}\;y = 1 + k_{A} - x $$

(112)

whereas the asymptotes for Eq. 111 are:

$$ y = a_{B} \; {\text{and}}\;x = 1 + k_{B} - y $$

(113)

If k _B  > k _A , the examination of the monotonicity of Eqs. 110 and 111 and the horizontal and vertical asymptotes imply that there are two intersection points (x ₁, y ₁) and (x ₂, y ₂) such that:

$$ 0 < x_{1} < a_{A} < x_{2} \;{\text{and}}\;0 < y_{1} < a_{B} < y_{2} $$

(114)

as shown in Fig. 8. k _B  > k _A implies that the diagonal asymptote for Eq. 110 is below the diagonal asymptote for Eq. 111. Consequently, there is a third intersection point (x ₃, y ₃) such that:

$$ x_{2} < x_{3} \;{\text{and}}\;y_{3} < 0 $$

(115)

Fig. 8

Graphical representation of solutions of the equilibrium equations when K _DA  ≠ K _DB (upper panel) and K _DA  = K _DB (lower panel). The equilibrium equations Eqs. 27 and 28 are equivalent to a system of two hyperbolic equations represented by the solid lines. Their intersection coordinates (x ₁, y ₁), (x ₂, y ₂), (x ₃, y ₃) (upper panel), and (x ₁, y ₂), (x ₂, y ₂) (lower panel) are all possible solutions of the system. The dashed lines represent the asymptotes for the hyperbolas. In case K _DA  = K _DB (equivalent to k _A  = k _B ) the diagonal asymptotes collapse to a single one reducing the number of solutions to two. The vertical and horizontal asymptotes intersect the axes at a_A and a_B, respectively. Only the solution (x ₁, y ₁) is inside the rectangle of vertices defined by 0, a _A , and a _B

If k _B  < k _A , the positions of the diagonal asymptotes reverses and the third intersection (x ₃, y ₃) satisfies the following:

$$ x_{3} < 0\;{\text{and}}\;y_{2} < y_{3} $$

(116)

If k _B  = k _A , then the existence of (x ₁, y ₁) and (x ₂, y ₂) satisfying Eq. 109 is a consequence of the same argument. Since the diagonal asymptotes collapse into one (see Fig. 8), there is no third intersection point. A formal proof of Existence Theorem not referring to a geometric interpretation of Eqs. 104 and 105 presented in Fig. 8 follows below.

Define the functions:

$$ f(x) = 1 - x - \frac{{k_{A} x}}{{a_{A} - x}},x \ne a_{A} \;{\text{and}}\;g(y) = 1 - y - \frac{{k_{B} y}}{{a_{B} - y}},\;y \ne a_{B} $$

(117)

Since the derivatives are negative:

$$ \frac{df}{dx}(x) = - 1 - \frac{{k_{A} a_{A} }}{{(a_{A} - x)^{2} }} < 0\;{\text{and}}\;\frac{dg}{dy}(y) = - 1 - \frac{{k_{B} a_{B} }}{{(a_{B} - B)^{2} }} < 0 $$

(118)

both functions are strictly decreasing. Because a discontinuity at x = a _A , there are two solutions to the equation:

$$ f\left( x \right) = 0 $$

(119)

$$ x_{a} = \frac{1}{2}\left( {1 + a_{A} + k_{A} - \sqrt {(1 + a_{A} + k_{A} )^{2} - 4a_{A} } } \right) $$

(120)

and

$$ x_{b} = \frac{1}{2}\left( {1 + a_{A} + k_{A} + \sqrt {(1 + a_{A} + k_{A} )^{2} - 4a_{A} } } \right) $$

(121)

One can verify by direct calculation that:

$$ 0 < x_{a} < \min \{ 1,a_{A} \} \le \max \{ 1,a_{A} \} < x_{b} $$

(122)

Similarly, there are two solutions to the equation:

$$ g\left( y \right) = 0 $$

(123)

$$ y_{a} = \frac{1}{2}\left( {1 + a_{B} + k_{B} - \sqrt {(1 + a_{B} + k_{B} )^{2} - 4a_{B} } } \right) $$

(124)

and

$$ y_{b} = \frac{1}{2}\left( {1 + a_{B} + k_{B} + \sqrt {(1 + a_{B} + k_{B} )^{2} - 4a_{B} } } \right) $$

(125)

Additionally

$$ 0 < y_{a} < \min \{ 1,a_{B} \} \le \max \{ 1,a_{B} \} < y_{b} $$

(126)

Because function g(y) is strictly decreasing and continuous in the intervals (−∞, a _B ) and (a _B , ∞), there exist inverse functions h ₁(x) and h ₂(x), respectively, such that:

$$ g\left( {h_{1} \left( x \right)} \right) = x\;{\text{and}}\;g\left( {h_{2} \left( x \right)} \right) = x, - \infty < {\text{ x }} < \infty , $$

(127)

To show existence of (x ₁, y ₁) consider a new function F ₁(x) = f(x) − h ₁(x) defined on the interval 0 ≤ x ≤ x _a . Then Eq. 126 implies that:

$$ F_{ 1} \left( 0 \right) = { 1} - y_{a} > 0 $$

(128)

As an inverse to a decreasing function h ₁(x) is also decreasing and Eq. 122 implies h ₁(x _a ) > h ₁(1) = 0, and consequently

$$ F_{ 1} \left( {x_{a} } \right) = 0 -h_{ 1} \left( {x_{a} } \right) < 0 $$

(129)

Because the function F ₁(x) is continuous, and it changes the sign at the ends of the interval [0, x _a ], the intermediate value theorem guarantees there exists a 0 < x ₁ < x _a such that:

$$ F_{ 1} \left( {x_{1} } \right) = 0 $$

(130)

Let y ₁ = h ₁(x ₁). Then Eqs. 130, 127, and 117 imply that (x ₁, y ₁) is a solution to Eqs. 104 and 105. Since x _a  < a _A , then x ₁ < a _A . This and Eq. 104 also yields that x₁ + y₁ < 1.

To show existence of (x ₂, y ₂) consider a new function F ₂(x) = f(x) − h ₂(x) defined on the interval a _A  < x ≤ x _b . By definition h ₂(x _b ) > a _B  > 0, and consequently

$$ F_{2} \left( {x_{b} } \right) = 0- h_{2} \left( {x_{b} } \right) < 0 $$

(131)

From Eq. 117 it follows that:

$$ \mathop {\lim }\limits_{{x \to a_{A} + }} F_{2} (x) = + \infty $$

(132)

The intermediate value theorem implies there exists a a _A  < x ₂ < x _b such that:

$$ F_{ 2} \left( {x_{ 2} } \right) = 0 $$

(133)

Let y ₂ = h ₂(x ₂). By definition of h ₂(x), y ₂ > a _B . Also, Eqs. 133, 127, and 117 imply that (x ₂, y ₂) is a solution to Eq. 104.

To show existence of (x ₃, y ₃) for the case k _A  < k _B consider a new function F ₃(x) = F(x) − h ₁(x) defined on the interval x _b  ≤ x < ∞. The function h ₁(x) is decreasing and Eq. 112 implies h ₁(x _b ) < h ₁(1) = 0. Hence

$$ F_{ 3} \left( {x_{b} } \right) = 0 - h_{ 1} \left( {x_{b} } \right) > 0 $$

(134)

Eq. 117 implies that:

$$ f(x) - 1 + x - k_{A} \to 0\;{\text{as}}\;x \to \infty ,\; {\text{and}} \; g(y) - 1 + y - k_{B} \to 0\;{\text{as}}\;y \to - \infty $$

(135)

As a decreasing function h ₁(x) → −∞ as x → ∞. Consequently, Eq. 135 implies that:

$$ g(h_{1} (x)) - 1 + h_{1} (x) - k_{B} \to 0 \;{\text{as}}\;x \to \infty $$

(136)

Hence and from Eq. 127

$$ h_{1} (x) - 1 + x - k_{B} \to 0\; {\text{as}}\;x \to \infty $$

(137)

Thus

$$ F_{3} (x) \to k_{A} - k_{B} < 0\;{\text{as}}\;x \to \infty $$

(138)

The function F ₃(x) changes its sign at the ends of the interval x _b  ≤ x < ∞. The intermediate value theorem implies that there exists x _b  < x ₃ < ∞ such that:

$$ F_{ 3} \left( {x_{ 3} } \right) = 0 $$

(139)

Since x ₂ < x _b , then x ₂ < x ₃. Let y ₃ = h ₁(x ₃), then y ₃ < h ₁(1) = 0. Also Eqs. 137, 127, and 117 imply that (x ₃, y ₃) is a solution to Eq. 104.

A similar argument holds to show existence of (x ₃, y ₃) for the case k _A  > k _B . Consider a function F ₄(x) = f(x) − h ₂(x) defined on the interval −∞ < x ≤ 0. Eqs. 117, 123, and 126 imply that:

$$ F_{ 4} \left( 0 \right) = { 1 }-y_{b} < 0 $$

(140)

The same derivations as above lead to:

$$ F_{4} (x) \to k_{A} - k_{B} > 0\; {\text{as x}} \to \infty $$

(141)

The intermediate value theorem implies that there exists x ₃ < 0 such that:

$$ F_{ 4} \left( {x_{ 3} } \right) = 0 $$

(142)

Let y ₃ = h ₂(x ₃). Since h ₂(x) is decreasing y ₃ > h ₂(0) = y _b  > y ₂, and Eq. 117 implies that y ₃ > y ₂. Also Eqs. 137, 127, and 117 imply that (x ₃, y ₃) is a solution to Eq. 104.

To show uniqueness of (x ₁, y ₁), (x ₂, y ₂), (x ₃, y ₃) for k _A  ≠ k _B one can notice that x ₁, x ₂, and x ₃ pairwise distinct. There are also roots of a polynomial obtained from Eqs. 104 and 105 as follows. One can calculate from Eq. 104 the term:

$$ y(a_{A} - x) = (1 - x)(a_{A} - x) - k_{A} x $$

(143)

To enforce this term in Eq. 105 multiply both sides by (a _A -x)²:

$$ ((1 - x)(a_{A} - x) - y(a_{A} - x))(a_{B} (a_{A} - x) - y(a_{A} - x)) = k_{B} y(a_{A} - x)^{2} $$

(144)

Eq. 143 implies that:

$$ k_{A} x = (1 - x)(a_{A} - x) - y(a_{A} - x) $$

(145)

Substituting Eqs. 143 and 145 into A38 yields:

$$ k_{A} x(a_{B} (a_{A} - x) - (1 - x)(a_{A} - x) + k_{A} x) = k_{B} (a_{A} - x)((1 - x)(a_{A} - x) - k_{A} x) $$

(146)

which can further transformed to

$$ k_{A} a_{B} x(a_{A} - x) - \left( {k_{A} x + k_{B} (a_{A} - x)} \right)\left( {(1 - x)(a_{A} - x) + k_{A} x} \right) = 0 $$

(147)

A leading term of the polynomial in Eq. 147 is (k _B  − k _A )x ³. Therefore Eq. 147 is a cubic equation with three distinct roots x ₁, x ₂, and x ₃. If (x*, y*) is a solution to Eqs. 104 and 105, then x* must be a solution to Eq. 147 and hence x* = x _i for some i = 1, 2, 3. Eq. 104 implies that x* ≠ a _A and Eq. 143 yields:

$$ y^{\ast} = \frac{{(1 - x^{\ast} )(a_{A} - x^{\ast} ) - k_{A} x^{\ast} }}{{a_{A} - x^{\ast} }} $$

(148)

Since (x _i , y_i) is a solution to Eq. 104 as well y _i can be expressed by the right hand side of Eq. 148 with x _i substituted for x* and hence y* = y _i .

To show uniqueness of (x ₁, y ₁) and (x ₂, y ₂) for k _A  = k _B one can notice that then the polynomial equation Eq. 147 reduces to a quadratic equation since the highest order term (k _B  − k _A )x ³ vanishes. This quadratic equation has two distinct roots x ₁ and x ₂. If (x*, y*) is a solution to Eqs. 104 and 105 then x* must be also a solution to the quadratic equation Eq. 147, and consequently x* = x _i for some i = 1, 2. Then y* = y _i by the same argument as above. This completes proof of Existence Theorem.

Derivation of Eqs. 40, 43, and 57

For the case k _A  ≠ k _B , to solve Eqs. 104 and 105 one can add them side by side:

$$ (1 - x - y)(a_{A} + a_{B} - x - y) = k_{A} x + k_{B} y $$

(149)

Multiplying Eq. 104 by k_B and Eq. 105 by k_A followed and adding equation side by side yields:

$$ (1 - x - y)(k_{B} a_{A} + k_{A} a_{B} - k_{B} x - k_{A} y) = k_{A} k_{B} (x + y) $$

(150)

Since

$$ k_{B} x + k_{A} y = (k_{A} + k_{B} )(x + y) - (k_{A} x + k_{B} y) $$

(151)

Eq. 151 can be substituted in Eq. 150:

$$ (1 - x - y)(k_{B} a_{A} + k_{A} a_{B} + k_{A} x + k_{B} y - (k_{A} + k_{B} )(x + y)) = k_{A} k_{B} (x + y) $$

(152)

With introducing a new variable:

$$ z = x + y $$

(153)

Eq. 152 becomes:

$$ (1 - z)(k_{B} a_{A} + k_{A} a_{B} + k_{A} x + k_{B} y - (k_{A} + k_{B} )z) = k_{A} k_{B} z $$

(154)

The right hand side of Eq. 149 coincides with a term in Eq. 154 that can be replaced by the left hand side of Eq. 149, resulting in:

$$ (1 - z)(k_{B} a_{A} + k_{A} a_{B} + (1 - z)(a_{A} + a_{B} - z) - (k_{A} + k_{B} )z) = k_{A} k_{B} z $$

(155)

The only unknown in Eq. 50 is z and ordering the terms by the power of z produces a cubic equation Eq. 43.

If k _A  = k _B , then Eq. 149 assumes the following form:

$$ (1 - z)(a_{A} + a_{B} - z) = k_{A} z $$

(156)

Rearranging terms in Eq. 156 and ordering them by the power of z yields Eq. 57. In order to express C _A and C _B in terms of z, one should notice that according to Eq. 153:

$$ C_{Atot} - C_{A} + C_{Btot} - C_{B} = R_{tot} z $$

(157)

Upon substitution of Eq. 157 to the Eqs. 27 and 28 they reduce to:

$$ R_{tot} (1 - z)C_{A} = K_{DA} (C_{Atot} - C_{A} ) $$

(158)

$$ R_{tot} (1 - z)C_{B} = K_{DB} (C_{Btot} - C_{B} ) $$

(159)

Solving Eq. 158 for C _A and Eq. 159 for C _B results in Eq. 40.

Appendix 2

Derivation of Eqs. 63 and 64

Differentiating both sides of Eqs. 27 and 28 leads to:

$$ \begin{aligned} & (R_{tot} - C_{Atot} - C_{Btot} + 2C_{A} + C_{B} + K_{DA} )\frac{{dC_{A} }}{dt} + C_{A} \frac{{dC_{B} }}{dt} \\& \quad = K_{DA} \frac{{dC_{Atot} }}{dt} - C_{A} \left(\frac{{dR_{tot} }}{dt} - \frac{{dC_{Atot} }}{dt} - \frac{{dC_{Btot} }}{dt}\right) \\ \end{aligned} $$

(160)

$$ \begin{aligned} & C_{B} \frac{{dC_{A} }}{dt} + (R_{tot} - C_{Atot} - C_{Btot} + C_{A} + 2C_{B} + K_{DB} )\frac{{dC_{B} }}{dt} \\ &\quad = K_{DB} \frac{{dC_{Btot} }}{dt} - C_{B} \left(\frac{{dR_{tot} }}{dt} - \frac{{dC_{Atot} }}{dt} - \frac{{dC_{Btot} }}{dt}\right) \\ \end{aligned} $$

(161)

Rearranging terms in Eqs. 160 and 161 so that dC _A /dt and dC _B /dt are unknowns leads to:

$$ a\frac{{dC_{A} }}{dt} + b\frac{{dC_{B} }}{dt} = e $$

(162)

$$ c\frac{{dC_{A} }}{dt} + d\frac{{dC_{B} }}{dt} = f $$

(163)

where

$$ a = R_{tot} - C_{Atot} - C_{Btot} + 2C_{A} + C_{B} + K_{DA} $$

(164)

$$ b = C_{A} $$

(165)

$$ c = C_{B} $$

(166)

$$ d = R_{tot} - C_{Atot} - C_{Btot} + C_{A} + 2C_{B} + K_{DB} $$

(167)

$$ e = K_{DA} \frac{{dC_{Atot} }}{dt} - C_{A} \left(\frac{{dR_{tot} }}{dt} - \frac{{dC_{Atot} }}{dt} - \frac{{dC_{Btot} }}{dt}\right) $$

(168)

$$ f = K_{DB} \frac{{dC_{Btot} }}{dt} - C_{B} \left(\frac{{dR_{tot} }}{dt} - \frac{{dC_{Atot} }}{dt} - \frac{{dC_{Btot} }}{dt}\right) $$

(169)

The system of two linear equations Eqs. 162 and 163 has a unique solution defined by the Cramer’s rule [17] if

$$ ad - bc \ne 0 $$

(170)

Then

$$ \frac{{dC_{A} }}{dt} = \frac{ed - bf}{ad - bc} $$

(171)

$$ \frac{{dC_{B} }}{dt} = \frac{af - ec}{ad - bc} $$

(172)

Replacing the derivatives in Eqs. 168 and 169 by the right hand sides of differential equations Eqs. 22, 24, and 26 and using the variables CP _Atot , CP _Btot , ans RP _tot defined by Eqs. 67–69 one can notice that:

$$ a = E + C_{A} $$

(173)

$$ d = F + C_{B} $$

(174)

$$ e = K_{DA} CP_{Atot} - C_{A} (RP_{tot} - CP_{Atot} - CP_{Btot} ) $$

(175)

$$ f = K_{DB} CP_{Btot} - C_{B} (RP_{tot} - CP_{Atot} - CP_{Btot} ) $$

(176)

Upon performing the calculations ad-bf, af-ec, and ad-bc become equal to the numerators and denominators of the ratios in Eqs. 63 and 64. The conditions in Eq. 29 imply that the left hand sides of the equilibrium equations are positive, and consequently E > 0 and F > 0. This guaranties that:

$$ ad - bc = EF + FC_{A} + EC_{B} > 0 $$

(177)

and the condition Eq. 170 is satisfied.