Inertial-Type Algorithm for Solving Split Common Fixed Point Problems in Banach Spaces

Abstract

In this paper, motivated by the works of Kohsaka and Takahashi (SIAM J Optim 19:824–835, 2008) and Aoyama et al. (J Nonlinear Convex Anal 10:131–147, 2009) on the class of mappings of firmly nonexpansive type, we explore some properties of firmly nonexpansive-like mappings [or mappings of type (P)] in p-uniformly convex and uniformly smooth Banach spaces. We then study the split common fixed point problems for mappings of type (P) and Bregman weak relatively nonexpansive mappings in p-uniformly convex and uniformly smooth Banach spaces. We propose an inertial-type shrinking projection algorithm for solving the two-set split common fixed point problems and prove a strong convergence theorem. Also, we apply our result to the split monotone inclusion problems and illustrate the behaviour of our algorithm with several numerical examples s. The implementation of the algorithm does not require a prior knowledge of the operator norm. Our results complement many recent results in the literature in this direction. To the best of our knowledge, it seems to be the first to use the inertial technique to solve the split common fixed point problems outside Hilbert spaces.

1 Introduction

Let X be a nonempty set and $T:X\rightarrow X$ be a mapping. A point $x\in X$ is called a fixed point of T if $Tx = x$. We shall denote the set of fixed points of T by F(T). The identity mapping on X is denoted by I.

Let $E_1$ and $E_2$ be real Banach spaces and $A:E_1\rightarrow E_2$ be a bounded linear operator with the adjoint operator $A^*$. Let C and Q be nonempty closed convex subsets of $E_1$ and $E_2$, respectively. The Split Feasibility Problem (in short, SFP) can be formulated as:

$$\begin{aligned} \text {find}~ x\in C ~\text {such that}~ Ax\in Q. \end{aligned}$$

(1.1)

The SFP was first introduced by Censor and Elfving [13] in the framework of Hilbert spaces for modeling inverse problems which arise from phase retrievals and medical image reconstruction. The SFP has applications in signal processing, radiation therapy, data denoising and data compression (see [4, 10, 12, 14, 19, 22, 50] for details).

A generalization of the SFP (1.1) is the Split Common Fixed Point Problem (in short, SCFPP). Let $T_i : E_1 \rightarrow E_1$, $i = 1, 2, ..., n$ and $U_j : E_2 \rightarrow E_2$, $j = 1, 2, ..., m$ be nonlinear mappings such that $F(T_i)$ and $F(U_j)$ are nonempty. The SCFPP is formulated as:

$$\begin{aligned} \text {find} \quad x\in \cap _{i=1}^m F(T_i) \quad \text {such that}\quad Ax\in \cap _{j=1}^n F(U_j). \end{aligned}$$

(1.2)

In particular, for $m =n =1$, then SCFPP (1.2) becomes the two-set SCFPP, which is formulated as:

$$\begin{aligned} \text {find}~ x\in F(T) ~\text {such that}~ Ax\in F(U). \end{aligned}$$

(1.3)

The two-set SCFPP (1.3) was first studied by Censor and Segal [15] in the framework of Hilbert spaces for the case where T and U are nonexpansive mappings. They proposed the following algorithm:

$$\begin{aligned} \left\{ \begin{array} {l l} x_0\in C,\\ x_{n+1} = T[x_n-\gamma A^*(I - U)Ax_n], \end{array} \right. \end{aligned}$$

where $\gamma \in (0, \frac{2}{\lambda })$ with $\lambda$ being the spectral radius of the operator $A^*A$, and under some suitable conditions proved a weak convergence theorem. In 2011, Moudafi [32] also studied the SCFPP for quasi-nonexpansive mappings in infinite-dimensional Hilbert spaces. By modifying the Mann’s iteration, Moudafi [32] proposed the following algorithm (1.4) for solving the two-set SCFPP and obtained a weak convergence theorem:

$$\begin{aligned} \left\{ \begin{array} {l l} x_0\in C,\\ y_n = x_n - \gamma \beta A^*(I - U)Ax_n,\\ x_{n+1} = (1-\alpha _n)y_n+\alpha _nTy_n, \end{array} \right. \end{aligned}$$

(1.4)

where $I - T$ and $I-U$ are demiclosed at zero, $\gamma \in (0, \frac{1}{\lambda \beta })$ for $\beta \in (0, 1)$ and $\lambda$ being the spectral radius of the operator $A^*A$.

Recently, some authors have studied the SCFPP (1.3) for a pair of mappings of different classes in Banach spaces. In 2015, Tang. et al. [53] studied the SCFPP (1.3) for an asymptotic nonexpansive mapping and a $\tau$-quasi-strict pseudocontractive mapping in the setting of two Banach spaces. They proved weak and strong convergence theorems.

Let E be a smooth, strictly convex and reflexive Banach space. Let H be a Hilbert space and C be a nonempty closed convex subset of H. Let B be a maximal monotone operator of H into $2^H$ such that $dom(B)\subset C$. Let $A: H\rightarrow E$ be a bounded linear operator such that $A\ne 0$, $\{T_i\}_{i=1}^{\infty }: C\rightarrow H$ be an infinite family of $k_i$-demimetric and demiclosed mappings and U be a firmly nonexpansive-like mapping on E. In 2018, Y. Song [43] studied the generalized split feasibility problem of the form:

$$\begin{aligned} \text {find}~x\in \cap _{i=1}^{\infty }F(T_i)\cap B^{-1}(0)\cap A^{-1}F(U). \end{aligned}$$

(1.5)

It is noted that if $B=0$, then (1.5) becomes the SCFPP (1.3). They proposed an Halpern type iterative algorithm for solving the problem (1.5) and proved a strong convergence theorem.

Also very recently, Takahashi [52] studied the SCFPP for generalized demimetric mappings in two Banach spaces. They used the hybrid method and shrinking projection method to find a solution to the problem and proved strong convergence theorems.

We note that the algorithms proposed for the SCFPP in [43, 52, 53] require a prior estimate of the norm of the bounded linear operator. This in practice is not always easy to compute. For more on SCFPP and related optimization problem, see [23,24,25, 27, 35, 41, 47, 48, 51, 54] and the references therein.

In fixed point theory, it is more desirable to work with an algorithm that has a high rate of convergence. A way of achieving this is by incorporating inertial term in the algorithm. This idea was proposed originally by Polyak [37]. It can be seen as a discrete version of a second-order time dynamical system used to speed up convergence rate of the smooth convex minimization problem. The main idea of these methods is to make use of two previous iterates to update the next iterate, which results in speeding up the algorithm’s convergence. Recently, authors have shown considerable interest in studying inertial type algorithms, see for example [26, 28, 42, 54] and the references therein.

Motivated by the above works, in this paper we study the two-set SCFPP for mappings of type (P) and Bregman weak relatively nonexpansive mappings in p- uniformly convex and uniformly smooth Banach spaces. We propose an inertial-type shrinking projection algorithm with the step size independent on the prior estimate of the norm of the bounded linear operator and prove strong convergence theorem. Our result seems to be the first to consider an inertial-type algorithm for SCFPP in Banach spaces.

This paper is organized as follows. In Sect. 2, we give some useful definitions, notations and lemmas, which are needed for the analysis of our algorithm. In Sect. 3, the algorithm and its strong convergence theorem are presented. In Sect. 4, we apply our main result to the split monotone inclusion problem. In Sect. 5, we give numerical examples to illustrate the behaviour of our algorithm. We conclude in Sect. 6.

2 Preliminaries

In this section, we give some definitions and results which will be needed in proving our main result in the next section.

Let E be a real Banach space with the norm $\Vert \cdot \Vert$, C be a nonempty closed convex subset of E and $E^*$ be the dual with the norm $\Vert \cdot \Vert _*$. We shall denote the value of the functional $x^*\in E^*$ at $x\in E$ by $\langle x^*, x\rangle$. For a sequence $\{x_n\}$ of E and $x\in E$, we denote the strong convergence of $\{x_n\}$ and weak convergence of $\{x_n\}$ to x by $x_n\rightarrow x$ and $x_n\rightharpoonup x$, respectively. The normalized duality mapping $J: E\rightarrow 2^{E^*}$ is defined by

$$\begin{aligned} Jx = \{x^*\in E^*: \langle x^*, x\rangle = \Vert x\Vert ^2 = \Vert x^*\Vert _*^2\}{,} \end{aligned}$$

(2.1)

for all $x\in E$. Let $U:=\{x\in E: \Vert x\Vert =1\}$. E is said to be smooth if the limit

$$\begin{aligned} \lim _{t\rightarrow 0}\frac{\Vert x+ty\Vert -\Vert x\Vert }{t} \end{aligned}$$

(2.2)

exists for all $x, y \in U$. E is said to be strictly convex if $\Vert x+y\Vert <2$ whenever $x, y\in E$ and $x\ne y$. Let $1<q\le 2\le p <\infty$ with $\frac{1}{p}+\frac{1}{q} = 1$. The modulus of convexity of E is the function $\delta _E: (0, 2]\rightarrow [0, 1]$ defined by

$$\begin{aligned} \delta _{E}(\epsilon ):= \inf \bigg \{1-\left\| \frac{x+y}{2}\right\| : \Vert x\Vert = \Vert y\Vert =1, \Vert x-y\Vert \ge \epsilon \bigg \}. \end{aligned}$$

E is said to be uniformly convex if $\delta _{E}(\epsilon )>0$ and p-uniformly convex if there exists a constant $C_p > 0$ such that $\delta _{E}(\epsilon )\ge C_p\epsilon ^p$, for any $\epsilon \in (0, 2]$. The $L_p$ space is 2-uniformly convex for $1<p\le 2$ and p-uniformly convex for $p\ge 2$. It is known that every uniformly convex Banach space is strictly convex and reflexive.

The modulus of smoothness of E is the function $\rho _{E}: [0, \infty )\rightarrow [0, \infty )$ defined by

$$\begin{aligned} \rho _{E}(\tau ):=\sup \bigg \{\frac{\Vert x+\tau y\Vert +\Vert x-\tau y\Vert }{2} - 1: \Vert x\Vert =\Vert y\Vert =1\bigg \}. \end{aligned}$$

E is called uniformly smooth if $\lim _{\tau \rightarrow 0^+}\frac{\rho _{E}(\tau )}{\tau }=0$ and q-uniformly smooth if there exists $C_q>0$ such that $\rho _{E}(\tau )\le C_q\tau ^q$. Every uniformly smooth Banach space is smooth and reflexive. The generalized duality mapping $J^E_p: E \rightarrow 2^{E^*}$ is defined by

$$\begin{aligned} J^{E}_p(x) = \{u^*\in E^*: \langle u^*, x\rangle = \Vert x\Vert ^p,~\Vert u^*\Vert _* = \Vert x\Vert ^{p-1}\}. \end{aligned}$$

(2.3)

If $p=2$, (2.3) becomes the normalized duality mapping (2.1). It is known that $J^E_p(x) = \Vert x\Vert ^{p-2}J(x)$ for all $x\in X$, $x\ne 0$. It is also known that E is uniformly smooth if and only if $J^E_p$ is norm-to-norm uniformly continuous on bounded subsets of E and E is smooth if and only if $J^E_p$ is single valued. Moreover, E is p-uniformly convex (smooth) if and only if $E^*$ is q-uniformly smooth (convex). If E is p-uniformly convex and uniformly smooth, then the duality mapping $J^E_p$ is norm-to-norm uniformly continuous on bounded subsets of E (see [17, 30, 56]). Examples of generalized duality mapping are given below:

Example 2.1

[1] Let $E:=\ell _p(\mathbb {R})$ and $x = (x_1, x_2, x_3,\ldots )\in \ell _p$ $(1<p<\infty )$. Then the generalized duality mapping $J^E_p$ is given by

$$\begin{aligned} J_p^E(x) = (|x_1|^{p-1}sgn(x_1), |x_2|^{p-1}sgn(x_2), \ldots ). \end{aligned}$$

Example 2.2

[1] Let $E:=L_p([\alpha , \beta ])$ $(1<p<\infty )$, where $\alpha , \beta \in \mathbb {R}$ and let $f\in E$. Then the generalized duality mapping $J^E_p$ is given by

$$\begin{aligned} J^E_p(f)(t) = |f(t)|^{p-1}sgn(f(t)). \end{aligned}$$

Xu and Roach [56] proved the following inequality for q-uniformly smooth Banach spaces.

Lemma 2.3

Let $x, y\in E$. If E is a q-uniformly smooth Banach space, then there exists a $C_q>0$ such that

$$\begin{aligned} \Vert x-y\Vert ^q\le \Vert x\Vert ^q - q\langle J^{E^*}_q(x), y \rangle +C_q\Vert y\Vert ^q. \end{aligned}$$

Definition 2.4

A function $f:E\rightarrow \mathbb {R}\cup \{+\infty \}$ is said to be

• (1) proper if its effective domain $D(f) = \{x\in E:f(x)<+\infty \}$ is nonempty,

• (2) convex if $f(\lambda x+(1-\lambda )y)\le \lambda f(x)+(1-\lambda )f(y)$ for every $\lambda \in (0, 1)$, $x, y \in D(f),$

• (3) lower semicontinuous at $x_0\in D(f)$ if $f(x_0)\le \lim \inf _{x\rightarrow x_0} f(x)$.

Let $x\in \text {int dom} f$. For any $y\in E$, the right-hand derivative of f at x denoted by $f^0(x,y)$ is defined by

$$\begin{aligned} f^0(x,y):=\lim _{t\rightarrow 0^+}\frac{f(x+ty)-f(x)}{t} . \end{aligned}$$

(2.4)

If the limit as $t\rightarrow 0$ in (2.4) exists for any y, then the function f is said to be Gâteaux differentiable at x (see, for instance [36], Definition 1.3, p. 3). In this case the gradient of f at x is the function $\nabla f(x)$ which is defined by $\langle \nabla f(x), y\rangle = f^0(x, y)$ for any $y\in E$. The function f is said to be Gâteaux differentiable if it is Gâteaux differentiable for any $x\in \text {int dom}f$(see also, [9]).

Let $f:E\rightarrow \mathbb {R}\cup \{+\infty \}$ be a proper, convex and lower semicontinuous function and $x\in \text {int dom} f$. The subdifferential of fat x is the convex set defined by

$$\begin{aligned} \partial f(x) = \{x^*\in E^*: f(y)\ge \langle x^*, y -x\rangle + f(x) \quad \forall \quad y\in E\}. \end{aligned}$$

If $\partial f(x)\ne \emptyset$, then f is said to be subdifferentiable at x.

Given a Gâteaux differentiable function f, the bifunction $\Delta _f: E \times E\rightarrow [0, +\infty )$ given as

$$\begin{aligned} \Delta _f(x, y): = f(x)-f(y)-\langle \nabla f(y), x - y\rangle , ~\forall ~ x, y\in E \end{aligned}$$

(2.5)

is called the Bregman distance with respect to f, (see [49]). In particular, let $f(x)=\frac{1}{p}\Vert x\Vert ^p$. In this case the duality mapping $J^E_p$ is the derivative of f. The Bregman distance $\Delta _p: E \times E\rightarrow [0, +\infty )$ is defined by

$$\begin{aligned} \Delta _p(x, y)&: =&\frac{\Vert x\Vert ^p}{p}- \frac{\Vert y\Vert ^p}{p}-\langle J_p^E(y), x-y\rangle \nonumber \\= & {} \frac{\Vert x\Vert ^p}{p} + \frac{\Vert y\Vert ^p}{q}-\langle J_p^E(y), x\rangle . \end{aligned}$$

(2.6)

Note that $\Delta _p(x, y)\ge 0$ and $\Delta _p(x, y) = 0$ if and only if $x = y$ (see e.g. [7]). In general, the Bregman distance is not symmetric and is not a metric. However, it possesses some distance-like properties. From (2.6) one can show that the following equality called three-point identity is satisfied:

$$\begin{aligned} \Delta _p(x, y)+\Delta _p(y, z)-\Delta _p(x, z) = \langle J^E_p(z) - J^E_p(y), x - y\rangle ~ \forall ~ x, y, z\in E. \end{aligned}$$

(2.7)

In particular,

$$\begin{aligned} \Delta _p(x, y)+\Delta _p(y, x) = \langle J^E_p(x) - J^E_p(y), x - y\rangle ~ \forall ~ x, y\in E. \end{aligned}$$

For p-uniformly convex space, the metric and Bregman distance satisfy the following relation [40]:

$$\begin{aligned} \tau \Vert x - y\Vert ^p\le \Delta _p(x, y)\le \langle J^{E}_p(x) - J^{E}_p(y), x -y\rangle , \end{aligned}$$

(2.8)

where $\tau > 0$ is some fixed number. If $f(x) = \Vert x\Vert ^2$, the Bregman distance is the Lyapunov functional $\phi : E \times E \rightarrow [0, +\infty )$ defined by

$$\begin{aligned} \phi (x, y) := \Vert x\Vert ^2 - 2\langle Jy, x\rangle + \Vert y\Vert ^2. \end{aligned}$$

(2.9)

The metric projection

$$\begin{aligned} P_Cx := \arg \min _{y\in C}\Vert x-y\Vert , ~x\in E, \end{aligned}$$

is the unique minimizer of the norm distance (see [20]). It can be characterized by the following variational inequality:

$$\begin{aligned} \langle J^E_p(x-P_Cx), z - P_Cx\rangle \le 0, \forall z\in C. \end{aligned}$$

Moreover, the metric projection is nonexpansive, i.e. $\Vert P_Cx - P_Cy\Vert \le \Vert x-y\Vert , \forall x,y\in C$. Similar to the metric projection, the Bregman projection defined by

$$\begin{aligned} \Pi _C(x) := argmin_{y\in C}\Delta _p(y, x), ~ x\in E, \end{aligned}$$

(2.10)

is the unique minimizer of the Bregman distance (see [39]). It can also be characterized by the variational inequality:

$$\begin{aligned} \langle J^E_p(x) - J^E_p(\Pi _Cx), z - \Pi _Cx\rangle \le 0, \quad \forall z\in C, \end{aligned}$$

from which one can derive that

$$\begin{aligned} \Delta _p(y, \Pi _Cx)+\Delta _p(\Pi _Cx, x)\le \Delta _p(y, x), \quad \forall y\in C. \end{aligned}$$

(2.11)

If E is a real Hilbert space, then $\Pi _C = P_C$, see [2, 21] for details. Associated with the Bregman distance is the functional $V_p: E\times E^*\rightarrow [0, +\infty )$ defined by

$$\begin{aligned} V_p(x, \bar{x}) := \frac{1}{p}\Vert x\Vert ^p - \langle \bar{x}, x \rangle +\frac{1}{q}\Vert \bar{x}\Vert ^q, \quad x\in E, \bar{x}\in E^*. \end{aligned}$$

Clearly, $V_p(x, \bar{x})\ge 0$ and the following properties are satisfied:

$$\begin{aligned} V_{p}(x, \bar{x}) = \Delta _p(x, J^{E^*}_q(\bar{x})), ~ \forall x\in E, \bar{x}\in E^*, \end{aligned}$$

(2.12)

and

$$\begin{aligned} V_{p}(x, \bar{x})+\langle \bar{y}, J^{E^*}_q(\bar{x})-x\rangle \le V_p(x, \bar{x}+\bar{y}),~ \forall x\in E, \bar{x}, \bar{y}\in E^*. \end{aligned}$$

(2.13)

Also, $V_p$ is convex in the second variable. Thus for all $z\in E$,

$$\begin{aligned} \Delta _p\left( z, J^{E^*}_q\left( \sum ^{N}_{i=1}t_iJ^{E}_px_i\right) \right) \le \sum ^{N}_{i}t_i\Delta _p(z, x_i), \end{aligned}$$

where $\{x_i\}\subset E$ and $\{t_i\}\subset (0, 1)$ with $\sum _{i=1}^{N}t_i = 1$.

A point $x^*\in C$ is called an asymptotic fixed point of T if C contains a sequence $\{x_n\}$ which converges weakly to $x^*$ such that $\lim _{n\rightarrow \infty }\Vert x_n - Tx_n\Vert =0$. We denote the set of asymptotic fixed points of T by $\hat{F}(T)$. A point $x^*\in C$ is called a strong asymptotic fixed point of T if C contains a sequence $\{x_n\}$ which converges strongly to $x^*$ such that $\lim _{n\rightarrow \infty }\Vert x_n - Tx_n\Vert =0$. We denote the set of strong asymptotic fixed points of T by $\tilde{F}(T)$. It follows from the definitions that $F(T)\subset \tilde{F}(T)\subset \hat{F}(T)$.

Definition 2.5

A mapping T from C to C is said to be

• (1) Bregman quasi-nonexpansive if $F(T)\ne \emptyset$ and

  $$\begin{aligned} \Delta _p(x^*, Ty)\le \Delta _p(x^*, y),~ \forall y \in C, x^*\in F(T), \end{aligned}$$

• (2) Bregman weak relatively nonexpansive if $\tilde{F}(T)\ne \emptyset$, $\tilde{F}(T)=F(T)$ and

  $$\begin{aligned} \Delta _p(x^*, Ty)\le \Delta _p(x^*, y),~ \forall y\in C, x^*\in F(T), \end{aligned}$$

• (3) Bregman relatively nonexpansive if $F(T)\ne \emptyset$, $\hat{F}(T)=F(T)$ and

  $$\begin{aligned} \Delta _p(x^*,Ty)\le \Delta _p(x^*, y),~ \forall y\in C, x^*\in F(T). \end{aligned}$$

It is known that for a Bregman quasi-nonexpansive mapping $T: C\rightarrow C$, the fixed point set F(T) is closed and convex (see [38]). From the definitions, it is clearly seen that the class of Bregman quasi-nonexpansive contains the class of Bregman weak relatively nonexpansive and the class of Bregman weak relatively nonexpansive contains the class of Bregman relatively nonexpansive. The next examples illustrate these inclusions.

Example 2.6

(See [16]) Let $E= \ell _2(\mathbb {R})$, where $\ell _2(\mathbb {R}) := \{\sigma = (\sigma _1, \sigma _2, \ldots , \sigma _n, \ldots ), \sigma _i\in \mathbb {R}: \sum _{i=1}^{\infty }|\sigma _i|^2<\infty \}$, $\Vert \sigma \Vert = (\sum _{i=1}^{\infty }|\sigma _i|)^{\frac{1}{2}}$ $\forall$ $\sigma \in E$ and let $f(x) = \frac{1}{2}\Vert x\Vert ^2$ for all $x\in E$. Let $\{x_n\} \subset E$ be a sequence defined by $x_0 = (1, 0, 0, 0, \ldots ), x_1 = (1, 1, 0, 0, \ldots ), x_2 = (1, 0, 1, 0, \ldots ), \ldots , x_n = (\sigma _{n, 1}, \sigma _{n, 2}, \sigma _{n, 3} \ldots ), \ldots ,$ where

$$\begin{aligned} \sigma _{n, k}=\left\{ \begin{array} {l l} 1\quad \text {if}\quad k = 1, n+1,\\ 0\quad \text {if}\quad \text {otherwise},\quad \forall \quad n\ge 0, \end{array} \right. \end{aligned}$$

$n\in \mathbb {N}$. Define the mapping $T: E\rightarrow E$ by

$$\begin{aligned} Tx=\left\{ \begin{array} {l l} \frac{n}{n+1}x\quad \text {if}\quad x = x_n,\\ -x\quad \text {if}\quad x\ne x_n. \end{array} \right. \end{aligned}$$

It can be shown that T is a Bregman quasi-nonexpansive, precisely Bregman weak relatively nonexpansive mapping but not a Bregman relatively nonexpansive mapping (see also [34]).

The next example is a Bregman quasi-nonexpansive mapping which is neither Bregman weak relatively nonexpansive nor Bregman relatively nonexpansive.

Example 2.7

[34, 44] Let E be a smooth Banach space, let k be an even number in $\mathbb {N}$ and let $f: E\rightarrow \mathbb {R}$ be defined by $f(x) = \frac{1}{k}\Vert x\Vert ^k$, $x\in E$. Let $x_0\ne 0$ be an element of E. Define the mapping $T:E \rightarrow E$ by

$$\begin{aligned} Tx=\left\{ \begin{array} {l l} (\frac{1}{2}+\frac{1}{2^{n+1}})x_0 \quad \text {if}\quad x = (\frac{1}{2}+\frac{1}{2^{n}})x_0,\\ -x\quad \text {if}\quad x\ne (\frac{1}{2}+\frac{1}{2^{n}})x_0, \end{array} \right. \end{aligned}$$

for all $n\ge 0$. It can be verified that T is a Bregman quasi-nonexpansive mapping which is neither Bregman weak relatively nonexpansive nor Bregman relatively nonexpansive.

One of the most important class of nonlinear mappings in Hilbert space is the class of firmly nonexpansive mappings. It includes all metric projections onto a closed convex set and all resolvents of a monotone operator. Kohsaka and Takahashi [29] proposed the class of firmly nonexpansive type mappings, which contains the firmly nonexpansive mappings in Hilbert spaces and resolvents of maximal monotone operators in Banach spaces. It is classified into three types; namely, type (P), type (Q) and type (R). In this study, we consider the class of firmly nonexpansive-like mappings (or mappings of type (P)).

Definition 2.8

(See [6]) Let E be a smooth Banach space and C a nonempty subset of E. A mapping $U: C\rightarrow E$ is said to be a mapping of type (P) if

$$\begin{aligned} \langle J(x - Ux) - J(y - Uy) , Ux - Uy\rangle \ge 0{,} ~\forall ~ x, y \in C. \end{aligned}$$

(2.14)

From the definition, it is easy to see that if E is a Hilbert space, then U is firmly nonexpansive-like of type (P) if and only if it is firmly nonexpansive, i.e. $\Vert Ux - Uy\Vert ^2\le \langle Ux - Uy, x - y\rangle {,} ~ \forall ~ x, y\in C$. We recall the following result.

Lemma 2.9

(See [5]) Let E be a smooth Banach space, C a nonempty subset of E and $U: C\rightarrow E$ a firmly nonexpansive-like mapping (mapping of type (P)). Then the following hold.

• (1) If C is closed and convex, then so is F(U).

• (2) $\hat{F}(U) = F(U)$.

Henceforth, we refer to a firmly nonexpansive-like mapping as mapping of type (P). In this study, we consider E as p-uniformly convex and uniformly smooth. Consequently, we modify Definition 2.8 to accommodate the generalized duality mapping (2.3). Here and hereafter, E is a p-uniformly convex and uniformly smooth Banach space.

Definition 2.10

Let E be a p-uniformly convex and uniformly smooth Banach space and C a nonempty subset of E. A mapping $U: C\rightarrow E$ is said to be of type (P) if

$$\begin{aligned} \langle J^E_p(x - Ux) - J^E_p(y - Uy), Ux - Uy\rangle \ge 0{,}~\forall ~ x, y \in C. \end{aligned}$$

(2.15)

Example 2.11

Let E be a p-uniformly convex and uniformly smooth Banach space and C a nonempty closed convex subset of E. Then the metric projection $P_C$ is a mapping of type (P).

Example 2.12

Let $E:=L_p([\alpha , \beta ])$ $(2\le p <\infty )$, where $\alpha , \beta \in \mathbb {R}$ and let $f\in E$. The mapping $U: E\rightarrow E$ defined by $U(f(x)) = \frac{1}{2}f(x)$ is of type (P). To see this, let $f, g\in E$, we obtain from (2.8) that

$$\begin{aligned}&\langle J^{E}_p(f(x) - U(f(x))) - J^E_p(g(x) - U(g(x))), f(x) - g(x) \rangle \nonumber \\&\quad = \langle J^{E}_p(\frac{1}{2}f(x)) - J^E_p(\frac{1}{2}g(x)), f(x) - g(x) \rangle \nonumber \\&\quad \ge \frac{\tau }{2^{p-1}}\Vert f(x) - g(x)\Vert ^p \ge 0. \end{aligned}$$

(2.16)

The following lemmas will be needed in the next section.

Lemma 2.13

[34] Let E be a smooth and uniformly convex real Banach space. Let $\{x_n\}$ and $\{y_n\}$ be bounded sequences in E. Then $\lim _{n\rightarrow \infty }\Delta _p(x_n, y_n) = 0$ if and only if $\lim _{n\rightarrow \infty }\Vert x_n - y_n\Vert = 0$.

Lemma 2.14

[56] Let $q\ge 1$ and $r>0$ be two fixed real numbers. Then, a Banach space E is uniformly convex if and only if there exists a continuous, strictly increasing and convex function $g: \mathbb {R}^+\rightarrow \mathbb {R}^+$, $g(0)=0$ such that for all $x, y\in B_r$ and $0\le \lambda \le 1$,

$$\begin{aligned} \Vert \lambda x+(1-\lambda )y\Vert ^q\le \lambda \Vert x\Vert ^q+(1-\lambda )\Vert y\Vert ^q - W_q(\lambda )g(\Vert x-y\Vert ), \end{aligned}$$

where $W_q(\lambda ):=\lambda ^q(1-\lambda )+\lambda (1-\lambda )^q$ and $B_r:=\{x\in E:\Vert x\Vert \le r\}.$

3 Main Results

In this section, we present our inertial-type algorithm and prove the strong convergence of the sequence generated to a solution of the SCFPP for mapping of type (P) and Bregman weak relatively nonexpansive mapping in p-uniformly convex and uniformly smooth Banach spaces. We assume $1<q\le 2\le p <\infty$ with $\frac{1}{p}+\frac{1}{q} = 1$.

Let $E_1, E_2$ be p-uniformly convex and uniformly smooth Banach spaces with duals $E_1^*, E_2^*$, respectively. Let $C=C_1$ be nonempty closed and convex subset of $E_1$. Let $T: E_1\rightarrow E_1$ be a Bregman weak relatively nonexpansive mapping and $U: E_2 \rightarrow E_2$ be a mapping of type (P). Let $A: E_1\rightarrow E_2$ be a bounded linear operator. We consider the following SCFPP:

$$\begin{aligned} \text {find}~x\in F(T)~\text {such that}~Ax\in F(U). \end{aligned}$$

(3.1)

We shall denote the solution set of the SCFPP (3.1) by $\Gamma$ and assume that $\Gamma \ne \emptyset$. We first prove the following lemma.

Lemma 3.1

Let E be a p-uniformly convex and uniformly smooth Banach space, C a nonempty closed convex subset of E, and $U: C\rightarrow E$ a mapping of type (P). Then the following hold:

• (1) $y\in F(U)$ if and only if $\langle J^E_p(x - Ux), Ux - y \rangle \ge 0$, for every $x\in C$;

• (2) F(U) is closed and convex;

• (3) $\tilde{F}(U) = F(U)$.

Proof

(1)  Let $y\in F(U)$. Then it follows from (2.15) that $\langle J^E_p(x - Ux), Ux - y\rangle \ge 0$, for every $x\in C$. Conversely, suppose $\langle J^E_p(x - Ux), Ux - y\rangle \ge 0$, for every $x\in C$. Then in particular

$$\langle J^E_p(y - Uy), Uy - y\rangle \ge 0.$$

The last inequality implies that $\Vert y - Uy\Vert ^p\le 0$. Hence $y = Uy$.

(2)  Let $\{x_n\}\subset F(U)$ be a sequence such that $x_n\rightarrow x$ as $n\rightarrow \infty$. Then

$$\begin{aligned} \langle J^E_p(x - Ux), Ux - x_n \rangle \rightarrow \langle J^E_p(x - Ux), Ux - x \rangle \ge 0 ~ \text {as}~ n\rightarrow \infty . \end{aligned}$$

Therefore, $\Vert x - Ux\Vert ^p\le 0$. Hence $x\in F(U)$. Which shows that F(U) is closed.

Let $x^*, y^*\in F(U)$. Then for all $\lambda \in (0, 1)$, $\lambda x^* + (1-\lambda ) y^*\in C$. Let $w = \lambda x^* + (1-\lambda ) y^*$. We want to show that $w\in F(U)$. Since $x^*, y^*\in F(U)$, we have that

$$\begin{aligned} \lambda \langle J^E_p(x - Ux), Ux - x^*\rangle \ge 0 \end{aligned}$$

(3.2)

and

$$\begin{aligned} (1-\lambda )\langle J^E_p(x - Ux), Ux - y^*\rangle \ge 0. \end{aligned}$$

(3.3)

From (3.2) and (3.3), we get that $\langle J^E_p(x - Ux), Ux - w \rangle \ge 0$. Hence $w\in F(U)$ and so F(U) is convex.

(3)  It is clear that $F(U)\subset \hat{F}(U)$. Let $x\in \hat{F}(U)$. Then there exists a sequence $\{x_n\}\subset C$ which converges weakly to x such that $\Vert Ux_n - x_n\Vert \rightarrow 0$ as $n\rightarrow \infty$. Since U is a mapping of type (P), from (2.15) we obtain

$$\begin{aligned} \langle J^E_p(x - Ux) - J^E_p(x_n - Ux_n), Ux - Ux_n \rangle \ge 0. \end{aligned}$$

Taking limit as $n\rightarrow \infty$ in the last inequality gives

$$\begin{aligned} \langle J^E_p(x - Ux), Ux - x\rangle \ge 0, \end{aligned}$$

which implies that $\Vert x - Ux\Vert ^p\le 0$. Hence $x\in F(U)$. We then obtain that $F(U) = \hat{F}(U)$. Since $F(U)\subset \tilde{F}(U)\subset \hat{F}(U)$, we conclude that $F(U) = \tilde{F}(U) = \hat{F}(U)$.

In what follows, we present our inertial-type algorithm.

Algorithm 3.2

Let $E_1, E_2$ be p-uniformly convex and uniformly smooth Banach spaces with duals $E_1^*, E_2^*$, respectively. Let $C=C_1$ be nonempty closed and convex subset of $E_1$. Let $T: E_1\rightarrow E_1$ be a Bregman weak relatively nonexpansive mapping and $U: E_2 \rightarrow E_2$ be a mapping of type (P). Let $A: E_1\rightarrow E_2$ be a bounded linear operator with its adjoint $A^*: E_2^* \rightarrow E_1^*$. Select $x_0, x_1\in E_1$, let $\{\theta _n\}$ be a real sequence such that $-\theta \le \theta _n\le \theta$ for some $\theta >0$ and $\{\alpha _n\}\subset (0, 1)$ be a real sequence satisfying $\liminf _{n\rightarrow \infty } \alpha _n>0$. Assuming that the $(n-1)$th and nth-iterates have been constructed, then we calculate the $(n+1)$th-iterate $x_{n+1} \in E_1$ via the formula

$$\begin{aligned} \left\{ \begin{array} {l l} w_n = P_CJ^{E^*_1}_q[J^{E_1}_px_n+\theta _n(J^{E_1}_px_n - J^{E_1}_px_{n-1})],\\ v_n = J^{E^*_1}_q[J^{E_1}_pw_n - \mu _nA^*J^{E_2}_p(I - U)Aw_n],\\ y_n = J^{E^*_1}_q[\alpha _nJ^{E_1}_pv_n+(1-\alpha _n)J^{E_1}_pT(v_n)],\\ C_{n+1} = \{z\in C_n: \Delta _p(z, y_n)\le \Delta _p(z, w_n)\},\\ x_{n+1} = \Pi _{C_{n+1}}x_0, \forall n\ge 1. \end{array} \right. \end{aligned}$$

(3.4)

Assume for small $\epsilon > 0$, the step size $\mu _n$ is chosen such that

$$\begin{aligned} \mu _n^{q-1}\in \bigg (0, \frac{q\Vert Aw_n - UAw_n\Vert ^p}{C_q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q}\bigg ),\quad n\in \Omega , \end{aligned}$$

(3.5)

where the index set $\Omega :=\{n\in \mathbb {N}: Aw_n - UAw_n\ne 0\}$, otherwise $\mu _n = \mu$, where $\mu$ is any non-negative real number.

We first prove the following lemmas which will be used to prove the convergence of Algorithm 3.2.

Lemma 3.3

The sequence $\{\mu _n\}$ defined by (3.5) is well-defined.

Proof

Let $x^*\in \Gamma$, then $x^* = Tx^*$ and $Ax^* = UAx^*$. Thus,

$$\begin{aligned}&\Vert Aw_n - UAw_n\Vert ^p \\&\quad = \langle J^{E_2}_p(I- U)Aw_n, Aw_n - UAw_n\rangle \\&\quad = \langle J^{E_2}_p(I- U)Aw_n, Aw_n - Ax^*+UAx^* - UAw_n \rangle \\&\quad = \langle J^{E_2}_p(I- U)Aw_n, Aw_n - Ax^*\rangle + \langle J^{E_2}_p(I- U)Aw_n, UAx^* - UAw_n\rangle \\&\quad = \langle A^*J^{E_2}_p(I- U)Aw_n, w_n - x^* \rangle + \langle J^{E_2}_p(I- U)Aw_n, UAx^* - UAw_n \rangle \\&\quad \le \Vert w_n - x^*\Vert \Vert A^*J^{E_2}_p(I- U)Aw_n\Vert _*+ \Vert UAx^* - UAw_n\Vert \Vert J^{E_2}_p(I- U)Aw_n\Vert _*\\&\quad = \Vert w_n - x^*\Vert \Vert A^*J^{E_2}_p(I- U)Aw_n\Vert _*+ \Vert UAx^* - UAw_n\Vert \Vert (I- U)Aw_n\Vert ^{p-1}. \end{aligned}$$

Consequently, for $n\in \Omega$, that is $\Vert (I - U)Aw_n\Vert > 0$, we obtain that $\Vert w_n - x^*\Vert \Vert A^*J^{E_2}_p(I- U)Aw_n\Vert _* >0$ and $\Vert UAx^* - UAw_n\Vert \Vert (I- U)Aw_n\Vert ^{p-1}>0$. Since $\Vert UAx^* - UAw_n\Vert \Vert (I- U)Aw_n\Vert ^{p-1}>0$, we have that $\Vert A^*J^{E_2}_p(I- U)Aw_n\Vert _* \ne 0$. This implies that $\mu _n$ is well-defined.

Lemma 3.4

For every $n\ge 1$, $\Gamma \subset C_n$ and $x_{n+1}$ defined by Algorithm 3.2 is well-defined.

Proof

By our construction, $C_1 = C$ is closed and convex. Suppose $C_k$ is closed and convex for some $k\in \mathbb {N}$. Then

$$\begin{aligned} C_{k+1}= & {} \{z\in C_k: \Delta _p(z, y_k)\le \Delta _p(z, w_k)\}\\= & {} \left\{ z\in C_k: \frac{\Vert z\Vert ^p}{p}+\frac{\Vert y_k\Vert ^p}{q} - \langle J^{E_1}_py_k, z \rangle \le \frac{\Vert z\Vert ^p}{p}+\frac{\Vert w_k\Vert ^p}{q} - \langle J^{E_1}_pw_k, z \rangle \right\} \\= & {} \{z\in C_k: \Vert y_k\Vert ^p - \Vert w_k\Vert ^p\le q \langle J^{E_1}_py_k - J^{E_1}_pw_k, z\rangle \}, \end{aligned}$$

from which it follows that $C_{k+1}$ is closed. Let $z_1, z_2 \in C_{k+1}$ and $\lambda _1, \lambda _2\in (0, 1)$ such that $\lambda _1 + \lambda _2 = 1$, then we have that

$$\begin{aligned} \Vert y_k\Vert ^p - \Vert w_k\Vert ^p\le q\langle J^{E_1}_py_k - J^{E_1}_pw_k, z_1\rangle \end{aligned}$$

(3.6)

and

$$\begin{aligned} \Vert y_k\Vert ^p - \Vert w_k\Vert ^p\le q\langle J^{E_1}_py_k - J^{E_1}_pw_k, z_2\rangle . \end{aligned}$$

(3.7)

From (3.6) and (3.7) we then have that

$$\begin{aligned} \Vert y_k\Vert ^p - \Vert w_k\Vert ^p\le q\langle J^{E_1}_py_k - J^{E_1}_pw_k, \lambda _1z_1 + \lambda _2z_2\rangle . \end{aligned}$$

(3.8)

By convexity, $\lambda _1z_1 + \lambda _2z_2\in C_k$. Therefore from (3.8), we conclude that $\lambda _1z_1 + \lambda _2z_2\in C_{k+1}$ and hence $C_{k+1}$ is convex. Thus, we have that $C_n$ is convex for all $n\in \mathbb {N}$.

Furthermore, since $\Gamma \ne \emptyset$ by assumption, it implies that $C_{n+1}\ne \emptyset$. To show that $\Gamma \subset C_{n}$, $\forall n\ge 1$. Let $x^*\in \Gamma$. Then $x^*\in F(T)$ and $Ax^*\in F(U)$, and therefore by construction i.e. (3.4), $\Gamma \subset C_1$. Suppose $x^*\in \Gamma \subset C_n$, then

$$\begin{aligned} \Delta _p(x^*, y_n)= & {} \Delta _p(x^*, (1-\alpha _n) J^{E_1}_pv_n + \alpha _nJ^{E_1}_pT(v_n))\nonumber \\\le & {} (1-\alpha _n)\Delta _p(x^*, v_n) + \alpha _n\Delta _p(x^*, T(v_n))\nonumber \\\le & {} \Delta _p(x^*, v_n). \end{aligned}$$

(3.9)

Also using (2.10), Lemma 2.3 and definition of Bregman distance, we get

$$\begin{aligned} \Delta _p(x^*, v_n)= & {} \Delta _p(x^*, J^{E^*_1}_q(J^{E_1}_pw_n - \mu _nA^*J^{E_2}_p(I-U)Aw_n))\nonumber \\= & {} \frac{\Vert x^*\Vert ^p}{p} - \langle J_p^{E_1}w_n - \mu _nA^{*}J_p^{E_2}(I - U)AW_n, x^* \rangle \nonumber \\&+ \frac{\Vert J_p^{E_1}w_n - \mu _n A^{*}J_p^{E_2}(I- U)Aw_n\Vert _*^q}{q} \nonumber \\\le & {} \frac{\Vert x^*\Vert ^p}{p} - \langle J_p^{E_1}w_n - \mu _nA^{*}J_p^{E_2}(I - U)AW_n, x^* \rangle + \frac{\Vert J^{E_1}_pw_n\Vert _*^q}{q} \nonumber \\&- \mu _n\langle J^{E_2}_p(I-U)Aw_n, Aw_n\rangle + \frac{C_q}{q}\mu _n^q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q\nonumber \\= & {} \frac{\Vert x^*\Vert ^p}{p} - \langle J_p^{E_1}w_n, x^*\rangle + \frac{\Vert J^{E_1}_pw_n\Vert _*^q}{q} - \mu _n\langle J^{E_2}_p(I-U)Aw_n, Aw_n - Ax^* \rangle \nonumber \\&+ \frac{C_q}{q}\mu _n^q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert ^q_*\nonumber \\= & {} V_p(x^*, J^{E_1}_pw_n) - \mu _n\langle J^{E_2}_p(I-U)Aw_n, Aw_n - Ax^*\rangle \nonumber \\&+\frac{C_q}{q}\mu _n^q\Vert A^*J^{E_2}_p(I-U)Ax_n\Vert _*^q\nonumber \\= & {} \Delta _p(x^*, w_n) - \mu _n\langle J^{E_2}_p(I-U)Aw_n, Aw_n\nonumber \\&-Ax^* \rangle + \frac{C_q}{q}\mu _n^q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q. \end{aligned}$$

(3.10)

We know from Lemma 3.1 that $\langle J^{E_2}_p(I-U)Aw_n, UAw_n - Ax^* \rangle \ge 0$. Therefore,

$$\begin{aligned} \langle J^{E_2}_p(I-U)Aw_n, Aw_n - Ax^*\rangle= & {} \langle J^{E_2}_p(I-U)Aw_n, Aw_n - UAw_n+UAw_n - Ax^*\rangle \nonumber \\= & {} \Vert Aw_n - UAw_n\Vert ^p + \langle J^{E_2}_p(I-U)Aw_n, UAw_n - Ax^*\rangle \nonumber \\\ge & {} \Vert Aw_n - UAw_n\Vert ^p. \end{aligned}$$

(3.11)

Substituting (3.11) in (3.10) will yield

$$\begin{aligned} \Delta _p(x^*, v_n)\le & {} \Delta _p(x^*, w_n) - \mu _n\Vert Aw_n - UAw_n\Vert ^p + \frac{C_q}{q}\mu _n^q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q\nonumber \\\le & {} \Delta _p(x^*, w_n) - \mu _n\bigg (\Vert Aw_n - UAw_n\Vert ^p - \frac{C_q}{q}\mu _n^{q-1}\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q\bigg )\nonumber \\\end{aligned}$$

(3.12)

$$\begin{aligned}\le & {} \Delta _p(x^*, w_n), \end{aligned}$$

(3.13)

where (3.13) follows from the condition on the step size (3.5). Hence from (3.9) and (3.13), we obtain that $\Delta _p(x^*, y_n) \le \Delta _p(x^*, w_n)$, which shows that $\Gamma \subset C_{n+1}$, $\forall$ $n\in \mathbb {N}$.

Lemma 3.5

The sequences $\{x_n\}$, $\{y_n\}$, $\{v_n\}$ and $\{w_n\}$ are bounded.

Proof

We know from Algorithm 3.2 that $x_n = \Pi _{C_n}x_0$ and $C_{n+1} \subseteq C_n$, $\forall$ $n\ge 1$. Then from (2.10), we have that $\Delta _p(x_n, x_0)\le \Delta _p(x_{n+1}, x_0)$. This shows that $\{\Delta _p(x_n, x_0)\}$ is nondecreasing. Also, since $\Gamma \subset C_{n+1}$ it implies that $\Delta _p(x_n, x_0)\le \Delta _p(x_{n+1}, x_0)\le \Delta _p(x^*, x_0)$, $\forall$ $x^*\in \Gamma$. Therefore from (2.8), we conclude that $\{x_n\}$ is bounded. Since $\{x_n\}$ is bounded, it follows from the construction that $\{y_n\}$, $\{v_n\}$ and $\{w_n\}$ are bounded.

Lemma 3.6

Let the sequences $\{x_n\}$, $\{y_n\}$, $\{v_n\}$ and $\{w_n\}$ be as defined in Algorithm 3.2. Assuming that for small $\epsilon >0$,

$$\begin{aligned} \mu _n\in \bigg (\epsilon , \bigg (\frac{q\Vert Aw_n - UAw_n\Vert ^p}{C_q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q}-\epsilon \bigg )^{\frac{1}{q-1}}\bigg ),\quad n\in \Omega . \end{aligned}$$

(3.14)

Then

• (i) $\lim _{n\rightarrow \infty }\Vert x_{n+1} - x_n\Vert = 0;$

• (ii) $\lim _{n\rightarrow \infty }\Vert w_{n} - x_n\Vert = 0;$

• (iii) $\lim _{n\rightarrow \infty }\Vert v_{n} - Tv_n\Vert = 0;$

• (iv) $\lim _{n\rightarrow \infty }\Vert x_{n} - v_n\Vert = 0;$

• (v) $\lim _{n\rightarrow \infty }\Vert A^*J^{E_2}_p(I - U)Aw_n\Vert _* = 0 ~ \text {and}~ \lim _{n\rightarrow \infty }\Vert (I - U)Aw_n\Vert = 0$.

Proof

From the proof of Lemma 3.5 we have that $\{\Delta _p(x_n, x_0)\}$ is a nondecreasing bounded sequence in $\mathbb {R}$. Hence $\lim _{n\rightarrow \infty }\Delta _p(x_n, x_0)$ exists. Using (2.11),

$$\begin{aligned} \Delta _p(x_{n+1}, \Pi _{C_n}x_0) + \Delta _p(\Pi _{C_n}x_0, x_0)\le \Delta _p(x_{n+1}, x_0). \end{aligned}$$

(3.15)

Therefore

$$\begin{aligned} \Delta _p(x_{n+1}, x_n)\le \Delta _p(x_{n+1}, x_0) - \Delta _p(x_n, x_0)\rightarrow 0. \end{aligned}$$

(3.16)

Applying Lemma 2.13, we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{n+1} - x_n\Vert =0. \end{aligned}$$

(3.17)

This establishes (i).

Let $t_n = J^{E^*_1}_q[J^{E_1}_px_n+\theta _n(J^{E_1}_px_n - J^{E_1}_px_{n-1})]$. It then follows that

$$\begin{aligned} J^{E_1}_pt_n - J^{E_1}_px_n = \theta _n(J^{E_1}_px_n - J^{E_1}_px_{n-1}). \end{aligned}$$

Then by the uniform continuity of $J^{E_1}_p$ on bounded subsets of $E_1$, we obtain that

$$\begin{aligned} \Vert J^{E_1}_pt_n - J^{E_1}_px_n\Vert _*= & {} \Vert {\theta _n}(J^{E_1}_px_n - J^{E_1}_px_{n-1})\Vert _*\nonumber \\\le & {} \theta \Vert J^{E_1}_px_n - J^{E_1}_px_{n-1}\Vert _*\rightarrow 0 \quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

(3.18)

By the uniform continuity of $J^{E^*_1}_q$ on bounded subsets of $E_1^*$ and (3.17), we obtain that $\lim _{n\rightarrow \infty }\Vert t_n - x_n\Vert = 0.$ Therefore,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n - x_n\Vert = \lim _{n\rightarrow \infty }\Vert P_Ct_n - x_n\Vert \le \lim _{n\rightarrow \infty }\Vert t_n - x_n\Vert = 0. \end{aligned}$$

(3.19)

This establishes (ii). Combining (i) and (ii) will give $\lim _{n\rightarrow \infty }\Vert x_{n+1} - w_n\Vert = 0.$

Furthermore, since $x_{n+1}\in C_{n+1}$, it follows from our construction that

$$\begin{aligned} \Delta _p(x_{n+1}, y_n)\le \Delta _p(x_{n+1}, w_n)\rightarrow 0\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

Therefore by Lemma 2.13, we get that $\lim _{n\rightarrow \infty }\Vert x_{n+1} - y_n\Vert = 0.$ This together with (3.17) yields

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n - y_n\Vert = 0. \end{aligned}$$

(3.20)

From (3.19) and (3.20), we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert y_n - w_n\Vert = 0. \end{aligned}$$

(3.21)

Let $x^*\in F(T)$. Then

$$\begin{aligned} \Delta _p(x^*, y_n)= & {} \Delta _p(x^*, J^{E^*_1}_q[(1-\alpha _n)J^{E_1}_pv_n + \alpha _nJ^{E_1}_pTv_n])\nonumber \\= & {} V_p(x^*, (1-\alpha _n)J^{E_1}_pv_n + \alpha _nJ^{E_1}_pTv_n)\nonumber \\= & {} \frac{\Vert x^*\Vert ^p}{p} - \langle (1-\alpha _n)J^{E_1}_pv_n + \alpha _nJ^{E_1}_pTv_n, x^*\rangle \nonumber \\&+\frac{1}{q}\Vert (1-\alpha _n)J^{E_1}_pv_n + \alpha _nJ^{E_1}_pTv_n\Vert _*^q\nonumber \\\le & {} \frac{\Vert x^*\Vert ^p}{p} - \langle (1-\alpha _n)J^{E_1}_pv_n, x^*\rangle -\alpha _n \langle J^{E_1}_pTv_n, x^* \rangle +\frac{(1-\alpha _n)}{q}\Vert v_n\Vert ^p\nonumber \\&+ \frac{\alpha _n}{q}\Vert Tv_n\Vert ^p - \frac{W_q(\alpha _n)}{q}g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*) \end{aligned}$$

(3.22)

$$\begin{aligned}= & {} (1-\alpha _n)\Delta _p(x^*, v_n) + \alpha _n\Delta _p(x^*, Tv_n) - \frac{W_q(\alpha _n)}{q}g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*)\nonumber \\= & {} \Delta _p(x^*, v_n) - \frac{W_q(\alpha _n)}{q}g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*)\nonumber \\\le & {} \Delta _p(x^*, w_n) - \frac{W_q(\alpha _n)}{q}g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*), \end{aligned}$$

(3.23)

where (3.22) and (3.23) follow from Lemma 2.14 and (3.13), respectively. Then from (3.23), we have that

$$\begin{aligned} \frac{W_q(\alpha _n)}{q}g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*)\le & {} \Delta _p(x^*, w_n) - \Delta _p(x^*, y_n)\nonumber \\= & {} \langle J^{E_1}_py_n - J^{E_1}_pw_n, x^* - w_n \rangle - \Delta _p(y_n, w_n)\nonumber \\\le & {} \langle J^{E_1}_py_n - J^{E_1}_pw_n, x^* - w_n\rangle \nonumber \\= & {} \Vert x^* - w_n\Vert \Vert J^{E_1}_py_n - J^{E_1}_pw_n\Vert _*. \end{aligned}$$

(3.24)

Since $J^{E^*_1}_q$ is norm-to-norm uniformly continuous on bounded subsets of $E^*_1$, taking the limit of (3.24) as $n\rightarrow \infty$ gives $\frac{W_q(\alpha _n)}{q}g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*)\rightarrow 0$. Thus we obtain that

$$\begin{aligned} g(\Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*)\rightarrow 0 \quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

By the continuity of g, the last limit implies that

$$\begin{aligned} \Vert J^{E_1}_pv_n- J^{E_1}_pTv_n\Vert _*\rightarrow 0 \quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

(3.25)

Since $J^{E^*_1}_q$ is norm-to-norm uniformly continuous on bounded subsets of $E_1^*$, (3.25) implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_n - Tv_n\Vert =0. \end{aligned}$$

(3.26)

This establishes (iii).

Also, using Lemma (2.13), (3.26) implies that $\lim _{n\rightarrow \infty }\Delta _p(v_n, Tv_n) =0$. Therefore,

$$\begin{aligned} \Delta _p(v_n, y_n)= & {} \Delta _p(v_n, J^{E^*_1}_q[(1-\alpha _n)J^{E_1}_pv_n + \alpha _nJ^{E_1}_pTv_n])\nonumber \\\le & {} (1-\alpha _n)\Delta _p(v_n, v_n) + \alpha _n\Delta _p(v_n, Tv_n)\nonumber \\= & {} \alpha _n\Delta _p(v_n, Tv_n) \rightarrow 0\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

(3.27)

Furthermore by Lemma 2.13, we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_n - y_n\Vert = 0. \end{aligned}$$

(3.28)

Consequently, from (3.20) and (3.28), we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_n - v_n\Vert = 0, \end{aligned}$$

(3.29)

which establishes (iv), and from (3.21) and (3.28), we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_n - w_n\Vert = 0. \end{aligned}$$

(3.30)

Also from (3.12), we have that

$$\begin{aligned} \mu _n\bigg (\left\| Aw_n - UAw_n \right\| ^p- & {} \frac{C_q}{q}\mu _n^{q-1}\left\| A^*J^{E_2}_p(I-U)Aw_n\right\| _*^q\bigg )\nonumber \\\le & {} \Delta _p(x^*, w_n) - \Delta _p(x^*, v_n)\nonumber \\= & {} \langle J^{E_1}_pv_n - J^{E_1}_pw_n, x^* - w_n \rangle - \Delta _p(v_n, w_n)\nonumber \\\le & {} \langle J^{E_1}_pv_n - J^{E_1}_pw_n, x^* - w_n \rangle \nonumber \\= & {} \Vert x^* - w_n\Vert \Vert J^{E_1}_pv_n - J^{E_1}_pw_n\Vert _*. \end{aligned}$$

(3.31)

Passing to the limit as $n \rightarrow \infty$ in (3.31) and using (3.30), we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }(\Vert Aw_n - UAw_n\Vert ^p - \frac{C_q}{q}\mu _n^{q-1}\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q) = 0. \end{aligned}$$

(3.32)

Note that by the choice of our step size, it holds that

$$\begin{aligned} \mu _n^{q-1} < \frac{q\Vert Aw_n - UAw_n\Vert ^p}{C_q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _{*}^q} - \epsilon . \end{aligned}$$

(3.33)

Simplifying (3.33) further gives

$$\begin{aligned} \frac{\epsilon C_q}{q}\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q < (\Vert Aw_n - UAw_n\Vert ^p - \frac{C_q}{q}\mu _n^{q-1}\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q). \end{aligned}$$

(3.34)

By passing to the limit as $n\rightarrow \infty$ in (3.34) and using (3.32), we obtain that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q = 0, \end{aligned}$$

(3.35)

and consequently,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _* = 0 \quad \text {and}\quad \lim _{n\rightarrow \infty }\Vert (I-U)Aw_n\Vert = 0. \end{aligned}$$

(3.36)

This establishes (v).

Theorem 3.7

The sequence $\{x_n\}$ generated by Algorithm 3.2 converges strongly to $u\in \Gamma$, where $u = \Pi _{\Gamma }x_0$.

Proof

Since $\{\Delta _p(x_n, x_0)\}$ is nondecreasing and bounded in $\mathbb {R}$, it implies that there exists $l\in \mathbb {R}$ such that $\Delta _p(x_n, x_0)\rightarrow l$ as $n\rightarrow \infty$. Using (2.11), we get that for every $m, n\in \mathbb {N}$,

$$\begin{aligned} \Delta _p(x_m, x_n)= & {} \Delta _p(x_m, \Pi _{C_n}x_0)\\\le & {} \Delta _p(x_m, x_0) - \Delta _p(x_n, x_0)\rightarrow 0. \end{aligned}$$

Therefore from Lemma 2.13, we have that $\Vert x_m - x_n\Vert \rightarrow 0$ as $m, n\rightarrow \infty$. This shows that $\{x_n\}$ is a Cauchy sequence in C. Since C is a closed convex subset of a Banach space, it implies that there exists $u\in C$ such that $x_n\rightarrow u$ as $n\rightarrow \infty$. It then follows from Lemma 3.6 that $w_n\rightarrow u$ and $v_n\rightarrow u$ as $n\rightarrow \infty$. By the linearity of A, we have that $Aw_n\rightarrow Au$ as $n\rightarrow \infty$. We have shown in Lemma 3.6 that $\Vert v_n - Tv_n\Vert \rightarrow 0$ as $n\rightarrow \infty$, this together with the fact that T is Bregman weak relatively nonexpansive implies that $u\in F(T)$. We have also shown in Lemma 3.6 that $\Vert (I - U)Aw_n\Vert \rightarrow 0$ as $n\rightarrow \infty$, which implies that $Au \in \tilde{F}(U)$. Then from Lemma 3.1(iii), we obtain that $Au\in F(U)$. It then implies that $u\in \Gamma$.

Lastly, we prove that $u= \Pi _{\Gamma }x_0$. Suppose there exists $v\in \Gamma$ such that $v = \Pi _{\Gamma }x_0$. Then

$$\begin{aligned} \Delta _p(v, x_0)\le \Delta _p(u, x_0). \end{aligned}$$

(3.37)

Since $\Gamma \in C_n$ for all $n\ge 1$, we have that $\Delta _p(x_n, x_0)\le \Delta _p(v, x_0).$ Now by the lower semicontinuity of the norm, we have that

$$\begin{aligned} \Delta _p(u, x_0)= & {} \frac{\Vert u\Vert ^p}{p}+\frac{\Vert x_0\Vert ^p}{q} - \langle J^{E_1}_px_0, u\rangle \nonumber \\\le & {} \liminf _{n\rightarrow \infty }\bigg (\frac{\Vert x_n\Vert ^p}{p}+\frac{\Vert x_0\Vert ^p}{q} - \langle J^{E_1}_px_0, x_n\rangle \bigg )\nonumber \\= & {} \liminf _{n\rightarrow \infty }\Delta _p(x_n, x_0)\nonumber \\\le & {} \limsup _{n\rightarrow \infty }\Delta _p(x_n, x_0)\nonumber \\\le & {} \Delta _p(v, x_0). \end{aligned}$$

(3.38)

Then from (3.37) and (3.38), we have that

$$\begin{aligned} \Delta _p(v, x_0)\le \Delta _p(u, x_0)\le \Delta _p(v, x_0). \end{aligned}$$

(3.39)

(3.39) implies that $u=v$. Hence $u = \Pi _{\Gamma }x_0$.

We next present some consequences of our main results. Firstly, if $\theta _n = 0$, we obtain the following non-inertial shrinking projection algorithm.

Corollary 3.8

Let $E_1, E_2$ be p-uniformly convex and uniformly smooth Banach spaces with duals $E_1^*, E_2^*$, respectively. Let $C=C_1$ be nonempty closed and convex subset of $E_1$. Let $T: E_1\rightarrow E_1$ be a Bregman weak relatively nonexpansive mapping and $U: E_2 \rightarrow E_2$ be a mapping of type (P). Let $A: E_1\rightarrow E_2$ be a bounded linear operator with its adjoint $A^*: E_2^* \rightarrow E_1^*$. Select ${x_0}\in E_1$ and let $\{\alpha _n\}\subset (0, 1)$ be a real sequence satisfying $\liminf _{n\rightarrow \infty } \alpha _n>0$. Assuming that the nth-iterate $x_n\in E_1$ has been constructed, then we calculate the $(n+1)th$-iterate $x_{n+1}\in E_1$ via the formula

$$\begin{aligned} \left\{ \begin{array} {l l} w_n = P_Cx_n,\\ v_n = J^{E^*_1}_q[J^{E_1}_pw_n - \mu _nA^*J^{E_2}_p(I - U)Aw_n],\\ y_n = J^{E^*_1}_q[\alpha _nJ^{E_1}_pv_n+(1-\alpha _n)J^{E_1}_pT(v_n)],\\ C_{n+1} = \{z\in C_n: \Delta _p(z, y_n)\le \Delta _p(z, w_n)\},\\ x_{n+1} = \Pi _{C_{n+1}}{x_0}, \forall n\ge 1. \end{array} \right. \end{aligned}$$

(3.40)

Assume for small $\epsilon > 0$, the step size $\mu _n$ is chosen such that

$$\begin{aligned} \mu _n\in \bigg (\epsilon , \big (\frac{q\Vert Aw_n - UAw_n\Vert ^p}{C_q\Vert A^*J^{E_2}_p(I-U)Aw_n\Vert _*^q}-\epsilon \big )^{\frac{1}{q-1}}\bigg ),\quad n\in \Omega , \end{aligned}$$

(3.41)

where the index set $\Omega :=\{n\in \mathbb {N}: Aw_n - UAw_n\ne 0\}$, otherwise $\mu _n = \mu$, where $\mu$ is any non-negative real number. Then $\{x_n\}$ converges strongly to $u\in \Gamma$, where $u = \Pi _{\Gamma }{x_0}$.

Also, by letting U be the metric projection mapping onto a closed convex subset Q of $E_2$ in Algorithm 3.2, i.e. $U = P_Q$ , we obtain the following result as a solution to split feasibility and fixed point problems.

Corollary 3.9

With reference to the data in Algorithm 3.2, let Q be a nonempty closed convex subset of $E_2$ and $U = P_Q$. Assuming $\Theta :=\{x\in C: x\in F(T), Ax\in Q\}\ne \emptyset$. Then the sequence $\{x_n\}$ generated by Algorithm 3.2 converges strongly to $u\in \Theta$, where $u = \Pi _{\Theta }x_0$.

4 Application

4.1 Split Monotone Inclusion Problem

Let E be a smooth, strictly convex and reflexive Banach space with dual $E^*$. Let $B:E\rightarrow 2^{E^*}$ be a multivalued mapping. The graph of B denoted by gr(B) is defined by $gr(B)=\{(x, u)\in E\times E^*: u\in Bx\}$. B is called a non-trivial operator if $gr(B)\ne \emptyset$. B is called a monotone mapping if $\forall$ $(x, u), (y, v)\in gr(B)$, $\langle x -y, u - v\rangle \ge 0.$

B is said to be a maximal monotone operator if the graph of B is not a proper subset of the graph of any other monotone mapping.

Let $T_1:E_1\rightarrow 2^{E_1^{*}}$ and $T_2:E_2\rightarrow 2^{E_2^{*}}$ be maximal monotone mappings and $A: E_1\rightarrow E_2$ be bounded linear operator. The Split Monotone Inclusion Problem (in short, SMIP) is to find

$$\begin{aligned} x\in E_1 ~\text {such that}~ x\in T_1^{-1}(0)\cap A^{-1}(T_2^{-1}(0)). \end{aligned}$$

(4.1)

Many authors have studied the SMIP (see [11, 31, 33, 46, 55]) and applied it to solve some real-life problems which include modeling intensity-modulated radiation therapy treatment planning, sensor networks in computerized tomography and data compression, see [10, 12, 13]. Very recently, Bello and Sheu [8] studied the problem in p-uniformly convex and uniformly smooth Banach spaces. They proposed an algorithm and proved a strong convergence theorem with the step size not depending on the prior knowledge of the norm of the bounded linear operator. Our purpose here is to apply our algorithm to solve the SMIP (4.1).

For all $r>0,$ the mapping $K_r:=(I+rJ^{E^*_2}_qT_2)^{-1}$ is called the metric resolvent of $T_2$. It is easy to see that $F(K_r) = {T_2}^{-1}(0)$. Also note that if $x\in ran(I + rJ^{E^*_2}_qT_2)$, then $J^{E_2}_p(x - K_rx)\in r^{{p-1}}T_2K_rx$. Therefore for every $x, y \in ran(I+rJ^{E^*_2}_qT_2)$, we have that

$$\begin{aligned} \langle J^{E_2}_p(x - K_rx) - J^{E_2}_p(y - K_ry), K_rx - K_ry\rangle \ge 0, \end{aligned}$$

(4.2)

by the monotonicity of $T_2$. This implies that $K_r$ is a mapping of type (P). Similarly, let $T_1: E_1\rightarrow 2^{{E_1}^*}$ be a maximal monotone operator. For every $r>0$, the Bregman resolvent associated with $T_1$ is denoted by $Res_{rT_1}$ and is defined by

$$\begin{aligned} Res_{rT_1}:=(J^{E_1}_p + rT_1)^{-1}\circ J^{E_1}_p: {E_1}\rightarrow 2^{E_1}. \end{aligned}$$

It is known that $Res_{rT_1}$ is Bregman weak relatively nonexpansive and $F(Res_{rT_1})={T_1}^{-1}(0)$ for each $r>0$.

It then implies that our algorithm can be used to solve the SMIP (4.1). We shall denote the solution set of (4.1) by $SMIP(T_1, T_2)$. An application of our main result is the following.

Theorem 4.1

Let $U = K_r$ and $T = Res_{rT_1}$ in Algorithm 3.2. Assuming $SMIP(T_1, T_2)\ne \emptyset$. Then the sequence $\{x_n\}$ generated by Algorithm 3.2 converges strongly to $u\in {SMIP(T_1, T_2)}$, where $u = \Pi _{SMIP(T_1, T_2)}x_0$.

Table 1 Numerical results for Example 5.1

Fig. 1

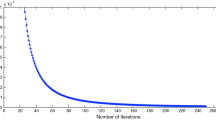
Example 5.1: Top left: Case Ia; Top right: Case Ib; Bottom left: Case Ic; Bottom right: Case Id

5 Numerical Examples

We next give some numerical examples to validate our results and to illustrate the performance of our Algorithm 3.2.

Example 5.1

Let $E_1= E_2 = \mathbb {R}$ and $C = C_1= [0, 3]$. Let $T: E_1\rightarrow E_1$ be defined by

$$\begin{aligned} Tx = \left\{ \begin{array} {l l} 0~\text {if}~x\ne 3,\\ 2~\text {if}~ x= 3, \end{array} \right. \end{aligned}$$

(5.1)

$\forall x\in E_1$ and $U: E_2\rightarrow E_2$ be defined by $Ux = \frac{1}{2}x,~\forall x\in E_2.$ Then T is weak relatively nonexpansive and U is firmly nonexpansive. Let $A: E_1\rightarrow E_2$ be a mapping defined by $Ax = \frac{2}{3}x$, $\forall x\in E_1.$ We choose $\theta _n = \frac{(-1)^n+3}{10n}$ and $\alpha _n= \frac{n+1}{4n}$. Then Algorithm 3.2 gives

$$\begin{aligned} \left\{ \begin{array} {l l} w_n = P_C[x_n+\frac{(-1)^n+3}{10n}(x_n - x_{n-1})],\\ v_n = [w_n - \mu _n(\frac{2}{9}w_n)],\\ y_n = [\frac{n+1}{4n}v_n+\frac{3n-1}{4n}T(v_n)],\\ C_{n+1} = \{z\in C_n: |z- y_n|\le |z - w_n|\},\\ x_{n+1} = P_{C_{n+1}}x_0, \forall ~ n\ge 1, \end{array} \right. \end{aligned}$$

(5.2)

where the step size $\mu _n$ is chosen such that

$$\begin{aligned} \mu _n\in \bigg (0, \frac{2|Aw_n - UAw_n|^2}{|A^*(I-U)Aw_n|^2}\bigg ). \end{aligned}$$

Using MATLAB R2015(a), we compute and compare the numerical outputs of Algorithms 3.2 and (3.40). We choose different values of $x_0$ and $x_1$ and plot the graphs of errors = $|x_{n+1} - x_{n}|$ against number of iterations n. The stopping criterion used for the computation is $|x_{n+1}-x_{n}|< 10^{-7}$ and the initial values are given below:

Case Ia::

$x_0 = 2.6; ~~ x_1 = 1.8$;

Case Ib::

$x_0 = 9.4; ~~ x_1 = 6.0$;

Case Ic::

$x_0 = 2.6; ~~ x_1 = 3.8$;

Case Id::

$x_0 = -9.4; ~~ x_1 = 7.8.$

The computational results are shown in Table 1 and Fig. 1.

Example 5.2

Let $E_1=E_2 = \ell _2(\mathbb {R})$, where $\ell _2(\mathbb {R}) := \{\sigma = (\sigma _1, \sigma _2, \ldots , \sigma _i, \ldots ), \sigma _i\in \mathbb {R}: \sum _{i=1}^{\infty }|\sigma _i|^2<\infty \}$, $\Vert \sigma \Vert _{\ell _2} = (\sum _{i=1}^{\infty }|\sigma _i|^2)^{\frac{1}{2}}$, $\forall$ $\sigma \in E_1.$ Let $C=C_1:= \{x \in E_1:||x||_{\ell _2}\le 1\}$. Let $T: E_1\rightarrow E_1$ be as defined in Example 2.6 and define $U: E_2\rightarrow E_2$ by $Ux = \frac{1}{2}x$, $\forall x\in E_2.$ Then U is a mapping of type (P). Let $A: E_1\rightarrow E_2$ be a mapping defined by $Ax = \frac{2}{3}x$. We choose $\theta _n = \frac{2n+1}{10n}$ and $\alpha _n= \frac{n+1}{4n}$. Then Algorithm 3.2 becomes

$$\begin{aligned} \left\{ \begin{array} {l l} w_n = P_CJ^{E_1}_q[J^{E_1}_px_n+\frac{1}{2n}(J^{E_1}_px_n - J^{E_1}_px_{n-1})],\\ v_n = J^{E_1}_q[J^{E_1}_pw_n - \mu _n\frac{2}{3}J^{E_2}_p(\frac{1}{3}w_n)],\\ y_n = J^{E_1}_q[\frac{n+1}{4n}J^{E_1}_pv_n+\frac{3n-1}{4n}J^{E_1}_pT(v_n)],\\ C_{n+1} = \{z\in C_n: \Delta _p(z, y_n)\le \Delta _p(z, w_n)\},\\ x_{n+1} = \Pi _{C_{n+1}}x_0, \forall ~ n\ge 1, \end{array} \right. \end{aligned}$$

(5.3)

where the stepsize $\mu _n$ is chosen as defined in (3.5). Using MATLAB R2015(a) and $\Vert x_{n+1} - x_{n}\Vert _{\ell _2} < 10^{-7}$ as stopping criterion, we compute and compare the numerical outputs of Algorithms 3.2 and (3.40) using four different starting values as follows:

Case IIa::

$x_0 = (4,2,1,\ldots ); ~~ x_1 = (25,5,1,\ldots )$;

Case IIb::

$x_0 = (-9,3,-1,\ldots ); ~~ x_1 = (10,-1,0.1,\ldots )$;

Case IIc::

$x_0 = (1,\frac{-1}{4}, \frac{1}{16},\ldots ); ~~ x_1 = (\frac{1}{\sqrt{3}}, \frac{1}{3}, \frac{1}{\sqrt{27}},\ldots )$;

Case IId::

$x_0 = (3, \frac{3}{2}, \frac{3}{4},\ldots ); ~~ x_1 = (-5, 1, -0.2,\ldots ).$

We thus plot the graphs of errors against number of iterations in each case. The computational result can be found in Table 2 and Fig. 2.

Table 2 Numerical results for Example 5.2

Fig. 2

Example 5.2: Top left: Case IIa; Top right: Case IIb; Bottom left: Case IIc; Bottom right: Case IId

Table 3 Numerical results for Example 5.3

Fig. 3

Example 5.3: Top left: Case IIIa; Top right: Case IIIb; Bottom left: Case IIIc; Bottom right: Case IIId

The next example is to illustrate the application given in Sect. 4.

Example 5.3

Let $E_1=E_2 = \ell _2(\mathbb {R})$, where $\ell _2(\mathbb {R}) := \{\sigma = (\sigma _1, \sigma _2, \ldots , \sigma _i, \ldots ), \sigma _i\in \mathbb {R}: \sum _{i=1}^{\infty }|\sigma _i|^2<\infty \}$, $\Vert \sigma \Vert _{\ell _2} = (\sum _{i=1}^{\infty }|\sigma _i|^2)^{\frac{1}{2}}$, $\forall$ $\sigma \in E_1.$ Let $C=C_1:= \{x \in E_1:||x||_{\ell _2}\le 1\}$. Let $T_1: E_1\rightarrow E_1$ be defined by $T_1x = 3x$, $\forall x\in E_1$ and define $T_2: E_2\rightarrow E_2$ by $T_2y = 7y$, $\forall y\in E_2.$ Let $A: E_1\rightarrow E_2$ be a mapping defined by $Ax = \frac{1}{4}x$. Then $T_1$ and $T_2$ are maximal monotone operators. One can easily verify that $Res_{rT_1}x = \frac{x}{1+3r}$, $\forall x\in E_1$ and $K_ry = \frac{y}{1+7r}$, $\forall y\in E_2$, $r>0$. Note that in this case, $SMIP(T_1,T_2)=\{\mathbf{0} = (0,0,\ldots )\}$. Therefore by Theorem 4.1, the sequence $\{x_n\}$ generated by Algorithm 3.2 converges strongly to $\mathbf {0}$. We choose $r=3$, $\theta _n = \frac{2n+1}{10n}$, $\alpha _n= \frac{n+1}{4n}$ and $\mu = 0.35$. Using MATLAB R2015(a), we test Algorithms 3.2 and (3.40) for the following initial values:

Case IIIa::

$x_0 = (4,2,1,\ldots ); ~~ x_1 = (3, -\frac{1}{3} \frac{1}{27},\ldots )$;

Case IIIb::

$x_0 = (-2, \frac{1}{2},-\frac{1}{8},\ldots ); ~~ x_1 = (-12, 4, -\frac{4}{3},\ldots )$;

Case IIIc::

$x_0 = (10, 2, 0.4,\ldots ); ~~ x_1 = (2, 1, \frac{1}{2},\ldots )$;

Case IIId::

$x_0 = (7, \sqrt{7},1,\ldots ); ~~ x_1 = (18,6,2,\ldots ).$

We thus plot the graphs of errors against number of iterations in each case. The computational result can be found in Table 3 and Fig. 3.

Table 4 Numerical results for Example 5.4

Fig. 4

Example 5.4: Top left: Case IVa; Top right: Case IVb; Bottom left: Case IVc; Bottom right: Case IVd

Example 5.4

Let $E_1=E_2 = \ell _3(\mathbb {R})$, where $\ell _3(\mathbb {R}) := \{x = (x_1, x_2, \ldots , x_i, \ldots ), x_i\in \mathbb {R}: \sum _{i=1}^{\infty }|x_i|^3<\infty \}$ with the norm $\Vert x\Vert _{\ell _3} = (\sum _{i=1}^{\infty }|x_i|^3)^{\frac{1}{3}}$, $\forall x \in E_1.$ Let $C=C_1:= \{x \in E_1:||x||_{\ell _3}\le 1\}$. For all $x\in E_1$, we define $A:E_1\rightarrow E_2$ by

$$\begin{aligned} Ax = \left( x_1, \frac{x_2}{\sqrt{2}}, \frac{x_3}{\sqrt{3}},\ldots \right) . \end{aligned}$$

Let $(e_n)$ be a sequence in $\ell _3(\mathbb {R})$ defined by $e_n = (\delta _{n,1}, \delta _{n,2}, \ldots , )$ for each $n\in \mathbb {N}$, where

$$\begin{aligned} \delta _{n,i} = {\left\{ \begin{array}{ll} 1~\text {if}~ n=i,\\ 0~\text {if}~n\ne i. \end{array}\right. } \end{aligned}$$

(5.4)

Let $f(x) = \frac{1}{3}\Vert x\Vert ^3_{\ell _3}$ for all $x\in \ell _3(\mathbb {R})$. We define $T:E_1\rightarrow E_1$ by

$$\begin{aligned} Tx = {\left\{ \begin{array}{ll} \frac{x}{n+1}~\text {if}~ x = e_n,\\ \frac{x}{2}~\text {if}~x\ne e_n. \end{array}\right. } \end{aligned}$$

(5.5)

Note that $\tilde{F}(T)=\{\mathbf{0}=(0, 0,\ldots )\}=F(T)$. Let $x\in E_1$. If $x = e_n$, for some $n\in \mathbb {N}$, then

$$\begin{aligned} \Delta _3(\mathbf{0}, Tx)= & {} f(\mathbf{0}) - f(Tx) - \langle J^{E_1}_3(Tx), \mathbf{0} - Tx\rangle \\= & {} f(\mathbf{0}) - \frac{1}{(n+1)^3}f(x) - \frac{1}{(n+1)^3}\langle J^{E_1}_3x, \mathbf{0} - x\rangle \\= & {} \frac{1}{(n+1)^3}\big (f(\mathbf{0}) - f(x) - \langle J^{E_1}_3x, \mathbf{0} - x\rangle \big )\\\le & {} \Delta _3(\mathbf{0}, x). \end{aligned}$$

If $x \ne e_n$, then

$$\begin{aligned} \Delta _3(\mathbf{0}, Tx)= & {} f(\mathbf{0}) - f(Tx) - \langle J^{E_1}_3(Tx), \mathbf{0} - Tx\rangle \\= & {} f(\mathbf{0}) - \frac{1}{8}f(x) - \frac{1}{8}\langle J^{E_1}_3x, \mathbf{0} - x\rangle \\= & {} \frac{1}{8}\big (f(\mathbf{0}) - f(x) - \langle J^{E_1}_3x, \mathbf{0} - x\rangle \big )\\\le & {} \Delta _3(\mathbf{0}, x). \end{aligned}$$

It therefore follows that T is Bregman weak relatively nonexpansive. We define $U:E_2\rightarrow E_2$ by $Ux = \frac{3x}{4}$, $x\in E_2$. Furthermore, we choose $\mu _n = 0.0001$, $\theta _n = \frac{2n}{10n+3}$ and $\alpha _n = \frac{2n+1}{13n}$. We make different choices of initial values $x_0$ and $x_1$ as follows:

Case IVa::

$x_0 = (8, 4, 2, \ldots ), x_1 = (6, -2, \frac{2}{3}, \ldots );$

Case IVb::

$x_0 = (3, -\frac{3}{2}, \frac{3}{4}, \ldots ), x_1 = (-1, \frac{1}{\root 3 \of {2}}, -\frac{1}{\root 3 \of {4}},\ldots );$

Case IVc::

$x_0 = (-2, \root 3 \of {4}, -\root 3 \of {2}, \ldots ), x_1 = (3, \root 3 \of {3}, 1, \ldots );$

Case IVd::

$x_0 = (4, 0.4, 0.04 \ldots ), x_1 = (5, \frac{5}{4}, \frac{5}{16}, \ldots ).$

Fig. 5

Example 5.5: Top left: Original image; Top right: Blurred Image; Bottom left: Restored image by Algorithm 3.2 with SNR = 35.0321; Bottom right: Restored image by Algorithm (3.40) with SNR = 34.9926

Fig. 6

Example 5.5: Top left: Original image; Top right: Blurred Image; Bottom left: Restored image by Algorithm 3.2 with SNR = 42.1303; Bottom right: Restored image by Algorithm (3.40) with SNR = 42.0827

Using MATLAB R2015(a), we compare the performance of Algorithms 3.2 and (3.40). The stopping criterion used for our computation is $\Vert x_{n+1}-x_n\Vert _{\ell _3}<10^{-7}$. The duality mapping is computed using the formula in Example 2.1 and the Bregman projection is calculated using Proposition 5.1 in Alber and Butnariu [3] for a fixed constant $k>0$. We plot the graphs of errors against the number of iterations in each case. The numerical results and figures are shown in Table 4 and Fig. 4, respectively.

Fig. 7

Example 5.5: Top left: Original image; Top right: Blurred Image; Bottom left: Restored image by Algorithm 3.2 with SNR = 32.8327; Bottom right: Restored image by Algorithm (3.40) with SNR = 32.8150

Table 5 Numerical comparison of SNR (dB) values of Algorithms 3.2 and (3.40)

Fig. 8

Example 5.5: Top: Cameraman.tif ($256\times 256$); Middle: Pout.tif ($291\times 240$); Bottom: Tire.tif ($205\times 232$)

Next, we apply our main result to an inverse problem stemming from image restoration problem. For most of the contents, we follow the recent works of Cholamjiak et al. [18] and Suparatulatorn et al. [45].

Example 5.5

(Image Deblurring) We recall the following linear model used in image restoration problem:

$$\begin{aligned} y = A\bar{x}+\xi , \end{aligned}$$

where $\bar{x}$ is the original image, y is the degraded image, A is a blurring matrix and $\xi$ is the noise. For a grayscale image of M pixels wide and N pixels height, each pixel value is known to be in the range [0, 255]. Let $D:=M\times N$. Then the underlying real Hilbert space is $\mathbb {R}^D$ equipped with the standard Euclidean norm $\Vert \cdot \Vert _2$, and $C = [0, 255]^D$. Our aim here is to recover the original image $\bar{x}$ given the data of the blurred image y and A. An approach to estimate an approximation of $\bar{x}$ is to recast the deblurring problem as the following convex minimization problem:

$$\begin{aligned} \min _x\Vert Ax - y\Vert _2. \end{aligned}$$

(5.6)

Setting $Q = \{y\}$, $T = P_C$ and $U = P_Q$, then (5.6) is equivalent to the following SCFPP:

$$\begin{aligned} \text {find}~ x\in F(T)~\text {such that}~Ax\in F(Q). \end{aligned}$$

It then follows that our Algorithm 3.2 can be used to solve the problem. Using MATLAB R2015(a), we apply Algorithm 3.2 to recover the original image $\bar{x}$ from the burred image y. The quality of the restored image is measured by the signal-to-noise ratio (SNR) in decibel (dB) as follows:

$$\begin{aligned} SNR:=20\log _{10}\frac{\Vert \bar{x}\Vert _2}{\Vert x - \bar{x}\Vert _2}, \end{aligned}$$

where $\bar{x}$ is the original image and x is the restored image. The larger the SNR, the better the quality of the restored image. The initial values for our experiments are $x_0= 0\in \mathbb {R}^D$ and $x_1= 1\in \mathbb {R}^D$. The gray test images for our experiments are Cameraman, Pout and Tire. Each test image is degraded by Gaussian $7\times 7$ blur kernel with standard deviation 4. We choose $\theta _n = \frac{n}{10n+5}$ and $\alpha _n = \frac{n}{3n+1}$. We test our Algorithms 3.2 and (3.40). The original, blurred and restored images by each of the algorithms are shown in Figs. 5, 6 and 7.

The computational results are shown in Table 5 and Fig. 8.

Remark 5.6

From the computational results, we see that Algorithm 3.2 performs better than Algorithm (3.40) in both CPU time taken and number of iteration. This illustrates the efficiency of the inertial extrapolation term.

6 Conclusion

We study the Split Common Fixed Point Problem (SCFPP) for a new mapping of type (P) in p-uniformly convex and uniformly smooth Banach spaces. We then propose an inertial shrinking projection algorithm and proved a strong convergence theorem for solving the SCFPP for mapping of type (P) and Bregman weak relatively nonexpansive mapping in p-uniformly convex and uniformly smooth Banach space. In addition, the implementation of our algorithm does not require an a priori estimate of the norm of the bounded linear operator. Lastly, we give numerical examples to demonstrate the performance of our algorithm and also apply our results to image deblurring problem.