A unified algorithm for solving variational inequality and fixed point problems with application to the split equality problem

Abstract

In this paper, we propose a new extragradient method consisting of the hybrid steepest descent method, a single projection method and an Armijo line searching the technique for approximating a solution of variational inequality problem and finding the fixed point of demicontractive mapping in a real Hilbert space. The essence of this algorithm is that a single projection is required in each iteration and the step size for the next iterate is determined in such a way that there is no need for a prior estimate of the Lipschitz constant of the underlying operator. We state and prove a strong convergence theorem for approximating common solutions of variational inequality and fixed points problem under some mild conditions on the control sequences. By casting the problem into an equivalent problem in a suitable product space, we are able to present a simultaneous algorithm for solving the split equality problem without prior knowledge of the operator norm. Finally, we give some numerical examples to show the efficiency of our algorithm over some other algorithms in the literature.

1 Introduction

Throughout this paper, let C be a nonempty closed convex subset of a real Hilbert space H with norm $||\cdot ||$ and inner product $\langle \cdot , \cdot \rangle .$ The variational inequality problem (VIP) is defined as:

$$\begin{aligned} \text{ Find }~~x \in C \quad \text{ such } \text{ that } \,\langle Ax, y - x \rangle \ge 0, \quad \forall ~y \in C, \end{aligned}$$

(1.1)

where $A: C \rightarrow H$ is a nonlinear operator. We denote the set of solutions of VIP (1.1) by VI(C, A). The VIP is an important tool in economics, decision making, engineering mechanics, mathematical programming, transportation, operation research, etc. (see, for example Aubin 1998; Glowinski et al. 1981; Khobotov 1987; Kinderlehrer and Stampachia 2000; Marcotte 1991).

It is well known that $x^\dagger$ solves the VIP (1.1) if and only if $x^\dagger$ solves the fixed point equation

$$\begin{aligned} x^\dagger = P_C(x^\dagger - \lambda A x^\dagger ), \quad \lambda >0, \end{aligned}$$

(1.2)

or equivalently, $x^\dagger$ solves the residual equation

$$\begin{aligned} r_{\lambda }(x^\dagger ) = 0, \quad \text {where}\quad r_{\lambda }(x^\dagger ): = x^\dagger - P_C(x^\dagger - \lambda Ax^\dagger ), \end{aligned}$$

(1.3)

for an arbitrary positive constant $\lambda$; see Glowinski et al. (1981) for details. Obviously, (1.3) is obtained from (1.2).

Several iterative methods have been introduced for solving the VIP and its related optimization problems; see (Jolaoso et al. 2019; Taiwo et al. 2019a, b, c). One of the earliest methods for solving VIP is the extragradient method introduced by Korpelevich (1976). The extragradient method was stated as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_1 \in C,\\ y_k = P_C(x_k - \lambda Ax_k), \\ x_{k+1} = P_C(x_k - \lambda Ay_k), \quad k \ge 1, \end{array}\right. } \end{aligned}$$

(1.4)

where $\lambda \in \left( 0, \frac{1}{L}\right)$, $A:C \rightarrow {\mathbb {R}}^n$ is monotone and Lipschitz continuous with Lipschitz constant L. This extragradient method has further been extended to infinite-dimensional spaces by many authors; see for example (Apostol et al. 2012; Ceng et al. 2010; Censor et al. 2012; Denisov et al. 2015).

As an improvement of the extragradient algorithm, (1.4), Censor et al. (2011b) introduced the following subgradient extragradient algorithm for solving the VIP in a real Hilbert space H:

$$\begin{aligned} {\left\{ \begin{array}{ll}x_1 \in C,\\ y_k = P_C(x_k - \lambda Ax_k),\\ D_k = \{w\in H: \langle x_k -\lambda Ax_k - y_k, w- y_k \rangle \le 0\},\\ x_{k+1} = P_{D_k}(x_k -\lambda Ay_k). \end{array}\right. } \end{aligned}$$

(1.5)

In (1.5), the second projection $P_C$ of the extragradient algorithm (1.4) was replaced with a projection onto a half-space $D_k$ which is easier to evaluate. Under some mild assumptions, Censor et al. (2011b) obtained a weak convergence result for solving VIP using (1.5).

The second problem which we involve in this paper is finding the fixed point of an operator $T:H \rightarrow H.$ A point $x \in H$ is called a fixed point of T if $x = Tx.$ The set of fixed points of T is denoted by F(T). Motivated by the result of Yamada et al. (2001), Tian (2010) considered the following general viscosity type iterative method for approximating the fixed points of a nonexpansive mapping:

$$\begin{aligned} x_{k+1} = \alpha _n \gamma f(x_k) + ( 1- \mu \lambda _k B)Tx_k, \quad ~ \forall ~k \ge 1, \end{aligned}$$

(1.6)

where $f: H \rightarrow H$ is a $\rho$-Lipschitz mapping with $\rho >0$ and $B:H \rightarrow H$ is a $\kappa$-Lipschitz and $\eta$-strongly monotone mapping with $\kappa > 0$ and $\eta >0.$ Under some certain conditions, Tian (2010) proved that the sequence $\{x_n\}$ generated by (1.6) converges strongly to a fixed point of T which also solves the variational inequality

$$\begin{aligned} \langle (\gamma B - \mu f)x^*, x - x^* \rangle \ge 0, \quad ~ \forall ~ x \in F(T). \end{aligned}$$

In Nadezhkina and Takahashi (2006), Nadezhkina and Takahashi proposed the following algorithm for finding a common solution of VIP (1.1) and F(T), where T is nonexpansive and A is monotone and L-Lipschitz continuous:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_k = P_C(x_k - \lambda _k Ax_k), \\ x_{k+1} = \alpha _k x_k + (1-\alpha _k)TP_C(x_k - \lambda _k Ay_k), \quad k \ge 1, \end{array}\right. } \end{aligned}$$

(1.7)

where $\{\lambda _k\}\subset [a,b]$ for some $a,b \in \left( 0, \frac{1}{L}\right)$ and $\{\alpha _k\} \subset (0,1)$. The sequence $\{x_k\}$ generated by (1.7) converges weakly to a solution $x \in \Gamma := VI(C,A)\bigcap F(T).$

Also, Censor et al. (2011b) studied the approximation of common solution of the VIP and fixed point problem for a nonexpansive mapping T in a real Hilbert space. They proposed the following subgradient extragradient algorithm and proved its weak convergence to a solution $u^* \in F(T)\cap VI(C,A)$:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 \in H, \\ y_k = P_C\left( x_k - \lambda Ax_k \right) ,\\ D_k = \{ w \in H: \langle x_k - \lambda Ax_k - y_k, w - y_k \rangle \le 0 \},\\ x_{k+1} = \alpha _k x_k + (1-\alpha _k)TP_{D_k}(x_k - \lambda A y_k). \end{array}\right. } \end{aligned}$$

(1.8)

To obtain strong convergence, Censor et al. (2011a) combined the subgradient extragradient method and the hybrid method to obtain the following effective scheme for solving the VIP (1.1) and finding the fixed point of a nonexpansive mapping T.

$$\begin{aligned} {\left\{ \begin{array}{ll} y_k = P_C(x_k - \lambda Ax_k),\\ D_k = \{w \in H: \langle x_k - \lambda A x_k - y_k, w - y_k \rangle \le 0\},\\ z_k = P_{D_k}(x_k - \lambda Ay_k),\\ t_k = \alpha _k x_k + (1-\alpha _k)[\beta _k z_k + (1-\beta _k)Tz_k],\\ C_k = \{ z\in H: ||t_k -z|| \le ||x_k -z||\},\\ Q_k = \{z\in H: \langle x_k -z, x_k - x_0 \rangle \le 0 \},\\ x_{k+1} = P_{C_k\cap Q_k}(x_0). \end{array}\right. } \end{aligned}$$

(1.9)

As an improvement on (1.9), Maingé (2008) proposed the following hybrid extragradient viscosity method which does not involve computing the projection onto the intersection $C_k \cap Q_k$:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_k = P_C(x_k - \lambda _k Ax_k),\\ z_k = P_C(x_k - \lambda _k Ay_k),\\ x_{k+1} = [(1-w)I + wT]t_k, ~~~~ t_k = z_k - \alpha _k Bz_k, \end{array}\right. } \end{aligned}$$

(1.10)

where $\lambda _k >0$, $\alpha _k >0$ and $w \in [0,1]$ are suitable parameters, $T: H \rightarrow H$ is $\beta$-demicontractive mapping, $A: C \rightarrow H$ is a monotone and L-Lipschitz continuous mapping and $B:H \rightarrow H$ is $\eta$-strongly monotone and $\kappa$-Lipschitz continuous mapping. Maingé (2008) proved that the sequence $\{x_k\}$ generated by (1.10) converges strongly to the unique solution $x^* \in VI(C,A)\cap F(T).$

Recently, Hieu et al. (2018) modified algorithm (1.10) and proposed the following two-step extragradient viscosity method for solving similar problem in a Hilbert space:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_k = P_C(x_k - \lambda _k A x_k),\\ z_k = P_C(y_k - \rho _k A y_k),\\ t_k = P_C(x_k - \rho _k Az_k),\\ x_{k+1} = (1-\beta _k)v_k + \beta _k Tv_k, \quad ~ v_k = t_k - \alpha _k Bt_k, \end{array}\right. } \end{aligned}$$

(1.11)

where $\rho _k >0$, $0 \le \lambda _k \le \rho _k,$ $\beta _k \in [0,1],$ A, T and B are as defined for (1.10). We observe that, although algorithm (1.11) does not contain (1.4), the algorithm (1.11) requires more computation of projections onto the feasible set. This can be costly if the feasible set has a complex structure which may affect the usage of the algorithm.

Motivated by the above results, in this paper, we present a unified algorithm which consists of the combination of hybrid steepest descent method (also called general viscosity method Tian 2010) and a projection method with an Armijo line searching rule for finding a common solution of VIP (1.1) and fixed point of $\beta$-demicontractive mapping in a Hilbert space. Our contributions in this paper can be highlighted as follows:

• Our proposed algorithm requires only one projection onto the feasible set and no other projection along each iteration process. This is in contrast to the above-mentioned methods and many other recent results (such as Dong et al. 2016; Kanzow and Shehu 2018; Thong and Hieu 2018a, b; Vuong 2018) which require more than one projection onto the feasible set in each iteration process.

• The underlying operator A of the VIP considered in our result is pseudo-monotone. This extends the above results where the operator is assumed to be monotone. Note that every monotone operator is pseudo-monotone, but the converse is not always true (as seen in Example 2.2).

• In our result, the step size $\lambda _k$ is determined via an Armijo line search rule. This is very important because it helps us to avoid finding a prior estimate of the Lipschitz constant L of the operator A used in the above-mentioned results. In practice, it is very difficult to approximate this Lipschitz constant.

• The strong convergence guaranteed by our algorithm makes it a good candidate method for approximating a common solution of VIP (1.1) and fixed point problem.

Finally, we present an application of our result for solving the split equality problem in Hilbert spaces.

2 Preliminaries

In this section, we present some basic notions and results that are needed in the sequel. We denote the strong and weak convergence of a sequence $\{x_n\} \subseteq H$ to a point $p \in H$ by $x_n \rightarrow p$ and $x_n \rightharpoonup p,$ respectively.

Definition 2.1

A mapping $A:C \rightarrow H$ is called

• (a) $\eta$-strongly monotone on C if there exists a constant $\eta >0$ such that $\langle Ax -Ay, x-y \rangle \ge \eta ||x-y||^2,$ for all $x,y \in C;$

• (b) $\alpha$-inverse strongly monotone on C if there exists a constant $\alpha >0$ such that $\langle Ax -Ay, x - y\rangle \ge \alpha ||Ax - Ay||^2$ for all $x,y \in C;$

• (c) monotone on C if $\langle Ax - Ay, x- y\rangle \ge 0$ for all $x,y \in C;$

• (d) pseudo-monotone on C if for all $x,y \in C$, $\langle Ax, y -x \rangle \ge 0 \Rightarrow \langle Ay, y -x \rangle \ge 0;$

• (e) L-Lipschitz continuous on C if there exists a constant $L >0$ such that $||Ax- Ay|| \le L||x-y||$ for all $x,y \in C.$

If A is $\eta$-strongly monotone and L-Lipschitz continuous, then, A is $\frac{\eta }{L^2}$-inverse strongly monotone. Also, we note that every monotone operator is pseudo-monotone, but the converse is not true (see the Example 2.2 below).

Example 2.2

Khanh and Vuong (2014) Let $E = \ell _2$, the real Hilbert space whose elements are the square summable sequences of real scalars, i.e.,

$$\begin{aligned} E = \{x = (x_1,x_2,\ldots ,x_k, \ldots )\Bigg |\sum _{k=1}^\infty |x_k|^2 < +\infty \}. \end{aligned}$$

The inner product and norm on E are given by

$$\begin{aligned} \langle x,y \rangle = \sum _{k=1}^\infty x_ky_k \quad \text {and}\quad ||x|| = \sqrt{\langle x,x \rangle }, \end{aligned}$$

where $x = (x_1, x_2,\dots ,x_k,\ldots ),$ and $y = (y_1, y_2, \ldots , y_k, \ldots ).$

Let $\alpha ,\beta \in {\mathbb {R}}$ such that $\beta> \alpha> \frac{\beta }{2}>0$ and

$$\begin{aligned} C = \{ x \in E: ||x|| \le \alpha \} \quad \text {and}\quad Ax = (\beta - ||x||)x. \end{aligned}$$

It is easy to verify that $VI(C,A) = \{0\}$. Now, let $x,y \in C$ such that $\langle Ax, y-x\rangle \ge 0$, i.e.,

$$\begin{aligned} (\beta - ||x||)\langle x, y-x \rangle \ge 0. \end{aligned}$$

Since $\beta> \alpha> \frac{\beta }{2} > 0,$ the last inequality implies that $\langle x, y-x\rangle \ge 0.$ Hence,

$$\begin{aligned} \langle Ay, y-x\rangle= & {} (\beta - ||y||)\langle y, y-x \rangle \\\ge & {} (\beta - ||y||)\langle y, y-x \rangle - (\beta - ||y||)\langle x, y-x \rangle \\= & {} (\beta - ||y||)||y-x||^2 \ge 0. \end{aligned}$$

This means that A is pseudo-monotone on C. To show that A is not monotone on C, let us consider $x = \Big (\dfrac{\beta }{2}, 0,\ldots ,0,\ldots \Big ),~~ y= (\alpha ,0,\ldots ,0, \ldots ) \in C.$ Then, we have

$$\begin{aligned} \langle Ax- Ay, x-y \rangle = \left( \dfrac{\beta }{2}-\alpha \right) ^{3} <0. \end{aligned}$$

Definition 2.3

A mapping $P_C:H \rightarrow C$ is called a metric projection if for any point $w \in H,$ there exists a unique point $P_Cw \in C$ such that

$$\begin{aligned} ||w -P_Cw|| \le ||w - y||,\quad ~ \forall ~ y\in C. \end{aligned}$$

We know that $P_C$ is a nonexpansive mapping and satisfies the following characterization.

• (i) $\langle x-y, P_C x - P_C y \rangle \ge ||P_C x-P_C y||^2,$ for every $x,y \in H;$

• (ii) for $x \in H$ and $z\in C$, $z = P_C x \Leftrightarrow$

  $$\begin{aligned} \langle x-z, z-y \rangle \ge 0, ~~\forall y \in C; \end{aligned}$$

  (2.1)

• (iii) for $x \in H$ and $y \in C$,

  $$\begin{aligned} ||y-P_C(x)||^2 + ||x- P_C(x)||^2 \le ||x-y||^2. \end{aligned}$$

  (2.2)

The normal cone of a nonempty closed convex subset C of H at a point $x \in C$, denoted by $N_C(x),$ is defined as

$$\begin{aligned} N_C(x) = \{ u \in H : \langle u, y-x \rangle \le 0, ~~\forall y \in C\}. \end{aligned}$$

Next, we recall some basic concepts of nonexpansive mapping and its generalization.

Definition 2.4

Let $T:C \rightarrow C$ be a nonlinear operator. Then T is called (see for example, Maingé 2008)

• (i) nonexpansive if

  $$\begin{aligned} ||Tx - Ty|| \le ||x-y||,\quad \forall ~ x,y \in C; \end{aligned}$$

• (ii) quasi-nonexpansive mapping if $F(T) \ne \emptyset$ and

  $$\begin{aligned} ||Tx - p|| \le ||x -p||,\quad \forall ~x \in C, p \in F(T); \end{aligned}$$

• (iii) k-strictly pseudocontractive if there exists a constant $k \in [0,1)$ such that

  $$\begin{aligned} ||Tx - Ty||^2 \le ||x-y||^2 + k||(I-T)x - (I-T)y||^2 \quad \forall ~x,y \in C; \end{aligned}$$

• (iv) $\beta$-demicontractive mapping if there exists $\beta \in [0,1)$ such that

  $$\begin{aligned} ||Tx - p||^2 \le ||x - p||^2 +\beta ||x- Tx||^2, \quad \forall ~x \in C, p \in F(T). \end{aligned}$$

  (2.3)

The following results will be used in the sequel.

Lemma 2.5

(Marino and Xu 2007; Zegeye and Shahzad 2011) In a real Hilbert space H, the following inequalities hold:

• (i) $||x-y||^2 = ||x||^2 - 2\langle x, y \rangle + ||y||^2 , ~~~\forall x,y \in H;$

• (ii) $||x+y||^2 \le ||x||^2 + 2\langle y, x+y \rangle , ~~\forall x,y \in H;$

• (iii) $||\alpha x + (1-\alpha )y ||^2 = \alpha ||x||^2 + (1-\alpha )||y||^2 - \alpha (1-\alpha )||x-y||^2, ~~\forall x,y \in H$ and $\alpha \in [0,1].$

It is well known that the demicontractive mappings have the following property.

Lemma 2.6

(Maingé 2008, Remark 4.2, pp 1506) Let T be a $\beta$-demicontractive self-mapping on H with $F(T) \ne \emptyset$ and set $T_w :=(1-w)I+wT$ for $w \in (0,1].$ Then

• (i) $T_w$ is a quasi-nonexpansive mapping if $w \in [0, 1 - \beta ]$;

• (ii) F(T) is closed and convex.

Definition 2.7

(See Lin et al. 2005; Mashreghi and Nasri 2010) The Minty Variational Inequality Problem (MVIP) is defined as finding a point ${\bar{x}} \in C$ such that

$$\begin{aligned} \langle Ay, y - {\bar{x}} \rangle \ge 0, \quad \forall y \in C. \end{aligned}$$

(2.4)

We denote by M(C, A) the set of solution of (1.1). Some existence results for the MVIP have been presented in Lin et al. (2005). Also, the assumption that $M(C,A) \ne \emptyset$ has already been used for solving VI(C, A) in finite dimensional spaces (see e.g., Solodov and Svaiter 1999). It is not difficult to prove that pseudo-monotonicity implies property $M(C,A) \ne \emptyset$, but the converse is not true. Indeed, let $A:{\mathbb {R}} \rightarrow {\mathbb {R}}$ be defined by $A(x) = \cos (x)$ with $C = [0, \frac{\pi }{2}]$. We have that $VI(C,A) = \{0, \frac{\pi }{2}\}$ and $M(C,A) = \{0\}$. But if we take $x = 0$ and $y = \frac{\pi }{2}$ in Definition 2.1(d), we see that A is not pseudo-monotone.

Lemma 2.8

(See Mashreghi and Nasri 2010) Consider the VIP (1.1). If the mapping $h:[0,1] \rightarrow E^{*}$ defined as $h(t) = A(tx + (1-t)y)$ is continuous for all $x,y \in C$ (i.e., h is hemicontinuous), then $M(C,A) \subset VI(C,A)$. Moreover, if A is pseudo-monotone, then VI(C, A) is closed, convex and $VI(C,A) = M(C,A).$

The following lemma was proved in ${\mathbb {R}}^n$ in Fang and Chen (2015) and can easily be extended to a real Hilbert space.

Lemma 2.9

Let H be a real Hilbert space and C be a nonempty closed and convex subset of H. For any $x \in H$ and $\lambda >0,$ we denote

$$\begin{aligned} r_{\lambda }(x):= x - P_C(x - \lambda Ax), \end{aligned}$$

(2.5)

then

$$\begin{aligned} \min \{1,\lambda \}||r_{1}(x)|| \le ||r_{\lambda }(x)||\le \max \{1,\lambda \}||r_{1}(x)||. \end{aligned}$$

Lemma 2.10

(Lemma 2.2 of Witthayarat et al. 2012) Let B be a k-Lipschitzian and $\eta$-strongly monotone operator on a Hilbert space H with $k>0,$ $\eta >0,$ $0<\mu <\frac{2\eta }{k^2}$ and $0<\alpha <1.$ Then $S:=(I-\alpha \mu B):H \rightarrow H$ is a contraction with a contractive coefficient $1-\alpha \tau$ and $\tau = \frac{1}{2}\mu (2\eta - \mu k^2).$

Lemma 2.11

(Xu 2002) Let $\{a_n\}$ be a sequence of nonnegative real numbers satisfying the following relation:

$$\begin{aligned} a_{n+1} \le (1-\alpha _n)a_n + \alpha _n \sigma _n + \gamma _n, \quad n\ge 1, \end{aligned}$$

where

• (i) $\{\alpha _n\}\subset [0,1],$ $\sum \nolimits _{n=1}^{\infty }\alpha _n = \infty ,$

• (ii) $\limsup \nolimits _{n\rightarrow \infty }\sigma _n \le 0,$

• (iii) $\gamma _n \ge 0,$ ($n \ge 1)$ and $\sum \nolimits _{n=1}^\infty \gamma _n < \infty .$

Then, $a_n \rightarrow 0$ as $n \rightarrow \infty$.

Lemma 2.12

(Maingé 2008) Let $\{a_n\}$ be a sequence of real numbers such that there exists a subsequence $\{n_i\}$ of $\{n\}$ with $a_{n_i} < a_{n_i+1}$ for all $i \in {\mathbb {N}}$. Consider the integer $\{m_k\}$ defined by

$$\begin{aligned} m_k = \max \{j \le k: a_j < a_{j+1}\}. \end{aligned}$$

Then $\{m_k\}$ is a nondecreasing sequence verifying $\lim _{n \rightarrow \infty }m_n = \infty ,$ and for all $k \in {\mathbb {N}},$ the following estimates hold:

$$\begin{aligned} a_{m_k} \le a_{m_k+1} \quad \mathrm{and} \quad a_k \le a_{m_k+1}. \end{aligned}$$

3 Main results

In this section, we give a precise statement of our algorithm and discuss its strong convergence.

Let C be a nonempty closed and convex subset of a real Hilbert space H. Let $A:H \rightarrow H$ be a pseudo-monotone and L-Lipschitz continuous operator and $T:H \rightarrow H$ be a $\beta$-demicontractive mapping with constant $\beta \in [0,1)$ and demiclosed at zero. Suppose Sol $:= VI(C,A)\bigcap F(T) \ne \emptyset ,$ let $B:H \rightarrow H$ be a k-Lipschitzian and $\eta$-strongly monotone mapping with $k>0$ and $\eta >0$ and $f:H \rightarrow H$ be a $\rho$-Lipschitz mapping with $\rho >0$. Let $0< \mu < \frac{2\eta }{k^2}$ and $0< \xi \rho < \tau ,$ where $\tau = \frac{1}{2}\mu (2\eta - \mu k^2).$ Let $\{\alpha _k\}$ and $\{v_k\}$ be sequences in (0, 1) and $\{x_k\}$ be generated by the following algorithm:

To establish the convergence of Algorithm 3.1, we make the following assumption:

• (C1) $\lim \nolimits _{k\rightarrow \infty }\alpha _k = 0$ and $\sum \limits _{k=0}^{\infty } \alpha _k = \infty ;$

• (C2) $\liminf \nolimits _{k \rightarrow \infty }\lambda _{k}>0;$

• (C3) $\liminf \nolimits _{k \rightarrow \infty }(v_{k}-\beta )v_{k}>0$.

Remark 3.2

Observe that if $x_k = y_k$ and $x_k - Tx_k = 0$, then we are at a common solution of the variational inequality (1.1) and fixed point of the demicontractive mapping T. In our convergence analysis, we will implicitly assume that this does not occur after finitely many iterations so that our Algorithm 3.1 generates infinite sequences. We will see in the following result that the Algorithm 3.1 is well defined. To do this, it suffices to show that the Armijo line searching rule defined by (3.2) is well defined and $\delta _k \ne 0.$

Lemma 3.3

There exists a nonnegative integer $l_k$ satisfying (3.2). In addition,

$$\begin{aligned} \delta _k \ge \frac{1 -\theta }{(1+\theta )^2}. \end{aligned}$$

(3.7)

Proof

Let $r_{\lambda _k}(x_k) = x_k - P_C(x_k - \lambda _k Ax_k)$ and suppose $r_{\gamma ^{k_0}}(x_k) = 0$ for some $k_0 \ge 1.$ Take $l_k = k_0$ which satisfies (3.2). Suppose $r_{\gamma ^{k_1}}(x_k) \ne 0$ for some $k_1 \ge 1$ and assume the contrary, that is,

$$\begin{aligned} {\gamma ^{l}}||Ax_k - A(P_C(x_k - \gamma ^{l}Ax_k))|| > {\theta }||r_{\gamma ^{l}}(x_k)||. \end{aligned}$$

Then it follows from Lemma 2.9 and the fact that $\gamma \in (0,1)$ that

$$\begin{aligned} ||Ax_k - A(P_C(x_k - \gamma ^{l}Ax_k))||> & {} \frac{\theta }{\gamma ^{l}}||r_{\gamma ^{l}}(x_k)|| \nonumber \\\ge & {} \frac{\theta }{\gamma ^{l}}\min \{1,\gamma ^{l}\}||r_1(x_k)|| \nonumber \\= & {} \theta ||r_1(x_k)||. \end{aligned}$$

(3.8)

Since $P_C$ is continuous, we have that

$$\begin{aligned} P_C(x_k- \gamma ^{l}Ax_k) \rightarrow P_C(x_k),~~~~ l \rightarrow \infty . \end{aligned}$$

We now consider two cases, namely when $x_k \in C$ and $x_k \notin C.$

• (i) If $x_k \in C,$ then $x_k = P_Cx_k$. Now since $r_{\gamma ^{k_1}}(x_k) \ne 0$ and $\gamma ^{k_1} \le 1$, it follows from Lemma 2.9 that

  $$\begin{aligned} 0< & {} ||r_{\gamma ^{k_1}}(x_k)|| \le \max \{1, \gamma ^{k_1}\}||r_1(x_k)|| \\= & {} ||r_1(x_k)||. \end{aligned}$$

  Letting $l \rightarrow \infty$ in (3.7), we have that

  $$\begin{aligned} 0 = ||Ax_k - Ax_k|| \ge \theta ||r_1(x_k)|| > 0. \end{aligned}$$

  This is a contradiction and so (3.2) is valid.

• (ii) $x_k \notin C,$ then

  $$\begin{aligned} \gamma ^{l}||Ax_k - Ay_k|| \rightarrow 0,\quad l \rightarrow \infty , \end{aligned}$$

  (3.9)

  while

  $$\begin{aligned} \lim _{l\rightarrow \infty }\theta ||r_{\gamma ^{l}}(x_k)|| = \lim _{l\rightarrow \infty }\theta ||x_k - P_C(x_k - \gamma ^{l}Ax_k)|| = \theta ||x_k - P_Cx_k|| > 0. \end{aligned}$$

  This is a contradiction. Therefore, the Armijo line searching rule in (3.2) is well defined.

On the other hand, since A is Lipschitz continuous, then, we have from (3.2) and (3.3):

$$\begin{aligned} \langle x_k - y_k, d(x_k,y_k)\rangle= & {} \langle x_k - y_k, x_k - y_k - \lambda _k (Ax_k - Ay_k) \rangle \nonumber \\= & {} ||x_k - y_k||^2 - \lambda _k \langle x_k - y_k, Ax_k - Ay_k \rangle \nonumber \\\ge & {} ||x_k - y_k||^2 - \lambda _k ||x_k - y_k||||Ax_k - Ay_k|| \nonumber \\\ge & {} ||x_k - y_k||^2 - \theta ||x_k -y_k||^2 \nonumber \\= & {} (1-\theta )||x_k - y_k||^2. \end{aligned}$$

(3.10)

Also,

$$\begin{aligned} ||d(x_k,y_k)||= & {} ||x_k - y_k - \lambda _k(Ax_k - Ay_k)|| \nonumber \\\le & {} ||x_k - y_k|| + \lambda _{k}||Ax_k - Ay_k|| \nonumber \\\le & {} (1+\theta )||x_k -y_k||. \end{aligned}$$

(3.11)

Therefore from (3.5), (3.10) and (3.11), we get

$$\begin{aligned} \delta _k= & {} \frac{\langle x_k - y_k, d(x_k,y_k)\rangle }{||d(x_k,y_k)||^2} \\\ge & {} \frac{(1-\theta )}{(1+\theta )^2}. \end{aligned}$$

$\square$

Now, we prove that the sequences $\{x_k\},\{y_k\}$ and $\{w_k\}$ generated by Algorithm 3.1 are bounded.

Lemma 3.4

The sequence $\{x_k\}$ generated by Algorithm 3.1 is bounded. In addition, the following inequality is satisfied:

$$\begin{aligned} ||w_k -x^*||^2 \le ||x_k -x^*||^2 - \frac{(2 -\sigma )}{\sigma }||w_k -x_k||^2, \end{aligned}$$

(3.12)

where $x^* \in Sol$.

Proof

Let $x^* \in$ Sol, then by Lemma 2.5 (i), we obtain

$$\begin{aligned} ||w_k - x^*||^2= & {} ||x_k -x^* - \sigma \delta _kd(x_k,y_k)||^2 \nonumber \\= & {} ||x_k -x^*||^2 - 2\sigma \delta _k \langle x_k - x^*, d(x_k, y_k) \rangle + \sigma ^2 \delta _k^2||d(x_k,y_k)||^2.\nonumber \\ \end{aligned}$$

(3.13)

Observe that

$$\begin{aligned} \langle x_k -x^*, d(x_k,y_k) \rangle = \langle x_k -y_k, d(x_k,y_k) \rangle + \langle y_k -x^*, d(x_k,y_k) \rangle . \end{aligned}$$

(3.14)

Since $y_k = P_C(x_k - \lambda _k Ax_k)$ and $x^* \in$ Sol, then by the variational characterization of $P_C$, we have

$$\begin{aligned} \langle x_k -\lambda _k Ax_k -y_k , y_k - x^* \rangle \ge 0, \end{aligned}$$

(3.15)

and from the pseudo-monotonicity of A, we have

$$\begin{aligned} \langle Ay_k,y_k -x^* \rangle \ge 0. \end{aligned}$$

(3.16)

Hence, combining (3.15) and (3.16), with the fact that $\lambda _k > 0$, we get

$$\begin{aligned} \langle d(x_k,y_k), y_k -x^* \rangle \ge 0. \end{aligned}$$

(3.17)

Thus from (3.17) and (3.14) , we get

$$\begin{aligned} \langle x_k -x^*, d(x_k,y_k) \rangle \ge \langle x_k - y_k, d(x_k,y_k) \rangle . \end{aligned}$$

(3.18)

Therefore, (3.13) yields

$$\begin{aligned} ||w_k -x^*||^2\le & {} ||x_k -x^*||^2 -2\sigma \delta _k \langle x_k -y_k, d(x_k,y_k) \rangle + \sigma ^2 \delta _k^2||d(x_k,y_k)||^2 \nonumber \\= & {} ||x_k -x^*||^2 -2\sigma \delta _k \langle x_k -y_k, d(x_k,y_k) \rangle + \sigma ^2 \delta _k \langle x_k - y_k, d(x_k,y_k) \rangle \nonumber \\= & {} ||x_k -x^*||^2 - \sigma (2 - \sigma )\delta _k \langle x_k -y_k, d(x_k,y_k) \rangle . \end{aligned}$$

(3.19)

From the definition of $\delta _k$ and $w_k$, we have

$$\begin{aligned} \delta _k\langle x_k -y_k, d(x_k,y_k) \rangle= & {} ||\delta _k d(x_k,y_k)||^2 \nonumber \\= & {} \frac{1}{\sigma ^2}||w_k -x_k||^2 . \end{aligned}$$

(3.20)

Substituting (3.20) into (3.19), we have

$$\begin{aligned} ||w_k -x^*||^2 \le ||x_k -x^*||^2 - \frac{(2-\sigma )}{\sigma }||w_k - x_k||^2. \end{aligned}$$

Hence,

$$\begin{aligned} ||w_k -x^*||^2 \le ||x_k -x^*||^2. \end{aligned}$$

(3.21)

Now, let $T_v = vT + (1 - v)I$, then by Lemma 2.6, $T_v$ is quasi-nonexpansive. Using Lemma 2.10, we have

$$\begin{aligned} ||x_{k+1} -x^*||= & {} ||\alpha _k \xi f(x_k) + (1-\alpha _k \mu B)T_{v_k}w_k - x^*|| \nonumber \\= & {} ||\alpha _k(\xi f(x_k) - \mu Bx^*) + (I-\alpha _k\mu B)T_{v_k}w_k - (I-\alpha _k\mu B)x^*|| \nonumber \\= & {} ||(I-\alpha _k\mu B)(T_{v_k}w_k - x^*) + \alpha _k (\xi f(x_k) - \mu Bx^* + \xi f(x^*) - \xi f(x^*))|| \nonumber \\\le & {} ||(I{-}\alpha _k\mu B)(T_{v_k}w_k {-} x^*)|| {+} \alpha _k \xi ||f(x_k) {-} f(x^*)|| {+} \alpha _k||\xi f(x^*) {-} \mu Bx^*|| \nonumber \\\le & {} (1-\alpha _k \tau )||T_{v_k}w_k -x^*|| + \alpha _k \xi \rho ||x_k -x^*|| + \alpha _k ||\xi f(x^*) - \mu Bx^*|| \nonumber \\\le & {} (1-\alpha _k \tau )||w_k - x^*|| + \alpha _k \rho ||x_k -x^*|| + \alpha _k||\xi f(x^*) - \mu Bx^*|| \nonumber \\\le & {} (1-\alpha _k\tau )||x_k -x^*|| + \alpha _k \xi \rho ||x_k -x^*|| + \alpha _k||\xi f(x^*) - \mu Bx^* || \nonumber \\= & {} (1-\alpha _k(\tau - \xi \rho ))||x_k -x^*|| + \alpha _k(\tau -\xi \rho )\frac{ ||\xi f(x^*) - \mu B(x^*)||}{\tau - \xi \rho } \nonumber \\\le & {} \max \left\{ ||x_k -x^*||, \frac{ ||\xi f(x^*) - \mu B(x^*)||}{\tau - \xi \rho } \right\} \nonumber \\&\vdots&\nonumber \\\le & {} \max \left\{ ||x_1 -x^*||, \frac{ ||\xi f(x^*) - \mu B(x^*)||}{\tau - \xi \rho } \right\} . \end{aligned}$$

(3.22)

This implies that $\{||x_k - x^*||\}$ is bounded and so $\{x_k\}$ is bounded in H. Consequently, from (3.21), $\{w_k\}$ is bounded and since A is continuous, then $\{Ax_k\}$ is bounded and therefore $\{y_k\}$ is bounded too. $\square$

Lemma 3.5

The sequence $\{x_n\}$ generated by Algorithm 3.1 satisfies the following estimates:

• (i) $s_{k+1} \le (1-a_k)s_k + a_kb_k ,$

• (ii) $-1 \le \limsup \nolimits _{k \rightarrow \infty }b_k < + \infty$,

where $s_k = ||x_k -x^*||^2, \quad a_k = \frac{2\alpha _k(\tau - \xi \rho )}{1 - \alpha _k \xi \rho },$ $b_k = \frac{\alpha _k\tau ^2 M_1}{2(\tau - \xi \rho )} + \frac{1}{\tau - \xi \rho }\langle \xi f(x^*) - \mu B(x^*), x_{k+1} - x^* \rangle ,$ for some $M_1 >0,$ $x^* \in Sol.$

Proof

Let $x^* \in \mathrm{Sol},$ then from Lemma 2.5FPar52.5 (ii) and (3.6), we have

$$\begin{aligned} ||x_{k+1} - x^*||^2= & {} ||\alpha _k \xi f(x_k) + (1-\alpha _k \mu B)T_{v_k}w_k - x^*||^2 \\= & {} ||\alpha _k (\xi f(x_k) - \mu B(x^*)) + (1-\alpha _k \mu B)T_{v_k}w_k - (1- \alpha _k \mu B)x^* ||^2 \\\le & {} ||(1{-}\alpha _k \mu B)T_{v_k}w_k {-} (1{-} \alpha _k \mu B)x^*||^2 {+} 2\alpha _k \langle \xi f(x_k) {-} \mu B(x^*), x_{k+1} {-} x^* \rangle \\\le & {} (1-\alpha _k \tau )^2||w_k - x^*||^2 + 2\alpha _k \xi \langle f(x_k) -f(x^*), x_{k+1} - x^* \rangle \\&+\, 2 \alpha _k \langle \xi f(x^*) - \mu B(x^*), x_{k+1} - x^* \rangle \\\le & {} (1-\alpha _k\tau )^2 ||x_k -x^*||^2 + 2\alpha _k \xi \rho ||x_k -x^*||||x_{k+1} -x^*|| \\&+\, 2 \alpha _k \langle \xi f(x^*) - \mu B(x^*), x_{k+1} -x^* \rangle \\\le & {} (1-\alpha _k\tau )^2 ||x_k -x^*||^2 + \alpha _k\xi \rho (||x_k -x^*||^2 + ||x_{k+1} -x^*||^2) \\&+ \,2 \alpha _k \langle \xi f(x^*) - \mu B(x^*), x_{k+1} -x^* \rangle . \end{aligned}$$

This implies that

$$\begin{aligned} ||x_{k+1} {-}x^*||^2\le & {} \frac{(1{-}\alpha _k\tau )^2{+}\alpha _k \xi \rho }{1 {-} \alpha _k \xi \rho }||x_k {-}x^*||^2 {+} \frac{2\alpha _k}{1 {-} \alpha _k \xi \rho }\langle \xi f(x^*) {-} \mu B(x^*), x_{k+1} {-}x^* \rangle \\= & {} \left( 1 - \frac{2\alpha _k(\tau - \xi \rho )}{1 - \alpha _k \xi \rho }\right) ||x_k - x^*||^2 + \frac{\alpha _k^2 \tau ^2}{1-\alpha _k \xi \rho }||x_k -x^*||^2 \\&+\, \frac{2 \alpha _k}{1-\alpha _k\xi \rho }\langle \xi f(x^*) - \mu B(x^*), x_{k+1} -x^* \rangle \\\le & {} \left( 1 - \frac{2\alpha _k(\tau - \xi \rho )}{1 - \alpha _k \xi \rho }\ \right) ||x_k - x^*||^2 \\&+ \frac{2\alpha _k (\tau - \xi \rho )}{1 - \alpha _k \xi \rho } \left\{ \frac{\alpha _k\tau ^2 M_1}{2(\tau - \xi \rho )} + \frac{1}{\tau - \xi \rho }\langle \xi f(x^*) - \mu B(x^*), x_{k+1} - x^* \rangle \right\} \\= & {} (1-a_k)s_k + a_k b_k, \end{aligned}$$

where the exisence of $M_1$ follows from the boundedness of $\{x_k\}$. This established (i).

Next, we prove (ii). Since $\{x_k\}$ is bounded and $\alpha _k \in (0,1)$, we have that

$$\begin{aligned} \sup _{k \ge 0}b_k \le \sup _{k \ge 0} \dfrac{1}{2(\tau - \xi \rho )}\Big (\tau ^2 M_1 + 2||\xi f(x^*) - \mu B(x^*)|||| x_{k+1} - x^*|| \Big )<\infty . \end{aligned}$$

We next show that $\limsup _{k \rightarrow \infty }b_k \ge -1.$ Assume the contrary that $\limsup _{k \rightarrow \infty }b_k < -1$, which implies that there exists $k_0 \in {\mathbb {N}}$ such that $b_k \le -1$ for all $k \ge k_0$. Hence, it follows from (i) that

$$\begin{aligned} s_{k+1}\le & {} (1 - a_k) s_k + a_kb_k \\< & {} (1- a_k) s_k - a_k \\= & {} s_k - a_k(s_k +1) \\\le & {} s_k - 2(\tau - \xi \rho )\alpha _k. \end{aligned}$$

By induction, we get that

$$\begin{aligned} s_{k+1} \le s_{k_0}- 2(\tau - \xi \rho )\sum _{i= k_0}^{k}\alpha _i \qquad \text {for all}~~k \ge k_0. \end{aligned}$$

Taking $\limsup$ of both sides in the last inequality, we have that

$$\begin{aligned} \limsup _{k \rightarrow \infty }s_k \le s_{k_0} - \lim _{k \rightarrow \infty }2(\tau - \xi \rho )\sum _{i= k_0}^{k}\alpha _i = -\infty . \end{aligned}$$

This contradicts the fact that $\{s_k\}$ is a nonnegative real sequence. Therefore, $\limsup _{k \rightarrow \infty }b_k \ge -1.$ $\square$

Lemma 3.6

Let $\{x_{k_j}\}$ be a subsequence of the sequence $\{x_k\}$ generated by Algorithm 3.1 such that $x_{k_j} \rightharpoonup p \in C.$ Suppose $||x_k - y_k|| \rightarrow 0$ as $k \rightarrow \infty$ and $\liminf _{j\rightarrow \infty }\lambda _{k_j} >0.$ Then,

• (i) $0 \le \liminf _{j\rightarrow \infty }\langle Ax_{k_j}, x - x_{k_j} \rangle$, for all $x \in C;$

• (ii) $p \in VI(C,A).$

Proof

• (i) Since $y_{k_j} = P_C(x_{k_j} - \lambda _{k_j} Ax_{k_j}),$ from the variational characterization of $P_C$ (i.e., (2.1)), we have

  $$\begin{aligned} \langle x_{k_j} - \lambda _{k_j} Ax_{k_j} - y_{k_j}, x- y_{k_j} \rangle \le 0, \quad ~ \forall ~x \in C. \end{aligned}$$

  Hence,

  $$\begin{aligned} \langle x_{k_j} - y_{k_j},x- y_{k_j} \rangle\le & {} \lambda _{k_j} \langle Ax_{k_j}, x - y_{k_k} \rangle \\= & {} \lambda _{k_j} \langle Ax_{k_j}, x_{k_j} - y_{k_j} \rangle + \lambda _{k_j} \langle Ax_{k_j}, x - x_{k_k} \rangle . \end{aligned}$$

  This implies that

  $$\begin{aligned} \langle x_{k_j} - y_{k_j},x- y_{k_j} \rangle +\lambda _{k_j} \langle Ax_{k_j}, y_{k_j} - x_{k_j} \rangle \le \lambda _{k_j} \langle Ax_{k_j}, x - x_{k_k} \rangle . \end{aligned}$$

  (3.23)

  Fix $x \in C$ and let $j \rightarrow \infty$ in (3.23), since $||x_{k_j} - y_{k_j}|| \rightarrow 0$ and by condition (C2), $\liminf _{j\rightarrow \infty }\lambda _{k_j} >0$, we have

  $$\begin{aligned} 0 \le \liminf _{j\rightarrow \infty }\langle Ax_{k_j}, x - x_{k_j} \rangle , \quad \forall ~x \in C. \end{aligned}$$

  (3.24)

• (ii) Let $\{\epsilon _j\}$ be a sequence of decreasing non-negative numbers such that $\epsilon _j \rightarrow 0$ as $j \rightarrow \infty .$ For each $\epsilon _j,$ we denote by N the smallest positive integer such that

  $$\begin{aligned} \langle Ax_{k_j}, x - x_{k_j} \rangle + \epsilon _j \ge 0, \quad \forall ~ j \ge N, \end{aligned}$$

  where the existence of N follows from (i). This implies that

  $$\begin{aligned} \langle Ax_{k_j}, x + \epsilon _j t_{k_j} - x_{k_j} \rangle \ge 0, \quad \forall j \ge N, \end{aligned}$$

  for some $t_{k_j} \in H$ satisfying $1 = \langle Ax_{k_j}, t_{k_j} \rangle$ (since $Ax_{k_j} \ne 0$). Since A is pseudo-monotone, then we have from (i) that

  $$\begin{aligned} \langle A(x+\epsilon _j t_{k_j}), x + \epsilon _j t_{k_j} - x_{k_j} \rangle \ge 0, \quad \forall j \ge N, \end{aligned}$$

  which implies that

  $$\begin{aligned} \langle Ax, x - x_{k_j} \rangle \ge \langle Ax - A(x + \epsilon _jt_{k_j}), x + \epsilon _jt_{k_j} - x_{k_j} \rangle - \epsilon _j\langle Ax, t_{k_j} \rangle \quad \forall ~j \ge N. \end{aligned}$$

  (3.25)

  Since $\epsilon _j \rightarrow 0$ and A is continuous, the right hand side of (3.25) tends to zero. Thus, we obtain that

  $$\begin{aligned} \liminf _{j\rightarrow \infty }\langle Ax, x - x_{k_j} \rangle \ge 0, \quad \forall ~x \in C. \end{aligned}$$

  Hence,

  $$\begin{aligned} \langle Ax, x - p \rangle = \lim _{j\rightarrow \infty }\langle Ax, x - x_{k_j} \rangle \ge 0, \quad \forall ~x \in C. \end{aligned}$$

  Therefore from Lemma 2.8FPar82.8, we obtain that $p \in VI(C,A).$

$\square$

We are now in a position to prove the convergence of our Algorithm.

Theorem 3.7

Let C be a nonempty closed and convex subset of a real Hilbert space H. Let $A:H \rightarrow H$ be a pseudo-monotone and L-Lipschitz continuous operator and $T:H \rightarrow H$ be a $\beta$-demicontractive mapping with constant $\beta \in [0,1)$ and demiclosed at zero. Suppose $Sol:= VI(C,A)\bigcap F(T),$ let $B:H \rightarrow H$ be a k-Lipschitz and $\eta$-strongly monotone mapping with $k>0$ and $\eta >0$ and $f:H \rightarrow H$ be a $\rho$-Lipschitz mapping with $\rho >0$. Let $0< \mu < \frac{2\eta }{k^2}$ and $0< \xi \rho < \tau ,$ where $\tau = \frac{1}{2}\mu (2\eta - \mu k^2).$ Let $\{\alpha _k\}$ and $\{v_k\}$ be sequences in (0, 1),  $\{x_k\}$ such that Assumptions (C1)–(C3) are satisfied. Then, sequence $\{x_k\}$ generated by Algorithm 3.1 converges strongly to a point $x^\dagger$, where $x^\dagger = P_{Sol}(I - \mu B + \xi f)(x^\dagger )$ is a unique solution of the variational inequality

$$\begin{aligned} \langle (\mu B - \xi f)x^\dagger , x^\dagger -x \rangle \le 0,\quad \forall ~~x \in Sol. \end{aligned}$$

(3.26)

Proof

Let $x^* \in$ Sol and put $\Gamma _k : = ||x_k -x^*||^2.$ We divide the proof into two cases.

Case I: Suppose that there exists $k_0 \in {\mathbb {N}}$ such that $\{\Gamma _k\}$ is monotonically non-increasing for $k\ge k_0.$ Since $\{\Gamma _k\}$ is bounded (from Lemma 3.4), then $\{\Gamma _k\}$ converges and therefore

$$\begin{aligned} \Gamma _k - \Gamma _{k+1} \rightarrow 0, \quad n \rightarrow \infty . \end{aligned}$$

(3.27)

Let $z_k = (1-v_k)w_k + v_k Tw_k,$ then using Lemma 2.5 (iii), we have

$$\begin{aligned} ||z_k -x^*||^2= & {} ||(1-v_k)(w_k - x^*) + v_k (Tw_k -x^*)||^2 \nonumber \\= & {} (1-v_k)||w_k -x^*||^2 + v_k||Tw_k - x^*||^2 - v_k(1-v_k)||w_k - Tw_k||^2 \nonumber \\\le & {} (1-v_k)||w_k -x^*||^2 + v_k(||w_k -x^*||^2 \nonumber \\&+ \beta ||w_k -Tw_k||^2) - v_k (1-v_k)||w_k -Tw_k||^2 \nonumber \\= & {} ||w_k -x^*||^2 -v_k(1 -v_k - \beta )||w_k -Tw_k||^2. \end{aligned}$$

(3.28)

Then, from Lemma ( 2.5) (ii) and (3.12), we have

$$\begin{aligned} ||x_{k+1} -x^*||^2= & {} ||\alpha _k \xi f(x_k) + (1-\alpha _k \mu B)z_k -x^* ||^2 \nonumber \\= & {} ||\alpha _k (\xi f(x_k) - \mu B(x^*)) + (1-\alpha _k \mu B)(z_k -x^*)||^2 \nonumber \\\le & {} ||(1-\alpha _k \mu B)(z_k - x^*)||^2 + 2 \alpha _k \langle \xi f(x_k) - \mu Bx^*, x_{k+1} -x^* \rangle \nonumber \\\le & {} (1-\alpha _k \tau )^2(||w_k -x^*||^2 - v_k(1 -v_k - \beta )||w_k - Tw_k||^2) \nonumber \\&+ 2 \alpha _k \langle \xi f(x_k) - \mu Bx^*, x_{k+1} -x^* \rangle \nonumber \\\le & {} (1-\alpha _k \tau )^2\left( ||x_k - x^*||^2 - \frac{2-\sigma }{\sigma }||w_k -x_k||^2\right) \nonumber \\&- \,(1-\alpha _k \tau )v_k(1-v_k -\beta )||w_k -Tw_k||^2 \nonumber \\&+ 2 \alpha _k \langle \xi f(x_k) - \mu Bx^*, x_{k+1} -x^* \rangle . \end{aligned}$$

(3.29)

Hence,

$$\begin{aligned} (1-\alpha _k \tau )^2\left( \frac{2 -\sigma }{\sigma }\right) ||w_k - x_k||^2\le & {} (1-\alpha _k \tau )^2||x_k -x^*||^2 -||x_{k+1} -x^*||^2 \\&+\, 2 \alpha _k \langle \xi f(x_k) - \mu Bx^*, x_{k+1} -x^* \rangle \\\le & {} \Gamma _k -\Gamma _{k+1} - \alpha _k M + 2 \alpha _k \langle \xi f(x_k) - \mu Bx^*, x_{k+1} -x^* \rangle , \end{aligned}$$

for some $M>0$. Since $\alpha _k \rightarrow 0$ and from (3.27), we have

$$\begin{aligned} \left( \frac{2 -\sigma }{\sigma }\right) ||w_k - x_k||^2 \rightarrow 0, \quad n \rightarrow \infty . \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{k \rightarrow \infty }||w_k -x_k|| = 0. \end{aligned}$$

(3.30)

From 3.20)3.20, we have

$$\begin{aligned} \langle x_k - y_k, d(x_k,y_k) \rangle \le \frac{(1+\theta )^2}{(1-\theta )\sigma ^2}||w_k -x_k||^2. \end{aligned}$$

(3.31)

Using (3.10), we have

$$\begin{aligned} ||x_k -y_k||^2 \le \frac{(1+\theta )^2}{(1-\theta )^2\sigma ^2}||w_k - x_k||^2. \end{aligned}$$

(3.32)

From (3.30) and (3.32), we have

$$\begin{aligned} ||x_k - y_k|| \rightarrow 0, ~~~~~n \rightarrow \infty . \end{aligned}$$

(3.33)

Therefore,

$$\begin{aligned} ||w_k - y_k|| \le ||w_k -x_k|| + ||x_k - y_k|| \rightarrow 0, ~~~n \rightarrow \infty . \end{aligned}$$

(3.34)

Also from (3.29), we have

$$\begin{aligned} (1-\alpha _k \tau )^2v_k(1-v_k -\beta )||w_k -Tw_k||^2\le & {} (1-\alpha _k \tau )^2||x_k -x^*||^2 - ||x_{k+1} -x^*||^2 \\&+\, 2 \alpha _k \langle \xi f(x_k) - \mu Bx^*, x_{k+1} -x^* \rangle \\\le & {} \Gamma _k - \Gamma _{k+1} - \alpha _kM + 2 \alpha _k \langle \xi f(x_k) \\&-\, \mu Bx^*, x_{k+1} -x^* \rangle , \end{aligned}$$

for some $M>0$. Since $\alpha _k \rightarrow 0$ and from (3.27), we have

$$\begin{aligned} v_k(1-v_k -\beta )||w_k -Tw_k||^2 \rightarrow 0, \quad n \rightarrow \infty . \end{aligned}$$

Therefore from condition (C3), we have

$$\begin{aligned} \lim _{k \rightarrow \infty }||w_k -Tw_k|| = 0. \end{aligned}$$

(3.35)

Furthermore, from (3.34),

$$\begin{aligned} ||z_k -w_k||= & {} ||(1-v_k)w_k + v_k Tw_k - w_k|| \nonumber \\= & {} v_k ||w_k - Tw_k|| \rightarrow 0, \quad n \rightarrow \infty , \end{aligned}$$

(3.36)

and

$$\begin{aligned} ||x_{k+1} -z_k||= & {} ||\alpha _k \xi f(x_k) + (1-\alpha _k \mu B)z_k - z_k || \nonumber \\= & {} \alpha _k || \xi f(x_k) - \mu B(z_k)|| \rightarrow 0, \quad n \rightarrow \infty . \end{aligned}$$

(3.37)

Therefore from (3.30), (3.36) and (3.37), we have

$$\begin{aligned} ||x_{k+1}- x_{k}||\le & {} ||x_{k+1} - z_k|| + ||z_k - w_k||+||w_k -x_k|| \rightarrow 0, ~~~~ n \rightarrow \infty . \end{aligned}$$

(3.38)

Since $\{x_k\}$ is bounded, there exists $\{x_{k_l}\}$ of $\{x_k\}$ such that $x_{k_l} \rightharpoonup p$ as $l \rightarrow \infty .$ From (3.35) and the demiclosedness of $I-T$ at zero, we have that $p \in F(T).$ Also, since $||x_k - y_k|| \rightarrow 0,$ we have from Lemma  that $p \in VI(C,A)$. Therefore, $p \in \mathrm{Sol}:= VI(C,A) \cap F(T).$

Next we show that $\limsup _{k \rightarrow \infty }\langle (\mu B - \xi f)x^*, x^* - x_k \rangle \le 0,$ where $x^* = P_\mathrm{Sol}(I -\mu B + \xi f)x^*$ is the unique solution of the variational inequality

$$\begin{aligned} \langle (\mu B - \xi f)x^*, x - x^* \rangle \ge 0, \quad \forall ~x \in \mathrm{Sol}. \end{aligned}$$

We obtain from (2.1) and (3.38) that

$$\begin{aligned} \limsup _{k \rightarrow \infty } \langle (\mu B - \xi f)x^*, x^* - x_{k+1} \rangle= & {} \limsup _{l \rightarrow \infty }\langle (\mu B - \xi f)x^*, x^* - x_{k_l+1} \rangle \nonumber \\= & {} \lim _{l\rightarrow \infty }\langle (\mu B - \xi f)x^*, x^*- p \rangle \nonumber \\\le & {} 0. \end{aligned}$$

(3.39)

Finally, we show that $\{x_k\}$ converges strongly to $x^*$. By Lemma 3.5 (i) we obtain

$$\begin{aligned} \Gamma _{k+1} \le (1-a_k) \Gamma _k + a_k b_k, \end{aligned}$$

(3.40)

where $a_k = \frac{2\alpha _k(\tau - \xi \rho )}{1 - \alpha _k \xi \rho },$ $b_k = \frac{\alpha _k\tau ^2 M_1}{2(\tau - \xi \rho )} + \frac{1}{\tau - \xi \rho }\langle \xi f(x^*) - \mu B(x^*), x_{k+1} - x^* \rangle ,$ for some $M_1 >0.$ It is easy to see that $a_k \rightarrow 0$ and $\sum _{k=1}^\infty a_k = \infty .$ Also by (3.39), $\limsup _{k \rightarrow \infty }b_k \le 0.$ Therefore, using Lemma 2.11 in (3.40), we obtain

$$\begin{aligned} \lim _{k \rightarrow \infty }||x_k -x^*|| = 0, \end{aligned}$$

and hence $\{x_k\}$ converges strongly to $x^*$ as $k \rightarrow \infty .$

Case II: Assume that $\{\Gamma _{k}\}$ is not monotonically decreasing. Let $\tau : {\mathbb {N}} \rightarrow {\mathbb {N}}$ be a mapping for all $k \ge k_0$ (for some $k_0$ large enough) defined by

$$\begin{aligned} \tau (k): = \max \{j\in {\mathbb {N}}: j \le k , \Gamma _{j} \le \Gamma _{j+1}\}. \end{aligned}$$

Clearly, $\tau$ is a non-decreasing sequence, $\tau (k) \rightarrow 0$ as $k \rightarrow \infty$ and

$$\begin{aligned} 0 \le \Gamma _{\tau (k)} \le \Gamma _{\tau (k)+1}, \quad \forall ~k \ge k_0. \end{aligned}$$

Following similar process as in Case I, we have

$$\begin{aligned}&||w_{\tau (k)} - Tw_{\tau (k)}|| \rightarrow 0, \quad k\rightarrow \infty , \\&\quad ||x_{\tau (k)+1} - x_{\tau (k)}|| \rightarrow 0, \quad k \rightarrow \infty , \end{aligned}$$

and

$$\begin{aligned} \limsup _{k \rightarrow \infty } \langle (\mu B - \xi f)x^*, x^* - x_{\tau (k)+1} \rangle . \end{aligned}$$

(3.41)

Since $\{x_{\tau (k)}\}$ is bounded, there exists a subsequence of $\{x_{\tau (k)}\}$ still denoted by $\{x_{\tau (k)}\}$ which converges weakly to $z \in C.$ By similar argument as in Case I, we conclude that $z \in \mathrm{Sol}:= VI(C,A)\cap F(T).$ From Lemma 3.5 (i), we have

$$\begin{aligned} \Gamma _{\tau (k)+1} \le (1-a_{\tau (k)})\Gamma _{\tau (k)} + a_{\tau (k)}b_{\tau (k)}. \end{aligned}$$

(3.42)

Also, $a_{\tau (k)} \rightarrow 0$ as $k \rightarrow \infty$ and $\limsup _{k \rightarrow \infty }b_{\tau (k)} \le 0$.

Since $\Gamma _{\tau (k)} \le \Gamma _{\tau (k)+1}$ and $a_{\tau (k)} >0$, we have

$$\begin{aligned} ||x_{\tau (k)} -x^*|| \le b_{\tau (k)}. \end{aligned}$$

This implies that

$$\begin{aligned} \limsup _{k \rightarrow \infty }||x_{\tau (k)} -x^*||^2 = 0, \end{aligned}$$

and thus

$$\begin{aligned} \lim _{k \rightarrow \infty }||x_{\tau (k)} -x^*|| = 0. \end{aligned}$$

Also from (3.42), we obtain

$$\begin{aligned} \limsup _{k \rightarrow \infty }||x_{\tau (k)+1}-x^*||^2 \le \limsup _{k \rightarrow \infty }||x_{\tau (k)} - x^*||^2. \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{k \rightarrow \infty }||x_{\tau (k)+1} -x^*|| = 0. \end{aligned}$$

Furthermore, for $k \ge k_0$, it is easy to see that $\Gamma _{\tau (k)} \le \Gamma _{\tau (k)+1}$ if $k \ge \tau (k)$ (that is $\tau (k) < k$), because $\Gamma _j \ge \Gamma _{j+1}$ for $\tau (k)+1 \le j \le k$. As a consequence, we obtain that for all $k \ge k_0,$

$$\begin{aligned} 0 \le \Gamma _k \le \max \{\Gamma _{\tau (k)}, \Gamma _{\tau (k)+1}\} = \Gamma _{\tau (k)+1}. \end{aligned}$$

Hence, $\Gamma _k \rightarrow 0$ as $k \rightarrow \infty$. That is, $\{x_k\}$ converges strongly to $x^*$. This completes the proof. $\square$

4 Application to split equality problem

Let $H_1,H_2$ and $H_3$ be real Hilbert spaces, let $C \subset H_1$ and $Q \subset H_2$ be nonempty closed convex sets, let $A:H_1 \rightarrow H_3$ and $B:H_2 \rightarrow H_3$ be bounded linear operators. The Split Equality Problem (shortly, SEP) is to find (see Moudafi 2013, 2014)

$$\begin{aligned} x \in C, y \in Q \quad \text {such that} \, Ax = By. \end{aligned}$$

(4.1)

The SEP allows asymmetric and partial relations between the variables x and y. If $H_2 =H_3$ and $B = I$ (the identity mapping), then the SEP reduces to the Split Feasibility Problem (SFP) which was introduced by Censor and Elfving (1994) and defined as

$$\begin{aligned} \text {find} \quad x \in C \quad \text {such that}\, Ax \in Q. \end{aligned}$$

(4.2)

The SEP (4.1) covers many situations, such as for instance in domain decomposition for PDE’s, game theory and intensity-modulated radiation therapy (IMRT) (Attouch et al. 2008; Censor et al. 2006; Moudafi 2014). A great numbers of articles have been published on iterative methods (most of which are projection methods) for solving the SEP (4.1) in literature; see, for instance (Jolaoso et al. 2018; Ogbuisi and Mewomo 2016, 2018; Okeke and Mewomo 2017).

In this section, we adapt our Algorithm 3.1 to solve the SEP (4.1). Before that, let us first prove some lemmas which will be of help.

Lemma 4.1

(Dong and Jiang 2018) Let $S = C \times Q \subset H:= H_1 \times H_2.$ Define $K:= [A, -B]: H_1 \times H_2 \rightarrow H_1 \times H_2$ and let $K^*$ be the adjoint operator of K, then the SEP (4.1) can be modified as

$$\begin{aligned} \text {Find} ~~~z = (x,y)\in S \quad \text {such that} \quad Kw = 0, \end{aligned}$$

(4.3)

where $w = \left[ \begin{array}{l} x \\ y \end{array} \right]$ is the vector associated with z.

Lemma 4.2

Let $H = H_1 \times H_2$, define $M: H \rightarrow H$ by $M(w) = M(u,v) := (\phi _1(u),\phi _2(v)),$ $w=(u,v) \in H$, where $\phi _i:H \rightarrow H$ are $k_i$-Lipschitz and $\eta _i$-strongly monotone mapping with $k_i >0$ and $\eta _i >0,$ $i =1,2.$ Then, M is k-Lipschitz and $\eta$-strongly monotone where $k = \max \{k_1,k_2\}$ and $\eta = \min \{\eta _1,\eta _2\}.$

Proof

Let $x = (x_1,y_1),$ $y = (x_2,y_2) \in H,$ then we have

$$\begin{aligned} \langle Mx - My, x-y \rangle= & {} \langle (\phi _1(x_1),\phi _2(y_1)) - (\phi _1(x_2), \phi _2(y_2)), (x_1 - x_2, y_1 - y_2) \rangle \\= & {} \langle (\phi _1(x_1) - \phi _1(x_2), \phi _2(y_1) - \phi _2(y_2)), (x_1 - x_2, y_1 - y_2) \rangle \\= & {} \langle \phi _1(x_1) - \phi _1(x_2), x_1 - x_2 \rangle + \langle \phi _2(y_1) - \phi _2(y_2), y_1 - y_2 \rangle \\\ge & {} \eta _1||x_1 - x_2||^2 + \eta _2||y_1 - y_2||^2 \\\ge & {} \min \{\eta _1,\eta _2\}(||x_1 - x_2||^2 + ||y_1 - y_2||^2) \\= & {} \eta ||x-y||^2. \end{aligned}$$

Hence, M is $\eta$-strongly monotone , where $\eta = \min \{\eta _1,\eta _2\}.$ Also,

$$\begin{aligned} ||Mx - My||^2= & {} ||(\phi _1(x_1),\phi _2(y_1)) - (\phi _1(x_2), \phi _2(y_2))||^2 \nonumber \\= & {} ||(\phi _1(x_1) - \phi _1(x_2), \phi _2(y_1) - \phi _2(y_2))||^2 \nonumber \\= & {} ||\phi _1(x_1) - \phi _1(x_2)||^2 +||\phi _2(y_1) - \phi _2(y_2)||^2 \nonumber \\\le & {} k_1^2 ||x_1 - x_2||^2 + k_2^2||y_1 - y_2||^2 \nonumber \\\le & {} \max \{k_1^2,k_2^2\}(||x_1 - x_2||^2 + ||y_1 - y_2||^2) \nonumber \\= & {} k^2||x-y||^2. \end{aligned}$$

Hence M is k-Lipschitz with $k = \max \{k_1,k_2\}.$ $\square$

In a similar process as in Lemma 4.2, we can prove the following results.

Lemma 4.3

Let $H:= H_1 \times H_2$, let $f:H \rightarrow H$ be defined by $f(u,v) = (f_1(u), f_2(v)),$ $w = (u,v) \in H$, $f_i:H_i \rightarrow H_i$ is $\rho _i$-Lipschitz mapping with $\rho _i >0$, $i =1,2.$ Then f is $\rho$-Lipschitz mapping with $\rho = \sqrt{\max \{\rho _1,\rho _2\}}.$

Lemma 4.4

Let $H:= H_1 \times H_2$, let $T:H \rightarrow H$ be defined by $T(u,v) = (T_1(u), T_2(v)),$ $w = (u,v) \in H$, $T_i:H_i \rightarrow H_i$ is $\beta _i$-demicontractive mapping with $\beta _i \in [0,1)$, $i =1,2.$ Then T is $\beta$-demicontractive mapping with $\beta = {\max \{\beta _1,\beta _2\}}.$

We now adapt our algorithm to solve the SEP.

Let H,  S,  and K be as defined in Lemma 4.1. Let T be as defined in Lemma 4.4 such that

$$\begin{aligned}\Gamma := \{(x,y)\in F(T_1)\times F(T_2):Ax = By\}\ne \emptyset .\end{aligned}$$

Let M and f be as defined in Lemmas 4.2 and 4.3, respectively, such that $0< \mu < \frac{2\eta }{k^2}$ and $0< \xi \rho < \tau$, where $\tau = \frac{1}{2}\mu (2\eta - \mu k^2).$ Let $\{\alpha _k\}$ and $\{v_k\}$ be sequences in (0, 1) and $\{z_k\} = \{(x_k,y_k)\}$ be generated by the following Algorithm.

Remark 4.6

Let $z = (x,y)$, we know that

$$\begin{aligned} P_S(z) = \big (P_C(x), P_Q(y)\big ). \end{aligned}$$

Also, since

$$\begin{aligned} K = [A, -B], \quad \text {and} \quad K^* = \left[ \begin{array}{l} A^*\\ -B^* \end{array}\right] , \end{aligned}$$

then

$$\begin{aligned} K^*Kw= & {} \left[ \begin{array}{ll} A^*A &{}- A^*B\\ -B^*A &{} B^*B \end{array}\right] \left[ \begin{array}{l} x\\ y \end{array}\right] \nonumber \\= & {} \left[ \begin{array}{l} A^*(Ax-By)\\ B^*(Ax-By) \end{array}\right] . \end{aligned}$$

(4.9)

Define the function $F: H_1 \times H_2 \rightarrow H_1$ by

$$\begin{aligned} F(x,y) = A^*(Ax-By), \end{aligned}$$

and $G: H_1 \times H_2 \rightarrow H_2$ by

$$\begin{aligned} G(x,y) = B^*(By- Ax). \end{aligned}$$

Now, by setting $z_k = (x_k,y_k),$ $y_k = (u_k,v_k)$ and $w_k = (s_k,t_k)$ in Algorithm 4.5, Algorithm 4.5 can be rewritten in the following simultaneous form:

We now prove the convergence of Algorithm 4.7 using Algorithm 3.1.

Observe that

$$\begin{aligned} ||s_k -x^*||^2 + ||t_k - y^*||^2= & {} ||x_k -x^* - \sigma \delta _k c_k||^2 + ||y_k - y^* - \sigma \delta _k d_k||^2 \nonumber \\\le & {} ||x_k - x^*||^2 + ||y_k - y^*||^2 \nonumber \\&- 2\sigma \delta _k (\langle x_k - x^*, c_k \rangle + \langle y_k - y^*, d_k \rangle ) \nonumber \\&+ \sigma ^2 \delta _k^2 (||c_k||^2 +||d_k||^2). \end{aligned}$$

(4.15)

But,

$$\begin{aligned} \langle x_k - x^*, c_k \rangle + \langle y_k - y^*, d_k \rangle= & {} \langle x_k - u_k, c_k \rangle + \langle u_k - x^*, c_k \rangle \\&\langle y_k - v_k, d_k \rangle + \langle v_k - y^*, d_k \rangle , \end{aligned}$$

and

$$\begin{aligned} \langle u_k - x^*, c_k \rangle + \langle v_k - y^*, d_k \rangle \ge 0. \end{aligned}$$

Hence,

$$\begin{aligned} \langle x_k - x^*, c_k \rangle + \langle y_k - y^*, d_k \rangle \ge \langle x_k - u_k, c_k \rangle + \langle y_k - v_k, d_k \rangle . \end{aligned}$$

(4.16)

Therefore from (4.15) and (4.16), we have

$$\begin{aligned} ||s_k - x^*||^2 + ||t_k -y^*||^2\le & {} ||x_k -x^*||^2 + ||y_k -y^*||^2 -2\sigma \delta _k(\langle x_k -u_k, c_k \rangle \nonumber \\&+\langle y_k -v_k, d_K\rangle ) + \sigma ^2 \delta _k^2 (||c_k||^2 +||d_k||^2). \end{aligned}$$

(4.17)

From the definition of $\delta _k$ and (4.12), we have

$$\begin{aligned} \delta _k(\langle x_k -u_k, c_k \rangle + \langle y_k -v_k, d_k \rangle )= & {} \delta _k^2(||c_k||^2 + ||d_k||^2) \nonumber \\= & {} \frac{1}{\sigma ^2}(||s_k-x_k||^2 + ||t_k -y_k||^2). \end{aligned}$$

(4.18)

Hence from (4.17) and (4.18), we get

$$\begin{aligned} ||s_k - x^*||^2 + ||t_k -y^*||^2\le & {} ||x_k -x^*||^2 + ||y_k -y^*||^2 \nonumber \\&- \left( \frac{2 - \sigma }{\sigma }\right) (||s_k -x_k||^2 + ||t_k -y_k||^2).\nonumber \\\le & {} ||x_k -x^*||^2 + ||y_k - y^*||^2. \end{aligned}$$

(4.19)

Following similar approach as in (3.22), we get

$$\begin{aligned} ||x_{k+1} -x^*|| + ||y_{k+1} - x^*||\le & {} \max \bigg \{||x_1 - x^*|| +||y_1 - y^*||, \nonumber \\&\frac{||\xi _1 f_1(x^*) - \mu _1 \phi _1(x^*)||}{\tau _1 - \xi \rho _1} \nonumber \\&+ \frac{||\xi _2 f_2(y^*) - \mu _2 \phi _2(y^*)||}{\tau _2 - \xi _2 \rho _2} \bigg \}. \end{aligned}$$

(4.20)

Hence $\{||x_{k+1} -x^*||+||y_{k+1} -y^*||\}$ is bounded and, consequently, $\{||x_{k}-x^*||\},$ $\{||y_{k}- y^*||\}$ are bounded. Thus, $\{x_k\}$ and $\{y_k\}$ are bounded.

Lemma 4.8

Suppose $\Gamma := \{(x,y)\in C\times Q:Ax = By\}\ne \emptyset .$ Let $\lambda _n$ be a sequence in $(0, \frac{2}{||A||^2+||B||^2}),$ such that (4.11) holds and suppose $\liminf _{n\rightarrow \infty }\lambda _n(2 - \lambda _n(||A||^2+||B||^2))>0,$ $||x_k - u_k||\rightarrow 0, ||y_k -v_k|| \rightarrow 0$ as $k \rightarrow \infty$. Then, there exist $({\bar{x}},{\bar{y}})\in \Omega$ such that $x_{k_j} \rightharpoonup {\bar{x}}$ and $y_{k_j} \rightharpoonup {\bar{y}},$ where $\{x_{k_j}\}$ and $\{y_{k_j}\}$ are subsequences of $\{x_k\}$ and $\{y_k\}$ generated by Algorithm  4.7.

Proof

Let $(x^*,y^*) \in \Omega ,$ then from (4.10), we have

$$\begin{aligned} ||u_k -x^*||^2= & {} ||P_C(x_k - \lambda _kF(x_k,y_k)) -x^*||^2 \nonumber \\\le & {} ||x_k - \lambda _k (A^*(Ax_k- By_k)) - x^*||^2 \nonumber \\\le & {} ||x_k - x^*||^2 - 2 \lambda _k\langle Ax_k - Ax^*, Ax_k - By_k \rangle \nonumber \\&+\, \lambda _k^2||A||^2||Ax_k - By_k||^2. \end{aligned}$$

(4.21)

Similarly, we have

$$\begin{aligned} ||v_k - y^*||^2\le & {} ||y_k - y^*||^2 + 2 \lambda _k \langle By_k - By^*, Ax_k - By_k \rangle \nonumber \\&+\, \lambda _k^2 ||B||^2 ||Ax_k - By_k||^2. \end{aligned}$$

(4.22)

Adding (4.21 and (4.22) while noting that $Ax^* = By^*$, we have

$$\begin{aligned} ||u_k -x^*||^2 +||v_k - y^*||^2\le & {} ||x_k -x^*||^2 + ||y_k-y^*||^2 \nonumber \\&\quad -\, \lambda _k(2-\lambda _k(||A||^2+||B||^2))||Ax_k - By_k||^2.\qquad \end{aligned}$$

(4.23)

Also, note that

$$\begin{aligned} ||u_k -x^*||^2 + ||v_k -y^*||^2= & {} ||u_k - x_k||^2 + 2\langle u_k - x_k, x_k - x_k -x^*\rangle + ||x_k - x^*||^2 \nonumber \\&~~ +\, ||v_k - y_k||^2 + 2\langle v_k - y_k, y_k - y^* \rangle + ||y_k - y^*||^2.\nonumber \\ \end{aligned}$$

(4.24)

Then from (4.23) and (4.24), we have

$$\begin{aligned} \lim _{k \rightarrow \infty }||Ax_k - By_k|| = 0. \end{aligned}$$

(4.25)

Without loss of generality, we may assume that $x_{k_j} \rightharpoonup {\bar{x}}$ and $y_{k_j} \rightharpoonup {\bar{y}}$ for some ${\bar{x}} \in H_1$ and ${\bar{y}} \in H_2$. Since $\{x_k\}$ is a sequence in C, we know that ${\bar{x}} \in C$. Similarly, ${\bar{y}} \in Q.$ Since $x_{k_j} \rightharpoonup {\bar{x}}$ and $y_{k_j} \rightharpoonup {\bar{y}},$ it follows that $Ax_{k_j} \rightharpoonup A{\bar{x}}$ and $By_{k_j} \rightharpoonup B{\bar{y}}.$ Hence, $Ax_{k_j} - By_{k_j} \rightharpoonup A{\bar{x}} - B{\bar{y}}.$ By the lower semicontinuity of the squared norm, we have

$$\begin{aligned} ||A{\bar{x}} - B{\bar{y}}||^2 \le \liminf _{k \rightarrow \infty }||Ax_{k_j} - By_{k_j}||^2 = \lim _{k \rightarrow \infty }||Ax_{k} - By_{k}||^2 = 0. \end{aligned}$$

Hence, $A{\bar{x}} = B{\bar{y}}.$ Therefore, $({\bar{x}},{\bar{y}}) \in \Omega .$ $\square$

Now using Lemma 4.8 and following the line of argument in Theorem 3.7, we can prove the following result.

Theorem 4.9

Let H,  S,  and K be as defined in Lemma 4.1. Let T be as defined in Lemma 4.4 such that $\Gamma := \{(x,y)\in F(T_1)\times F(T_2):Ax = By\}\ne \emptyset .$ Let M and f be as defined in Lemmas 4.2 and 4.3, respectively, such that $0< \mu < \frac{2\mu }{k^2}$ and $0< \xi \rho < \tau$, where $\tau = \frac{1}{2}\mu (2\eta - \mu k^2).$ Let $\{\alpha _k\}$ and $\{v_k\}$ be sequences in (0, 1) satisfying condition (C1) and (C3) and let $\lambda _n$ be a sequence in $(0, \frac{2}{||A||^2+||B||^2}),$ such that (4.11) holds and $\liminf _{n\rightarrow \infty }\lambda _n(2 - \lambda _n(||A||^2+||B||^2))>0.$ Then the sequence $\{(x_k,y_k)\}$ generated by Algorithm  4.7 converges strongly to a solution $(u,v) \in \Gamma .$

5 Numerical examples

In this section, we present three numerical examples which demonstrate the performance of our Algorithm 3.1. Let $T: H \rightarrow H$ be defined by

$$\begin{aligned} Tx = {\left\{ \begin{array}{ll} -\frac{9}{2}x, \quad &{} \mathrm{if}\, x \le 0, \\ -2x, \quad &{} \mathrm{if} \, x > 0. \end{array}\right. } \end{aligned}$$

(5.1)

It easy to see that T is demicontractive mapping with $\beta = \frac{77}{121},$ and $F(T) = \{0\}$. We let $f =I,$ $B = \frac{1}{2}I,$ then $\rho =1$ and $\eta = 1 = k.$ Hence $0< \mu < \frac{2\eta }{k^2} = 2.$ Let us choose $\mu = 1$ so that $\tau = \frac{1}{2}\mu (2\eta - \mu k^2) = 1.$ As $0< \xi \rho < \tau ,$ we have $\xi \in (0,2).$ Without loss of generality, we choose $\xi = 1.$

In each example, we fix the stopping criterion as ${||x_{k+1}-x_{k}||}=\epsilon <10^{-5}$, $\sigma = 0.7$, $\gamma = 0.54$, $\lambda _k = 0.15$ and let $\alpha _k = \frac{1}{k+1}$ and $v_k = \frac{2k+3}{4k + 12}$. The projection onto the feasible set C is carried out by using the MATLAB solver ‘ fmincon ’ and the projection onto an hyperplane $Q = \{x \in H: \langle a,x\rangle = 0\}$ is defined by

$$\begin{aligned} P_Q(x) = x -\frac{\langle a,x \rangle }{||a||^2}a. \end{aligned}$$

Example 5.1

First, we consider the Hp-Hard problem. Let $A: {\mathbb {R}}^m \rightarrow {\mathbb {R}}^m$ define by $Ax = Mx+q$ where

$$\begin{aligned} M =NN^{T} + S+D, \end{aligned}$$

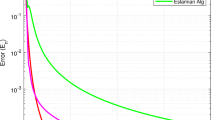
N is an $m\times m$ matrix, S is an $m \times m$ skew-symmetric matrix, D is an $m \times m$ diagonal matrix, whose diagonal entries are nonnegative so that M is positive definite and q is a vector in ${\mathbb {R}}^m$. The feasible set $C\subset {\mathbb {R}}^m$ is the closed and convex polyhedron which is defined as $C = \{x = (x_1,x_2,\dots , x_m) \in {\mathbb {R}}^m: Qx \le b\}$, where Q is a $l \times m$ matrix and b is a nonnegative vector. It is clear that A is monotone (hence, pseudo-monotone) and L-Lipschitz continuous with $L = ||M||$. For experimental purpose, all the entries of N, S, D and b are generated randomly as well as the starting point $x_1 \in [0,1]^m$ and q is equal to the zero vector. In this case, the solution to the corresponding variational inequality is $\{0\}$ and also, $\mathrm{Sol} : = VI(C,A) \cap F(T) =\{0\}$. We take $m = 10, 50, 100$ and compare the output of Algorithm  3.1 with Algorithm (1.11) and Algorithm (1.8). The numerical results are reported in Table 1 and Fig. 1.

Table 1 Numerical results for Example 5.1

Fig. 1

Example 5.1, top left: $m = 50$; top right: $m=100$; bottom: $m=200$

Example 5.2

Let $H = L^2([0,2\pi ])$ with norm $||x|| = (\int _{0}^{2\pi }|x(t)|^2\mathrm{d}t)^{\frac{1}{2}}$ and inner product $\langle x,y \rangle = \int _{0}^{2\pi }x(t)y(t)\mathrm{d}t,$ $x,y \in H.$ The operator $A:H \rightarrow H$ is defined by $Ax(t) = \frac{1}{2}\max \{0,x(t)\},$ $t \in [0,2\pi ]$ for all $x \in H$. It can easily be verified that A is Lipschitz continuous and monotone. The feasible set $C = \{x \in H: \int _{0}^{2\pi }(t^2+1)x(t)\mathrm{d}t \le 1\}$. Observe that $\mathrm{Sol} = \{0\}.$ We choose the following starting points and compare the result of Algorithm  3.1 with Algorithms (1.11) and (1.9).

$$\begin{aligned} \mathrm{(i)}~ x_1 = \frac{1}{3}t^2 \exp (-3t),\quad \mathrm{(ii)}~x_1= \frac{1}{20}\sin (3\pi t) \cos (2\pi t), \quad \mathrm{(iii)}~x_1= \frac{1}{50}\cos (3t)\exp (2t). \end{aligned}$$

The numerical results are shown in Table 2 and Fig. 2.

Table 2 Numerical results for Example 5.2

Fig. 2

Example 5.2, Left: $x_1 = \frac{1}{3}t^2 \exp (-3t)$; Middle: $x_1 = \frac{1}{200}\sin (3\pi t)\cos (2\pi t)$; Right: $x_1 = \frac{1}{50}\cos (3t)\exp (2t)$

Example 5.3

Finally, we consider the Kojima–Shindo nonlinear complementarity problem (NCP) which was considered in Malitsky (2015), where $n = 4$ and the mapping A is defined by

$$\begin{aligned} A(x_1,x_2,x_3,x_4) = \left[ \begin{array}{l} 3x_1^2 + 2x_1x_2 + 2x_2^2 + x_3 + 3x_4 -6 \\ 2x_1^2+x_1 + x_2^2 + 10x_3 + 2x_4-2 \\ 3x_1^2 + x_1x_2 + 2x_2^2 + 2x_3 + 9x_4 -9\\ x_1^2 + 3x_2^2 + 2x_3 + 3x_4 -3 \end{array} \right] . \end{aligned}$$

(5.2)

The feasible set $C = \{x \in {\mathbb {R}}_{+}^4: x_1 + x_2 + x_3 +x_4 = 4\}$. We choose the following starting points and test our Algorithm 3.1 with Algorithm (1.11).

$$\begin{aligned} \mathrm{(i)}~x_1 = (2,0,0,2)', \quad \mathrm{(ii)}~ x_1 = (1,1,1,1)', \quad \mathrm{(iii)} ~x_1 = (1,2,0,1)'. \end{aligned}$$

The results are summarized in Table 3 and Fig. 3.

Table 3 Numerical results for Example 5.3

Fig. 3

Example 5.3, left: $x_1 = (2,0,0,2)'$; middle: $x_1 = (1,1,1,1)'$; right: $x_1 = (1,2,0,1)'$

Remark 5.4

In conclusion, one can see from the above examples that

• there is no significant difference in terms of number of iterations between Algorithms 3.1 and (1.11), for Example 5.1. However, Algorithm 3.1 performs better than Algorithm (1.11) in terms of time of execution. This can be due to the greater number of projections in Algorithm 1.11 .

• Algorithm 3.1 converges faster than Algorithms (1.8) and (1.9) in terms of number of iteration and cpu time taken for execution.

• In addition, when the feasible set is complex, Algorithm 3.1 is more preferable than Algorithm (1.9) or (1.11).