Introduction

Design optimization is very important for complex product design process, which allows designers to locate optimal solutions within design space. Recently, the utilization of optimization has increased dramatically in product design. The nature of complex products includes complex structure, intensive technology, long development cycle, etc. The design proscess involves the integration of multidisciplinary knowledge and the coordination of multiple professionals, which makes the computer simulations of complex products are extremely time-consuming and the optimizations are quite difficult. Optimization in design has the following characteristics (Forrester et al. 2008; Jones et al. 1998; Shahriari et al. 2016): High-dimensional, Black-box and Expensive in terms of computer simulations (HBE). These characteristics lead to a situation where a huge design space must be explored, which means that designers must expend considerable time and cost for computer simulations to find an optimal design solution.

Most engineering designs require a large number of experiments and/or computer simulations to evaluate design solutions (Liu et al. 2016; Sahnoun et al. 2016). A single computer simulation of complex product can take many hours, days, or even months to complete. One of the effective ways to solve this issue is to build a surrogate model to replace the computer simulations, and then use this to obtain an optimal solution. A surrogate model is a low-cost mathematical model used to replace the time-consuming computer simulation (Vidal and Archer 2016). Surrogate models have been used for tasks such as optimization, design space exploration, and sensitivity analysis (Gorissen and Dhaene 2010) due to their low computational expense. When enough simulation data are available, surrogate models can be used to support designers in finding an optimal solution since building a high-accuracy surrogate model is easy. However, when only limited simulation data are available, building a high-accuracy surrogate model is quite difficult. Therefore, developing new method for building surrogate models and conducting optimization with limited simulation data is a critical and challenging research problem which requires more research focus.

Integrating engineering knowledge and limited simulation data provides a new way to build a surrogate model and conducting design optimization when only limited simulation data are available. Existing hybrid methods try to extract synergistic rules from domain theory (Monisha and Peter 2017; Towell and Shavlik 1994) or knowledge from historical datasets (Yu et al. 2008; Zhang et al. 2019) to optimize the settings of the neural network structure. Although these methods can be used to build surrogate models and integrate the extra information, the performances of the surrogate model are heavily dependent on the algorithms used to extract knowledge. For integrating synergistic rules, it also replies on rules-to-network algorithms. Besides, these methods cannot integrate the mapping knowledge directly that designers hold, which contains useful information that is not contained in the limited simulation data. In this work, we develop a method which is capable of building surrogate model and conducting design optimization synchronously by integrating limited simulation data and shape knowledge, which is a specific kind of engineering knowledge. Our method realizes the direct integration of the engineering knowledge owned by designers. Besides, we use GP as a surrogate model which requires less data to train comparing with neural networks.

The rest of the paper is structured as follows. In section 2 there is an evaluation of some related research works and the research gaps are also pointed out. In section three the details of the proposed method are described. In section four several experiments are conducted to verify this method. In section five the empirical results are analyzed and discussed while in section six there is a summary of this work and some contributions are presented.

Related work

Optimization in engineering design

The use of optimization techniques in engineering design has been on the rise steadily as the computational capabilities of the computers are increasing (Liu et al. 2018). Optimization has a wide range of applications in engineering design, such as structural design [e.g., pressure vessel design (Fatemeh et al. 2019), welded beam design (Du et al. 2018)], shape optimization (Daróczy et al. 2018; Fengjie and Lahmer 2018), topology optimization (e.g., airfoil (Bhattacharyya et al. 2019), fluid (Yoshimura et al. 2017), inverse optimization [Johnson–Cook model (Ning et al. 2018)], processing planning (Pratap et al. 2018; Zhang et al. 2018), product designs (Du et al. 2019), etc. Routine tasks such as design optimization, sensitivity analysis and design space exploration usually require thousands or even millions of simulation evaluations (Sefat et al. 2012). For many engineering design problems, however, a single simulation is extremely time-consuming which is a main obstacle to implement design optimization.

One way of alleviating this burden is by exploiting surrogate models for optimization. Yoshimura et al. (Yoshimura et al. 2017) proposes a non-gradient-based approach applied to fluid problems. This paper uses genetic algorithm for topology optimization assisted by the Kriging surrogate model. Song et al. (Song et al. 2016) conducts a sensitivity analysis and carries out a reliability based design optimization by taking into account the uncertainties in the TWB configuration. Wang et al. (2017) proposes a novel surrogate-assisted particle swarm optimization combining uncertainty and performance based criteria for expensive problems.

Among the optimization techniques based on surrogate models, Bayesian optimization is a state-of-the-art global optimization method with two attractive advantages. One is that it can be applied to problems where it is vital to optimize a performance criterion while keeping the number of evaluations small (Calandra et al. 2016). Another is that it considers the uncertainty which is ubiquitous in engineering design in conducting the sampling (updating) process. While Bayesian optimization is a popular probabilistic approach when limited data are available, as indicated in Trucano et al. (2006), the prior surrogate model are often difficult to specify due to the lack of prior knowledge. Subjectively assigned prior distributions may yield unstable posterior distributions (Aughenbaugh and Herrmann 2007), which undermines the advantage of Bayesian updating. Therefore, our research focuses on the integration of engineering knowledge and limited simulation data into the prior surrogate model to improve the accuracy of it. The model itself is refined and its demand for sampling is further reduced in the updating process, which is more suitable for limited data problems.

Actually, the performance of surrogate model depends on two key factors: (1) the type of surrogate models, such as neural network, Kriging, response surface model and so on, and (2) the information contained in training data. When only limited data are available, it’s challenging to build a high-accurate surrogate model. The following two subsections summarize the ways of building surrogate models with limited data from two perspectives: data augmentation and knowledge integration.

Building surrogate models by data augmentation

Limited simulation data brings serious challenges for building surrogate models in the domain of engineering design (Dougherty et al. 2015). The main difficulty is that information contained in limited data is often insufficient. Currently, two types of methods from artificial intelligent provide ideas and ways to build surrogate models with limited simulation data. One such method is data augmentation, and the other is knowledge integration.

Data augmentation refers to the generation of new data records based on existing information. It can be implemented in many ways, for example, interpolation (Amsallem et al. 2009; Zhao et al. 2017), noise injection (Bella et al. 2007; Fortuna et al. 2009), data sampling (Gorissen and Dhaene 2010), and virtual sample generation (Kang et al. 2019; Li et al. 2013, 2018a; Tsai and Li 2008). For these methods, virtual samples can also be generated based on prior knowledge (Li et al. 2003, 2012). Although these methods can improve accuracy, they also have limitations. For data augmentation, new errors will inevitably be introduced. Besides, the information contained in new data is still similar with existing data or knowledge.

Building Surrogate Models by Integrating Knowledge

Knowledge integration is used to add some restrictions to the model. There are two ways to be addressed separately, including regularization and transfer learning (Min et al. 2017). For the model regularization, only very simple knowledge can be integrated when defining regularization terms while with transfer learning it is difficult to interpret and integrate different data.

The main way is integrating more complex knowledge into surrogate models. In this way, currently, there are only a few related studies about integrating engineering knowledge and limited simulation data in the domain of engineering design (Kotlowski and Slowinski 2013). Hence, we also review papers in the domains of artificial intelligence and machine learning. The existing methods can be classified from two perspectives: the types of knowledge studied and the types of models (Gaussian process, neural network) integrating knowledge and data. Different authors use various designations for knowledge, such as knowledge (Nagarajan et al. 2018), prior knowledge (Aguirre and Furtado 2007; Parrado-Hernández et al. 2012), constraints(Wang and Welch 2018; Wang and Berger 2016), hints (Abu-Mostafa 1990; Sill 1998; Sill and Abu-Mostafa 1997) etc.

Gaussian processes and neural networks are the two main methods for integrating knowledge. There are many works for integrating knowledge and data using neural networks. The main mechanism is usually realized by putting constraints on the parameters of a neural network. Abu-Mostafa (1990) propose a method using neural networks to learn from hints, as expressed by a set of data. Sill (1998) and Sill and Abu-Mostafa (1997) further develops this work, and proposes a general method for incorporating monotonicity information into neural networks. Based on this work, Daniels and Velikova (2010) presents a monotonic neural network, and Gupta et al. (2018) presented a neural network with shape constraints. Different from these methods, our previous work (Hao et al. 2018) proposes the integration of limited simulation data and engineering knowledge through an evolutionary neural network.

Another mechanism builds a hybrid learning network which use both knowledge and data during learning through connectionist machine learning. Towell and Shavlik (1994) describes a hybrid learning system knowledge-based artificial neural networks (KBANN) which uses both synergistic rules and classified training examples. An extension of this approach (Shavlik 1994) initializes an RNN by synergistic knowledge expressed as a Finite State Automaton (FSA). Hybrid methods have been used in product design. Monisha and Peter (2017) uses a knowledge based neural network (KBNN) for designing of triple band planar inverted-F antenna (PIFA). Prior knowledge is used in the form of trained radial basis function network (RBFN) in addition with back propagation network (BPN). Yu et al. (2008) creates a learning-based hybrid method named KBANN-DT, which combines knowledge-based artificial neural network (KBANN) and CART decision tree (DT). The KBANN is applied to realizing the mapping between customer needs and product specifications which integrates both two knowledge resources, i.e., domain theory and historical database. Zhang et al. (2019) proposes a knowledge-based artificial neural network (ANN) to model the relationship between customer requirement attributes and product service system (PSS) base types. The initial structure of ANN is defined by domain knowledge which is extracted from the data of historical configuration instance data sets using a priori algorithm.

Although, it is possible to integrate the data and knowledge using the neural network, there are limitations. The first is that these methods require deliberately specifying the structure of the neural networks and/or the normalization terms, which is an experience-based process and is also very difficult. The second is that neural networks requires more data to train compared with other models. The third limitation is that it’s very hard to form a universal method for integrating different kinds of knowledge into neural networks, which means for different knowledge totally different structure and normalization terms must be designed.

Gaussian process (GP) is a popular tool for function estimation which allows a straightforward combination of function and derivative observations in a prior model. Wu and Feb (2017) exploited exact derivative values in GP which are hard to acquire in real-word problems. Some types of prior knowledge have been successfully incorporated including monotonicity (Riihimäki and Vehtari 2010; Wang and Welch 2018; Wang and Berger 2016), monotonic convex or concave (Lenk and Choi 2017; Wang and Berger 2016), unimodality (Andersen et al. 2017; Jauch and Peña 2016; Li et al. 2018b). The method of Wang and Welch (2018) is designed for a dominant function which is composed of functions with monotonicity constraints. Preliminary work (Riihimäki and Vehtari 2010) also study Gaussian processes with monotonicity information, which paves the way for much following research. For unimodality work, unfortunately, (Andersen et al. 2017) has to resort to approximate inference to compute intractable posterior distributions and focused on univariate problems to provide proof of concept. As the dimensions get larger and larger, the reliability of Jauch and Peña (2016) will be reduced and it eventually fails. The method proposed by Li et al. (2018b) is only limited for the problems of producing something with a target value. However, for many engineering design problems, the performances of products are supposed to be larger or smaller as possible. Therefore, we can safely conclude that none of the existing works solves our problem with multiple knowledge including monotonicity, unimodality, multimodal and any shape that can be decomposed as several monotonic intervals, thus the problem remains open.

The above two methods are used for integrating data and knowledge. However, they are mainly applied to tuning the hyperparameters of machine learning models and thus rarely are used to build surrogate models in the domain of engineering design. In this paper we develop a method for building surrogate models and conducting design optimization by integrating shape engineering knowledge and limited simulation data through Bayesian optimization (BO-DK4DO).

Method

Limited simulation data and engineering knowledge

  1. (1)

    Limited simulation data

Limited simulation data means that the data are inadequate to describe the design space for building an accurate surrogate model. This data commonly includes design variables and their corresponding performances. For the purposes of this work, a limited simulation dataset has the following characteristics:

  • The amount of data is limited

If a solution and its performances are regarded as a piece of data, the dataset only contains a few such pairs. However, there is no predetermined threshold value that determines whether a dataset is limited simulation data or not, this depends on the accuracy we want to achieve. For a 1-dimension Lipschitz-continuous function, which satisfies Eq. (1), the amount of data must reach \( \left({{\raise0.7ex\hbox{$C$} \!\mathord{\left/{\vphantom {C {2\epsilon}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2\epsilon}$}}} \right)^{2} \) to get a model that has the prediction error \( \epsilon \) (Brochu et al. 2010).

$$ || f\left( {x_{1} } \right) - f\left( {x_{2} } \right) || \le {\text{C}} || x_{1} - x_{2} ||$$
(1)

If we have a 1-dimension function and want to get a model has prediction error 0.05 (assuming C is 1), then we need 100 data records. From the above analysis, it can be said that all datasets are limited simulation data to some extent, since we always require higher accuracy.

  • The information is incomplete

A dataset must contain information about the mapping between design solutions and its performances. If a dataset contains a substantial number of data records that cover the entire design space, then it contains almost all information about the mapping. In contrast, if a dataset contains data records that only cover a portion of the design space, then it contains incomplete information about the mapping. When the amount of data is limited, the information contained is incomplete. When the amount of data is large, but the information is repeated, it will also lead to incomplete information.

In this work, we assume a zero-mean Gaussian process prior

$$ p(\varvec{f}|\varvec{X}) = N\left( {\varvec{f}|0,K\left( {\varvec{X},\varvec{X}} \right)} \right) $$
(2)

where \( \varvec{f} \) is a vector of the real performances of a solution \( \varvec{X} \).

Limited simulation data can be regarded as noisy observations \( \varvec{y} \) of the real values \( \varvec{f} \) of the performance because a simulation model will never accurately model all the details. The relationships between \( \varvec{f} \) and \( \varvec{y} \) follows a Gaussian distribution as shown in Eq. (3).

$$ p(\varvec{y}|\varvec{f}) = N\left( {\varvec{y} |\varvec{f},\sigma^{2} \varvec{I}} \right) $$
(3)

where \( \sigma \) is the variance of noise,\( \varvec{I} \) is the identity matrix, and \( \varvec{y} = \varvec{f} + \vartheta \), \( \vartheta \sim N\left( {0,\sigma^{2} } \right) \).

  1. (2)

    Shape engineering knowledge

Engineering knowledge plays a critical role in building surrogate models, especially when only limited simulation data are available. The knowledge is assumed to be correct in this paper, which is summarized by designers in long-term working. The definition of shape knowledge in this paper is the combination of monotonicity knowledge, which is monotonic in one or more piecewise domains. Monotonicity knowledge means that \( f(x) \) is monotonically decreasing or increasing against \( x \) over a specific range (Sill 1998). Table 1 shows more details about the monotonicity and shape engineering knowledge in formula, description and graph. In formula, we can see that monotonicity is a special case of shape when \( {\text{n}} = 1 \) and x conforms to monotonicity formula. In this paper, knowledge can be described in the form of rule. All the descriptions of monotonicity knowledge are listed in Table 1. Due to the diversity of shape engineering knowledge, we only list some of them.

Table 1 The definition of monotonicity and shape engineering knowledge
Full size table

In our experience we have found that shape engineering knowledge are more common than other kinds in the domain of engineering design. Also, it is easy for designers to give this type of knowledge articulately. Thus, this paper focuses on shape engineering knowledge.

Framework of BO-DK4DO

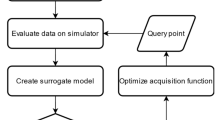
BO-DK4DO is used to build high accuracy surrogate models and find the optimal solution when only limited simulation data are available by integrating engineering knowledge. The underlying idea of this method is integration while updating limited simulation data are modeled by a Gaussian process and used as prior process, while the shape engineering knowledge by another Gaussian process and uses it as a likelihood process. To calculate the posterior process, the information from both of the prior process and likelihood process are integrated through Bayes rule. The updating is used to guide the process of collecting new data points automatically, which means the posterior process determines where to sample a new data point. The whole framework is shown in Fig. 1.

Fig. 1
figure 1

The general framework of the proposed method (BO-DK4DO)

Full size image

As shown in Fig. 1, the following steps are contained in the proposed method.

  • Step 1: Modeling limited simulation data by a Gaussian process;

  • Step 2: Modeling engineering knowledge by a Gaussian process;

  • Step 3: Calculating a posterior Gaussian process using Bayes Rule;

  • Step 4: Sampling new data from the posterior Gaussian process;

  • Step 5: Run computer simulations to obtain the performance of the newly sampled data;

  • Step 6: If conditions (number of iterations or required maximum value) are meet, go to Step 7 else go to Step 1 for next iteration;

  • Step 7: Obtain the optimal value based on the posterior Gaussian process.

The first three steps are to integrate limited simulation data and engineering knowledge and they are illustrated in “Integrating knowledge and data (integration)” section. The step 4 is the updating process, and it is illustrated in “Sampling new data point (updating)” section.

Integrating knowledge and data (integration)

To model engineering knowledge and limited simulation data, we first assume a zero-mean Gaussian process (prior GP) \( {\mathcal{G}\mathcal{P}}\left( {0,\varvec{K}_{prior} } \right) \) and choose a squared exponential (SE) function as the covariance function [Eq. (4)].

$$ \varvec{K}_{prior} \left( {\varvec{x}^{i} ,\varvec{x}^{j} } \right) = {{\varepsilon }}e^{{ - \frac{{\left| {\left| {\varvec{x}^{i} - \varvec{x}^{j} } \right|} \right|^{2} }}{{2l^{2} }}}} $$
(4)

where \( {{\varepsilon }} \) controls the output variance. \( l \) is length scale which is a free parameter to control the strength of correlation.

Essentially, in engineering design, data and knowledge can be regarded as the mapping relationships between design variables and performances. Therefore, surrogate model is used to reflect this mapping information. Besides, in engineering design, the obtained data often contain noise and uncertainty. To deal with uncertainty, Gaussian distribution is commonly used in engineering background because of simplicity. A Gaussian Process is a collection of random variables, any finite number of these random variables have joint Gaussian distribution (Rasmussen et al. 2006). In complex engineering design, GP do a better job of accurately representing the portion of the design space that is of interest to the engineer (Wang et al. 2005). Therefore, we use Gaussian process to model data and knowledge in this work. Besides, the mean of the GP does not influence the learning process, therefore, we set the mean to 0.

Based on the above assumption, single monotonicity engineering knowledge is first integrated into the prior GP. Because the monotonicity engineering knowledge can be expressed by partial derivatives easily, we build a joint Gaussian distribution to model the relationship between the function values and the partial derivatives using the following steps.

Step 1: a finite number \( N \) of locations \( \varvec{X} \) are sampled, and the observation values and function values are indicated by \( \varvec{y} \) and \( \varvec{f} \) respectively. \( D = \left[ {\varvec{X},\varvec{y}} \right] \) indicates the limited simulation data.

All function values \( \varvec{f} \) follows Gaussian process (GP) \( P\left( \varvec{f} \right) = {\mathcal{G}\mathcal{P}}\left( {\varvec{f},\varvec{K}_{{\varvec{X},\varvec{X}}} } \right) \) and the \( \varvec{K}_{{\varvec{X},\varvec{X}}} \) can be calculated using Eq. (4). With this model, the function value \( f^{0} \) of a new point \( \varvec{x}^{0} \varvec{ } \) can be calculated using Eqs. (5) and (6) based on marginal distribution when only \( \varvec{X},\varvec{y} \) are known. However, these two equations do not contain the information from monotonicity engineering knowledge.

$$ E\left[ {f^{0} \left| {\varvec{x}^{0} ,\varvec{X},\varvec{y} } \right.} \right] = \varvec{K}\left( {\varvec{x}^{0} ,\varvec{X}} \right)\left( {\varvec{K}\left( {\varvec{X},\varvec{X}} \right) + \sigma^{2} \varvec{I}} \right)^{ - 1} \varvec{y} $$
(5)
$$\begin{aligned} Var\left[ {f^{0} \left| {\varvec{x}^{0} ,\varvec{X},\varvec{y} } \right.} \right] &= \varvec{K}\left( {\varvec{x}^{0} ,\varvec{x}^{0} } \right) - \varvec{K}(\varvec{x}^{0} ,\varvec{X})\\ &\quad \times \left( {\varvec{K}(\varvec{X},\varvec{X}} \right) + \sigma^{2} \varvec{I})^{ - 1} \varvec{K}\left( {\varvec{X},\varvec{x}^{0} } \right)\end{aligned} $$
(6)

Step 2: a finite number \( M \) of locations, \( \bar{\varvec{X}}, \) where the function values are samples which are known to be monotonic against the \( d^{th} \) variable, and the values and signs of the partial derivatives are indicated by \( \varvec{f^{\prime}} \) and \( \varvec{m} \) respectively.

To express the monotonicity, the probit likelihood \( P\left( {\varvec{m} |\varvec{f^{\prime}}} \right) \) is assumed to follow a distribution as shown in Eqs. (7) and (8) based on existing works (Riihimäki and Vehtari 2010).

$$ P\left( {\varvec{m} |\varvec{f}^{{\prime }} } \right) = \mathop \prod \limits_{i = 1}^{M} {{\Phi }}\left( {\frac{{f_{i}^{{\prime }} }}{v}} \right) $$
(7)
$$ {{\Phi }}\left( x \right) = \mathop \smallint \limits_{ - \infty }^{x} N\left( {t |0,1} \right)dt $$
(8)

where \( v \) controls the strictness of the monotonicity engineering knowledge and it was fixed to \( v = 10^{ - 2} \) in all experiments;

Step 3: the \( \varvec{f} \) and \( \varvec{f}^{{\prime }} \) are also assumed to follow a joint GP \( P\left( {\varvec{f},\varvec{f^{\prime}}} \right) = {\mathcal{G}\mathcal{P}}\left( {\varvec{\mu}_{{\varvec{joint}}} ,\varvec{K}_{joint} } \right) \), where

$$\begin{aligned} \varvec{\mu}_{{\varvec{joint}}} = \left[ {\begin{array}{*{20}c} \varvec{f} \\ {\varvec{f}^{{\prime }} } \\ \end{array} } \right], \varvec{K}_{joint} = \left[ {\begin{array}{*{20}c} {\varvec{K}_{{\varvec{X},\varvec{X}}} } & {\varvec{K}_{{\varvec{X},\bar{\varvec{X}}}} } \\ {\varvec{K}_{{\bar{\varvec{X}},\varvec{X}}} } & {\varvec{K}_{{\bar{\varvec{X}},\bar{\varvec{X}}}} } \\ \end{array} } \right] \end{aligned}$$
(9)

According to Bayes rule, this joint GP can be updated using Eq. (10) to derive the joint posterior GP when some observation values \( \varvec{y} \) and the signs of partial derivatives \( \varvec{m} \) are obtained.

$$ \begin{aligned} P\left( {\varvec{f},\varvec{f}^{{\prime }} |\varvec{y},\varvec{m}} \right) & = \frac{{P\left( {\varvec{y},\varvec{m} |\varvec{f},\varvec{f}^{{\prime }} } \right)P\left( {\varvec{f},\varvec{f}^{{\prime }} } \right)}}{{P\left( {\varvec{y},\varvec{m}} \right)}}\\ &= \frac{{P\left( {\varvec{y} |\varvec{f}} \right)P\left( {\varvec{m} |\varvec{f}^{{\prime }} } \right)P\left( {\varvec{f},\varvec{f}^{{\prime }} } \right)}}{{P\left( {\varvec{y},\varvec{m}} \right)}} \\ & = \frac{1}{Z}P\left( {\varvec{f},\varvec{f}^{{\prime }} } \right)P\left( {\varvec{y} |\varvec{f}} \right)P\left( {\varvec{m} |\varvec{f}^{{\prime }} } \right) \\ \end{aligned} $$
(10)

where \( Z \) is a normalization term, \( P\left( {\varvec{f},\varvec{f}^{{\prime }} } \right) \) is the joint Gaussian distribution, \( P\left( {\varvec{y} |\varvec{f}} \right) \) is the observation model introduced in “Limited simulation data and engineering knowledge” section [Eq. (3)].

Since \( P\left( {\varvec{m} |\varvec{f}^{{\prime }} } \right) \) is not a GP, which makes the calculation of the posterior difficult. Therefore, this work adopts an expectation propagation algorithm to calculate the posterior.

The EP algorithm approximates the posterior distribution in Eq. (10) with

$$\begin{aligned} q\left( {\varvec{f},\varvec{f}^{{\prime }} |\varvec{y},\varvec{m}} \right) &= \frac{1}{{Z_{EP} }}P\left( {\varvec{f},\varvec{f}^{{\prime }} |\varvec{X},\bar{\varvec{X}}} \right)P\left( {\varvec{y} |\varvec{f}} \right)\\ &\quad \times \mathop \prod \limits_{i = 1}^{M} t_{i} \left( {\bar{Z}_{i} ,\bar{\mu }_{i} ,\bar{\sigma }_{i}^{2} } \right)\end{aligned} $$
(11)

where \( t_{i} \left( {\bar{Z}_{i} ,\bar{\mu }_{i} ,\bar{\sigma }_{i}^{2} } \right) = \bar{Z}_{i} N(f_{i}^{{\prime }} |\bar{\mu }_{i} ,\bar{\sigma }_{i}^{2} ) \) are local likelihood approximations with site parameters \( \bar{Z}_{i} \), \( \bar{\mu }_{i} \) and \( \bar{\sigma }_{i}^{2} \). The posterior is a product of Gaussian distributions, and can be simplified to

$$ q\left( {\varvec{f},\varvec{f}^{{\prime }} |\varvec{y},\varvec{m}} \right) = N(\left[ {\varvec{X},\bar{\varvec{X}}} \right]|\hat{\varvec{\mu }},{\hat{{\Sigma }}}) $$
(12)

The posterior mean is \( \hat{\varvec{\mu }} = {\hat{\Sigma}}\Sigma^{-1}{\varvec{\mu}} \) and the covariance \( {\hat{{\Sigma }}} = \left( {K_{joint}^{ - 1} + {{\Sigma }}^{ - 1} } \right)^{ - 1} \), where

$$ \varvec{\mu}= \left[ {\begin{array}{*{20}c} {\textbf{y}} \\ {\bar{\varvec{\mu }}} \\ \end{array} } \right],\quad {{\Sigma }} = \left[ {\begin{array}{*{20}c} {\sigma^{2} \varvec{I}} & 0 \\ 0 & {{\bar{{\Sigma }}}} \\ \end{array} } \right] $$
(13)

\( {\bar{\varvec{\upmu }}} \) is the vector of site means \( \bar{\mu }_{i} \), and \( {\bar{{\Sigma }}} \) is a diagonal matrix with site variances \( \bar{\sigma }_{i}^{2} \) on the diagonal.

With the above model, the function value \( f^{0} \) of a new point \( \varvec{x}^{0} \varvec{ } \) can be calculated by Eq. (14) and (15) based on the marginal distribution when \( \varvec{X},\varvec{y},\varvec{ \bar{X}}, \varvec{m} \) are given.

$$ E\left[ {f^{0} \left| {\varvec{x}^{0} ,\varvec{X},\varvec{y},\varvec{ \bar{X}}, \varvec{m} } \right.} \right] = \varvec{K}\left( {\varvec{x}^{0} ,\left[ {\varvec{X},\bar{\varvec{X}}} \right]} \right)\left( {\varvec{K}_{joint} + \sigma^{2} \varvec{I}} \right)^{ - 1}\varvec{\mu} $$
(14)
$$\begin{aligned} Var\left[ {f^{0} \left| {\varvec{x}^{0} ,\varvec{X},\varvec{y},\bar{\varvec{X}}, \varvec{m} } \right.} \right] & = \varvec{K}\left( {\varvec{x}^{0} ,\varvec{x}^{0} } \right) - \varvec{K}\left( {\varvec{x}^{0} ,\left[ {\varvec{X},\bar{\varvec{X}}} \right]} \right)\\&\quad (\varvec{K}_{joint} + \sigma^{2} \varvec{I})^{ - 1} \varvec{K}\left( {\left[ {\varvec{X},\bar{X}} \right],\varvec{x}^{0} } \right)\end{aligned} $$
(15)

With the above methods, monotonicity engineering knowledge is represented as derivatives signs and can be integrated with limited simulation data. However, to integrate shape engineering knowledge, two issues should be addressed further. The first is how to represent shape engineering knowledge while the second is what mathematical operations can be adopted for integrating this knowledge. For the first issue, we divided the original domain of shape engineering knowledge into piecewise domains and in one or more domains the shape engineering knowledge is monotonic. Based on that, we randomly sample some data points from the domain where we know the latent function are monotonic for different variables. Each point is expressed as \( \left[ {\varvec{x} , + d} \right] \), where \( d \) represents the \( d{\text{th}} \) variable and the \( + / - \) indicates the latent function is positive or negative with the \( d{\text{th}} \) variable. For the second issue, we revise Eqs. (7)–(16) which takes the variables into consideration.

$$ P\left( {\varvec{m} |\varvec{f}^{{\prime }} } \right) = \mathop \prod \limits_{i = 1}^{M} {{\Phi }}\left( {\frac{{\partial f_{i} }}{{\partial x_{d} }}\frac{1}{v}} \right) $$
(16)

Sampling new data point (updating)

The joint posterior GP shown in Eq. (10) is a surrogate model. With this surrogate model, the value of each point becomes a Gaussian distribution, and the mean and variance can be calculated using Eqs. (14) and (15). Therefore, we need to balance the mean and variance to find the optimal value for the next iteration. The mean \( \mu \) indicates the value that the objective function is expected to be, while variance \( \sigma \) represents the uncertainty of the value. The value of this point may fall in the interval \( \left( {\mu - \sigma , \mu + \sigma } \right) \). When looking for the maximum value, the latent value of a point with a small mean (Point B in Fig. 2) but a high uncertainty may be larger than the point (Point A in Fig. 2) with a larger mean but low uncertainty (Fig. 2). If we only consider the mean and select A, we will lose the chance of obtaining a higher value by using a point B.

Fig. 2
figure 2

One dimensional Gaussian process inference of the posterior mean (blue line) and posterior deviation (half of the height of the gray envelope). The latent value of point B may be higher than point A (Color figure online)

Full size image

To address this issue, an acquisition function is adopted which can balance the mean and variance. The new sample \( \varvec{x}_{n + 1} \) can be determined by maximizing the acquisition function as shown in Eq. (17)

$$ \varvec{x}_{n + 1} = argmax\, \alpha (\varvec{x}|D_{n} ) $$
(17)

where \( D_{n} \) represent the limited simulation data at the nth iteration and \( \alpha \) indicates the acquisition function. As shown in Fig. 1, after \( \varvec{x}_{n + 1} \) is determined and the simulation data is obtained, the data will be further added into the limited simulation data to form a new dataset \( D_{n + 1} \) for the next iteration. Therefore, we find that the acquisition function plays a very critical role in the updating process. Currently, several different acquisition functions are proposed and selected, such as the probability of improvement (PI) (Kushner 1964), Expected Improvement (EI) (Calvin et al. 2012; Srinivas et al. 2010), Gaussian process upper confidence bound (GP-UCB) (Srinivas et al. 2010), Thompson sampling (Russo and Van Roy 2014) and entropy search (Hennig and Schuler 2012). Considering the cost and time of objective function evaluation, we would like to make the convergence rate of the algorithm fast, which means to get close to the optimum as quickly as possible. Therefore, we use GP-UCB as the acquisition function in this work, Eq. (18).

$$ \alpha_{n} \left( \varvec{x} \right) = \mu_{n - 1} \left( \varvec{x} \right) + \sqrt {\beta_{n} } \sigma_{n - 1} \left( \varvec{x} \right) $$
(18)

where \( \beta_{n} \) denotes a positive trade-off parameter and was fixed to 0.1 in this paper. \( \mu_{n - 1} \left( \varvec{x} \right) \) is the mean and \( \sigma_{n - 1} \left( \varvec{x} \right) \) is the variance.

This function has been studied extensively in the literature (Schneider 2015; Smola 2012). It was first proposed and analyzed by Srinivas et al. (2010) in the noisy setting and extended to the noiseless case by Smola (2012). Srinivas et al. (2010) found that GP-UCB acquisition function is currently known to has the fastest convergence rate for GP global optimization. Srinivas theoretically proved that (1) the asymptotic property of BO with GP-UCB is to be no-regret \( \left( {\mathop {\lim }\nolimits_{{{\text{T}} \to \infty }} \frac{{R_{T} }}{T} = 0} \right) \) and (2) the cumulative regret \( R_{t} \) increases sub-linearly with the growth of \( {\text{T}} \) rounds \( \left( {R_{T} = \mathop \sum \nolimits_{t = 1}^{T} r_{t} } \right) \). This work provides the theatrical foundation why we use this acquisition function.

Experiments with BO-DK4DO

The proposed method is verified by two groups of experiments: including benchmark functions and an engineering problem.

Benchmark functions

In this paper, six commonly used single-objective benchmark functionsFootnote 1 are adopted, and they are (1) Matyas, (2) Rastrigin, (3) Sphere (5 dimensions), (4) Styblinski-Tang (5 dimensions), (5) Sphere (7 dimensions), (6) Styblinski-Tang (7 dimensions). These functions are named B1, B2, B3, B4, B5 and B6 in the following sections, and all these functions have a maximum value. The limited simulation data is sampled by Latin hypercube sampling from these functions and the engineering knowledge is obtained by analyzing these functions, as shown in Table 2. In this table, the optimum is the extreme value of the corresponding function while samples are the initial number of data points used to build a surrogate model.

Table 2 The benchmark functions and the engineering knowledge
Full size table

The proposed method (BO-DK4DO) is compared with general BO (GBO) which does not integrate engineering knowledge. Each experiment is run 20 times and all empirical results are the average value of the 20 runs. The empirical results are shown in “Benchmark functions” section.

Engineering optimization problem

As an engineering material, steel is very popular in industry. The material processing process is very complex due to many variables and constraints must be considered. To meet the desired properties, many trials are required to get an optimal solution, which is an expensive and time-consuming process. Luckily, designers have accumulated some pieces of shape knowledge through previous trials. Typically, our method is useful for dealing with such problem. Figure 3 shows the hot rod rolling (HRR) process for creating a round rod from a lab of steel, which forms the input material for automotive steel gear production. The final properties of steel depend heavily on the microstructure generated after cooling.

Fig. 3
figure 3

Hot rod rolling (HRR) process chain

Full size image

Tensile strength (TS) is a key property of steel, which indicates the resistance to break under the tensile load. In this experiment, we try to build a surrogate model which learns the mapping between TS and a group of variables, including the composition of Si ([Si]), the composition of N ([N]), ferrite grain size (\( D_{\alpha } \)), the pearlite interlamellar spacing (\( S_{0} \)) and the phase fractions of ferrite (\( X_{f} \)). Table 3 shows the details of the variables and performance while Table 4 shows the related engineering knowledge. To verify the proposed method, the HRR problem is run for 20 times. For each run, we first collect a dataset with 6 data points and the method iterate 11 times to find an optimal solution.

Table 3 The variables and performance for HRR
Full size table
Table 4 The engineering knowledge of HRR
Full size table

Results and discussion

Benchmark functions

The empirical results of benchmark functions are listed in Table 5. In this table, the iteration indicates the number of iterations (Step 1 to Step 6 shown in Fig. 1) the algorithms run, and the corresponding empirical results are obtained at this stage. This paper compares the proposed BO-DK4DO and general Bayesian optimization (GBO), and in this table “BO-DK4DO-N” uses N pieces of engineering knowledge which are integrated with limited simulation data.

Table 5 The empirical results of benchmark functions
Full size table

After N iterations, the methods can find the maximum value. This paper adopts the following six metrics to measure the performance. All the experiments are run on ThinkPad E470c with Intel(R) Core(TM) i5-6200U CPU @ 2.3 GHz 2.4 GHz and 8 GB RAM.

  1. (1)

    The average means (AM) indicates the average current maximum value of the 20 runs of the experiments for a certain iteration. A higher AM value indicates a greater rate of convergence to the real maximum.

    $$ {\text{AM}}_{i} = \frac{1}{n}\mathop \sum \limits_{p = 1}^{n} x_{pi} $$
    (19)

    where \( n \) is the times of experiments. \( x_{pi} \) represents the value of the ith iteration in the pth experiment. Accordingly, \( {\text{AM}}_{i} \) is the mean of ith iteration.

  2. (2)

    The Rank-AM is the order of these methods in terms of the AM value. If the order is 1, the corresponding method has the maximal AM.

  3. (3)

    The scaled standard error (SSE) measures the stability of the 20 maximums found after N running. A lower SSE implies a higher stability and robust capability to find the real maximum.

    $$ {\text{SSE}}_{i} = \left( {\frac{{\frac{1}{n}\mathop \sum \nolimits_{p = 1}^{n} \left( {x_{pi} - {\text{AM}}_{i} } \right)^{2} }}{n}} \right)^{{\frac{1}{2}}} $$
    (20)

    Similarly, \( {\text{SSE}}_{i} \) is the standard error of ith iteration. The numerator is the standard error formula, which we scaled for the showing on the figure.

  4. (4)

    The Rank- SSE is the order of these methods in terms of the SSE value. If the order is 1, the corresponding method has the minimal SSE.

  5. (5)

    The relative difference (RD) is the proximity of real maximum and \( {\text{AM}} \) found at certain iteration. The smaller the value, the closer of real maximum and AM. The real maximum is titled as “optimum” in Table 5.

    $$ {\text{RD}} = \frac{{{\text{optimum}} - {\text{AM}}}}{\text{optimum}} $$
    (21)
  6. (6)

    The relative time (RT) indicator calculated by Eq. (22).

    $$ {\text{RT}} = \frac{{T_{1} - T_{2} }}{{T_{2} }} $$
    (22)

    Where \( T_{1} \) and \( T_{2} \) represent the time of two methods, respectively.

From Table 5, several results can be seen. The first and most important finding is that the integration of engineering knowledge (no matter single or multiple pieces of engineering knowledge) with limited simulation data brings a higher AM and a lower SSE. This implies that the integration of engineering knowledge tends to accelerate the speed of convergence with higher robustness.

The second finding is that when multiple pieces of engineering knowledge are integrated, the AM is further increased while the SSE is decreased. We can see from Table 5 that at last iteration of BO-DK4DO-3 has the maximal AM and minimal SSE, which implies it’s the best method. BO-DK4DO-2 has a relatively small AM and bigger SSE, but the performance is obviously better than BO-DK4DO-1 and GBO.

The third finding is that although in many situations the performance of BO-DK4DO-1 is better than that of GBO, there are indeed some situations where GBO outperformed BO-DK4DO-1, which have an outline border in Table 5. From the corresponding values of AM and SSE, we find the differences are very small. This finding again tells us that it is better to integrate multiple pieces of engineering knowledge with limited simulation data to obtain an obvious improvement in terms of the performance.

Figure 4 shows the AM and SSE for every iteration, from which we obtain another observation. This observation can be expressed as the most obvious difference between GBO and BO-DK4DO occurs in the first few iterations, where BO-DK4DO has obvious advantages. When many iterations (more than 10) are finished, the performances of BO-DK4DO and GBO tend become closer. Because most computer simulations are expensive and time-consuming, the performance in the first few iterations influence the applicability of the methods significantly. From this point of view, the proposed BO-DK4DO is far better than GBO.

Fig. 4
figure 4

The iteration process of GBO and BO-DK4DO on benchmark functions

Full size image

To further discuss the efficiency of our method quantitatively, we use RD to compare BO-DK4DO-N with GBO shown in Table 6. Meanwhile, due to the time required for each iteration is almost the same, we show and compare the total time of a run in Table 7. The RT shown in the table is also the average RT of each iteration.

Table 6 Comparative results between GBO and BO-DK4DO-N of benchmark functions
Full size table
Table 7 Comparison of relative program run time of GBO and BO-DK4DO for benchmark functions
Full size table

Table 6 indicates that BO-DK4DO has a better performance in terms of convergence when the initial samples are relatively small (3, 6 and 8 shown in Table 2). As the complexity of the problem increases, BO-DK4DO becomes more competitive in terms of RD. The RD of GBO can be reduced by increasing the number of iterations. However, it is not guaranteed to achieve the performance of BO-DK4DO.

There are two phenomena need to be addressed. The first is that for B3, the RD of BO-DK4DO-1 is higher than GBO in the last two iterations, with a final difference of 0.35%. However, in the tenth iteration, BO-DK4DO-1 has already reached 0.86%, while GBO is still up to 8.03%. The second is that for B5, the RD of BO-DK4DO-1 is higher than GBO in the last two iterations, with a final difference of 0.42%. However, in the twelfth iteration, BO-DK4DO-1 has already reached 0.82%, while GBO is still up to 4.10%. The above analysis implies that the proposed method is able of reducing the interactions without sacrificing of the solution.

As shown in Table 7, we can see that when more pieces of engineering knowledge are integrated, the computational time also increases. Meanwhile, the convergence speed is also increasing rapidly inferred from Table 6. Take B4 and B6 as examples, GBO’s RD on B4 is 83.59% in the 5th iteration and GBO’s RD on B6 is 93.11% in the 6th iteration, while our method is only 24.80%, 13.63%, 10.09% for B4 and 47.37%, 16.13%, 12.58% for B6 respectively. Considering here are situations where the time required for a single simulation is often hours, days or even more, our proposed method is effective which is often cheaper than performing additional costly simulations of the unknown function.

For the functions B3 and B5 with errors highlighted in Table 5 Line Rank-AM, correspondingly, compared with B4 and B6 shown in Table 7, the RT increases faster as multiple knowledge integrated. To be noted, in the 5th iteration, for B3 and B5, the RD for GBO is 32.87% and 20.02%, while our method is only 2.12%, 0.01%, 0% for B3 and 1.25%, 0.37%, 0.13% for B5. To meet the same requirements for optimal solution, our method is able to save up many iterations.

As shown in Table 7, For B4 and B6 (Their name is Styblinski-Tang), as the dimension increases, the RT of all methods only increase slightly, which means if we have a big number of design variables, the RT will not increase obvious. Therefore, the proposed method is capable for complex product designs with many variables.

Engineering optimization problems

In this paper, we use BO-DK4DO and GBO to maximize the tensile strength of the rolling steel. Four methods are compared including GBO, BO-DK4DO-1, BO-DK4DO-3 and BO-DK4DO-5. The empirical results are shown in Table 8.

Table 8 The empirical results of HRR
Full size table

From Table 8, we have similar findings with the benchmark experiments and the control system experiments. The first is that the BO-DK4DO is efficient of integrating engineering knowledge with limited simulation data and this integration is helpful for finding the optimal solution efficiently. The second is that the integration of engineering knowledge decreases the SSE, which implies that it increases the robustness of the methods. In other words, BO-DK4DO is less affected by the distribution of the initial points. It can be seen more clearly in Fig. 5, we take the last iteration of 20 runs as an example.

Fig. 5
figure 5

The predicted values of the last iteration of the 20 runs

Full size image

In this experiment, one thing is different from the benchmark experiments where the performance is increasing as long as engineering knowledge is integrated. When adding the first piece of engineering knowledge, GBO has a better performance compare with BO-DK4DO-1, and this can be seen more specific in Fig. 6. However, when adding more than one (three or five) pieces of engineering knowledge, the method gains obvious advantages compare with GBO. This phenomenon occurs because GP with engineering knowledge tends to favor smooth functions, but the real function is not smooth. Figure 7 shows the range of the function within the domain 0.18 to 0.3, which is also the domain of the first piece of engineering knowledge. The fixed value of \( x_{2} \), \( x_{3} \), \( x_{4} \) and \( x_{5} \) are 0.009, 8, 0.25 and 0.1 respectively.

Fig. 6
figure 6

The iteration process of GBO and BO-DK4DO on HRR

Full size image
Fig. 7
figure 7

The relationship between \( x_{1} \) and \( y_{1} \) of the HRR

Full size image

To compare the efficiency of these methods, Table 9 show the average runtime at each iteration. The computational time of each iteration in both methods is nearly the same.

Table 9 The average program run time at each iteration for the HRR
Full size table

As shown in Table 8, though the latent function of HRR is non-smooth, both BO-DK4DO-3 and BO-DK4DO-5 do better than GBO, with 765.16 MPa and 770.16 MPa in the last iteration, while BO-DK4DO-1 is 756.09 finally. Meanwhile, form Table 10, as the RT of GBO is set to 0, the RT of BO-DK4DO-1, BO-DK4DO-3, BO-DK4DO-5 for the HRR are 2.61, 3.64 and 4.83.

Table 10 Comparison of relative program run time (11 iterations) for the HRR
Full size table

Note that the reduction of the number of experiments is also significant, as shown in Fig. 6 We only show the available value against iteration in this figure, the difference of real cost is much larger. In this case, the target value is over 755 MPa. BO-DK4DO-5 and BO-DK4DO-3 takes 3 and 5 iterations respectively to reach the target while the BO-DK4DO-1 and GBO takes 11 and 8 iterations. To apply the method to real-world problems, the computation time should include not only the program run time which is consumed to find the optimal solution but also the simulation time used for sampling. Therefore, the total computation time is defined as follows in this paper.

$$ T = T_{p} + T_{s} $$
(23)

where \( T_{p} \) is the program run time to obtain the target value and \( T_{s} \) is the simulation time.

In the HRR problem, the average sampling time for generating a data point in the simulation is about 3.5 h (12600 s), which is at least 2 orders of magnitude larger than the total program run time for all methods.

Figure 8 show the \( T_{p} \) and \( T_{s} \) for all methods. Mapping to the real time, BO-DK4DO-3 and BO-DK4DO-5 are able to save up to 37.41% and 62.43% of total computation time \( T \), which firmly establishes the utility of using multiple engineering knowledge through our proposed method. Actually, we can ignore the \( T_{p} \) in Eq. (23) due to the huge magnitude difference. For many complex engineering problems, the computation time is the equivalent of the simulation time.

Fig. 8
figure 8

Comparison of \( T_{p} \) and \( T_{s} \) of GBO and BO-DK4DO for the HRR

Full size image

Closure

Surrogate models are widely used in simulation-based design, and many engineering problems are solved with the support of surrogate models. However, enough data are required to build a highly accurate surrogate model, which are not available for many real-world engineering problems. Therefore, developing methods for building high-accuracy surrogate models and implement optimization designs are still a challenge. In this paper, we present a method to integrate limited simulation data and shape engineering knowledge to build surrogate models and conduct design optimizations based on Bayesian optimization, which is called BO-DK4DO. The proposed method is verified using 6 benchmark functions and HRR problem. By the analysis of the empirical results, we find (1) the proposed method is capable of integrating shape engineering knowledge and limited simulation data efficiently; (2) the integration of engineering knowledge brings satisfactory improvement in terms of finding optimum values; (3) when more pieces of engineering knowledge are integrated, the performance of the methods are further improved.

By this paper, three-fold contributions are made. The first is that the notion of integration engineering knowledge and available limited data to build surrogate models and implementing design optimization. The notion expands the application of surrogate models to scenarios where only limited simulation data are available. The second is the adoption of Bayesian optimization and a probabilistic model (Gaussian process) to model the engineering knowledge and limited simulation data. This natural adoption of uncertainty of the proposed method provides a new way and tools for further research about the uncertainty of engineering knowledge and limited simulation data. The last contribution is that a computational method to accomplish the above idea is implemented, and the proposed method is demonstrated through 6 benchmark functions and a real-world engineering design problem. We suggest that this method is foundational for further development.