Keywords

1 Introduction

Surrogate Assisted Optimization (SAO) has been applied widely in the practical engineering [1]. The SAOs [2, 3] have advantages over traditional methods when dealing with highly computational cost problems, such as simulation-based design. However, most of high nonlinear and high dimensional problems still cannot be handled, especially for expensive simulation evaluations. Usually, 10 or more dimensional problems can be considered high if the corresponding evaluation is time consuming, and such problems widely exist in various disciplines [4, 5].

Region-based optimization is one branch of optimization methods. For an optimization problem, the design space can be partitioned multiple sub-region to search the global optimum. Partitioning multiple regions is often done with the DIRECT optimization algorithm. The method is a global optimization method first motivated by Lipschitz optimization, which has been proven to be effective in a wide range of application domains [6, 7]. The algorithm centers on a space-partitioning scheme that divides large hyperrectangles into small ones. The center of each hyperrectangle, considered as a representing point of the hyperrectangle, is evaluated via the objective function. At each iteration, a set of potentially optimal hyperrectangles are selected for further divisions. However, for most of high nonlinear and high dimensional problems still cannot be handled. On the other hand, Xu et al. partitioned the design space into multiple cells to improve the accuracy of the global surrogate [8].

In this study, an adative region-based global optimization is suggested. The method intends to generate multiple sub-regions and sample sets within each sub-region. With the generation of multiple sub-regions, a local surrogate is built from the sample set within each sub-region to predicate the optimum of the sub-region. At each iteration, a global surrogate is built from all the sample sets to predicate the optimal sub-region. One crucial advantage of the proposed method is to use local surrogate to exploit the global optimum and global surrogate to explore the optimal sub-region.

The next section of this paper describes the general idea behind the multiscale surrogate assisted global optimization method in details. Sections 3 and 4 present numerical experiments and discuss the test results compared with three nature-inspired methods and three surrogate assisted methods. Section 5 presents concluding remarks.

2 Adative Region-Based Global Method Optimization Formulations (MSAO)

The general formulation of an optimization problem is considered:

$$ \begin{array}{*{20}l} {\mathop {\text{Min}}\limits_{{\mathbf{X}}} } \hfill & {{\text{Y = }}f ({\mathbf{X}} )} \hfill \\ {s.t.} \hfill & {{\mathbf{X}} = \left[ {x_{1} ,x_{2} , \ldots ,x_{D} } \right]^{\text{T}} , { }{\mathbf{X}} \in\Omega } \hfill \\ \end{array} $$
(1)

where \( {\mathbf{X}} \) is the design variable vector, D is the number of design variables. \( f ({\mathbf{X}} ) \) is the objective function. \( \Omega \) is the constraint subset of the D dimensional space.

To help designers to concentrate on these sub-regions rather than the whole design space, the suggested method partitions the space into multiple sub-regions and assigns multiple sample points to each sub-region as presented in Fig. 1. Figure 1 illustrates the partition of a two-dimensional space into four sub-regions, which requires three center points. In this example, the center points are placed randomly in the design space. For the shape of the sub-region, hyperrectangles are employed to partition the entire design space into a set of hyperrectangle cells. The ith rectangles cell, represents the surrounding region of center point P i.

Fig. 1.
figure 1

Two-dimensional partitioning example showing data points and three sub-regions.

Full size image

2.1 Generation of New Samples

Once the sub-regions have divided with assigning multiple sample points, the local surrogates are built within the sub-region. The local optimization is repeatedly obtained by using gradient optimization method to generate new points (Point 1). However, the new point needs meet two criteria:

  1. (1)

    The new point should not be too close to existing points within the sub-region

  2. (2)

    Due to updating the size of the sub-region based on the new point, the new point should not be too close to the center points of other sub-regions.

When the new point is too close to existing points within the sub-region, then an exploration point should be added. To explore the sub-region, the sample set should be updated by adding a point to the database that maximizes the uncertainty of the local surrogate (Point 2) [9]. The exploration could prevent the new point from crowding the same area, allowing one point to capture the behavior in the sub-region. If the Point 2 could not meet the second criterion, the sub-region could not find a new point (Table 1).

Table 1. Comparison of two points to decide where to place the center of a sub-region and update the size of the region.
Full size table

2.2 Dynamic Partitioning

The cooperative optimization process performed by local surrogates and global surrogate is suggests in per optimization iteration. The purpose of this method is to have each local surrogate predicate a single optimum, and the global surrogate could explore a single optimal sub-region per iteration. Therefore, as a part of the cooperative optimization process, a self-organizing mechanism is proposed to dynamically partition the sub-regions which adapts to the search space. By self-organizing, the size of the sub-regions will be updated and terminated depending on the cooperative optimization process. The size of the sub-regions will be extended when the new points is to improve the current optimum and reduce the uncertainty of the local surrogate (updating), and will be terminated when the sub-region could not exploit the optimum (termination).

The method of space partitioning focuses on moving the sub-regions’ centers to different local optima. As a result, each sub-region can choose a surrogate that is accurate around the local optimum, and the new sub-region can also explore the whole design space. Then it begins optimization by choosing a surrogate, fitting it and optimizing on this surrogate. As a result, the new sub-region could be arranged multiple new points. Then, the center of the sub-region is moved to the “best” point in the sub-region to tradeoff distance and objective function value. This is done by comparing the center at the last iteration to the last point added by the sub-region.

2.2.1 Update or Terminate the Size of the Sub-region

Once a sub-region has added a new point in its database, it will check whether to update the size of the region and moved its center to the best point, or to terminate the udpdating of the region. These operations assign search resources non-uniformly in the design space so that sub-regions are not redundant and can efficiently improve the accuracy of the local surrogate.

2.2.2 Create a New Sub-region

The sub-regions might reach a point where there is no improvement made by the optimization in several iterations (i.e., the sub-region couldnot generate new point). To improve exploration, a new sub-region is created in the design space per iterations. This parameter is called the stagnation threshold. To create a new sub-region, a new center point is created by minimizing the global surrogate, thus forming a new sub-region. The design space is then repartitioned. If the new sub-region might be too close to other sub-region, the sub-region could be created by maximizing the uncertainty of the global surrogate.

2.3 The Optimization Method is Summarized as Follows

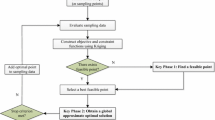
The flowchart of the MSAO method is shown in Fig. 2.

Fig. 2.
figure 2

Flowchart of the MSAO method.

Full size image

3 Numerical Experiment

This section compares the accuracy and efficiency of the methods presented in this study for three numerical examples. Six methods are compared: three nature-inspired methods (GA [10], DE [11], and PSO [12]), three surrogate assisted methods (EGO [13], MSEGO [14], and MPS [15]).

3.1 Test Functions

In this section, three test cases with different features are used to demonstrate the applicability of the methods. These test cases are classified two groups: the first group is a set of low dimensional test cases. These test cases are in favor of sequential sampling optimization methods considering both exploration and exploitation; the second group is a high dimensional test case with highly nonlinear regions. These cases are summarized in Table 2.

Table 2. Summary of test cases
Full size table

3.2 Test Scheme

To obtain more stable prediction, all functions are tested with 100 replications. A Latin Hypercube Sampling (LHS) is employed to create an initial sample set where sample points are infilled in the design space and sub-regions. The number of initial sample points is 3D for low dimension and 10D for high dimension. Furthermore, to compare the performance method with different method within the limited Number of the Function Evalutions (NFEs), the NFEs is the stopping criterion used in this study. The details are summarized in Table 3.

Table 3. Multi-agent parameters for example problems
Full size table

4 Results and Discussion

4.1 Rosenbrock Function

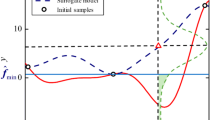
Figure 3 shows the real function, global surrogate, local surrogate, and the region with sample points in different cycles. As shown in Fig. 3(a–c), the centers of the regions are based on the initial samples are created by the LHS, and the size of the region is set by the initial size. Then the next initial samples are included and created by the LHS. As shown in Fig. 3(d–f), the number of the region is 2 instead of 4 since the new sample is too close to the other sample within the disappeared region. Moreover, by the manner, the optimal region can be catched, and the other region can be removed. As shown in Fig. 3(g–i), there are two remaining regions. The large one is the optimal region to exploit the next global optimum. The small one is the most uncertainty region to explore the region of the global optimum.

The results of the different methods for Rosenbrock2 are shown in Fig. 4.

Fig. 3.
figure 3

Contour plots of the real function and KRG model in different cycles

Full size image
Fig. 4.
figure 4

The results of the different methods for Rosenbrock2 (60NFEs)

Full size image

Figure 6 shows that the Ymin of each method is close to the real optimum in the limited number of samples, suggesting that none of the EGOs can handle such a complicated multimodal function. However, it is clear that the convergence result of the EGO is retively good and reliable.

4.2 Schwefel Function

Figure 5 shows the real function, global surrogate, local surrogate, and the region with sample points in different cycles. As shown in Fig. 5(a–c), the centers of the regions are based on the initial samples are created by LHS, and the size of the region is set by the initial size. Then the next initial samples are included and created by the LHS. As shown in Fig. 5(d–f), the number of the region is 4 since the distances between the new samples of the current region and the other samples of the current region are suitable to generate new samples. Moreover, by the manner, the current region can be extended to find more local optimum. As shown in Fig. 5(g–i), the number of the region is 3 instead of 5 since the distances between the new samples of the disappeared regions and the other samples of the disappeared regions are too short or the size of the disappeared region is too large.

Fig. 5.
figure 5

Contour plots of the real function and KRG model in different cycles

Full size image

Figure 6 shows that the Ymin of each method is near to the real optimum in the limited number of samples, suggesting that none of these methods can handle such a complicated multimodal function. However, it is clear that the convergence result of the MASO is retively good and reliable.

Fig. 6.
figure 6

The results of the different methods for Schwefel2 (60NFEs)

Full size image

4.3 Rastrigin Function

Figure 7 shows that the Ymin of each method is near to the real optimum in the limited number of samples, suggesting that none of these methods can handle such a complicated multimodal function. However, it is clear that the convergence result of the DE is retively good and reliable.

Fig. 7.
figure 7

The results of the different methods for Rastrigin 10 (1000 NFEs)

Full size image

5 Conclusion Remarks

This paper provided a novel multiscale surrogate assisted global optimization method to address the global optimization problem. The method is compared with six global methods. It is observed that the MASO method has the potential to improve the efficiency of the optimization method by dynamically partitioning the design space. In practice, this is an ideal scenario as one would not want to waste resources on searching for poor sub-region.

For Schwefel and Rosenbrock function, it is observed that the MSAO method outperforms nature-inspired methods in terms of efficiency and reliability. However, the MSAO method might not outperform other surrogate assisted optimization (EGO, MSEGO). For Rastrigin function, none of methods obtains the global optimum. It is observed that the MSAO method outperforms other surrogate assisted optimization (EGO, MSEGO) in terms of efficiency and reliability. However, the MSAO method might not outperform the nature-inspired methods.

In the future, a more in-depth look at the advantages of using multiple sub-regions per iteration can be studied. There is the possibility to explore asynchronous sub-regions that partition the starting points for local optimization in the space and update the global surrogate as new points are added.