1 Introduction

In real-world problems, the optimization goals mostly consist of multiple conflicting objectives. Thus, optimizing all the objectives simultaneously leads to multiple solutions that are mathematically equal. The solution for such a problem can be presented in the form of a Pareto set.

One of the techniques to attain the Pareto set is using weighted sum of the objectives [1,2,3], which can be optimized by standard single objective optimization algorithms. However, there are many ways to define the weighted sum function and to determine the proper coefficients, relying on experts opinion is fundamental [4]. Another alternative is using approaches based on Multi-objective Evolutionary Algorithms (MOEAs) [5,6,7], but the number of required function evaluations often is very high. This represents a clear limitation when optimizing engineering systems, whose performance are typically analyzed via computationally expensive and time-consuming simulations.

In this framework, surrogate-based optimization is a popular approach [8]: the idea is to approximate the desired design objective using a data-driven surrogate model. Several models are commonly used, including but not limited to Gaussian processes [9,10,11], Neural networks [12, 13], Polynomial chaos expansion [14, 15], and Tree-structured Parzen estimator [16] . Such model is built based on a limited number of (expensive) simulations and is cheap-to-evaluate. Examples include optimization of electronic circuits performance [17,18,19], the shape of airplane components [20,21,22], and the strength of adhesive joints [23].

A popular technique for surrogate-based optimization is Bayesian Optimization (BO) based on a Gaussian Process (GP) as surrogate model. The technique [24] proposes fast and efficient hypervolume-based BO for multi-objective problems. However, the technique [24] implicitly assumes that all of the objectives can be evaluated with the same computational cost.

This condition does not always hold in multi-objective optimization problems. Typically, some objectives are cheap to compute. For example, the footprint of electrical devices [25] and time of gluing in the adhesive bonding case [26]. Many multi-objective BO techniques [27,28,29] do not take into account the objectives with very cheap computational cost. In practice, cheap objectives are often modeled with the same surrogate model cost as the expensive ones. This can be an unnecessary burden to the optimization process.

In this work, we extend the standard hypervolume-based acquisition functions to deal with cheap-to-evaluate functions. More specifically, we focus on the bi-objective case, which can be easily extended later on. Instead of modeling the cheap function with a GP, we directly integrate it in the hypervolume-based acquisition functions. We derive the formula analytically resulting in two hypervolume-based acquisition functions: Cheap Hypervolume Expected Improvement (CHVEI) and Cheap Hypervolume Probability of Improvement (CHVPOI).

For evaluating its performance, we consider four analytical benchmark functions [30], and two realistic design problems in microwave engineering. We show that the proposed method performs better than state-of-the-art approaches. Since the cheap objective is computed directly, the inaccuracies introduced by modeling are eliminated.

This paper is organized as follows: Sect. 2 introduces the GP probabilistic model and BO. Section 3 presents the hypervolume-based bi-objective BO. Our extension to the hypervolume-based acquisition function is described in Sect. 4. Then, Sect. 5 presents relevant experimental results on benchmark functions and realistic design problems. Finally, conclusions are drawn in Sect. 6.

2 Bayesian optimization

2.1 Optimization procedure

In global optimization, the goal is to find an optimizer \({\varvec{x}}^*\) of an unknown objective function \(f({\varvec{x}})\), which can be mathematically described as:

$$\begin{aligned} {\varvec{x}}^{\star }=\underset{{\varvec{x}} \in {\mathcal {X}}}{\arg \max } f({\varvec{x}}) \end{aligned}$$
(1)

where \({\mathcal {X}} \in {\mathbb {R}}^{d}\) is the design space. The unknown objective function \(f({\varvec{x}})\) typically does not have gradient information and is very expensive to evaluate, for example in terms of time or economic cost. Thus, a data-efficient algorithm to find \({\varvec{x}}^*\) is desired.

BO is a global optimization method that aims to minimize the number of function evaluations needed to estimate the global optimum of a function. It relies on two elements: a model of the objective function and a sequential sampling strategy. The idea is to iteratively refine the model until the solution to the optimization problem can be found. The sampling strategy relies on the model to estimate which data point should be acquired next. In order to do so, the sampling strategy relies on a function called acquisition function. The acquisition function balances the trade-off between exploration and exploitation, based on the surrogate model. Usually, the acquisition function has an analytical form that can be computed easily [10].

Before running the BO routine, we first need to generate initial points to train the model. In this paper, the Latin Hypercube Design (LHD) [31] is used. Then, the acquisition function is optimized based on the trained model. After a new point is selected, it is evaluated on the true objective function and the result is used to update the surrogate model. These steps are repeated until a suitable stopping criterion is met. The flowchart of BO is shown in Fig. 1.

Fig. 1
figure 1

General flowchart of Bayesian optimization. The two key components are the surrogate model and the acquisition function. The query point from the previous iteration is added to the surrogate model. Thus, the samples in the dataset are increased sequentially

Full size image

2.2 Gaussian processes

The most common choice for the surrogate model for BO is a GP. It is analytically tractable and provides a predictive distribution given new input data. In a more formal definition, GP defines a prior over functions \(f({\varvec{x}})\sim GP(m({\varvec{x}}),k({\varvec{x}}, \varvec{x'}))\).

GP is fully specified by its mean function \(m({\varvec{x}})\) and positive semi-definite covariance function \(k({\varvec{x}}, \varvec{x'})\). Following previous work [24], we assume a zero mean function and train the GP on a set of data by maximizing the likelihood using the L-BFGS algorithm. The predictive distribution with a zero mean function of new data \(X_{\star }= [{\varvec{x}}_{\star 1},\ldots ,{\varvec{x}}_{\star N}]\) can be calculated using:

$$\begin{aligned} \mu \left( X_{\star }\right)&={\mathbb {E}}\left( {\varvec{f}}_{\star } \mid X_{\star }, {\mathcal {D}}_{n}\right) =K_{\star \mathrm {x}} K_{\mathrm {xx}}^{-1} {\varvec{y}} \end{aligned}$$
(2)
$$\begin{aligned} \sigma ^{2}\left( X_{\star }\right)&= {\text {Var}}\left( {\varvec{f}}_{\star } \mid X_{\star }, {\mathcal {D}}_{n}\right) =K_{\star \star }-K_{\star \mathrm {x}} K_{\mathrm {xx}}^{-1} K_{\star \mathrm {x}}^{T} \end{aligned}$$
(3)

where \({\mathcal {D}}_{n}\) is the observed data, \(\mu \left( X_{\star }\right)\) is the predictive mean, and \(\sigma ^{2}\left( X_{\star }\right)\) is the predictive variance, and \(K_{\mathrm {xx}} = k({\varvec{x}}_{i},{\varvec{x}}_{j})\), \(K_{\star \mathrm {x}} = k({\varvec{x}}_{\star i},{\varvec{x}}_{j})\), \(K_{\star \star }=k({\varvec{x}}_{\star i},{\varvec{x}}_{\star j})\). For the covariance function, the Matérn 5/2 kernel [32] is used and defined as:

$$\begin{aligned} k\left( {\varvec{x}}, {\varvec{x}}^{\prime }\right)&=\alpha \left( 1+\sqrt{5} r+\frac{5}{3} r^{2}\right) \exp (-\sqrt{5} r), \nonumber \\ r&=\left\| \sum _{m=1}^{d} \frac{\left( x_{m}-x_{m}^{\prime }\right) ^{2}}{l_{m}^{2}}\right\| _{2} \end{aligned}$$
(4)

This kernel is chosen as it does not put strong smoothness assumptions on the target function compared to the other kernels [33]. Thus, it is more suitable for real-world cases such as the engineering design problems.

3 Multi-objective Bayesian optimization

3.1 Pareto optimality

In real life optimization problem, typically there are multiple conflicting objectives. This leads to solutions that cannot be improved in any of the objectives without sacrificing at least one of other objectives. These solutions are called Pareto optimal solutions, represented as a Pareto set [34].

For minimization problems with m objectives, the notation \({\varvec{x}}_{b} \succ {\varvec{x}}_{a}\) means that \({\varvec{x}}_{b}\) dominates \({\varvec{x}}_{a}\) if, and only if \(f_{j}\left( {\varvec{x}}_{b}\right) \le f_{j}\left( {\varvec{x}}_{a}\right) , \forall j \in \{1, . ., m\}\) and \(\exists j \in \{1, . ., m\}\) such that \(f_{j}\left( {\varvec{x}}_{b}\right) <f_{j}\left( {\varvec{x}}_{a}\right)\). In other words, \({\varvec{x}}_{b}\) is not worse than \({\varvec{x}}_{a}\) in all objectives and better in at least one objective. The Pareto set can then be defined by:

$$\begin{aligned} {\varvec{P}}=\left\{ {\varvec{x}} \in {\mathbb {R}}^{d} \mid \not \exists \varvec{x^{\prime }} \in {\mathbb {R}}^{d}: \varvec{x^{\prime }} \succ {\varvec{x}}\right\} \end{aligned}$$
(5)

where m is the number of the objectives. Mathematically, the points inside the resulting Pareto set are equal. Also we denotes the Pareto front, the Pareto optimal solutions in output space as \({\mathcal {P}}\). In practice, after the optimal Pareto set is obtained, the decision makers can choose which point to use based on their preference.

3.2 Multi-objective hypervolume-based acquisition function

In multi-objective optimization problems, instead of calculating the improvement towards a single maximum, we want to get the improvement over the Pareto set \({\varvec{P}}\). For the hypervolume-based acquisition function, this improvement can be calculated using the hypervolume indicator \({\mathcal {H}}({\mathcal {P}})\). This indicator denotes the volume of the dominated region, bounded by a reference point r which needs to be dominated by all points in \({\mathcal {P}}\) [35]. The contribution of new points \({\varvec{y}}\) to \({\mathcal {P}}\) can be estimated by using the exclusive hypervolume (also called hypervolume contribution) \({\mathcal {H}}_{exc}\) as:

$$\begin{aligned} {\mathcal {H}}_{exc}({\varvec{y}}, {\mathcal {P}})={\mathcal {H}}({\mathcal {P}} \cup \{{\varvec{y}}\})-{\mathcal {H}}({\mathcal {P}}) \end{aligned}$$
(6)

Using \({\mathcal {H}}_{exc}\), we can define the improvement function for the hypervolume-based multi-objective case as:

$$\begin{aligned} I({\varvec{y}}, {\mathcal {P}})=\left\{ \begin{array}{ll} {\mathcal {H}}_{{\text {exc}}}({\varvec{y}}, {\mathcal {P}}) &{} \text{ if } {\varvec{y}} \text{ is } \text{ not } \text{ dominated } \text{ by } {\mathcal {P}} \\ 0 &{} \text{ otherwise } \end{array}\right. \end{aligned}$$
(7)

Next, we will build the acquisition function for multi-objective settings upon this improvement function. In order to make the formula simpler, given the predictive distribution defined in Eqs. (2) and (3), the probability density function \(\phi _{j}\) and cumulative density function \(\varPhi _{j}\) are compactly defined as:

$$\begin{aligned} \phi _{j}\left[ y_{j}\right]&:=\phi _{j}\left[ y_{j} ;\,\, \mu _{j}({\varvec{x}}), \sigma _j({\varvec{x}})\right] \end{aligned}$$
(8)
$$\begin{aligned} \varPhi _{j}\left[ y_{j}\right]&:=\varPhi _{j}\left[ y_{j} ;\,\, \mu _{j}({\varvec{x}}), \sigma _j({\varvec{x}})\right] \end{aligned}$$
(9)

Then, the hypervolume-based multi-objective POI (HVPOI) [24] is defined as follows:

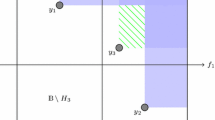
$$\begin{aligned} {\text {HVPOI}}[I]&= I(\mu ({\varvec{x}}), {\mathcal {P}}) \int _{{\varvec{y}} \in A} \prod _{j=1}^{m} \phi _{j}\left[ y_{j}\right] d y_{j} \end{aligned}$$
(10)

where \(\mu ({\varvec{x}})\) is a GP prediction at \({\varvec{x}}\) and A is the non-dominated region, see Fig. 2. m is the number of objectives, \({\varvec{y}}\) is the objective vector inside region A.

Furthermore, we can define the hypervolume-based EI (HVEI) [24] as:

$$\begin{aligned} {\text {HVEI}}[I]=\int _{{\varvec{y}} \in A} I({\varvec{y}}, {\mathcal {P}}) \prod _{j=1}^{m} \phi _{j}\left[ y_{j}\right] d y_{j} \end{aligned}$$
(11)

Note that these acquisition functions are intractable. To mitigate this problem, Couckuyt et al. [24] suggests calculating the hypervolume from the set of disjoint cells built from the lower and upper bound of the Pareto front. This approach is more computationally efficient compared to the uniform grid search [36].

However, these multi-objective acquisition functions implicitly assume that the models of all objectives must be computed, regardless of the computational cost of evaluating each objective. A problem might arise using this assumption: If we have a cheap but complex objective function, the GP might introduce inaccuracies as well as a waste of computational resources.

4 Cheap-expensive hypervolume-based acquisition function

Without loss of generality, let us consider problems where two objective functions can be defined, where one is expensive \(f_1\) and the other is cheap \(f_2\). Our extended approach models \(f_1\) into a GP and uses it to predict new data \(\varvec{x^*}\) and estimate the corresponding mean \(\mu _1\) and variance \(\sigma ^{2}_{1}\) in the acquisition function calculation. Next, \({\varvec{y}} :=(y_1,y_2)\) is used to compute the improvement function \(I({\varvec{y}}, {\mathcal {P}})\), where \(y_1\) and \(y_2\) are potential observation and observation of \(f_1\) and \(f_2\), respectively. Here, \({\mathcal {P}} = \{(p_{1}^{1},p_{2}^{1}),(p_{1}^{2},p_{2}^{2}),\ldots ,(p_{1}^{M},p_{2}^{M})\}\), where \(p_{1}^{m}\) denotes the expensive dimension sorted in ascending order. Then it follows that \(p_{2}^{m}\), the cheap dimension, is sorted in descending order. Next, the Cheap Hypervolume EI (CHVEI) is defined as follows:

$$\begin{aligned} {\text {CHVEI}}(x) = \int _{(y)\in A}I({\varvec{y}}, {\mathcal {P}})\phi (y_1)dy_1 \end{aligned}$$
(12)
Fig. 2
figure 2

Illustration of the non-dominated region and the way the cheap objective function evaluation \(y_2\) is incorporated into the hypervolume-based acquisition function. \(P_i\) are the points in the Pareto set. The blue dotted curve illustrates the prediction of the expensive objective \(y_1\). The orange dot is the reference point, used as the bound to calculate the hypervolume

Full size image

Using \({\mathcal {P}}\) we define horizontal and vertical cells as shown in Fig. 2. Based on these cells, we can derive the closed form of the CHVEI as follows:

$$\begin{aligned} {\text {CHVEI}}(x) = \sum _{m} \sum _{k}\left( u_{2}^{k}-y_{2}\right) ^+ \int _{l_{1}^{m}}^{u_{1}^{m}}\left( u_{1}^{k}-\max \left( l_{1}^{k}, l_{1}^{m}\right) \right) \phi (y_{1}) d y_{1} \end{aligned}$$
(13)

where m is the cell of interest, k is the cell improvement relative to m, l is lower bound, u is upper bound and \(z^+=\max (z,0)\). Then, we can calculate the closed form solution of CHVEI. For cells of interest (\(m = k\)), the integrals on Eq. 13 are the definition of the single-objective EI [37] defined as:

$$\begin{aligned} \left( u_{1}^{k}-\mu _{1}({\varvec{x}})\right) \left( \varPhi [u^{m}_{1}]- \varPhi [l^{m}_{1}]\right) + \sigma _{1}^{2}({\varvec{x}})\left( \phi [u^{m}_{1}]-\phi [l^{m}_{1}]\right) \end{aligned}$$
(14)

while the integral for cells on the right of the cells of interest (\(l^{k}_{1} \ge u^{m}_{1}\)) are calculated by:

$$\begin{aligned} \left( u^{k}_{1}-l^{k}_{1}\right) \left( \varPhi \left[ u^{m}_{1}\right] - \varPhi \left[ l^{m}_{1}\right] \right) \end{aligned}$$
(15)

and 0 for cells in the left (\(u^{k}_{1}<l^{m}_{1}\)).

It is important to mention that the cheap objective is directly incorporated in the acquisition function, thus avoiding the inaccuracies due to modeling the cheap objective with a surrogate model. This is favorable especially when the cheap objective function has a complex dynamic behaviour in the design space. Additionally, it leads to a reduced computational complexity of the overall algorithm. The proposed BO approach based on CHVEI is summarized in Algorithm 1.

figure a

A similar approach can be used to define the cheap version of bi-objective POI as follows:

$$\begin{aligned} {\text {CHVPOI}}(x) =&\sum _{m=1}^{M-1} (p_{2}^{m}-y_2)^+(p_{1}^{m}-y_1)^+ (\varPhi _1\left[ p_{1}^{(m+1)}\right] \nonumber \\&\quad -\varPhi _1\left[ p_{1}^{m}\right] ) \end{aligned}$$
(16)

Now, a BO routine based on CHVPOI can be defined as for the CHVEI: the only difference with the approach described in Algorithm 1 is that Eq. (16) is used instead of \(\mathrm {CHVEI}(x)\).

5 Result and discussion

The proposed BO approach is implemented using the GPFlowOpt library [38] in python. For the initial data, 21 points are arranged using a Latin-Hypercube Design [31]. The acquisition function is optimized using the best solution of Monte Carlo sampling, further fine-tuned by a gradient-based optimizer. We consider four variants of the well known DTLZ benchmark functions [30] and two real-life electrical device design optimization problems to validate the proposed method.

In all experiments, the CHVEI and CHVPOI acquisition functions are compared with the standard HVEI and HVPOI, as well as random sampling. Additionally, we also compare against the MOEA algorithms SMS-EMOA [39] and NSGA-II [40]. We used hypervolume indicator metrics to assess the quality of the Pareto set per iteration, where the computational budget is fixed to 100 function evaluations for all methods except the MOEA, that uses a budget of 250 function evaluations instead. This choice guarantees a fair comparison, since MOEA needs more evaluations compared to approaches based on BO. Finally, when optimizing electrical devices we inspect the quality of the Pareto set by checking the design layout and its corresponding responses visually.

5.1 DTLZ benchmark functions

We consider four variants of the DTLZ functions: DTLZ1, DTLZ2, DTLZ5, and DTLZ7, as indicated in Table 1. DTLZ2 and DTLZ5 have a smooth set of Pareto solution, while DTLZ1 and DTLZ7 have a disjoint Pareto set.

Table 1 We configure the DTLZ benchmark functions for 5 dimensional inputs, 2 outputs, and a fixed reference point r
Full size table

The final hypervolume indicator is shown in Table 2. Overall results show that CHVPOI always performs better than the other methods, even compared to the MOEAs with 250 function evaluations budget.

Figure 3 shows the hypervolume indicator evolution with respect to the function evaluations number: the CHVEI and CHVPOI achieve a better hypervolume indicator in less iterations compared with their standard counterpart HVEI and HVPOI, respectively. Additionally, CHVEI and CHVPOI offer the best performance compared with all other methods for DTLZ1 and DTLZ7, while standard HVPOI is better than CHVEI in iteration 100 for the functions DTLZ2 and DTLZ5, that have a smooth Pareto solution. This is because EI based methods are less exploitative compared to the POI based methods.

Table 2 Hypervolume with \(95\%\) confidence interval of the DTLZ benchmark experiments
Full size table
Fig. 3
figure 3

Evolution of hypervolume indicator for the DTLZ benchmark functions. (a) and (d) are less smooth functions, DTLZ1 and DTLZ7 respectively. While (b) DTLZ2 and (c) DTLZ5 are smoother functions

Full size image

Furthermore, we randomly sample 1 million points for all the benchmark functions to approximate the true Pareto set of the functions. Next, we calculate the distance of the sampled-based Pareto set and the Pareto set obtained via BO-based approaches and MOEAs. This metric is used to measure the convergence of the results with respect to approximate ”true” Pareto set: the lower the value, the more accurate the approximation. It is defined as:

$$\begin{aligned} {\text {CM}}(P,{\hat{P}}) = \frac{1}{n}\sum _j^{n} \min _i ||P_i - {\hat{P}}_j||_2 \end{aligned}$$
(17)

\({\hat{P}}\) is a vector of Pareto front obtained by the algorithm, P is an approximation of true Pareto front obtained, for instance, by random sampling.

The convergence measure in Table 3 shows that CHVPOI is better in most cases except on DTLZ7. As we see in Fig. 3d, the hypervolume indicator does not improve much after iteration 10, indicating that the method is finding the extrema faster, which results in a less uniform Pareto set. This is prevalent in hypervolume-based improvement functions: since hypervolume is a product, it samples less in regions where at least one objective has a very small improvement.

Table 3 The convergence measure with \(95\%\) confidence interval of the DTLZ benchmark experiments
Full size table

5.2 Microstrip low-pass filter

Our first engineering problem is the design of a two-port low-pass stepped impedance microstrip filter device [41]. The simulator for the device is implemented in the MATLAB RF Toolbox (Mathworks Inc., Natick, MA, USA). The corresponding layout is presented in Fig. 4.

Fig. 4
figure 4

Top-view of microstrip low-pass filter. We use 1 widths \(w_{1}=w_{3}=w_{5}\) and 3 different lengths \(l_1\), \(l_3\), \(l_5\) as design parameters

Full size image

The filter is a cascade of 6 microstrip lines, each specified by width and length, where by design \(w1 = w3 = w5\) and \(w2 = w4 = w6\). The cross-section view of each microstrip is depicted in Fig. 5.

Fig. 5
figure 5

The cross-section view of each microstrip. For \(w_n = w_1 = w_3 = w_5\), the values changes within the optimization iterations, while for \(w_n = w_2 = w_4 = w_6\) the values are fixed at 0.428 mm

Full size image

Our target design is a filter with a 3 dB cut-off frequency at 2.55 GHz. To achieve this, we define the design goals as follows:

$$\begin{aligned} \left| S_{21} \right| \ge {-3}\,\hbox {dB} \quad \text {for} \; \quad&0\,\hbox {GHz} \le {\text {freq}} \le {{2.55}\,\hbox {GHz}} \end{aligned}$$
(18)
$$\begin{aligned} \left| S_{21} \right| \le {-3}\,\hbox {dB} \quad \text {for} \; \quad&{{2.55}\,\hbox {GHz}} \le {\text {freq}} \end{aligned}$$
(19)

where \(\left| S_{21} \right|\) is the magnitude of the element \(S_{21}\) of the scattering matrix, and freq is the frequency. Visually, the target response is illustrated in Fig. 6. We also want to optimize the cost to produce the device, by minimizing the footprint of the filter. Hence, the target design and the area of the filter are used as our expensive and cheap objective, respectively.

Fig. 6
figure 6

Example of the desired response for the microstrip low-pass filter

Full size image

In the optimization problem formulation, the chosen design parameters are the length and the width of the first, third and fifth microstrips, indicated as \(l_1\), \(l_3\), \(l_5\), \(w_1\), \(w_3\), \(w_5\), (see Fig. 4). Note that, these microstrips have the same width by design [41]: the width of all three microstrips is one single design parameter indicated as \(w_{1,3,5}\). The other geometrical and electrical characteristics of the filter are chosen according to Table 4.

Table 4 Microstrip low-pass filter design parameters
Full size table

To achieve our optimization goals, we formulate our objectives as follows:

$$\begin{aligned} f_1&= -\min _{{\text {freq}} \in [1, f_{pass}]} S_{21}({\text {freq}}) + \max _{{\text {freq}} \in [f_{stop}, 5]} S_{21}(freq) \end{aligned}$$
(20)
$$\begin{aligned} f_2&= \log \left( \sum _{n=1}^{3}w_{1,3,5}\;l_{2n-1}\right) \end{aligned}$$
(21)

In the first objective defined in Eq. (20), we want a response that assumes values as high as possible until \(f_{\text {pass}}\), and as low as possible for frequencies above \(f_{stop}\). This ensures that our device has a low-pass filter behavior, as shown in Fig. 6. The second cheap objective expressed in Eq. (21) represents the \(\log\) of sum of the three microstrips’s area, this means that the goal is to minimize the footprint of the filter. The \(\log\) term is to ensure numerical stability of the second objective. We solve this problem with our proposed methods. The hypervolume per iteration of all methods is shown in Fig. 7.

Fig. 7
figure 7

Hypervolume indicator evolution for low-pass filter case. The hypervolume is calculated using (1, 0) as the reference point

Full size image

Comparison of the hypervolume indicator of all methods for a predefined computational budget is presented in Table 5. CHVPOI performs better compared to the other benchmark methods, while CHVEI performs worse in terms of hypervolume indicator compared to HVEI. To check this unexpected behavior, we evaluate the quality of the pareto set by using the same convergence measure adopted for the DTLZ functions. In particular, the Pareto set is approximated via 50000 evaluations on random points in the design space and the distance metric defined in Eq. (17) is computed for CHVEI and HVEI. The result show that CHVEI gives a better convergence measure (0.0127 ± 0.0009) than the HVEI (0.0468 ± 0.0027). This means that the CHVEI yields a Pareto front that is spread more evenly along the approximated true front than the HVEI. The full convergence measure results are described in Table 5.

Table 5 Hypervolume and convergence measure with \(95\%\) confidence interval of the low-pass filter example experiments
Full size table

5.3 Tapped-line filter

The second engineering example is a tapped-line filter [42, 43], implemented in the Advanced Design System simulator (Keysight EEsof EDA). The full layout of this device is shown in Fig. 8.

Fig. 8
figure 8

Top-view of Tapped-line Filter. The two conductors (in gray) are placed on a dielectric substrate [19, 20]

Full size image

The design requirements for this filter are described in Eq. (22) and (23), as:

$$\begin{gathered} \left| {S_{{21}} } \right| \ge - 3\,{\text{dB}}\,{\text{for}}\;4.75\,{\text{GHz}}\, \le \,{\text{freq}}\, \le \,5.25\,{\text{GHz}} \hfill \\ \left| {S_{{21}} } \right| \le - 20\,{\text{dB}}\,{\text{for}}\;3.0\,{\text{GHz}}\, \le \,{\text{freq}}\, \le 4.0\,{\mkern 1mu} {\text{GHz}} \hfill \\ \end{gathered}$$
(22)
$$\quad \quad \quad \quad {\text{and}}\;6.0\, {\text{GHz}}\, \le \, {\text{freq}}\, \le \, 7.0\, {\text{GHz}}$$
(23)

where \(\left| S_{21} \right|\) is the magnitude of the element \(S_{21}\) of the scattering matrix, and freq is the frequency. The requirements in Eqs. (22) and (23) lead to the to response depicted in Fig. 9: the desired filter response is lower than \({-20}\,\hbox {dB}\) in the low and high frequency parts (called stopbands) and higher than \({-3}\,\hbox {dB}\) in the mid part (passband of the filter).

Fig. 9
figure 9

The target response of the tapped-line filter. The red horizontal lines indicate the values \(-3\)dB and \(-20\)dB in Eqs. (22) and (23)

Full size image

The design requirements shown above are used as the first optimization goal. For the second cheap objective, the footprint of the device is used. We formulate these objectives as follows:

$$\begin{aligned} f_1 =&\max _{{\text {freq}} \in [3, fs_{1}]} S_{21}({\text {freq}})-\min _{freq \in [fp_{1}, fp_{2}]} S_{21}({\text {freq}})\times 10 \end{aligned}$$
(24)
$$\begin{aligned}&+\max _{{\text {freq}} \in [fs_{2}, 7]}S_{21}({\text {freq}}) \nonumber \\ f_2 \,=\,&(L_1+10) \times (4 \times 2 + g) \end{aligned}$$
(25)

where \(fs_1 = {4}\,\hbox {GHz}\), \(fp_1 = {4.75}\,\hbox {GHz}\), \(fp_2 = {2.25}\,\hbox {GHz}\) and \(fs_2 = {6}\,\hbox {GHz}\). Equation (24) ensures that the filter’s response follows the design requirements. To balance the value, we put a higher weight for the response in the passband. Equation (25) represents the footprint of the device.

The variables for the optimization are the displacement \(L_1\) (mm) and the spacing g (mm) between the two conductors. Additionally, the dielectric constant \(\epsilon\) (mil), and height h (mm) of the substrate are also considered as design parameters. The corresponding design space is shown in Table 6.

Table 6 Tapped line filter design parameters
Full size table
Fig. 10
figure 10

Evolution of hypervolume for tapped-line filter case. (20, 20) is used as the reference point to calculate the hypervolume

Full size image

Using these settings, we run the optimization with our proposed methods and other benchmark methods. The results in Fig. 10 show that CHVEI and CHVPOI get a higher hypervolume indicator faster than the other methods. Additionally, in Table 7 we can see that our methods have higher hypervolume indicator compared to the MOEAs: SMSEMOA and NSGA2b, even with a lower function evaluation budget.

Table 7 Hypervolume with \(95\%\) confidence interval of the tapped-line filter example experiments
Full size table

6 Conclusion

We proposed the Cheap Hypervolume Expected Improvement (CHVEI) and Cheap Hypervolume Probability of Improvement (CHVPOI) which can directly exploit cheap-to-evaluate objective functions. The direct evaluation can speed up the optimization process and removes possible inaccuracies introduced by surrogate modeling. To evaluate the performance of the proposed method, we apply our algorithm to multiple benchmark functions and two engineering design problems. We evaluate the performance of the CHVEI and CHVPOI by measuring the hypervolume indicator and convergence measure at each iteration. It is shown that in the engineering design problems our proposed methods outperform the standard hypervolume-based methods, random sampling, and Genetic algorithm-based methods. In future works we will extend the algorithm for \(n>2\) objectives, and consider the case of noisy objective functions.