A bi-fidelity Bayesian optimization method for multi-objective optimization with a novel acquisition function

Abstract

In engineering design optimization, there are often multiple conflicting optimization objectives. Bayesian optimization (BO) is successfully applied in solving multi-objective optimization problems to reduce computational expense. However, the expensive expense associated with high-fidelity simulations has not been fully addressed. Combining the BO methods with the bi-fidelity surrogate model can further reduce expense by using the information of samples with different fidelities. In this paper, a bi-fidelity BO method for multi-objective optimization based on lower confidence bound function and the hierarchical Kriging model is proposed. In the proposed method, a novel bi-fidelity acquisition function is developed to guide the optimization process, in which a cost coefficient is adopted to balance the sampling cost and the information provided by the new sample. The proposed method quantifies the effect of samples with different fidelities for improving the quality of the Pareto set and fills the blank of the research domain in extending BO based on the lower confidence bound (LCB) function with bi-fidelity surrogate model for multi-objective optimization. Compared with the four state-of-the-art BO methods, the results show that the proposed method is able to obviously reduce the expense while obtaining high-quality Pareto solutions.

1 Introduction

Simulation models have been widely used in engineering design optimization. However, obtaining the Pareto solutions of multi-objective optimization problems usually requires many evaluations of objective functions. The evaluation processes of objective functions rely on time-consuming simulation models, which increases the burden of the optimization tasks. To solve this problem, surrogate models, such as Kriging models (Jerome et al. 1989; Liu et al. 2018; Williams et al. 2021), radial basis function models (Sóbester et al. 2005; Zhou et al. 2017), support vector regression models (Shi et al. 2020), are commonly adopted to replace expensive simulations in engineering design optimization.

Bayesian optimization (Shahriari et al. 2016) is a typical surrogate-based optimization method, which is able to balance the exploitation and exploration by utilizing the uncertainty term of the surrogate model with an acquisition function (Jeong et al. 2005). Commonly used acquisition functions include the probability of improvement (PI) (Ruan et al. 2020), expected improvement (EI) (Jones 2001; Zhan et al. 2022), and lower confidence bound (LCB) (Srinivas et al. 2012; Zheng et al. 2016). In recent years, extending these single-objective BO methods to multi-objective optimization has also gained much attention. For example, Knowles (2006) proposed the ParEGO method, which extended the EI function to multi-objective optimization. Emmerich et al. (2011) combined the hypervolume improvement with the EI function, which clarifies the regions where the Pareto frontier can be improved by establishing the monotonicity properties. Zhan et al. (2017) expanded the EI function into a matrix form (EIM), where the elements of the matrix are the EI value corresponding to each objective. Shu et al. (2020) defined an acquisition function for multi-objective optimization problems, considering convergence and diversity of the Pareto frontier.

However, these methods only utilize the high-accuracy samples to build the surrogate model, which still expends much computational cost (Chen et al. 2016). A potential way to further reduce the expense is adopting the multi-fidelity (MF) surrogate model (Zhang et al. 2018a, b), constructed based on a few costly high-fidelity (HF) samples and plenty of cheap low-fidelity (LF) samples. There are three main MF surrogate modeling methods: the scaling function method (Choi et al. 2009; Li et al. 2017), the space mapping method (Leifsson et al. 2015), and the Co-Kriging method (Kennedy et al. 2000; Perdikaris et al. 2015; Singh et al. 2017). Moreover, several new MF modeling methods have been proposed in the past few years, such as the method proposed by Eweis-Labolle et al. (2022), which utilizes latent-map Gaussian processes and outperforms the space mapping method. With above MF surrogate models gaining much attention, several multi-fidelity BO methods have been developed. For example, Zhang et al. (2018a, b) proposed a multi-fidelity method with an extension of Co-Kriging model, hierarchical Kriging (HK) model (Han et al. 2012), which avoids the construction of cross covariance in Co-Kriging. Jiang et al. (2019) proposed a new method to obtain the new sample and fidelity level, extended BO based on the LCB function with MF surrogate model. However, very limited work is accomplished for multi-objective optimization with BO based on the MF surrogate model. He et al. (2022) introduced a novel method for multi-objective problems, combining the HK model and EIM method. The blank of the research domain in extending BO based on the LCB function with MF surrogate model for multi-objective optimization still needs to fill. The bi-fidelity (BF) surrogate model is the surrogate model with two different fidelities, which is the special case of the MF surrogate model and needs to be considered first.

In this paper, a bi-fidelity BO method for multi-objective optimization is proposed, which utilizes the advantages of the bi-fidelity surrogate model and BO framework to further reduce the expense. In the method, a novel acquisition function is developed, in which a cost coefficient considering a cost ratio between different fidelity levels is introduced to balance the sampling cost and information of the new sample. The proposed method is compared with four state-of-the-art BO methods using several numerical examples and two engineering design optimization problems. The results show that the proposed method presents prominent performance in computational cost, especially for solving high-dimension problems.

The remainder of the paper is organized as follows. In Sec. 2, the technical background of the multi-objective optimization, HK model, and Bayesian optimization are recalled. Sec. 3 introduces the proposed method in detail. In Sec. 4, the results of comparative study between the proposed method and other state-of-the-art methods are presented. Sec. 5 summarizes this paper with conclusions and future work provided.

2 Background

2.1 Multi-objective optimization

Multi-objective optimization exists multiple conflicting objectives to optimize, and the optimization problem can be formulated as follows:

$$\begin{array}{*{20}c} {\min F(x) = \left\{ {f_{1} (x),f_{2} (x), \ldots ,f_{i} (x), \ldots ,f_{M} (x)} \right\}} \\ {s.t.\;g_{j} \left( x \right) \le 0,j = 1,2, \ldots ,q} \\ {x_{lb} \le x \le x_{ub} } \\ \end{array}$$

(1)

where the dimension of objective functions $\, F({\text{x}}) \,$ is $\, M$, ${\text{x}} = (x_{1} ,x_{2} ,...,x_{N} )^{T}$ denotes N-dimension design variable vector with lower/upper bounds of ${\text{x}}_{lb}$ and ${\text{x}}_{ub}$, ${\text{g}} = (g_{1} ,g_{2} ,...,g_{q} )$ is the constrain vector that can be simple linear or nonlinear.

The multi-objective improvement functions are usually employed as acquisition functions in BO for multi-objective optimization. Euclidean distance improvement function (Keane 2006), maximin distance improvement function (Svenson et al. 2016), and hypervolume (HV) (Yang et al. 2019) improvement function are three state-of-the-art multi-objective improvement functions. The Euclidean distance improvement function can be expressed as follows:

$$I({\text{x}}) = \mathop {\min }\limits_{j = 1}^{k} \sqrt {\sum\limits_{i = 1}^{m} {(f_{i}^{j} - y_{i} ({\text{x}}))^{2} } }$$

(2)

where $f_{i}^{j}$ is the jth Pareto solution of the ith objective, $y_{i} ({\text{x}})$ is the prediction of the ith objective.

The maximin distance improvement function is expressed as follows:

$$I({\text{x}}) = - \mathop {\max }\limits_{j = 1}^{k} \left[ {\mathop {\min }\limits_{i = 1}^{m} (y_{i} ({\text{x}}) - f_{i}^{j} )} \right]$$

(3)

Before the HV improvement function is introduced in detail, firstly the concept of the HV should be clarified. With a reference point dominated by the Pareto set, the HV of the dominated region can be measured as follows:

$$H(p) = {\text{Volume}} (y \in {\mathbf{\mathbb{R}}}^{M} |p \prec y \prec R)$$

(4)

where $p \prec y \prec R$ means the dominated region bounded by current Pareto $p$ and the reference point, Volume (·) is the HV indicator.

The HV improvement is the difference of the HV indicator between the current Pareto set and Pareto set with the next sample. It can be formulated as follows:

$$I(y) = H(p \cup y) - H(p)$$

(5)

where $p \cup y$ represents the Pareto set obtained by the non-dominated-sort method after the new sample y added. $I(y)$ is the HV improvement beyond the current Pareto set after adding a new sample $\, y \,$. Figure 1 presents the 2D example of the HV improvement. The light gray area is the HV of current Pareto set and the dark gray area illustrates the $I(y)$. A higher HV improvement means a better-quality improvement beyond the current Pareto set.

Fig.1

2-dimension example of the HV improvement

More information about these improvement functions can be consulted in Svenson’s work (2016).

2.2 Hierarchical kriging (HK) model

Kriging model (Williams et al. 2006) is an interpolative surrogate model, which originated from the geostatistics and was applied to fit expensive simulation (Jerome et al. 1989).

HK model is a MF surrogate model based on the Kriging model, which takes LF prediction as an overall trend of the MF model with the HF function adopted to be a correction. To build an HF surrogate model for expensive function, first we build a Kriging model with LF samples, which is adopted thereafter to assist the construction of the MF model. The LF Kriging model is expressed as follows:

$$Y_{l} ({\text{x}}) = \beta_{0,l} + Z_{l} ({\text{x}})$$

(6)

where $\beta_{0,l}$ is the mean term and $Z_{l} ({\text{x}})$ is a random process with variance $\sigma^{2}$ and zero mean. One of the most commonly used spatial correlation functions between the error term of two points ${\text{ x }}$ and ${\text{ x}}^{\prime}$, named the Gaussian correlation function, is given as follows:

$${\text{cov}} (Z({\text{x}}),Z({\text{x}}^{\prime})) = \sigma^{2} \exp \left\{ { - \sum\limits_{i = 1}^{d} {\theta_{i} \left| {x_{i} - x_{i}^{^{\prime}} } \right|^{2} } } \right\}$$

(7)

where $\sigma^{2}$ is the variance of the $Z({\text{x}})$,$\, d \,$ is the dimension of design variables, and ${\uptheta } = \left\{ {\theta_{1} ,\theta_{2} ,...,\theta_{d} } \right\}$ is a “roughness” parameter associated with dimension i.

The prediction of mean and mean-squared error (MSE) from LF model at any unobserved points can be formulated as follows:

$$\hat{y}_{l} (x) = \beta_{0,l} + {\text{r}}_{l}^{T} (x){\text{R}}_{l}^{ - 1} (f_{l} ({\text{x}}) - {1}\beta_{0,l} )$$

(8)

$$s_{l}^{2} (x) = \sigma^{2} (1 - {\text{r}}_{l}^{T} (x){\text{R}}_{l}^{ - 1} {\text{r}}_{l} (x) + \frac{{(1 - {1}^{T} {\text{R}}_{l}^{ - 1} {\text{r}}_{l} (x))^{2} }}{{{1}^{T} {\text{R}}_{l}^{ - 1} {1}}})$$

(9)

respectively, where $\beta_{0,l} = ({1}^{T} {\text{R}}_{l}^{ - 1} {1})^{ - 1} {1}^{T} {\text{R}}_{l}^{ - 1} f_{l} ({\text{x}})$, $f_{l} ({\text{x}})$ is the LF response of samples ${\text{ x}}$,${1}$ is a vector filled with 1, ${\text{R}}_{l}$ is the covariance matrix with $R_{l,mn} = {\text{cov}} (Z({\text{x}}^{m} ),Z({\text{x}}^{n} ))$ as elements, and ${\text{r}}_{l}$ is a vector of correlation between the unobserved point and samples. Above hyperparameters $\beta_{0,l}$, $\sigma^{2}$, $\theta_{i}$ are calculated by Maximum Likelihood Estimation (MLE).

Taking the predicted value of the LF model to construct the prior mean of the HF Kriging model, it will be built as follows:

$$Y({\text{x}}) = \beta_{0} \hat{y}_{l} ({\text{x}}) + Z({\text{x}})$$

(10)

where the $\hat{y}_{l} ({\text{x}})$ is the prediction of the LF model scaled by a constant factor $\beta_{0}$, $Z({\text{x}})$ is a random process with zero mean and a covariance of ${\text{cov}} (Z({\text{x}}),Z({\text{x}}^{^{\prime}} ))$.

The prediction of mean value and mean-squared error (MSE) of HK model at the unobserved point can be formulated as follows:

$$\hat{y}(x) = \beta_{0} \hat{y}_{l} ({\text{x}}) + {\text{r}}^{T} (x){\text{R}}^{ - 1} (f_{h} ({\text{x}}) - \beta_{0} f_{l} ({\text{x}}))$$

(11)

$$\begin{gathered} MSE\left\{ {\hat{y}(x)} \right\} = \sigma^{2} \left\{ {1 - {\text{r}}^{T} (x){\text{R}}^{ - 1} {\text{r}}(x) + } \right. \\ \left. {\left[ {{\text{r}}^{T} (x){\text{R}}^{ - 1} f_{l} ({\text{x}}) - \hat{y}_{l} ({\text{x}})} \right]\left[ {f_{l} ({\text{x}})^{T} {\text{R}}^{ - 1} f_{l} ({\text{x}})} \right]^{ - 1} \left[ {{\text{r}}^{T} (x){\text{R}}^{ - 1} f_{l} ({\text{x}}) - \hat{y}_{l} ({\text{x}})} \right]^{T} } \right\} \\ \end{gathered}$$

(12)

respectively, where $\beta_{0} = \left[ {f_{l} ({\text{x}})^{T} {\text{R}}^{ - 1} f_{l} ({\text{x}})} \right]^{ - 1} f_{l} ({\text{x}})^{T} {\text{R}}^{ - 1} f_{h} ({\text{x}})$ is a scaling factor, and $f_{h} ({\text{x}})$ is the high-fidelity response of sample points ${\text{ x}}$.

More details about hierarchical Kriging model are introduced in Han’s work (2012).

2.3 Bayesian optimization based on the LCB function

Bayesian optimization is a type of the surrogate model-based method for expensive optimization problems. The BO method utilizes the uncertainty and prediction information from surrogate model to quantify the improvement or probability of improvement between new sample and current optimum, which can balance the exploitation and exploration. EI and LCB functions are commonly used acquisition functions (Tran et al. 2019). With the number of objectives increased, due to the complexity of the non-dominated region, a piecewise integral approach is often used to calculate the EI value, where the integral region is commonly resolved into some regular cells (Zhan et al. 2017). Hence, such improvement-based acquisition function as above multi-objective EI criteria becomes so complicated that the EI value is hard to be calculated. On the contrary, an outstanding advantage using LCB function is that it is no need to calculate such tedious piecewise integral like EI and PI function. This property economizes many computational resources from the calculation of high-dimension integrals.

Given the samples $\left\{ {x_{1} ,x_{2} ,...,x_{N} } \right\}$ and their associated response $\left\{ {f_{1} ,f_{2} ,...,f_{N} } \right\}$, LCB function is formulated as follows:

$$f_{LCB} ({\text{x}}) = \hat{f}({\text{x}}) - ks({\text{x}})$$

(13)

where $\hat{f}({\text{x}})$ represents the prediction value of surrogate model, $s({\text{x}})$ is the square root of uncertainty, $k$ is a parameter balanced the exploitation and exploration. In multi-objective optimization, the form of LCB function will be a vector (Shu et al. 2020):

$$\begin{gathered} f_{LCB} ({\text{x}}) = \left[ {f_{LCB,1} ({\text{x}}),f_{LCB,2} ({\text{x}}),...,f_{LCB,M} ({\text{x}})} \right] \\ where \, f_{LCB,i} ({\text{x}}) = \hat{f}_{i} ({\text{x}}) - k_{i} s_{i} ({\text{x}}) \\ \end{gathered}$$

(14)

where M is the number of objectives, each objective is fitted by the surrogate model respectively, and $s_{i} (x)$ is the square root of the posterior predictive variance. A larger value of the coefficient $k_{i}$ represents that the algorithm is encouraged to search the solution in the uncertain region, conversely a small value encourages exploitation in the current optimum region.

More information about EI, PI, and other acquisition functions can be consulted in following reference papers (Jones et al. 1998) (Ruan et al. 2020; Shahriari et al. 2016).

3 Proposed method

In this section, a bi-fidelity BO method for multi-objective optimization is proposed. Firstly, the cost and HV improvement after adding a new sample with different fidelity are analyzed, then the new acquisition function is introduced in detail. Finally, the terminal condition and procedure of the method are presented.

3.1 Predicted HV improvement after adding a new sample with different fidelities

The LCB function utilizes the predicted mean and uncertainty to measure the worth of each point in the unobserved area. The HV improvement function is employed to quantify the predicted quality improvement after adding a new sample in the proposed method, as presented in Eqs. (4) and (5). The HV improvement function can be formulated as follows:

$$I_{LCB} (x) = H(p \cup f_{LCB} (x)) - H(p)$$

(15)

where the $f_{LCB} (x)$ is the LCB function defined in Eq. (14). Figure 2 presents the Pareto set and predicted HV improvement after adding a new sample ($I_{LCB} (x)$) in 2D objective space. The red point in Fig. 2 represents the $f_{LCB} ({\text{x}})$ at sample x.

Fig.2

2-dimension example of Pareto set and predicted HV improvement

Figure 3 presents the HV improvement while the surrogate model has two fidelity levels and the HV improvement functions are formulated, respectively, as follows:

$$I_{LCB}^{l} (x) = H(p \cup f_{LCB}^{l} (x)) - H(p)$$

(16)

$$I_{LCB}^{h} (x) = H(p \cup f_{LCB}^{h} (x)) - H(p)$$

(17)

where the $I_{LCB}^{l} (x)$ and $I_{LCB}^{h} (x)$ denote the HV improvement after adding HF and LF samples, respectively,$f_{LCB}^{l} (x)$ and $f_{LCB}^{h} (x)$ are expressed as follows:

$$f_{LCB}^{l} (x) = \left[ {f_{LCB,1}^{l} (x),f_{LCB,2}^{l} (x),...,f_{LCB,M}^{l} (x)} \right]$$

(18)

$$f_{LCB}^{h} (x) = \left[ {f_{LCB,1}^{h} (x),f_{LCB,2}^{h} (x),...,f_{LCB,M}^{h} (x)} \right]$$

(19)

respectively, where

$$\, f_{LCB,i}^{l} (x) = \hat{f}_{i} (x) - k_{i} \beta_{0} s_{i}^{l} (x)$$

(20)

$$f_{LCB,i}^{h} (x) = \hat{f}_{i} (x) - k_{i} s_{i}^{h} (x)$$

(21)

Fig.3

the predicted HV improvement after adding HF and LF samples

$s_{i}^{h} (x)$ is the error term arising from the lack of an HF sample in HK model, $\beta_{0} s_{i}^{l} (x)$ is the error of the LF model prediction because of the lack of a LF sample (Zhang et al. 2018a, b).

The light gray area in Fig. 3 is the HV of the current Pareto frontier. The blue and dark gray areas represent the HV improvement after adding the LF sample ($I_{LCB}^{l} (x)$) and the HF sample ($I_{LCB}^{h} (x)$) beyond current Pareto set, respectively. It should be noted that the $I_{LCB}^{h} (x)$ includes the blue area, which denotes the HV indicator of the region between $f_{LCB}^{h} (x)$ and the Pareto set. In most circumstances, the $I_{LCB}^{h} (x)$ is larger than the corresponding $I_{LCB}^{l} (x)$ due to the discrepant uncertainty term so that there is a conflict between computational cost and HV improvement of the sample with different fidelity.

3.2 The proposed acquisition function

As illustrated in the following Fig. 4, the predicted HV improvement can be partitioned into two parts, one from the predicted mean and the other from the uncertainty region.

Fig.4

the predicted HV improvement of the predicted mean after adding new samples

The green region in Fig. 4 means the HV improvement of the predicted mean after adding a new sample ($I_{LCB}^{\mu } (x)$) and it is expressed as follows:

$$I_{LCB}^{\mu } (x) = H(p \cup \hat{f}(x)) - H(p)$$

(22)

$$\hat{f}({\text{x}}) = [\hat{f}_{1} ({\text{x}}),\hat{f}_{2} ({\text{x}}),...,\hat{f}_{i} ({\text{x}}),...,\hat{f}_{M} ({\text{x}})]$$

(23)

where $\hat{f}_{i} (x)$ means the prediction mean of each objective. The blue and dark gray areas represent the HV improvement as the same as shown in Fig. 3, and they can be expressed as $I_{LCB}^{l} (x)$ and $I_{LCB}^{h} (x)$ calculated by Eqs. (16) and (17).

To balance the cost and improvement of a new sample with different fidelity, here a novel improvement function with different fidelity is introduced, which can be expressed as follows:

$$I(x,t) = \left\{ \begin{gathered} (I_{LCB}^{l} (x) - I_{LCB}^{\mu } (x)) \times CR(t) + I_{LCB}^{\mu } (x) \, t = 1 \hfill \\ (I_{LCB}^{h} (x) - I_{LCB}^{\mu } (x)) \times CR(t) + I_{LCB}^{\mu } (x) \, t = 2 \hfill \\ \end{gathered} \right.$$

(24)

where $t = 1$ and $t = 2$ represent the improvement function with low fidelity and high fidelity, respectively, $CR(t)$ is the cost coefficient that is formulated as follows:

$$CR(t) = \left\{ \begin{gathered} c \, t = 1 \hfill \\ 1 \, t = 2 \hfill \\ \end{gathered} \right.$$

(25)

where $c \ge 1$, which is the ratio of cost between HF and LF simulations. With the cost coefficient applied, the HV improvement with LF sample is expanded proportionally by controlling the computational cost to the same level for different fidelities. Thus, the HV improvement with different fidelities can be reasonably compared and choose the most appropriate one. When the cost ratio $c$ is larger than one, it is invidious to compare $I_{LCB}^{l} (x)$ with corresponding $I_{LCB}^{h} (x)$ after multiplying the cost coefficient $CR(t)$ because the predicted mean with all fidelity levels has no discrepancy between each other in BF surrogate model. Hence, the effect of the cost coefficient on the HV improvement of the predicted mean should be eliminated.

As the cost coefficient $CR(t)$ with HF level is equal to 1, the term where $t = 2$ in Eq. (24) can be regarded as follows:

$$(I_{LCB}^{h} (x) - I_{LCB}^{\mu } (x)) \times 1 + I_{LCB}^{\mu } (x) = I_{LCB}^{h} (x)$$

(26)

and the $I(x,t)$ can be simplified as follows:

$$I(x,t) = \left\{ \begin{gathered} (I_{LCB}^{l} (x) - I_{LCB}^{\mu } (x)) \times CR(t) + I_{LCB}^{\mu } (x) \, t = 1 \hfill \\ I_{LCB}^{h} (x) \, t = 2 \hfill \\ \end{gathered} \right.$$

(27)

When the $f_{LCB} ({\text{x}})$ locates in dominated region, all of terms in $I(x,t)$ is equal to zero and it cannot estimate which fidelity level is more appropriate. On the other hand, the algorithm of optimizing the acquisition function, such as genetic algorithm (GA) (Jin 2011), adopts random sampling to obtain the initial population, whereas Pareto solutions usually only occupy a narrow region relative to the whole design space. Therefore, GA may not be able to acquire a solution located in the area of Pareto set during the searching process, which leads to the decline of search efficiency in optimization process. Figure 5 illustrates the situation that the LCB function locates in dominated region of Pareto frontier.

Fig.5

the LCB function located in dominated region

To address this issue, we refer to our previous work (Shu et al. 2020), a novel acquisition function is defined as follows:

$$a(x,t) = \left\{ \begin{gathered} I(x,t), \, where \, f_{LCB} \, is{\text{ non - dominated}} \hfill \\ - \mathop {\min }\limits_{{{\text{i}} = 1,2,...q}} (\left\| {f_{LCB} (x) - f(X_{i} )} \right\|_{2} ), \, where \, f_{LCB} \, is{\text{ dominated}} \hfill \\ \end{gathered} \right.$$

(28)

where $I(x,t)$ is Eq. (27), $X_{i}$ ($i = 1,2,...,q$) denotes the current Pareto solution, $\left\| {f_{LCB} (x) - f(X_{i} )} \right\|_{2}$ means the Euclidean distance between $f_{LCB} (x)$ and the Pareto solution $X_{i}$. The acquisition function makes an encouragement to help GA find the solution close to the Pareto frontier so that the optimization efficiency can be improved.

3.3 Procedure and termination condition

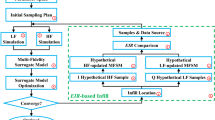
The proposed method, based on BF model and LCB function for multi-objective optimization (BF-MOLCB), follows a process as illustrated in Fig. 6. In the study, the Latin hypercube sampling (LHS) (Wang 2003) policy is applied to generate two initial sample sets for two fidelity levels. With the corresponding responses of initial samples evaluated, the current Pareto frontier can be obtained by the non-dominated sorting method (Deb et al. 2002).

Fig.6

the flowchart of the proposed method

The procedure of the BF-MOLCB is summarized in the flowchart as shown in Fig. 6, includes

• Step 1 Generate two sample sets for LF and HF model by LHS.

• Step 2 Evaluate the true responses of the corresponding samples.

• Step 3 Construct the LF Kriging models for each objective utilizing the DACE toolbox (Lophaven et al. 2002).

• Step 4 Construct the hierarchical Kriging model based on LF Kriging model and HF samples. The initial value of the hyperparameter $\theta$ is set to be 1. The region of $\theta$ is set to be $[10^{ - 6} ,10^{3} ]$.

• Step 5 Obtain the current Pareto frontier by the non-dominated sorting method.

• Step 6 Judge the termination criterion, if it is not satisfied, go to step 7. Otherwise, the method is stopped and output the solution.

• Step 7 Maximize the proposed acquisition function to obtain a new sample, turn back to step 2.

A stop criterion is adopted to terminate the optimization process after the following two conditions are satisfied:

• (1) After the algorithm finds at least 20 solutions, thus, the Pareto set will provide enough choice to the decision maker; Or the computational expense gets the maximum budget, defined as 200 in this paper.

• (2) The discrepancy of the quality metrics in two adjacent iterations represents the variation of the current Pareto frontier. Hence, when the ratio of the difference and the current HV value is less than a specific value (e.g., 0.1% in this paper), the algorithm will be terminated, which is defined as follows:

  $$HV_{T} = \frac{{HV_{i} - HV_{i - 1} }}{{HV_{i} }}$$

  (29)

where the $HV_{i}$ means the HV value of the ith iteration (Shu et al. 2020).

4 Examples and results analysis

In this section, four numerical examples and an engineering design problem are adopted to test the efficiency and applicability of the proposed method. The formulations and true Pareto solutions of the four numerical examples (Shu et al. 2019) are summarized in Table 1. There are two single-fidelity BO methods (Sun et al. 2021; Zhan et al. 2017) only utilizing HF simulations and other two bi-fidelity BO methods (He et al. 2022) to compare with the proposed BF-MOLCB method: (1) Euclidean distance-based EIM method (EIMe), (2) Euclidean distance-based LCBM method (LCBMe), (3) Hypervolume-based VFEIM method (VFEIMh), and (4) VFEMHVI method.

Table 1 The formulation of the four numerical examples

4.1 Numerical examples

ZDT1, ZDT2, FON, and POL examples are solved by above methods and the results are compared in this part. The cost of the initial sample is set as 10*n (n is the dimension of design variable), where the cost of the bi-fidelity method is formulated by an equivalent calculation as follows:

$$COST = \frac{{N_{l} }}{CR} + N_{h}$$

(30)

where $N_{l}$/$N_{h}$ denotes the number of LF/HF samples. For initial sampling, $N_{l}$ and $N_{h}$ are set as 5*n*CR and 5*n, respectively. The $CR$ is the ratio of cost between LF and HF samples, which is set to be 4 in the following numerical test problems. To obtain the HV indicator, a reference point is set in each test function, as the shown in Table 2.

Table 2 Reference points to calculate HV indicator in each test function

Firstly, a detailed comparison between these methods is demonstrated using the example ZDT1 (dimension $n = 3$). Each method is run 10 times, where the statistics of the HV indicator and computational expense (COST) are recorded. The comparison results of HV and COST using different methods are summarized in Table 3, including the mean, median value, and STDs of HV and COST from 10 runs. The best indicators are shown in bold in the Table. Figure 7 illustrates the box charts of the HV and COST obtained from different methods in ZDT1 problem.

Table 3 The compared results of different methods for ZDT1 problem

Fig.7

the box chart of the HV and COST. a HV, b COST

As the HV indicators presented in Table 3, the LCBMe method, the VFEMHVI method, and proposed method have the most ideal Pareto frontier approximation quality according to the HV indicator. Meanwhile, the minimum mean and STD value of the COST demonstrate that the proposed method enables to have an ideal performance with lowest computational expense simultaneously, in which the COST means of the proposed method have 55.67%, 43.74%, 46.03%, and 28.13% decline over EIMe, LCBMe, VFEIMh, and VFEMHVI, respectively. Figure 7 illustrates the comparison over different methods intuitively. It can be seen that COST indicator of the proposed method has the most inconspicuous abnormal value in this box chart.

Table 4 presents the average computational expense required to obtain different number of Pareto solutions in ZDT1, further comparing the efficiency of finding Pareto solutions over these methods. As shown in Table 4, the proposed method always has the lowest value of the average computational expense. It is important to find enough Pareto solutions to provide adequate options for designers.

Table 4 The average computational expense required to obtain different number of Pareto solutions for ZDT1 problem

The quality of Pareto frontier is also a considerable metric in multi-objective optimization problems, which directly determines the information provided for designers. Hence, it is necessary to compare the quality of Pareto frontier from different methods. There are several figures illustrating the Pareto frontier with the lowest HV indicator over 10 runs, as shown in Fig. 8. In the ZDT1 problem, the most ideal Pareto frontier are still obtained by the VFEMHVI method and the proposed method, but the advantage is not evident enough, in which the difference of the HV means between the proposed method and VFEMHVI is lower than 0.01. Other methods also have nonnegligible competitiveness in this case.

Fig.8

Pareto frontier with the lowest HV indicator in 10 runs on ZDT1 problem

The comparisons of remaining examples are summarized in Tables 5 and 6. All these methods present satisfactory performance in obtaining the Pareto solutions on FON and ZDT2 problems with $n = 3$ and the proposed method still has the lowest computational cost and ideal HV indicators. A very diverse phenomenon appears in POL problem. Even though the discrepancy of the cost among different methods is not significant enough, the cost of the proposed method is slightly higher than other single-fidelity methods and VFEIMh method. However, the proposed method has the highest HV indicator, which means it enables to obtain a Pareto set with better quality than other methods. Similar to Fig. 8, Fig. 9 illustrates the Pareto frontier with the lowest HV indicator in 10 runs on POL problem. It can be seen that the Pareto solutions obtained by the proposed method uniformly distribute on the true Pareto frontier, which is obviously better than VFEIMh and other single-fidelity methods. The VFEMHVI method has the same situation but its expense is 3.43% higher than the proposed method.

Table 5 The compared results of different methods for ZDT2 (n = 3), POL and FON problems

Table 6 The compared results of different methods for high-dimension ZDT2 problems

Fig.9

Pareto frontier with the lowest HV indicator in the 10 runs on POL problem

Fig.10

Parameterization of the torque arm (Shu et al. 2020)

Additionally, there are several high-dimension test problems (ZDT2 problem with dimension $n = 68{,}\,10$) for measuring the ability to solve the optimization problems under more complex cases. The proposed method reveals a prominent performance in these problems, as shown in Table 6. The “/” symbol denotes that the termination criterion cannot be satisfied when the computational expense reaches the maximum budget 200. For these high-dimension problems, the proposed method always has the lowest computational expense and ideal quality of Pareto frontiers. In the ZDT2 problem with $n = 6$, single-fidelity methods sometimes fail to obtain 20 Pareto solutions before the maximum budget reached. The performance of the VFEMHVI and the proposed BF-MOLCB method has notable improvement, in which the COST means of the proposed method have 52.89%, 62.87%, 60.24%, and 34.70% decline over EIMe, LCBMe, VFEIMh, and VFEMHVI, respectively. The VFEMHVI method can obtain the largest HV indicator. The proposed method can also obtain an ideal Pareto frontier (difference of HV between the VFEMHVI and the proposed method is less than 0.01% of the whole HV), meanwhile the computational expense of the proposed method is much lower than the VFEMHVI. In the test problem with $n = 8,10$, all single-fidelity methods cannot meet the termination criterion until the maximum budget 200 reached. The cost of the VFEIMh and VFEMHVI method is also unsatisfactory. Especially in ZDT2 with $n = 10$, only the proposed method can still obtain a satisfactory Pareto frontier with controllable computational expense.

Comparing these test problems in terms of the dimensions, low-dimension problems ($n = 2,3$) have a smaller difference in the computational cost between these methods, whereas the corresponding discrepancy in high-dimension problems is much more noteworthy. Therefore, the bi-fidelity surrogate models have better performance than single-fidelity models in approximating the complex problems, which confirms the research significance of utilizing bi-fidelity models in BO to solve the multi-objective optimization problems.

4.2 Engineering case

In this section, two engineering examples, torque arm and honeycomb structure vibration isolator design optimization, are adopted to verify the performance of the proposed method. The torque arm is fixed at the left end. The load on the torque arm, $P_{1} = 8.0kN$ and $P_{2} = 4.0kN$, is exerted at the right end (Fig. 10).

Six design variables are applied for the torque in this example, including $\alpha ,b_{1} ,D_{1} ,h,t_{1} ,t_{2}$, and $t_{2}$. The optimization problem is expressed as follows:

$$\begin{gathered} \min f_{1} = V(\alpha ,b_{1} ,D_{1} ,h,t_{1} ,t_{2} ) \\ \min f_{2} = \max \_d(\alpha ,b_{1} ,D_{1} ,h,t_{1} ,t_{2} ) \\ where \, 3\deg \le \alpha \le 4.5\deg ; \, 25mm \le b_{1} \le 35mm \\ 90mm \le D_{1} \le 120mm; \, 20mm \le h \le 30mm \\ 12mm \le t_{1} \le 22mm; \, 8mm \le t_{2} \le 12mm \\ \end{gathered}$$

(31)

where $V$ is the total volume, $\max \_d$ is the maximum displacement of the torque arm, and the Young’s modulus is 200 GPa and Poisson’s ratio is 0.3. In this example, the reference point is [1000;10] and the cost ratio between high- and low-fidelity samples is 4.

Each method is run 10 times, where the average of the HV indicator and computational expense is recorded, as the shown in Table 7. All of these methods can meet the termination condition; thereinto, the proposed method has the best performance in the quality of Pareto solutions due to the highest HV indicator. However, the cost of the proposed method is higher than other methods. The reason why this phenomenon appears is that the non-dominated solutions obtained by the single-fidelity methods and the VFEIMh method early on have satisfied the termination criterion, which leads the method cannot obtain an ideal Pareto set. There are some figures in Fig. 11 used to show the Pareto frontier with the lowest HV indicator in 10 runs on this torque arm problem. Obviously, the Pareto solutions obtained from proposed method distribute uniformly on the true Pareto frontier, distinctly better than other single-fidelity methods and VFEIMh.

Table 7 The comparison with different methods for the torque arm problem

Fig.11

Pareto frontier with the lowest HV indicator in 10 runs on the torque arm problem

To compare the proposed method with other methods more fairly, the same budget is adopted to compare the quality of the Pareto solution set, which is set 100 in this study. Each method works 10 times repeatedly, terminated when the cost of optimization process reaches 100, and summarizes the median, mean, and std value of the HV indicator. The results are shown in Table 8. It can be seen that the median and mean value of the HV indicator obtained by the proposed method are still better than other methods; meanwhile, the least std value reveals the stability of the proposed method. Even the HV indicators obtained by the single-fidelity methods and the VFEIMh method after 100 iterations are still less than the corresponding value when the proposed method has obtained 20 Pareto solutions (5488.2470 on average), whereas the proposed method only costs 35.93 on average to obtain 20 Pareto solutions in optimization process. The VFEMHVI method also has a good performance, which has slight discrepancy with the proposed method.

Table 8 The comparison with the same budget for the torque arm problem

Figure 12 intuitionally presents the Pareto frontier of the lowest HV indicator with the same budget. The Pareto frontiers obtained by the single-fidelity methods are much better than before but still distributed unevenly. The diversity of the Pareto solutions is also worser than the proposed method obtained, in which a fixed area many non-dominated solutions intensively distributed. Compared with other two bi-fidelity method, the proposed method still has the best performance in the torque arm optimization problem.

Fig.12

Pareto frontier of the lowest HV indicator with the same budget

In the vibration isolator optimization problem, six design variables are applied, including $\theta ,D,R_{f} ,L,t_{h}$, and $t_{l}$ as shown in Fig. 13. The ratio of the natural frequency $e$ and the Equivalent strain $\varepsilon_{\max }$ are set as the goal of the multi-objective optimization problem to minimize. The nonlinear coefficient $\xi$, the transverse-longitudinal stiffness ratio $R_{k}$, the total height $H$, and the dimensional coordination conditions $T_{s}$ are set as the constraints, in which $\xi$ and $R_{k}$ should be evaluated by computationally expensive simulations while the $H$ and $T_{s}$ can be obtained by mathematical formulas. The optimization problem is expressed as follows:

$$\begin{gathered} \min \, e(\theta ,D,R_{f} ,L,t_{h} ,t_{l} ) = \left| {1 - \frac{f}{{f_{0} }}} \right| \\ \varepsilon_{\max } (\theta ,D,R_{f} ,L,t_{h} ,t_{l} ) \\ s.t. \, g_{1} = 1 - \frac{\xi }{0.75} \le 0,g_{2} = 1 - \frac{{R_{k} }}{1.2} \le 0,g_{3} = \frac{H}{70} - 1 \le 0,g_{4} = T_{s} \le 0 \\ \end{gathered}$$

(32)

where the parameters are shown in Tables 9, 10, and 11.

Fig.13

The vibration isolator and the geometry of a honeycomb cell (Qian et al. 2021)

Table 9 Fixed parameters

Table 10 Physical meaning and ranges of design variables

Table 11 Objective and constraint functions and their boundary conditions

The vibration isolator test problem is modeled and simulated using ANSYS 18.2, in which high- and low-fidelity levels are set via adjusting the dimension of the mesh division. The number of mesh division of the high-fidelity analysis model in the direction of inclined beam thickness $t_{l}$ is set as 6, and the corresponding number in the low-fidelity analysis model is set as 2, as shown in Fig. 14. The cost coefficient is set as 3. The penalty function is used to handle the constraints which are obtained by mathematical formulas. For constraints which need time-consuming simulations to obtain, this paper addresses them based on the method proposed by Schonlau (1998), which was extended to solve multi-fidelity optimization problems in our previous work (Shu et al. 2021). The reference point is set as [10;0.2].

Fig.14

The mesh division for high- and low-fidelity finite element. a Fine mesh. b Coarse mesh (Qian et al. 2021)

Each method is run 10 times, where the average of the HV indicator and computational expense is recorded, as the shown in Table 12. All of these methods can meet the termination condition; thereinto, the proposed method has the best performance in the quality of Pareto solutions due to the highest HV indicator. With regard to the computational expense, there is only a small variation between these methods, in which the EIMe has the lowest cost and the VFEMHVI is the highest one. Other three methods are almost the same level. However, the proposed method has notable advantage in term of the HV indicator, especially comparing with the EIMe, the LCBMe, and the VFEIMh method. Figure 15 illustrates the Pareto frontier with the lowest HV indicator in 10 runs. It can be seen that the Pareto frontier obtained from proposed method is better than other methods obtained.

Table 12 The comparison with different methods for the engineering problem

Fig.15

Pareto frontier with the lowest HV indicator in 10 runs on the engineering problem

5 Conclusion

A bi-fidelity Bayesian optimization method for multi-objective optimization is proposed. In the proposed method, the LCB functions are adopted to utilize the uncertainty of surrogate model. On this basis, a novel acquisition function is defined, in which a cost coefficient balances the computational expense and accuracy of new sample points with different fidelity levels. Then, the new sample can be determined by maximizing the proposed acquisition function.

Four numerical test problems with different dimensions and two real-world engineering design optimization problems are applied to investigate the feasibility and efficiency of the proposed method. Some conclusions are drawn as follows:

• 1) The effect of samples with different fidelities for improving the quality of the current Pareto set is quantified in the proposed method;

• 2) The proposed method balances the cost and effect of samples with different fidelities, which can utilize the LF samples to potentially further reduce the computational expense;

• 3) Compared with other two state-of-the-art single-fidelity methods and two bi-fidelity methods, the proposed method shows prominent performance in computational cost and improving of Pareto solutions, especially for solving high-dimension problems.

In the future, several potential directions are worth exploring. First, the acquisition function of choosing new samples from multiple fidelities (> 2) still remains to be researched and tested. Second, combined with the research from Foumani et al. (2022), other acquisition functions like EI and PI can be utilized in multi-objective optimization with multi-fidelity model. Last but not the least, the proposed method can be extended to solve multi-objective robust optimization problems.