1 Introduction

Miniaturization of field-effect transistors enables improved functionality and higher packaging density of electronic devices [1–3]. However, the progressive downscaling of complementary metal–oxide–semiconductor (CMOS) technology places certain restrictions on device performance due to the subthreshold slope (SS) limit of 60 mV/decade for MOSFETs [3–6]. Meanwhile, the growing demand for low-power devices has attracted attention from many researchers. Recently, the tunnel field-effect transistor (TFET) has emerged as a new device of interest, setting the pace in the semiconductor industry [6–9]. A major concern regarding MOSFETs is that the channel shrinkage frequently applied in TFETs results in short-channel effects (SCEs). The TFET employs a band-to-band tunneling (BTBT) mechanism, which reduces the OFF-state current (\(I_\mathrm{{OFF}}\)), and thereby the subthreshold slope (SS) to below 60 mV/decade [6–10]. Also, the SOI TFET exhibits better performance in terms of SCEs due to the presence of a tunneling barrier at the source–channel interface [11]. To improve TFET performance, various techniques such as gate engineering [12, 13], material engineering [14–16], and dielectric engineering [17, 18] have been proposed to enable improved gate control over the channel. Research has also been carried out on dual- and triple-material gates, resulting in improved device performance by reducing SCEs [14–16].

Recently, such research has been extended to another level through employment of workfunction engineering of the gate metal, resulting in excellent gate control and immunity to SCEs [19–36]. Improved analog performance and reduced SCEs can be realized by introducing linear variation of the mole fraction in the gate metal (\(\text {A}_X \text {B}_{1-X}\)) from the source to drain end. Continuous workfunction variation of nanowire gate metal has already been reported, and fabricated on a single substrate by exploiting various methods [37, 38]. In this paper, subthreshold slope minimization is considered as one of the key techniques to achieve the objective of low power consumption. Here, a new binary metal alloy with linearly modulated workfunction is applied as the gate electrode to achieve greater gate controllability for the single-gate SOI tunnel FET. The present model reduces the leakage current, which further helps in reducing the subthreshold slope. Here, the electric field is customized to reduce the asymmetric and uneven nature of the surface potential as well as the drain-induced barrier lowering (DIBL) effect, thereby reducing SCEs [25]. The improved initial tunneling distance in OFF-state results in SS below 45 mV/decade for the workfunction-modulated TFET (WM-TFET). The enhanced scalability of the present model is also investigated, and its accuracy validated using the 2-D TCAD Sentaurus device simulator [39].

2 Physical model and electrostatic analysis

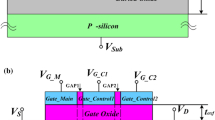
A schematic of the structure of the workfunction-modulated single-gate SOI TFET (WM-TFET) is shown in Fig. 1. The proposed structure is designed with a SOI substrate having channel length (\(L_\mathrm{{C}}\)) of 40 nm and source/drain length (\(L_\mathrm{{S}} /L_\mathrm{{D}}\)) of 20 nm. The source and drain regions are heavily doped with trivalent and pentavalent impurity concentration (\(p^+\)/\(n^+\)) of \(10^{20}\,\mathrm{{cm}}^{-3}\), respectively. The intrinsic channel region is lightly doped with concentration of \(N=10^{15}\,\mathrm{{cm}}^{-3}\). The buried oxide thickness, gate oxide thickness, and silicon body thickness are taken as 2, 2, and 10 nm, respectively. The dielectric constant of the silicon and gate oxide are denoted as \(\varepsilon _{\mathrm{{Si}}} \) and \(\varepsilon _{\mathrm{{ox}}} \), respectively. The present analytical model was developed using a gate metal (\(\text {A}_X \text {B}_{1-X}\)) with spatially modulated workfunction to enhance gate control; the workfunction at the source and drain interface is \(\Phi _{\mathrm{{MA}}} =4.2\) eV and \(\Phi _{\mathrm{{MB}}} =5\) eV, respectively, while the instantaneous workfunction, \(\Phi _{\mathrm{{Mi}}} \left( X \right) \), of the metal gate contact along the x-axis can be represented as a function of the mole fraction (\(0\le X\le 1\)) as

$$\begin{aligned} \Phi _{\mathrm{{Mi}}} \left( x \right) =\Phi _{\mathrm{{MA}}} +\frac{\left( {\Phi _{\mathrm{{MB}}}-\Phi _{\mathrm{{MA}}} } \right) }{L_\mathrm{{c}}}x. \end{aligned}$$
(1)

This variation of the workfunction along the x-axis is formulated based on the assumption that the two pure metals (A and B) have equivalent density of states [20–22]. The potential profile (\(\Phi ({x,y})\)) in the channel region can be expressed in terms of the two-dimensional (2-D) Poisson equation in the rectangular coordinate system as

$$\begin{aligned} \frac{\partial ^{2}\Phi \left( {x,y} \right) }{\partial ^{2}x}+\frac{\partial ^{2}\Phi \left( {x,y} \right) }{\partial ^{2}y}=\frac{qN}{\varepsilon _{\mathrm{{Si}}} }. \end{aligned}$$
(2)

Here, the effect of fixed and trapped charges on the surface potential is assumed to be negligible. The solution of Eq. 2 can be found by considering a parabolic approximation [6–8], using the required boundary conditions at the respective interfaces:

$$\begin{aligned}&\left. {\Phi _\mathrm{{s}} \left( x \right) } \right| _{x=0} =V_{\mathrm{{bis}}}\end{aligned}$$
(3)
$$\begin{aligned}&\left. {\Phi _\mathrm{{s}} \left( x \right) } \right| _{x=L_\mathrm{{c}} } =V_{\mathrm{{bid}}} +V_{\mathrm{{DS}}}\end{aligned}$$
(4)
$$\begin{aligned}&\left. {E\left( {x,y} \right) } \right| _{y=0} =\left( {\frac{\Phi _\mathrm{{s}} \left( x \right) -V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}} }{t_{\mathrm{{ox}}} }} \right) \frac{\varepsilon _{\mathrm{{ox}}} }{\varepsilon _{\mathrm{{Si}}} }\end{aligned}$$
(5)
$$\begin{aligned}&\left. {E\left( {x,y} \right) } \right| _{y=t_{\mathrm{{Si}}} } =0, \end{aligned}$$
(6)

where \(V_{\mathrm{{bis}}} \) and \(V_{\mathrm{{bid}}} \) represent the built-in potentials at the source–channel and channel–drain interface, respectively. The gate–source voltage (\(V_{\mathrm{{GS}}}\)) and drain–source voltage (\(V_{\mathrm{{DS}}}\)) are applied at the corresponding gate and drain terminal. Moreover, the instantaneous flat-band voltage (\(V_{\mathrm{{FBi}}}\)) can be evaluated using the modulated metal workfunction (\(\Phi _{\mathrm{{Mi}}}\)) and silicon workfunction (\(\Phi _{\mathrm{{Si}}}\)) as

$$\begin{aligned} V_{\mathrm{{FBi}}} =\Phi _{\mathrm{{Mi}}} -\Phi _{\mathrm{{Si}}}. \end{aligned}$$
(7)

The surface potential along the lateral direction can be evaluated using the solution of Eq. 2

$$\begin{aligned} \Phi _\mathrm{{s}} \left( x \right) =A_\mathrm{{m}} \text {e}^{kx}+B_\mathrm{{m}} \text {e}^{-kx}-\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}+V_{\mathrm{{GS}}} -V_{\mathrm{{FBi}}}, \end{aligned}$$
(8)

where k is defined as the natural normalized length, expressed as

$$\begin{aligned} k=\sqrt{\frac{\varepsilon _{\mathrm{{ox}}} }{t_{\mathrm{{Si}}} t_{\mathrm{{ox}}} \varepsilon _{\mathrm{{Si}}} }}. \end{aligned}$$
(9)

The coefficients \(A_\mathrm{{m}} \) and \(B_\mathrm{{m}} \) can be evaluated using the boundary conditions in (3) and (4) as

$$\begin{aligned}&A_\mathrm{{m}} =\frac{\left( {V_{\mathrm{{bid}}} +V_{\mathrm{{DS}}} +\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}-V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}} } \right) \text {e}^{kL_\mathrm{{c}} }-(V_{\mathrm{{bis}}} +\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}-V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}})}{\text {e}^{2kL_\mathrm{{c}} }-1}\nonumber \\\end{aligned}$$
(10)
$$\begin{aligned}&B_\mathrm{{m}} =\frac{(V_{\mathrm{{bis}}} +\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}-V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}} )\text {e}^{2kL_\mathrm{{c}} }-\left( {V_{\mathrm{{bid}}} +V_{\mathrm{{DS}}} +\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}-V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}}} \right) \text {e}^{kL_\mathrm{{c}}}}{\text {e}^{2kL_\mathrm{{c}}}-1}.\nonumber \\ \end{aligned}$$
(11)

The electric field along the x-axis has a substantial impact on the driving current capability and subthreshold slope of the device; it is primarily related to the surface potential of the device and can be determined by differentiating the potential w.r.t. the x-axis as

$$\begin{aligned} E_x \left( {x,y} \right) =-\frac{\partial \Phi _\mathrm{{s}} \left( {x,y} \right) }{\partial x}=k\left( {-A_\mathrm{{m}} \text {e}^{kx}+B_\mathrm{{m}} \text {e}^{-kx}} \right) .\nonumber \\ \end{aligned}$$
(12)
Fig. 1
figure 1

Schematic cross-sectional view of an n-channel workfunction-modulated TFET (WM-TFET)

Full size image

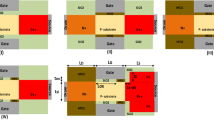
The drain current of the proposed model can be determined using the tunneling volume in the channel region. In ON-state, charge carriers tunnel from occupied states of the source valence band to unoccupied states of the channel conduction band, thus improving the tunneling volume in the channel. The initial tunneling distance (\(x_\mathrm{{i}}\)) is defined as the shortest distance from the tunneling junction when the source valence band and channel conduction band are lined up [8, 12, 40] as shown in Fig. 2. For lower values of \(\hbox {V}_{\mathrm{{GS}}}\), the distance between the source valance band and channel conduction band is high, thus preventing carrier tunneling in OFF-state. As \(\hbox {V}_{\mathrm{{GS}}}\) is gradually increased, this tunneling distance is progressively reduced, thereby increasing the ON-state current.

$$\begin{aligned}&\left. {\Phi _\mathrm{{s}} \left( x \right) } \right| _{x=x_\mathrm{{i}} } =\left. {\Phi _\mathrm{{s}} \left( x \right) } \right| _{x=0} +\frac{E_\mathrm{{g}} }{q}\end{aligned}$$
(13)
$$\begin{aligned}&x_\mathrm{{i}} =\left( {\frac{1}{k}\ln \frac{\left( {V_{\mathrm{{bis}}} +\frac{E_\mathrm{{g}} }{q}+\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}-V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}} } \right) +\sqrt{\left( {V_{\mathrm{{bis}}} +\frac{E_\mathrm{{g}} }{q}+\frac{qN}{\varepsilon _{\mathrm{{Si}}} k^{2}}-V_{\mathrm{{GS}}} +V_{\mathrm{{FBi}}} } \right) ^{2}-4A_\mathrm{{m}} B_\mathrm{{m}} }}{2A_\mathrm{{m}} }} \right) . \end{aligned}$$
(14)

The initial tunneling distance plays a significant role in determining both the drain current and subthreshold slope of the device. The drain current of the proposed model can be determined by integrating the BTBT generation rate (\(G_{\mathrm{{BTBT}}}\)) over a finite volume as

$$\begin{aligned} I_\mathrm{{D}} =q\smallint A_\mathrm{{c}} E_{{x}} E_{\mathrm{{avg}}} \hbox {exp}\left( {-\frac{B_\mathrm{{c}} }{E_{\mathrm{{avg}}} }} \right) \,\text {d}v, \end{aligned}$$
(15)

where \(E_{\mathrm{{avg}}} =\frac{E_\mathrm{{g}} }{qx}\) is defined as the average electric field. The magnitude of Kane’s tunneling process-dependent parameters \(A_\mathrm{{c}}\) and \(B_\mathrm{{c}} \) are considered as \(9.6615\times 10^{18}\,\mathrm{{cm}}^{-1}\mathrm{{s}}^{-1}\mathrm{{V}}^{-2}\) and \(3\times 10^{7}\,\mathrm{{V}}\,\mathrm{{cm}}^{-1}\), respectively [8].

$$\begin{aligned} I_\mathrm{{D}} =q\mathop \smallint \limits _0^{t_{\mathrm{{Si}}} } \mathop \smallint \limits _{x_\mathrm{{i}} }^{L_\mathrm{{c}} } A_\mathrm{{c}} E_{{x}} \frac{E_\mathrm{{g}} }{qx} \exp \left( {-\frac{B_\mathrm{{c}} q}{E_\mathrm{{g}} }x} \right) \,\text {d}y \, \text {d}x. \end{aligned}$$
(16)

Neglecting the minimal effect of the exponential and polynomial terms at the channel–drain interface, the final drain current equation can be formulated as [12]

$$\begin{aligned}&I_\mathrm{{D}} =A_\mathrm{{c}} kt_{\mathrm{{Si}}} E_\mathrm{{g}} \left[ {\frac{A_\mathrm{{m}} }{\left( {k-\frac{B_\mathrm{{c}} q}{E_\mathrm{{g}} }} \right) }E\left( {x_\mathrm{{i}} } \right) -\frac{B_\mathrm{{m}} }{\left( {k+\frac{B_\mathrm{{c}} q}{E_\mathrm{{g}} }} \right) }F\left( {x_\mathrm{{i}} } \right) } \right] ,\nonumber \\\end{aligned}$$
(17)
$$\begin{aligned}&\hbox {where }E=\frac{\text {e}^{x\left( {k-\frac{B_\mathrm{{c}} q}{E_\mathrm{{g}}}} \right) }}{x}\, \mathrm{{and}} \, F=\frac{\text {e}^{-x\left( {k+\frac{B_\mathrm{{c}} q}{E_\mathrm{{g}} }} \right) }}{x}. \end{aligned}$$
(18)

The subthreshold slope (SS) of a device indicates the sharpness of the transition from OFF- to ON-state. The SS for a device can be determined as the gate voltage change required to achieve a one-decade change in drain current:

$$\begin{aligned} \mathrm{{SS}}=\left. {\left( {{\text {d} \log (I_\mathrm{{D}} )}/{\text {d}V_{\mathrm{{GS}}} }} \right) ^{-1}} \right| _{V_{\mathrm{{DS}}} = \mathrm{{const}}}. \end{aligned}$$
(19)
Fig. 2
figure 2

ON-state energy band diagram of the TFET and WM-TFET models

Full size image

Similarly, the transconductance (\(g_\mathrm{{m}}\)) of a device is defined as the first-order differential of the drain current w.r.t. the gate voltage for constant drain voltage, i.e., \(g_\mathrm{{m}} =\left. {\frac{\partial I_\mathrm{{D}}}{\partial V_{\mathrm{{GS}} }}} \right| _{V_{\mathrm{{DS}}} = \mathrm{{const}}} \). Both of these factors, i.e., \(g_\mathrm{{m}} \) and SS, provide information about the switching speed of the device. Also, the transconductance generation factor (TGF), which is one of the important figures of merit, can be evaluated as the ratio of the transconductance to drain current for fixed gate voltage and drain voltage, i.e., \(\text {TGF}=g_\mathrm{{m}} /I_\mathrm{{D}}\). The gain of the device per unit power dissipation can also be determined from the TGF [9].

3 Results and discussion

The accuracy of the presented analytical model was corroborated using the 2-D TCAD Synopsis Sentaurus device simulator. The carrier transport phenomenon in the model was analyzed using Kane’s nonlocal BTBT model [8]. Several other models, such as the Shockley–Read–Hall (SRH) recombination model, bandgap-narrowing model, and electron-barrier tunneling model, were also considered. Here, doping-dependent mobility models and high-field saturation models were also used to explore the driving capability of the present model. The results for the proposed model are compared with results for a conventional TFET with gate metal workfunction of 4.2 eV.

Considering the effect of the workfunction modulation, the variation of the surface potential and absolute lateral electric field for the present model are illustrated in Fig. 3a and b, respectively. The significant impact of the spatially modulated metal alloy is evident from the surface potential characteristics in the channel region, thus affecting the gate control capability. However, for the present model, the surface potential remains unchanged in the source and drain regions, as for the conventional TFET. Similarly, the lateral electric field (Fig. 3b) shows equivalent values in the source and drain region, whereas it varies marginally in the channel region due to the impact of the workfunction variation. The lateral electric field is one of the important parameters for calculation of the drain current.

Fig. 3
figure 3

Comparison of a the surface potential and b lateral electric field variation along the x-axis for both models at constant gate voltage

Full size image

The surface potential variation for the WM-TFET model with different gate voltages is illustrated in Fig. 4a. It is clearly evident that, with increasing gate voltage, the gate control over the channel increases, thereby increasing the surface potential. The increased slope of the surface potential results in reduced tunneling distance in ON-state, thus improving the drain current at higher gate voltage. Figure 4b shows the influence of the drain voltage on the surface potential distribution for both models. The impact is significant at the channel–drain interface. Figure 4b reveals the reduced drain-induced barrier lowering (DIBL) effect, as the slope of the surface potential is unaffected by change in the drain voltage.

Fig. 4
figure 4

Surface potential variation along the x-axis for the WM-TFET model with different values of a gate voltage and b drain voltage

Full size image

Figure 5 displays the variation in the initial tunneling distance for the WM-TFET model with respect to gate voltage at constant \(V_{\mathrm{{DS}}} \), compared with the conventional TFET model. The present model exhibits higher initial tunneling distance in OFF-state, resulting from the spatially modulated workfunction, and thus significantly reduced OFF-current and SS. On the other hand, the proposed model provides marginally higher initial tunneling distance in ON-state compared with the conventional TFET, thus exhibiting poor ON-current performance.

Fig. 5
figure 5

Variation of the initial tunneling distance for both models w.r.t. gate voltage

Full size image

The average and point SS for both models are illustrated in Fig. 6a, b. The transfer characteristic for both models is shown on linear and logarithmic scales in Fig. 6a. It is evident that the conventional TFET model provides higher ON-current compared with the WM-TFET. On the other hand, the proposed model exhibits steeper subthreshold slope as a result of the workfunction modulation of the linearly graded metal alloy. The model shows significantly reduced average SS compared with the basic model. In Fig. 6b, the point SS is plotted with respect to drain current for both models. \(I_{60} \) is one of the figures of merit, determining the maximum drain current for SS = 60 mV/decade [41]. The drain current \(I_{60} \) was evaluated for the proposed model to investigate the impact of the workfunction modulation. The present model exhibits higher \(I_{60}\) (\(\sim 1\,\hbox {decade}\)) compared with the TFET model.

Fig. 6
figure 6

a Drain current as function of gate voltage, and b variation of the point SS w.r.t. drain current for constant gate voltage and drain voltage

Full size image

Figure 7a shows the \(I_\mathrm{{D}} - V_{\mathrm{{GS}}}\) characteristics for both models for different gate oxide thickness (\(t_{\mathrm{{ox}}}\)) values and the resulting average SS. Each reduction in \(t_{\mathrm{{ox}}}\) leads to an increase in the drain current for both models. However, the WM-TFET model exhibits steeper SS for each gate oxide thickness due to the enhanced control of the linearly modulated gate over the channel. Similarly, Fig. 7b indicates the effect of gate oxide scaling on \(I_{60}\) for both models. It is evident that the \(I_{60} \) value for the present model is improved as the gate oxide thickness is reduced, as for the TFET model.

Fig. 7
figure 7

a Drain current (\(\log I_\mathrm{{D}}\)) as a function of gate voltage. b Point SS as a function of drain current for different gate oxide thicknesses

Full size image

The \(I_\mathrm{{D}} - V_{\mathrm{{GS}}} \) characteristics of both the TFET and WM-TFET models for different silicon body thickness (\(t_{\mathrm{{Si}}}\)) values along with the average SS are illustrated in Fig. 8a. The average SS is reduced further with reduction in \(t_{\mathrm{{Si}}} \) for the WM-TFET model compared with the conventional TFET model, revealing the impact of the workfunction modulation on the channel. Thus, downscaling of the body thickness results in higher drain current performance and low power consumption (low OFF-current and SS) for the present model, as for the TFET model. Figure 8b shows the variation of the point SS for both models w.r.t. drain current for different values of silicon body thickness. The impact of the spatial modulation of the metal alloy workfunction is evident in Fig. 8b, with improved \(I_{60} \) as \(t_{\mathrm{{Si}}}\) is reduced.

Fig. 8
figure 8

a Drain current (\(\log I_\mathrm{{D}}\)) as a function of gate voltage, and b point SS as a function of drain current for different silicon body thicknesses

Full size image

Figure 9a and b illustrate the transconductance and TGF for both models as functions of gate voltage. For constant drain voltage, the transconductance of the conventional TFET model is higher compared with the present model due to the marginal difference in drain current behavior between the models, indicating a lower amplification capability for the present model. The unit power dissipation gain factor TGF for both device models is shown in Fig. 9b. The TGF gain factor is quite high for the proposed model at low gate voltage, due to the steep slope of the transfer characteristics. This is a result of the introduction of the linearly graded gate in the TFET.

Fig. 9
figure 9

a Variation of transconductance (\(\log g_\mathrm{{m}}\)) and b TGF w.r.t. gate voltage for both models at \(V_{\mathrm{{DS}}} =1\) V

Full size image

4 Conclusions

The performance in terms of various electrical parameters such as the surface potential, electric field, initial tunneling distance, drain current, average SS, \(I_{60} \), transconductance, and unit gain TGF is investigated for the WM-TFET model. Prominently improved efficiency is exhibited by the present model compared with the conventional TFET, with significantly improved \(I_{60} \) and reduced average SS (\(\sim 14\,\hbox {mV/decade}\)). Also, the effect of downscaling the gate oxide and silicon body thicknesses on the variation of the average and point SS of the WM-TFET is investigated. This model represents one potential solution for ultralow-power applications due to its low OFF-current and steeper SS.