1 Introduction

Junctionless field effect transistors (JLFETs) have been studied as a promising alternative for MOSFETs in sub-100 nm regime. The junctionless FET, also known as a gated resistor has several advantages over the conventional MOSFET, like diminished short channel effects (SCEs), nearly ideal subthreshold slope (\(\hbox {SS} \sim \)60 mV/dec), high \(\hbox {I}_{\mathrm{ON}}/\hbox {I}_{\mathrm{OFF}}\) ratio, and low source/drain series resistance [1]. Besides, the absence of any metallurgical junctions in the device offers a simplified low thermal budget fabrication process. Analyzing and developing accurate models for JLFETs, hence, is important for circuit designs and simulations.

However, the subthreshold leakage current (diffusion current) for the JLFETs is considerably high and flows through the center of the channel due to low concentration of the depletion charge carriers. To turn OFF the device properly and to achieve a lower value of subthreshold leakage current, we need to use a gate material with a high work function (\({\sim }5.6\) eV), which is technologically challenging. Instead, the electrostatic performance of the device can be significantly improved by incorporating a step in the surface potential profile using a Dual Material Gate (DMG). The DMG concept has been widely studied to demonstrate the simultaneous suppression of the SCEs and enhancement of trans-conductance, due to the introduction of a step function in the channel surface potential [2–11]. Recently, improvements in electrical characteristics have been demonstrated by using the DMG structure in planar JLFETs and junctionless nanowire transistors [12, 13]. In addition, the DMG structure is compatible with the current CMOS fabrication technology [14, 15]. Therefore, developing a pseudo two-dimensional (2-D) analytical surface potential model for a dual material double gate junctionless field effect transistor (DMDG JLFET) is of great interest. An accurate surface potential model is useful to develop the drain current model of DMDG JLFET.

In this paper, therefore we report an analytical model for the surface potential of a DMDG JLFET by solving the 2-D Poisson’s equation. The model results are verified by comparing them with the 2-D simulated results from ATLAS [16]. Most of the models developed for DG JLFET did not account for depletion into the source and drain regions. In this paper, the depletion regions extending into source \((\hbox {d}_{\mathrm{S}})\) and drain (\(\hbox {d}_{\mathrm{D}}\)) are also considered [10, 17].

2 Two dimensional model for surface potential

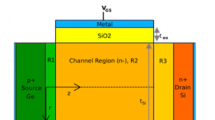
A schematic cross sectional view of the DMDG JLFET is shown in Fig. 1. It is a junctionless device with uniform doping in the entire silicon channel. The gate is made up of two different metals laterally merged together, where, the work function of metal in gate1 (\(\hbox {M}_{1}\)) is greater than that of gate2 (\(\hbox {M}_{2}\)) i.e. \(\phi _{M1} >\phi _{M2} \) for an n-doped structure and vice-versa for a p-doped structure. The 2-D Poisson’s equation for the potential distribution in the channel can be written as:

$$\begin{aligned}&\frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial x^{2}}+\frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial y^{2}}\nonumber \\&\quad =\frac{qN_D }{\varepsilon _{si} }\left[ {e^{\left( {\frac{\phi -V}{V_t }} \right) }-1} \right] \quad for\; 0\le x\le L;-t_{si} \le y\le 0\nonumber \\ \end{aligned}$$
(1)

where \(\phi \left( {x,y} \right) \) is the potential at any point (x, y) in the channel, \(N_D\) is the channel doping concentration, \(\varepsilon _{si} \) is the dielectric constant of silicon, V is the quasi-Fermi potential, \(V_t \) is the thermal voltage, \(t_{si} \) is the channel thickness and L is the channel length.

Fig. 1
figure 1

Cross sectional view of an a dual material double gate junctionless field effect transistor (DMDG JLFET)

Full size image

The parabolic nature of potential across the channel has already been demonstrated [18, 19]. Hence, the potential profile in the vertical direction, i.e., the y-dependence of \(\phi \left( {x,y} \right) \) can be approximated by a simple parabolic function:

$$\begin{aligned} \phi \left( {x,y} \right) =\phi _s \left( x \right) +a_1 \left( x \right) y+a_2 \left( x \right) y^{2};\hbox {}-t_{si} \le y\le 0 \end{aligned}$$
(2)

where \(\phi _s \left( x \right) \) is the surface potential and arbitrary coefficients \(a_1 \left( x \right) \) and \(a_2 \left( x \right) \) are functions of x only.

In the DMDG JLFET, we have two different gate metals with different work functions. Therefore, the flatband voltage for the two gates would be different. Since, the flat band voltages \(V_{FB1}\) and \(V_{FB2} \), respectively, depend upon the work functions \(\phi _{M1}\) and \(\phi _{M2} \), they can be written as

$$\begin{aligned} V_{FB1} =\phi _{M1} -\phi _{si}\,and\,V_{FB2} =\phi _{M2} -\phi _{si} \end{aligned}$$
(3)

where \(\phi _{si} \) is the silicon work function. In the DMDG JLFET structure, since the gate is divided into two parts (\(\hbox {M}_{1}\) and \(\hbox {M}_{2})\), the potential under the two gates can be written as

$$\begin{aligned}&\phi _1 \left( {x,y} \right) =\phi _{s1} \left( x \right) +a_{11} \left( x \right) y+a_{12} \left( x \right) y^{2}\nonumber \\&\qquad for\,0\le \hbox {x}\le L_1 ;-t_{si} \big /2\le y\le 0 \end{aligned}$$
(4)
$$\begin{aligned}&\phi _2 \left( {x,y} \right) =\phi _{s2} \left( x \right) +a_{21} \left( x \right) y+a_{22} \left( x \right) y^{2}\nonumber \\&\qquad {for}\,L_1 \le \hbox {x}\le L_1 +L_2 ;-\frac{t_{si} }{2}\le y\le 0 \end{aligned}$$
(5)

3 Boundary conditions

The Poisson’s equation under two gates can be solved using following boundary conditions:

  1. (1)

    Electric flux at the gate-oxide interface is continuous for both metal gate s

    $$\begin{aligned} \varepsilon _{Si} \frac{\phi _1 \left( {x,y=0} \right) }{\partial y}= & {} C_{ox} \left( {V_{GS1}^{\prime } -\phi _{s1} \left( x \right) } \right) \,for\,M_1 \end{aligned}$$
    (6)
    $$\begin{aligned} \varepsilon _{Si} \frac{\phi _2 \left( {x,y=0} \right) }{\partial y}= & {} C_{ox} \left( {V_{GS2}^{\prime } -\phi _{s2} \left( x \right) } \right) \,for\,M_2 \end{aligned}$$
    (7)

    where \(V_{GS1}^{\prime } =V_{GS} -V_{FB1}\,\hbox {and}\,V_{GS2}^{\prime } =V_{GS} -V_{FB2},C_{ox} =\frac{\varepsilon _{ox} }{t_{ox}}\)

    \(\varepsilon _{ox} \) is the dielectric constant of the oxide and \(t_{ox} \) is the oxide thickness, \(V_{GS} \) is the gate to source bias voltage.

  2. (2)

    Surface potential at the interface of the two dissimilar metals is continuous

    $$\begin{aligned} \phi _{s_1 } \left( {L_1 } \right) =\phi _{s_2 } \left( {L_1 } \right) \end{aligned}$$
    (8)
  3. (3)

    Electric field at the interface of the two dissimilar metals is continuous

    $$\begin{aligned} \phi _{s_1 }^{\prime } \left( {L_1 } \right) =\phi _{s_2 }^{\prime } \left( {L_1 } \right) \end{aligned}$$
    (9)
  4. (4)

    By accounting for the extra depletion into the source region, we can approximate the potential at the source end to be

    $$\begin{aligned} \phi _{s_1 } \left( {x=0} \right) =V-\frac{qN_d d_S^2 }{2\varepsilon _{Si} } \end{aligned}$$
    (10)

    where \(d_S \) is the extra depletion into the source region [17].

  5. (5)

    By accounting for the extra depletion into the drain region, we can approximate the potential at the drain end to be

    $$\begin{aligned} \phi _{s_2 } \left( {x=L_1 +L_2 } \right) =V+V_{DS} -\frac{qN_d d_D^2 }{2\varepsilon _{Si} } \end{aligned}$$
    (11)

    where \(d_D \) is the extra depletion into the drain region, \(V_{DS} \) is the drain to source bias voltage [17].

  6. (6)

    From the boundary condition (10), the electrical field at the source end should be continuous i.e.

    $$\begin{aligned} \phi _{S_1 }^{\prime } \left( {x=0} \right) =-\frac{qN_d d_S }{\varepsilon _{Si} } \end{aligned}$$
    (12)
  7. (7)

    From the boundary condition (11), the electrical field at the drain end should be continuous i.e.

    $$\begin{aligned} \phi _{S_2 }^{\prime } \left( {x=L_1 +L_2 } \right) =\frac{qN_d d_D }{\varepsilon _{Si} } \end{aligned}$$
    (13)

4 Modes of operation

According to the applied gate voltage, the operation of the DMDG JLFET can be categorized into three modes: (i) full depletion, (ii) partial depletion, and (iii) near flatband. In this section, the general surface potential functions for all the three modes are discussed. This approach helps in arriving at the final surface potential model in the DMDG JLFET for different modes of operation.

4.1 Full depletion model (\(V_{G}<V_{th}\))

When the applied gate voltage (\(\hbox {V}_{\mathrm{G}}\)) is less than the threshold voltage (\(\hbox {V}_{\mathrm{th}}\)), the channel is completely depleted. Since, the concentration of mobile charges is almost negligible in the channel, the exponential term can be neglected from the Poisson’s equation and can be simplified as

$$\begin{aligned} \frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial x^{2}}+\frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial y^{2}}=\frac{-qN_D }{\varepsilon _{si}};-t_{si} /2\le y\le 0 \end{aligned}$$
(14)

Since, the device is a symmetric structure, the electric field at the center of the device is zero i.e.

$$\begin{aligned} \frac{\phi \left( {x,y=-t_{si} /2} \right) }{\partial y}=0 \end{aligned}$$
(15)

The constants \(a_{i1} \left( x \right) \,and \, a_{i2} \left( x \right) \) are deduced from the boundary conditions (6, 7) and (15). Substituting their values in (4) and (5) and then in (14), we obtain

$$\begin{aligned} \phi _{s_i }^{{\prime }{\prime }} -\alpha \phi _{s_i } =\beta _i \end{aligned}$$
(16)

where \(\alpha =\frac{2C_{ox} }{t_{si} \in _{si} }\,and\,\beta _i =-\left[ {\frac{qN_D }{\varepsilon _{si} }+\alpha \left( {V_G -\phi _{M_i } +\phi _{si} } \right) } \right] \)

(\(\beta _i \) corresponds to gate ‘i’)

4.2 Partial depletion (\(V_{th}<V_{G}<V_{FB}\))

When the applied gate voltage is between the threshold voltage and the flatband voltage, the channel is partially depleted, leaving a neutral region at the center of the structure. In the depletion region, therefore, the Poisson’s equation can be simplified as

$$\begin{aligned} \frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial x^{2}}+\frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial y^{2}}=\frac{-qN_D }{\varepsilon _{si} };-y_d \le y\le 0 \end{aligned}$$
(17)

To model the surface potential function in the partial depletion, we need to calculate the depletion thickness (\(y_d\)) of the channel (refer to Fig. 2). Assuming uniform \(y_d \) in the channel, it is calculated through one dimensional (1-D) model of the surface potential in the depletion region. Assuming the origin to be at the center of the device, 1-D model is developed given as

$$\begin{aligned}&\phi \left( {x,y} \right) =\frac{-qN_D }{2\varepsilon _{si} }(\left| y \right| -y_0 )^{2}-E_0 (\left| y \right| -y_0 )+V-V_t ;\nonumber \\&\qquad \quad y_0\le \left| y \right| \le t_{si} /2 \end{aligned}$$
(18)

where \(y_0\) is the point from the origin where the depletion region starts, \(E_0 \) is the electric field at \(\hbox {y}=y_0\).

Fig. 2
figure 2

DMDG JLFET illustrating partial mode under both gate1 and gate2

Full size image

Since, the potential profile across the channel is parabolic in nature, the electric field can be approximated as E=Ky in the neutral region (\(0\le \left| y \right| \le y_0)\), where K is a constant. We obtain a concise expression for \(E_0 \) by the finite difference method using the potential relation \(\phi \left( {x,y_0 } \right) =V-V_t \) i.e.

$$\begin{aligned}&\frac{\phi \left( {x,y=y_0 } \right) }{\partial y}=Eo=\frac{-8V_t y_d }{t_{Si}^2 } \end{aligned}$$
(19)
$$\begin{aligned}&y_d =\frac{t_{si} }{2}-y_0 \end{aligned}$$
(20)

Using Eqs. (19) and (20) in (18), then using Eq. (6) or (7), the depletion thickness \(y_d \) can be calculated as

$$\begin{aligned} y_d =\frac{-b+\sqrt{b^{2}-4ac}}{2a} \end{aligned}$$
(21)

where

Also, \(y_d \) being the magnitude of depletion thickness, it remains unchanged with respect to the change in the origin.

The potential in the neutral region follows a simple parabolic potential approximation where the potential at the center of the device is approximated to be V, i.e.

$$\begin{aligned} \phi \left( {x,y=-t_{si} /2} \right) =V \end{aligned}$$
(22)

The constants \(a_{i1} \left( x \right) \,and\, a_{i2} \left( x \right) \) are deduced from the boundary conditions (6, 7) and (19). Substituting their values in (4) and (5) and then in (17), we obtain,

$$\begin{aligned} \phi _{s_i }^{{\prime }{\prime }} -\alpha \phi _{s_i } =\beta _i \end{aligned}$$
(23)

where \(\alpha =\frac{C_{ox} }{y_d \varepsilon _{si} }\,and\,\beta _i =-\left[ {\frac{qN_D }{\varepsilon _{si} }+\alpha \left( {V_G -\phi _{M_i } +\phi _{si} } \right) } \right] \)

(\(\beta _i \) corresponds to gate ‘i’)

4.3 Near flatband (\(|V_{G} \sim V_{FB}| \le V_t)\)

Around the flatband voltage, the carrier concentration in the entire channel is approximately equal to \(\hbox {N}_{\mathrm{D}}(\sim 10^{19} /\hbox {cm}^{3}\)). On further increasing the gate voltage, negative charges accumulate at the surface changing the curvature of the band diagram [18]. Using Taylor’ series, the Poisson’s equation can be approximated as

$$\begin{aligned}&\frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial x^{2}}+\frac{\partial ^{2}\phi \left( {x,y} \right) }{\partial y^{2}}=\frac{qN_D }{\varepsilon _{si} }\left( {\frac{\phi -V}{V_t }} \right) ;\nonumber \\&\quad -t_{si} \big /2\le y\le 0 \end{aligned}$$
(24)

The constants \(a_{i1} \left( x \right) anda_{i2} \left( x \right) \) are deduced from the boundary conditions (6, 7) and (15). Substituting their values in (4) and (5) and then in (24), we obtain

$$\begin{aligned} \phi _{s_i }^{{\prime }{\prime }} -\alpha \phi _{s_i } =\beta _i \end{aligned}$$
(25)

where

$$\begin{aligned}&\alpha =\frac{2C_{ox} }{t_{si} \varepsilon _{si} }+\frac{qN_D }{\varepsilon _{si} V_t }\,and\\&\beta _i=-\left[ {\frac{qN_D }{\varepsilon _{si} V_t }+\alpha \left( {V_G -\phi _{M_i } +\phi _{si} } \right) } \right] \end{aligned}$$

(\(\beta _i \) corresponds to gate ‘i’)

5 Combination of operating modes

Since \(\phi _{M1} >\phi _{M2} \), the threshold and the flatband voltages for gate1 are larger than that of gate2 (\( V_{th1} >V_{th2} \& V_{FB1} >V_{FB2} )\). Therefore, on applying a gate voltage, the channels under the two gate regions will be in different operating modes. Hence, we need to model the surface potential for different combinations of the operating modes. The surface potential model for a particular combination of operating modes is developed from the previously obtained general surface potential model depending upon the operating mode, exhibited under the respective gate. In addition, on applying a gate voltage, the depletion thicknesses\((y_{d1} ,y_{d2} )\) under the two gates will be different.

5.1 Full depletion (gate1) and partial depletion (gate2)

When \(\hbox {V}_{G }< \hbox {V}_{\mathrm{th1}}\) (threshold voltage of gate1) and \(\hbox {V}_{\mathrm{th2} }< \hbox {V}_{\mathrm{G}} < \hbox {V}_{\mathrm{FB2},}\) the channel under gate1 is fully depleted and the channel under gate2 is partially depleted. Using equations (16) and (23) for gate1 and gate2 respectively, the surface potential functions can be written as

$$\begin{aligned} \phi _{s_1 } \left( x \right)= & {} A_1 e^{\lambda _1 x}+B_1 e^{-\lambda _1 x}-\frac{\beta _1 }{\alpha };\,0\le \hbox {x}\le L_1 \end{aligned}$$
(26)
$$\begin{aligned} \phi _{s_2 } \left( x \right)= & {} A_2 e^{\lambda _2 \left( {x-L_1 } \right) }+B_2 e^{-\lambda _2 \left( {x-L_1 } \right) }-\frac{\beta _2 }{\alpha };0\le \hbox {x}\le L_2\nonumber \\ \end{aligned}$$
(27)

where \(A_1 ,A_2 ,B_1 ,\hbox {and}\,B_2 \) are deduced using the boundary conditions (8–13) as shown below in (33).

5.2 Partial depletion (gate1) and partial depletion (gate2)

When \(\hbox {V}_{\mathrm{G}} >\hbox {V}_{\mathrm{th1}}\) (threshold voltage of gate1) and \(\hbox {V}_{\mathrm{th2}}<\hbox {V}_{\mathrm{G}} <\hbox {V}_{\mathrm{FB2},}\) the channel under both the gates is partially depleted. This results in the formation of depletion regions of thickness \(y_{d1} \) and \(y_{d2} \) under gate1 and gate2, respectively. Using equation (23) for both the gates, the surface potential functions can be written as

$$\begin{aligned} \phi _{s_1 } \left( x \right)= & {} A_1 e^{\lambda _1 x}+B_1 e^{-\lambda _1 x}-\frac{\beta _1 }{\alpha };\,0\le \hbox {x}\le L_1 \end{aligned}$$
(28)
$$\begin{aligned} \phi _{s_2 } \left( x \right)= & {} A_2 e^{\lambda _2 \left( {x-L_1 } \right) }+B_2 e^{-\lambda _2 \left( {x-L_1 } \right) }-\frac{\beta _2 }{\alpha };0\le \hbox {x}\le L_2\nonumber \\ \end{aligned}$$
(29)

where \(A_1 ,A_2 ,B_1 ,\hbox {and}\,B_2 \) are deduced using the boundary conditions (8–13) as shown below in (33).

5.3 Partial depletion (gate1) and near flatband (gate2)

When \(\hbox {V}_{\mathrm{th1}}<\hbox {V}_{\mathrm{G}}<\hbox {V}_{\mathrm{FB1}}\) and \(\hbox {V}_{\mathrm{G}} >\hbox {V}_{\mathrm{FB2}}\) channel under gate1 is partially depleted with a depletion thickness (\(y_{d1}\)) and the channel under gate2 is in near flat band mode. In near flat band mode, there is no depletion in the channel. Hence, the depletion width into the drain region is zero (\(d_D =0\)). Using Eqs. (23) and (25) for gate1 and gate2 respectively, the surface potential functions can be written as

$$\begin{aligned} \phi _{s_1 } \left( x \right)= & {} A_1 e^{\lambda _1 x}+B_1 e^{-\lambda _1 x}-\frac{\beta _1 }{\alpha };\,0\le \hbox {x}\le L_1 \end{aligned}$$
(30)
$$\begin{aligned} \phi _{s_2 } \left( x \right)= & {} A_2 e^{\lambda _2 \left( {x-L_1 } \right) }+B_2 e^{-\lambda _2 \left( {x-L_1 } \right) }-\frac{\beta _2 }{\alpha };0\le \hbox {x}\le L_2\nonumber \\ \end{aligned}$$
(31)

where \(A_1 ,A_2 ,B_1 ,\hbox {and}\,B_2 \) are deduced using the boundary conditions (8–12) as shown below in (33).

5.4 Threshold voltage

At threshold, the channel is completely depleted. Therefore, on substituting \(y_d =-t_{si} /2\) in equation (21) and solving for the gate voltage, we get the threshold voltage as

$$\begin{aligned} V_{th} =V_{FB1} -\frac{qN_D }{8\varepsilon _{si} }t_{si} ^{2} -\frac{qN_D }{2\varepsilon _{ox} }t_{si} t_{ox} +V-3V_t -\frac{4C_{si} }{C_{ox} }V_t \end{aligned}$$
(32)

In the case of DMG structure, due to the coexistence of metal gates \(\hbox {M}_{1}\) and \(\hbox {M}_{2}\), with different work functions, the threshold voltage of DMDG JLFET is solely determined by the metal gate with a higher work function i.e. \(\phi _{M1}\) [3].

$$\begin{aligned} d_S= & {} \frac{-b_S +\sqrt{b_S^2 -4a_S c_S }}{2a_S }and\nonumber \\&d_D =\frac{-b_D +\sqrt{b_D^2 -4a_D c_D }}{2a_D }\nonumber \\ a_S= & {} \frac{qN_d }{2\varepsilon _{si} },b_S =\frac{qN_d }{\varepsilon _{si} \lambda _1 },c_S =-\frac{\beta _1 }{\alpha _1 }-V\,and\nonumber \\ a_D= & {} \frac{qN_d }{2\varepsilon _{si} },b_D =\frac{qN_d }{\varepsilon _{si} \lambda _2 },c_D =-\frac{\beta _2 }{\alpha _2 }-V-V_d\nonumber \\ \lambda _i= & {} \sqrt{\alpha _i };B_1 =0.5\left( {\frac{\beta _1 }{\alpha _1 }+V-\frac{qN_d }{2\varepsilon _{si} }d_S^2 +\frac{qN_d }{\varepsilon _{si} \lambda _1 }d_S } \right) \nonumber \\ A_{2}= & {} \left\{ {{\begin{array}{l} {0.5\left( {\frac{\beta _2 }{\alpha _2 }+V+V_d -\frac{qN_d }{2\varepsilon _{si} }d_D^2 +\frac{qN_d }{\varepsilon _{si} \lambda _2 }d_D } \right) e^{-\lambda _2 L_2 }}\\ \quad {Full\;and\;Partial\;depletion\;modes} \\ {\frac{\left[ {\left( {V+V_d +\frac{\beta _2 }{\alpha _2 }} \right) (\lambda _1 +\lambda _2 )e^{(\lambda _2 L_2 )}+\left( {\frac{\beta _1 }{\alpha _1 }-\frac{\beta _2 }{\alpha _2 }} \right) \lambda _1 -2\lambda _1 B_1 e^{-\lambda _1 L_1 }} \right] }{\lambda _1 -\lambda _2 +(\lambda _1 +\lambda _2 )e^{(2\lambda _{2} L_{2} )}}}\\ {\quad Near\;flatband\;mode} \\ \end{array} }} \right. \nonumber \\ A_1= & {} \frac{\left[ {2A_2 -\left( {1-\frac{\lambda _1 }{\lambda _2 }} \right) B_1 e^{-\lambda _1 L_1 }+\frac{\beta _1 }{\alpha _1 }-\frac{\beta _2 }{\alpha _2 }} \right] e^{-\lambda _1 L_1 }}{1+\frac{\lambda _1 }{\lambda _2 }}\nonumber \\ B_2= & {} \left[ \left( {1-\frac{\lambda _1 }{\lambda _2 }} \right) A_1 e^{\lambda _1 L_1} +\left( {1+\frac{\lambda _1 }{\lambda _2 }} \right) B_1 e^{-\lambda _1 L_1 }\right. \nonumber \\&\left. -\,\frac{\beta _1 }{\alpha _1 }+\frac{\beta _2 }{\alpha _2 } \right] *0.5 \end{aligned}$$
(33)

In the above equations, values of \(\alpha _i ,\beta _i ,\lambda _i\) are used from the Sect. 4 depending upon the operating mode, exhibited by the respective gate.

6 Model verification and discussion

To verify the proposed analytical model, the 2-D device simulator ATLAS is used to simulate the potential distribution within the silicon channel [16]. A DMDG JLFET structure is implemented in ATLAS, having a uniformly n-doped (\(\hbox {N}_{\mathrm{D}}{\sim }10^{19}/\hbox {cm}^{3})\) source, drain and channel regions. The typical values of the work functions of gate metals M1 and M2 are chosen to be 5.2 and 4.7 eV, respectively. The Shockley–Read-Hall recombination model and the Fermi–Dirac carrier statistics are used in the simulation. The device channel length is 100 nm and source/drain lengths are 10 nm each to avoid parasitic resistance effects. The other device parameters used are; channel thickness (\(\hbox {t}_{\mathrm{si}}) = 10\,\hbox {nm}, \hbox {L}_{1} = \hbox {L}_{2} = 50\,\hbox {nm}\), gate oxide thickness (\(\hbox {t}_{\mathrm{ox}}) = 2\,\hbox {nm}\), and \(\hbox {V}_{\mathrm{S}} = \hbox {V}_{\mathrm{D}} = 0\). The threshold voltages for the two gates, calculated from (32), are \(\hbox {V}_{\mathrm{th1}} = 0.23\,\hbox {V}, \hbox {V}_{\mathrm{th2} }= -0.27\,\hbox {V}\). Figure 3 shows the surface potential variation with respect to different values of (a) impurity concentration, (b) gate oxide thickness and (c) silicon film thickness. Irrespective of which one of these parameters is varied, the surface potential converges to the quasi-Fermi potential (\({\sim }\)0.5294 V) as the gate voltage approaches the flatband voltage. The reason for this convergence is that the electric field and the space charge concentration would be zero when the device is in the near flatband mode. In addition, due to the absence of the depletion region the impact of oxide or silicon channel capacitance reduces in near flat band condition. We observe from Fig. 3 that the model shows good agreement with the simulation results. In Fig. 4, the surface potential along the channel is shown for \(\hbox {V}_{\mathrm{G}} = -0.1\) and 0.1 V. At these gate voltages, the channel under gate1 is fully depleted and the channel under gate2 is partially depleted. In addition, it is evident from the figure that the proposed analytical model accounts for the depletion into the source and drain region and the model values are in good agreement with the simulation results. Similarly, Fig. 5 shows the surface potential along the channel for \(\hbox {V}_{\mathrm{G}} = 0.4\) and 0.45 V.

Fig. 3
figure 3

The surface potential of DMDG JLFET under gate1 versus gate voltage for different values of a impurity concentration, b gate oxide thickness, and c silicon film thickness

Full size image
Fig. 4
figure 4

The surface potentials versus position along the channel for full depletion under gate1 and partial depletion under gate2 for \(\hbox {V}_{\mathrm{G}}= -0.1\) and 0.1 V

Full size image
Fig. 5
figure 5

The surface potentials versus position along the channel for partial depletion under both gate1 and gate2 for \(\hbox {V}_{\mathrm{G}}= 0.4\) and 0.45 V

Full size image

At these gate voltages, the channel under both gate1 and gate2 is partially depleted. We observe that the error between the model and the simulation results is negligible (\({\le } 2\,\%\)). Even this small error is due to the fact that the electric field approximation (18) used in the partial depletion model does not hold good for the gate voltages around flatband. Figure 6 compares the surface potentials along the channel for \(\hbox {V}_{\mathrm{G}} = 0.5\) and 0.6 V from our model with simulations. At these gate voltages, the channel under gate1 is partially depleted and the channel under gate 2 is in near flat band condition. The channel under the gate2 is entirely neutral due to absence of any space charges. Therefore, the surface potential plot is completely flat and in conjunction with the quasi-Fermi potential for gate2. Therefore, at \(\hbox {V}_{\mathrm{G}} = 0.5\,\hbox {V}, \phi _{s_2}\) is equal to V (\({\sim }0.5294\,\hbox {V}\)), as is expected. When \(\hbox {V}_{\mathrm{G}}= 0.6\,\hbox {V}\), the channel under gate2 enters the accumulation regime. The model results match well with the simulation results even when the gate voltage exceeds the flatband voltage of the channel under gate2. In Fig. 7, the potential distributions across the channel from our model and simulations are compared for all the operating modes.

Fig. 6
figure 6

The surface potential versus position along the channel for partial depletion under gate1 and near flatband (\(\hbox {V}_{\mathrm{G}}= 0.5\,\hbox {V}\)) / accumulation (\(\hbox {V}_{\mathrm{G}}= 0.6\,\hbox {V}\)) under gate2

Full size image
Fig. 7
figure 7

Potential distribution versus position across the channel for a full depletion, b partial depletion, c near flatband condition

Full size image

In Fig. 8, the threshold voltage calculated from the analytical model (32) for different impurity concentrations is compared with those obtained from 2-D simulation, extracted from the commonly used maximum transconductance method [3], for different values of gate oxide thickness and silicon film thickness. We observe that for a given channel doping, the threshold voltage decreases with an increase in either the gate oxide thickness or the silicon film thickness. The proposed analytical model accurately predicts the potential distribution for the entire silicon channel. The model is continuous and is valid for all the operating modes, making it suitable to develop the drain current model of a DMG JLFET.

Fig. 8
figure 8

Threshold voltage of DMDG JLFET for various a oxide thickness and b silicon thickness as a parameter of impurity concentration for \(\hbox {V}_{\mathrm{D}}= 1.0\,\hbox {V}\)

Full size image

7 Conclusions

In this paper, we have developed a pseudo 2-D analytical model for the surface potential of a DMDG JLFET. This model uses a parabolic approximation to find the surface potential under the two metal gates. The extra depletion extending into the source \((\hbox {d}_{\mathrm{S}})\) and the drain regions (\(\hbox {d}_{\mathrm{D}}\)) is accounted for a better accuracy of the model. In the partial depletion mode, a model for the channel depletion thickness (\(\hbox {y}_{\mathrm{d}}\)) is also developed and is further used to model both the surface potential and the threshold voltage. The model accurately predicts the surface potentials for all the different combination of operating modes exhibited under the two metal gates. The dependence of the surface potential and threshold voltage on the device parameters such as doping concentration, gate oxide and silicon film thicknesses is demonstrated. The accuracy of the model is validated against 2-D numerical simulations.