A surface-potential based drain current model for short-channel symmetric double-gate junctionless transistor

Abstract

Junctionless transistors, which do not have any pn junction in the source-channel-drain path have become an attractive candidate in sub-20 nm regime. They have homogeneous and uniform doping in source-channel-drain region. Despite some similarities with conventional MOSFETs, the charge-potential relationship is quite different in a junctionless transistor, due to its different operational principle. In this report, models for potential and drain current are formulated for shorter channel symmetric double-gate junctionless transistor (DGJLT). The potential model is derived from two dimensional Poisson’s equation using “variable separation technique”. The developed model captures the physics in all regions of device operation i.e., depletion to accumulation region without any fitting parameter. The model is valid for a range of channel doping concentrations, channel thickness and channel length. Threshold voltage and drain-induced barrier lowering values are extracted from the potential model. The model is in good agreement with professional TCAD simulation results.

1 Introduction

Junctionless transistors (JLT) avoid the ultrahigh doping concentration gradients at the junctions and high thermal budgets, and hence their fabrication steps are comparatively easier than junction-based metal oxide field-oxide transistors (JB MOSFETs). They offer low OFF-state currents and hence can be scaled to lower channel lengths compared to JB MOSFETs. JLT has near ideal subthreshold slope (SS $\sim$60 mV/dec), high ON-state to OFF-state current ratio ($I_{ON}/I_{OFF}>10^{7}$), low drain induced barrier lowering etc. There is less degradation of mobility with gate voltage and temperature in JLT than classical transistors [1]. The transconductance in junctionless (JL) transistor is however lesser compared to JB transistor. Device variability and the parasitic source/drain resistances are acknowledged as important limitations of the JL nanowire field-effect transistors [2].

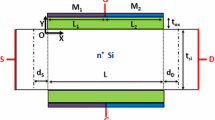
The working physics of a DGJLT is different from JB MOSFET counterpart. A cross-sectional view of symmetric n-channel DGJLT is shown in Fig. 1. JLT has highly doped $({\sim }8\times 10^{18}-8\times 10^{19}\;\hbox {cm}^{-3})$ channel to have desirable threshold voltage $(V_{T})$. Also, to have full depletion in the subthreshold region, channel should be adequately thin. For gate voltage $V_{GS}<V_{T}$, the channel of a DGJLT is fully depleted. When $V_{GS}$ exceeds $V_{T}$, the channel becomes partially depleted. When $V_{GS}$ = flat band voltage $(V_{FB})$, bulk current flows and on further increasing $V_{GS}$, surface current dominates in the channel current [3].

Fig. 1

Cross-sectional view of symmetric n-channel double-gate junctionless transistor (DGJLT)

Looking at the low leakage currents and many advantages as mentioned above, a JLT can be a prospective candidate for low power circuit design applications in future technology nodes, and therefore, an analytical compact model of junctionless transistor is sought after. Since the device physics of DGJLT is fundamentally different than the JB MOSFETs [1], the existing models for DG JB MOSFETs do not directly apply. There are many reports on analytical/semi-analytical modelling for potential and drain current either for long-channel or short-channel length junctionless transistor in double-gate, trigate or gate-all-around architecture till date [2–27]. Some of them are valid only in subthreshold region and some are applicable from subthreshold to accumulation region. There are few potential models for shorter channel length double-gate junctionless transistors which are valid in subthreshold region only. Jiang et al. proposed a physics-based analytical model of electrostatic potential for short-channel junctionless double-gate MOSFETs (JLDGMTs) operated in the subthreshold regime only, by solving 2D Poisson’s equation in channel region using method of series expansion similar to Green’s function. Jin et al. derived potential model by solving 2-D Poisson’s equation using “variable separation technique” for deep nanoscale short channel asymmetric junctionless double-gate MOSFETs valid in the subthreshold region. Holtij et al. reported analytical 2D potential model within ultra-scaled junctionless double-gate MOSFETs valid in the subthreshold regime using the Schwarz–Christoffel transformation. Also, some of the models are developed piecewise (region-wise) and some are non-piecewise. Accurate potential and drain current models, valid from depletion to accumulation regions of operation, for shorter channel length double-gate junctionless transistor, are still rare in literature. In this work, potential and drain current models, covering all regions of operation, are targeted for a shorter channel length double-gate junctionless transistor (DGJLT). A two-part approach, known as the “variable separation technique” is applied to derive the channel potential, in which the total potential is divided into long channel part and short channel part. Such a method gives quite accurate results in short channel regime, because, while deriving the short channel part of potential, one can include a large set of eigen values and details will be presented later in Sect. 2.2. In this work, we have obtained good accuracy with two eigen values, however, if more number of iterations are used, correspondingly, the simulation time may increase. Threshold voltage and drain induced barrier lowering (DIBL) parameters are extracted from the model. The potential model as well as the extracted parameters is then compared to professional TCAD simulation results.

2 Potential model derivation

The Poisson’s equation considering both fixed and mobile charges in the silicon region can be written as

$$\begin{aligned} \frac{d^{2}\Psi (x,y)}{dx^{2}}+\frac{d^{2}\Psi (x,y)}{dy^{2}}=\frac{qN_D }{\varepsilon _{si} }\left( {e^{\left( {\Psi (x,y)-V} \right) /U_T }-1} \right) \nonumber \\ \end{aligned}$$

(1)

where, $\Psi (x,y)$ is the channel potential, $\varepsilon _{si}$ is the permittivity of silicon, V is electron quasi-Fermi potential, $U_{T}=kT/q$ is the thermal voltage, $N_{D}$ is the channel doping concentration and q is the charge of electron. Hole density is neglected as compared to electron density. The coordinates, x and y are as shown in Fig 1. Equation (1) has no direct analytical solution. One way to solve (1) is variable separation technique, which states that the total potential can be divided into long channel part (1D) and short channel part (2D) i.e.,

$$\begin{aligned} \Psi (x,y)=\Psi _I (y)+\Psi _{II} (x,y) \end{aligned}$$

(2)

where, $\Psi _I(y)$ is the potential which is related to only y direction (long channel part) and $\Psi _{II}(x,y)$ is the potential variation related to both x and y directions (short channel part) with boundary conditions, as stated below.

2.1 Expression for $\Psi _{I}(y)$

$\Psi _I (y)$ is expressed as

$$\begin{aligned} \frac{d^{2}\Psi _I}{dy^{2}}=\frac{qN_D }{\varepsilon _{si} }\left( {e^{\left( {\Psi (y)-V} \right) /U_T }-1} \right) \end{aligned}$$

(3)

with boundary conditions

$$\begin{aligned} \begin{aligned}&\displaystyle {\frac{\partial \Psi }{\partial y}} \Bigg |_{y=\pm \dfrac{T_{si} }{2}}=\Psi _{S} =\dfrac{C_{ox} }{\varepsilon _{si} }\left( {V_{GS} -V_{FB} -\Psi \left( {\dfrac{T_{si} }{2}} \right) } \right) \\&\displaystyle \frac{\partial \Psi }{\partial y} \Bigg |_{y=0} =0 \end{aligned} \end{aligned}$$

(4)

Equation (4) has no closed form solution even though it looks simple. Integrating (4), we obtain

$$\begin{aligned} E_{S} ^{2}=\frac{2qN_D U_T }{\varepsilon _{si} }\left[ {e^{\left( {\Psi _{S} -V} \right) /U_T }-e^{\left( {\Psi _{0} -V} \right) /U_T }-\left( {\frac{\Psi _{S} -\Psi _{0} }{U_T }} \right) } \right] \nonumber \\ \end{aligned}$$

(5)

where, $\Psi _{S}$ and $\Psi _{0}$ are the potentials at the surface and centre of the channel respectively. Thus, once the relation between $\Psi _{S}$ and $\Psi _{0}$ is known, the potential at any point in the silicon body can be determined. The Gauss’s law connects the surface potential with gate voltage as

$$\begin{aligned} Q_{SC} =-2\varepsilon _{si} \left. {\frac{d\Psi }{dx}} \right| _{x=\pm \frac{T_{si} }{2}} =-2C_{ox} (V_G -V_{FB} -\Psi _{S} )\qquad \end{aligned}$$

(6)

$Q_{SC}$ being the space charge density per unit area, $C_{ox} =\varepsilon _{ox}/T_{ox}$ is the oxide capacitance, $V_{FB}$ is the flat band voltage. Combining (5) and (6)

$$\begin{aligned}&(V_G -V_{FB} -\Psi _{S} )^{2}\nonumber \\&\quad =\frac{2qN_D \varepsilon _{si} U_T }{C_{ox}^{2}}\left[ {e^{\left( {\Psi _{S}-V} \right) /U_T }-e^{\left( {\Psi _{0} -V} \right) /U_T }-\left( {\frac{\Psi _{S} -\Psi _{0}}{U_{T}}} \right) } \right] \nonumber \\ \end{aligned}$$

(7)

(a) For depletion region $\left( {V_{FB} <V_G <V_{FB} +V_{DS}} \right) {\textit{ with }} V_{DS} >0$, after some mathematical reformulations, the Eq. (7) can be written as [4]

$$\begin{aligned} \psi _{S}= & {} V_G -V_{TH} -\frac{qN_D T_{si}}{8C_{si} }\nonumber \\&-\,V_T {\textit{Lambertw}}\left[ {\frac{qN_D T_{si}}{4C_{ox} U_T }e^{\left( {V_G -V_{TH} -V} \right) /U_T}} \right] \end{aligned}$$

(8)

where, Lambertw is the Lambert W-function, which is the inverse of the function $\hbox {z}=\hbox {W(z)}\times \hbox {e}^{\mathrm{W(z)}}$. $V_{T}$ is the threshold voltage and $\left( {\Psi _{0}-\Psi _{S}}\right)$ is the difference between centre and surface potentials, given by,

$$\begin{aligned}&V_T =V_{FB} -qN_D T_{si} /2C_{eff} \nonumber \\&C_{eff}^{-1}=(4C_{si})^{-1}+(C_{ox})^{-1},\; C_{si} =\varepsilon _{si} /T_{si}\nonumber \\&\Psi _{0} -\Psi _{S} =qN_{D} T_{si}^{2}/8\varepsilon _{si} \end{aligned}$$

(9)

The expression of $V_{T}$ in (9) is valid when channel length is higher. The $V_{T}$ for shorter-channel device is given in Sect. 2.3.

(b) For accumulation region $\left( {V_G >V_{FB} +V_{DS} } \right)$

The relation between centre and surface potentials $\left\{ {\Psi _{S}-\Psi _{0}\left( {=\alpha , \hbox {say}} \right) }\right\}$ is given by [5]

$$\begin{aligned} \Psi _{S}-\Psi _{0} =\frac{qN_{D}T_{si}^{2}}{8\varepsilon _{si}}\left( {e^{\frac{\Psi _{0} -V}{U_T}}-1} \right) \end{aligned}$$

(10)

Equation (10) can also be expressed as [17]

$$\begin{aligned}&\Psi _{S} -\Psi _{0}\nonumber \\&\quad =-\frac{qN_D T_{si}}{8C_{si} }+U_{T} {\textit{Lambertw}}\left[ {\frac{qN_D T_{si} }{8C_{si} U_T }e^{\frac{qN_D T_{si} }{8C_{si} U_T }}e^{\frac{\Psi _{S} -V}{U_T }}} \right] \nonumber \\ \end{aligned}$$

(11)

Now, using (7) and (11), the relation between surface potential with gate voltage can be obtained as [17]

$$\begin{aligned}&(V_G -V_{FB} -\Psi _{S} )^{2}\nonumber \\&\quad =\,{\textit{sign}}(\alpha )\left( {\frac{q^{2}N_D ^{2}T_{si} \varepsilon _{si} }{C_{ox} ^{3}}} \right) \nonumber \\&\qquad \times \, \left[ {e^{\left( {\Psi _{S} -V} \right) /U_T }-1-\left( {1+\frac{8C_{si} U_T }{qN_D T_{si} }} \right) } \right. \nonumber \\&\qquad \times \, \left. {\left\{ {-\frac{qN_D T_{si} }{8C_{si} U_T }+{\textit{Lambertw}}\left[ {\frac{qN_D T_{si} }{8C_{si} U_T }e^{\frac{qN_D T_{si} }{8C_{si} U_T }}e^{\frac{\Psi _{S} -V}{U_T }}} \right] } \right\} }\right] \nonumber \\ \end{aligned}$$

(12)

For accumulation region $\left( {V_{GS} >V_{FB} +V_D } \right)$, $\alpha >0$. Equation (12) can be solved numerically. The centre potential can be derived using Eqs. (8)–(12), as explained in [18].

2.2 Expression for $\Psi _{II} (x,y)$

$\Psi _{II}(x,y)$ is expressed as

$$\begin{aligned} \frac{d^{2}\Psi _{II} (x,y)}{dx^{2}}+\frac{d^{2}\Psi _{II} (x,y)}{dy^{2}}=0 \end{aligned}$$

(13)

with the boundary conditions

$$\begin{aligned}&\Psi _{II} (0,y)=V_{bi} -\Psi _I (y) \nonumber \\&\Psi _{II} (L,y)=V_{DS} +V_{bi} -\Psi _I (y) \nonumber \\&\varepsilon _{si} \frac{\partial \Psi _{II} \left( {T_{si} /2,x} \right) }{\partial x}=-C_{ox} \Psi _{II} \left( {\frac{T_{si} }{2},x} \right) \nonumber \\&\left. {\frac{\partial \Psi _{II} }{\partial y} } \right| _{y=0} =0 \end{aligned}$$

(14)

Equation (13) is a mixed boundary value problem and it is already solved by many groups [28, 29]. The final solution is

$$\begin{aligned} \Psi _{II} (x,y)=\left\{ {A_{0} e^{\frac{2\mu _n \left( {x-L} \right) }{T_{si}}}+A_1 e^{-\frac{2\mu _n x}{T_{si}}}} \right\} \times \cos \left( {\mu _n y} \right) \end{aligned}$$

(15)

where,

$$\begin{aligned} A_{0}= & {} B_1 \left[ {V_{DS} +V_{bi} \left( {1-e^{-\frac{2\mu _n L}{T_{si} }}} \right) } \right] -B_2 \Psi _{S\hbox {(Long)}} \nonumber \\ A_{1}= & {} B_1 \left[ {V_{bi} \left( {1-e^{-\frac{2\mu _n L}{T_{si} }}} \right) -V_{DS} e^{-\frac{2\mu _n L}{T_{si} }}} \right] -B_2 \Psi _{S\hbox {(Long)}}\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned} B_1= & {} \frac{4\times Sin(\mu _n)}{2\mu _n+Sin(2\mu _n )\left( {1-e^{-\frac{2\mu _n L}{T_{si}}}} \right) },\nonumber \\ B_{2}= & {} \frac{4\mu _n \times Cos\left( {\frac{\mu _n }{2}} \right) \left( {1-e^{-\frac{2\mu _n L}{T_{si} }}} \right) }{2\mu _n +Sin(2\mu _n )\left( {1-e^{-\frac{2\mu _n L}{T_{si} }}} \right) } \end{aligned}$$

(17)

$\Psi _{S\hbox {(Long)}}$ is the long channel surface potential. The eigenvalue $\mu _{n}$ is the periodic $\hbox {n}^{\mathrm{th}}$ root of this equation and is determined using the permittivity and thickness values of both silicon and oxide. It can have infinite possible values for $\upmu$, however, first 1-2 iteration(s) give quite good result.

$$\begin{aligned} 2\mu _{n}\tan \left( {\mu _{n}}\right) =\frac{\varepsilon _{ox}T_{si} }{T_{ox} \varepsilon _{si}} \end{aligned}$$

(18)

Now, putting the expressions of $\Psi _{I}(y)$ and $\Psi _{II}(x,y)$ in Eq. (2), the total potential in the channel region of a shorter channel DGJLT can be determined.

2.3 Threshold voltage and DIBL value extraction

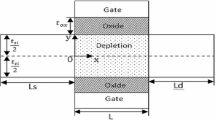
A schematic plan for calculating the threshold voltage $(V_{T})$ is given in Fig. 2. The threshold voltage is given by the following expression, and it is valid for longer as well as shorter channel length devices [30]

$$\begin{aligned} V_T =V_{GS}+\Delta V_{GS}\left( {\frac{U_T \ln \left( {N_D /n_i} \right) -\Psi _{\min (V_{GS1})}}{\Psi _{\min (V_{GS2})} -\Psi _{\min (V_{GS1})}}}\right) \end{aligned}$$

(19)

$\Psi _{\min (V_{GS1})}$ and $\Psi _{\min (V_{GS1})}$ are the minimum potentials at two gate-to-source voltages $V_{GS1}$ and $V_{GS2}$. Assuming a linear relationship between $\Psi _{\min }$ and $V_{GS}$, in the subthreshold region, threshold voltage can be extracted using (13).

Fig. 2

Schematic plan for calculating the threshold voltage. Here, $V_{T}=V_{GS}$ at $U_{T}{\textit{ln}}(N_{D}/n_{i})=\Psi _{\mathrm{min}}$ and $\Delta V_{GS}$ is the difference between two voltages in the subthreshold region

Drain induced barrier lowering (DIBL) is defined as the change in threshold voltage when drain voltage changes from 50 mV to 1 V i.e.,

$$\begin{aligned} \left. {{\textit{DIBL}}=V_{T}}\right| _{V_{DS} =50mV} -\left. {V_T}\right| _{V_{DS} = 1 \mathrm{V}} \end{aligned}$$

(20)

2.4 Discussion and verification of model

To validate the model results, they are compared with electrical characteristics of the devices simulated using 2D ATLAS device simulator with version 5.19.20.R [31]. Lombardi mobility model is employed, accounting for the dependence on the impurity concentrations as well as the transverse and longitudinal electric field values. Shockley-Read-Hall (SRH) recombination model is included in the simulation to account for leakage currents. Because of high channel doping concentration, Fermi-Dirac carrier statistics without impact ionization is utilized in the simulations. Band gap narrowing model (BGN) is also incorporated to take care of the band gap narrowing effect which may arise due to highly doped channel regions. Quantum effect is not considered here. Channel doping concentration $N_{D}$ of $5\times 10^{18}$ and $1\times 10^{19}\; \hbox {cm}^{-3}$, equivalent gate oxide thickness (EOT) = 2 nm, silicon thickness $(T_{si})=10$, 15 nm are considered for TCAD simulation. Channel width (W) is $1\upmu \hbox {m}$. In addition, p-type polysilicon is used having doping concentration $10^{20}\;\hbox {cm}^{-3}$. The interface charge concentration $(N_{SS})$ is considered as $5\times 10^{10}\;\hbox {cm}^{-3}$. A constant mobility $(\mu _{e})$ of $100\;\hbox {cm}^{2}$/V.s is assumed. For channel length of $1\;\upmu \hbox {m}$, source/drain extension length $(L_{S}/L_{D})$ is taken as 50 nm; and for channel length of 30 nm-80 nm, $L_{S}/L_{D}$ is taken as 10 nm to avoid parasitic resistance effect. Calculations are done on Mathematica computational software. Figure 3 shows the surface potential with respect to gate voltage, for different values of $V_{D}=0$ V, 50 mV, 0.5 V and 1 V respectively for a channel length of $1\;\upmu \hbox {m}$. The simulation and model curves are in close agreement. Figure 4 shows the surface potential with respect to gate voltage, for different values of $V_{D}=0$ V, 50 mV, 0.5 V and 1 V respectively for a channel length of 30 nm. The marginal difference may be due to the inclusion of source and drain extension resistances in TCAD characteristics; and the exclusion of fringing electric fields in the model. Figure 5a, b shows the potential along the channel direction, 0.5 nm away from the $\hbox {Si-SiO}_{2}$ interface, at $\hbox {V}_{\mathrm{DS}}= 50$ mV and 1 V respectively keeping $\hbox {V}_{\mathrm{GS}}=0$ V for gate lengths of 80 and 30 nm. Both the simulation and model plots are in close agreement. There is marginal difference of potential towards the drain side between model and simulation. For example, for L = 30 nm at $\hbox {V}_{\mathrm{DS}}=1$ V this difference are 86.4 mV. Figure 6a, b show the threshold voltage and drain induced barrier lowering characteristics extracted from model and simulation, for different gate lengths. The values obtained from model and simulations are in close agreement. The marginal difference of threshold voltage between model and TCAD results for say, L = 20 nm and L = 60 nm are 0.013 and 0.003 V respectively. The difference of DIBL between model and TCAD results are 9 mV and 1 mV for L = 20 nm and L = 60 nm respectively.

Fig. 3

Surface potential with respect to gate voltage near the drain side for $V_{D}=0$ V, 50 mV, 0.5 V and 1 V. $L=1\;\upmu \hbox {m}$, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}=5\times 10^{18}\;\hbox {cm}^{-3}$ and source/drain extension $\hbox {length}=50~\hbox {nm}$. Flat band voltage $(V_{FB})$ considered is ${\sim }1.1$ eV

Fig. 4

Surface potential with respect to gate voltage near the drain side for $V_{D}=0$ V, 50 mV, 0.5 V and 1 V. $L=30$ nm, $T_{si}=15\;\hbox {nm}$, $T_{ox}=2$ nm, $N_{D}=5\times 10^{18}\;\hbox {cm}^{-3}$ and source/drain extension length = 10 nm. Flat band voltage $(V_{FB})$ considered is ${\sim }1.1$ eV

Fig. 5

Surface potential along the channel for a $L=80$ nm (long channel) at $V_{D}=50$ mV, 1 V, b $L=30$ nm (short channel). $T_{si}=10$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$, $V_{GS}=0$ V and source/drain extension length=10 nm. Flat band voltage $(V_{FB})$ considered is ${\sim }1.1$ eV

Fig. 6

a Threshold voltage $(V_{T})$ at $V_{DS}=50$ mV for $\hbox {L}=20$ to 60 nm, b drain induced barrier lowering (DIBL) for $L=20$ to 60 nm. $T_{si}=10$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$

3 Drain current model

The mobile charge density $Q_{m}$ can be written as

$$\begin{aligned} Q_{m}=Q_{SC}-Q_{d} \end{aligned}$$

(21)

$Q_d =qN_D T_{si}$ is the fixed charge density. The drain current can be expressed as (using (7))

$$\begin{aligned} I_{D}= & {} -\mu \frac{W}{L}\int \limits _{0}^{V_{DS} } {Q_m dV} \nonumber \\= & {} -\mu \frac{W}{L}\int \limits _{0}^{V_{DS}}{\left[ {2C_{ox} \left( {V_G -V_{FB} -\Psi _{S}}\right) +Q_d}\right] dV} \end{aligned}$$

(22)

It is assumed that $V_{S}=0$ and $V_{D}=V_{DS}$. W is the width of the device and $\Psi _{S}$ (long-channel part + short-channel part) is the surface potential. Figure 7 shows the drain current with respect to gate voltage for different values of $N_{D}$ i.e., $8\times 10^{18}\;\hbox {cm}^{-3}$ and $1\times 10^{19}\;\hbox {cm}^{-3}$ at a drain voltage of 1 V. Same current values are plotted in both logarithmic (left) and linear (right) scales. The model results (symbols) are in close agreement with TCAD simulation (lines) in all regions of device operation, i.e., from subthreshold to accumulation regions. The subthreshold slope obtained from model is almost equal to TCAD results. As expected, current saturates at higher gate voltages. Also, saturation current increases with increase in channel doping concentration, as usual. The current in the accumulation region is obtained numerically. The subthreshold slope extracted from model and TCAD are in close agreement for long as well as short channel DGJLT. For example, for a DGJLT with $L=30\hbox {nm}$, $T_{si}=10$ nm, $T_{ox}=2$ nm and $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$, the subthreshold slope is 63 mV/dec as extracted from TCAD, which is almost similar to the value extracted from model. Figure 8 shows the transfer characteristic for Tsi=10 nm, L=30nm, $T_{ox}=2$ nm and $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ at gate voltages $V_{GS}$ of 50 mV and 1 V. Both TCAD (solid line) and model results (symbols) are in close agreement. Figure 9 shows the drain current with respect to gate voltage for $L=80$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}= 1\times 10^{19}\;\hbox {cm}^{-3}$ at $V_{DS}=1$ V. Lines show the TCAD simulations and symbols shows model results. TCAD (solid line) and model results (symbols) are in good agreement. Figure 10 presents the drain current with respect to drain voltage for different values of $N_{D}\; i.e$., $8\times 10^{18}\;\hbox {cm}^{-3}$ and $1\times 10^{19}\;\hbox {cm}^{-3}$ at a gate voltage of 1 V. The models (symbols) are in close accord with TCAD simulation (lines). The transconductance with respect to gate voltage for L=30 nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ at $V_{DS}=1$ V is shown in Fig. 11. TCAD simulations (symbols) and model results (lines) are not in close match at higher gate voltages. Figure 12 shows the output conductance with respect to drain voltage for $L=30$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ at $V_{GS}=1$ V. Both TCAD and model results are in close agreement.

Fig. 7

Drain current with respect to gate voltage for $N_{D}=5\times 10^{18}\;\hbox {cm}^{-3}$ and $1\times 10^{19}\;\hbox {cm}^{-3}$. $L=30$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $V_{DS}=1$ V and source/drain extension $\hbox {length}=10~\hbox {nm}$. Flat band voltage $(V_{FB})$ considered is ${\sim }1.1$ eV. Lines show the TCAD simulations and symbols shows model results

Fig. 8

Drain current with respect to gate voltage for $T_{si}=10$ nm, $L=30$ nm, $T_{ox}=2$ $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ and source/drain extension length = 10 nm at $V_{DS}=50$ mV and 1 V. Lines show the TCAD simulations and symbols shows model results

Fig. 9

Drain current with respect to gate voltage for $L=80$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ and source/drain extension length=10 nm at $V_{DS}=50$ mV and 1 V. Lines show the TCAD simulations and symbols shows model results

Fig. 10

Drain current with respect to drain voltage for $N_{D}=5\times 10^{18}\;\hbox {cm}^{-3}$ and $1\times 10^{19}\;\hbox {cm}^{-3}$. $L=30$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $V_{GS}=1$ V and source/drain extension $\hbox {length}=10~\hbox {nm}$. Flat band voltage $(V_{FB})$ considered is ${\sim }1.1$ eV. Lines show the TCAD simulations and symbols shows model results

Fig. 11

Transconductance with respect to gate voltage for $L=30$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ at $V_{DS}=1$ V and source/drain extension $\hbox {length}=10~\hbox {nm}$. Lines show the TCAD simulations and symbols shows model results

Fig. 12

Drain current and output conductance with respect to drain voltage for $L=30$ nm, $T_{si}=15$ nm, $T_{ox}=2$ nm, $N_{D}=1\times 10^{19}\;\hbox {cm}^{-3}$ at $V_{GS}=1$ V and source/drain extension length $=$ 10 nm. Lines show the TCAD simulations and symbols shows model results

4 Conclusion

In this work, we have proposed a semi-analytical model to calculate the channel surface potential as well as drain current for shorter channel length symmetric double-gate junctionless transistor by a two parts approach. Carrier mobility is assumed to be constant and the quantum effects are not considered. The model is valid in depletion to accumulation regions of operation. Threshold voltage and drain induced barrier lowering parameters were extracted from model. Assessment of the model with TCAD simulations confirms its legitimacy. Consideration of short-channel and quantum effects in the model is another scope for future research.