Introduction

The relative balance between hydrophilic and hydrophobic non-bonded molecular interactions is of central importance to the fields of chemistry [15], biophysics [70] and pharmacology [47]. Within the field of pharmacology, accurate characterization of these physiochemical properties is critical, as they affect all aspects of the drug design process, such as: availability [47], potency [75] and toxicity [48]. Tuning the hydrophobicity of a ligand affects its ability to diffuse across cellular membranes, alters its ability to bind to targets and impacts its clearance properties.

One way of rigorously quantifying a ligand’s hydrophilicity is the free energy required to transfer a molecule from a bulk apolar environment (k), e.g. octanol or hexane, to a bulk aqueous environment, \(\Delta G^{k \rightarrow {\text{aq}}}\), in the limit of infinite dilution. In the pharmaceutical sciences, this transfer free energy is often cast as a partition coefficient, \(P_{k}\), the ratio of concentrations of the solute in the two immiscible phases, which is trivially related to the transfer free energy, where \(k_{\text{B}}\) is the Boltzmann constant and T is the absolute temperature. Because of this, it is frequently expressed as a common logarithm (\(\log P_{k}\)).

$$P_{k}= {\frac{[{\text{A}}]_k}{[{\text{A}}]_{\text{aq}}}}$$
(1)
$${\Delta } G^{k \rightarrow {\text{aq}}}= k_{\text{B}} T \ln (10) \log P_{k}$$
(2)

Since many drug molecules contain ionizable groups that may exist in multiple protomeric states under physiological \({\text{pH}}\) conditions, the reality is often more complicated than the two-state model implied by partition coefficients. Solute aggregation, and the water dragging effect [18, 19] can also lead to non-negligible populations of solute molecules in “other” states. To account for these deviations from ideal behavior, we can combine the definition of a partition coefficient with a looser definition of relevant solute states. By including protonation, tautomerization, multimerization, etc., we obtain the definition of a distribution coefficient, \(D_{k}\) (Eq. 3).

$$D_{k} = {\frac{\sum _i \gamma _i [{\text{A}}]_{k,i}}{\sum _j \gamma _j [{\text{A}}]_{\text{aq},j}}}$$
(3)

The summation is over all states i and j in the apolar and aqueous environments, respectively. Equation 3 introduced the activity coefficient, \(\gamma\), to account for further, subtler deviations from ideal behavior, however in this work we will ignore this effect, and assume \(\gamma \equiv 1\).

While distribution coefficients are reliably and quickly characterized experimentally, [13, 46, 61] analogous physics-based computational predictions are expensive, and typically limited to neutral solutes [8, 32]. The accurate characterization of ionizable solutes, and thus \({\text{p}}K_{\text{a}}\) values remains a challenge. Most successful computational approaches to \({\text{p}}K_{\text{a}}\) prediction involve significant fitting to experimental data, [45, 77] or relative \({\text{p}}K_{\text{a}}\) calculations [11]. Accurately modeling the precise experimental conditions poses further challenges to the computational prediction of distribution coefficients. For example, the partitioning between aqueous and organic phases is exquisitely sensitive to the water content of the organic phase [1]. In experiments, both polar [29] and apolar [43] solutes are known to aggregate in the interfacial region, and thus deplete in the bulk phase.

Even without the complexities associated with predicting distribution coefficients, accurate prediction of partition coefficients still requires properly accounting for the change of solute–solvent interactions between apolar and polar phases. Previous SAMPL small molecule challenges have emphasized the calculation of hydration free energies for small molecules, [22, 55, 65] a not-dissimilar task from our current charge. The lessons learned in this regard from our previous work in SAMPL4, [40, 58] in which we showed the effectiveness of using quantum mechanical [39] based potential energy calculations in combination with the non-Boltzmann Bennett (NBB) free energy method [41], should be directly applicable in this current challenge [2].

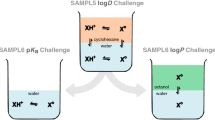
In this work we predict the partitioning between aqueous and cyclohexane phases for 53 small drug-like molecules in the SAMPL5 blind prediction challenge (Figs. 1, 2). We use various computational techniques ranging from molecular dynamics (MD) simulations to quantum mechanical potential energy evaluations (QM), combining the best aspects of these approaches via the NBB free energy estimator. These QM-NBB calculations with implicit solvent yield predictions with a root mean squared deviation from experiment (RMSD) that ranks second among the various entries. We also attempt to account for deviations from non-ideal behavior using QM based \({\text{p}}K_{\text{a}}\) and protomeric calculations. When these corrections are applied to partition predictions, the resulting distribution predictions are found to correlate more strongly with experimental results, than those predictions made without the corrections. The results of the underlying molecular mechanics (MM) free energy simulations, as well as QM/MM multi-scale free energy results are discussed in a companion paper in the same issue [38]. The vast majority of the data in this work were generated in a blind fashion, before the conclusion of the SAMPL5 challenge, the exceptions being the inclusion of additional protomeric states of molecule 83 and additional dimerization states of molecule 50. These additional results are discussed in the body of this text, and do not appear in any tabulated results.

Fig. 1
figure 1

Chemical structures of the molecules did not deviate significantly from their reference states (\({<}0.01\) kcal mol\(^{-1}\))

Full size image
Fig. 2
figure 2

Chemical structures of the molecules that were determined to have multiple protomeric states

Full size image

Methods

Free energy methods

We will first predict the partition coefficients, \(\log P_{\text{chex}}\), by calculating the transfer free energy from cyclohexane to water, \({\Delta } G^{{\text{chex}} \rightarrow {\text{aq}}} = {\Delta } G^{*}_{\text{aq}} - {\Delta } G^{*}_{\text{chex}}\), for the reference states of the molecules in the challenge, as they were provided by D3R. Here, the “\(*\)” denotes the standard state of 1 mol L\(^{-1}\), and will be implied for the rest of this work. The most straightforward approach for estimating the free energy difference between a sampled state i and an unsampled state j is by application of Zwanzig’s equation [80]. This approach is used to obtain the free energy difference by the following

$${\Delta } G^{i \rightarrow j} = - \beta ^{-1} \ln \langle \exp [-\beta (U_j - U_i) ] \rangle _i,$$
(4)

where \(\beta ^{-1} = k_{\text{B}} T\) is the thermodynamic temperature, and \(U_i\) is the potential energy of a configuration evaluated using the indicated Hamiltonian, and the angular brackets indicate an ensemble average over state i. In principle this approach can be used to obtain a free energy value from an expensive QM based potential energy surface, using an ensemble generated using a cheaper MM based force field. This strategy is preferable to obtaining a free energy directly from ab initio MD, which would be prohibitively expensive. The accuracy of this approach is strictly limited by the similarity between the QM and the MM potential energy surfaces, as well as by the system size. Because of the presence of numeric instabilities in this method, alternative approaches are often preferable [5, 12, 17, 20, 23, 26, 30, 31, 33, 42, 54, 56, 60, 62, 63].

By drawing configurations from both states i and j, one can obtain the minimum variance estimate between these states by applying Bennett’s Acceptance Ratio (BAR) [6].

$${\Delta } G^{i \rightarrow j} = - \beta ^{-1} \ln \left( {\frac{\langle f(\beta [U_i - U_j +C]) \rangle _j}{\langle f(\beta [U_j - U_i -C]) \rangle _i}}\right) + C$$
(5)

where f is the Fermi function

$$f(x) = {\frac{1}{1+ \exp (x)}}$$
(6)

and C is a constant. An iterative solution is obtained, such that the ratio in Eq. 5 converges to unity. BAR is very commonly applied to studying free energy changes in chemical processes. More recently, a multistate variant has been derived [64], and it should be adopted when simultaneously considering the free energy differences between more than two states, such as in a chain of states during an alchemical transformation process. One strict disadvantage of using BAR is that it requires configurations to be drawn from both states i and j. This can make direct application of BAR to QM based calculation too computationally demanding.

Similar to the Zwanzig equation, we can use the non-Boltzmann Bennett method to estimate the free energy of an unsampled state i by using configurations drawn from a sampled state \(i^{\prime }\). This is accomplished by biasing the sampled states \(i^{\prime }\) and \(j^{\prime }\) using the potential energy difference between i and \(i^{\prime }\) by the following function.

$$V^{\text{b}}_{i} = U_{i^{\prime }} - U_{i}.$$
(7)

The correct ensemble averages in the unsampled states i and j are then recovered from the biased states by applying Torrie and Valleau’s relationship [71] to calculate the unbiased ensemble average, \(\langle X \rangle _i\), from configurations taken from a biased state \(i^{\prime }\).

$$\langle X \rangle _i = {\frac{ \left\langle X \exp \left( \beta V^{\text{b}} _i \right) \right\rangle _{i^{\prime }} }{ \left\langle \exp \left( \beta V^{\text{b}} _i\right) \right\rangle _{i^{\prime }}} }$$
(8)

By combining Eqs. 5 and 8 one obtains the NBB equation, allowing us to estimate the free energy difference between two unsampled states i and j, that are typically too expensive to explicitly sample.

$${\Delta } G^{i \rightarrow j} = - \beta ^{-1} \ln \left( {\frac{\langle f(\beta [U_i - U_j +C]) \exp ( \beta V^{\text{b}} _j ) \rangle _{j^{\prime }} \langle \exp ( \beta V^{\text{b}} _i ) \rangle _{i^{\prime }} }{\langle f(\beta [U_j - U_i -C]) \exp ( \beta V^{\text{b}} _i ) \rangle _{i^{\prime }} \langle \exp ( \beta V^{\text{b}} _j ) \rangle _{j^{\prime }} }} \right) + C$$
(9)

MD simulation

All MD simulations were carried out using the PERT module [10] of the CHARMM simulation package [9, 10] and the CHARMM General Force Field (CGenFF) for organic molecules. [73] The aqueous phase was modeled with 1906 TIP3P water molecules [34] and six pairs of sodium and chlorine ions, to approximately reproduce the ionic strength of the reported experimental conditions (\({\text{pH}}\)  7.4, 136 mM NaCl, 2.6 mM KCl, 7 mM \({\text{Na}}_3{\text{PO}}_4\), 1.46 mM \({\text{KH}}_2{\text{PO}}_4\), 0.27 M DMSO and 0.18 M acetonitrile). The cubic simulation boxes were pre-equilibrated with 0.5 ns of constant pressure dynamics, resulting in unit cells with edges varying between 38.55 and 38.75 Å in length. The apolar phase was modeled with 337 cyclohexane molecules and cubic box sizes with edges varying from 39.93 to 40.18 Å in length. Long range electrostatics were represented using smooth particle mesh Ewald summation [14], while Lennard–Jones interactions used a switching window at 10 Å, before being truncated at 12 Å. A Nosé-Hoover thermostat [28] maintained the canonical ensemble during the 0.5 ns equilibration runs, and during the 5 ns production runs. All simulations used a 1 fs timestep and SHAKE constraints on all hydrogen valence terms. Geometric configurations were saved every 1000 steps for later analysis and post-processing.

Transfer free energies were calculated by turning off all non-bonded solute interactions, both in the cyclohexane and the aqueous phases. This alchemical mutation was carried out in five steps. In step 1, the charges on the cyclohexane phase solute were decremented to zero over six states (\(\lambda = 0.00, 0.25, 0.50, 0.75, 0.90\) and 1.00). We refer to this process as “uncharging”. In step 2, we decremented the Lennard-Jones interactions in the gas phase over 24 equidistant states (\(\lambda = 0, {1}/{23}, \ldots , {22}/{23}, 1\)). We refer to this process as “vanishing”. For molecules 65, 83 and 92 an additional state at \(\lambda = 0.022\) was used to achieve convergence as these are the largest and most flexible molecules. In step 3, we transfer the non-interacting ligand, \({\text{A}}^{({\text{n}},\varnothing )}\), from the cyclohexane to the aqueous phase. The free energy of this process is equivalent to zero. Step 4 and step 5 negate the vanishing process and uncharging processes, respectively, in the aqueous phase, using the same alchemical scheme employed in the cyclohexane phase. The alchemical scheme is summarized in Eq. 10,

$${\text{A}}^{(+,{\text{LJ}})}_{\text{chex}} \mathop{\rightarrow}\limits^{{\Delta} G_1} {\text{A}}^{({\text{n}},{\text{LJ}})}_{\text{chex}} \mathop{\rightarrow}\limits^{{\Delta } G_2} {\text{A}}^{({\text{n}},\varnothing )}_{\text{chex}} \mathop{\rightarrow}\limits^{{\Delta } G_3} {\text{A}}^{({\text{n}},\varnothing )}_{\text{a}q} \mathop{\rightarrow}\limits^{{\Delta } G_4} {\text{A}}^{({\text{n}},{\text{LJ}})}_{\text{aq}} \mathop{\rightarrow}\limits^{{\Delta } G_5} {\text{A}}^{(+,{\text{LJ}})}_{\text{aq}},$$
(10)

where “+” denotes the fully-charged states, and “n” denotes uncharged states.

To enhance sampling, \(\lambda\)-Hamiltonian Replica Exchange [67, 68] was used to attempt exchanges between neighboring \(\lambda\)-states every 1000 steps. Because these \(\lambda\)-states are already required for the underlying BAR free energy calculation, multiplexing the alchemical states together via replica exchange provides accelerated convergence, for marginal cost. Soft-core potentials were used to avoid the endpoint problem [7, 76].

QM calculations

All QM calculations in this work were performed using Gaussian 09 [21]. Transfer free energies were calculated by using a standard QM optimization approach. To calculate QM based partition coefficients, We used an “adiabatic” protocol at the M06-2X/6-31+G(d) level of theory [78, 79] with the SMD implicit solvent [50, 51, 59]. In this scheme, geometry optimizations are carried out in both the cyclohexane and aqueous phases. Next, the Hessian matrices are computed for both phases, and are used to compute the thermal corrections (to 298.15 K) for each molecule in the harmonic limit. Finally, a single point calculation (SPC) was computed on the static geometries using a larger (6-311++G(d,p)) basis set, in both phases, to attempt to further improve the computed transfer free energies, and to explore the efficacy of the 6-311++G(d,p) basis set. All QM optimizations were performed with “Tight” wave function and geometry convergence criteria and by using“UltraFine” numerical quadrature as required by M06-2X.

Due to the large size of molecule 83, QM optimizations on this ligand instead used the cheaper BLYP/6-31G(d) [4, 44, 53] method in conjunction with the SMD implicit solvent We estimated the transfer free energy as the difference of vertical solvation free energies from the gas phase into the appropriate bulk phase. Specifically, this was calculated as the hydration free energy less the solvation free energy in cyclohexane. The default options for wavefunction and geometric convergence, as well as default numerical quadrature were also used to speed up the calculations. Harmonic entropy contributions were ignored, as the frequency calculations were too expensive. Some of our previous work [37] has indicated the effectiveness of the BLYP functional for HFE predictions, despite its simplicity (and significantly reduced cost) with respect to M06-2X.

QM-NBB calculations

We also estimated the transfer free energies using NBB combined with two different QM methods: M06-2X/6-31+G(d) and OLYP/DZPFootnote 1 [16, 25, 27, 44, 53]. In this approach, configurations are drawn from the explicit solvent MD calculations, the explicit solvent is removed and energies are computed using single point QM calculations with the SMD implicit solvent. Because the solvent degrees of freedom are treated implicitly, there now exists sufficient overlap, with NBB biasing, to connect the cyclohexane state to the aqueous state directly. In this case 4N QM calculations are required, where N is the number of configurations drawn from the two chemical states, and the NBB equation simplifies to the following.

$$V^{\text{b}}_{i} = U_{i, {\text{MM}}} - U_{i, {\text{QM}}}$$
(11)
$${\Delta } G^{{\text{chex}} \rightarrow {\text{aq}}} _{\text{QM}} = C + \beta ^{-1} \ln \left( {\frac{\langle f(\beta [U_{\text{chex,QM}} - U_{\text{aq,QM}} +C]) \exp ( \beta V^{\text{b}} _{\text{aq}} ) \rangle _{\text{aq,MM}} \langle \exp ( \beta V^{\text{b}} _{\text{chex}} ) \rangle _{\text{chex,MM}} }{\langle f(\beta [U_{\text{aq,QM}} - U_{\text{chex,QM}} -C]) \exp ( \beta V^{\text{b}} _{\text{chex}} ) \rangle _{\text{chex,MM}} \langle \exp ( \beta V^{\text{b}} _{\text{aq}} ) \rangle _{\text{aq,MM}} }} \right)$$
(12)

While this approach requires a large number of single point QM calculations, \(4 \times 5000\) per molecule in this study, these costs can be mitigated by the use of looser wave function convergence criteria and coarser numerical quadrature than was was used for the analogous QM optimization calculations. This increased performance ca. fivefold and incurred a loss of \({<}0.005\) kcal mol\(^{-1}\) in precision. These calculations also have the advantage of being “embarrassingly” parallel, allowing us to efficiently use any and all available computer resources, especially older marginal hardware with poor networking capabilities.

Protomer and \({\text{p}}K_{\text{a}}\) corrections

Because the goal of the SAMPL5 challenge is to predict the distribution coefficients between cyclohexane and water, rather than the partition coefficients, we must incorporate contributions from states that significantly deviate from the neutral reference structures. Using QM based \({\text{p}}K_{\text{a}}\) calculations [11, 49], we will account for populations of the acidic and basic ligands in their conjugate forms (\({\Delta } G_{{\text{p}}K_{\text{a}}}\)). Our corrections will also address the presence of protomers (\({\Delta } G_{\text{taut}}\)). While our submissions did not include corrections for the effects of dimerization (\({\Delta } G_{\text{dimer}}\)) or water dragging (\({\Delta } G_{\mu {\text{solv}}}\)) [18, 19], we will demonstrate that ignoring these phenomena may diminish the accuracy of distribution predictions as well.

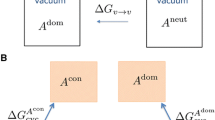
Our \({\text{p}}K_{\text{a}}\) calculations used both an “absolute” and a “relative” protocol [11, 49]. In the absolute protocol we use the usual thermocycle (Fig. 3) to obtain an expression for the free energy of deprotonating \({\text{AH}}^{+}\), in the aqueous phase. Values for \(G({\text{AH}}^{+}_{\text{aq}})\) and \(G({\text{A}}_{\text{aq}})\) are obtained directly from the QM calculations. The value of \(G({\text{H}}^{+}_{\text{gas}})\) is analytic [52], while \({\Delta } G_{\text{solv}}({\text{H}}^{+})\) is experimentally determined [69]. A final factor of \(R T \ln (24.46)\) is also included to account for change of standard state from 1 atm L\(^{-1}\), denoted “\(\circ\)”, in the gas phase to 1 mol L\(^{-1}\) in the aqueous phase. Physically, this term corresponds to the loss of entropy when compressing an ideal gas from 1 to 24.46 atm (1 M), and is 1.89 kcal mol\(^{-1}\) at 298.15 K. Errors from the QM calculation of hydrating the charged ligand and uncertainties associated with the experimental value of hydrating a free proton (\({\Delta } G_{\text{solv}}({\text{H}}^{+}) = -265.9\) kcal mol\(^{-1}\)) [69], are thought to limit the accuracy of the absolute scheme [11]. Once the quantity \({\Delta } G_{\text{aq}}\) has been obtained, it can be readily converted into a \({\text{p}}K_{\text{a}}\) value using Eq. 13, where \(R = k_{\text{B}}/ N_{\text{A}}\) is the usual gas constant.

Fig. 3
figure 3

The thermodynamic cycle used for absolute \({\text{p}}K_{\text{a}}\) calculations in this work

Full size image
$${\Delta } G_{\text{aq}} = {\text{p}}K_{\text{a}} R T \ln (10)$$
(13)

Alternatively, relative \({\text{p}}K_{\text{a}}\) corrections may be preferable (Eq. 14), as the two main sources of error stated above are explicitly removed. The correctness of relative \({\text{p}}K_{\text{a}}\) calculations instead depends upon the choice of an appropriate analog ligand, L, and the availability of reliable experimental data, \({\text{p}}K^{\text{exp}}_{\text{a}}\), obtained under conditions (temperature, concentration and ionic strength) mirroring those for the system of interest. If any of these conditions are not sufficiently met, the relative \({\text{p}}K_{\text{a}}\) calculations can vastly underperform their absolute counterparts. For more information about the specific analogs used in this work, please see Table 3 and Figure S1.

$${\text{p}}K^{\text{rel}}_{\text{a}} ({\text{AH}}^{+}) = {\text{p}}K^{\text{exp}}_{\text{a}} ({\text{LH}}^{+}) + \left[ {\Delta } G^{*}_{\text{aq}} ({\text{AH}}^{+}) - {\Delta } G^{*}_{\text{aq}} ({\text{LH}}^{+}) \right] / \left[ RT \ln (10) \right]$$
(14)

Both \({\text{p}}K_{\text{a}}\) schemes can be combined with either adiabatic or vertical hydration free energy (HFE) calculations from QM. The adiabatic scheme is as described above. In the the vertical solvation scheme, gas phase optimized geometries optimized at the M06-2X/6-31+G(d) level of theory are used for a single point energy calculation in the aqueous phase at the same level of theory in the SMD implicit solvent. This approach neglects solvent relaxation effects during solvation process and may not be appropriate for some of the larger more flexible molecules in the SAMPL5 data set. A simple combination of these various approaches yields the four total \({\text{p}}K_{\text{a}}\) correction schemes we used in our submissions. Once we calculated the \({\text{p}}K_{\text{a}}\) values from our various approaches, we obtained relative populations of conjugate pairs using the Henderson–Hasselbalch equation at \({\text{pH}} =7.4\). These populations are then converted into free energy corrections (\({\Delta } G_{{\text{p}}K_{\text{a}} }\)) from the neutral reference state.

Other corrections, such as \({\Delta } G_{\text{taut}}\), can be obtained by appropriately combining Eqs. 1 and 3. We then cast the difference between QM calculated \(\log P_k\) and \(\log D_k\) values as a free energy correction (Eq. 15) from the reference transfer free energy, to a transfer free energy that has additional states included to model the correction of interest. This correction, originally derived from QM calculations, may then be applied to a transfer free energy obtained from any method of choice (Eq. 16).

$$\log D_{\text{QM}}= \log P_{\text{QM}} + {\frac{ {\Delta } G_{\text{corr}}}{k_{\text{B}} T \ln (10)}}$$
(15)
$$\log P_{\text{chex}}= \left[ {{\Delta }} G^{{\text{chex}}\rightarrow{\text{aq}}} + {{\Delta }} G_{\text{corr}} \right] / [k_{\text{B}} T \ln (10)]$$
(16)

Results and discussion

In this section, individual and collective descriptors, such as RMSD, of partition and distribution coefficients will be given in logarithmic units, which are dimensionless, and thus will not be explicitly listed. These results can be expressed as free energies using the conversion \(1 \log = 1.36\) kcal mol\(^{-1}\), at \(25~^{\circ }{\text{C}}\). When comparing predictions with an experiment, a “−” sign indicates that the prediction is more hydrophilic than experiment, while a “+” indicates that our prediction is too hydrophobic.

Being one of the most popular and effective quantum chemistry methods in use today, the M06-2X/6-31+G(d)/SMD level of theory yielded \(\log P_{\text{chex}}\) predictions that served as a good reference point by which we could evaluate the accuracy and efficiency of the rest of our submissions to the SAMPL5 challenge. When combined with the vertical solvation protocol (the adiabatic protocol performs similarly, submission 28), these predictions agreed relatively well with experiment, sixth overall (submission 27, RMSD = 2.58), but correlated poorly with experiment (Kendall’s \(\tau = 0.46\)). While we chose to include both frequency and single point corrections with a triple-\(\zeta\) basis set, with our adiabatic protocol, neither of these corrections changed the collective behavior of our predictions significantly (Figure S2). The most significant outlying result, by far, is for 83. We did not identify the correct protomeric state for this molecule in either the cyclohexane or aqueous phases. Using the incorrect protomer as the basis for our predictions, our value for \(\log P_{\text{chex}}({\mathbf{83}})\) is too hydrophilic by 12.45. The results from these submissions are explicitly tabulated in Table 1.

Table 1 Predicted values for partition coefficients using the various QM methods presented in this work, in units of \(\log {\text{P}}\), as they were submitted to the challenge
Full size table

After consulting with other participants at the D3R meeting, and then identifying more stable protomers in both phases, our predicted partition value is in much better agreement with experiment, but is still far too hydrophilic \({\Delta }_{\text{exp}} = -7.11\). The RMSD for this submission is also significantly reduced to 2.25 units by using the proper tautomers for 83, now ranking it amongst the best submissions by RMSD. The correlation with experiment is still very poor however, and is significantly worse than the result obtained by the top performing COSMO-RS submission (submission 16, \({\text{RMSD}} = 2.1 \pm 0.2\), \(\tau = 0.73 \pm 0.04\)) [36, 35]. The extreme sensitivity of these results to the inclusion of two additional protomers for a single molecule in the data set, dramatically underscores the difficult nature of these calculations.

While a detailed analysis of the results from the underlying MM free energy simulations are discussed in a companion paper to this work, [38] it is important to briefly introduce and discuss them. Running the simulations using reference states where all protonizable groups are neutral, and protomers are incorrectly assigned for at least three molecules (50, 56 and 83), yields extremely poor results. The CGenFF fixed charge force field, in combination with the BAR free energy estimator, provides partition predictions that significantly deviate from experiment (submission 38, \({\text{RMSD}} = 5.6 \pm 0.4\), \(\tau = 0.25 \pm 0.08\)). Applying our corrections based on absolute \({\text{p}}K_{\text{a}}\) calculations (Table 3) and adiabatic solvation free energy calculations, improves this result dramatically (Fig. 4), reducing the deviation from experiment and increasing the correlation (submission 10, \({\text{RMSD}} = 3.14\), \(\tau = 0.49\)).

Fig. 4
figure 4

Our partition estimations from MM BAR (submission 38) plotted against experiment. We have applied our QM based free energy corrections (adiabatic/absolute scheme, submission 10), shifting the predicted values towards more hydrophilic values. These corrections account for multiple protomeric states and for ligand ionization due to the presence of protonizable groups. These corrections substantially reduce the RMSD and increase the correlation of these predictions with respect to experimentally determined values

Full size image

The predicted partition coefficients (Table 1) using the QM-NBB free energy estimator combined with the OLYP/DZP level of theory had a relatively low deviation from experiment (submission 02, \({\text{RMSD}} = 2.3 \pm 0.3\), \(\tau = 0.48 \pm 0.07\)), ranking second by RMSD, but a relatively mediocre correlation (Fig. 5). After applying our free energy corrections based on absolute \({\text{p}}K_{\text{a}}\) calculations and adiabatic solvation free energy, the resulting distribution coefficients deviate further from experiment, however the correlation with experiment increases (submission 54, \({\text{RMSD}} = 2.68\), \(\tau = 0.53\)). While we did not address dimerization in our SAMPL5 submissions, our subsequent analysis indicated that these effects can be substantial. For example, molecule 50 will likely dimerize in the apolar phase, significantly decreasing its lipophobicity. Similarly, for molecule 74, the water dragging effect may diminish its lipophobicity as well, as its many alcohol groups can strongly coordinate a water molecule. Similarly the effect of polar impurities in the apolar phase was not investigated either. Our QM-NBB calculations using M06-2X did not perform significantly differently from the analogous OLYP calculations. This is an advantageous result from an efficiency perspective, as OLYP is a pure functional, and does not have a kinetic energy density term, nor a Hartree–Fock exchange, making it significantly cheaper than M06-2X. However, this result is also disappointing, because it closes an obvious path for trivially improving the quality of partition predictions by improving the quality of our QM functional.

Fig. 5
figure 5

Partition coefficient estimations from our QM-NBB OLYP/DZP free energy calculations (left, submission 02). After application of our free energy corrections (adiabatic/absolute scheme, the resulting distribution coefficients correlate more strongly with experiment, but are significantly too hydrophilic, and systematically overestimate the hydrophilicity (right, submission 54)

Full size image

The quality of \({\text{p}}K^{\text{rel}}_{\text{a}}\) calculations (Table 2) is exquisitely dependent upon the choice of analog molecule (Table 3). In many cases, an obvious choice will present itself, and the resulting \({\text{p}}K^{\text{rel}}_{\text{a}}\) calculation is likely to be more accurate than its absolute analog. In other cases, choosing an appropriate chemical analog will be difficult or impossible. One example is the acidic phenolic hydrogen in 17. Phenol is a poor choice of analog for this system, because this proton is stabilized by an intramolecular hydrogen bond with the neighboring basic heterocyclic nitrogen. By directly comparing the \({\text{p}}K^{\text{rel}}_{\text{a}}\) and \({\text{p}}K^{\text{abs}}_{\text{a}}\) predictions (Fig. 6), we may be able to blindly assess the quality of our free energy corrections without any a priori knowledge of the distribution coefficients.

Table 2 The original free energy corrections from reference to equilibrium conditions using the various solvation and \({\text{p}}K_{\text{a}}\) schemes, as submitted to the SAMPL5 challenge
Full size table
Table 3 Chemical names and experimental \({\text{p}}K_{\text{a}}\) values for analog molecules used in relative \({\text{p}}K_{\text{a}}\) calculation schemes
Full size table
Fig. 6
figure 6

Differences in free energy corrections calculated using the two different \({\text{p}}K_{\text{a}}\) calculation schemes, both of the free energy corrections in this figure used the adiabatic solvation protocol. When the two sets of corrections strongly deviate, it may be a sign of poor analog selection in the \({\text{p}}K^{\text{rel}}_{\text{a}}\) calculations

Full size image

Conclusions

The OLYP/DZP QM method with SMD implicit solvation model performed very strongly relative to other submissions when combined with the NBB free energy estimator (submission 02). Overall, this submission ranked second by RMSD, but had only a mediocre correlation as estimated by Kendall’s \(\tau\). While this particular combination of density functional and basis set is unusual, this protocol [58] was designed using HFE data from the SAMPL4 challenge [55] as a target. The cost of the QM-NBB approach is relatively high relative to simple QM optimization, due to the large number of configurations that must be evaluated (\({\approx }4 \times 5000\)) for each molecule. This cost is mitigated somewhat by the embarrassingly parallel nature of these energy evaluations.

The M06-2X/6-31+G(d) QM optimization calculations with SMD implicit solvent also performed well, ranking sixth overall by RMSD (submission 27). This submission was made because the required QM calculations were a strict subset of the calculations required for our \({\text{p}}K_{\text{a}}\) predictions. The M06-2X and SMD approaches are ubiquitous in the literature, [50, 59] and serves as a good “control” to help us understand how our more complicated and more expensive free energy methods compare against other popular approaches. These predictions also had mediocre correlation as estimated by Kendall’s \(\tau\).

By including our \({\text{p}}K_{\text{a}}\) and protomeric corrections with our partition predictions (specifically our corrections based on adiabatic solvation free energies and an absolute \({\text{p}}K_{\text{a}}\) scheme), our resulting distribution predictions enjoyed increased correlation for all tested methods. Unfortunately, in many of our best performing methods, such as QM-NBB with OLYP/DZP, our corrections increased our RMSD values. This occurred because our \(\log P_{\text{chex}}\) predictions were already too hydrophilic relative to experiment. Our corrections, as submitted to the SAMPL5 challenge, exacerbated this problem, further increasing the hydrophilicity of our predictions, because our corrections summed over additional aqueous phase states, further tipping the balance of our predictions towards the hydrophilic.

Our \({\text{p}}K_{\text{a}}\) corrections indicated that some of our reference states, under which our MD simulations were performed, were very far from equilibrium. Molecule 83 for example, has a protomer in the apolar phase that is ca. 10 kcal mol\(^{-1}\) from the state we modeled with MD. Differences this large, cannot likely be corrected for using QM optimization calculations on one configuration.

Our \({\text{p}}K_{\text{a}}\) corrections were performed using the QM optimization protocol, which, while successful overall, suffers from over representing the global minimum structure, as conformational entropy of neighboring low-lying configurations is neglected. This effect should be particularly troublesome for larger molecules that were very common in this challenge, as well as for the many ionic conjugates that were ubiquitous in this data set. The accuracy of our \({\text{p}}K_{\text{a}}\) corrections could likely be improved by using a NBB scheme here as well. This approach will be the subject of follow up work.