Simultaneous Quantum Transmission and Teleportation of Unknown Photons Using Intra- and Inter-particle Entanglement Controlled-NOT Gates via Cross-Kerr Nonlinearity and P-Homodyne Measurements

Abstract

We propose an arbitrary controlled-unitary (CU) gate and a simultaneous quantum transmission and teleportation (SQTTP) scheme. The proposed CU gate utilizes photons with cross-Kerr nonlinearities (XKNLs), coherent superposition states (CSSs) and P-homodyne detectors and consists of the consecutive operation of a controlled-path (C-path) gate and a gathering-path (G-path) gate It is almost deterministic and feasible with current technology when strong CSSs and weak XKNLs are employed. Compared with the existing multi-qubit or controlled gates, which utilize XKNLs, coherent states, and X-homodyne detectors, the proposed CU gate can increase the feasibility of experimental realization, and enhance the robustness against the decoherence effect. Based on the CU gate, we present a SQTTP scheme that simultaneously transmits and teleports two unknown states of photons between two parties (Alice and Bob) using path-polarization intra-particle hybrid entanglement (IRHE) by transferring only a single photon. Consequently, it is possible to experimentally implement SQTTP with a certain success probability using the proposed CU gate.

1 Introduction

Quantum communication (QC) is a method to transfer information (quantum or classic) from one place to another by using quantum phenomena For this purpose, quantum information processing (QIP) protocols, such as quantum key distribution (QKD), quantum secret sharing (QSS), quantum secure direct communication (QSDC) and quantum teleportation (QTP) [1–16] have been thus far researched. Both the experimental implementation and the efficiency of QCs and QIPs depend on the two main resources of quantum operation and quantum entanglement.

The reliable quantum operations are performed by the realization of multi-qubit gates, such as the arbitrary controlled-unitary (CU) gates. Thus, for the experimental realization of QCs and QIPs with a certain success probability, quantum CU gates play a very important role; accordingly, the deterministic CU gates must be realized with experimental feasibility. Cross-Kerr nonlinearities (XKNLs) have been well studied, both experimentally and theoretically. In principle, the XKNL effect can induce efficient photon interactions with which photonic multi-qubit gates can be implemented, using far fewer physical resources than linear optical schemes [17–19]. Nemoto et al. proposed nearly deterministic controlled gates using an ancilla photon, linear optical elements, and quantum non-demolition (QND) detectors based on weak XKNLs, X-homodyne detectors, and feed-forwards [20]. This indicates that controlled gates can be experimentally realized by the weak XKNL with a large amplitude of the probe beam in a coherent state. In 2009, Lin et al. presented an almost deterministic controlled-path (C-path) gate and probabilistic controlled gates, such as controlled- σ _X (CNOT), Fredkin, Toffoli, and arbitrary CU gates, using XKNLs, coherent states, X-homodyne detectors, feed-forwards and no ancilla photon [21]. Thereafter, similar schemes for implementing photonic multi-qubit gates were developed. QCs and QIPs based on the implementation of multi-qubit gates via weak XKNLs [22–32] have also been investigated.

For a certain success probability, when designing multi-qubit gates using QNDs based on XKNLs, the feasibility of experimental implementation and the robustness against the decoherence effect during the process are two important considerations. The experimental realization of strong XKNLs is still difficult [33], because the nature of the Kerr medium is extremely weak [34]. Therefore, the multi-qubit gates should be implemented using weak XKNLs which are as weak as possible. However, as described in Ref. [20], for the condition α 𝜃 ² ≫ 1, we must use the extremely strong amplitude of the probe beam (coherent state); nevertheless, the decoherence effect between the probe beam (coherent state) and the photon is inevitable in a practice situation [35]. Consequently, for the deterministic distinguishability between the shifted and non-shifted phases in the coherent state, the devised multi-qubit gates must satisfy the requirements of using weak XKNLs and optimal (relatively smaller) amplitude of the coherent state to achieve the feasibility of experimental implementation and the robustness against the decoherence effect.

Regarding another resource, quantum entanglement, some QCs [1–12] have exploited the properties of inter-particle entanglement (IEE), which correlates identical types of degrees of freedom – for example, the spin or the polarization – of two or more particles. Both the experimental implementation and the efficiency of QCs and QIPs also depend on the experimental ease of implementation and the efficient maintenance of the entangled states. Therefore, to successfully achieve both experimental implementation and efficiency, various types of entanglement must be investigated.

Hybrid entanglement is the entanglement between different types of degrees of freedom (such as path, polarization, linear momentum, and spin) [36, 37] and intra-particle hybrid entanglement (IRHE) is hybrid entanglement within a single particle. IRHE – entangling degrees of freedom such as the polarization and the linear momentum [38, 39] or the polarization and the angular momentum [40] of a single photon or the path and the spin [41] of a single neutron – has been demonstrated theoretically and experimentally [38–43]. Since IRHE is correlated within a single particle, the technique utilizing this type of entanglement as a resource for an information processing scheme consumes fewer resources (photons) than the technique utilizing IEE.

Recently, researchers have shown that the path-spin intra-particle hybrid (IRH) entangled state of a single spin-1/2 particle could be transformed to the spin-spin IEE of two particles (QIP) [13]. Furthermore, QCs using IRHE have been suggested for QKD [14], unidirectional quantum teleportation (UQTP) [15], and unidirectional quantum transmission (UQT) [16] Another protocol for QC was recently proposed by Heo et al. [16] whose work achieved UQT of an unknown state of photon using a single photon’s path-polarization IRHE. Unlike the aforementioned studies [13, 15, 24] that utilized a BS and an SF to generate path-spin IRH entangled states, the protocol uses only a single polarizing beam splitter (PBS) to generate the entangled states. After passing the PBS, the unknown state of photon is transformed into a path-polarization IRH entangled state and is later reconstructed by Bob, as in Ref. [16]. Therefore the scheme using PBS in Ref. [16] uses fewer resources – number of photons and CNOT operations – to transmit or teleport an unknown state of photon (unidirectional QC) than the scheme in Ref. [15].

In this paper, we first propose a deterministic and experimentally feasible CU gate, which is composed of the consecutive operations of a C-path gate and a gathering-path (G-path) gate via weak XKNLs, coherent superposition states (CSSs), P-homodyne detectors, and feed-forwards. Comparing the existing multi-qubit gates [20–26] using XKNLs, coherent states and X-homodyne detectors, either the nonlinear phase shift 𝜃 or the amplitude of the coherent state α required in our CU gate will be relatively reduced while maintaining the same error probability. Thus, when this CU gate is experimentally implemented, it improves the feasibility and reduces the decoherence effect. Subsequently, we present a simultaneous quantum transmission and teleportation (SQTTP) scheme for two unknown states of photons exchanged between Alice and Bob by transmitting only one photon, using both IRHE and IEE via linear optical devices and the proposed CU gates.

This paper is organized as follows. In Section 2, we present a CU gate performed by the consecutive operation of a C-path gate and a G-path gate via XKNLs, CSSs, P-homodyne detectors, and feed-forwards. We demonstrate that this gate is almost deterministic using weak XKNLs. Furthermore, compared to the existing multi-qubit gates [20–26] using coherent states and X-homodyne detectors, our CU gate improves the feasibility of the experimental implementation and enhances the robustness against the decoherence effect using CSSs and P-homodyne detectors. In Section 3, we propose an SQTTP scheme that simultaneously transfers and teleports two unknown photons between Alice and Bob using both IRHE and IEE, by transferring only a single photon via optical elements, such as a polarizing beam splitter (PBS), two beam splitters (BSs), two spin flippers (SFs), polarizing detectors (P-Ds), and three CNOT operations by CU gates, as described in Section 2. Finally, we discuss the success probability and experimental implementation of the proposed CU gate and SQTTP in Section 4.

2 CU Gate with XKNLs, CSSs, P-Homodyne Detectors and Feed-Forwards

Let us consider two types of photon polarization: linear-polarization ($\left |H\right .\rangle$ is horizontal and $\left |V\right .\rangle$ is vertical) and circular-polarization ($\left |R\right .\rangle$ is right- and $\left |L\right .\rangle$ is left-circular). The relationships between the two types are given by:

$$ \begin{array}{l} \left|H\right.\rangle \equiv \left|+\right.\rangle =\frac{1}{\sqrt{2}} \left( {\left|R\right.\rangle +\left|L\right.\rangle} \right), \left|V\right.\rangle \equiv i\left|-\right\rangle =\frac{i}{\sqrt{2}} \left( {\left|R\right.\rangle -\left|L\right.\rangle} \right) \\ \left|R\right.\rangle \equiv \left|0\right\rangle =\frac{1}{\sqrt{2}} \left( {\left|H\right.\rangle -i\left|V \right.\rangle} \right), \left|L\right.\rangle \equiv \left|1\right.\rangle =\frac{1}{\sqrt{2}} \left( {\left|H\right.\rangle +i\left|V\right\rangle} \right). \\ \end{array} $$

(1)

Thus, the linearly polarized states correspond to the eigen states of $\sigma _{X} :\left \{ {\left |H\right .\rangle \equiv \left |+\right .\rangle ,\left |V\right .\rangle \equiv i\left |-\right .\rangle } \right \}$ and the circularly polarized states to the eigen states of $\sigma _{Z} :\left \{ {\left |R\right .\rangle \equiv \left |0\right \rangle ,\left |L\right .\rangle \equiv \left |1\right .\rangle } \right \}$ In order to explain the CU gate, we introduce the XKNL. The Hamiltonian of the XKNL has the form

$$ H_{Kerr} =\hslash \chi N_{1} N_{2} , $$

(2)

where N _i is the photon number operator and χ is the strength of nonlinearity of the Kerr medium. Let us assume that $\left |n\right .\rangle _{i}$ represents a state of n photons (signal), and the probe beam is in a coherent state $\left |\alpha \right .\rangle _{j}$. After passing through the Kerr medium, the state of the signal-probe system is given as follows:

$$ U_{Kerr} \left|n\right.\rangle_{1} \left|\alpha\right.\rangle_{2} =e^{i\theta N_{1} N_{2}} \left|n\right.\rangle_{1} \left|\alpha\right.\rangle_{2} =\left|n\right.\rangle_{1} \left|\alpha e^{in\theta} \right.\rangle_{2}, $$

(3)

where 𝜃 = χ t and t is the interaction time. During this interaction the signal photon is unaffected, and the phase of the probe beam $\left |\alpha \right .\rangle _{2}$ is shifted to $\left |\alpha e^{in\theta }\right .\rangle _{2}$ according to the number of photons n in the state $\left |n\right .\rangle _{1}$.

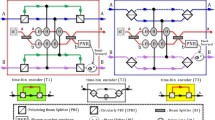
Now, we propose a deterministic CU gate that is composed of the consecutive operation of a C-path gate and a G-path gate, an arbitrary unitary operator U, XKNLs, CSSs, P-homodyne detectors feed-forwards, and linear optical elements such as PBSs BSs and wave-plates (WPs), as shown in Fig. 1. Suppose that the initial state of two photons is

$$ \left|\varphi\right.\rangle_{\text{int}} =\alpha \left|R\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|R\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} +\gamma \left|L\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\delta \left|L\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} , $$

(4)

where the superscripts describe photon paths and the subscripts c and t represent the control and target photon, respectively. Consequently, the final state $\left |{\Psi }\right .\rangle _{\text {fin}}$ which is performed by the CU gate will be

$$ \left|{\Psi}\right.\rangle_{\text{fin}} =\alpha \left|R\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|R\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} +\gamma \left|L\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{4}} \right)+\delta \left|L\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{4}} \right) $$

(5)

If U is σ _X , then the CU gate will be a CNOT gate: $\left |{\Psi }\right .\rangle _{\text {fin}} =\alpha \left |R\right .\rangle _{c}^{1} \left |R\right .\rangle _{t}^{4} +\beta \left |R\right .\rangle _{c}^{1} \left |L\right .\rangle _{t}^{4} +\gamma \left |L\right .\rangle _{c}^{1} \left |L\right .\rangle _{t}^{4} +\delta \left |L\right .\rangle _{c}^{1} \left |R\right .\rangle _{t}^{4}$. The probe beam is in a CSS $C\left ({\left |\alpha \right .\rangle +\left |-\alpha \right .\rangle } \right )$ with a normalization factor ${C=1 \left/ \sqrt{2+2e^{-2\alpha^{2}}}\right.}$.

Fig. 1

The CU gate (black box) comprises the consecutive operation of a C-path gate (red box) and a G-path gate (blue box) using XKNLs CSSs, P-homodyne detectors and feed-forwards. The CU gate is composed of three parts, the C-path gate, U operator, and G-path gate. First, in the C-path gate, the two photons (c and t) in the input state induce the controlled phase shifts 𝜃 and −𝜃 in the probe beam (CSS: $C\left ({\left |\alpha \right .\rangle +\left |-\alpha \right .\rangle } \right ))$ by the interaction of XKNLs. Then, we measure the probe beam with the P-homodyne detector, $\left |\mathrm {P}\right .\rangle \left .\langle {\mathrm {P}} \right |$, which projects the CSS to momentum space According to the measurement outcome P of the P-homodyne detector, we determine whether or not to operate the phase shifter ${\Phi } \left ({\mathrm {P}} \right )$ and the path-switch S on the target photon t by feed-forward. After passing the C-path gate, the path of the target photon is split according to the polarization of the control photon. The target photon goes through path 3 (or 4) when the control photon is $\left |H\right .\rangle$ (or $\left |V\right .\rangle )$. In the second step, the unitary operator U on path 4 is applied to the target photon. In the third step of the G-path gate, the XKNLs induce a phase shift 𝜃 in the probe beam (CSS: $C\left ({\left |\alpha \right .\rangle +\left |-\alpha \right .\rangle } \right ))$ according to the target photon t. Finally, to gather the target photon on the split path, we apply the unitary operator −σ _X and the phase shifter ${\Phi }^{\prime }\left ({\mathrm {P}} \right )$ to the control photon and the path-switch S to the target photon via the feed-forward, depending on the measurement outcome of the P-homodyne detector on the probe beam. Consequently, the CU gate performs a controlledunitary operation on the input state

In the C-path gate, (Fig. 1), after the control photon c passes through a WP, which performs like the Hadamard operator: $\left |R\right .\rangle \to \left |H\right .\rangle , \left |L\right .\rangle \to -i\left |V\right .\rangle , \left |H\right .\rangle \to \left |R\right .\rangle , \left |V\right .\rangle \to i\left |L \right .\rangle$, both the control photon c and target photon t pass through a PBS and a BS. When passing through the PBS, $\left |H\right .\rangle$ is transmitted and $\left |V\right .\rangle$ is reflected. The action of 50:50 BS is described by:

$$ a_{U}^{+} \to \frac{1}{\sqrt{2}} \left( {a_{U}^{+} +a_{D}^{+}} \right) , a_{D}^{+} \to \frac{1}{\sqrt{2}} \left( {a_{U}^{+} -a_{D}^{+}} \right), $$

(6)

where $a_{i}^{+}$ is a creation operator of a photon on path i (U is an Up path and D is a Down path). Subsequently, the two photons (c and t) interact with the probe beam in a CSS $C\left ({\left |\alpha \right .\rangle +\left |-\alpha \right .\rangle } \right )$ to introduce the phase shifts 𝜃 and -𝜃 in the Kerr medium as shown in Fig. 1. After passing through the PBS, the photon state is transformed to $\left |\varphi \right .\rangle _{01}$:

$$\begin{array}{@{}rcl@{}} \left|\varphi\right.\rangle_{01} &=&\frac{C}{\sqrt{2}} \left[ \left(\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} \right)\left(\left|\alpha e^{i\theta}\right.\rangle+\left|-\alpha e^{i\theta}\right.\rangle \right)\right.\nonumber\\[2pt]&&+\left. \left(-i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} -i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} \right)\left(\left|\alpha e^{-i\theta}\right.\rangle+\left|-\alpha e^{-i\theta}\right.\rangle \right)\right]\\[2pt]&&+\frac{C}{\sqrt{2}}\left(\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle _{t}^{4} -i\delta \left|V\right.\rangle_{c}^{1}\left|L\right\rangle _{t}^{4} \right)\left(\left|\alpha\right.\rangle \!+\! \left|-\alpha\right.\rangle\right).\end{array} $$

(7)

Then, the probe beam is measured by a P-homodyne detector [30–32] which projects the probe beam to momentum space. When α is real, the projection of $\left |\varphi \right .\rangle _{01}$ onto an eigen state $\left |P\right .\rangle$ of the observable P is given by:

$$\begin{array}{@{}rcl@{}} \left|\varphi\right.\rangle_{\text{P:}CP} &=&\langle\mathrm{P}\left|\varphi\right.\rangle_{01} \\ &=&C\left[s_{0} \cdot \sqrt{2} \cos \left(\alpha \cdot \mathrm{P} \right) \right]\cdot \left[ \alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3}\right.\\ &&-\left.i\gamma \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} -i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} \right] \\ &&+\frac{C}{\sqrt{2}} \left[s_{1 +}\right]\cdot \left[e^{-i\alpha \phi^{+}}\cdot \left(\alpha \left|H\right.\rangle_{c}^{1}\left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} \right)\right.\\ &&\left.+e^{i\alpha \phi^{+}}\cdot \left(-i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} -i\delta \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} \right)\right] \\ &&+\frac{C}{\sqrt{2}} \left[ {s_{1 -}} \right]\cdot \left[ e^{i\alpha \phi^{-}}\cdot \left(\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4}\right)\right.\\ &&+\left.e^{-i\ alpha \phi^{-}}\cdot \left(-i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} -i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} \right) \right], \end{array} $$

(8)

where we used the result $\langle \mathrm{P} \left|\alpha e^{\pm i\theta}\right.\!\rangle \!=\!\frac{1}{\sqrt[4]{2\pi}}\exp \left[{\!-\frac{1}{4}\!\left( {\mathrm{P}\mp\! 2\alpha \sin \theta} \right)^{2}\!-\!i\alpha \cos \theta\!\left( {\mathrm{P}\!\mp\alpha \sin \theta} \right)} \right]$.

$$ s_{0} =\frac{1}{\sqrt[4]{2\pi}}e^{-\frac{1}{4}\left( {\mathrm{P}} \right)^{2}},s_{1 \pm} =\frac{1}{\sqrt[4]{2\pi} }e^{-\frac{1}{4}\left( {\mathrm{P}\mp2\alpha \sin \theta}\right)^{2}}, \phi^{\pm} =\cos \theta \left( {\mathrm{P}\mp\alpha\sin \theta} \right). $$

(9)

In Fig. 2, we plot $s_{0} \cdot \sqrt {2} \left | {\cos \left ({\alpha \cdot \mathrm {P}} \right )} \right |$ (rapid oscillation) and s _1± (Gaussian curve) as a function of the P-homodyne measurement result of (8). These functions have peaks at $-2\alpha \sin \theta$, 0 and $2\alpha \sin \theta$, and the two midpoints between the three functions are $\mathrm {P}_{0 \pm } =\pm \alpha \sin \theta$, as shown in Fig. 2. Assuming that the distances $\left | {2\alpha \sin \theta } \right |$ (between the peak of $s_{0} \cdot \sqrt {2} \cos \left ({\alpha \cdot \mathrm {P}} \right )$ and the peaks of s _1±) and $\left | {4\alpha \sin \theta } \right |$ (between the peaks of s _1±) are sufficiently large, there is little overlap between the three functions. Then, a P-homodyne detector distinguishes the probe beam in the coherent states with a certain probability. If we obtain the measurement result P, which is in the regime of P₀₋ < P < P₀₊, we can construe that the state of the two photons c and t is:

$$ \left|\varphi\right.\rangle_{CP} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} -i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} . $$

(10)

This state $\left |\varphi \right .\rangle _{CP}$ is performed by the C-path operation, which switches path 3 of the target photon t to path 4 if the polarization of the control photon c is $\left |V\right .\rangle$, on the initial state $\left |\varphi \right .\rangle _{\text {int}}$ in (4). On the other hand, if the measurement result P is larger than P₀₊ or smaller than P₀₋, the state of the two photons is given by:

$$ \begin{array}{l} \left|\varphi\right.\rangle_{\text{P} > \text{P}_{0 +}} =e^{-i\alpha \phi^{+}}\cdot \left(\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4}\right)+e^{i\alpha \phi^{+}}\cdot \left(-i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3}-i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3}\right) \\ \left|\varphi\right.\rangle_{\text{P} < \text{P}_{0 -}} =e^{i\alpha \phi^{-}}\cdot \left(\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4}\right)+e^{-i\alpha \phi^{-}}\cdot \left(-i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3}-i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} \right), \end{array} $$

(11)

where the states $\left |\varphi \right .\rangle _{\text {P} > \text {P}_{0 +}}$ and $\left |\varphi \right .\rangle _{\text {P} < \text {P}_{0 -}}$ differ in the global phase. Subsequently, according to the feed-forward, which depends on the measurement result P, the phase shifter ${\Phi } \left ({\mathrm {P}} \right )$ and the path-switch S are performed on the target photon t in the state $\left |\varphi \right .\rangle _{\text {P} > \text {P}_{0 +}} \left ({\left |\varphi \right .\rangle _{\text {P} < \text {P}_{0 -}} } \right )$. The transformed state $\left |\varphi \right .\rangle _{F-F}$ will be:

$$ \begin{array}{l} {\left|\varphi\right.\rangle_{\text{P} > \text{P}_{0 +}} } \\ {\left|\varphi\right.\rangle_{\text{P} < \text{P}_{0 -}} } \\ \end{array} {~}^{\underrightarrow{\quad\text{feed-forward}\quad}} \left|\varphi\right.\rangle_{F-F} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} -i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} , $$

(12)

where the state $\left |\varphi \right .\rangle _{F-F}$ is the same as the state $\left |\varphi \right .\rangle _{CP}$ in (10). Consequently, the state $\left |\varphi \right .\rangle _{\text {P} > \text {P}_{0 +}} \left ({\left |\varphi \right .\rangle _{\text {P} < \text {P}_{0 -}} } \right )$ can be transformed to the state $\left |\varphi \right .\rangle _{CP}$ (the performed C-path operation) using feed-forward. The sum $\left ({P_{error}^{CP}} \right )$ of the error probabilities of the measurement which correspond to the overlap between S ₁₋ and $S_{0} \cdot \sqrt {2} \left | {\cos \left ({\alpha \cdot \mathrm {P}} \right )} \right |$, between S ₁₊ and $S_{0} \cdot \sqrt {2} \left | {\cos \left ({\alpha \cdot \mathrm {P}} \right )} \right |$, or between S ₁₊ and S ₁₋ in (8), is given by:

$$\begin{array}{@{}rcl@{}} P_{error}^{CP} &=&\left| C \right|^{2}\left[ { {\int}_{0}^{\mathrm{P}_{0 +}} {\left( { \left| {s_{1 +}} \right|^{2}+ \left| {s_{1 -}} \right|^{2} } \right)\text{dP}} \text{ + } {\int}_{\mathrm{P}_{0 +} }^{\infty} {\left( {\text{ 2}\left| {s_{0} \cdot \sqrt{2} \cos \left( {\alpha \cdot \mathrm{P}} \right)} \right|^{2}+ \left| {s_{1 -}} \right|^{2} } \right)\text{dP}} } \right] \\ &\approx& \left| C \right|^{2}\cdot \frac{3}{2}\left[ {1-\text{erf}\left( {\frac{2\alpha \sin \theta} {2\sqrt{2}} } \right)} \right]=\frac{3}{4}\left[ {1-\text{erf}\left( {\frac{2\alpha \sin \theta} {2\sqrt{2}} } \right)} \right], \end{array} $$

(13)

where erf(x) is a Gauss error function and $2\alpha \sin \theta$ is the amplitude of the distance between the functions $s_{0} \cdot \sqrt {2} \cos \left ({\alpha \cdot \mathrm {P}} \right )$ and s ₁₋ (or s ₁₊), as shown in Fig. 2. When α is real and ≫1, $\left | C \right |^{2}=1/2$. For the nearly deterministic C-path gate, $P_{error}^{CP}$ is smaller than 10⁻⁶ when $2\alpha \sin \theta \sim 2\alpha \theta >9$. This indicates that if we can choose the amplitude α of the probe beam to be sufficiently large, then the weak XKNL (𝜃 ≪ 1) can be utilized for the C-path gate. Thus, using weak XKNLs, a CSS and a P-homodyne detector with the condition 2α 𝜃 > 9, this C-path gate is nearly deterministic with a certain success probability ($P_{succ}^{CP} =1)$. After passing the C-path, the path of the target photon is split, as shown in (10).

Fig. 2

The probability distribution functions of the measurements of the probe beam in CSS, acquired by a P-homodyne measurement: The blue, black and red functions correspond to S ₁₋, $S_{0} \cdot \sqrt {2} \left | {\cos \left ({\alpha \cdot \mathrm {P}} \right )} \right |$ and S ₁₊, respectively. P₀₊ and P₀₋ are the midpoints of the three peaks

In the second step, the target photon in the state $\left | \right \rangle _{CP}$ (10) passes through an arbitrary unitary operator U on path 4. The transformed state $\left | \right \rangle _{U}$ is represented as:

$$ \left|\varphi\right.\rangle_{U} =\left( U \right)_{t}^{4} \left|\varphi\right.\rangle_{CP} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left(U\left|R\right.\rangle_{t}^{4} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left(U\left|L\right.\rangle_{t}^{4} \right). $$

(14)

For example, if U is σ _X , σ _Z or i σ _Y , then the state $\left | \right \rangle _{U}$ will be given by:

$$ \begin{array}{l} \left|\varphi\right.\rangle_{\sigma_{X}} =\left( {\sigma_{X}} \right)_{t}^{4} \left|\varphi\right.\rangle_{\alpha} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} -i\delta \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} , \\\left|\varphi\right.\rangle_{\sigma_{Z}} =\left( {\sigma_{Z}} \right)_{t}^{4} \left|\varphi\right.\rangle_{\alpha} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +i\delta \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} , \\\left|\varphi\right.\rangle_{i\sigma_{Y}} =\left( {i\sigma_{Y}} \right)_{t}^{4}, \left|\varphi\right.\rangle_{\alpha} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} +i\gamma \left|V\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} -i\delta \left|V\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} , \end{array} $$

(15)

These are the output states of the unitary operation of CNOT, controlled- σ _Z (CZ) or controlled- σ _Y (CY) on the initial state of the two photons (4), respectively. Since the path of the target photon is divided into the two paths 3 and 4 in (14), we use the G-path gate to merge the split path of the target photon to a single path.

In the G-path gate of the third step, as described in Fig. 1, the target photon in $\left |\varphi \right .\rangle _{U}$ passes through a BS. After the CSS $C\left ({\left |\alpha \right .\rangle +\left |-\alpha \right .\rangle } \right )$ is shifted to $C\left ({\left |\alpha e^{-i\theta }\right .\rangle +\left |-\alpha e^{-i\theta }\right .\rangle } \right )$ by the phase shifter, the target photon t induces a controlled phase shift 𝜃 in the probe beam by the interaction of XKNL. Then, the transformed state $\left |{\Psi }\right .\rangle _{01}$ is given by:

$$\begin{array}{@{}rcl@{}} \left|{\Psi}\right.\rangle_{01} &=&\frac{C}{\sqrt{2}} \left[\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4}\right.\\ &&\left.-i\gamma \left|L\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{4}} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left({U\left|L\right.\rangle_{t}^{4}} \right) \right]\left( {\left|\alpha\right.\rangle +\left|-\alpha\right.\rangle} \right) \\ &&+\frac{C}{\sqrt{2}} \left[-\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} -\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3}\right.\\ &&-\left.i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{3}} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{3}} \right) \right]\left( {\left|\alpha e^{-i\theta}\right.\rangle +\left|-\alpha e^{-i\theta}\right.\rangle}\right). \end{array} $$

(16)

Subsequently, the P-homodyne detector measures the probe beam. The projection of $\left |{\Psi }\right .\rangle _{01}$ onto an eigen state $\left |\mathrm {P}\right .\rangle$ of the observable P is given as follows:

$$\begin{array}{@{}rcl@{}} \left|{\Psi}\right.\rangle_{\text{P:}GP} &=&\langle {\mathrm{P}} \left|\psi\right.\rangle_{01} \\ &=&C\left[ {s_{0} \cdot \sqrt{2} \cos \left( {\alpha \cdot \mathrm{P}} \right)} \right]\cdot \left[ \alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right\rangle_{t}^{4} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{4}} \right)\right.\\ &&-\left.i\delta \left|V\right.\rangle_{c}^{1} \left(U\left|L\right.\rangle_{t}^{4} \right) \right] \\ &&+\frac{C}{\sqrt{2}} \left[ {s_{1 +}} \right]\cdot e^{i\alpha \phi^{+}}\cdot \left[ -\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} -\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{3}} \right)\right.\\ &&-\left.i\delta \left|V\right.\rangle_{c}^{1} \left({U\left|L\right.\rangle_{t}^{3}} \right) \right] \\ &&+\frac{C}{\sqrt{2}} \left[ {s_{1 -}} \right]\cdot e^{-i\alpha \phi^{+}}\cdot \left[ -\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3} -\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{3}} \right)\right.\\ &&-i\left.\delta \left|V\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{3}} \right) \right], \end{array} $$

(17)

where s ₀, s _1± and ϕ ⁺ are given in (9). If we obtain the measurement result P, which is in the regime of P₀₋ < P < P₀₊, we can construe that the state of the two photons c and t is:

$$ \left|{\Psi}\right.\rangle_{GP} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{4}} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{4}} \right). $$

(18)

The path of this state $\left |{\Psi }\right .\rangle _{GP}$ is merged with path 4 by the G-path gate. On the other hand, if the measurement result P is larger than P₀₊ or smaller than P₀₋, the state of the two photons is given by:

$$\begin{array}{@{}rcl@{}} \left|{\Psi}\right.\rangle_{\text{P} > \text{P}_{0 +}} =e^{i\alpha \phi^{+}}\cdot \left[ {-\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{3}} -\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{3}} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{3}} \right) \right] \\ \left|{\Psi}\right.\rangle_{\text{P} < \text{P}_{0 -}} =e^{-i\alpha \phi^{+}}\cdot \left[ {-\alpha\left|H\right.\rangle _{c}^{1} \left|R\right.\rangle_{t}^{3}} -\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{3} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{3}} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left( {U\left|L\right.\rangle_{t}^{3}} \right) \right], \end{array} $$

(19)

where the states $\left |{\Psi }\right .\rangle _{\text {P} > \text {P}_{0 +}}$ and $\left |{\Psi }\right .\rangle _{\text {P} < \text {P}_{0-}}$ have different global phases. Subsequently, we perform a −σ _X and the phase shifter ${\Phi }^{\prime }\left ({\mathrm {P}} \right )$ on the control photon c, and the path-switch S on the target photon t in the state $\left |{\Psi }\right .\rangle _{\text {P} > \text {P}_{0 +}} \left ({\left |{\Psi }\right .\rangle _{\text {P} < \text {P}_{0 -}} } \right )$ by feed-forward according to the measurement result P. The transformed state $\left |{\Psi }\right .\rangle _{F-F}$ will be:

$$ \begin{array}{l} \left|{\Psi}\right.\rangle_{\text{P} > \text{P}_{0+}} \\ {\left|{\Psi}\right.\rangle_{\text{P} < \text{P}_{0-}} } \end{array} {~}^{\underrightarrow{\quad\text{feed-forward}\quad}} \left|{\Psi}\right.\rangle_{F-F} =\alpha \left|H\right.\rangle_{c}^{1} \left|R\right.\rangle_{t}^{4} +\beta \left|H\right.\rangle_{c}^{1} \left|L\right.\rangle_{t}^{4} -i\gamma \left|V\right.\rangle_{c}^{1} \left( {U\left|R\right.\rangle_{t}^{4}} \right)-i\delta \left|V\right.\rangle_{c}^{1} \left({U\left|L\right.\rangle_{t}^{4}} \right), $$

(20)

where the state $\left |{\Psi }\right .\rangle _{F-F}$ is the same as the state $\left |{\Psi }\right .\rangle _{GP}$ in (18). Thus, the output state is always the state $\left |{\Psi }\right .\rangle _{GP}$. After passing the control photon c in the state $\left |{\Psi }\right .\rangle _{GP}$ through a WP, we finally obtain the output state $\left |{\Psi } \right .\rangle _{\text {fin}}$ which is performed by the operation of the CU gate, as in (5). When the G-path gate utilizes the same CSS amplitudes of $\left (\alpha \right )$ and phase shift $\left (\theta \right )$ as the C-path gate, the error probability $P_{error}^{GP}$ of this gate is the same as in (13); $P_{error}^{GP} =P_{error}^{CP}$. Consequently, the error probability $P_{error}^{CU}$ of the single CU gate, which is composed the consecutive operations of C- and G-path gates, is given by:

$$\begin{array}{@{}rcl@{}} P_{error}^{CU} &=&P_{error}^{CP} +P_{error}^{GP} -\left( {P_{error}^{CP} \cdot P_{error}^{GP}} \right)\qquad P_{error}^{CP} =P_{error}^{GP} \\ &=&2P_{error}^{CP} -\left( {P_{error}^{CP}} \right)^{2} \end{array} $$

(21)

where $P_{error}^{CP} =\frac {3}{4}\left [ {1-\text {erf}\left ({\frac {2\alpha \sin \theta } {2\sqrt {2}} } \right )} \right ]$, as in (13). Thus, the CU gate is nearly deterministic $\left ({P_{error}^{CU} <10^{-5}} \right )$ for $2\alpha \sin \theta \sim 2\alpha \theta >9$. Furthermore, our multi-qubit gate using CSS and a P-homodyne detector is experimentally more efficient than the existing multi-qubit gates that use the coherent state and an X-homodyne detector [20–26]. Compared with the C-path gate in Ref. [21], it has an error probability given by

$$ P_{error} =\frac{1}{2}\left[ {1-\text{erf}\left( {\frac{2\alpha \left( {1-\cos \theta} \right)}{2\sqrt{2}} } \right)} \right]\approx \frac{1}{2}\left[ {1-\text{erf}\left( {\frac{\alpha \theta^{2}}{2\sqrt{2}} } \right)} \right]. $$

(22)

This error probability is also applied to other multi-qubit gates [20, 22–26] via weak XKNLs using the coherent state and an X-homodyne detector. If we choose the same error probability (< 10⁻⁶), the condition of 2α 𝜃 > 9 is required for the deterministic operation of our C-path gate as in (13). However, for the same error probability (< 10⁻⁶), the condition α 𝜃 ² > 9 is required for the C-path gate in [21] Consequently, our method of using the CSS and P-homodyne detector can reduce the nonlinear phase shift or the strength of the coherent state, in the regime of 𝜃≪1 (weak XKNL) and α ≫ 1. Therefore our proposed CU gate not only increases the feasibility of experimental realization but also enhances the robustness against the decoherence effect.

3 Simultaneous Quantum Transmission and Teleportation (SQTTP) Scheme

Figure 3 shows the scheme for the simultaneous quantum transmission (QT) of the unknown photon state $\left |{\Psi }\right .\rangle _{T}$ from Alice to Bob and QTP of photon state $\left |\varphi \right .\rangle _{B}$ from Bob to Alice. Let us consider an unknown state of photon $\left |{\Psi }\right .\rangle _{T} =\alpha \left |H\right .\rangle _{T} +\beta \left |V\right .\rangle _{T}$ that Alice wants to send to Bob along path Q. After passing through the PBS, the initial state $\left |{\Phi }\right .\rangle _{int}$ becomes a path-polarization IRH entangled state $\left |{\Phi }\right .\rangle _{\text {IRHE}}$, as follows:

$$ \left|{\Phi}\right.\rangle_{int} =\alpha \left|H\right.\rangle_{T}^{Q} +\beta \left|V\right.\rangle_{T}^{Q} {~}^{\underrightarrow{\quad\text{PBS}\quad}} \left|{\Phi}\right.\rangle_{\text{IRHE}} =\alpha \left|H\right.\rangle_{T}^{P} +\beta \left|V\right.\rangle_{T}^{Q} , $$

(23)

with $\left | \alpha \right |^{2}+\left | \beta \right |^{2}=1$ Subsequently, Alice performs a CNOT operation in which the photon T in $\left |{\Phi }\right .\rangle _{\text {IRHE}}$ acts as a control qubit and the right-circularly polarized state $\left |R\right .\rangle _{a}$ is used as a target qubit. The possible results of the CNOT operation depend on the two types of polarized state (linear and circular) and can be summarized as follows:

$$\begin{array}{@{}rcl@{}} U_{CNOT} \left( {\left|H\right.\rangle_{1} \left|R\right.\rangle_{2}} \right)&=&\frac{1}{\sqrt{2}} \left( {\left|H\right.\rangle_{1} \left|H\right.\rangle_{2} -\left|V\right.\rangle_{1} \left|V\right.\rangle_{2}} \right),\notag\\U_{CNOT} \left( {\left|H\right.\rangle_{1} \left|L\right.\rangle_{2}} \right)&=&\frac{1}{\sqrt{2}}\left( {\left|H\right.\rangle_{1} \left|H\right.\rangle_{2} +\left|V\right.\rangle_{1} \left|V\right.\rangle_{2}} \right)\notag\\U_{CNOT} \left( {\left|V\right.\rangle_{1} \left|R\right.\rangle_{2}} \right)&=&\frac{1}{\sqrt{2}} \left( {\left|H\right.\rangle_{1} \left|V\right.\rangle_{2} +\left|V\right.\rangle_{1} \left|H\right.\rangle_{2}} \right),\notag\\U_{CNOT} \left( {\left|V\right.\rangle_{1} \left|L\right.\rangle_{2}} \right)&=&\frac{-1}{\sqrt{2} }\left( {\left|H\right.\rangle_{1} \left|V\right.\rangle_{2} -\left|V\right.\rangle_{1} \left|H\right.\rangle_{2}} \right) \end{array} $$

(23-1)

$$\begin{array}{@{}rcl@{}} &&U_{CNOT} \left( {\left|H\right.\rangle_{1} \left|H\right.\rangle_{2}} \right)=\left|H\right.\rangle_{1} \left|H\right.\rangle_{2}, U_{CNOT} \left( {\left|H\right.\rangle_{1} \left|V\right.\rangle_{2}} \right)=-i\left|V\right.\rangle_{1} \left|V\right.\rangle_{2} \\ &&U_{CNOT} \left( {\left|V\right.\rangle_{1} \left|H\right.\rangle_{2}} \right)=\left|V\right.\rangle_{1} \left|H \right.\rangle_{2} , U_{CNOT} \left( {\left|V\right.\rangle_{1} \left|V\right.\rangle_{2}} \right)=i\left|H\right.\rangle_{1} \left|V\right.\rangle_{2} \end{array} $$

(23-2)

where the states of photons 1 and 2 are used as the control and target qubit, respectively, and are defined with respect to $\left \{ {\left |H\right .\rangle \equiv \left |+\right .\rangle ,\left |V\right .\rangle \equiv i\left |-\right .\rangle } \right \}$, $\left \{ {\left |R\right .\rangle \equiv \left |0\right .\rangle ,\left |L\right .\rangle \equiv \left |1\right .\rangle } \right \}$ as in (1). In Fig. 4, the CNOT operations that Alice and Bob use to recover and teleport unknown photons in SQTTP, are practically implemented by CNOT gates (the consecutive operation of a C-path gate and a G-path gate via XKNLs, CSSs, P-homodyne detectors, and feed-forwards), as described in Section 2. According to (23-1), after the CNOT operation, the output state $\left |{\Phi }\right .\rangle _{Alice}$ of Alice becomes an inter-particle (IE) entangled state between the polarizations of the two photons T and a, which depend on the path in the following manner:

$$\begin{array}{@{}rcl@{}} \left|{\Phi}\right.\rangle_{\text{IRHE}} {~}^{\underrightarrow{\quad \text{CNOT} (T-a)\quad}} \left|{\Phi}\right.\rangle_{Alice} &=&\frac{1}{\sqrt{2}} \left[\alpha \left( \left|H\right.\rangle_{T}^{P} \left|H\right.\rangle_{a} -\left|V\right.\rangle_{T}^{P} \left|V\right.\rangle_{a} \right)\right.\\ &+&\left.\beta \left( \left|H\right.\rangle_{T}^{Q} \left|V\right.\rangle_{a} +\left|V\right.\rangle_{T}^{Q} \left|H\right.\rangle_{a} \right) \right]. \end{array} $$

(24)

Equation (24) can also be expressed as follows:

$$ \left|{\Phi}\right.\rangle_{Alice} =\frac{1}{\sqrt{2}} \left[ {\left(\alpha \left|H\right.\rangle_{T}^{P} +\beta \left|V\right.\rangle_{T}^{Q} \right)\left|H\right.\rangle_{a} -\left( {\alpha \left|V\right.\rangle_{T}^{P} -\beta \left|H\right.\rangle_{T}^{Q}} \right)\left|V\right.\rangle_{a}} \right]. $$

(25)

Equations (24) and (25) show that the state $\left |{\Phi }\right .\rangle _{Alice}$ can be expressed as a linear combination of IE entangled states between the polarizations of the two photons T and a as shown in (24), and also be expressed as a linear combination of IRH entangled states between the path and polarization of photon T as shown in (25) Alice transmits photon T in the state $\left |{\Phi }\right .\rangle _{Alice}$ to Bob’s side, while photon a remains on Alice’s side.

Fig. 3

The SQTTP scheme consists of a PBS and a CNOT operation on Alice’s side and two BSs, two SFs, two CNOT operations and two P-Ds on Bob’s side. $\left |{\Psi }\right .\rangle _{T} \left ({\left |\varphi \right .\rangle _{B}} \right )$ is an unknown state of photon that Alice (Bob) wants to send to Bob (Alice). $\left |R\right .\rangle _{a} \left ({\left |R\right .\rangle _{b}} \right )$ is recovered for the teleported (transferred) unknown state of photon by Bob (Alice) using the unitary operation $U_{A} \left ({U_{B}} \right )$. The suitable operation is determined by the information on the initial path of the transferred photon T, the measured path and polarization of photon T in P-D _B02, and the measured polarization of photon B in P-D _B01. The CNOT operation on Alice’s side reconstructs the teleported photon state from Bob to Alice $\left ({\left |\varphi \right .\rangle _{B} \to \left |R\right .\rangle _{a}} \right )$ while two CNOT operations on Bob’s side reconstruct the transmitted state of photon from Alice to Bob $\left ({\left |{\Psi } \right .\rangle _{T} \to \left |R\right .\rangle _{b}} \right )$ and teleport the unknown state of photon $\left ({\left |\varphi \right .\rangle _{B}} \right )$ from Bob to Alice

Fig. 4

The CNOT operations performed between the control photon T (the transmission photon: Alice’s unknown state $\left |{\Psi } \right .\rangle _{T} )$ and the target photons $a \quad b\left (B \right )$ [Alice’s recovering photon state $\left |R\right .\rangle _{a}$, Bob’s recovering (unknown) photon states $\left |R \right .\rangle _{a} \left ({\left |\varphi \right .\rangle _{B}} \right )$], shown in Fig. 3. These CNOT operations are implemented by the CU gates, in which the C-path and G-path gates are consecutively performed by XKNLs, CSSs, P-homodyne detectors, and feed-forwards, as described in Section 2. If the unitary operator U in the middle between the C-path and G-path gates is σ _X , then the CU gate will become a CNOT (controlled- σ _X ) gate. The details of this CNOT gate are presented in Appendix

On Bob’s side, after photon T in the state $\left |{\Phi }\right .\rangle _{Alice}$ passes the BS and SF (on path P), Bob performs a CNOT operation, in which photon T in $\left |{\Phi }\right .\rangle _{Alice}$ is used as a control qubit and the right-circularly polarized state of photon $\left |R\right .\rangle _{b}$ is used as a target qubit. According to the operations of the BS SF and CNOT in (23-1), the state $\left |{\Psi }\right .\rangle _{01}$ is given by:

$$\begin{array}{@{}rcl@{}} &&\left|\Phi\right.\rangle_{Alice} ^{\underrightarrow{\text{BS, SF}(\text{path P}), \text{CNOT} (T-b)}}\\ &&\left|\Psi\right.\rangle_{01} =\frac{1}{2\sqrt{2}} \left[\left(\left|H\right.\rangle_{T}^{P} \left|H\right.\rangle_{a} +\left|V\right.\rangle_{T}^{P} \left|V\right.\rangle_{a} \right)\left(\alpha \left|V\right.\rangle_{b} +\beta \left|H\right.\rangle_{b} \right)\right.\\ &&{\kern5.5pc}-\left(\left|H\right.\rangle_{T}^{P} \left|V\right.\rangle_{a} -\left|V\right.\rangle_{T}^{P} \left|H\right.\rangle_{a} \right)\left(\alpha \left|H\right.\rangle_{b} -\beta \left|V\right.\rangle_{b} \right) \\ &&{\kern5.5pc}-\left(\left|H\right.\rangle_{T}^{Q}\left|V\right.\rangle_{a} +\left|V\right.\rangle _{T}^{Q} \left|H \right.\rangle_{a} \right)\left(\alpha \left|V\right.\rangle_{b} +\beta \left|H\right.\rangle_{b}\right) \nonumber\\ &&{\kern5.5pc}\left.{+\left(\left|H\right.\rangle_{T}^{Q} \left|H\right.\rangle_{a} -\left|V\right.\rangle_{T}^{Q} \left|V\right.\rangle_{a} \right)\left(\alpha \left|H\right.\rangle_{b} -\beta \left|V\right.\rangle_{b} \right)} \right], \end{array} $$

(26)

where the operation U _{S F} of the SF is $U_{SF} =\left |H\right .\rangle \left .\langle V \right |+\left |V \right .\rangle \left .\langle H \right |$. By the CNOT operation in (26), the expansion coefficients α,β of Alice’s unknown photon T appear in Bob’s photon state b. The IEE between the two photons T and a is still maintained.

In order to teleport the unknown state of photon $\left |\varphi \right .\rangle _{B} =\chi \left |H\right .\rangle _{B} +\delta \left |V\right .\rangle _{B} \left ({\left | \chi \right |^{2}+\left | \delta \right |^{2}=1} \right )$ to Alice, Bob performs an SF (on path P) and a CNOT operation, in which photon T in $\left |{\Psi }\right .\rangle _{01}$ is used as a control qubit and the unknown state of photon $\left | \right .\rangle _{B}$ is used as a target qubit, according to (23-2). Subsequently, after photon T is injected into the BS, the final photon state $\left |{\Psi }\right .\rangle _{\text {Bob:} Q}$ is expressed as follows:

$$\begin{array}{@{}rcl@{}} &&\left|{\Psi}\right.\rangle_{01} {~}^{\underrightarrow{\quad\text{SF}(\text{path P})\text{, CNOT } (T-B),\text{BS}\quad}} \\ &&\left|{\Psi}\right.\rangle_{\text{Bob:}Q} =\frac{1}{2\sqrt{2}} \left[\left|H\right.\rangle_{T}^{Q} \left(\alpha \left|V\right.\rangle_{b} +\beta \left|H\right.\rangle_{b} \right)\left\{\left|R\right.\rangle_{B} \left( {\chi \left|V\right.\rangle_{a} -\delta \left|H\right.\rangle_{a}} \right)+\left|L\right.\rangle_{B} \left( {\chi \left|V\right.\rangle_{a} +\delta \left|H\right.\rangle_{a}} \right)\right\} \right. \\ &&\qquad\qquad -\left|V\right.\rangle_{T}^{P} \left(\alpha \left|H\right.\rangle_{b} -\beta \left|V\right.\rangle_{b} \right)\left\{ {\left|R\right.\rangle_{B} \left(\chi \left|V\right.\rangle_{a} -\delta \left|H\right.\rangle_{a} \right)+\left|L \right.\rangle_{B} \left( {\chi \left|V \right.\rangle_{a} +\delta \left|H\right.\rangle_{a}} \right)} \right\} \\ &&\qquad\qquad +\left|V\right.\rangle_{T}^{Q} \left(\alpha \left|V\right.\rangle_{b} -\beta \left|H\right.\rangle_{b} \right)\left\{ {\left|R\right.\rangle_{B} \left(\chi \left|H\right.\rangle_{a} +\delta \left|V\right.\rangle_{a} \right)+\left|L \right.\rangle_{B} \left( {\chi \left|H \right.\rangle_{a} +\delta \left|V\right.\rangle_{a}} \right)} \right\} \\ &&\qquad\qquad +\left.\left|H\right.\rangle_{T}^{P} \left(\alpha \left|H\right.\rangle_{b} +\beta \left|V\right.\rangle_{b} \right)\left\{ {\left|R\right.\rangle_{B} \left(\chi \left|H\right.\rangle_{a} +\delta \left|V\right.\rangle_{a} \right)+\left|L \right.\rangle_{B} \left( {\chi \left|H \right.\rangle_{a} +\delta \left|V\right.\rangle_{a}} \right)} \right\} \right], \end{array} $$

(27)

where the polarized state of photon B is expressed in terms of circular polarization $\left \{ {\left |R \right .\rangle _{c} ,\left |L\right .\rangle _{c}} \right \}$ If Alice transfers an unknown photon to Bob along path P, $\alpha \left |H\right .\rangle _{T}^{P} +\beta \left |V\right .\rangle _{T}^{P}$, and if Bob wants to send $\left | \varphi \right .\rangle _{B} =\chi \left |H\right .\rangle _{B} +\delta \left |V\right .\rangle _{B}$ to Alice, the final state $\left |{\Psi } \right .\rangle _{\text {Bob: } P}$ will be expressed as follows:

$$\begin{array}{@{}rcl@{}} &&\left|{\Psi}\right.\rangle_{\text{Bob: } P} =\frac{1}{2\sqrt{2}} \left[ {\left|H\right.\rangle_{T}^{P} \left( {\alpha \left|V\right.\rangle_{b} +\beta \left|H\right.\rangle_{b}} \right)\left\{ {\left|R\right.\rangle_{B} \left( {\chi \left|V\right.\rangle_{a} -\delta \left|H\right.\rangle_{a}} \right)+\left|L\right.\rangle_{B} \left( {\chi \left|V\right.\rangle_{a} +\delta \left|H\right.\rangle_{a}} \right)} \right\}} \right. \\ &&\qquad\qquad -\left|V\right.\rangle_{T}^{Q} \left( {\alpha \left|H\right.\rangle_{b} -\beta \left|V\right.\rangle_{b}} \right)\left\{ {\left|R\right.\rangle_{B} \left( {\chi \left|V\right.\rangle_{a} -\delta \left|H\right.\rangle_{a}} \right)+\left|L\right.\rangle_{B} \left( {\chi \left|V\right.\rangle_{a} +\delta \left|H\right.\rangle_{a}} \right)} \right\} \\ &&\qquad\qquad +\left|V\right.\rangle_{T}^{P} \left( {\alpha \left|V\right.\rangle_{b} +\beta \left|H \right.\rangle_{b}} \right)\left\{ {\left|R\right.\rangle_{B} \left( {\chi \left|H\right.\rangle_{a} +\delta \left|V\right.\rangle_{a}} \right)+\left|L \right.\rangle_{B} \left( {\chi \left|H\right.\rangle_{a} -\delta \left|V \right.\rangle_{a}} \right)} \right\} \\ &&\qquad\qquad \left. {+\left|H\right.\rangle_{T}^{Q} \left( {\alpha \left|H\right.\rangle_{b} -\beta \left|V\right.\rangle_{b}} \right)\left\{ {\left|R\right.\rangle_{B} \left( {\chi \left|H\right.\rangle_{a} +\delta \left|V \right.\rangle_{a}} \right)+\left|L \right.\rangle_{B} \left( {\chi \left|H\right.\rangle_{a} -\delta \left|V\right.\rangle_{a}} \right)} \right\}} \right]. \end{array} $$

(28)

Next, Bob measures both the path and the polarization of photon T in basis $\left \{ {\left |H\right .\rangle _{T} ,\left |V\right .\rangle _{T}} \right \}$ (using P-D _B02) and the polarization of photon B in basis $\left \{ {\left |R\right .\rangle _{c} ,\left |L\right .\rangle _{c}} \right \}$ (using P-D _B01) but Bob does not measure the polarization of photon b. After these measurements, the state of photon b collapse to one of four possible states and the state of photon a to one of eight possible states. Subsequently, Alice announces to Bob the initial path information of the transferred photon T and Bob communicates to Alice the measured path and polarization information of photon T and photon B through the public channel. By performing proper operations U _A on Alice’s target photon a and U _B on Bob’s target photon b, they can recover the teleported unknown state of photon $\chi \left |H\right .\rangle _{a} +\delta \left |V\right .\rangle _{a}$ and the transferred unknown state of photon $\alpha \left |H\right .\rangle _{b} +\beta \left |V\right .\rangle _{b}$ Table 1 summarizes all possible states of Alice’s and Bob’s target photons (photons a and b) and the optimal unitary operators (U _A and U _B ), which depend on the initial path information of the transferred photon T and the measured path and polarizations of photon T and photon B. Alice performs QT, in which the transferred photon T (from Alice to Bob) is in an unknown path-polarization IRH entangled state generated by a PBS, according to the method described in Ref. 16 Also, Bob can teleport his unknown state of photon B to Alice using IEE between the polarizations of the two photons T and a. Unlike QT of photons, during QTP, the sender (Bob) does not directly send an unknown state of photon but instead uses a classical channel to send the information about the state of photon, and the receiver (Alice) then uses the information to reconstruct its unknown state Consequently, SQTTP is a bidirectional QC (QT and QTP) using CNOT gates, as described in Section 2.

Table 1 The collapsed states of the photons (photons a and b) and the suitable unitary operations (U _A , U _B ) depending on Alice’s path and Bob’s measurement outcomes

4 Conclusion

In this paper, we proposed a scheme for SQTTP that performs mutual transfer of two unknown states of photons between Alice and Bob. This scheme is developed based on improvements applied to unidirectional QC to establish bidirectional QC, which are detailed in Ref. 16. Our protocol consists of both QT that transfers Alice’s unknown state of photon to Bob and QTP that simultaneously teleports Bob’s unknown state of photon to Alice. In our protocol, both participants simultaneously become message senders and message receivers by the transfer of only a single photon between them, as in the scheme from Ref. 16. To accomplish this exchange, the path and polarization of the transferred photon (Alice’s initial photon T) are entangled (IRHE) using a PBS and then Bob teleports his unknown state of photon B using the CNOT operation and the physical properties of IEE between photons T and a.

Because the SQTTP scheme is based on the CU (CNOT) gate, its success probability and realization feasibility strongly depend on the deterministic performance and the experimental implementation of the CU gate. Therefore, we propose a nearly deterministic CU gate that can be operated by the consecutive performance of C-path and G-path gates via weak XKNLs CSSs, P-homodyne detections and feed-forwards as described in Sec. 2 The error probability of the single CU gate is $P_{error}^{CU} =2P_{error}^{CP} -\left ({P_{error}^{CP}} \right )^{2}$, where $P_{error}^{CP} =\frac {3}{4}\left [ {1-\text {erf}\left ({{\text {2}\alpha \theta } \left / {2\sqrt {2}}\right . }\right )} \right ]$ is the error probability induced by the overlaps between the three functions $s_{0} \cdot \sqrt {2} \cos \left ({\alpha \cdot \mathrm {P}} \right )$, s ₁₋ and s ₁₊ of Fig. 2. Thus, the CU gate has $P_{error}^{CU} <1.02\times 10^{-5}$ (nearly deterministic) for 2α 𝜃 > 9. Additionally, the XKNL is not necessarily very large (𝜃 ≪ 1) because it can be compensated by using CSSs with very large amplitude.

On the other hand, the extremely strong amplitude of the probe beam (CSS) may give rise to a stronger decoherence effect (more difficult experimental implementation [35]). From this point of view, our CU gate can use a smaller probe beam amplitude compared to the existing multi-qubit gates (using the coherent state and X-homodyne detector) [20–26] because the requirement 2α 𝜃 > 9 in our deterministic CU gate is much more relaxed than the existing condition α 𝜃 ² > 9 in the multi-qubit gates [20–26]. Although natural XKNLs are extremely weak, 𝜃 ≈ 10⁻¹⁸ [34], it has been established that the nonlinearity magnitude could be largely improved, to about 𝜃 ≈ 10⁻² with the help of electromagnetically induced transparency (EIT) [44, 45], which is effectively employed in the multi-qubit gates. When the amplitude of the nonlinear phase shift 𝜃 is 10⁻², the amplitudes of the probe beams in our CU gate (CSS) and the existing multi-qubit gates (coherent state) should be $\alpha _{\left ({CSS} \right )} >450$ (in (13)) and $\alpha _{\left ({coherent} \right )} >90000$ (in (22)) for the same error probabilities as P _{e r r o r} < 10⁻⁶.

Furthermore, as shown in Fig. 5, if the same probe beam amplitude $\left ({\alpha =1000} \right )$ is utilized for the multi-qubit gates, the amplitudes of the XKNLs in our CU gate corresponding to $P_{error}^{CU}$ are weaker than those in the existing multi-qubit gates [20–26] corresponding to P _{e r r o r} . Consequently, the proposed CU gate, which uses the weak XKNLs, CSSs, P-homodyne detectors and feed-forwards, is almost deterministic $P_{error}^{CU} <1.02\times 10^{-5}$ for 2α 𝜃>9, and can reduce the nonlinear phase shift or the strength of the probe beam compared to the existing multi-qubit gates, which use the coherent state and X-homodyne detectors. Thus, our CU gate can improve the feasibility of experimental realization and the robustness against the decoherence effect with respect to present techniques. In conclusion, our scheme (SQTTP) is experimentally applicable with a certain success probability.

Fig. 5

Plots of the error probabilities of the C-path gate (black) using CSS and a P-homodyne detector and the existing multi-qubit gate (red) using coherent state and an X-homodyne detector, as a function of 𝜃 (the phase shift of the XKNL) for a probe beam amplitude of α = 1000. The black and red plots are the functions $P_{error}^{CP} =3\left .\left [ {1-\text {erf}\left ({2\alpha \theta } \left / {2\sqrt {2}} \right . \right )} \right ] \right / 4$ and $P_{error} =\left .\left [ 1-\text {erf}\left (\alpha \theta ^{2} \left / 2\sqrt {2} \right . \right ) \right ]\right /2$ respectively. For example, when 𝜃 = 0.0045, $P_{error}^{CP} \approx 5.1\times 10^{-6}$ and P _{e r r o r} ≈ 0.495

Appendix

1.1 CNOT Gates in SQTTP

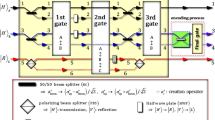
In Section 2, both the control photon and the target photon of the initial state are in a single path of the CU gate, as shown in (1). However, on Alice’s and Bob’s side of the SQTTP, the path of the control photon T is divided into two paths P and Q when path-polarization IRHE is generated as shown in Fig. 3. In our SQTTP scheme, we use a modified CNOT gate, such as in Fig. 4, which contains a split path of the control photon T. The details are shown in Fig. 6. For example, let us assume that the control photon is in a state $\frac {1}{\sqrt {2}} \left ({\left |H\right .\rangle _{c}^{P} +\left |V\right .\rangle _{c}^{Q}} \right )$ and the target photon in $\left |R \right .\rangle _{t}$. The initial state $\left |\emptyset \right .\rangle _{int}$ is given by:

$$ \left|{\emptyset}\right.\rangle_{int} =\frac{1}{\sqrt{2}} \left( {\left|H\right.\rangle_{c}^{P} \left|R\right.\rangle_{t}^{3} +\left|V\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{3}} \right), $$

(A.1)

where the target photon t is in path 3. After the control photon c passes through the two WPs, the two photons (c and t) are injected to the C-path gate Then, the state $\left |\emptyset \right .\rangle _{int}$ is changed to $\left |\emptyset \right .\rangle _{CP}$

$$\begin{array}{@{}rcl@{}} &&\left|\emptyset\right.\rangle_{int} {~}^{\underrightarrow{\quad\text{WPs} (\text{Control photon})\quad}} \frac{1}{\sqrt{2}} \left( {\left|R\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{3} +i\left|L\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{3}} \right) \\ &&{~}^{\underrightarrow{\quad\text{C-path gate}\quad}} \left|\emptyset\right.\rangle_{CP} =\frac{1}{2}\left( {\left|H\right.\rangle_{c}^{P} \left|R\right.\rangle_{t}^{3} +i\left|H\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{3} -i\left|V\right.\rangle_{c}^{P} \left|R\right.\rangle_{t}^{4} -\left|V\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{4}} \right). \end{array} $$

(A.2)

After the application of the unitary operator σ _X , G-path gate and two WPs, the state $\left |\emptyset \right .\rangle _{CP}$ is finally transformed to $\left |\emptyset \right .\rangle _{\text {fin}}$ as follows:

$$\begin{array}{@{}rcl@{}} &&\left|\emptyset\right.\rangle_{CP} {~}^{\underrightarrow{\quad\sigma_{X} (\text{Target photon : path 4})\quad}} \frac{1}{2}\left( {\left|H\right.\rangle_{c}^{P} \left|R\right.\rangle_{t}^{3} +i\left|H\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{3} -i\left|V\right.\rangle_{c}^{P} \left|L\right.\rangle_{t}^{4} -\left|V\right.\rangle_{c}^{Q} \left|L\right.\rangle_{t}^{4}} \right) \\ &&{~}^{\underrightarrow{\quad\text{G-path gate}\quad}} \frac{1}{2}\left( {\left|H\right.\rangle_{c}^{P} \left|R \right.\rangle_{t}^{4} +i\left|H\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{4} -i\left|V\right.\rangle_{c}^{P} \left|L\right.\rangle_{t}^{4} -\left|V\right.\rangle_{c}^{Q} \left|L\right.\rangle_{t}^{4}} \right) \\ &&{~}^{\underrightarrow{\quad\text{WPs} \left( {\text{Control photon}} \right)\quad}} \left|\emptyset \right.\rangle_{\text{fin}} =\frac{1}{2}\left( {\left|R\right.\rangle_{c}^{P} \left|R\right.\rangle_{t}^{4} +i\left|R\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{4} +\left|L\right.\rangle_{c}^{P} \left|L\right.\rangle_{t}^{4} -i\left|L\right.\rangle_{c}^{Q} \left|L\right.\rangle_{t}^{4}}\right) \\ && =\frac{1}{\sqrt{2}} \left[ {\frac{1}{\sqrt{2}} \left( {\left|R\right.\rangle_{c}^{P} \left|R\right.\rangle_{t}^{4} +\left|L\right.\rangle_{c}^{P} \left|L\right.\rangle_{t}^{4}} \right)+\frac{i}{\sqrt{2}} \left( {\left|R\right.\rangle_{c}^{Q} \left|R\right.\rangle_{t}^{4} -\left|L\right.\rangle_{c}^{Q} \left|L\right.\rangle_{t}^{4}} \right)} \right]. \end{array} $$

(A.3)

where the initial state is $\left |\emptyset \right .\rangle _{int} =\frac {1}{\sqrt {2}} \left ({\left |H \right .\rangle _{c}^{P}} \left |R\right .\rangle _{t}^{3} +\left |V\right .\rangle _{c}^{Q} \left |R\right .\rangle _{t}^{3} \right ),$ in (A.1).

Fig. 6

The CNOT gates in SQTTP scheme (Figs. 3 and 4): The split path (P and Q) of the control photon c and the single path of the target photon t, the multi-qubit gates perform the interaction of XKNLs to between CSSs and two photons (c and t) according to the path (P and Q), respectively. If the unitary operator U in the middle of the C-path and G-path gates is σ _X , then the CU gate becomes a CNOT gate