Quantum Private Comparison Protocol without a Third Party

Abstract

This paper presents a quantum private comparison (QPC) protocol based on Bell states. The proposed QPC protocol can secretly compare information of the two participants without the help of a third party (TP). The proposed protocol employs some decoy state photons and quantum SWAP gates to resist various outside attacks and internal attacks. This paper compares the presented quantum private comparison (QPC) protocol with other schemes in terms of different indicators. The results show that the proposed protocol has some advantages different from previous protocols.

1 Introduction

Ever since quantum mechanics was introduced into the cryptography field, numerous quantum cryptographic applications have been proposed, such as quantum secure direct communication (QSDC) [1, 2], quantum secret sharing (QSS) [3, 4], quantum public key cryptosystem (QPKC) [5, 6].

Recently, quantum private comparison (QPC) becomes an important branch of quantum cryptography, which can privately compare two parties’ undisclosed information for equality. In 2009 the first QPC protocol was presented by Yang and Wen based on Bell states and a hash function [7]. Since then numerous QPC protocols have been proposed to improve both the security and the qubit efficiency in [8,9,10,11,12,13,14,15,16], etc. Thus far, these protocols have accomplished the comparison work with the help of a semi-honest third party (TP). But a semi-honest TP might try to steal the players private inputs, while he cannot be corrupted by the adversary.

Although Lo (1997) pointed that a QPC may not be securely evaluated with a two-party scenario under the technology of that time in [17]. With the advance in quantum entanglement swapping, many papers reconstructed the two-party QPC protocols without the help of a TP. In 2014 Lin et al. presented a QPC without a TP based on entanglement swapping and a hash function [18]. In 2016 He proposed a QPC with two parties only based on single photon sequences and hash function [19]. Soon afterwards, He proposed the device-independent version of the QPC protocol [20]. One common feature of these protocols is that they require the help of hash functions to complete the comparison in [18,19,20].

Quantum private comparisons without third-party help are rare. In addition, publishing more efficient and safer protocols are necessary. For the above reasons, this paper present a new QPC protocol without a third party via using the Bell states and quantum SWAP gates. The paper is organized as follows. Section 2 introduces some basic concepts. Section 3 presents a QPC protocol. Section 4 analyzes the security of the QPC protocol. Section 5 concludes the paper.

2 Background

2.1 Permutation Operation

We summarize some basic concepts about permutations. By definition, a permutation of set A = {1,⋯ ,n} is simply a bijection $\pi : A\rightarrow A$. We usually write a permutation π by writing its values as a finite sequence π = (i₁,⋯ ,i_n), where π(j) = i_j and j = 1,⋯ ,n. We denote all permutations of the set A on S_n. For example, let A = {1,2,3}, then S₃ = {(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)}.

A transposition is a special permutation that fixes all but two integers, which are interchanged. For example, the following are some of the transpositions in S₃: (1,3,2),(3,2,1),(2,1,3). We define the special notation [s,t] to denote the transposition in S_n that interchanges s and t. For example, with n = 3, (1,3,2) = [2,3],(3,2,1) = [1,3],(2,1,3) = [1,2].

There are two basic facts about permutations. One is that every permutation can be written as the composition of transpositions. For example, with n = 3, (3,1,2) = [2,3][1,2]. Another is that a representation of a permutation as a composition of transpositions is not unique. For example, with n = 3, (3,1,2) = [2,3][1,2] = [1,3][2,3]. There are more details in [21].

Next we define a special permutation operation called N-level permutation by iterating the cyclic shift operation several times. Details as below.

Let π_k be a cyclic left-shift operation (shorted by $\lll k$) defined as π_k(i) = i + k mod r, that is

$$ \begin{array}{@{}rcl@{}} \pi_{k}: (1, 2, \cdots, r)\rightarrow (k+1, k+2, \cdots, r, 1, 2, \cdots, k), \end{array} $$

(1)

where non-negative integer k < r. Another cyclic right-shift operation has the same definition.

Let S = {a_{(1,⋯ ,1,1,1)},⋯ ,a_{(1,⋯ ,1,1,r)},a_{(1,⋯ ,1,2,1)},⋯ ,a_{(1,⋯ ,1,2,r)},⋯ ,a_{(r,⋯ ,r,1)},⋯ , $a_{(\underbrace {r, \cdots , r, r}_{N})}\}$ be a r^N-dimension set, where r,N ≥ 2. By (1), the cyclic left-shift operation $\pi ^{(j)}_{k_{j}}$ on set S is defined as

$$ \begin{array}{@{}rcl@{}} &&\pi^{(j)}_{k_{j}} \left( a_{(\underbrace{1, \cdots, 1}_{j-1}, 1, \underbrace{1, \cdots, 1, 1}_{N-j})}, \cdots, a_{(\underbrace{1, \cdots, 1}_{j-1}, 1, \underbrace{1, \cdots, 1, r}_{N-j})},\right.\\ && \quad\qquad \left. \cdots, a_{(\underbrace{r, \cdots, r}_{j-1}, r, \underbrace{r, \cdots, r, 1}_{N-j})}, \cdots, a_{(\underbrace{r, \cdots, r}_{j-1}, r, \underbrace{r, \cdots, r, r}_{N-j})}\right)\\ &=&\left( a_{(\underbrace{1, \cdots, 1}_{j-1}, \pi_{k_{j}}(1), \underbrace{1, \cdots, 1, 1}_{N-j})}, \cdots, a_{(\underbrace{1, \cdots, 1}_{j-1}, \pi_{k_{j}}(1), \underbrace{1, \cdots, 1, r}_{N-j})},\right.\\ && \quad\quad\left. \cdots, a_{(\underbrace{r, \cdots, r}_{j-1}, \pi_{k_{j}}(r), \underbrace{r, \cdots, r, 1}_{N-j})}, \cdots, a_{(\underbrace{r, \cdots, r}_{j-1}, \pi_{k_{j}}(r), \underbrace{r, \cdots, r, r}_{N-j})}\right) \end{array} $$

(2)

where 1 ≤ j ≤ N,1 ≤ k_j ≤ r.

Example 1

With N = 2,r = 3,k_j = 2,j = 2, it follows that

$$ \begin{array}{@{}rcl@{}} &&\pi^{(2)}_{2} (a_{(1, 1)}, a_{(1, 2)}, a_{(1, 3)}, a_{(2, 1)}, a_{(2, 2)}, a_{(2, 3)}, a_{(3, 1)}, a_{(3, 2)}, a_{(3, 3)}) \\ &=&(a_{(1, \pi_{2}(1))}, a_{(1, \pi_{2}(2))}, a_{(1, \pi_{2}(3))}, a_{(2, \pi_{2}(1))}, a_{(2, \pi_{2}(2))}, a_{(2, \pi_{2}(3))}, a_{(3, \pi_{2}(1))},\\ && a_{(3, \pi_{2}(2))}, a_{(3, \pi_{2}(3))})\\ &=&(a_{(1, 3)}, a_{(1, 1)}, a_{(1, 2)}, a_{(2, 3)}, a_{(2, 1)}, a_{(2, 2)}, a_{(3, 3)}, a_{(3, 1)}, a_{(3, 2)}). \end{array} $$

So the mathematical description of N-level permutation is

$$ \begin{array}{@{}rcl@{}} \pi=\pi^{(N)}_{k_{N}}\circ {\cdots} \circ \pi^{(1)}_{k_{1}}, \end{array} $$

(3)

where ∘ means the compound of operation and $\pi ^{(j)}_{k_{j}}$ is the cyclic left-shift operation in (2).

Example 2

With N = 2,r = 3,k₁ = 2,k₂ = 2, it performs $\pi =\pi ^{(2)}_{k_{2}}\circ \pi ^{(1)}_{k_{1}}$ operation and obtains

$$ \begin{array}{@{}rcl@{}} &&\pi^{(2)}_{k_{2}}\circ \pi^{(1)}_{k_{1}}(a_{(1, 1)}, a_{(1, 2)}, a_{(1, 3)}, a_{(2, 1)}, a_{(2, 2)}, a_{(2, 3)}, a_{(3, 1)}, a_{(3, 2)}, a_{(3, 3)}) \\ &=&\pi^{(2)}_{k_{2}}(a_{(\pi_{k_{1}}(1), 1)}, a_{(\pi_{k_{1}}(1), 2)}, a_{(\pi_{k_{1}}(1), 3)}, a_{(\pi_{k_{1}}(2), 1)}, a_{(\pi_{k_{1}}(2), 2)}, a_{(\pi_{k_{1}}(2), 3)}, a_{(\pi_{k_{1}}(3), 1)},\\ && a_{(\pi_{k_{1}}(3), 2)}, a_{(\pi_{k_{1}}(3), 3)}) \\ &=&\pi^{(2)}_{k_{2}}(a_{(3, 1)}, a_{(3, 2)}, a_{(3, 3)}, a_{(1, 1)}, a_{(1, 2)}, a_{(1, 3)}, a_{(2, 1)}, a_{(2, 2)}, a_{(2, 3)})\\ &=&(a_{(3, \pi_{2}(1))}, a_{(3, \pi_{2}(2))}, a_{(3, \pi_{2}(3))}, a_{(1, \pi_{2}(1))}, a_{(1, \pi_{2}(2))}, a_{(1, \pi_{2}(3))}, a_{(2, \pi_{2}(1))},\\ && a_{(2, \pi_{2}(2))}, a_{(2, \pi_{2}(3))})\\ &=&(a_{(3, 3)}, a_{(3, 1)}, a_{(3, 2)}, a_{(1, 3)}, a_{(1, 1)}, a_{(1, 2)}, a_{(2, 3)}, a_{(2, 1)}, a_{(2, 2)}). \end{array} $$

Now we define an induction operation of π as follows

$$ \begin{array}{@{}rcl@{}} \overline{\pi}= \pi^{(1)}_{k_{1}}\circ {\cdots} \circ \pi^{(N)}_{k_{N}}. \end{array} $$

(4)

Next we discuss the commutativity of N-level permutation. By the (2), (3) and (4), it directly fields the Proposition 1 as follows.

Proposition 1

Let π_A and π_B be two N-level permutations, $\overline {\pi _{A}}$ and $\overline {\pi _{B}}$ are induction operation of π_A and π_B respectively, then $\pi _{A}\circ \overline {\pi _{B}}=\pi _{B}\circ \overline {\pi _{A}}$.

Proof

The proof is easy. Let $\pi _{A}=\pi ^{(N)}_{k_{N}}\circ {\cdots } \circ \pi ^{(1)}_{k_{1}}$ and $\pi _{B}=\pi ^{(N)}_{s_{N}}\circ {\cdots } \circ \pi ^{(1)}_{s_{1}}$ be two N-level permutations. Then it has

$$ \begin{array}{@{}rcl@{}} &&\pi_{A}\circ \overline{\pi_{B}}(a_{(\underbrace{1, \cdots, 1, 1}_{N})}, \cdots, a_{(\underbrace{1, \cdots, 1, r}_{N})}, \cdots, a_{(\underbrace{r, \cdots, r, 1}_{N})}, \cdots, a_{(\underbrace{r, \cdots, r, r}_{N})})\\ &=&\pi^{(N)}_{k_{N}}\circ\cdots\circ \pi^{(1)}_{k_{1}}\circ \pi^{(1)}_{s_{1}}\circ\cdots\circ \pi^{(N)}_{s_{N}} (a_{(1, \cdots, 1, 1)}, \cdots, a_{(1, \cdots, 1, r)}, \cdots, a_{(r, \cdots, r, 1)},\\ && \cdots, a_{(r, \cdots, r, r)})\\ &=&\pi^{(N)}_{k_{N}}\circ\cdots\circ \pi^{(1)}_{k_{1}}(a_{(s_{1}+1, \cdots, s_{N-1}+1, s_{N}+1)}, \cdots, a_{(s_{1}+1, \cdots, s_{N-1}+1, s_{N}+r)}, \cdots,\\ && a_{(s_{1}+r, \cdots, s_{N-1}+r, s_{N}+1)}, \cdots, a_{(s_{1}+r, \cdots, s_{N-1}+r, s_{N}+r)})\\ &=&(a_{(k_{1}+s_{1}+1, \cdots, k_{N-1}+s_{N-1}+1, k_{N}+s_{N}+1)}, \cdots, a_{(k_{1}+s_{1}+1, \cdots, k_{N-1}+s_{N-1}+1, k_{N}+s_{N}+r)}, \cdots,\\ &&~~~~~~a_{(k_{1}+s_{1}+r, \cdots, k_{N-1}+s_{N-1}+r, k_{N}+s_{N}+1)}, \cdots, a_{(k_{1}+s_{1}+r, \cdots, k_{N-1}+s_{N-1}+r, k_{N}+s_{N}+r)}) \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} &&\pi_{B}\circ \overline{\pi_{A}}\left( a_{(\underbrace{1, \cdots, 1, 1}_{N})}, \cdots, a_{(\underbrace{1, \cdots, 1, r}_{N})}, \cdots, a_{(\underbrace{r, \cdots, r, 1}_{N})}, \cdots, a_{(\underbrace{r, \cdots, r, r}_{N})}\right)\\ &=&\pi^{(N)}_{s_{N}}\circ\cdots\circ \pi^{(1)}_{s_{1}}\circ \pi^{(1)}_{k_{1}}\circ\cdots\circ \pi^{(N)}_{k_{N}} (a_{(1, \cdots, 1, 1)}, \cdots, a_{(1, \cdots, 1, r)}, \cdots, a_{(r, \cdots, r, 1)}, \cdots,\\ && a_{(r, \cdots, r, r)})\\ &=&\pi^{(N)}_{s_{N}}\circ\cdots\circ \pi^{(1)}_{s_{1}}(a_{(k_{1}+1, \cdots, k_{N-1}+1, k_{N}+1)}, \cdots, a_{(k_{1}+1, \cdots, k_{N-1}+1, k_{N}+r)}, \cdots,\\ && a_{(k_{1}+r, \cdots, k_{N-1}+r, k_{N}+1)}, \cdots, a_{(k_{1}+r, \cdots, k_{N-1}+r, k_{N}+r)})\\ &=&(a_{(k_{1}+s_{1}+1, \cdots, k_{N-1}+s_{N-1}+1, k_{N}+s_{N}+1)}, \cdots, a_{(k_{1}+s_{1}+1, \cdots, k_{N-1}+s_{N-1}+1, k_{N}+s_{N}+r)}, \cdots,\\ && a_{(k_{1}+s_{1}+r, \cdots, k_{N-1}+s_{N-1}+r, k_{N}+s_{N}+1)}, \cdots, a_{(k_{1}+s_{1}+r, \cdots, k_{N-1}+s_{N-1}+r, k_{N}+s_{N}+r)}). \end{array} $$

It is clear that $\pi _{A}\circ \overline {\pi _{B}}=\pi _{B}\circ \overline {\pi _{A}}$. Thus it holds. □

Example 3

For N = 2,r = 2, let $\pi _{A}=\pi ^{(2)}_{1}\circ \pi ^{(1)}_{2}$ and $\pi _{B}=\pi ^{(2)}_{2}\circ \pi ^{(1)}_{1}$ be two 2-level permutations, then it has

$$ \begin{array}{@{}rcl@{}} &&\pi_{A}\circ \overline{\pi_{B}}(a_{(1,1)}, a_{(1,2)}, a_{(2,1)}, a_{(2,2)})\\ &=&\pi^{(2)}_{1}\circ \pi^{(1)}_{2}\circ \pi^{(1)}_{1}\circ \pi^{(2)}_{2}(a_{(1,1)}, a_{(1,2)}, a_{(2,1)}, a_{(2,2)})\\ &=&\pi^{(2)}_{1}\circ \pi^{(1)}_{2}(a_{(2,1)}, a_{(2,2)}, a_{(1,1)}, a_{(1,2)})\\ &=&(a_{(2,2)}, a_{(2,1)}, a_{(1,2)}, a_{(1,1)}) \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} &&\pi_{B}\circ \overline{\pi_{A}}(a_{(1,1)}, a_{(1,2)}, a_{(2,1)}, a_{(2,2)})\\ &=&\pi^{(2)}_{2}\circ \pi^{(1)}_{1}\circ \pi^{(1)}_{2}\circ \pi^{(2)}_{1}(a_{(1,1)}, a_{(1,2)}, a_{(2,1)}, a_{(2,2)})\\ &=&\pi^{(2)}_{2}\circ \pi^{(1)}_{1}(a_{(1,2)}, a_{(1,1)}, a_{(2,2)}, a_{(2,1)})\\ &=&(a_{(2,2)}, a_{(2,1)}, a_{(1,2)}, a_{(1,1)}) \end{array} $$

It is clear that $\pi _{A}\circ \overline {\pi _{B}}=\pi _{B}\circ \overline {\pi _{A}}$.

2.2 General Quantum SWAP Gates

In this subsection we introduce a quantum SWAP gate. The SWAP gate is seen as an important component in theory of quantum computation. For a n-qubit quantum systems |c₁,⋯ ,c_n〉, the general quantum SWAP gate in [22] will act as:

$$ \begin{array}{@{}rcl@{}} SWAP_{\pi}:|c_{1}, \cdots, c_{n}\rangle=|c_{i_{1}}, \cdots, c_{i_{n}}\rangle, \end{array} $$

(5)

where a permutation π = (i₁,⋯ ,i_n).

Let π be a permutation, then π = π₁ ∘⋯ ∘ π_m, where π_i is also a transposition, 1 ≤ i ≤ n. Since every permutation can be written as the composition of transpositions. By (5), we have

$$ SWAP_{\pi}=SWAP_{\pi_{1}}{\cdots} SWAP_{\pi_{m}}. $$

For example, in 3-qubit system, SWAP_(3,1,2)|c₁,c₂,c₃〉 = SWAP_[2,3]SWAP_[1,2]|c₁,c₂,c₃〉 = |c₃,c₁,c₂〉. Thus, it directly fields the following Proposition 2.

Proposition 2

Let π_A and π_B be two N-level permutations, $\overline {\pi _{A}}$ and $\overline {\pi _{B}}$ are induction operation of π_A and π_B respectively, then $SWAP_{\pi _{A}\circ \overline {\pi _{B}}}=SWAP_{\pi _{B}\circ \overline {\pi _{A}}}$ for n-qubit quantum system.

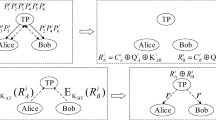
3 The Proposed Two-Party QPC Protocol

3.1 A Description of QPC Protocol

Alice and Bob are two parties who want to compare the equality of their secret messages with same bit-length, a,b ∈{0,1}^∗, respectively. They agree that the two Bell states $|\phi ^{0}\rangle =\frac {1}{\sqrt {2}}(|00\rangle +|11\rangle ), |\phi ^{1}\rangle =\frac {1}{\sqrt {2}}(|01\rangle +|10\rangle )$ represent the classical bits 0, 1, respectively. The proposed protocol can be depicted in steps as following.

Alice divides the secret message a into m groups, which are

$$ \begin{array}{@{}rcl@{}} &&X_{0}=\{a_{1}, \cdots, a_{r^{2}}\}=\{a_{(1,1)}, \cdots, a_{(1,r)}, \cdots, a_{(r,1)}, \cdots, a_{(r,r)}\},\\ &&X_{1}=\{a_{r^{2}+1}, \cdots, a_{2r^{2}}\}=\{a^{(1)}_{(1,1)}, \cdots, a^{(1)}_{(1,r)}, \cdots, a^{(1)}_{(r,1)}, \cdots, a^{(1)}_{(r,r)}\},\\ &&\cdots,\\ &&X_{m-1}=\{a_{(m-1)r^{2}+1}, \cdots, a_{(m-1)r^{2}}\}=\{a^{(m-1)}_{(1,1)}, \cdots, a^{(m-1)}_{(1,r)}, \cdots, a^{(m-1)}_{(r,1)}, \cdots, a^{(m-1)}_{(r,r)}\}. \end{array} $$

If |X_m− 1|≠r², Alice fills in the data alternately 0 and 1 after X_m− 1.

Bob does the same things for the secret message b and obtains

$$ \begin{array}{@{}rcl@{}} &&Y_{0}=\{b_{1}, \cdots, b_{r^{2}}\}=\{b_{(1,1)}, \cdots, b_{(1,r)}, \cdots, b_{(r,1)}, \cdots, b_{(r,r)}\},\\ &&Y_{1}=\{b_{r^{2}+1}, \cdots, b_{2r^{2}}\}=\{b^{(1)}_{(1,1)}, \cdots, b^{(1)}_{(1,r)}, \cdots, b^{(1)}_{(r,1)}, \cdots, b^{(1)}_{(r,r)}\},\\ &&\cdots,\\ &&Y_{m-1}=\{b_{(m-1)r^{2}+1}, \cdots, b_{(m-1)r^{2}}\}=\{b^{(m-1)}_{(1,1)}, \cdots, b^{(m-1)}_{(1,r)}, \cdots, b^{(m-1)}_{(r,1)}, \cdots, b^{(m-1)}_{(r,r)}\}, \end{array} $$

where a_(i,j),b_(i,j) ∈{0,1},i,j = 1,⋯ ,r², a_s,b_s ∈{0,1},s = 1,⋯ ,mr² and r ∈ Z⁺.

Step 1.:

Alice (Bob) selects two transpositions $\pi ^{(1)}_{k_{1}}, \pi ^{(2)}_{k_{2}}(\pi ^{(1)}_{s_{1}}, \pi ^{(2)}_{s_{2}})$ in (4). Then Alice (Bob) computes

$$\overline{\pi_{A}}(X_{0})=\overline{\pi_{A}}(a_{(1,1)}, \cdots, a_{(1,r)}, \cdots, a_{(r,1)}, \cdots, a_{(r,r)})=(a_{\overline{\pi_{A}}(1)}, \cdots, a_{\overline{\pi_{A}}(r^{2})})$$

$$ (\overline{\pi_{B}}(Y_{0})=\overline{\pi_{B}}(b_{(1,1)}, \cdots, b_{(1,r)}, \cdots, b_{(r,1)}, \cdots, b_{(r,r)})=(b_{\overline{\pi_{B}}(1)}, \cdots, b_{\overline{\pi_{B}}(r^{2})}))$$

for first group X₀(Y₀), where $\overline {\pi _{A}}=\pi ^{(1)}_{k_{1}}\circ \pi ^{(2)}_{k_{2}} (\overline {\pi _{B}}=\pi ^{(1)}_{s_{1}}\circ \pi ^{(2)}_{s_{2}} )$.

Step 2.:

Alice (Bob) encodes each bit of $\overline {\pi _{A}}(X_{0}) (\overline {\pi _{B}}(Y_{0}))$ and prepares r² Bell states as initial states. Alice (Bob) records these initial states as

$$S_{A}=\{|\phi^{a_{\overline{\pi_{A}}(1)}}\rangle_{1}, \cdots, |\phi^{a_{\overline{\pi_{A}}(r^{2})}}\rangle_{r^{2}}\} ~~~~(S_{B}=\{|\phi^{b_{\overline{\pi_{B}}(1)}}\rangle_{1}, \cdots, |\phi^{b_{\overline{\pi_{B}}(r^{2})}}\rangle_{r^{2}}\}),$$

where $|\phi ^{a_{\overline {\pi _{A}}(i)}}\rangle _{i}, |\phi ^{b_{\overline {\pi _{B}}(i)}}\rangle _{i}\in \{|\phi ^{0}\rangle , |\phi ^{1}\rangle \}, i=1, \cdots , r^{2}$. Further, Alice (Bob) divides them into two ordered sequences $S_{A_{1}}$ and $S_{A_{2}} (S_{B_{1}}$ and $S_{B_{2}})$ composed of the 1st and 2nd particles of each Bell state respectively, that is

$$ S_{A_{1}}=\{|\phi_{1}^{a_{\overline{\pi_{A}}(1)}}\rangle_{1}, \cdots, |\phi_{1}^{a_{\overline{\pi_{A}}(r^{2})}}\rangle_{r^{2}}\} ~~~~(S_{B_{1}}=\{|\phi_{1}^{b_{\overline{\pi_{B}}(1)}}\rangle_{1}, \cdots, |\phi_{1}^{b_{\overline{\pi_{B}}(r^{2})}}\rangle_{r^{2}}\}), $$

$$ S_{A_{2}}=\{|\phi_{2}^{a_{\overline{\pi_{A}}(1)}}\rangle_{1}, \cdots, |\phi_{2}^{a_{\overline{\pi_{A}}(r^{2})}}\rangle_{r^{2}}\} ~~~~(S_{B_{2}}=\{|\phi_{2}^{b_{\overline{\pi_{B}}(1)}}\rangle_{1}, \cdots, |\phi_{2}^{b_{\overline{\pi_{B}}(r^{2})}}\rangle_{r^{2}}\}). $$

Step 3.:

Alice (Bob) randomly prepares decoy photons $\otimes {D^{A}_{j}} (\otimes {D^{B}_{j}})$, where $|{D_{j}^{A}} \rangle$$(|{D^{B}_{j}}\rangle )\in \{|0\rangle , |1\rangle ,$$(|0\rangle +|1\rangle )/\sqrt {2}, (|0\rangle -|1\rangle )/\sqrt {2}\} (j=1, 2, \cdots , k)$. Then Alice (Bob) randomly inserts $\otimes {D^{A}_{j}} (\otimes {D^{B}_{j}})$ in $S_{A_{1}}(S_{B_{1}})$ to form a new sequence $S^{\prime }_{A_{1}}(S^{\prime }_{B_{1}})$, and sends it to Bob (Alice).

Step 4.:

After confirming that Bob (Alice) has received the quantum sequence $S^{\prime }_{A_{1}}(S^{\prime }_{B_{1}})$, Alice (Bob) informs the positions and the measurement bases of $\otimes {D^{A}_{j}} (\otimes {D^{B}_{j}})$ to Bob (Alice). Subsequently, Bob (Alice) extracts the particles in $\otimes {D^{A}_{j}} (\otimes {D^{B}_{j}})$ from $S^{\prime }_{A_{1}}(S^{\prime }_{B_{1}})$, and gets the sequence $S_{A_{1}}(S_{B_{1}})$. Thereafter, Alice and Bob can check the existence of an Eve by a predetermined threshold of error rate. If the error rate is limited in a predetermined threshold, there is no eve and the protocol continues. Otherwise, Alice and Bob abort the protocol and restart from Step 1.

Step 5.:

Bob (Alice) performs quantum swapping gate $SWAP_{\pi _{B}} (SWAP_{\pi _{A}})$ on quantum particle sequence $S_{A_{1}}(S_{B_{1}})$ and obtains

$$ S^{\prime\prime}_{A_{1}} = \{|\phi_{1}^{a_{\overline{\pi_{A}}(1)}}\rangle_{\pi_{B}(1)}, \cdots, |\phi_{1}^{a_{\overline{\pi_{A}}(r^{2})}}\rangle_{\pi_{B}(r^{2})}\} ~~(S^{\prime\prime}_{B_{1}}\! = \{|\phi_{1}^{b_{\overline{\pi_{B}}(1)}}\rangle_{\pi_{A}(1)}, \cdots, |\phi_{1}^{b_{\overline{\pi_{B}}(r^{2})}}\rangle_{\pi_{A}(r^{2})}\}). $$

Step 6.:

Bob (Alice) selects a binary random sequences $e^{B}=({e^{B}_{1}}, {e^{B}_{2}}, \cdots , e^{B}_{r^{2}})\in \{0, 1\}^{r^{2}}$$(e^{A}=({e^{A}_{1}}, {e^{A}_{2}}, \cdots , e^{A}_{r^{2}})\in \{0, 1\}^{r^{2}}$). Bob (Alice) performs unitary operation U on quantum particle sequence $S^{\prime \prime }_{A_{1}} (S^{\prime \prime }_{B_{1}})$ and obtains a new quantum particle sequence $\widetilde {S}^{\prime \prime }_{A_{1}} (\widetilde {S}^{\prime \prime }_{B_{1}})$, where U = I if ${e^{B}_{i}}=0$$({e^{A}_{i}}=0)$ and U is X-gate if ${e^{B}_{i}}=1$$({e^{A}_{i}}=1)$.

Step 7.:

Bob (Alice) randomly inserts $\otimes D^{\prime A}_{j} (\otimes D^{\prime B}_{j})$ in $\widetilde {S}^{\prime \prime }_{A_{1}}$ and $S_{B_{2}} (\widetilde {S}^{\prime \prime }_{B_{1}}$ and $S_{A_{2}})$ to form a new sequence $S^{\prime \prime \prime }_{A_{1}}(S^{\prime \prime \prime }_{B_{1}})$ and $S^{\prime }_{B_{2}} (S^{\prime }_{A_{2}})$, where $|D^{\prime A}_{j} \rangle (|D^{\prime B}_{j}\rangle )\in \{|0\rangle , |1\rangle , (|0\rangle +|1\rangle )/\sqrt {2}, (|0\rangle -|1\rangle )/\sqrt {2}\} (j=1, 2, \cdots , k)$. Then Bob (Alice) sends sequences $S^{\prime \prime \prime }_{A_{1}}(S^{\prime \prime \prime }_{B_{1}})$ and $S^{\prime }_{B_{2}} (S^{\prime }_{A_{2}})$ to Alice (Bob).

Step 8.:

Alice and Bob check the existence of an Eve just as Step 4 introduced, and obtains $\widetilde {S}^{\prime \prime }_{A_{1}}, S_{B_{2}}$ and $\widetilde {S}^{\prime \prime }_{B_{1}}, S_{A_{2}}$ respectively.

Step 9.:

Bob (Alice) performs quantum swapping gate $SWAP_{\pi _{B}} (SWAP_{\pi _{A}})$ on quantum particle sequence $S_{A_{2}}(S_{B_{2}})$, and obtains

$$ S^{\prime\prime}_{A_{2}} = \{|\phi_{2}^{a_{\overline{\pi_{A}}(1)}}\rangle_{\pi_{B}(1)}, \cdots, |\phi_{2}^{a_{\overline{\pi_{A}}(r^{2})}}\rangle_{\pi_{B}(r^{2})}\} ~~(S^{\prime\prime}_{B_{2}}\! = \{|\phi_{2}^{b_{\overline{\pi_{B}}(1)}}\rangle_{\pi_{A}(1)}, \cdots, |\phi_{2}^{b_{\overline{\pi_{B}}(r^{2})}}\rangle_{\pi_{A}(r^{2})}\}). $$

Step 10.:

Alice (Bob) obtains the sequence of classical results $\{a^{A_{1}}_{1}\oplus {e^{B}_{1}}, \cdots , a^{A_{1}}_{r^{2}}\oplus e^{B}_{r^{2}}, b^{B_{2}}_{1}, \cdots , b^{B_{2}}_{r^{2}}\}, (\{b^{B_{1}}_{1}\oplus {e^{A}_{1}}, \cdots , b^{B_{1}}_{r^{2}}\oplus e^{A}_{r^{2}}, a^{A_{2}}_{1}, \cdots , a^{A_{2}}_{r^{2}}\})$ from quantum particles $\widetilde {S}^{\prime \prime }_{A_{1}}S^{\prime \prime }_{B_{2}} (\widetilde {S}^{\prime \prime }_{B_{1}}S^{\prime \prime }_{A_{2}})$ after the |0〉,|1〉 basis measurement. Alice (Bob) computes the ${t^{A}_{i}}=a^{A_{1}}_{i}\oplus {e^{B}_{i}}\oplus b^{B_{2}}_{i}\oplus {e^{A}_{i}}$ (${t^{B}_{i}}=b^{B_{1}}_{i}\oplus {e^{A}_{i}}\oplus a^{A_{2}}_{i}\oplus {e^{B}_{i}}$), and obtains result $t^{A}=\{{t^{A}_{i}}, i=1, \cdots , r^{2}\}$ ($t^{B}=\{{t^{B}_{i}}, i=1, \cdots , r^{2}\}$). Alice and Bob publish the t^A and t^B respectively. If t^A = t^B, then they announce the compared secret information X₀ and Y₀ are identical, and perform the protocol for the next group X_j and Y_j,j = 1,⋯ ,m − 1. Otherwise, they announce the comparison are regarded as different.

3.2 An Example

Next, we taken an example when N = 2,r = 2. Suppose that Alice’s and Bob’s secret inputs are a = a_(1,1)a_(1,2)a_(2,1)a_(2,2) = 1001,b = b_(1,1)b_(1,2)b_(2,1)b_(2,2) = 1001.

Step 1.:

Alice selects two integers k₁ = 1,k₂ = 2 and computes

$$ \begin{array}{@{}rcl@{}} \overline{\pi_{A}}(a_{(1, 1)}, a_{(1, 2)}, a_{(2, 1)}, a_{(2, 2)}) &=&\pi^{(1)}_{k_{1}}\circ\pi^{(2)}_{k_{2}}(a_{(1, 1)}, a_{(1, 2)}, a_{(2, 1)}, a_{(2, 2)})\\ &=&(a_{(2, 1)}, a_{(2, 2)}, a_{(1, 1)}, a_{(1, 2)})=0110. \end{array} $$

Bob selects two integers s₁ = 1,s₂ = 1 and computes

$$ \begin{array}{@{}rcl@{}} \overline{\pi_{B}}(b_{(1, 1)}, b_{(1, 2)}, b_{(2, 1)}, b_{(2, 2)}) &=&\pi^{(1)}_{s_{1}}\circ\pi^{(2)}_{s_{2}}(b_{(1, 1)}, b_{(1, 2)}, b_{(2, 1)}, b_{(2, 2)})\\ &=&(a_{(2, 2)}, a_{(2, 1)}, a_{(1, 2)}, a_{(1, 1)})=1001. \end{array} $$

Step 2.:

Alice (Bob) encodes each bit and prepares 4 Bell states as initial states. Alice (Bob) records these initial states as

$$S_{A}=\{|\phi^{0}\rangle_{1}, |\phi^{1}\rangle_{2}, |\phi^{1}\rangle_{3}, |\phi^{0}\rangle_{4}\} ~~~~(S_{B}=\{|\phi^{1}\rangle_{1}, |\phi^{0}\rangle_{2}, |\phi^{0}\rangle_{3}, |\phi^{1}\rangle_{4}\}.$$

Further, Alice (Bob) divides them into two ordered sequences $S_{A_{1}}$ and $S_{A_{2}} (S_{B_{1}}$ and $S_{B_{2}})$ composed of the 1st and 2nd particles of each Bell state respectively, that is

$$ S_{A_{1}}=\{|{\phi_{1}^{0}}\rangle_{1}, |{\phi_{1}^{1}}\rangle_{2}, |{\phi_{1}^{1}}\rangle_{3}, |{\phi_{1}^{0}}\rangle_{4}\} ~~~~(S_{B_{1}}=\{|{\phi_{1}^{1}}\rangle_{1}, |{\phi_{1}^{0}}\rangle_{2}, |{\phi_{1}^{0}}\rangle_{3}, |{\phi_{1}^{1}}\rangle_{4}\}), $$

$$ S_{A_{2}}=\{|{\phi_{2}^{0}}\rangle_{1}, |{\phi_{2}^{1}}\rangle_{2}, |{\phi_{2}^{1}}\rangle_{3}, |{\phi_{2}^{0}}\rangle_{4}\} ~~~~(S_{B_{2}}=\{|{\phi_{1}^{1}}\rangle_{1}, |{\phi_{1}^{0}}\rangle_{2}, |{\phi_{2}^{0}}\rangle_{3}, |{\phi_{1}^{1}}\rangle_{4}\}). $$

Step 3.:

Alice (Bob) randomly inserts decoy photons in $S_{A_{1}}(S_{B_{1}})$ to form a new sequence $S^{\prime }_{A_{1}}(S^{\prime }_{B_{1}})$, and sends it to Bob (Alice).

Step 4.:

Alice and Bob check the presence of an Eve. There is no an Eve and the protocol continues. Otherwise, Alice and Bob abort the protocol and restart from Step 1.

Step 5.:

Bob (Alice) performs quantum swapping gate $SWAP_{\pi _{B}} (SWAP_{\pi _{A}})$ on quantum particle sequence $S_{A_{1}}(S_{B_{1}})$ and obtains

$$ S^{\prime\prime}_{A_{1}}=\{|{\phi_{1}^{0}}\rangle_{4}, |{\phi_{1}^{1}}\rangle_{3}, |{\phi_{1}^{1}}\rangle_{2}, |{\phi_{1}^{0}}\rangle_{1}\} ~~~~(S^{\prime\prime}_{B_{1}}=\{|{\phi_{1}^{0}}\rangle_{3}, |{\phi_{1}^{1}}\rangle_{4}, |{\phi_{1}^{1}}\rangle_{1}, |{\phi_{1}^{0}}\rangle_{2}\}). $$

Step 6.:

Bob (Alice) selects a binary random sequences e^B = (0,0,1,1)(e^A = (1,1,0,0)). Bob (Alice) performs unitary operation U on quantum particle sequence $S^{\prime \prime }_{A_{1}} (S^{\prime \prime }_{B_{1}})$ and obtains a new quantum particle sequence $\widetilde {S}^{\prime \prime }_{A_{1}} (\widetilde {S}^{\prime \prime }_{B_{1}})$, where U = I if ${e^{B}_{i}}=0$$({e^{A}_{i}}=0)$ and U is X-gate if ${e^{B}_{i}}=1$$({e^{A}_{i}}=1)$.

Step 7.:

Alice (Bob) randomly inserts decoy photons in $\widetilde {S}^{\prime \prime }_{A_{1}}$ and $S_{B_{2}} (\widetilde {S}^{\prime \prime }_{B_{1}}$ and $S_{A_{2}})$ to form a new sequence $S^{\prime \prime \prime }_{A_{1}}(S^{\prime \prime \prime }_{B_{1}})$ and $S^{\prime }_{B_{2}} (S^{\prime }_{A_{2}})$, and sends them to Bob (Alice).

Step 8.:

Alice and Bob check the existence of an Eve just as Step 4 introduced, and obtains $\widetilde {S}^{\prime \prime }_{A_{1}}, S_{B_{2}}$ and $\widetilde {S}^{\prime \prime }_{B_{1}}, S_{A_{2}}$ respectively.

Step 9.:

Bob (Alice) performs quantum swapping gate $SWAP_{\pi _{B}} (SWAP_{\pi _{A}})$ on quantum particle sequence $S_{A_{2}}(S_{B_{2}})$, and obtains

$$ S^{\prime\prime}_{A_{2}}=\{|{\phi_{2}^{0}}\rangle_{4}, |{\phi_{2}^{1}}\rangle_{3}, |{\phi_{2}^{1}}\rangle_{2}, |{\phi_{2}^{0}}\rangle_{1}\} ~~~~(S^{\prime\prime}_{B_{2}}=\{|{\phi_{2}^{0}}\rangle_{3}, |{\phi_{2}^{1}}\rangle_{4}, |{\phi_{2}^{1}}\rangle_{1}, |{\phi_{2}^{0}}\rangle_{2}\}). $$

Step 10.:

Alice (Bob) obtains the sequence of classical results {0,1,0,1,1,1,0,0}, ({0,1,1,0,0,0,0,0) from quantum particles $\widetilde {S}^{\prime \prime }_{A_{1}}S^{\prime \prime }_{B_{2}} (\widetilde {S}^{\prime \prime }_{B_{1}}S^{\prime \prime }_{A_{2}})$ after the |0〉,|1〉 basis measurement. Alice (Bob) computes the t^A = {0,1,0,1} (t^B = {0,1,0,1}). Alice and Bob publish the t^A and t^B respectively. The t^A = t^B, then they announce the compared secret information a and b are identical.

4 Analysis

4.1 Correctness

Alice and Bob use the N-level permutation to process secret information. They encode secret information and insert decoy states randomly. Then they send the first sequence of quantum particles to each other. Alice and Bob check the presence of an Eve. They use the quantum swapping gate $SWAP_{\pi _{B}}$ and $SWAP_{\pi _{A}}$ to process the sequence of quantum particles received separately. Before sending, Alice and Bob perform some unitary operations U on quantum particle sequences according to the random number sequences selected. Then they insert the decoy states in the sequence of quantum particles, and return to each other. After checking the presence of an Eve, they respectively obtain the sequence of quantum particles $\widetilde {S}^{\prime \prime }_{A_{1}}, S_{B_{2}}$ and $\widetilde {S}^{\prime \prime }_{B_{1}}, S_{A_{2}}$ from each other. Furthermore, they perform quantum swapping gate $SWAP_{\pi _{A}}$ and $SWAP_{\pi _{B}}$ on quantum particle sequence $S_{B_{2}}$ and $S_{A_{2}}$, separately. After the measurement, Alice and Bob obtain some corresponding encoding information respectively. That is, after performing 0, 1 basis measurement, Alice and Bob obtain the $a_{i}^{A_{1}}\oplus {e^{B}_{i}}, b^{B_{2}}_{i}$ and $b^{B_{1}}_{i}\oplus {e^{A}_{i}}, a^{A_{2}}_{i}$, respectively. Since Proposition 1, $\pi _{B}\circ \overline {\pi _{A}}=\pi _{A}\circ \overline {\pi _{B}}$ holds. From Table 1 we observe that when the secret information is the same, that is a_i = b_i, there is always ${t^{A}_{i}}\oplus {t^{B}_{i}}=0$. Otherwise, when a_i ≠ b_i, there is always ${t^{A}_{i}}\oplus {t^{B}_{i}}=1$. So our protocol is correctness.

Table 1 The mainly parameters and their values

4.2 Outsider Attack

In presented protocol, Alice and Bob exchange compared secret information under insecure channels. In order to ensure the security of information, all parties publicly check for the existence of an Eve. There are two steps need to detect the presence of an Eve in presented protocol.

Since the Eve doesn’t know the measuring bases, and the positions of all decoy photons in $S^{\prime }_{A_{1}}$ and $S^{\prime }_{B_{1}}$. Eve will lead to an error to each decoy photon with a probability of $\frac {1}{4}$. Thus, let n be the number of decoy photons, if n is large enough, then the probability of detecting Eve’s attack from the public discussion $1-(\frac {3}{4})^{n}$ is close to 1. In addition, in step 8, Alice and Bob check the existence of an Eve just as Step 4 introduced. Hence, the presented protocol can withstand some known outsider attacks, such as entanglement-measure attack, measurement-resend attack, and intercept-resend [23,24,25,26,27].

4.3 Insider Attack

In general, dishonest participant can learn the secret of other party’s partial information without being detected. This congenital advantage for any participants should be limited such that it doesn’t threaten the security of the presented protocol.

The presented protocol is symmetric, Alice and Bob can execute the same attack strategy. Without loss of generality, we consider the case that Bob learns the Alice’s secret.

For comparing private information a, Alice divides the secret information into some groups, rearranges them according to a cyclic left-shift operation π_A and encoding the new secret information using the Bell states on Step 1 and Step 2. At Step 3, Alice randomly inserts some decoy photons in $S_{A_{1}}$ and sends the quantum sequences to Bob. After checking the existence of an Eve, Bob can obtain the sequences of quantum particles $S_{A_{1}}$.

So Bob can distinguish between a_j = 0 and a_j = 1,j = π_A(i) if Bob can distinguish between the two states $\frac {|00\rangle +|11\rangle }{\sqrt {2}}$ and $\frac {|01\rangle +|10\rangle }{\sqrt {2}}$. Bob needs to distinguish between the density matrices

$$ \begin{array}{@{}rcl@{}} \rho^{A}&&=tr_{2}\left( \frac{|00\rangle+|11\rangle}{\sqrt{2}}\frac{\langle00|+\langle11|}{\sqrt{2}}\right)\\ &&=\frac{|0\rangle\langle0|+|1\rangle\langle1|}{2}= \left( \begin{array}{cc} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{array} \right) \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \sigma^{A}&&=tr_{2}\left( \frac{|01\rangle+|10\rangle}{\sqrt{2}}\frac{\langle01|+\langle10|}{\sqrt{2}}\right)\\ &&=\frac{|0\rangle\langle0|+|1\rangle\langle1|}{2}= \left( \begin{array}{cc} \frac{1}{2} & 0 \\ 0 & \frac{1}{2} \end{array} \right). \end{array} $$

It is clear that ρ^A = σ^A. Then Bob cann’t distinguish the Alice’s initial Bell states by measuring the first photon of the j-th state.

In Step 8, Bob can obtain the quantum particle sequence $S_{A_{2}}$. But Bob only knows the π_B and doesn’t know the π_A. The probability of obtaining another correct π_A is $\frac {1}{r^{2}}$, that is the order $\pi _{A}\overline {\pi _{B}}$ is secret for Bob. Through the particle sequences $S_{A_{1}}$ and $S_{A_{2}}$, Bob only guesses the correct Bell state or the corresponding message X₀ with a probability of $\frac {1}{r^{2}}$.

In addition, in Step 8, Bob obtains other quantum particle sequence $\widetilde {S}^{\prime \prime }_{B_{1}}$. Bob doesn’t obtain Alice’s secret information. The reason is that Bob does not know random number sequence e^A except e^B. So Bob only guesses the correct random numbers with $\frac {1}{2^{r^{2}}}$ successful probability. Furthermore, the presented protocol can resist the inside attacks.

4.4 Comparison

In this subsection, the comparisons of Lin et al.’s protocol [18], He’s protocol [19], and the proposed scheme is described in the following Table 2. The qubit efficiency η is defined as $\eta =\frac {\eta _{c}}{\eta _{q}}$, where η_c denotes the classical bits that can be employed, and η_q denotes the total photons.

Table 2 The comparison of the proposed protocol to the other QPCs

Lin et al. use Bell states to design their QPC protocol, in which two qubits can compare one bit of information. However, the qubit efficiency can be computed as 50%. In He’s protocol, single photon states are used to construct the QPC, in which one photons can compare one bit of information among two parties. Therefore, its qubit efficiency is 100%. Comparing these protocol, the presented protocol also uses the Bell states to construct the new QPC, It leads to the qubit efficiency of 50%.

Lin et al.’s and He’s scheme need more quantum devices such as quantum operations, and quantum measurement to perform the comparison. For Lin et al.’s and He’s scheme, both users have to perform one-to-one hash operation to encode the hash code of their information in advance, and encode each bit to the corresponding quantum states. In the proposed scheme, it does not require hash coding in advance.

In addition, in Lin et al.’s QPC, it need Bell-basis measurement to accomplish the comparison phase. In He’s scheme, it requires single photon measurements. In the proposed scheme, the two players only need to perform the {0,1}-basis measure to retrieve their own result of comparison. Thus, the proposed scheme is more efficient and practical.

5 Conclusion

In this paper, we described a protocol to compare the quantum secrets without a third party based on the Bell states and quantum SWAP gates. The proposed protocol has adopted quantum transmission strategy and the decoy state photons to prevent various types of eve attacks. In addition, Bob (Alice) only knows the π_B(π_A), and doesn’t know the π_A(π_B). Thus they have only the same order of information arrangement, but the $\pi _{A}\overline {\pi _{B}}=\overline {\pi _{A}}\pi _{B}$ is secret for two parties. The participants’ encoded secrets are protected by the entanglement of Bell states. So, it provides security for inside attackers. In summary, through the security analysis, the presented protocol is demonstrated to be secure against outsider attack and insider attack.